Комплексные числа примеры решения – Комплексные числа, примеры с решением

Операции над комплексными числами, с примерами

Рассмотрим операции над комплексными числами записанными в алгебраической, тригонометрической и показательной формах.

Сравнение

Два комплексных числа и называются равными, если , т.е. равны их действительные и мнимые части.

Два комплексных числа в тригонометрической форме и называются равными, если . То есть, если равны их модули, а аргументы отличаются на число, кратное .

Аналогично для чисел в показательной форме : два комплексных числа равны, если .

Сложение

Сложение комплексных чисел осуществляется в алгебраической форме и определяется следующим образом: суммой чисел и является число

   

Т.е. выполняется непосредственное суммирование действительных и мнимых частей.

Подробнее про сложение комплексных числе читайте в отдельной статье: Сложение комплексных чисел.

Вычитание

Вычитание комплексных чисел также осуществляется в алгебраической форме. Разность двух чисел и является число

   

Таким образом, чтобы вычесть из одного числа другое, выполняется непосредственное вычитание действительных и мнимых частей.

Умножение

Умножение комплексных чисел в алгебраической форме и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :

   

   

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Для произведения комплексных чисел в показательной форме выполняется следующее равенство:

   

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел в алгебраической форме и находится путем домножения числителя и знаменателя на сопряженное к знаменателю число:

   

Частное комплексных чисел в тригонометрической форме выполняется по формуле:

   

Частное комплексных чисел в показательной форме выполняется по формуле:

   

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Возведение в степень

Для возведения в степень комплексных чисел в тригонометрической форме верна формула Муавра:

   

В показательной форме комплексные числа возводятся в степень по следующей формуле:

   

Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.

Извлечение корня из комплексного числа

Для извлечения корня из комплексного числа применяют аналогичным образом формулу Муавра (если число не равно нулю):

   

   

Подробнее про извлечение корня читайте в отдельной статье: Извлечение корня из комплексного числа.

ru.solverbook.com

Показательная форма комплексного числа

Пусть комплексное число записано в тригонометрической форме , где — модуль комплексного числа. Используя формулу Эйлера, получаем

   

Формула Эйлера

Формула Эйлера связывает между собой тригонометрические и показательные функции:

   

где – экспонента, – мнимая единица.

Для комплексного числа выполняется:

   

В случае, когда – вещественное число , верно

   

Если – чисто мнимое число , верно

   

Используя формулу Эйлера, получаем:

   

Подробнее про формулу Эйлера читайте в отдельной статье: Формула Эйлера для комплексных чисел.

Примеры решения задач

Действия над комплексными числами в показательной форме

Умножение

Для произведения комплексных чисел в показательной форме верно равенство:

   

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел в показательной форме выполняется по формуле:

   

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Возведение в степень

Для возведения в степень комплексных чисел в показательной форме верна формула:

   

Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Комплексные числа задания

13

Комплексные числа (задачи для домашнего расчётного задания)

Комплексные числа Вариант № 1

Задание 1.Представить в тригонометрической и показательной формах.

z = .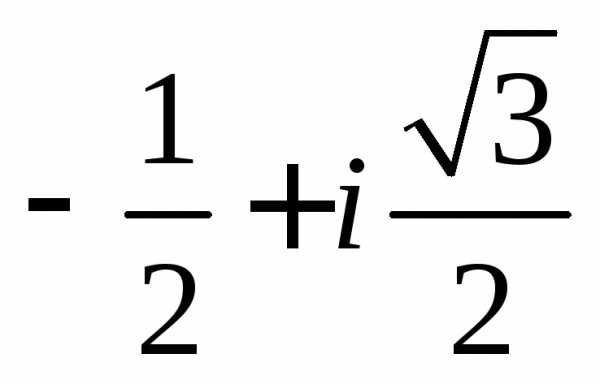

Задание 2.Определить модули и аргументы комплексных чисел.

z =.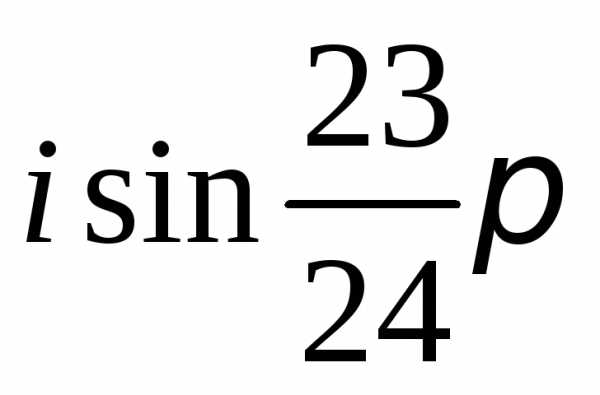

Задание 3.Вычислить выражения.

z =.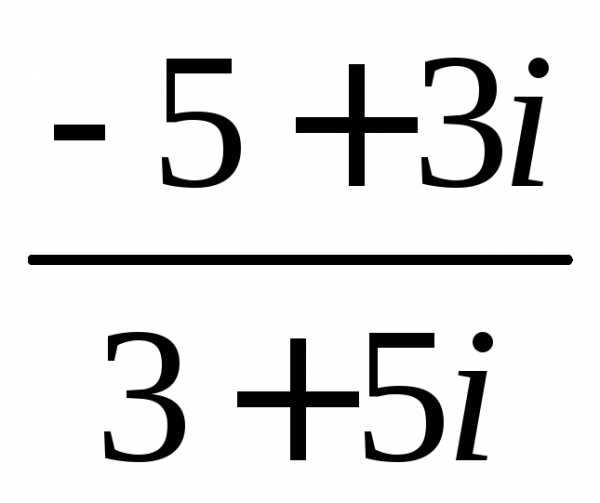

Задание 4.Решить уравнение или неравенство.

.

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 2

Задание 1.Представить в тригонометрической и показательной формах:

z =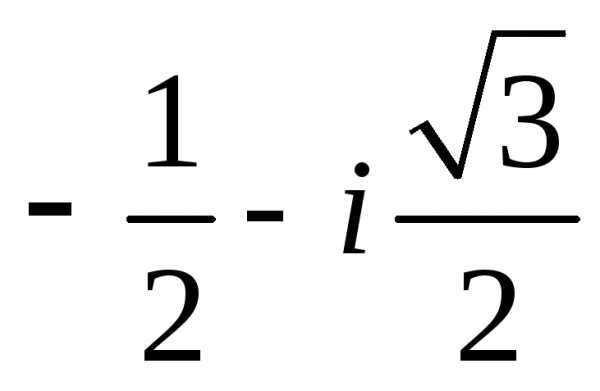

Задание 2.Определить модули и аргументы комплексных чисел:

z =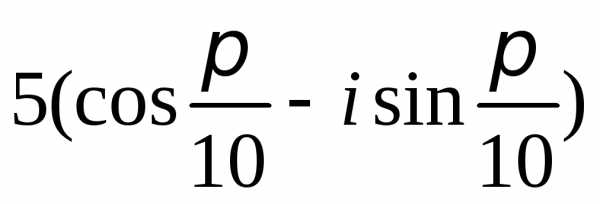

Задание 3.Вычислить выражения:

z =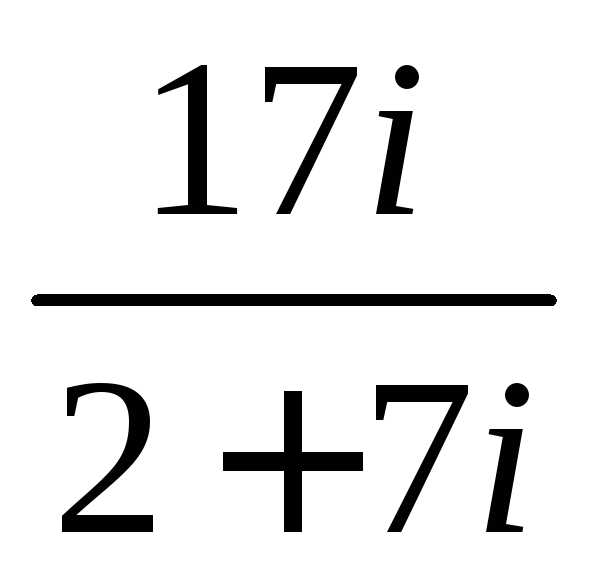

Задание 4.Решить уравнение или неравенство:

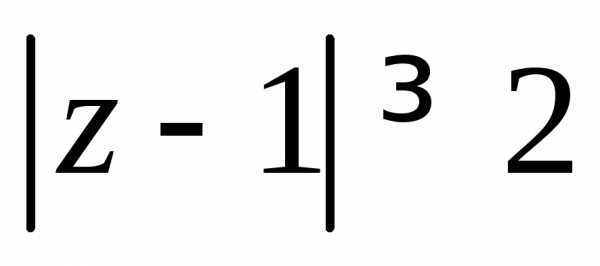
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 3

Задание 1.Представить в тригонометрической и показательной формах:

z =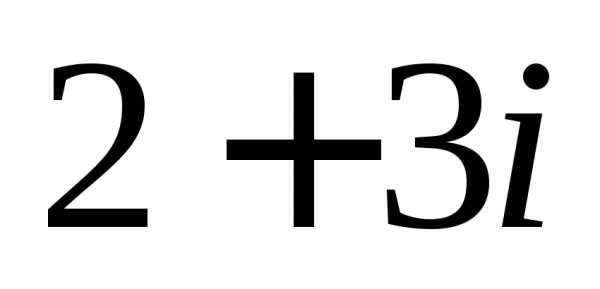

Задание 2.Определить модули и аргументы комплексных чисел:

z =

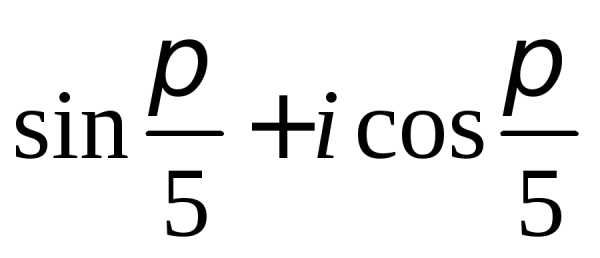
Задание 3.Вычислить выражения:

z =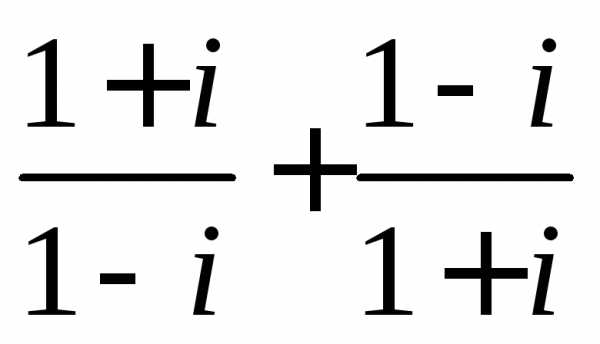

Задание 4.Решить уравнение или неравенство:

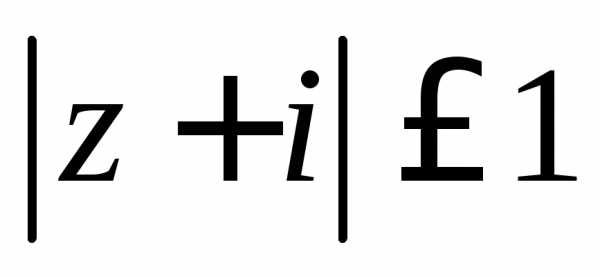
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 4

Задание 1.Представить в тригонометрической и показательной формах:

z =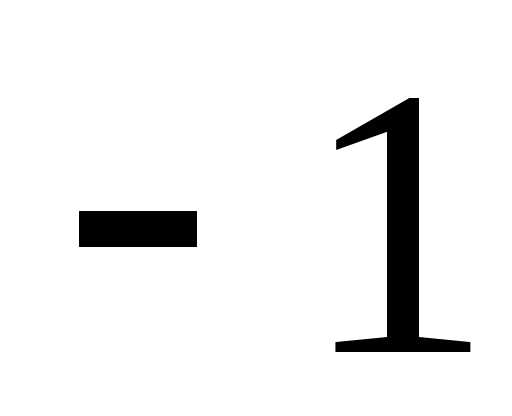

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =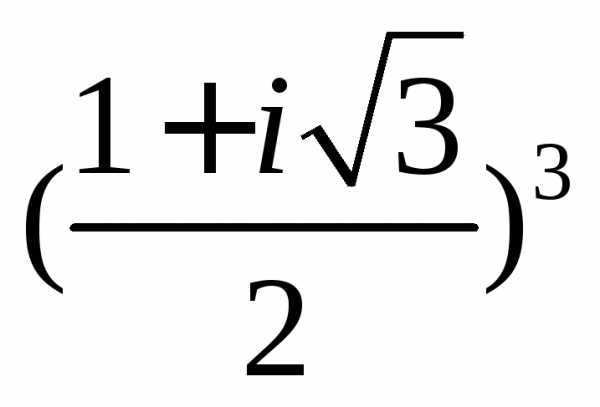

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 5

Задание 1.Представить в тригонометрической и показательной формах. Варианты:

z =

Задание 2.Определить модули и аргументы комплексных чисел. Варианты:

z =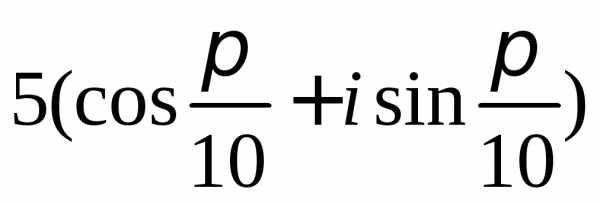

Задание 3.Вычислить выражения. Варианты:

z =

Задание 4.Решить уравнение или неравенство. Варианты:

Задание 5. Найти все значения корня.

Комплексные числа Вариант № 6

Задание 1.Представить в тригонометрической и показательной формах:

z =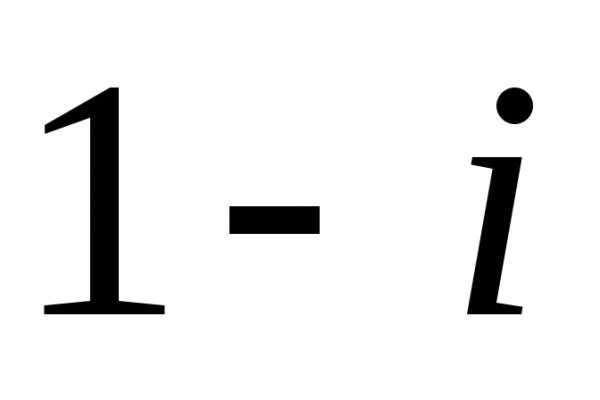

Задание 2.Определить модули и аргументы комплексных чисел:

z =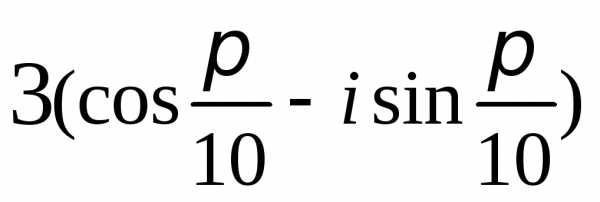

Задание 3.Вычислить выражения:

z =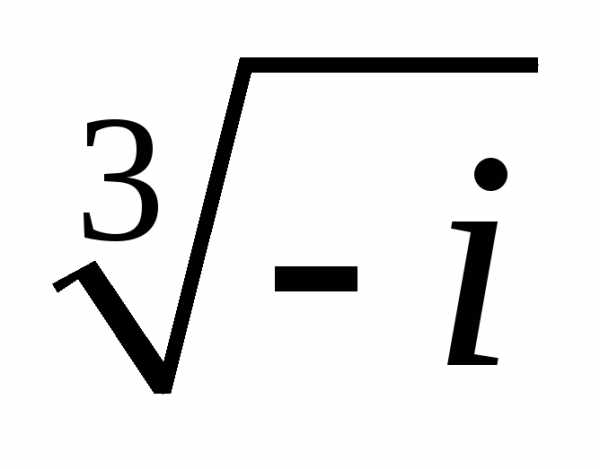

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня.

Комплексные числа Вариант № 7

Задание 1.Представить в тригонометрической и показательной формах:

z =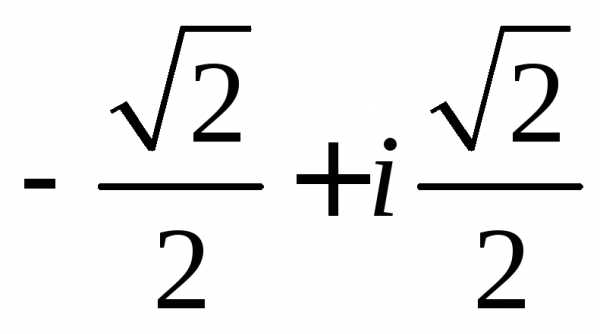

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =

Задание 4.Решить уравнение или неравенство:

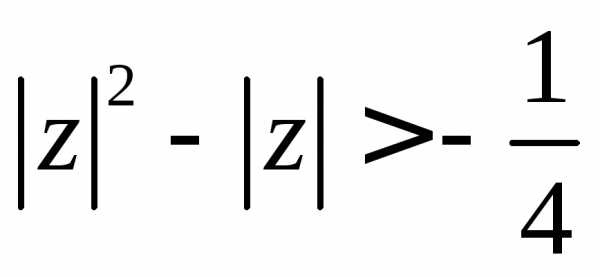
Задание 5. Найти все значения корня.

Комплексные числа Вариант № 8

Задание 1.Представить в тригонометрической и показательной формах:

z =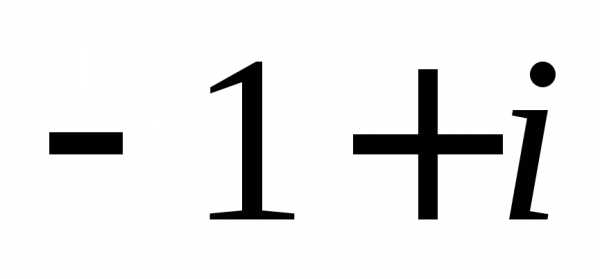

Задание 2.Определить модули и аргументы комплексных чисел:

z =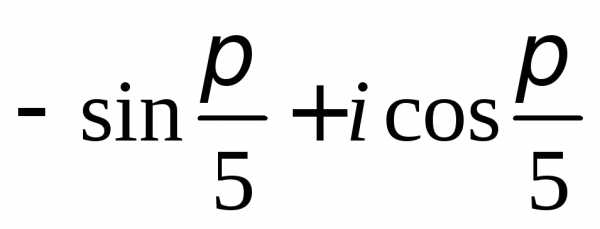

Задание 3.Вычислить выражения:

z =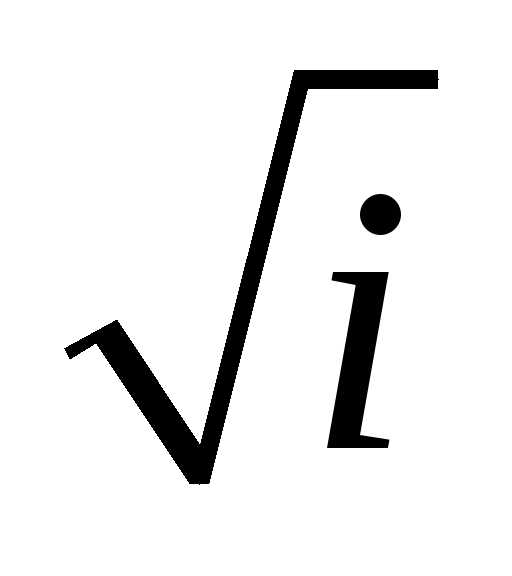

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 9

Задание 1.Представить в тригонометрической и показательной формах:

z =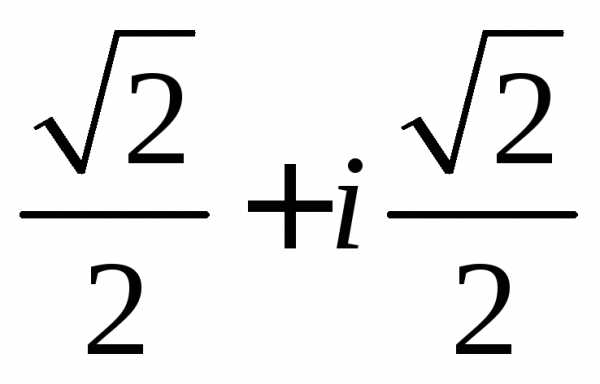

Задание 2.Определить модули и аргументы комплексных чисел:

z =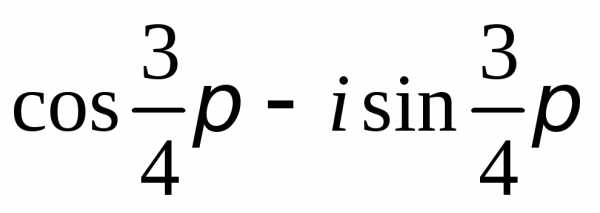

Задание 3.Вычислить выражения:

z =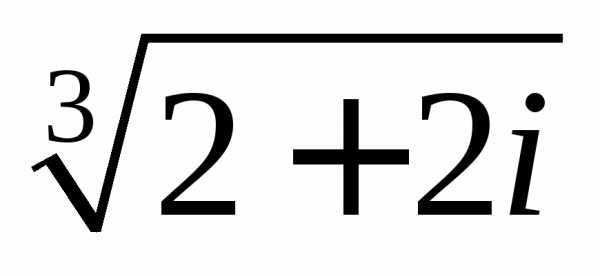

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 10

Задание 1.Представить в тригонометрической и показательной формах:

z =

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =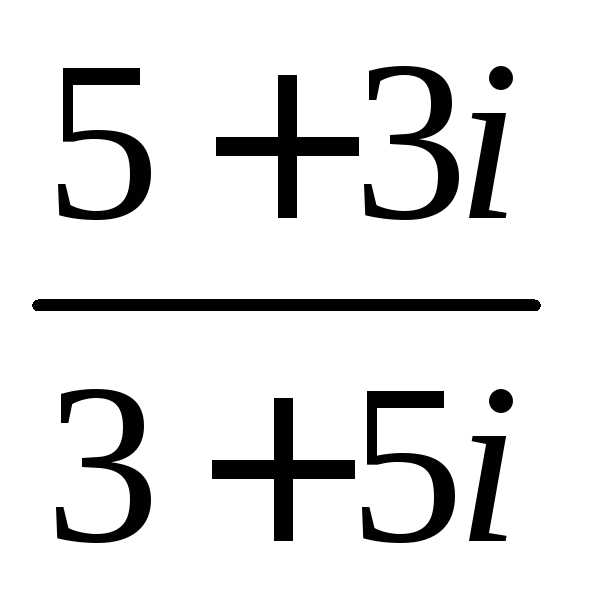

Задание 4.Решить уравнение или неравенство:

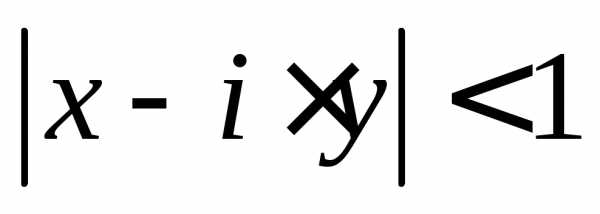
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 11

Задание 1.Представить в тригонометрической и показательной формах:

z =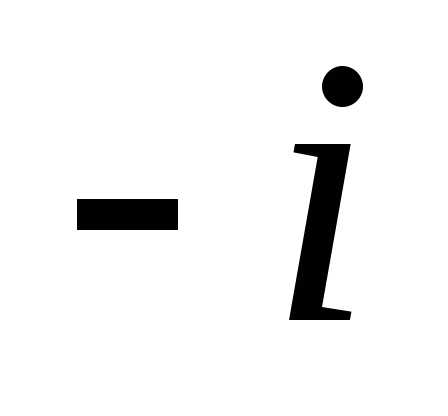

Задание 2.Определить модули и аргументы комплексных чисел:

z =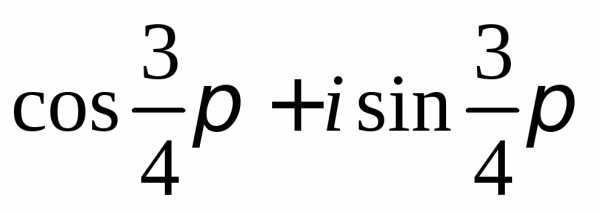

Задание 3.Вычислить выражения:

z =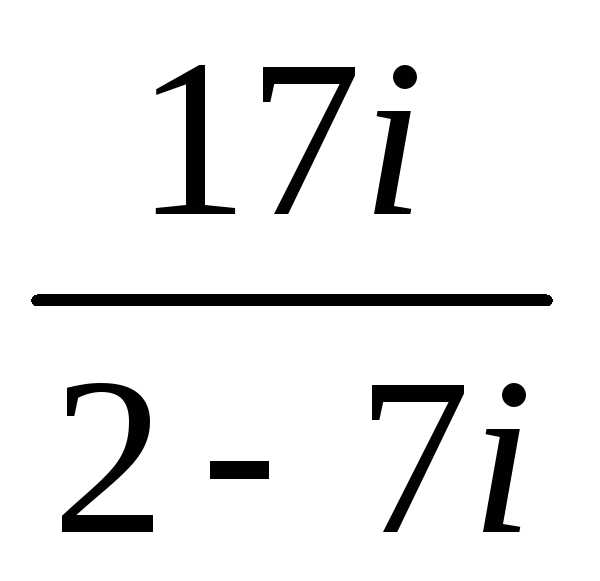

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 12

Задание 1.Представить в тригонометрической и показательной формах:

z =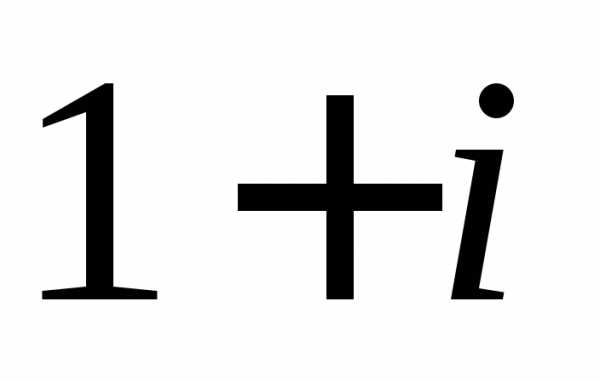

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =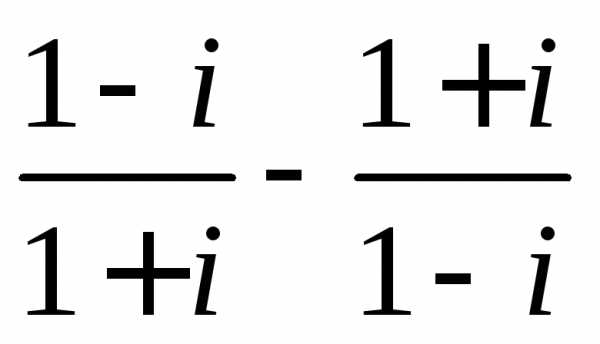

Задание 4.Решить уравнение или неравенство:

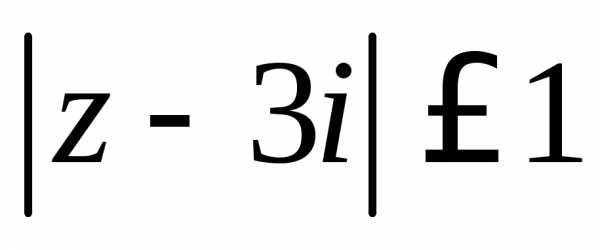
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 13

Задание 1.Представить в тригонометрической и показательной формах:

z =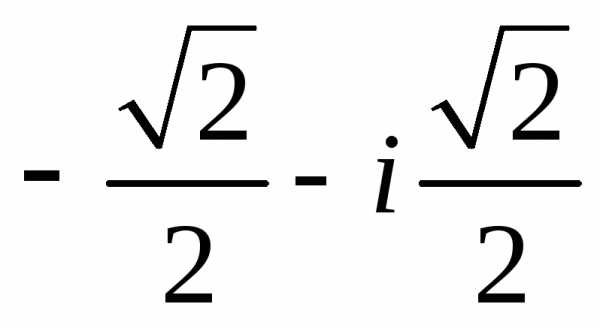

Задание 2.Определить модули и аргументы комплексных чисел:

z =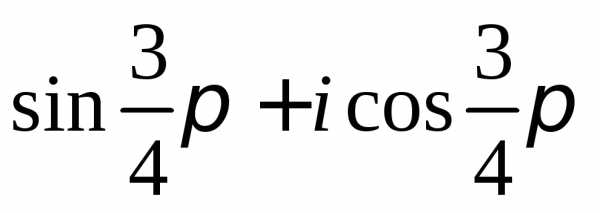

Задание 3.Вычислить выражения:

z =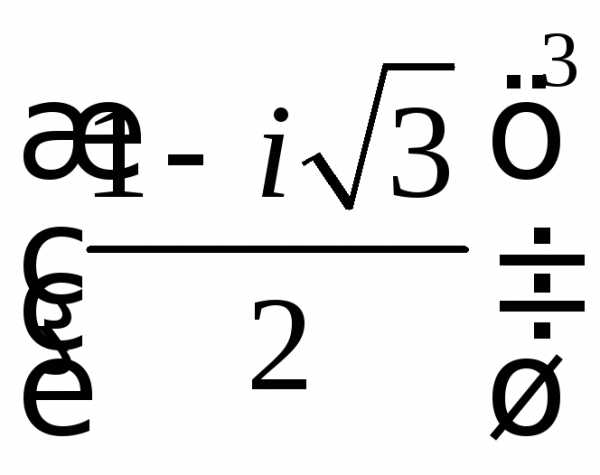

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 14

Задание 1.Представить в тригонометрической и показательной формах:

z =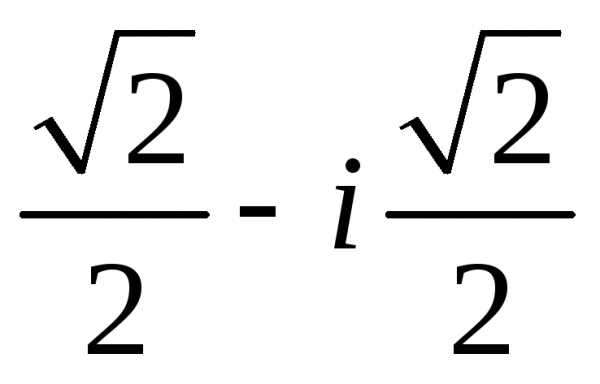

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 15

Задание 1.Представить в тригонометрической и показательной формах:

z =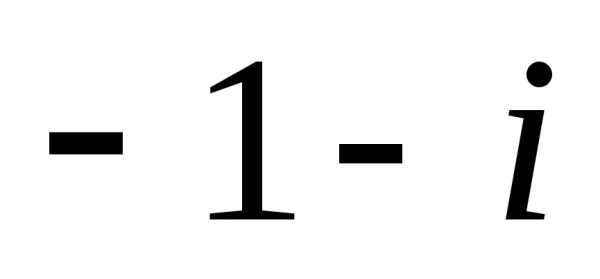

Задание 2.Определить модули и аргументы комплексных чисел:

z =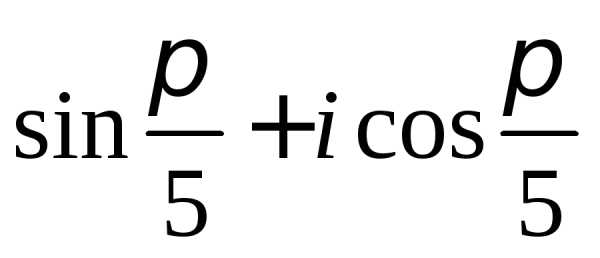

Задание 3.Вычислить выражения:

z =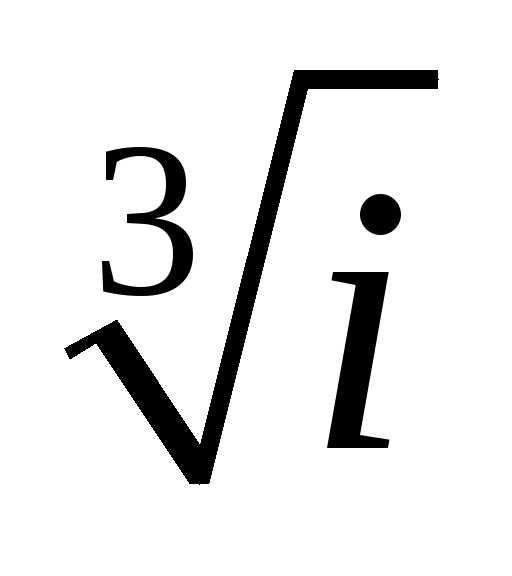

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 16

Задание 1.Представить в тригонометрической и показательной формах:

z =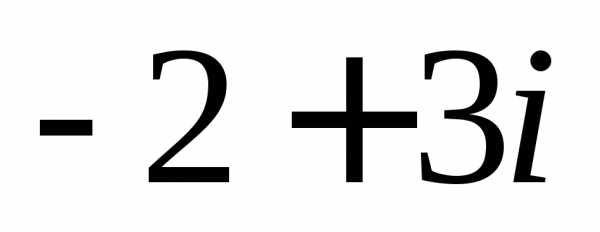

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =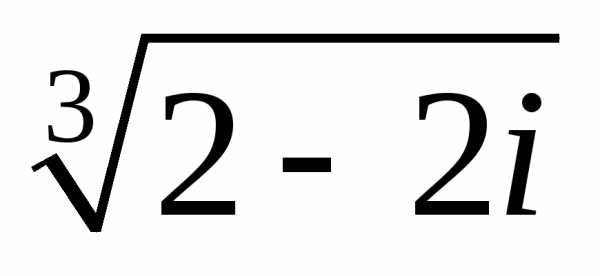

Задание 4.Решить уравнение или неравенство:

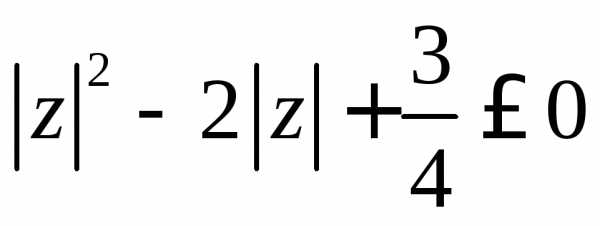
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 17

Задание 1.Представить в тригонометрической и показательной формах:

z =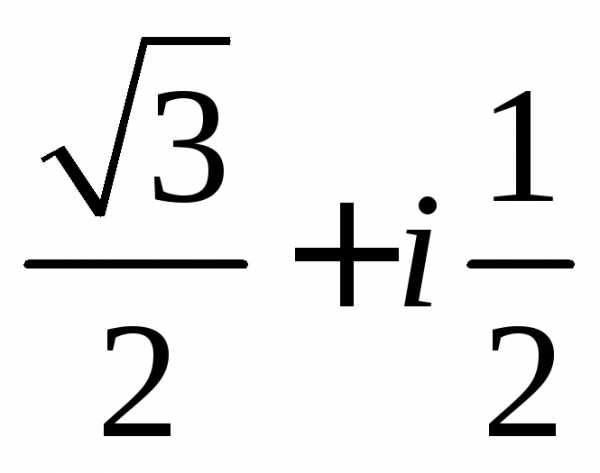

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =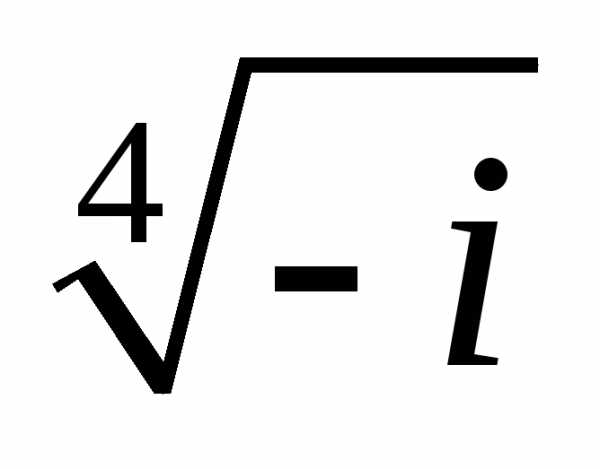

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 18

Задание 1.Представить в тригонометрической и показательной формах:

z =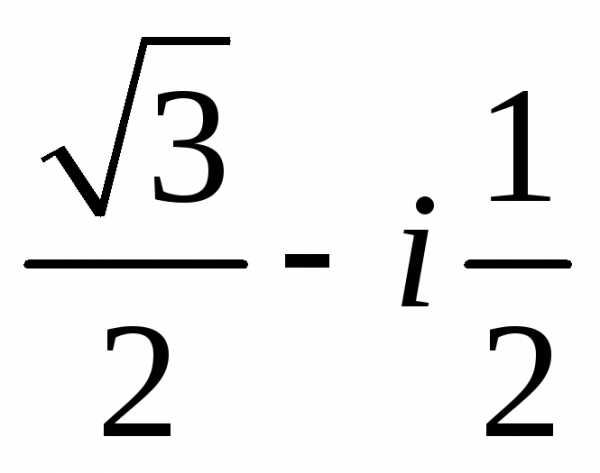

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =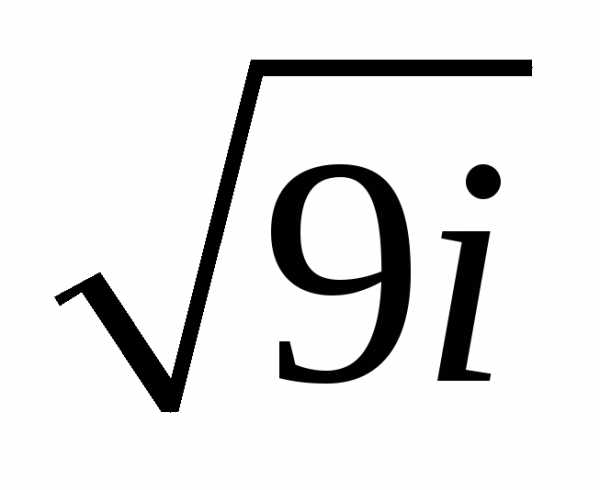

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 19

Задание 1.Представить в тригонометрической и показательной формах:

z =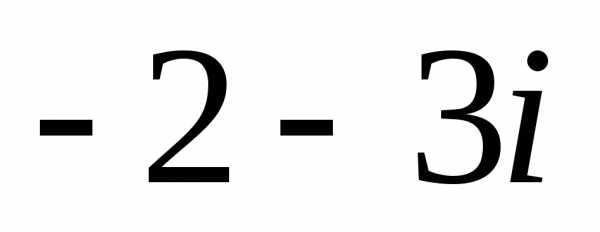

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =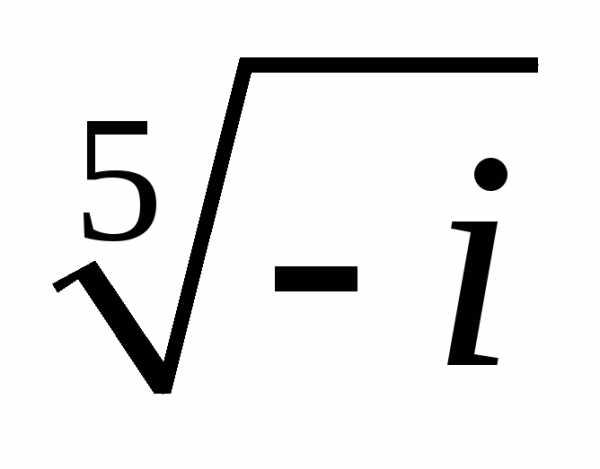

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 20

Задание 1.Представить в тригонометрической и показательной формах:

z =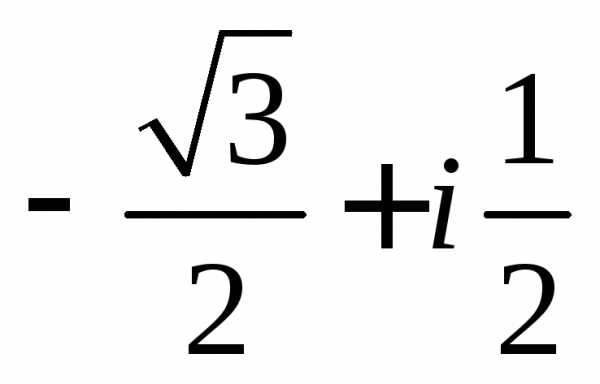

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =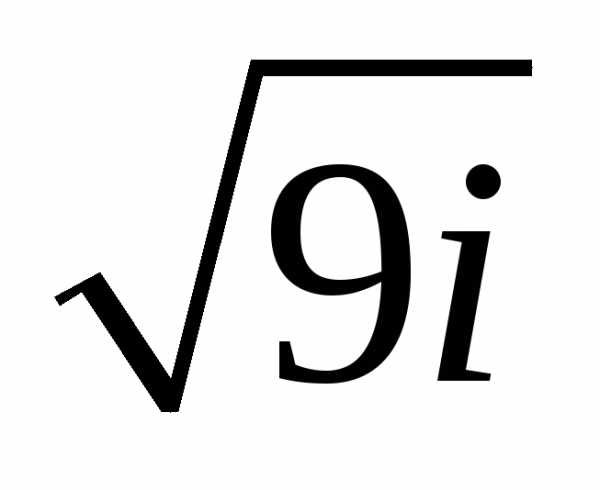

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 21

Задание 1.Представить в тригонометрической и показательной формах:

z =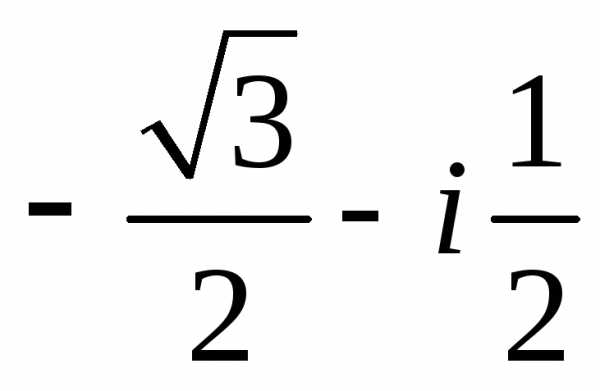

Задание 2.Определить модули и аргументы комплексных чисел:

z =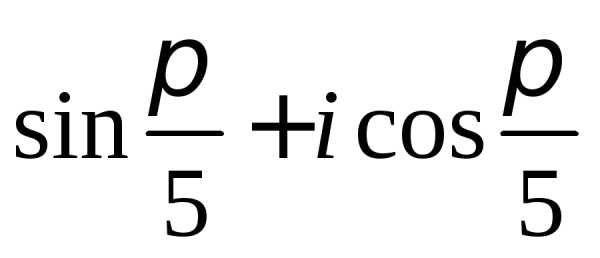

Задание 3.Вычислить выражения:

z =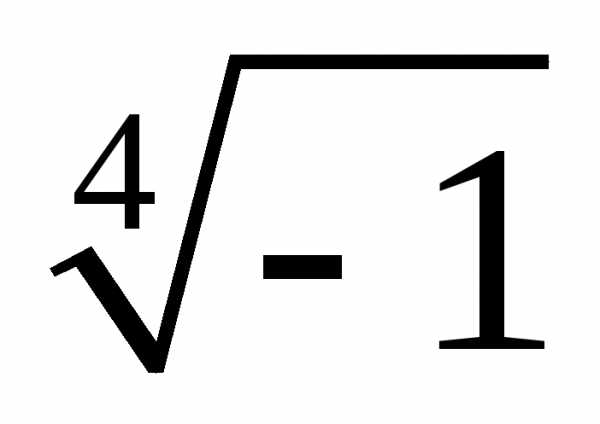

Задание 4.Решить уравнение или неравенство:

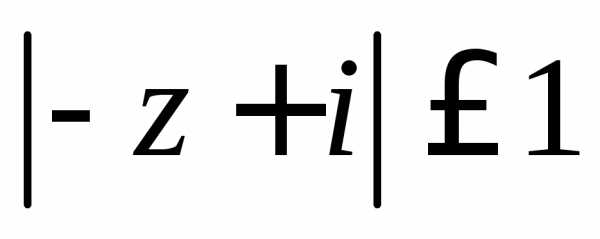
Задание 5. Найти все значения корня:

Комплексные числа Вариант № 22

Задание 1.Представить в тригонометрической и показательной формах:

z =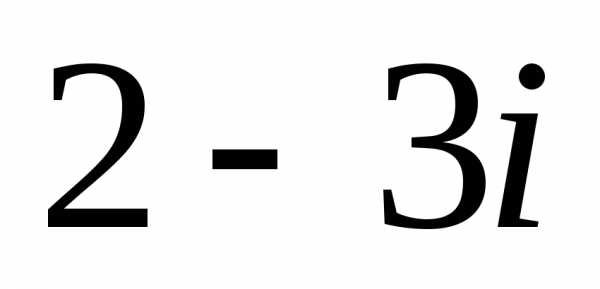

Задание 2.Определить модули и аргументы комплексных чисел:

z =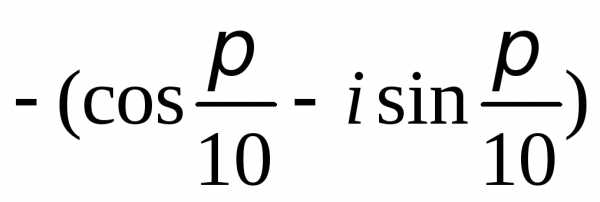

Задание 3.Вычислить выражения:

z =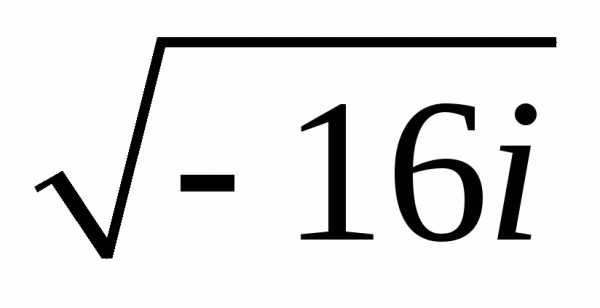

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 23

Задание 1.Представить в тригонометрической и показательной формах:

z =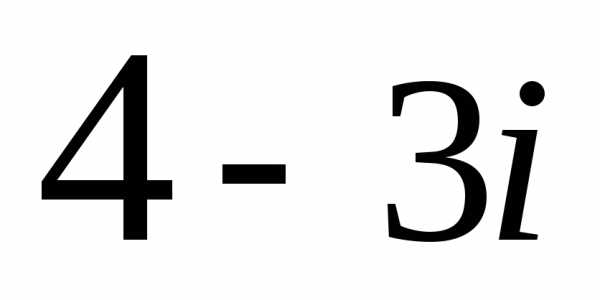

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =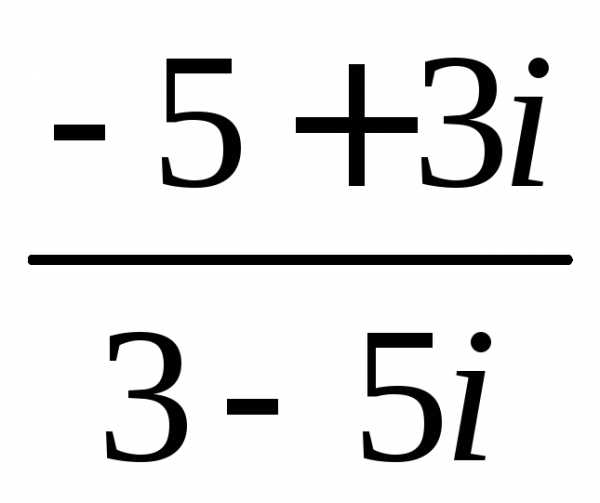

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 24

Задание 1.Представить в тригонометрической и показательной формах:

z =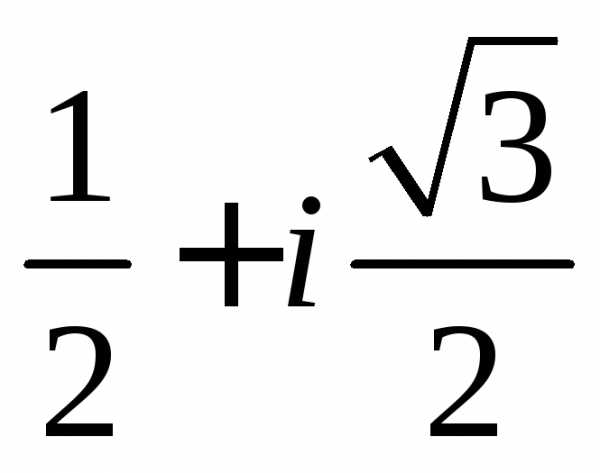

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =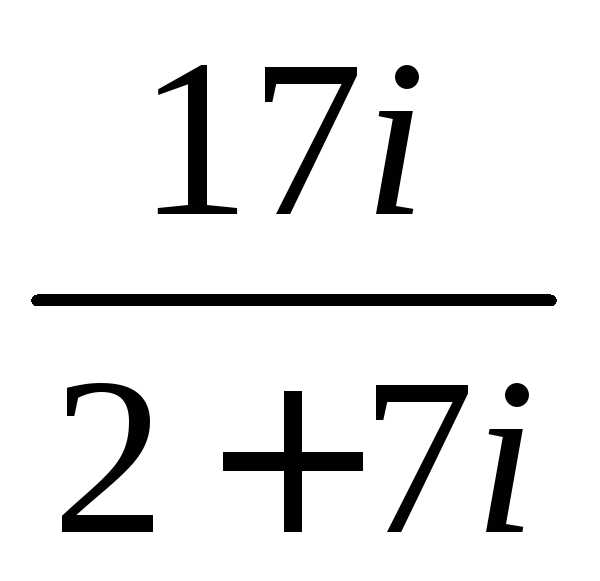

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 25

Задание 1.Представить в тригонометрической и показательной формах:

z =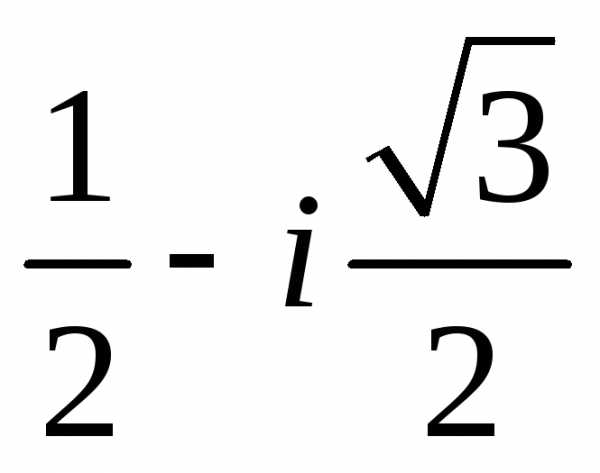

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =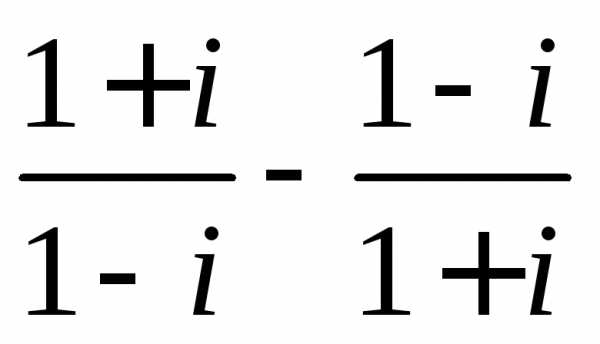

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 26

Задание 1.Представить в тригонометрической и показательной формах:

z =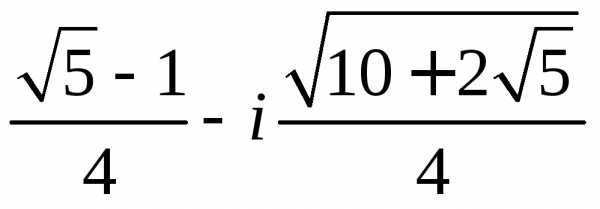

Задание 2.Определить модули и аргументы комплексных чисел:

z =

Задание 3.Вычислить выражения:

z =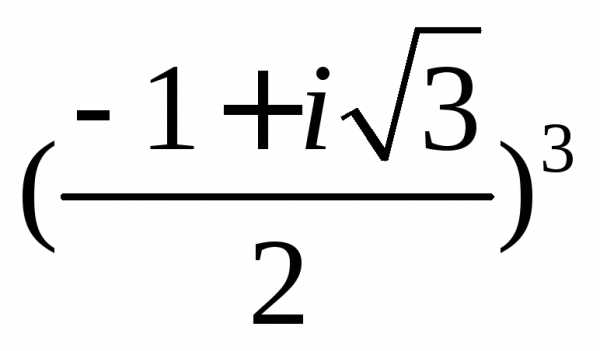

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Комплексные числа Вариант № 27

Задание 1.Представить в тригонометрической и показательной формах:

z =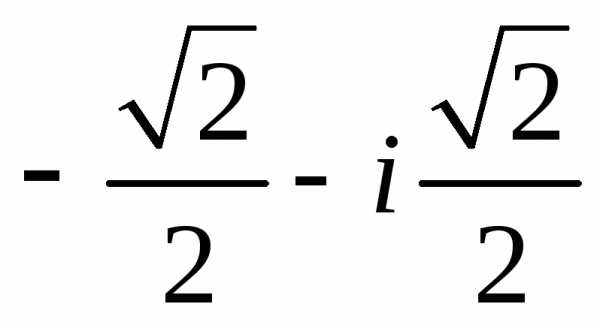

Задание 2.Определить модули и аргументы комплексных чисел:

z =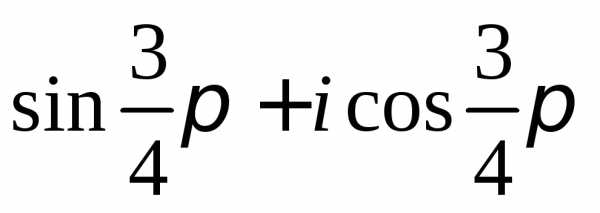

Задание 3.Вычислить выражения:

z =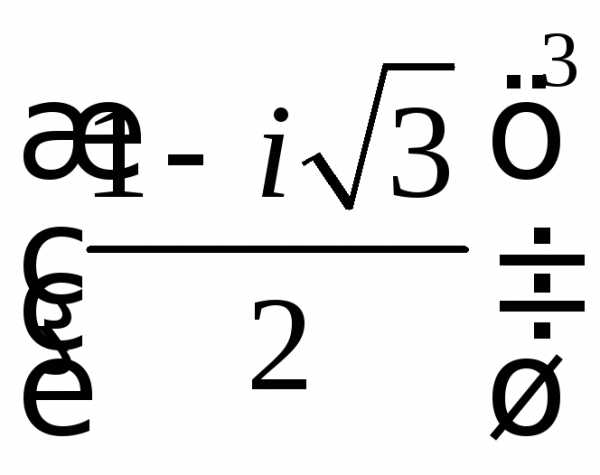

Задание 4.Решить уравнение или неравенство:

Задание 5. Найти все значения корня:

Образец решения заданий

Задание 1.

Представить в тригонометрической и показательной формах комплексное число z =.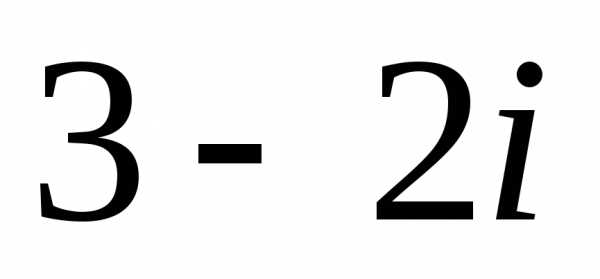

Решение. 1.Тригонометрическая форма комплексного числа имеет вид :

,

где —это модуль, а —аргумент комплексного числа.

Напомним, что аргумент комплексного числа определяется с точностью до , а его главное значение, оно обозначается через 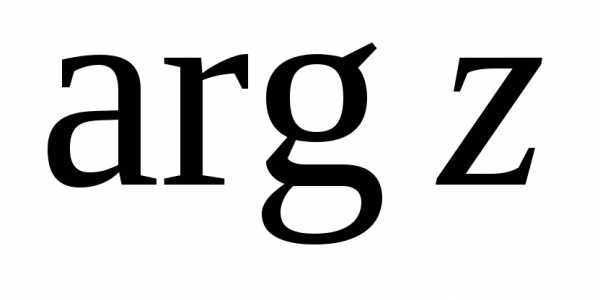,выбирается из диапазона 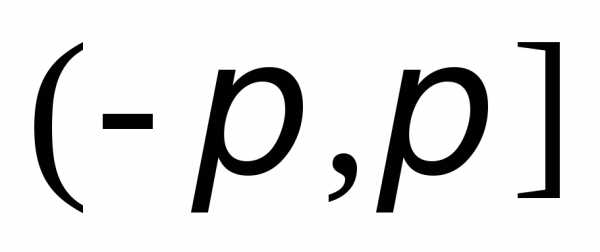.Для определенности, далее, будем считать, что .

По определению, 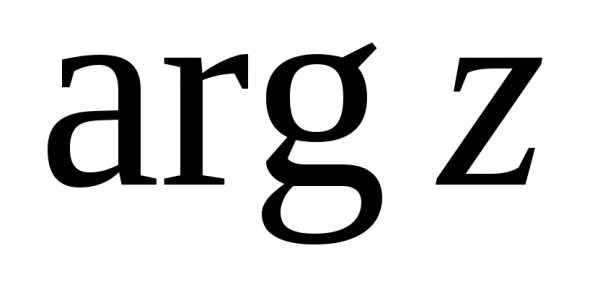–это угол, который образует вектор 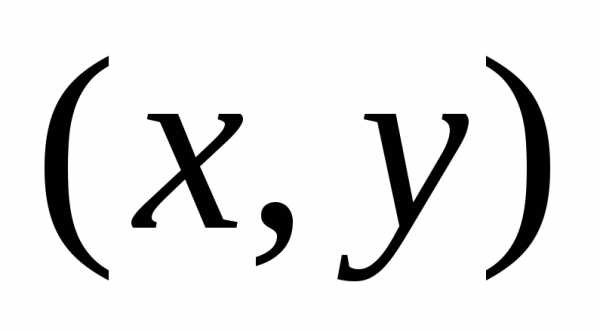с положительным направлением оси 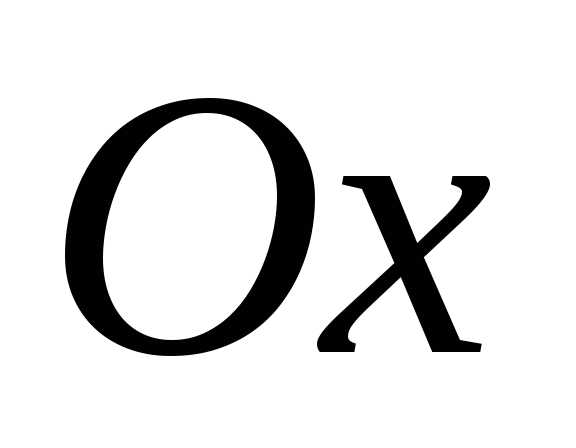и формально, его можно найти следующим образом.

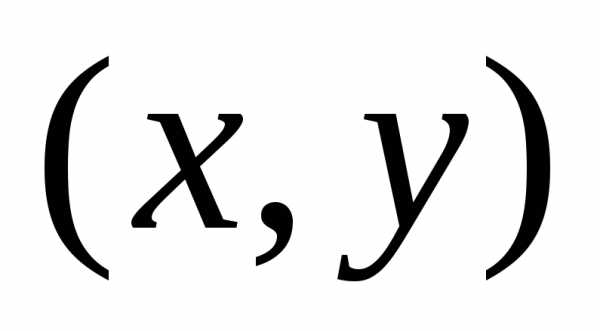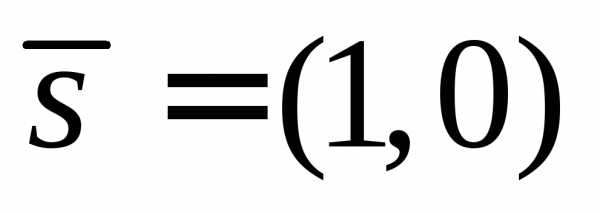Рассмотрим вектор , который соответствует комплексному числу ,и вектор , который является направляющим вектором оси 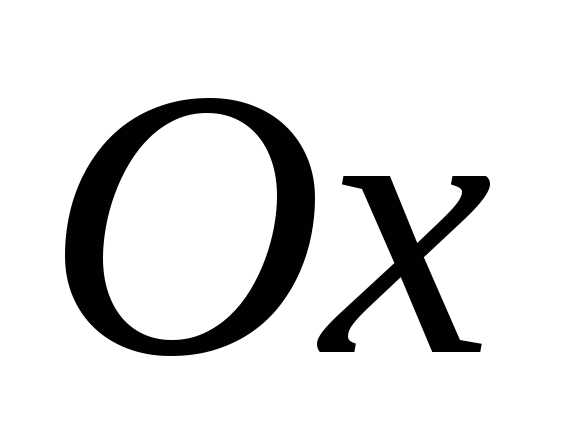. Тогда скалярное произведение этих векторов равно

,откуда и , следовательно,

. (1)

В нашем случае , вектор четверти. Учитывая это обстоятельство, а также то, что в выражении (1) необходимо положить 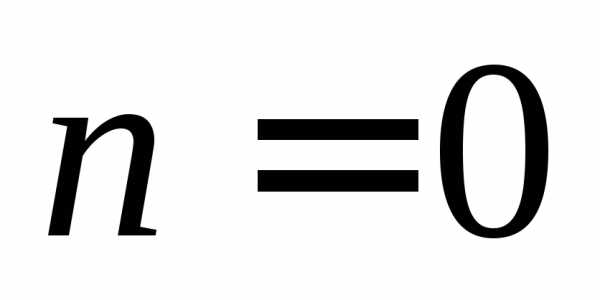.Таким образом ,

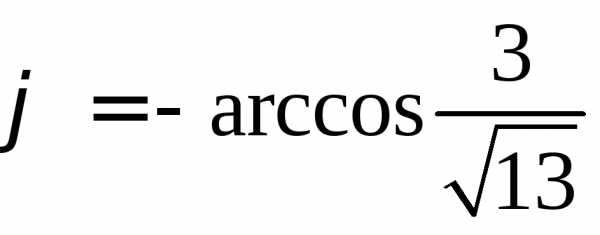и тригонометрическая форма данного числа следующая:

.(2)

2.Используя формулу Эйлера , выражение (2) можно записать так:

. Это и есть показательная форма данного комплексного числа.

Задание 2.Определить модуль и аргумент комплексного числа

Решение: Если комплексное число представлено в тригонометрической форме , где 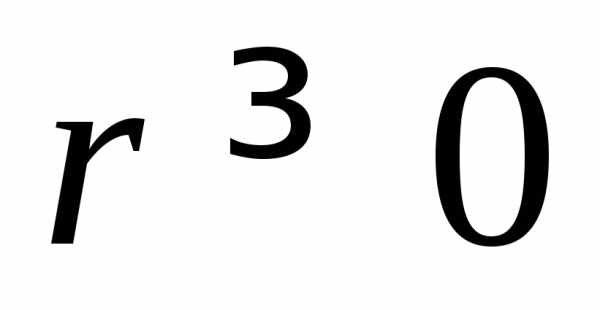,то число 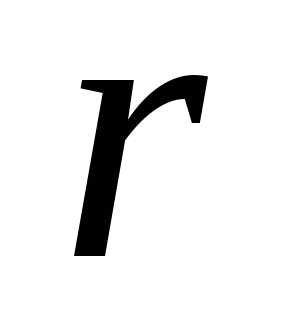является модулем, а число аргументом этого числа. Приведем данное число к тригонометрической форме. Имеем

— это уже тригонометрическая форма. Таким образом, модуль 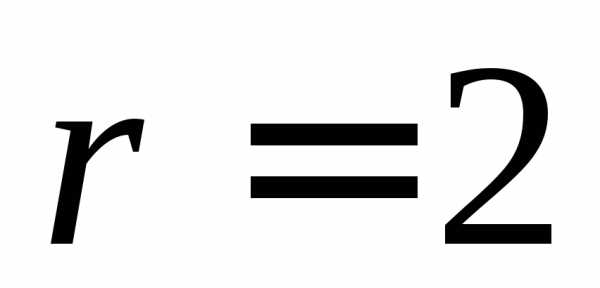,аргумент 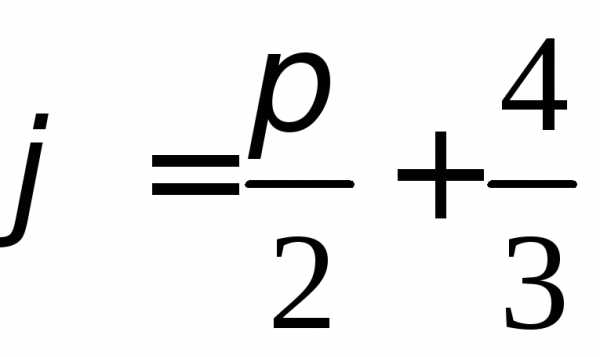.Точнее, это один из аргументов, т.к. любое число также является аргументом. Замечание:

Обычно, в тригонометрической форме комплексного числа указывают главное значение аргумента 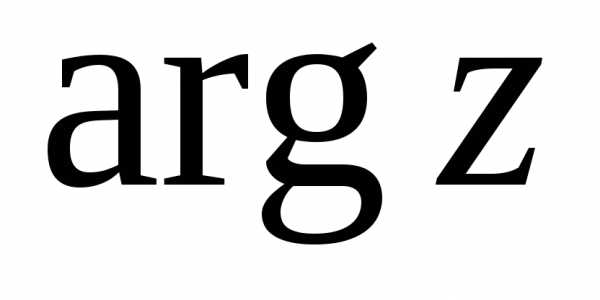,которое принадлежит интервалу 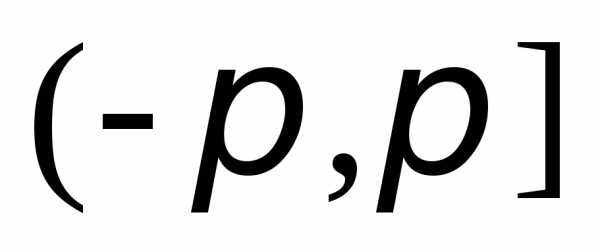.В данном случае число и является, следовательно, главным значением аргумента.

Задание 3. Вычислить выражение

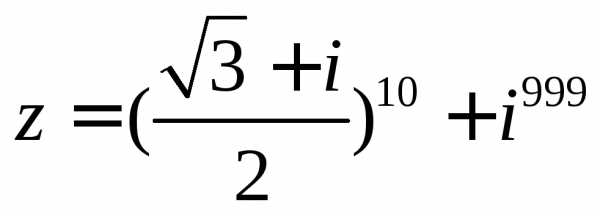.Решение:

Вычислим первое слагаемое. Для этого представим выражение, расположенное в скобках в тригонометрической форме, а затем используем формулу Муавра. Имеем .

2.Вычислим второе слагаемое

.

3.Таким образом,

.

Задание 4. Решить неравенство

Замечание:

Данное неравенство может быть решено исходя из геометрической интерпретации комплексных чисел и алгебраических операций между ними.

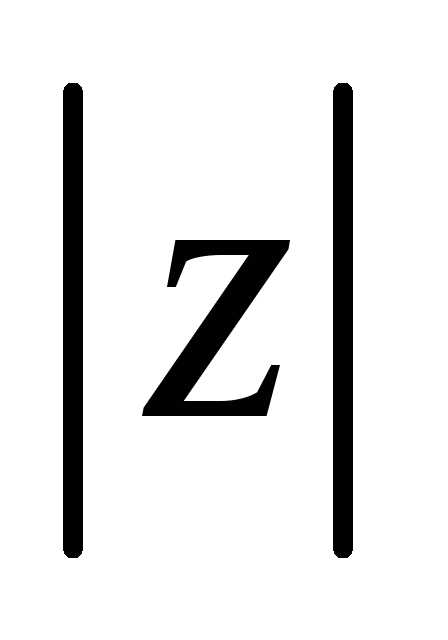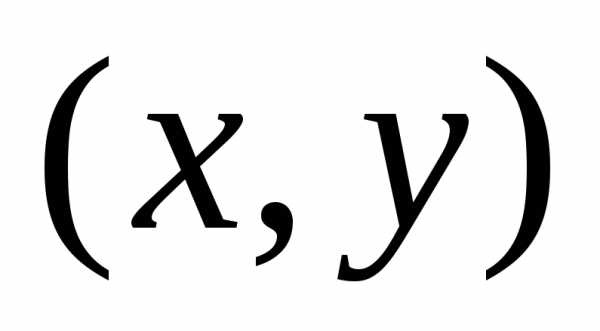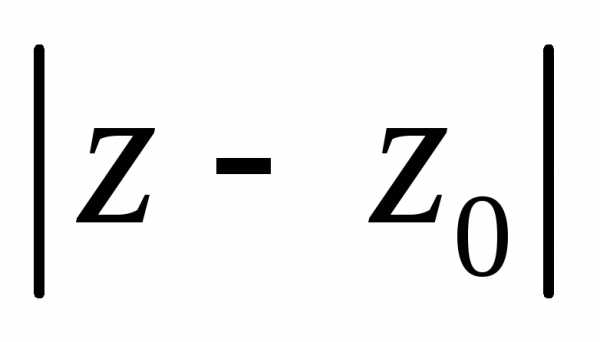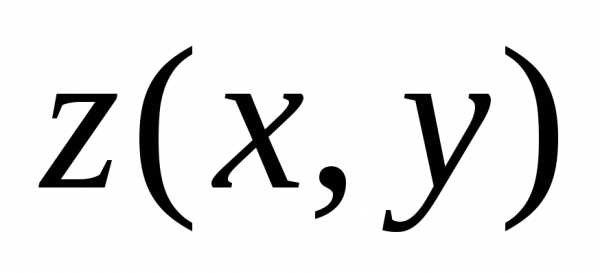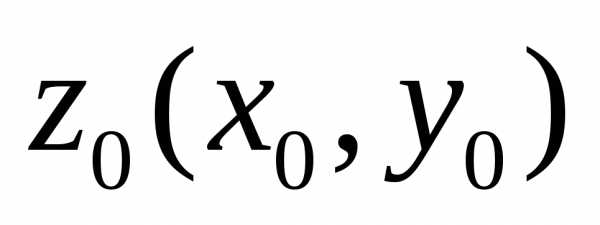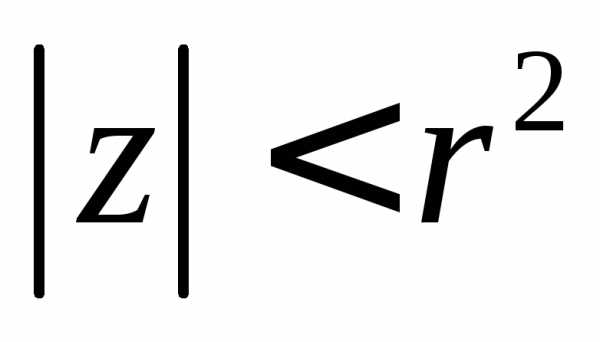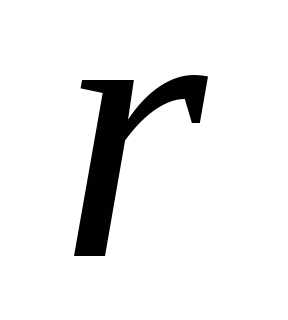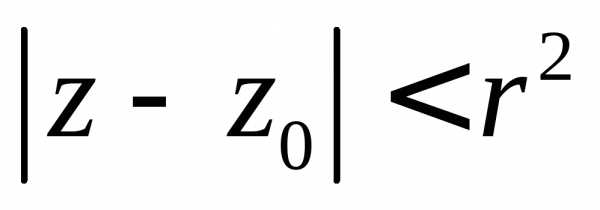Пусть и некоторые комплексные числа. Тогда представляет собой расстояние точки от начала координат, а представляет собой расстояние между точками и . Следовательно, неравенство описывает внутреннюю часть круга радиуса с центром в начале координат, а неравенство – внутреннюю часть круга с центром в точке .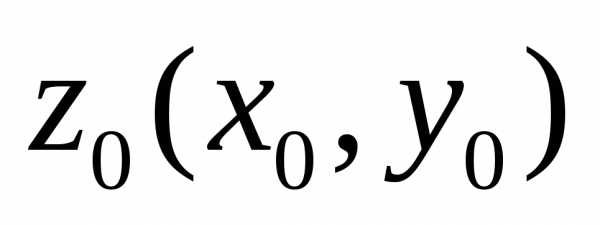

Решение:

Представим данное неравенство в одной из указанных в Замечании форм. Именно .Таким образом, неравенство описывает множество внутренних точек круга радиуса 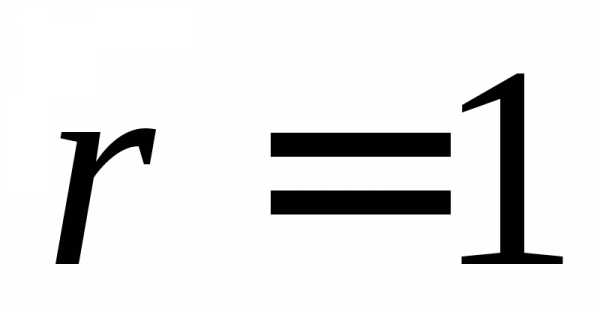с центром в точке 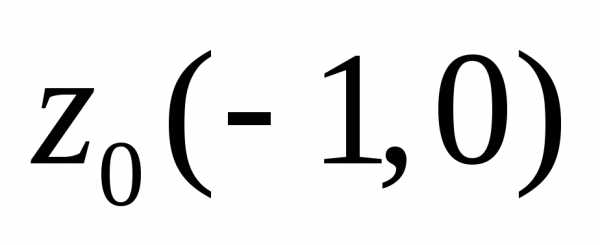.Его уравнение

studfiles.net

Комплексные числа

Содержание

§ 1.Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа

Комплексные равенства

Геометрическое изображение комплексных чисел

Модуль и аргумент комплексного числа

Алгебраическая и тригонометрическая формы комплексного числа

Арифметические действия над комплексными числами

Показательная форма комплексного числа

Формулы Эйлера

§ 2.Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел

Определение алгебраического уравнения -й степени

Основные свойства многочленов

Примеры решения алгебраических уравнений на множестве комплексных чисел

Вопросы для самопроверки

Глоссарий

§ 1. Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа )

Комплексным числомz называется выражение следующего вида:

Комплексное число в алгебраической форме,(1)

Где x, y Î;

i — это мнимая единица , определяемая равенством i 2 = –1.

Основные термины:

x = Re z — действительная часть комплексного числа z ;

y = Im z — мнимая часть комплексного числа z ;

— комплексно сопряженное число числу z ; — противоположное число числу z ; — комплексный ноль ; – так обозначается множество комплексных чисел.

Примеры

1)z = 1 + i Þ Re z = 1, Im z = 1,

= 1 – i, = –1 – i ;

2)z = –1 +

i Þ Re z = –1, Im z = , = –1 – i, = –1 –i ;

3)z = 5 + 0i = 5 Þ Re z = 5, Im z = 0,

= 5 – 0i = 5, = –5 – 0i = –5

Þ если Imz = 0, то z = x — действительное число;

4)z = 0 + 3i = 3i Þ Re z = 0, Im z = 3,

= 0 – 3i = –3i , = –0 – 3i = – 3i

Þ если Rez = 0, то z = iy — чисто мнимое число .

Комплексные равенства (Сформулируйте смысл комплексного равенства )

1)

;

2)

.

Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.

Примеры

1)

;

2)

.

Геометрическое изображение комплексных чисел (В чём состоит геометрическое изображение комплексных чисел? )

Комплексное число z изображается точкой (x , y ) на комплексной плоскости или радиус-вектором этой точки.

Знак z во второй четверти означает, что система декартовых координат будет использоваться как комплексная плоскость.

Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа? )

Модулем комплексного числа

называется неотрицательное действительное число .(2)

Геометрически модуль комплексного числа — это длина вектора, изображающего число z , или полярный радиус точки (x , y ).

Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x , y )).

Обозначение

, причем , или .

Для вычисления аргумента комплексного числа используется формула

Аргумент комплексного числа ,(3)

причем, при определении угла

по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z :

Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа? )

Так как геометрически очевидно, что

и , то

Тригонометрическая форма комплексного числа .(4)

Запись z = x + iy называется алгебраической формой комплексного числа z ; запись z = r (cosj + i sinj ) называется тригонометрической формой комплексного числа z .

Примеры

Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.

1)z = 1 + i Þ

, Þ

Þ

;

2)

Þ , Þ

Þ

;

3)

Þ , Þ Þ ;

4)

, ;

5)

,

mirznanii.com

Комплексные числа. примеры

Комплексные числа

Пример 1.

Указать, какие линии определяются этими уравнениями:

а) .

б) .

в) .

г) .

Решение:

а) .

Пусть , тогда

.

= .

.

,

.

Ответ: — окружность с центром в точке с координатами (0,5, 0) и радиусом 0,5.

б) .

Пусть , тогда

.

.

.

.

.

,

,

.

Ответ: — графиком является гипербола, ветви которой расположены во второй и четвертой четверти координатной плоскости.

в) .

Пусть , тогда

.

.

.

Ответ: — окружность с центром в начале координат и радиусом.

г) .

Пусть , тогда

.

.

= .

.

— возведем полученное уравнение в квадрат

,

— возведем ещё раз в квадрат, получим

,

–разделим обе части уравнения на 192,

.

Ответ: — каноническое уравнение эллипса.

Пример 2.

Построить множество точек на плоскости комплексной переменной z, которая определяется заданными условиями.

а) .

б).

в) .

г) .

д)

Решение.

а) .

Пусть , тогда

.

.

— Возведем систему в квадрат, получим

Ответ:

б) .

Пусть , тогда

.

.

= .

.

.

Ответ:

в) .

Пусть , тогда

.

Ответ:

г) .

Пусть , тогда

.

.

,

.

Ответ:

д)

Пусть , тогда

.

= .

.

.

,

Решим первое неравенство системы:

,

— возведем обе части неравенства в квадрат.

— раскрываем скобки, приводим подобные, получаем

.

Решим второе неравенство системы:

,

— возведем обе части неравенства в квадрат, получим

— ещё раз возведем в квадрат.

256

В итоге получаем систему

Ответ:

8

studfiles.net

Деление комплексных чисел, формула и примеры

Существует три формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная. Рассмотрим деление комплексных чисел в каждой из форм.

Деление в алгебраической форме

Частное комплексных чисел и находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

   

Деление в тригонометрической форме

Частное комплексных чисел в тригонометрической форме выполняется по формуле:

   

Таким образом, чтобы поделить два комплексных числа, нужно поделить их модули и найти разность аргументов.

Деление в показательной форме

Частное комплексных чисел в показательной форме выполняется по формуле:

   

Т.е. чтобы поделить два комплексных числа в показательной форме, нужно найти частное их модулей, а в показателе степени экспоненты найти разность их аргументов.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Мнимая часть комплексного числа, формула и примеры

Например. — комплексное число, действительной частью которого является вещественное число , а мнимой частью – вещественное число .

Если действительная часть комплексного числа равна нулю комплексное число называется чисто мнимым.

Например. где .

Комплексные числа являются расширением действительных (вещественных) чисел, у которых мнимая часть равна нулю.Любое действительное число может быть записано в форме комплексного числа: .

Например. Комплексные числа обозначают действительное число .

Геометрическая интерпретация комплексного числа

Можно изображать комплексные числа на комплексной плоскости следующим образом: действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.

Любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами: , и радиус-вектор (существуют также обозначения ) комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.

Историческая справка

К понятию мнимого числа впервые пришли математики Кардано и Бомбелли. Последний описывал возможность использовать мнимые величины при решении кубического уравнения . Само название «мнимых» корней закрепилось после работ Декарта. В XVIII веке Эйлер предложил использовать символ для обозначения мнимых чисел. Можно еще отметить исследования Муавра и Котса, также относящиеся к XVIII столетию. Несмотря на активное развитие математической теории, длительное время ученые с сомнением относились к полученным в отношении мнимых чисел результатам. Лишь позднее, в XIX столетии, математик и астроном Гаусс развил и популяризировал теорию мнимых чисел.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com