Синус, косинус и тангенс острого угла прямоугольного треугольника
На этом уроке мы познакомимся с синусом, косинусом и тангенсом – тригонометрическими функциями, связывающими острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Это очень важные понятия, которые будут встречаться не только в геометрии, но и в алгебре, физике и во многих других науках.
Напомним основные сведения о прямоугольном треугольнике (см. Рис. 1).
Рис. 1
;
– катеты; AB=c – гипотенуза.
Также в прямоугольном треугольнике сумма острых углов равна : .
Для прямоугольного треугольника также верна теорема Пифагора: .
Введём теперь понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Определение
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе.
, .
Определение
Косинусом острого угла прямоугольного треугольника
, .
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему катету.
, .
С помощью введённых понятий можно находить катеты или гипотенузу.
Например, из формулы: . Аналогично: .
Также можно получить формулу для связи длин двух катетов: .
При решении задач очень важно знать соотношения между синусом, косинусом и тангенсом острого угла прямоугольного треугольника.
Рассмотрим следующие две формулы: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Аналогично получаем: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Докажем теперь важную формулу, связывающую тангенс с синусом и косинусом:
ДоказательствоЗапишем определение синуса и косинуса острого угла прямоугольного треугольника: , . Тогда: . Доказано.
Аналогично: .
Рассмотрим следующую важную задачу.
Задача
Даны прямоугольные треугольники . Кроме того, .
Доказать:.
Доказательство
(так как оба треугольника прямоугольные с равными острыми углами). Значит, выполняется следующее соотношение: .
Отсюда получаем: .
.
.
Доказано.
Вывод: синус, косинус и тангенс не зависят от треугольника, а зависят только от угла.
Сформулируем и докажем одну из важнейших теорем, связывающих синус и косинус острого угла прямоугольного треугольника, – основное тригонометрическое тождество.
Основное тригонометрическое тождество: .
Примечание:
Доказательство
, тогда: (при доказательстве мы пользовались теоремой Пифагора: ).
Доказано.
Рассмотрим пример, иллюстрирующий связь тригонометрических функций.
Дано: – прямоугольный (), .
Найти:
Решение
Воспользуемся основным тригонометрическим тождеством: . Подставим в него известное нам значение синуса: . Отсюда: . Так как косинус, по определению, – это отношение катета к гипотенузе, то он может быть только положительным, поэтому: .
Найдём теперь тангенс угла, пользуясь формулой: .
Ответ: .
На этом уроке мы рассмотрели понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника, вывели некоторые их свойства и формулы связи между этими величинами. На следующем уроке мы познакомимся со значениями синуса, косинуса и тангенса для некоторых конкретных значений углов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Xvatit.com (Источник).
- Egesdam.ru (Источник).
Домашнее задание
- № 133(а-г), 134(а-г), Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Найдите синус, косинус и тангенс наименьшего угла египетского треугольника.
- Найдите косинус и тангенс острого угла прямоугольного треугольника, синус которого равен .
interneturok.ru
Синус, косинус угла треугольника
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Если у нас есть треугольник \(ABC\), рисунок выше, для которого \(С\)- прямой угол, то сторонами \(BC\) и \(AC\) будут катеты, а сторона \(AB\) — гипотенуза. Следовательно, по определению, синус угла \(ABC\) равен отношению катета \(АС\) к гипотенузе: синус угла \(ABC=\frac{AC}{AB}\) и синус угла \(BAC=\frac{BC}{AB}\).
косинус угла \(ABC=\frac{BC}{AB}\) и косинус угла \(BAC=\frac{AC}{AB}\).
Чаще всего известно лишь часть данных, например катет и угол, нужно выразить неизвестную величину. Подумайте, как это сделать.
Пример 1. Вычислим синус по двум катетам.
Берем тот же треугольник \(ACB\) с прямым углом \(С\) в котором мы знаем катеты: \(BC = 3\), \(AC = 4\). Для вычисления синуса угла с необходимо разделить катет на гипотенузу: \(sin ∠BAC = \frac{BC} { AB}\).
Гипотенузу вычислим из теоремы Пифагора: \(AC^2+BC^2=AB^2\) \(9+16=25\) \(AB=5\) откуда синус равен:
\(sin ∠ BAC = \frac{3}{5}\)
Пример 2. Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).
Самое главное помнить, что сумма всех углов в треугольнике равна 180 °.Найдем угол \(ABC\):
\(180\)° \(-30\)° \(-90\)°\(=60\)°.
\(sin\) \(60\)° возьмем из табличного значения: \(\frac{ \sqrt{3}} { 2}\)
Табличные значения \(sin\) и \(cos\):
Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат \((y)\) линия синуса, ось абсцисс \((x)\) – линия косинуса. Если вы забыли значения синуса и косинуса \(90\) и \(180\) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит \(x\), на втором \(y\) \((x,y)\);
Теорема синусов:
Теорема косинусов:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Синус в треугольнике | Треугольники
Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Определение.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Например,
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Вывод:
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
Например,
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
Тогда
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Тогда
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
Угол A в обоих треугольниках одинаков.
www.treugolniki.ru
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.
a, b — катеты
c — гипотенуза
α, β — острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β, γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике ( M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Калькулятор — вычислить, найти медиану, биссектрису, высоту
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L— биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
www-formula.ru
Вычисление синусов, косинусов в прямоугольном треугольнике.
Начинаем разбор Заданий №6 из открытого банка заданий по математике.
Тема объемная, поэтому отводим на нее несколько статей.
+ показать
Вам может быть полезно заглянуть сюда, чтобы вспомнить свойства прямоугольного треугольника.
Итак, сегодня вычисляем
Часть 1.
Углы в прямоугольном треугольнике
 Задача 1.
Задача 1.
Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение: + показать
Задача 2.
Один острый угол прямоугольного треугольника в 29 раз больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Решение: + показать Пусть один из острых углов треугольника равен градусов, тогда согласно условию задачи второй острый угол градусов. Так как сумма острых углов прямоугольного треугольника равна 90 градусов, то Тогда больший острый угол равен Ответ: 87.
Задача 3.
В треугольнике ABC угол C равен 90°, CH — высота, угол A равен . Найдите угол BCH. Ответ дайте в градусах.
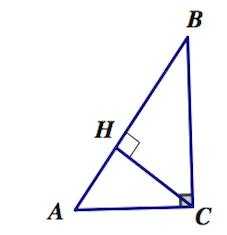
Решение: + показать Из прямоугольного треугольнике Тогда, так как угол – прямой, то Ответ: 89.
Задача 4.
Острый угол прямоугольного треугольника равен . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
Решение: + показать
Задача 5.
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Решение: + показать
Задача 6.
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен . Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Решение: + показать
Задача 7.
Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение: + показать Обратите внимание на эту задачу. Она может оказаться сложной, если не знать одного очень важного свойства медианы, проведенной к гипотенузе. А именно: Медиана, проведенная к гипотенузе, равна ее половине. Значит, треугольники и – равнобедренные. Ответ: 62.
Часть 2.
Нахождение значений синусов, косинусов, тангенсов углов в прямоугольном треугольнике
 Вы должны знать как находить синус, косинус, тангенс угла в прямоугольном треугольнике.
Вы должны знать как находить синус, косинус, тангенс угла в прямоугольном треугольнике.
А также знать некоторые связи между острыми углами прямоугольного треугольника (не только то, что их сумма равна 90 градусов, но и как они связаны при помощи тригонометрических функций), а также что еще связывает смежные углы помимо того, что их сумма 180 градусов. Заглянув сюда, вы найдете компактные таблицы-шпаргалки с необходимым справочным материалом для решения задач, что мы здесь рассматриваем.
Задача 1.
В треугольнике угол равен 90°, Найдите
Решение: + показать
Задача 2.
В треугольнике ABC угол C равен 90°, Найдите
Решение: + показать
Задача 3.
В треугольнике ABC угол C равен 90°, Найдите
Решение: + показать
Сначала найдем из основного тригонометрического тождества: Поскольку имеем дело с острым углом , то положителен. Тогда Ответ: 1,75.
Задача 4.
В треугольнике угол равен 90°, Найдите
Решение: + показать
Задача 5.
В треугольнике угол равен 90°, Найдите
Решение: + показать В задаче можно обращаться к тригонометрическим тождествам, но мы поступим так: Пусть , тогда . По теореме Пифагора () имеем: Тогда Ответ: 0,28.
Задача 6.
В треугольнике ABC угол C равен 90°, CH — высота, Найдите
Решение: + показать Мы уже знаем, что для острых углов прямоугольного треугольника выполняется: . В треугольнике Значит и Ответ: 0,8. 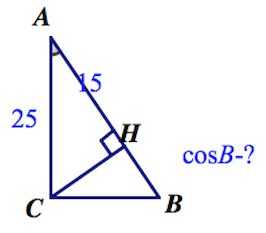
Задача 7.
В треугольнике ABC угол C равен 90°, синус внешнего угла при вершине A равен Найдите .
Решение: + показать
Задача 8.
В треугольнике ABC угол C равен 90°, косинус внешнего угла при вершине A равен Найдите .
Решение: + показать Уже говорили о том, что , поэтому Берем положительное значение , так как угол – острый: Ответ: 0,5.
Дожили до конца статьи? 🙂
Отдых не помешает!

ПРОДОЛЖЕНИЕ. Смотрите также статью «Прямоугольный треугольник. Вычисление длин».
egemaximum.ru
1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.
Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
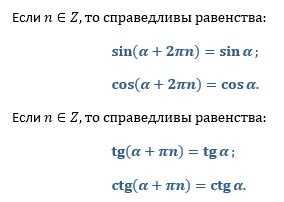
cknow.ru
Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.
В системе координат построим полуокружность радиуса \(1\) с центром в начале координат.

Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике \(AOX\):
sinα=AXAO;cosα=OXAO.
Так как радиус полуокружности \(R = AO = 1\), то sinα=AX;cosα=OX.
Длина отрезка \(AX\) равна величине координаты \(y\) точки \(A\), а длина отрезка \(OX\) равна величине координаты \(x\) точки \(A\):
Acosα;sinα.
Следовательно, для углов 0°≤α≤180° видно, что −1≤cosα≤1;0≤sinα≤1.
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
tgα=AXOX=sinαcosα.
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для 0°;90°;180°.
sin0°=0;cos0°=1;tg0°=0;sin90°=1;cos90°=0;tg90° не существует;sin180°=0;cos180°=−1;tg180°=0.
Рассмотрим оба острых угла в треугольнике \(AOX\). Если вместе они образуют 90°, то оба выразим через α.
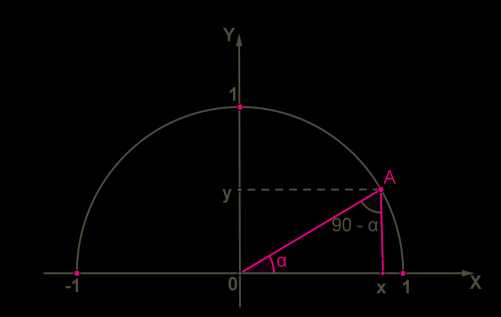
Если sinα=AXAO;cosα=OXAO, то sin90°−α=OXAO;cos90°−α=AXAO.
Видим, что справедливы равенства:
cos90°−α=sinα;sin90°−α=cosα.
Рассмотрим тупой угол, который также выразим через α.
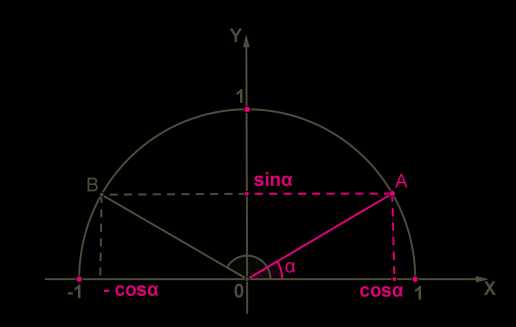
Справедливы следующие равенства:
sin180°−α=sinα;cos180°−α=−cosα.
Эти формулы называются формулами приведения:
cos90°−α=sinα;sin90°−α=cosα.
sin180°−α=sinα;cos180°−α=−cosα.
Если в треугольнике \(AOX\) применить теорему Пифагора, получаем AX2+OX2=1. Заменив отрезки соответственно синусом и косинусом, мы напишем
Главное тригонометрическое тождество
sin2α+cos2α=1.
Это тождество позволяет вычислить величину синуса угла, если дан косинус
(как уже отмечено, синус для углов 0°≤α≤180° только 0 или положительный):
sin2α+cos2α=1;sin2α=1−cos2α;sinα=1−cos2α
— или величину косинуса угла, если дан синус:
sin2α+cos2α=1;cos2α=1−sin2α;cosα=±1−sin2α.
Для острых углов косинус положительный, а для тупых углов берём отрицательное значение.
www.yaklass.ru

 Задача 1.
Задача 1.