Ортогональные и симметрические матрицы линейных преобразований
Матрица
А является симметрической, если она не
меняется при транспонировании, то есть
А=  Например, следующие матрицы симметрические
Например, следующие матрицы симметрические 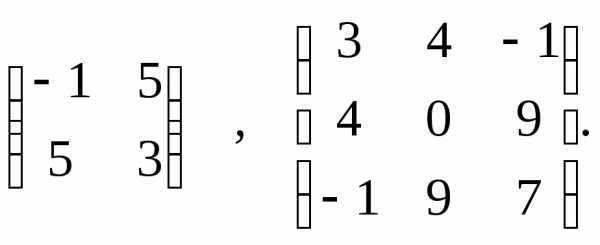
Свойства симметрических матриц:
Собственные значения симметрической матрицы – действительные числа.
Любая симметрическая матрица имеет по крайней мере один набор попарно перпендикулярных собственных векторов.
Симметрическая матрица может быть приведена к диагональному виду.
Матрица
Q называется ортогональной, если при
транспонировании она совпадает со своей
обратной матрицей, то есть Q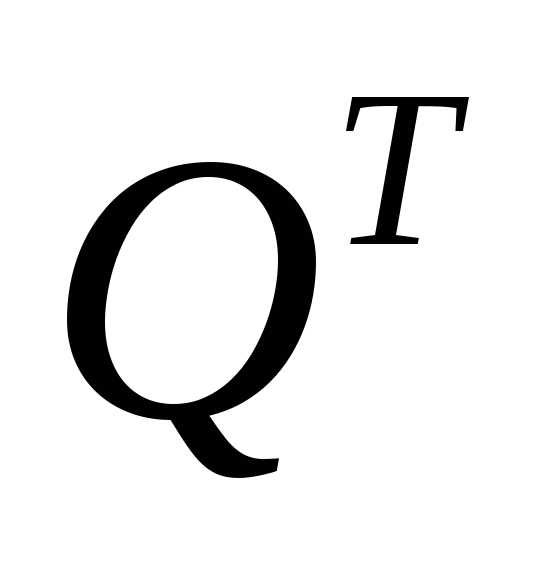 .
.
Свойства ортогональных матриц Q:
Если матрица ортогональная, то Q-1 также ортогональная.
Столбцы матрицы Q образуют ортонормированную систему векторов.
Для каждой симметрической матрицы
 существует такая ортогональная матрица
Q, что матрица
существует такая ортогональная матрица
Q, что матрица  является диагональной.
является диагональной.
На основании перечисленных свойств симметрических и ортогональных матриц (преобразований) можно составить план приведения симметрической матрицы к диагональному виду:
Найти собственные значения матрицы.
Сформировать базис из ортогональных собственных векторов.
Составить матрицу перехода С к базису из собственных векторов.
Столбцы матрицы С подвергнуть нормализации
(т.е. каждый собственный вектор разделить на его длину), в результате получится матрица Q.
Транспонируя матрицу Q, получим обратную матрицу Q-1.
Вычислим произведение диагональная матрица.
Пример. Привести симметрическую матрицу А к диагональному виду с помощью ортогональной матрицы Q, если
А= .
.
Решение. Составим характеристическое уравнение det(A-λE)=0,
Корни характеристического уравнения
действительные и различные числа. Определим собственные векторы. В систему уравнений
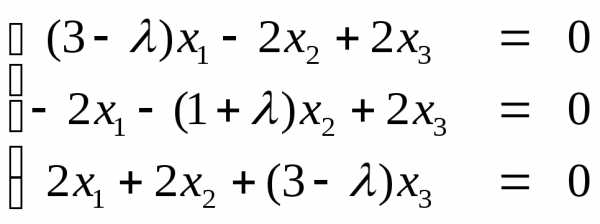 подставим собственные
значения.
подставим собственные
значения.
1) λ=λ1=-3 получим х3 — любое число, и не равно нулю. Пусть х3=-1., тогда имеем собственный вектор е1=(1, 2, -1).
Возьмем λ=λ2=3.
Пусть х3 =1. Второй собственный вектор е2=(-1, 1, 1).
3) Подставим λ=λ3=5.
Если х3=1, то е3=(1, 0, 1). Полученные собственные векторы попарно ортогональны:
Имеем ортогональный базис
Матрица перехода к
этому базису
— это ортонормированный базис. Матрица
Q= —
ортогональная матрица.
—
ортогональная матрица.
По
свойству  запишем обратную матрицу
запишем обратную матрицу
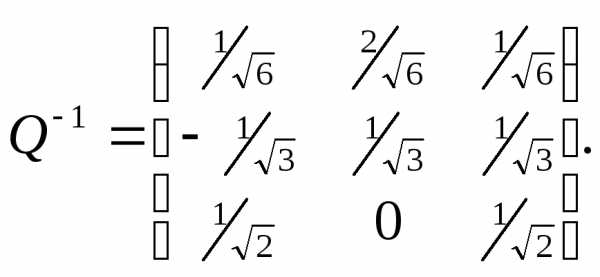 Вычислив произведение
трех матриц, получим диагональную
матрицу
Вычислив произведение
трех матриц, получим диагональную
матрицу 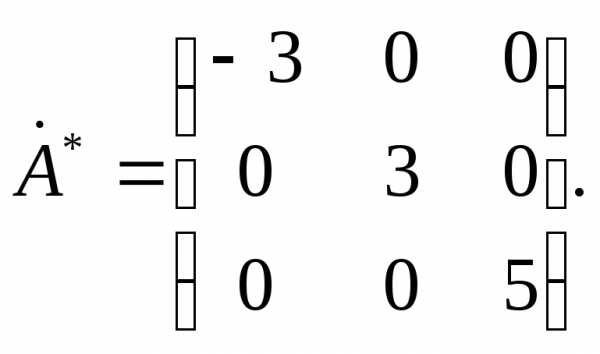
Рассмотрим теперь пример, в котором собственные числа не все различны.
Пример.
Привести к диагональному виду матрицу
А, определяющую линейное преобразование
в ортогональном базисе: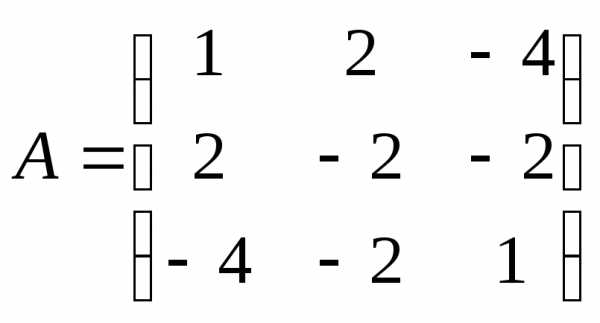
Решение. Составим характеристическое уравнение.
(*)
Решая уравнение, найдем собственные значения Для нахождения собственных векторов в систему уравнений
подставим сначала
двукратный корень λ=λ1=λ2=-3.
Получим следующую систему  которая сводится к одному уравнению:
которая сводится к одному уравнению:
2х1+х2-2х3=0 (**)
Из
последнего уравнения можно сделать
вывод, считая его скалярным произведением,
что все собственные векторы е1,
е2 , соответствующие кратному собственному
значению λ=-3, лежат в одной плоскости
и ортогональны вектору е=(2,1,-2), координаты
которого есть коэффициенты уравнения
(**). Следовательно, вектор е принадлежит
множеству собственных векторов,
соответствующих λ 3=6.
Этот факт можно проверить следующим
образом: подставим λ3=6
в систему (*), а затем подставим туда
координаты вектора е. Получим 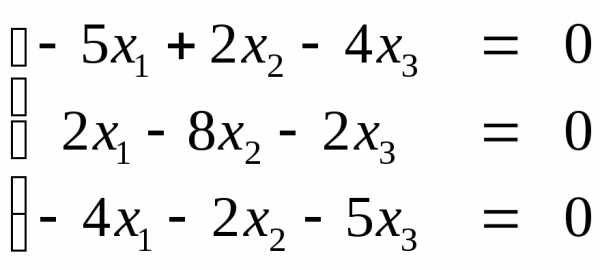 .
При х1=2
х2=1,
х3=-2:
-10+2+8=0 4-8+4=0, -8-2+10=0. Поэтому е3=е=(2,
1, -2). Теперь, пользуясь уравнением (**),
подберем решение х1=1,
х2=2,
х3=2
и обозначим собственный вектор е2=(1,
2, 2). Чтобы найти еще один собственный
вектор из бесчисленного множества
векторов, соответствующих λ=-3, примем
во внимание, что искомый вектор должен
быть ортогонален векторам е2 и е3 . Следовательно, его можно вычислить
как векторное произведение, т.е. е1=
.
При х1=2
х2=1,
х3=-2:
-10+2+8=0 4-8+4=0, -8-2+10=0. Поэтому е3=е=(2,
1, -2). Теперь, пользуясь уравнением (**),
подберем решение х1=1,
х2=2,
х3=2
и обозначим собственный вектор е2=(1,
2, 2). Чтобы найти еще один собственный
вектор из бесчисленного множества
векторов, соответствующих λ=-3, примем
во внимание, что искомый вектор должен
быть ортогонален векторам е2 и е3 . Следовательно, его можно вычислить
как векторное произведение, т.е. е1=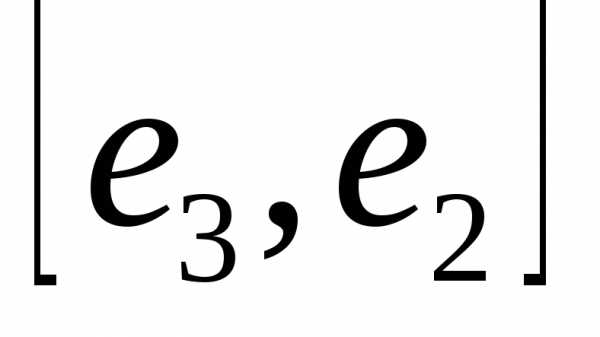 .
В координатной форме это выглядит
следующим образом:
.
В координатной форме это выглядит
следующим образом:
Таким образом, новый ортогональный базис из собственных векторов: е1=(6,-6,3), е2=(1,2,2), е3=(2,1,-2). Разделим каждый вектор на его длину и получим ортонормированный базис
Ортогональная матрица:
Обратная
матрица: Q-1=Qт=
Q-1=Qт=

Диагональная матрица, определяющая преобразование в новом ортонормированном базисе, найдется по формуле:
Ответ: 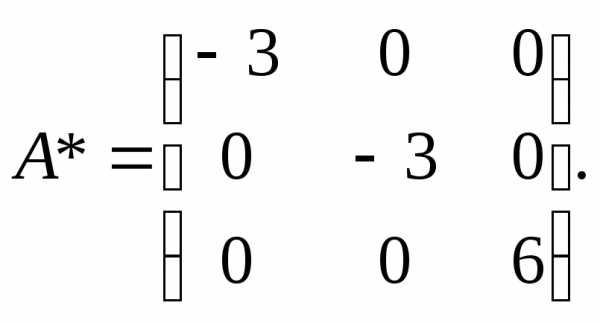
Если собственные значения симметрической матрицы в трехмерном линейном пространстве все одинаковы λ 1=λ2=λ3=λ, то матрица определяет преобразование подобия с коэффициентом λ. В этом случае все векторы пространства являются собственными векторами. В качестве нового базиса можно взять любую тройку единичных попарно ортогональных векторов, например е1=(1,0,0), е2=(0,1,0), е3=(0,0,1).
studfiles.net
Квадратичные формы
Квадратичной формойf(х1, х2,…,хn) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом:f(х1, х2,…,хn) =(aij=aji).
Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическаяматрица (т.е. матрица, симметричная относительно главной диагонали,aij=aji).
В матричной записи квадратичная форма имеет вид f(Х) = ХТAX, где
. В самом деле
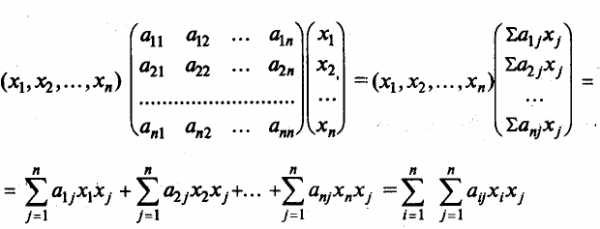
Например, запишем в матричном виде квадратичную форму .
Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С — невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = ХTАХ = (CY)TA(CY) = (YTCT)A(CY) =YT(C TAC)Y.
Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А*=CTAC.
Например, найдем квадратичную форму f(y1, y2), полученную из квадратичной формыf(х1, х2) = 2x12+ 4х1х2— 3х22линейным преобразованием .
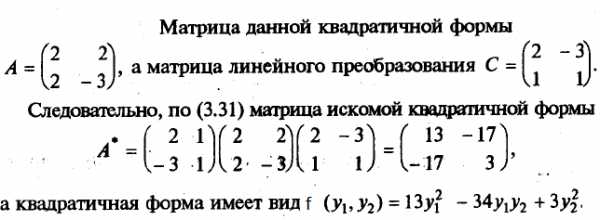
Квадратичная форма называется канонической(имеетканонический вид), если все ее коэффициентыaij= 0 приi≠j, т.е.f(х1, х2,…,хn) = a11 x12 + a22 x22+ … + ann xn2 = .
Ее матрица является диагональной.
Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.
Например, приведем к каноническому виду квадратичную форму f(х1, х2,х3) = 2x12+ 4х1х2— 3х22– х2х3.
Для этого вначале выделим полный квадрат при переменной х1:
f(х1, х2, х3) = 2(x12+ 2х1х2+ х22) — 2х22— 3х22– х2х3= 2(x1+ х2)2— 5х22– х2х3.
Теперь выделяем полный квадрат при переменной х2:
f(х1, х2, х3) = 2(x1+ х2)2– 5(х22– 2* х2*(1/10)х3+ (1/100)х32) — (5/100)х32= = 2(x1+ х2)2– 5(х2– (1/10)х3)2— (1/20)х32.
Тогда невырожденное линейное преобразование y1= x1+ х2,y2= х2– (1/10)х3иy3= x3приводит данную квадратичную форму к каноническому видуf(y1,y2,y3) = 2y12— 5y22— (1/20)y32.
Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами1). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называютзаконом инерции квадратичных форм.
Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х2:f(х1, х2,х3) = 2x12+ 4х1х2— 3х22– х2х3= -3х22– х2х3+ 4х1х2+ 2x12= -3(х22– — 2* х2((1/6) х3+ (2/3)х1) +((1/6) х3+ (2/3)х1) 2) – 3((1/6) х3+ (2/3)х1) 2+ 2x12= = -3(х2– (1/6) х3— (2/3)х1)2– 3((1/6) х3+ (2/3)х1)2+ 2x12=f(y1,y2,y3) = -3y12— -3y22+ 2y32, гдеy1= — (2/3)х1+ х2– (1/6) х3,y2= (2/3)х1+ (1/6) х3иy3= x1. Здесь положительный коэффициент 2 приy3и два отрицательных коэффициента (-3) приy1иy2(а при использовании другого способа мы получили положительный коэффициент 2 приy1и два отрицательных – (-5) приy2и (-1/20) приy3).
Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичную форму f(X) называютположительно(отрицательно)определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).
Например, квадратичная форма f1(X) = x12+ х22— положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf2(X) = -x12+ 2x1х2— х22— отрицательно определенная, т.к. представляет ее можно представить в видеf2(X) = -(x1— х2)2.
В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).
Теорема. Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).
Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.
Главным (угловым) миноромk-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().
Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.
Например, исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2+ 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(3 -) – 4 = (6 — 2- 3+2) – 4 =2— 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – положительно определенная.
Способ 2. Главный минор первого порядка матрицы А 1=a11= 2 > 0. Главный минор второго порядка2== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.
Исследуем на знакоопределенность другую квадратичную форму, f(х1, х2) = -2x12+ 4х1х2— 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+2) – 4 =2+ 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – отрицательно определенная.
Способ 2. Главный минор первого порядка матрицы А 1=a11= = -2 < 0. Главный минор второго порядка2== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).
И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2— 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(-3 -) – 4 = (-6 — 2+ 3+2) – 4 =2+- 10 = 0;D= 1 + 40 = 41;. Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).
Способ 2. Главный минор первого порядка матрицы А 1=a11= 2 > 0. Главный минор второго порядка2== -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).
1Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пустьf(х1, х2) = 2x1х2= x12+ 2x1х2 + х22— x12— х22=
= (x1+ х2)2— x12— х22= (x1+ х2)2– (x12— 2x1х2 + х22) — 2x1х2 = (x1+ х2)2– — (x1— х2)2— 2x1х2; 4x1х2= (x1+ х2)2– (x1— х2)2;f(х1, х2) = 2x1х2= (1/2)* *(x1+ х2)2– (1/2)*(x1— х2)2=f(y1,y2) = (1/2)y12– (1/2)y22, гдеy1= х1+ х2, аy2= х1– х2.
studfiles.net
Квадратичные формы
КВАДРАТИЧНЫЕ ФОРМЫ И ИХ ПРИМЕНЕНИЯ
Определение. Квадратичной формой 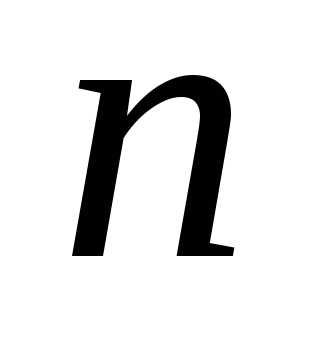 переменных,принимающих
числовые значения ,
называется числовая
функция вида
переменных,принимающих
числовые значения ,
называется числовая
функция вида
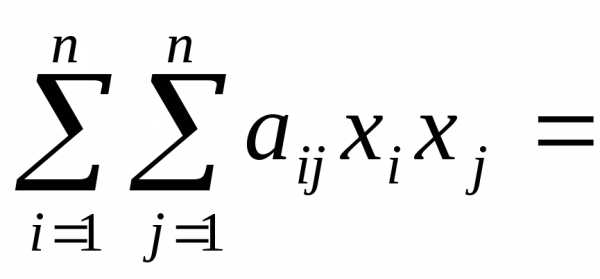 ,
,
где  —
числа,
называемые коэффициентами квадратичной
формы.
—
числа,
называемые коэффициентами квадратичной
формы.
Определение. Матрицей квадратичной формы 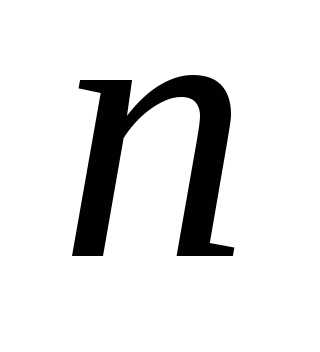 переменных,
называется симметрическая матрица
порядка
переменных,
называется симметрическая матрица
порядка 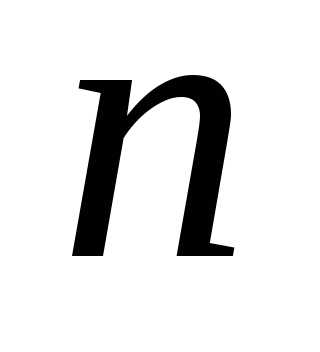 ,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных,
а каждый недиагональный элемент,
расположенный в
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных,
а каждый недиагональный элемент,
расположенный в  ой
строке
ой
строке ом
столбце,
равен половине коэфициента при
ом
столбце,
равен половине коэфициента при 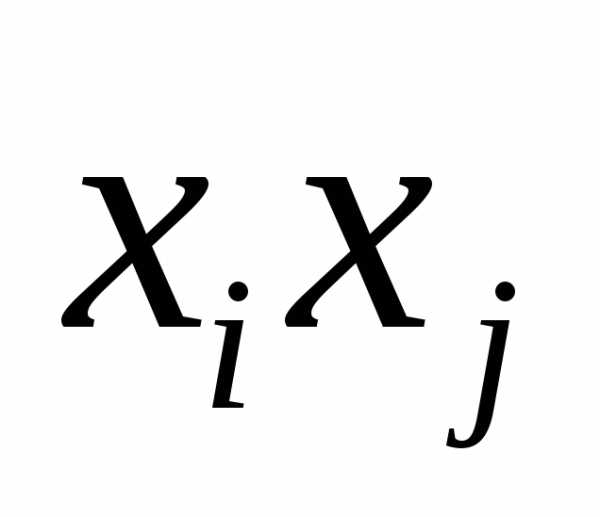 в квадратичной форме.
в квадратичной форме.
Определение. Рангом квадратичной формы называется
ранг её матри-цы.
Квадратичная форма может быть записана
в матричном виде
где 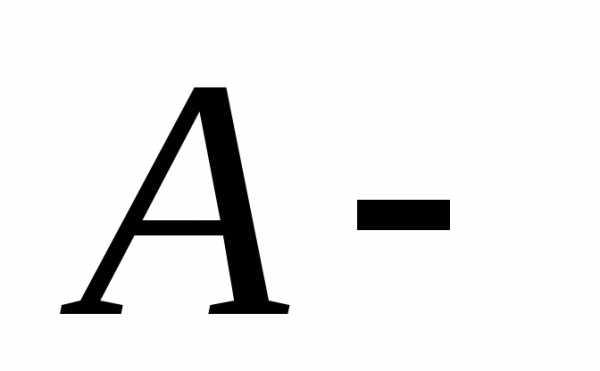 матрица
квадратичной формы и
.
матрица
квадратичной формы и
.
Определение.
Квадратичная форма называется канонической
(имеет канонический вид),
если коэфициенты 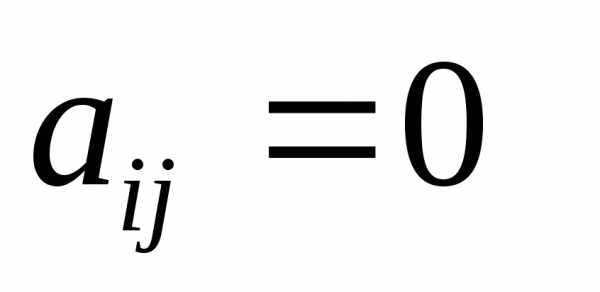 при
при 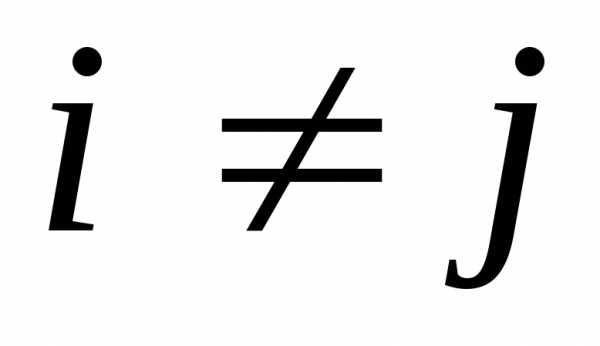 ,
то есть,
если матрица квадратичной формы
диагональная и следовательно
,
то есть,
если матрица квадратичной формы
диагональная и следовательно
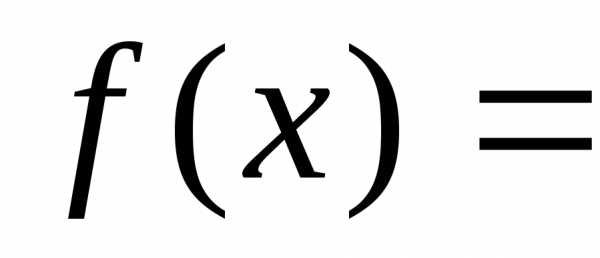 .,
.,
где
не все коэффициенты  равны
нулю.
равны
нулю.
Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Определение.
Нормальным
видом квадратичной
формы называется такой канонический
вид,
в котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны 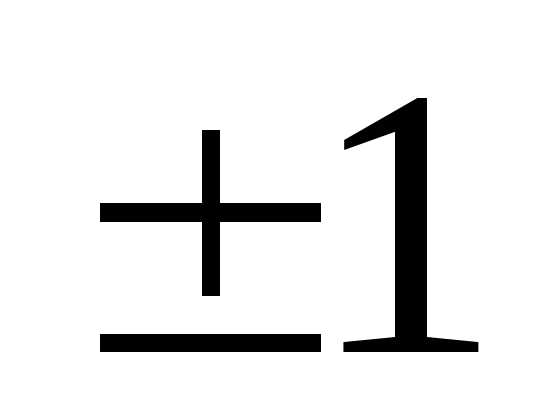 .
.
Определение.
Квадратичная
форма 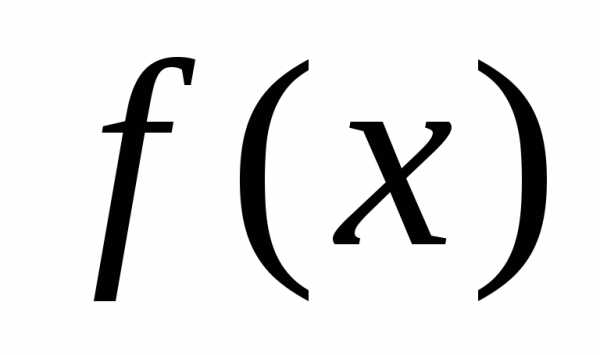 называется положительно
называется положительно
(отрицательно) определённой, если при всех
108
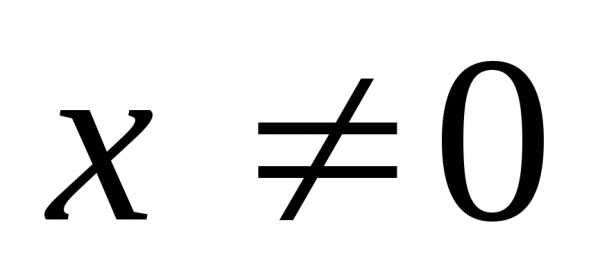 и
положительно (отрицательно)
полуопределённой,если
при всех
и
положительно (отрицательно)
полуопределённой,если
при всех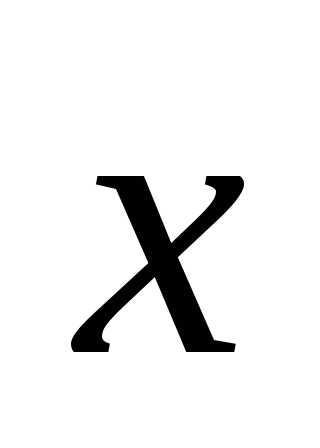 .
.
Теорема (критерий
Сильвестра).
Для того чтобы квадратичная
форма 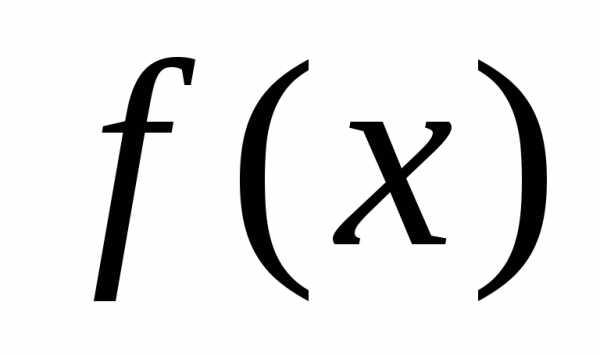 была положительно определённой,
необходимо и достаточно
чтобы все угловые миноры матрицы
квадратичной
формы
были положительны,то
есть,
чтобы
была положительно определённой,
необходимо и достаточно
чтобы все угловые миноры матрицы
квадратичной
формы
были положительны,то
есть,
чтобы
Здесь -угловые миноры матрицы квадратичной формы.
Следствие.
Для того чтобы квадратичная
форма 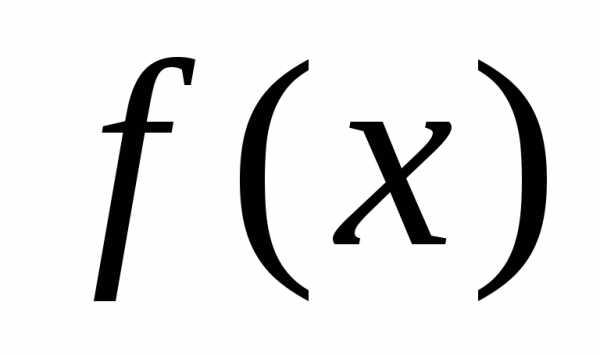 была отрицательно определённой,
необходимо и достаточно,
чтобы знаки угловых миноров матрицы
квадратичной
формы чередовались следующим образом:
была отрицательно определённой,
необходимо и достаточно,
чтобы знаки угловых миноров матрицы
квадратичной
формы чередовались следующим образом:
Примеры
1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
.
Решение. Следуя алгоритму метода Лагранжа,
выделим вначале в квад-ратичной форме
все члены, содержащие 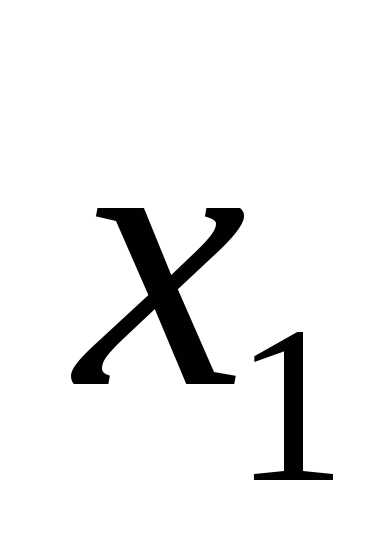 ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
.
Сделаем в этом выражении замену и подставим его в квадратичную форму. Получим:
.
Далее
выделим в 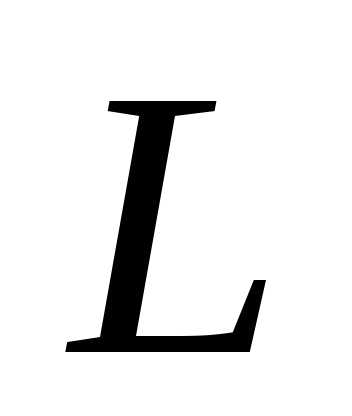 члены, содержащие
члены, содержащие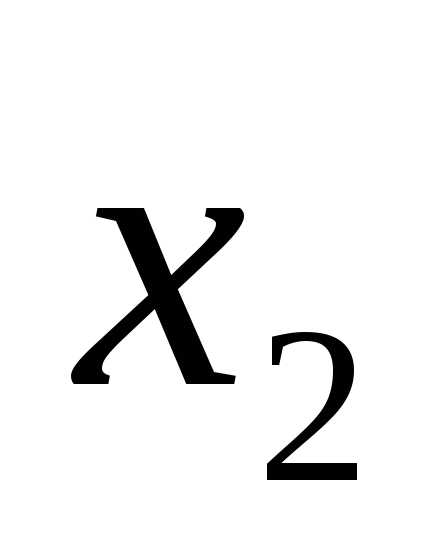 и проделаем с ними анало-гичную процедуру:
и проделаем с ними анало-гичную процедуру:
Если
положить
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также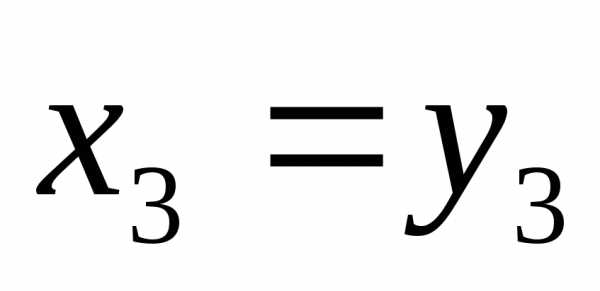 ,
тогда
,
тогда
109
канонический вид квадратичной формы есть
.
Соответствующее
преобразование от переменных 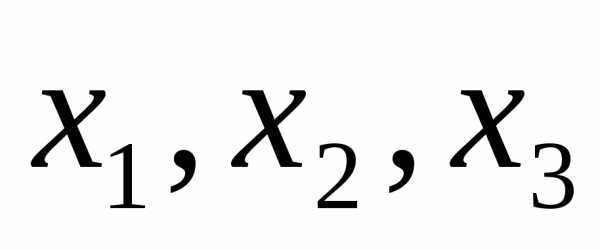 к переменным
к переменным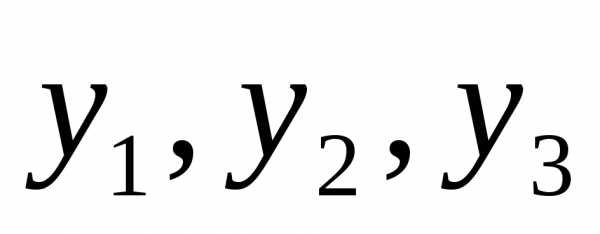 имеет вид:
имеет вид:
.
2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
.
Решение. В исходном базисе 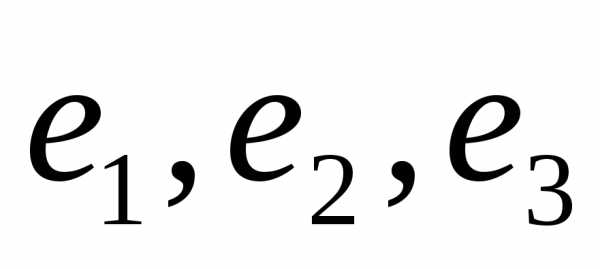 матрица оператора, соответствующая
данной квадратичной форме, есть
матрица оператора, соответствующая
данной квадратичной форме, есть
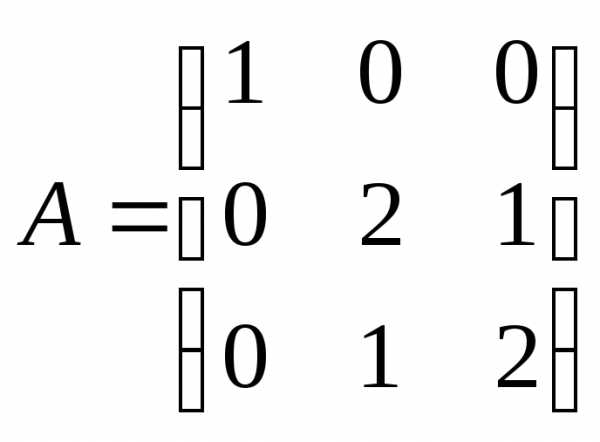 .
.
Эта
матрица будет определять
квадратичную форму канонического вида
в ортонормированном базисе 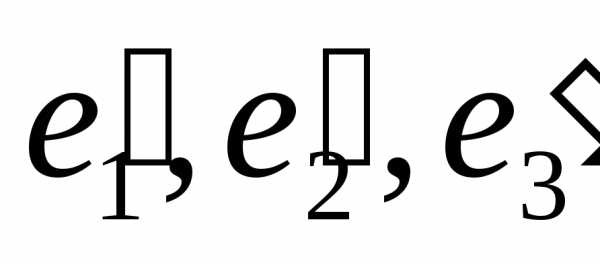 ,
составленном из собственных векторов
матрицы
,
составленном из собственных векторов
матрицы .
Найдем их.
.
Найдем их.
Характеристическое
уравнение для матрицы  имеет вид
имеет вид
.
Откуда следует
и .
Как известно собственные векторы матрицы находятся из уравнений
.
Для
случая 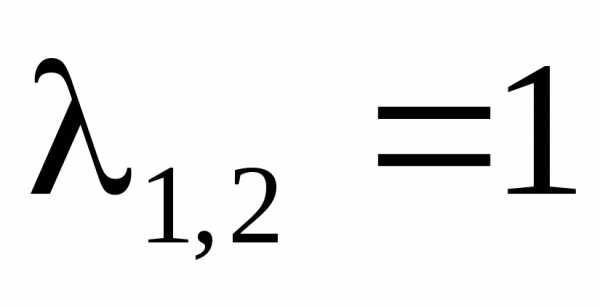 имеем:
имеем:

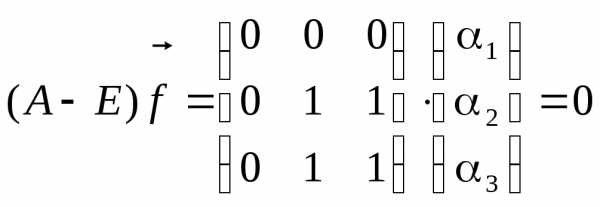 .
.
110
Ранг
матрицы этой системы уравнений
(относительно  )
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина  принимает произвольные значения, а
величины
принимает произвольные значения, а
величины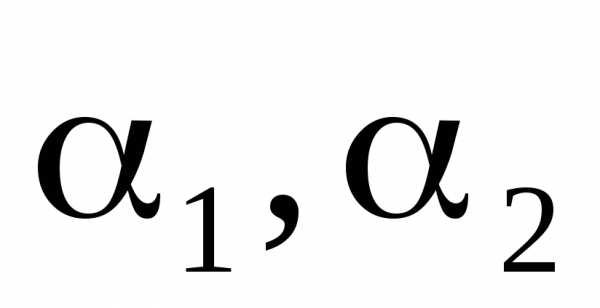 связаны соотношением.
В качестве собственных можно выбрать,
например, векторы
связаны соотношением.
В качестве собственных можно выбрать,
например, векторы
Эти
векторы ортогональны:
(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор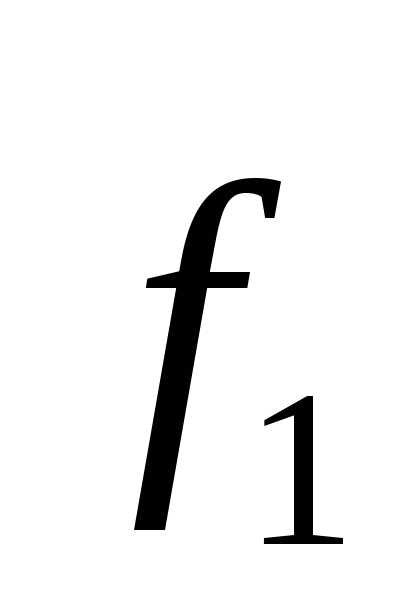 к тому же и нормирован. Откуда следует
—
к тому же и нормирован. Откуда следует
— .
Нормируем теперь вектор
.
Нормируем теперь вектор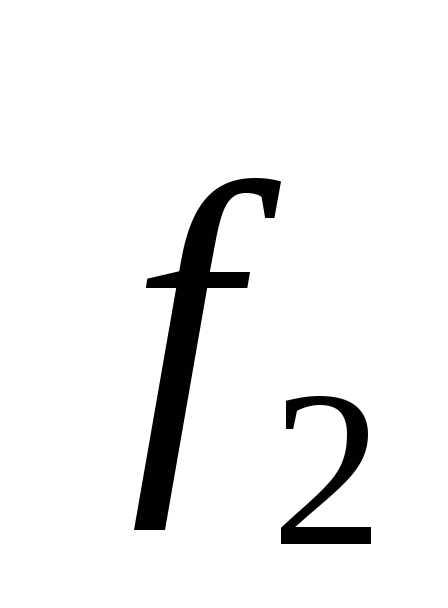 :
:
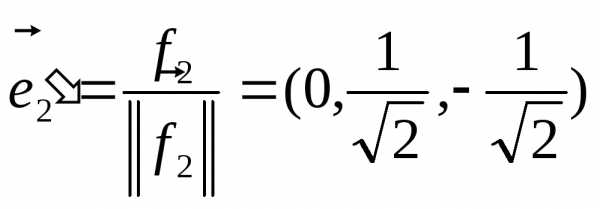 .
.
Для
случая 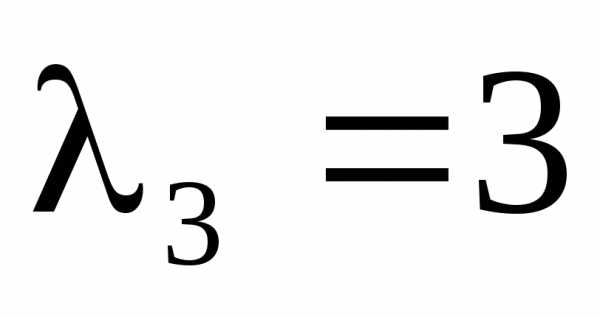 уравнение, определяющее собственный
вектор есть
уравнение, определяющее собственный
вектор есть

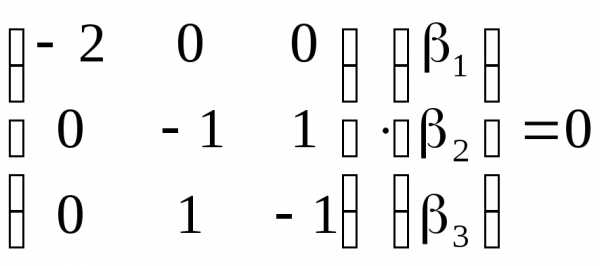 .
.
Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например, 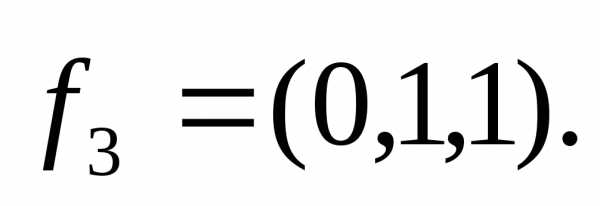 Отнормируем этот вектор:
Отнормируем этот вектор: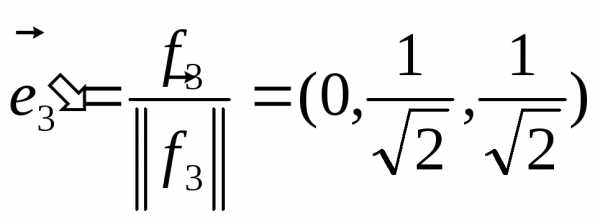 .
.
Теперь можно составить искомую матрицу ортогонального преобразования:
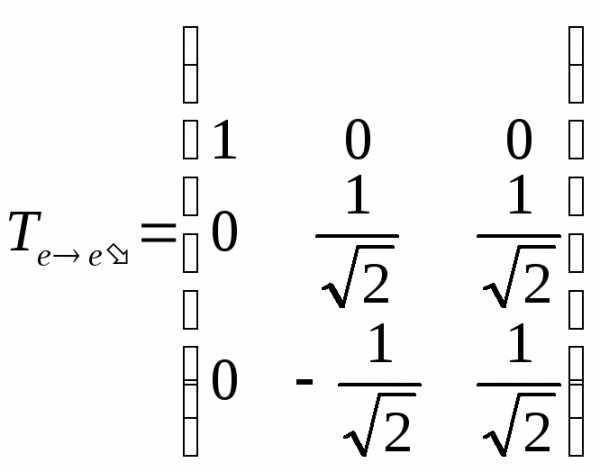 .
.
111
Исходная квадратичная форма будет иметь следующий канонический вид
.
При
этом переменные 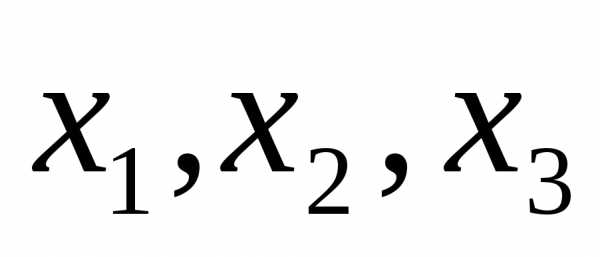 связаны с переменными
связаны с переменными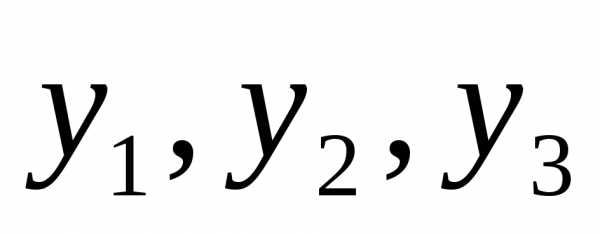 соотношением
соотношением
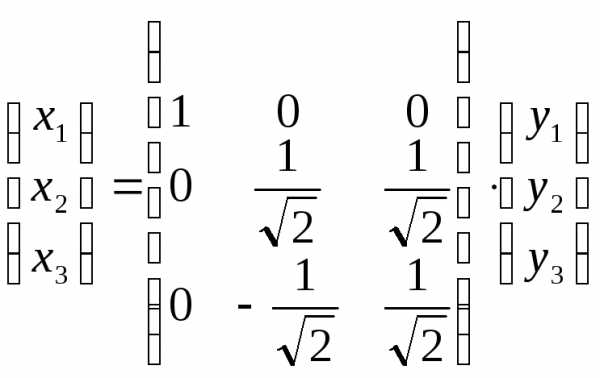 или
или
3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
.
Решение. Выделим в этом выражении квадратичную
форму 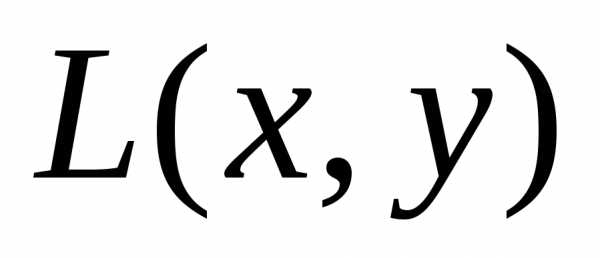 .
Это три первых слагаемых уравнения.
.
Это три первых слагаемых уравнения.
Матрица
квадратичной формы равна 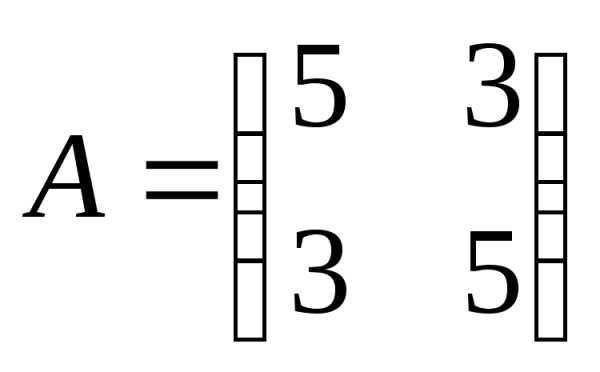 .
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
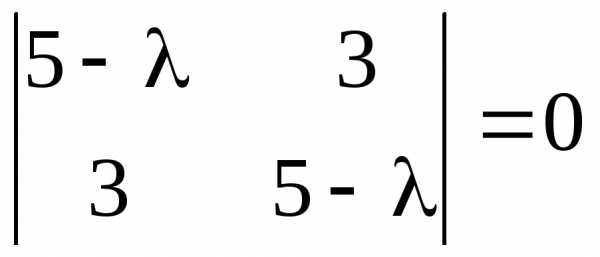 .
.
Его корни таковы: .
Найдём теперь собственные векторы, соответствующие этим корням и отнормрируем их. Для вектора , соответствующего
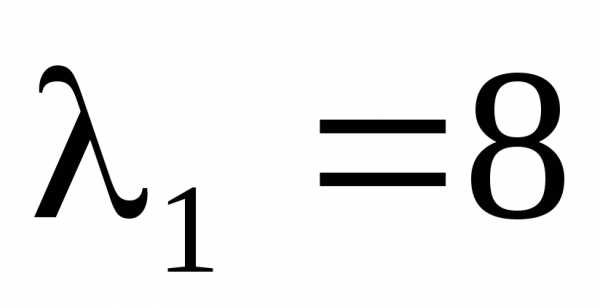 ,
имеем
,
имеем
112
В
итоге собственный вектор, соответствующий 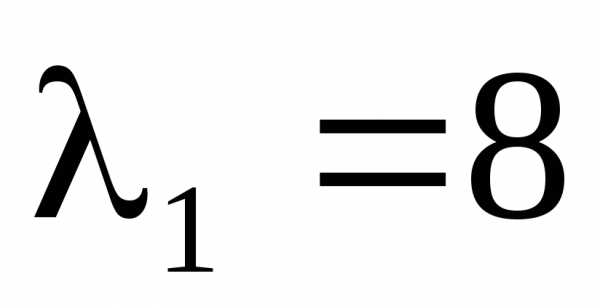 ,
можно выбрать в виде
,
можно выбрать в виде
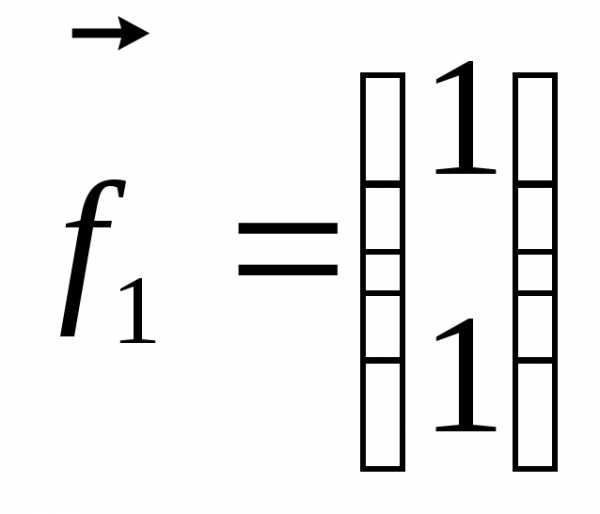 .
.
Анологичная процедура для собственного вектора даёт:
Откуда:
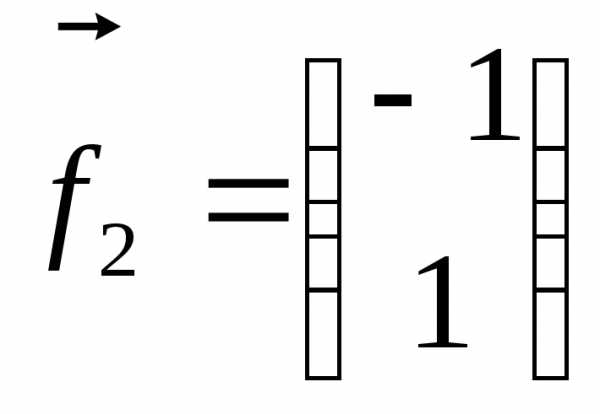 .
.
После нормировки полученных векторов имеем:
.
Эти векторы представляют собой ортонормированный базис новой системы координат. Матрица ортогонального оператора, приводящего квадратичную форму к каноническому виду, есть
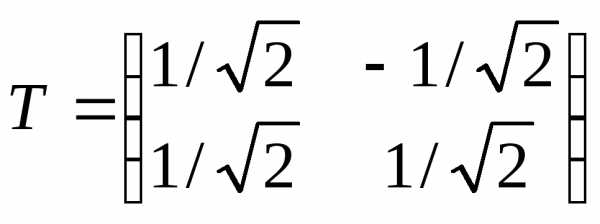
Связь
старых 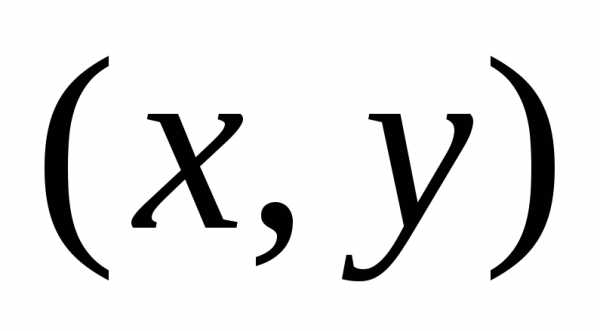 и новых
и новых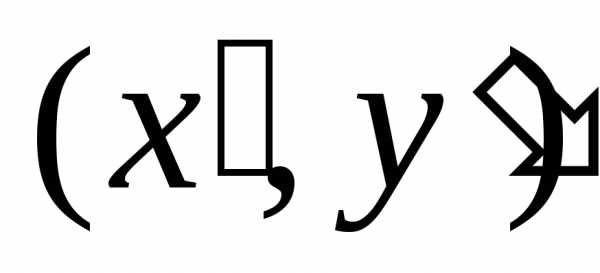 координат определяется соотношением.
координат определяется соотношением.
Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду
113
Это
есть каноническое уравнение эллипса в
системе координат 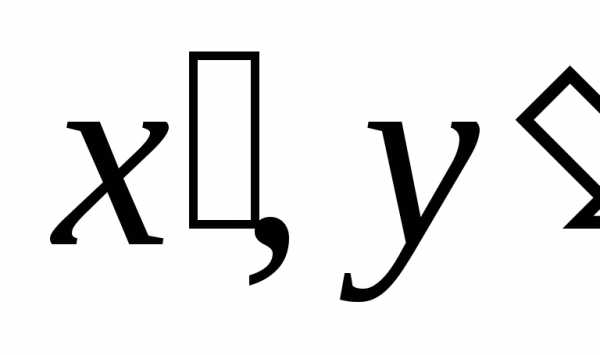 ,которая
получается из исходной её поворотом на
угол
,которая
получается из исходной её поворотом на
угол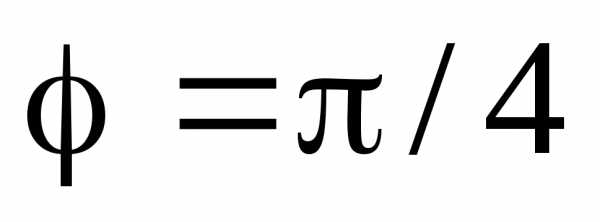 и
переносом начала координат в точку.
и
переносом начала координат в точку.
Записать матрицу квадратичной формы:
5.1. ;
5.2. ;
5.3. 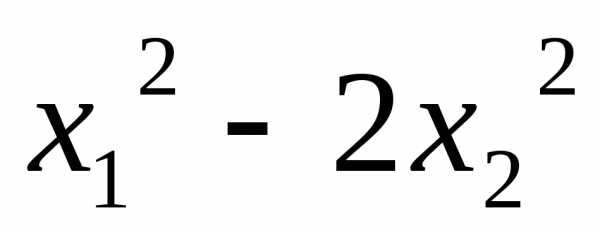 ;
;
5.4. ;
5.5. ;
5.6. ;
5.7. ;
5.8. ;
5.9. ;
5.10. ;
5.11. 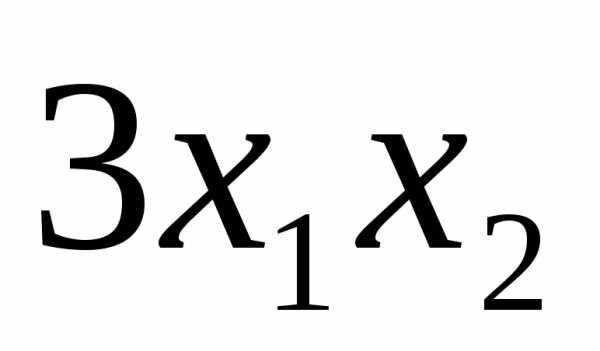 .
.
Найти ранг квадратичной формы:
5.12. ;
5.13. ;
5.14. ;
114
5.15. ;
5.16. ;
5.17. ;
5.18. ;
5.19. ;
5.20. .
Записать квадратичную форму в матричном виде:
5.21. ;
5.22. ;
5.23. 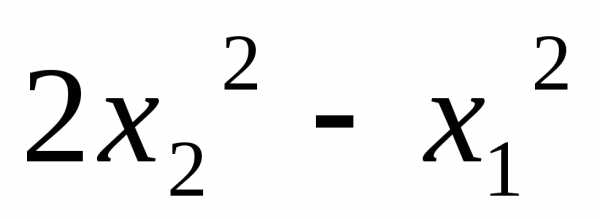 ;
;
5.24. ;
5.25. ;
5.26. ;
5.27. ;
5.28. ;
5.29. ;
5.30. .
Записать
квадратичную форму в виде 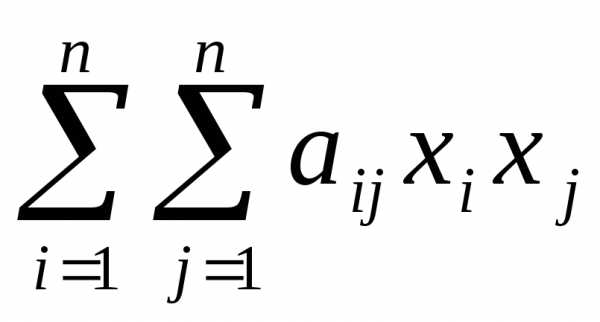 по
заданной
по
заданной
матрице :
5.31. 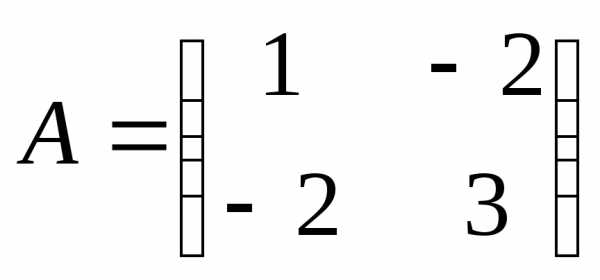 ;
5.32.
;
5.32.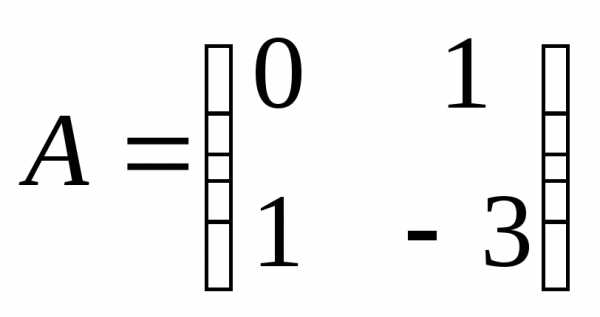 ;
;
5.33. 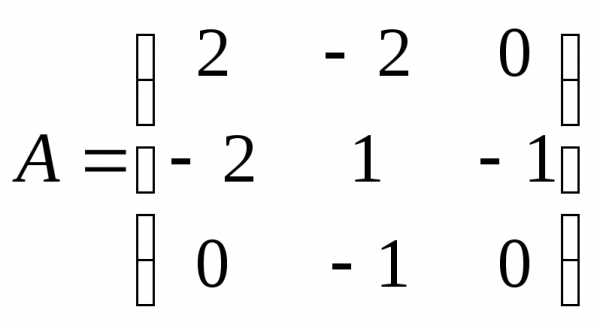 ;
5.34.
;
5.34.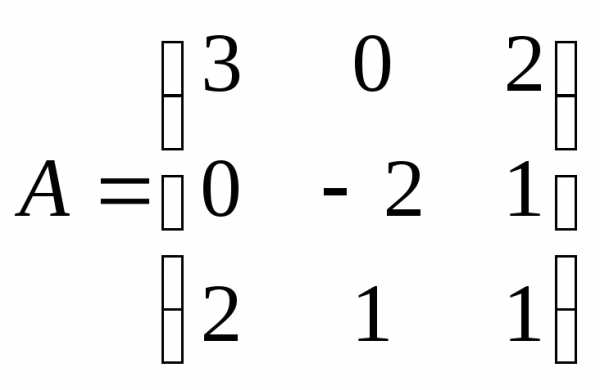 ;
;
115
5.35. 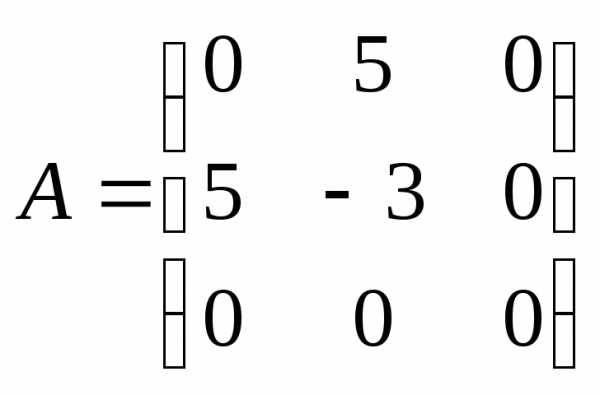 ;
5.36.
;
5.36. ;
;
5.37. 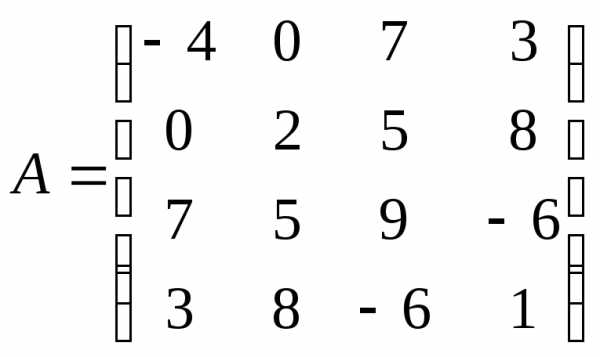 ;
5.38.
;
5.38.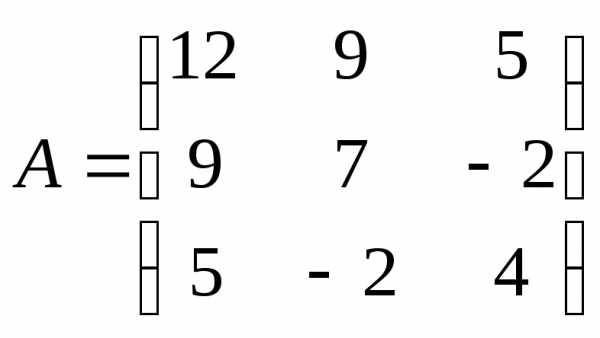 ;
;
5.39. 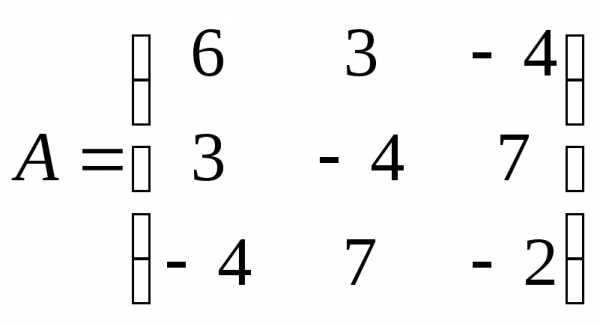 ;
5.40.
;
5.40. 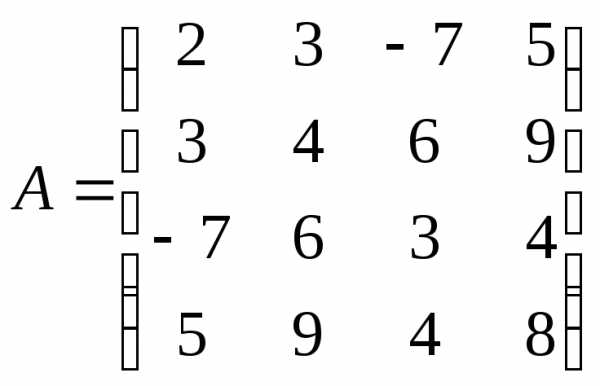 .
.
Привести квадратичную форму к каноническому виду методом
Лагранжа и записать соответствующее преобразование:
5.41. ;
5.42. ;
5.43. ;
5.44. ;
5.45. ;
5.46. ;
5.47.
5.48.
5.49.
5.50.
5.51. ;
116
5.52. .
Найти ортогональное преобразование, приводящее квадратичную
форму к каноническому виду и записать соответствующий кано-
нический вид квадратичной формы:
5.53. ;
5.54. ;
5.55. 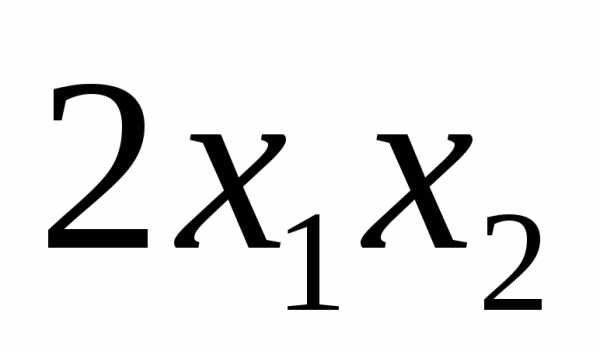 ;
;
5.56. ;
5.57. ;
5.58. ;
5.59. ;
5.60. ;
5.61. ;
5.62. .
Записать данное уравнение второго порядка в матричном виде и
определить, фигуру какого типа (эллиптического, гиперболическо-
го, параболического) оно определяет:
5.63.
5.64.
5.65.
5.66.
5.67.
5.68.
5.69.
5.70.
5.71.
5.72.
117
5.73.
5.74. .
Построить в прямоугольной системе координат Оху (O;i,j) фигуру,
определяемую данным уравне-нием, предварительно приведя его
к каноническому виду:
5.75.
5.76.
5.77.
5.78.
5.79.
5.80.
5.81.
5.82.
5.83.
5.84. .
Каждую из квадратичных форм исследовать на знакоопределённость
5.85.
5.86.
5.87.
5.88.
5.89.
5.90.
5.91.
5.92.
5.93. ;
5.94.
118
5.95. ;
5.96. .
119
studfiles.net
Квадратичные формы. приведение квадратичных форм к каноническому виду. критерий сильвестра
Задание 1. Составить матрицу квадратичной формы .
Решение. В общем виде квадратичная форма аргументов и задаётся следующим образом:
,
Где являются элементами матрицы квадратичной формы. Сравнивая заданную квадратичную форму с общим её видом, получим, что , , , , , , т. е. .
Ответ: .
Задание 2. Восстановить квадратичную форму по заданной матрице . Каждая ли из заданных матриц может соответствовать некоторой квадратичной форме? Почему?
А) ; б) .
Решение. Матрица квадратичной формы должна быть симметрической, т. е. .
а) Матрица не может быть матрицей квадратичной формы, так как , т. е. она не является симметрической.
Б) Матрице соответствует некоторая квадратичная форма, так как она является симметрической. Очевидно, , , , , , . Следовательно, квадратичная форма примет вид
.
Ответ: .
Задание 3. Задана квадратичная форма . Найти квадратичную форму , полученную из данной линейным преобразованием: , .
Решение. При невырожденном линейном преобразовании матрица квадратичной формы преобразуется в матрицу .
Выпишем матрицу заданной квадратичной формы: . Матрица заданного линейного преобразования , тогда . Следовательно,
,
т. е. .
Можно сделать проверку полученного результата непосредственной подстановкой в заданную квадратичную форму формулы преобразования координат:
.
Ответ: .
Задание 4. Привести к каноническому виду квадратичную форму .
Решение. Выпишем матрицу квадратичной формы: . Диагонализация матрицы квадратичной формы происходит в ОНБ из собственных векторов. Если – матрица перехода к такому базису, то координаты вектора в разных базисах связаны между собой соотношением:
,
Где в столбцах матрицы находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.
Составим характеристическое уравнение:
,
Значит, собственные значения , , .
Найдём собственные векторы, соответствующие найденным собственным значениям.
При : , откуда получаем однородную систему уравнений тогда .
При : , т. е. тогда .
При : , откуда получаем однородную систему уравнений
Из системы следует, что – свободная переменная. Примем , тогда
.
Векторы , , попарно ортогональны (в этом легко убедиться непосредственно!), тогда ОНБ составят векторы
, , .
Матрица перехода от ОНБ к ОНБ примет вид:
.
Замечание. О том чтобы матрица оказалась симметрической, следует помнить при построении собственных векторов , И .
Формулы перехода от координат к координатам :
, , .
Канонический вид заданной квадратичной формы:
.
Подстановкой приведенных формул преобразования координат в заданную квадратичную форму можно убедиться в правильности проведенных вычислений.
Ответ: .
Задание 5. Установить знакоопределённость квадратичной формы .
Решение.
Метод 1. Если все собственные значения , то квадратичная форма положительно определённая; если все – отрицательно определённая. Найдём собственные значения квадратичной формы. Для этого составим её матрицу:
И характеристическое уравнение:
Его корни , , т. е. все , а следовательно, квадратичная форма положительно определённая.
Метод 2. Знакоопределённость квадратичной формы можно установить и с помощью критерия Сильвестра, в соответствии с которым квадратичная форма положительно определённая, если все главные диагональные миноры матрицы положительны, т. е. , , …, , а если знаки этих миноров чередуются, т. е. , , , …, то квадратичная форма – отрицательно определённая.
Для данной квадратичной формы имеем:
, , , т. е. заданная квадратичная форма положительно определённая.
Ответ: квадратичная форма положительно определённая.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
2.1. Квадратичные формы
Определение: Квадратичной формой от n неизвестных называется сумма вида
, (1)
то есть
. (2)
Матрица , называется матрицей квадратичной формы (1), а ее ранг – рангом формы (1). Если ранг формы равен n, форма называется невырожденной (в этом случае ранг матрицы A равен n и матрица A невырожденная).
Cчитаем, что матрица A квадратичной формы – симметрическая.
Из формулы (2) видно, что квадратичная форма является однородным многочленом 2-й степени от переменных Кроме того, квадратичную форму можно считать функцией от вектора:
В матричном виде квадратичную форму записать:
Так как квадратичная форма – это функция от вектора, то ее вид зависит от базиса линейного пространства, и при изменении базиса матрица квадратичной формы также изменяется. Закон изменения матрицы дает следующая теорема.
Теорема: Квадратичная
форма от n неизвестных с матрицей A после выполнения
линейного преобразования неизвестных
с матрицей  превращается в квадратичную форму от
новых неизвестных с матрицей
превращается в квадратичную форму от
новых неизвестных с матрицей
Определение: Каноническим
видом квадратичной
формы называют
такой её вид (в некотором базисе), который
представляет собой сумму квадратов
неизвестных с некоторыми коэффициентами:
называют
такой её вид (в некотором базисе), который
представляет собой сумму квадратов
неизвестных с некоторыми коэффициентами:
Теорема: (Основная теорема о квадратичных формах). Всякая квадратичная форма с действительными коэффициентами может быть приведена некоторым невырожденным линейным преобразованием переменных к каноническому виду.
Пример: Квадратичную форму привести к каноническому виду посредством невырожденного линейного преобразования.
Решение. Соберём все слагаемые, содержащие
неизвестное 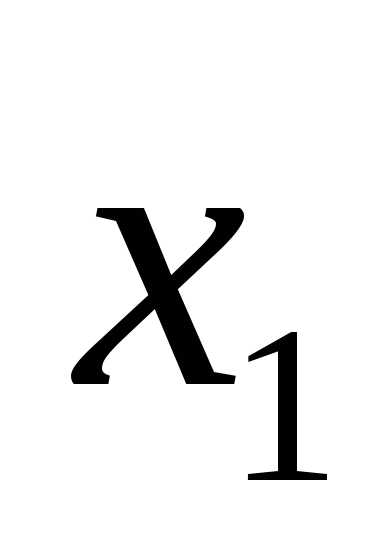 ,
и дополним их до полного квадрата
,
и дополним их до полного квадрата
.
(Так как .)Положим
 (3)
(3)
и
от неизвестных 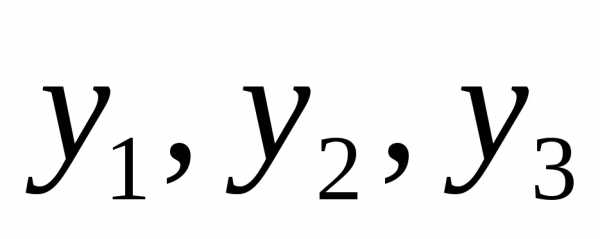 форма
форма примет вид.
Далее полагаем
примет вид.
Далее полагаем
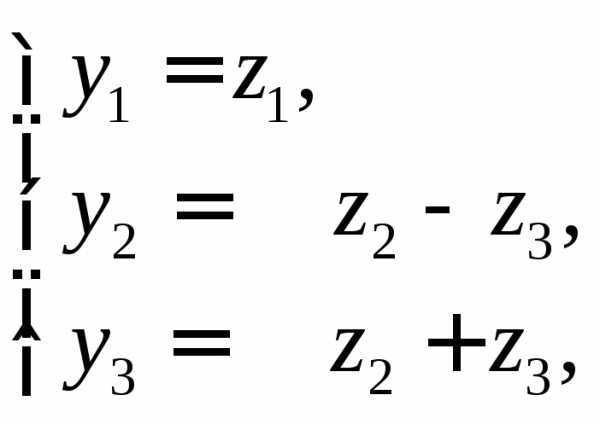
и
от неизвестных 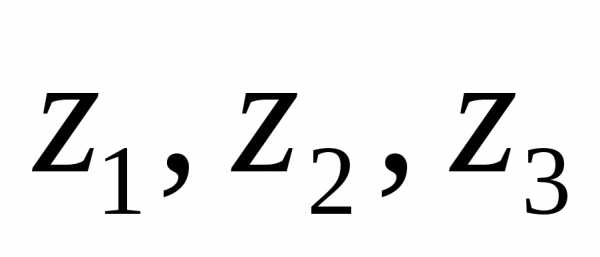 форма
форма примет уже канонический вид
примет уже канонический вид
. (4)
Разрешим
равенства (3) относительно 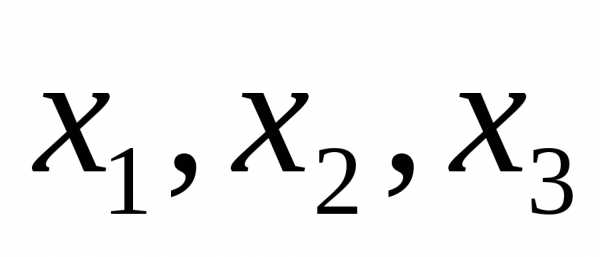 :
:
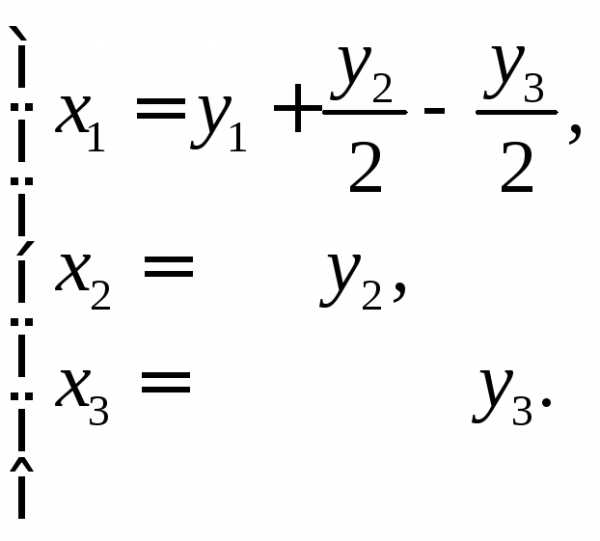
Последовательное
выполнение линейных преобразований 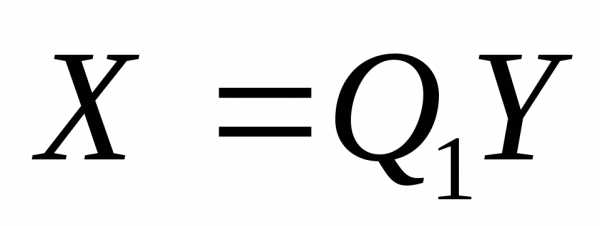 и
и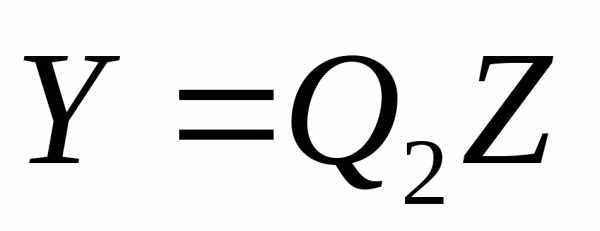 ,
где
,
где
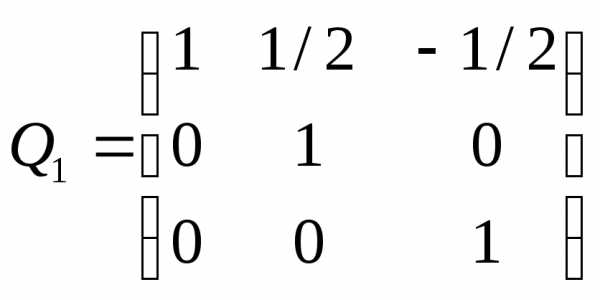 ,
, 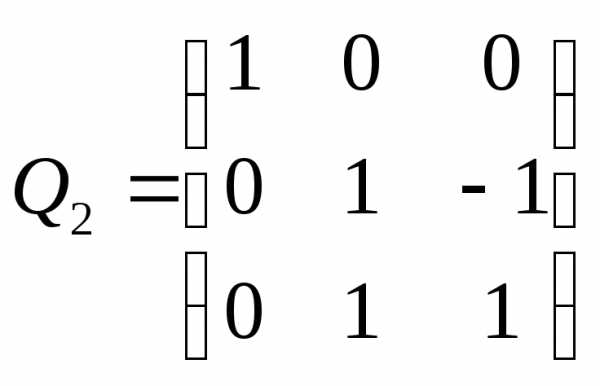
имеет матрицей
.
Линейное
преобразование неизвестных приводит
квадратичную форму  к каноническому виду (4). Переменные
к каноническому виду (4). Переменные 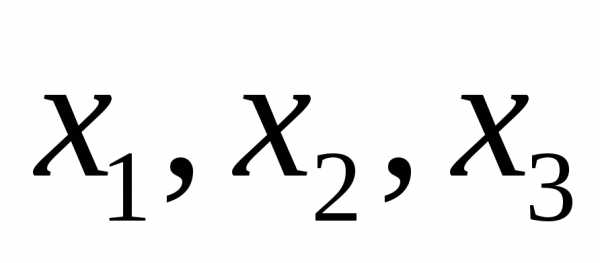 связаны с новыми переменными
связаны с новыми переменными соотношениями
соотношениями

Определение: Нормальным
видом квадратичной
формы называется сумма квадратов
неизвестных с коэффициентами « »
или «
»
или « ».
».
Определение: Квадратичная
форма называется положительно
определённой,
если при всех 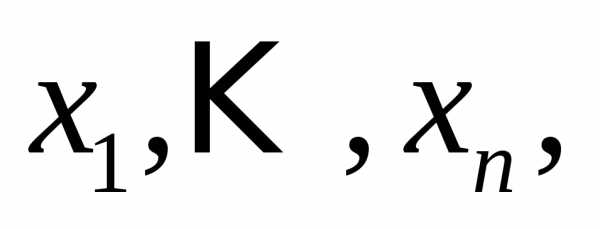 за исключениемКвадратичная форма называется отрицательно
определённой,
если при всех
за исключениемКвадратичная форма называется отрицательно
определённой,
если при всех
Теорема: Квадратичная
форма является положительно определённой
тогда и только тогда, когда  приводится к нормальному виду, содержащему n квадратов неизвестных с коэффициентами «+1»: Квадратичная
форма является отрицательно определённой
тогда и только тогда, когда
приводится к нормальному виду, содержащему n квадратов неизвестных с коэффициентами «+1»: Квадратичная
форма является отрицательно определённой
тогда и только тогда, когда  приводится к виду
приводится к виду
Определение: Пусть– квадратичная форма с матрицей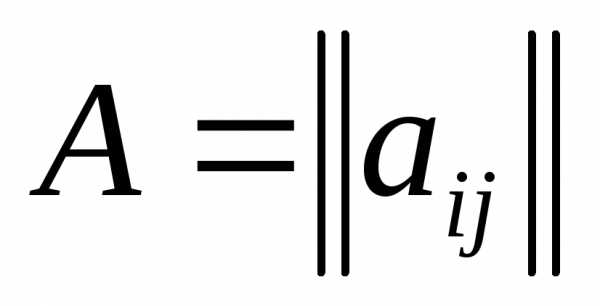 , .
Миноры
, .
Миноры 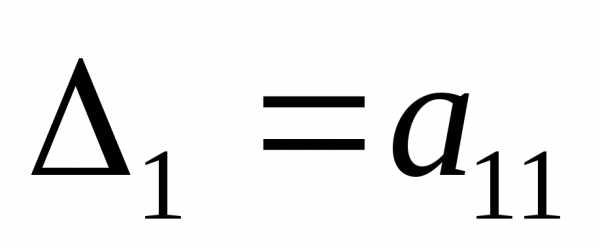 ,
, 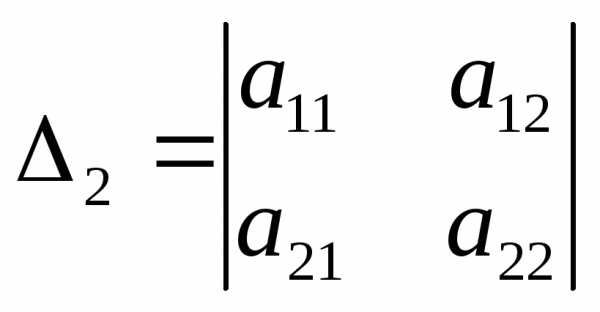 ,
,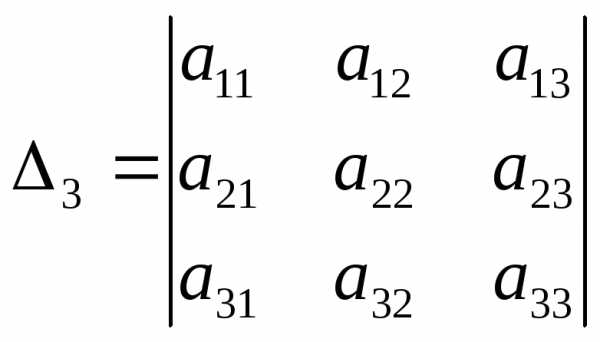 ,
…,
,
…,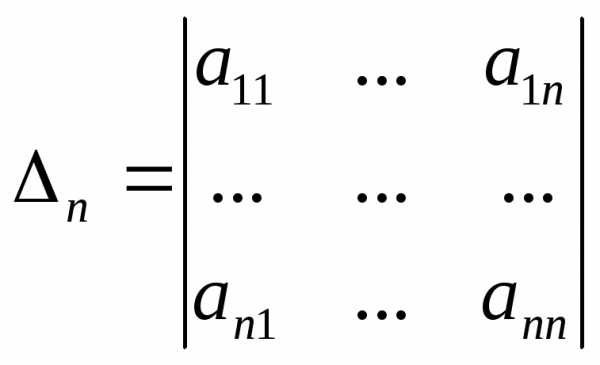 называютсяугловыми
минорами квадратичной формы
называютсяугловыми
минорами квадратичной формы 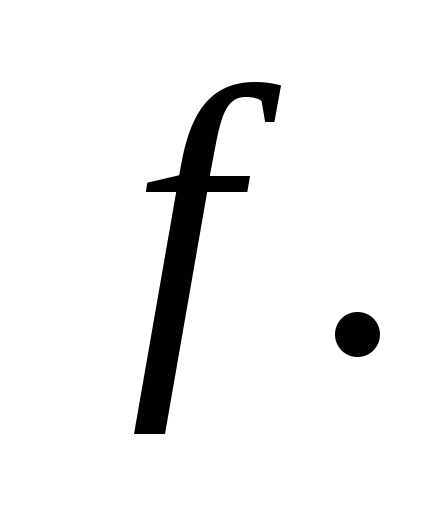
2.2. Критерий Сильвестра.
Теорема
(Критерий Сильвестра): Квадратичная
форма является положительно определённой
тогда и только тогда, когда все её угловые
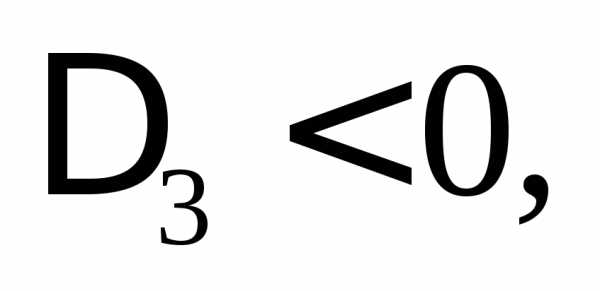
миноры строго положительны:
Квадратичная форма является отрицательно определённой
тогда и только тогда, когда её угловые
миноры удовлетворяют неравенствам: 
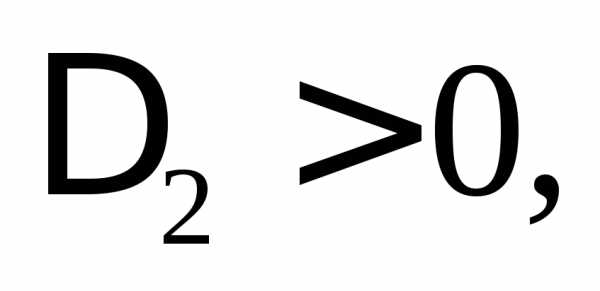
 и т.д.
и т.д.
Определение: Будем называть линейное преобразование
переменных 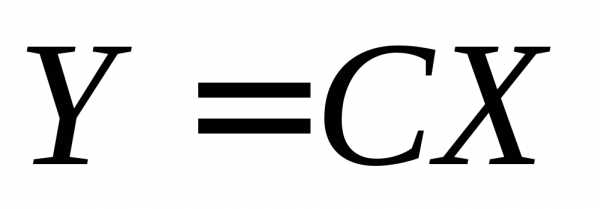 ортогональным,
если матрица
ортогональным,
если матрица  ортогональная,
т.е.
ортогональная,
т.е.
Сформулируем алгоритм приведения квадратичной формы к каноническому виду ортогональным преобразованием:
Находим собственные значения линейного оператора, решая характеристическое уравнение
Для каждого собственного значения находим собственные векторы, решая систему линейных уравнений (У этой системы мы должны найти фундаментальную систему решений).
Если собственное значение
 имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применитьпроцесс
ортогонализации Шмидта (изучите самостоятельно, читайте: Ржавинская Е. В., Олейник Т. А., Соколова
Т. В. Лекции по линейной алгебре и
аналитической геометрии, М., МИЭТ.
2007. )
имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применитьпроцесс
ортогонализации Шмидта (изучите самостоятельно, читайте: Ржавинская Е. В., Олейник Т. А., Соколова
Т. В. Лекции по линейной алгебре и
аналитической геометрии, М., МИЭТ.
2007. )Нормируем найденные собственные векторы, т.е. каждый вектор делим на его длину.
Записываем канонический вид квадратичной формы и преобразование координат, приводящее её к этому виду.
Пример: Привести данную квадратичную форму к каноническому виду ортогональным преобразованием координат:
Решение: Составим матрицу этой квадратичной формы:
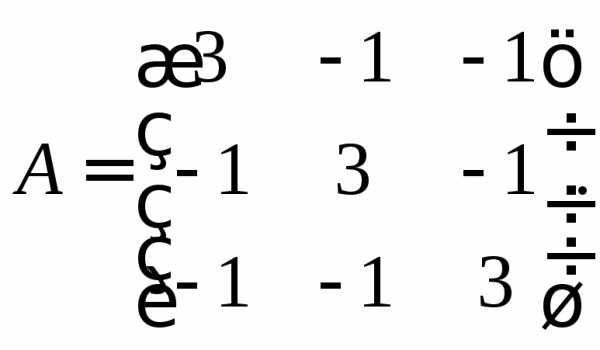
Составим характеристическое уравнение:
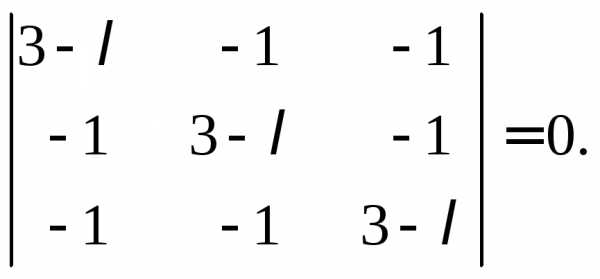
Отсюда
получаем:
Корни характеристического уравнения: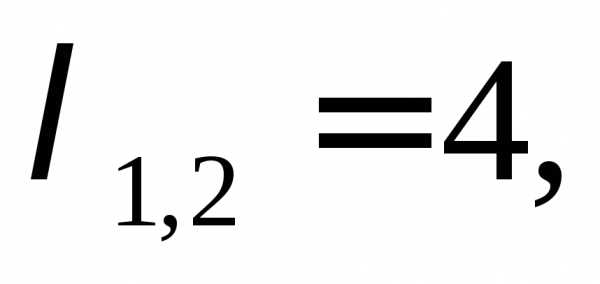
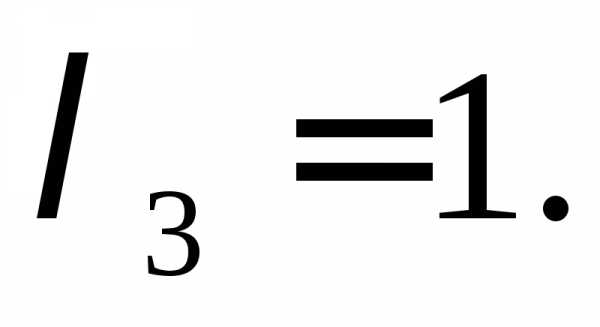
Для 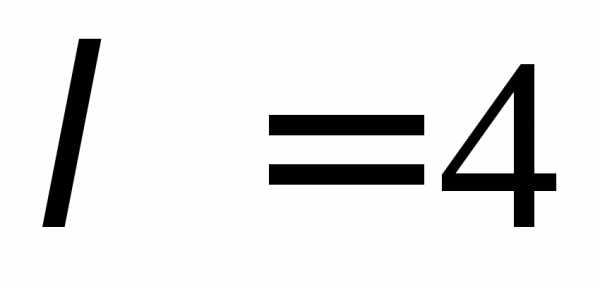 система уравнений, из которой находятся
собственные векторы, выглядит так:
система уравнений, из которой находятся
собственные векторы, выглядит так:
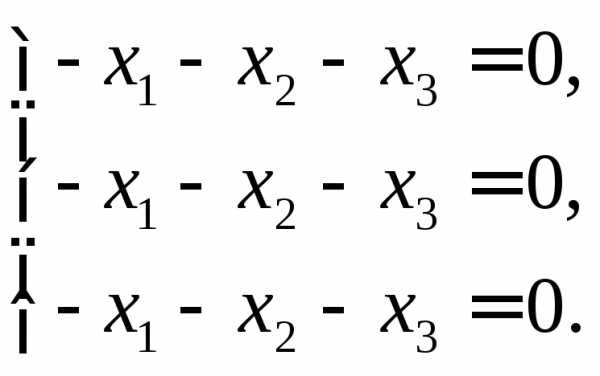
Её
фундаментальная система решений:
Эти векторы не ортогональны друг другу,
поэтому применим к нимпроцесс
ортогонализации Шмидта.
Положим 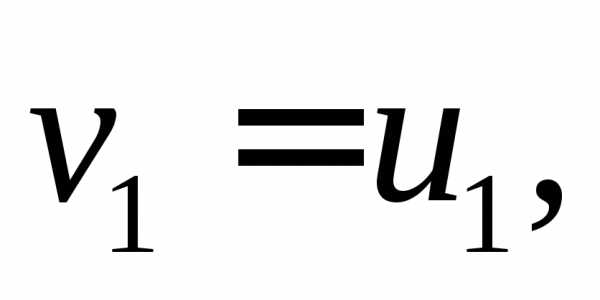 и подберём
и подберём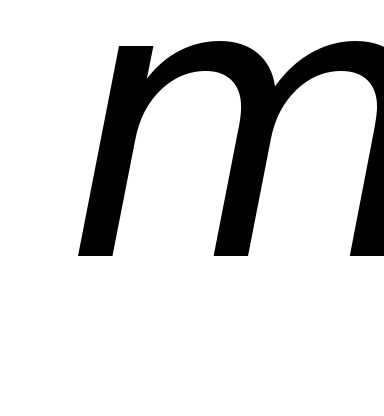 так, чтобы было выполнено условие
так, чтобы было выполнено условие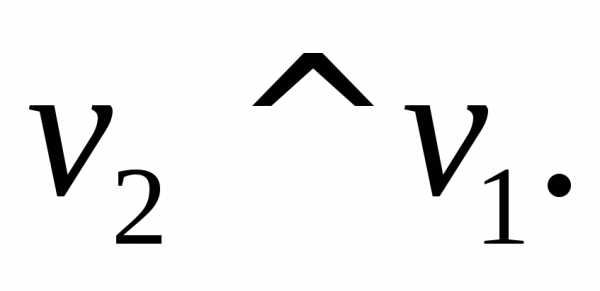 Имеем:
Имеем: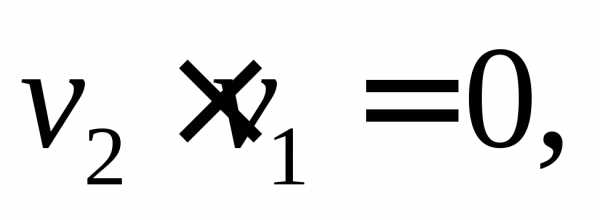 т.е.
т.е.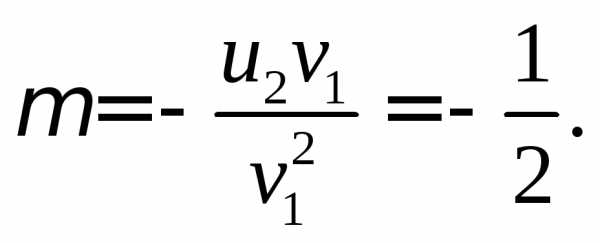 Следовательно,
Следовательно,
Запишем
теперь систему уравнений для 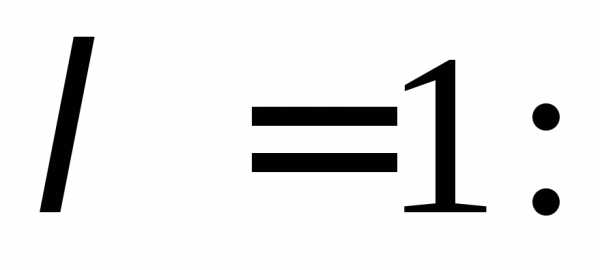
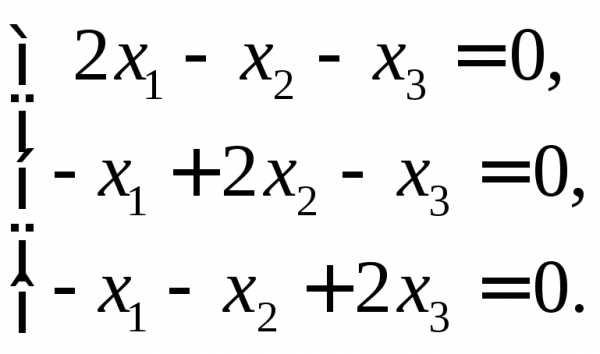
Её
ф.с.р. состоит из одного вектора:
Этот
вектор ортогонален векторам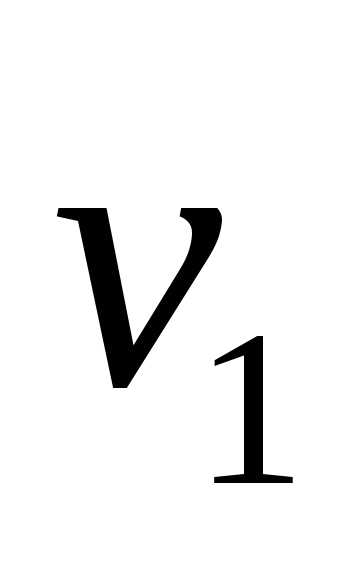 и
и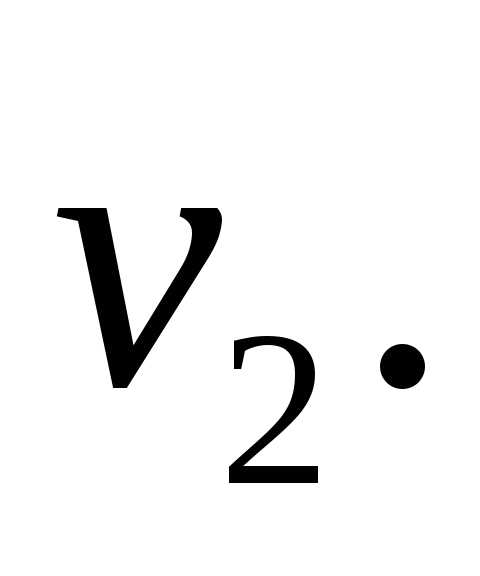
Пронормируем
векторы  разделив каждый вектор на его длину.
Получим ортонормированный базис из
собственных векторов:
разделив каждый вектор на его длину.
Получим ортонормированный базис из
собственных векторов: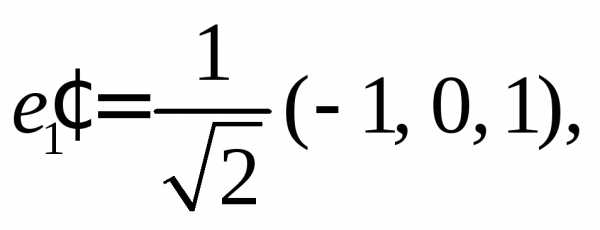
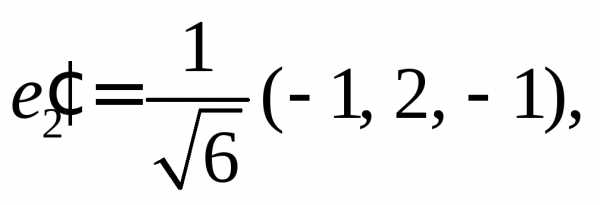
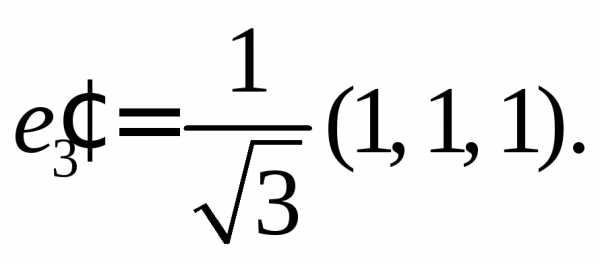
Матрица
перехода от исходного базиса
к новому базису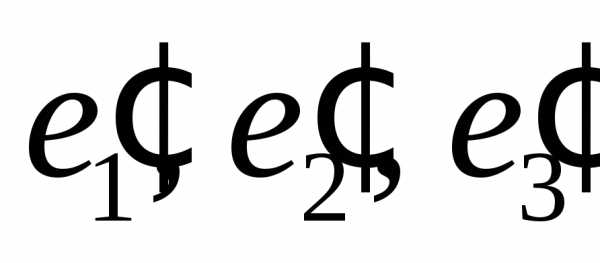 равна:
равна:
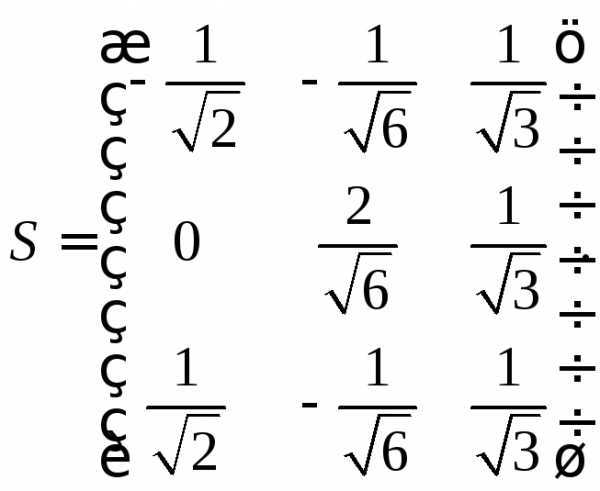
В новых координатах квадратичная форма будет иметь вид Старые координаты выражаются через новые следующим образом:
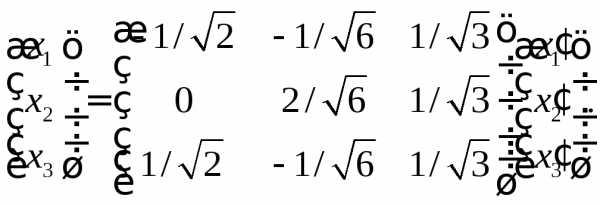
Обратные формулы:
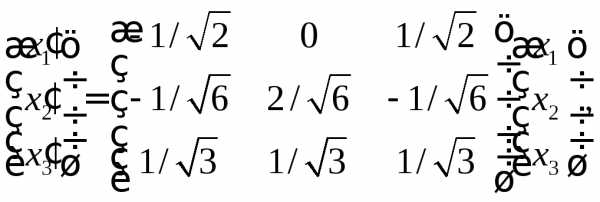
т.е.

studfiles.net
Квадратичные формы
Квадратичной формойf(х1, х2,…,хn) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом:f(х1, х2,…,хn) =(aij=aji).
Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическаяматрица (т.е. матрица, симметричная относительно главной диагонали,aij=aji).
В матричной записи квадратичная форма имеет вид f(Х) = ХТAX, где
. В самом деле
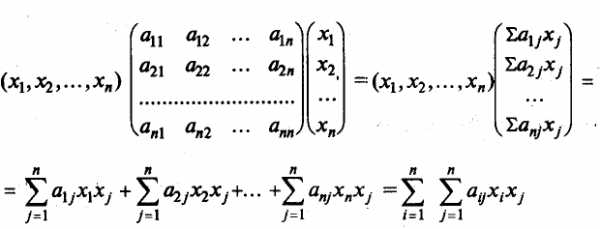
Например, запишем в матричном виде квадратичную форму .
Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С — невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = ХTАХ = (CY)TA(CY) = (YTCT)A(CY) =YT(CTAC)Y.
Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А*=CTAC.
Например, найдем квадратичную форму f(y1, y2), полученную из квадратичной формыf(х1, х2) = 2x12+ 4х1х2— 3х22линейным преобразованием .
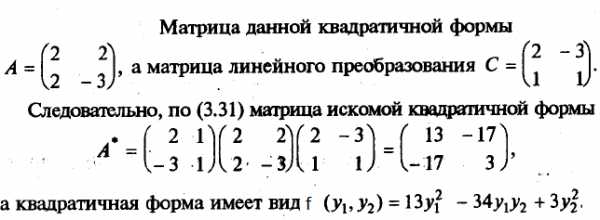
Квадратичная форма называется канонической(имеетканонический вид), если все ее коэффициентыaij= 0 приi≠j, т.е.f(х1, х2,…,хn) =a11x12+a22x22+ … +annxn2=.
Ее матрица является диагональной.
Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.
Например, приведем к каноническому виду квадратичную форму f(х1, х2,х3) = 2x12+ 4х1х2— 3х22– х2х3.
Для этого вначале выделим полный квадрат при переменной х1:
f(х1, х2, х3) = 2(x12+ 2х1х2+ х22) — 2х22— 3х22– х2х3= 2(x1+ х2)2— 5х22– х2х3.
Теперь выделяем полный квадрат при переменной х2:
f(х1, х2, х3) = 2(x1+ х2)2– 5(х22– 2* х2*(1/10)х3+ (1/100)х32) — (5/100)х32= = 2(x1+ х2)2– 5(х2– (1/10)х3)2— (1/20)х32.
Тогда невырожденное линейное преобразование y1= x1+ х2,y2= х2– (1/10)х3иy3= x3приводит данную квадратичную форму к каноническому видуf(y1,y2,y3) = 2y12— 5y22— (1/20)y32.
Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами1). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называютзаконом инерции квадратичных форм.
Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х2:f(х1, х2,х3) = 2x12+ 4х1х2— 3х22– х2х3= -3х22– х2х3+ 4х1х2+ 2x12= -3(х22– — 2* х2((1/6) х3+ (2/3)х1) +((1/6) х3+ (2/3)х1) 2) – 3((1/6) х3+ (2/3)х1) 2+ 2x12= = -3(х2– (1/6) х3— (2/3)х1)2– 3((1/6) х3+ (2/3)х1)2+ 2x12=f(y1,y2,y3) = -3y12— -3y22+ 2y32, гдеy1= — (2/3)х1+ х2– (1/6) х3,y2= (2/3)х1+ (1/6) х3иy3= x1. Здесь положительный коэффициент 2 приy3и два отрицательных коэффициента (-3) приy1иy2(а при использовании другого способа мы получили положительный коэффициент 2 приy1и два отрицательных – (-5) приy2и (-1/20) приy3).
Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичную форму f(X) называютположительно(отрицательно)определенной, если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).
Например, квадратичная форма f1(X) = x12+ х22— положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf2(X) = -x12+ 2x1х2— х22— отрицательно определенная, т.к. представляет ее можно представить в видеf2(X) = -(x1— х2)2.
В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).
Теорема. Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).
Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.
Главным (угловым) миноромk-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().
Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.
Например, исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2+ 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(3 -) – 4 = (6 — 2- 3+2) – 4 =2— 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – положительно определенная.
Способ 2. Главный минор первого порядка матрицы А 1=a11= 2 > 0. Главный минор второго порядка2== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.
Исследуем на знакоопределенность другую квадратичную форму, f(х1, х2) = -2x12+ 4х1х2— 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+2) – 4 =2+ 5+ 2 = 0;D= 25 – 8 = 17;. Следовательно, квадратичная форма – отрицательно определенная.
Способ 2. Главный минор первого порядка матрицы А 1=a11= = -2 < 0. Главный минор второго порядка2== 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).
И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х1, х2) = 2x12+ 4х1х2— 3х22.
Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид= (2 -)* *(-3 -) – 4 = (-6 — 2+ 3+2) – 4 =2+- 10 = 0;D= 1 + 40 = 41;. Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).
Способ 2. Главный минор первого порядка матрицы А 1=a11= 2 > 0. Главный минор второго порядка2== -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).
studfiles.net
§6. Квадратичные формы и их применения
1. Квадратичной формой 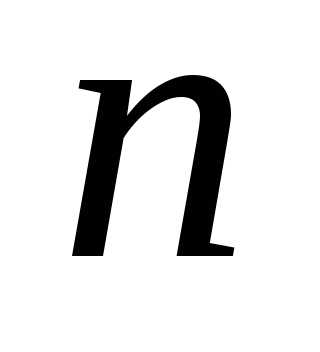 переменных,принимающих
числовые значения , называется числовая
функция вида
переменных,принимающих
числовые значения , называется числовая
функция вида
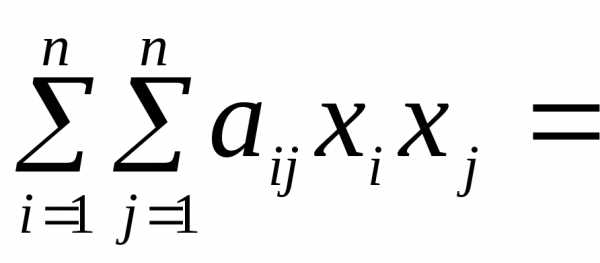 ,
,
где 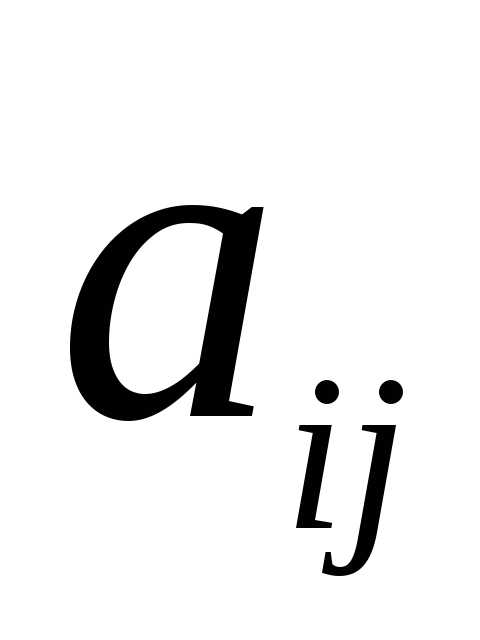 —
числа, называемые коэффициентами
квадратичной формы.
—
числа, называемые коэффициентами
квадратичной формы.
Матрицей
квадратичной формы  переменных,
называется симметрическая матрица
порядка
переменных,
называется симметрическая матрица
порядка ,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных, а каждый недиагональный
элемент, расположенный в
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных, а каждый недиагональный
элемент, расположенный в ой
строке
ой
строке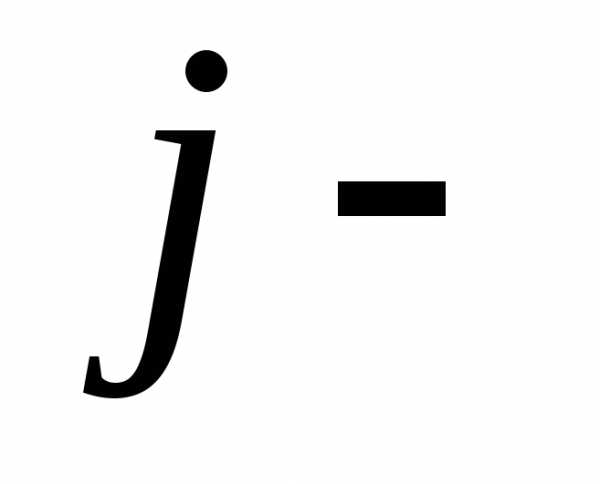 ом
столбце, равен половине коэффициента
при
ом
столбце, равен половине коэффициента
при 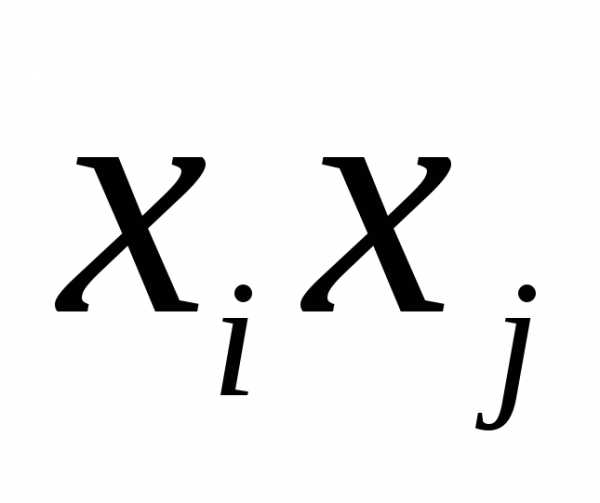 в квадратичной форме.
в квадратичной форме.
Рангом
квадратичной формы называется ранг её матрицы. Квадратичная
форма может быть записана в матричном
виде где 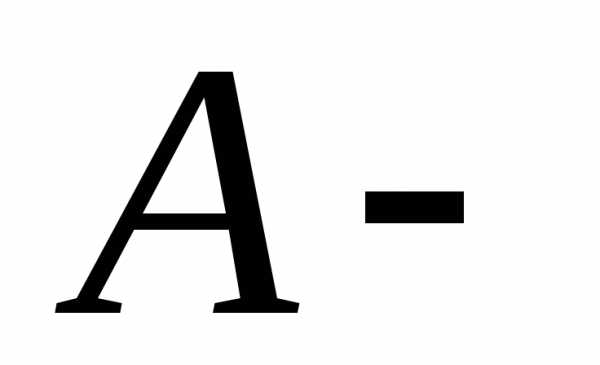 матрица
квадратичной формы и
.
матрица
квадратичной формы и
.
Квадратичная
форма называется канонической (имеет канонический вид), если коэффициенты 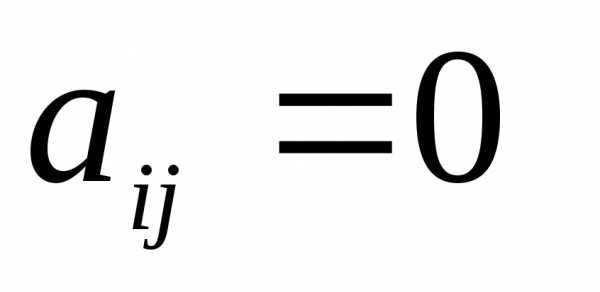 при
при 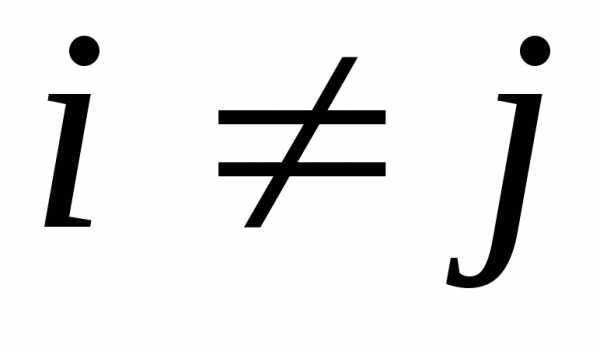 ,
то есть, если матрица квадратичной формы
диагональная и следовательно
,
то есть, если матрица квадратичной формы
диагональная и следовательно
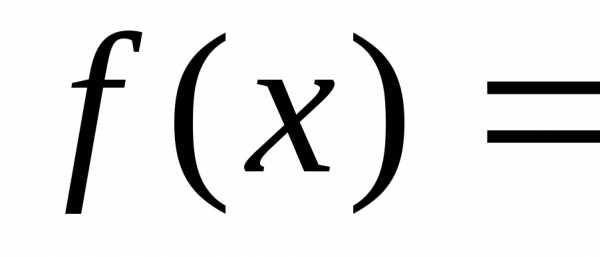 .,
.,
где
не все коэффициенты  равны нулю.
равны нулю.
ТЕОРЕМА (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.
Нормальным
видом квадратичной формы называется такой канонический вид, в
котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны  .
.
Квадратичная
форма 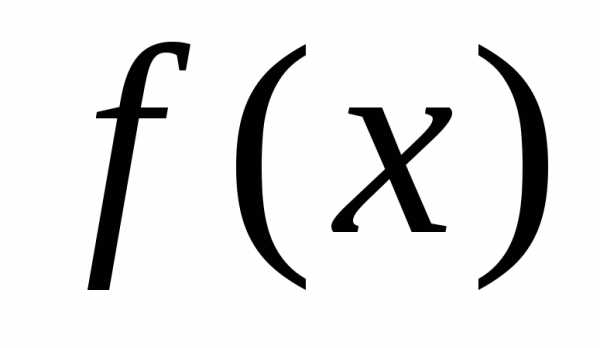 называется положительно (отрицательно)
определённой, если при всех
называется положительно (отрицательно)
определённой, если при всех 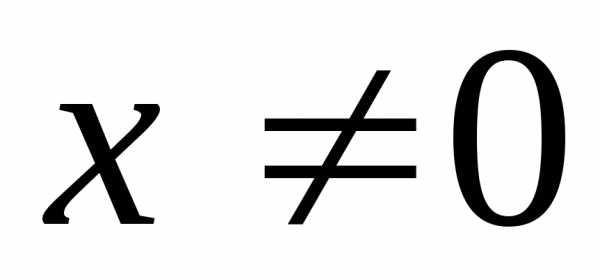 и положительно (отрицательно)
полуопределённой, если при всех
и положительно (отрицательно)
полуопределённой, если при всех 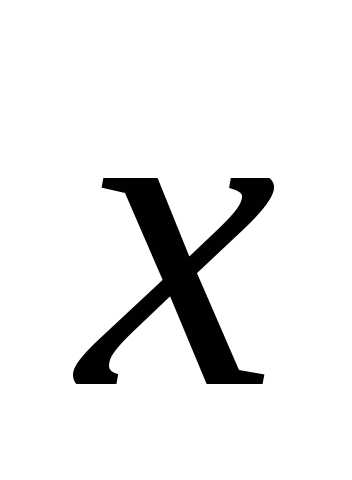 .
.
ТЕОРЕМА (критерий
Сильвестра). Для того чтобы квадратичная форма 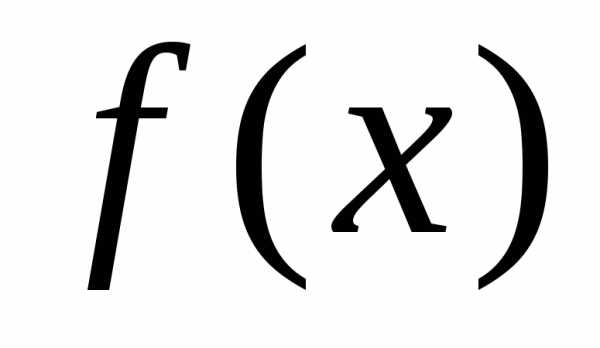 была положительно определённой,
необходимо и достаточно чтобы все
угловые миноры матрицы квадратичной
формы были положительны, то есть, чтобы
была положительно определённой,
необходимо и достаточно чтобы все
угловые миноры матрицы квадратичной
формы были положительны, то есть, чтобы
Здесь -угловые миноры матрицы квадратичной формы.
Следствие
Для
того чтобы квадратичная форма 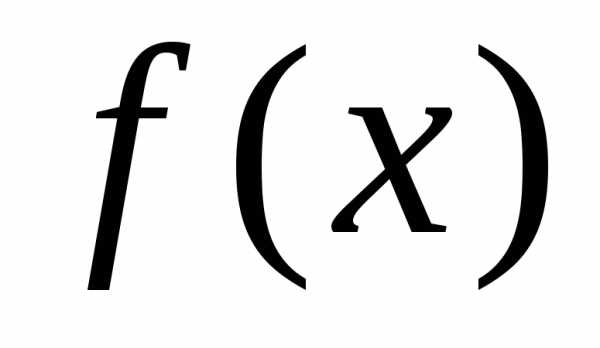 была отрицательно определённой,
необходимо и достаточно, чтобы знаки
угловых миноров матрицы квадратичной
формы чередовались следующим образом:
была отрицательно определённой,
необходимо и достаточно, чтобы знаки
угловых миноров матрицы квадратичной
формы чередовались следующим образом:
Типовые примеры
1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование
.
►Следуя
алгоритму метода Лагранжа, выделим
вначале в квадратичной форме все члены,
содержащие 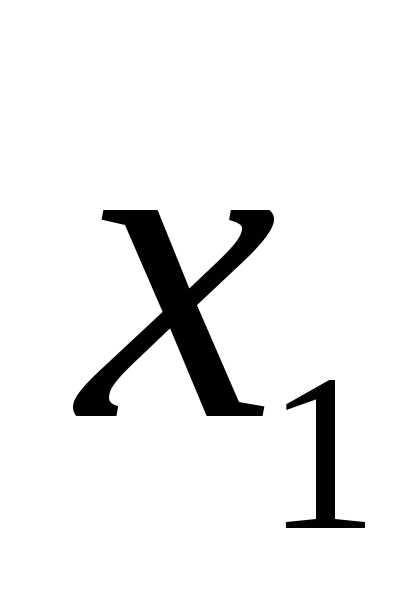 ,
и дополним их до полного квадрата:
,
и дополним их до полного квадрата:
.
Сделаем в этом выражении замену и подставим его в квадратичную форму. Получим:
.
Далее
выделим в  члены, содержащие
члены, содержащие 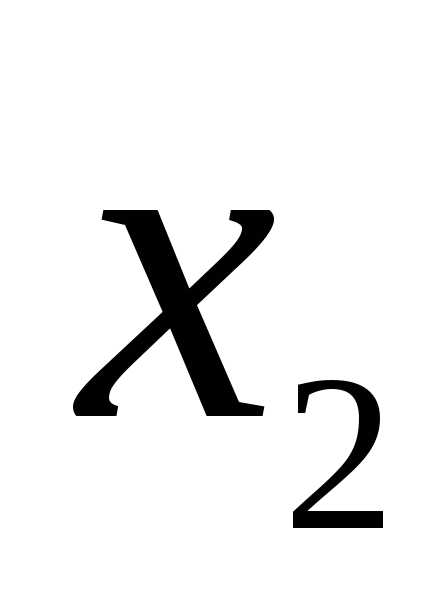 и проделаем с ними аналогичную процедуру:
и проделаем с ними аналогичную процедуру:
Если
положить
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также 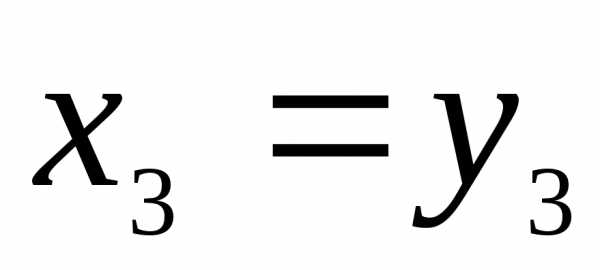 ,
тогда
,
тогда
канонический вид квадратичной формы есть
.
Соответствующее
преобразование от переменных 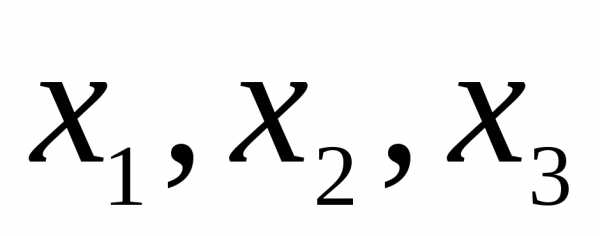 к переменным
к переменным 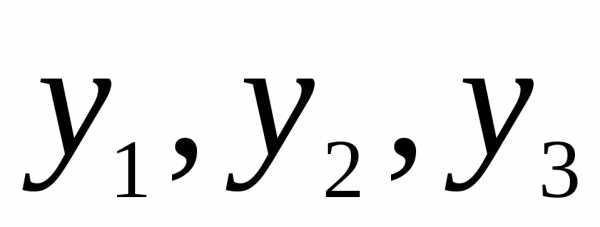 имеет вид:
имеет вид:
.◄
2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:
.
►В
исходном базисе 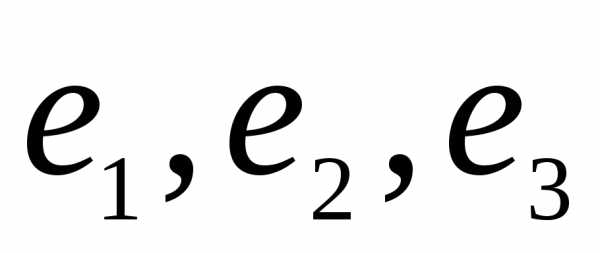 матрица оператора, соответствующая
данной квадратичной форме, есть
матрица оператора, соответствующая
данной квадратичной форме, есть
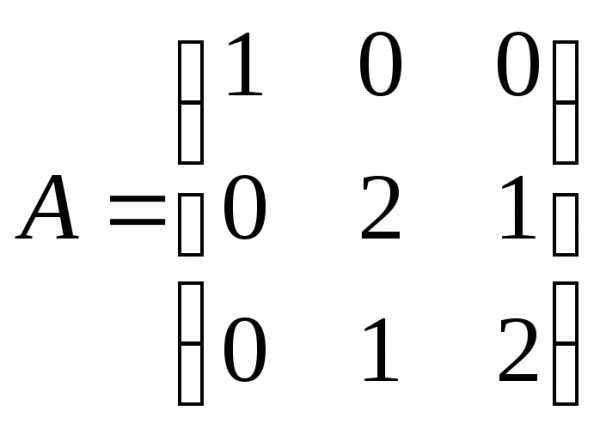 .
.
Эта
матрица будет определять квадратичную
форму канонического вида в ортонормированном
базисе 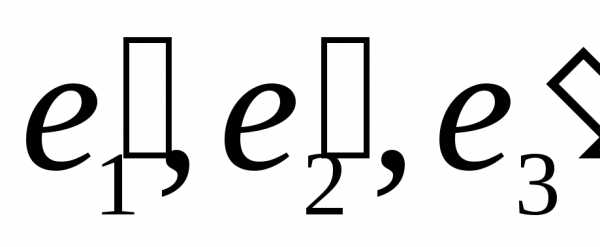 ,
составленном из собственных векторов
матрицы
,
составленном из собственных векторов
матрицы  .
Найдем их. Характеристическое уравнение
для матрицы
.
Найдем их. Характеристическое уравнение
для матрицы  имеет вид
имеет вид
.
Откуда следует
и .
Как известно собственные векторы матрицы находятся из уравнений
.
Для
случая  имеем:
имеем:
 .
.
Ранг
матрицы этой системы уравнений
(относительно  )
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.
Как
видно из данной системы, величина  принимает произвольные значения, а
величины
принимает произвольные значения, а
величины 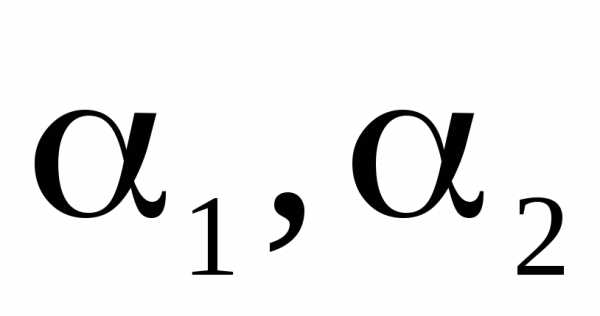 связаны соотношением
.
В качестве собственных можно выбрать,
например, векторы
связаны соотношением
.
В качестве собственных можно выбрать,
например, векторы
Эти
векторы ортогональны: 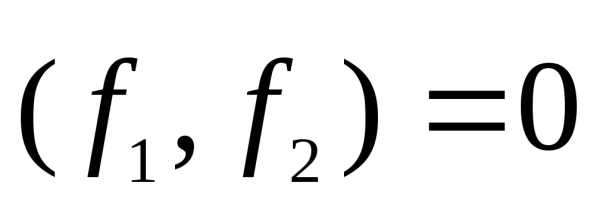 (если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор
(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор 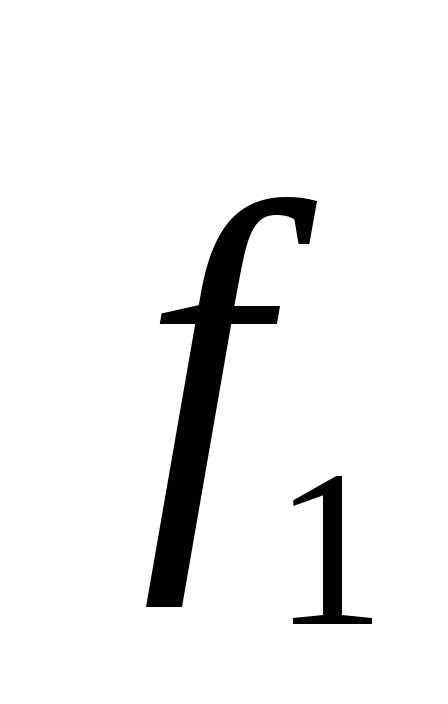 к тому же и нормирован. Откуда следует
—
к тому же и нормирован. Откуда следует
— 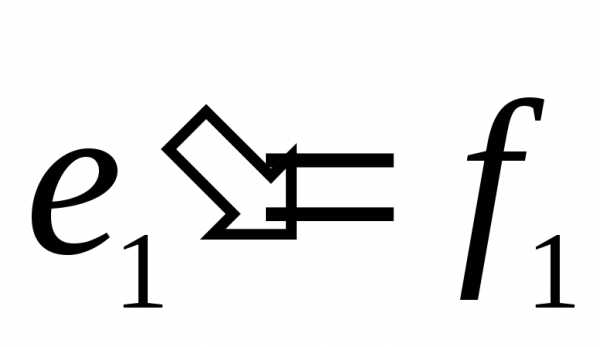 .
Нормируем теперь вектор
.
Нормируем теперь вектор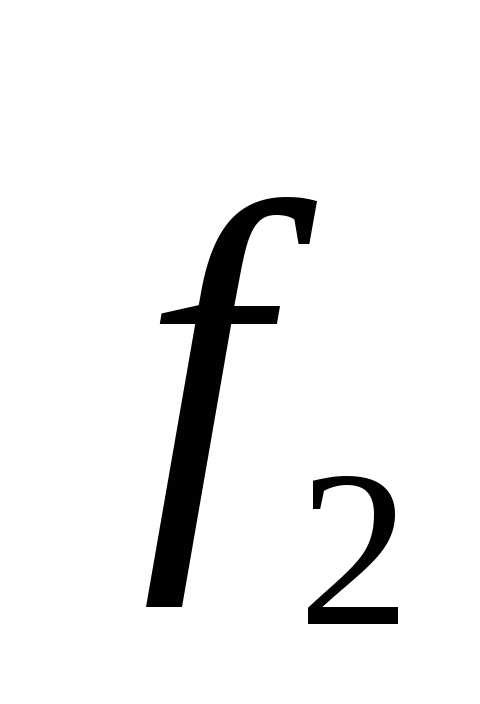 :
:
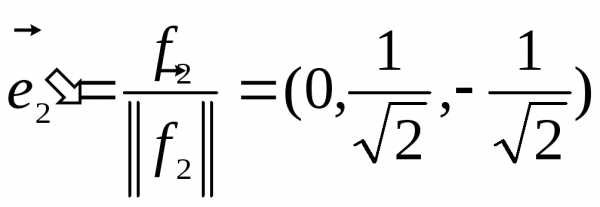 .
.
Для
случая  уравнение, определяющее собственный
вектор есть
уравнение, определяющее собственный
вектор есть

 .
.
Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например, Отнормируем этот вектор: 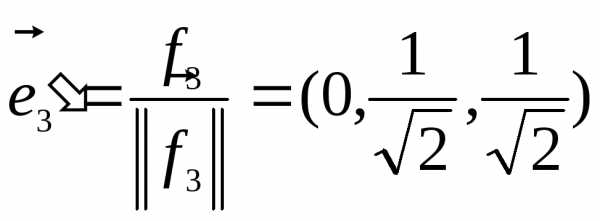 .
.
Теперь можно составить искомую матрицу ортогонального преобразования:
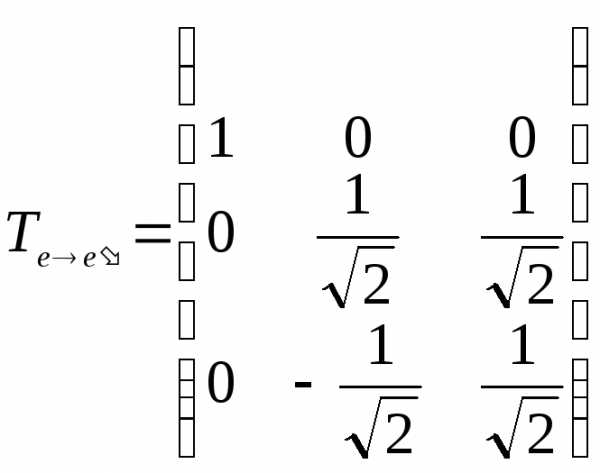 .
.
Исходная квадратичная форма будет иметь следующий канонический вид
.
При
этом переменные 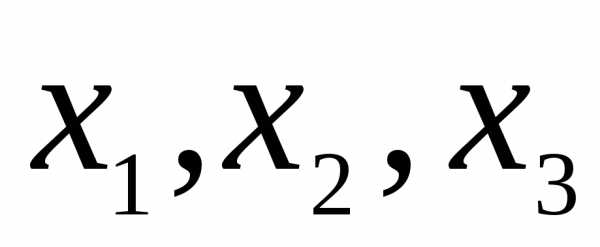 связаны с переменными
связаны с переменными  соотношением
соотношением
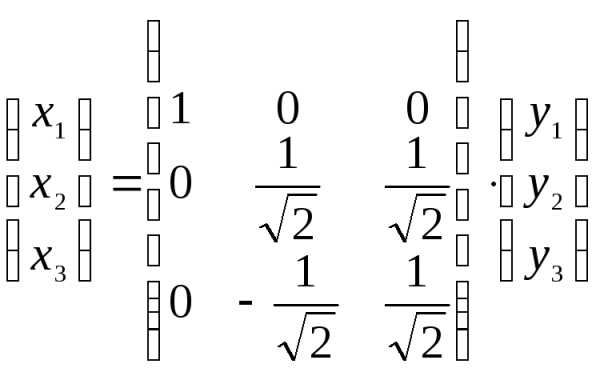 или
или
.◄
3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду
.
►Выделим
в этом выражении квадратичную форму  .
Это три первых слагаемых уравнения
.
.
Это три первых слагаемых уравнения
.
Матрица
квадратичной формы равна 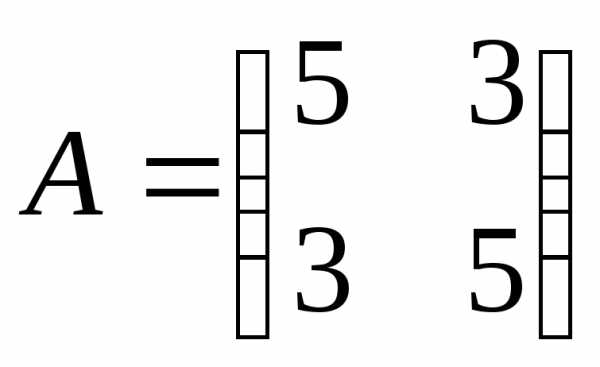 .
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид
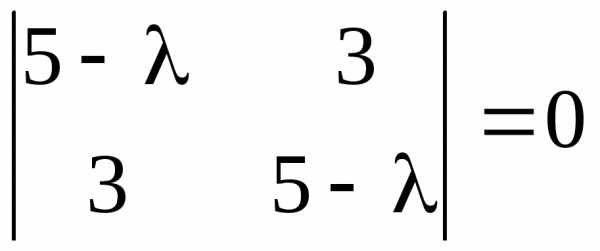 .
.
Его
корни таковы:
.
Найдём теперь собственные векторы,
соответствующие этим корням и ортонормируем
их. Для вектора
,
соответствующего 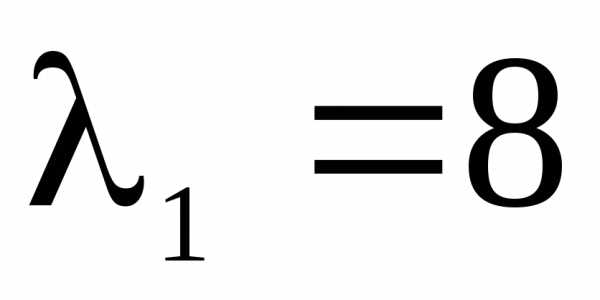 ,
имеем
,
имеем
В
итоге собственный вектор, соответствующий 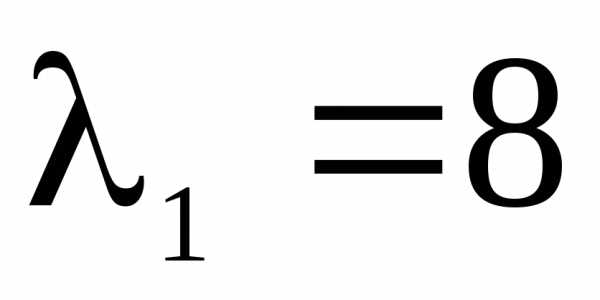 ,
можно выбрать в виде
,
можно выбрать в виде
 .
.
Аналогичная процедура для собственного вектора даёт:
Откуда:
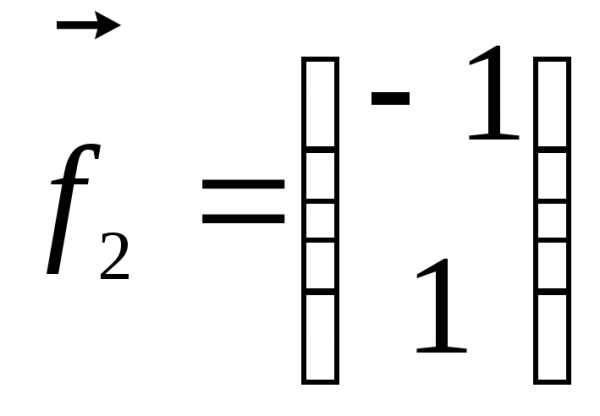 .
.
После нормировки полученных векторов имеем:
.
Эти векторы представляют собой ортонормированный базис новой системы координат. Матрица ортогонального оператора, приводящего квадратичную форму к каноническому виду , есть
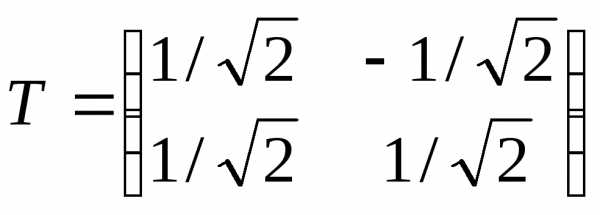
Связь
старых 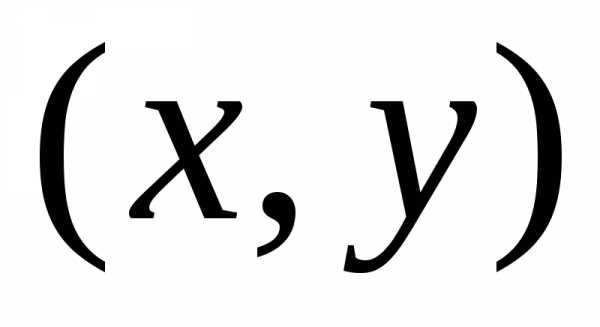 и новых
и новых  координат определяется соотношением
.
координат определяется соотношением
.
Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду
.
Это есть каноническое уравнение эллипса
в системе координат  ,которая
получается из исходной её поворотом на
угол
,которая
получается из исходной её поворотом на
угол 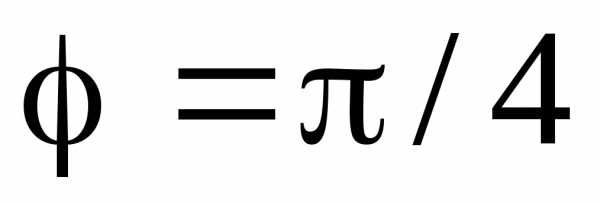 и
переносом начала координат в точку
.◄
и
переносом начала координат в точку
.◄
79
studfiles.net

 существует такая ортогональная матрица
Q, что матрица
существует такая ортогональная матрица
Q, что матрица  является диагональной.
является диагональной. имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применитьпроцесс
ортогонализации Шмидта (изучите самостоятельно, читайте: Ржавинская Е. В., Олейник Т. А., Соколова
Т. В. Лекции по линейной алгебре и
аналитической геометрии, М., МИЭТ.
2007. )
имеет кратность, большую 1 (в
характеристическом уравнении), то
векторы из ф.с.р. могут оказаться не
ортогональными друг другу – в этом
случае к ним надо применитьпроцесс
ортогонализации Шмидта (изучите самостоятельно, читайте: Ржавинская Е. В., Олейник Т. А., Соколова
Т. В. Лекции по линейной алгебре и
аналитической геометрии, М., МИЭТ.
2007. )