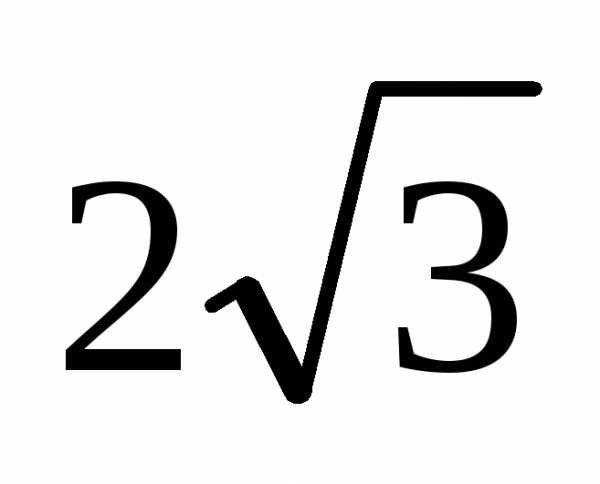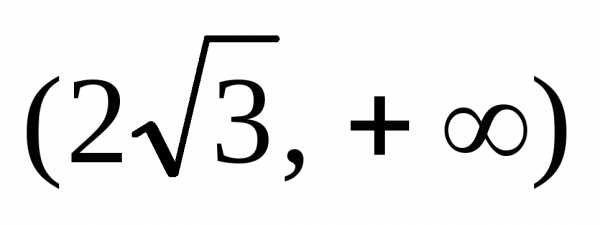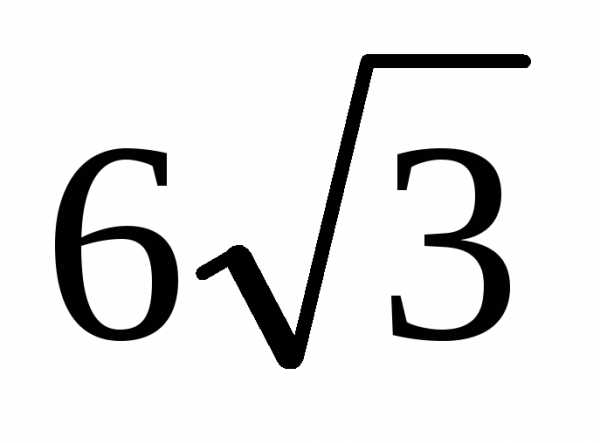Как найти вертикальную асимптоту функции
Разберемся как найти вертикальную асимптоту функции.
Вертикальная асимптота для функции у(x) — это такая прямая, которая проходит параллельно оси Оу и к которой неограниченно близко приближается функция у(x), когда асимптота стремится к бесконечности.
Вертикальная асимптота имеет уравнение вида:
Здесь const— какое-то постоянное число.
Рассмотрим условие существования вертикальной асимптоты, которая будет существовать в случае, если хоть один из следующих пределов функции у(х) в точке будет равен или :
или .
Заметим, что рассмотренные выше пределы также используют для того, чтобы проверить будет ли точка точкой разрыва функции y(x).
Именно поэтому вертикальные асимптоты функции ищут лишь в точках разрыва функции.
Пример.
Найдем вертикальные асимптоты функции .
Решение.
Сначала нужно определить точки разрыва:
Находим передел справа и предел слева в точке :
Получили, что прямая — вертикальная асимптота заданной функции.
Находим передел справа и предел слева в точке :
Получили, что и прямая — вертикальная асимптота заданной функции.
ru.solverbook.com
Как найти асимптоты функции
Функция может иметь асимптоты трех видов: горизонтальные (параллельны оси Ох), вертикальные (параллельны оси Оу) и наклонные (проходят под некоторым углом к оси Ох, как и к оси Оу).
Функция может асимптот может не иметь вообще, может иметь одну какую-то асимптоту, а может иметь и несколько разных или одинакового вида асимптот.
Рассмотрим на примере как найти асимптоты функции.
Пример.
Найти все виды асимптот функции .
1) Найдем наклонные асимптоты:
Уравнение наклонных асимптот имеет вид . Согласно определению асимптоты:
Найдем коэффициент k:
Найдем коэффициент b:
Получили уравнение наклонной асимптоты:
2) Найдем вертикальные асимптоты.
Сначала нужно определить точки разрыва:
Находим передел справа и предел слева в точке :
Получили, что прямая — вертикальная асимптота заданной функции.
Находим передел справа и предел слева в точке :
Получили, что и прямая — вертикальная асимптота заданной функции.
ru.solverbook.com
1.13. Асимптоты кривой
Литература: [3], гл. V, § 10
[5], Ч.1, гл. 6, § 6.5
Прямая называется асимптотой кривой y = f (x), если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность от начала координат (рис. 1.7).
Рис. 1.7
Различают вертикальные и наклонные асимптоты. Вертикальная асимптота имеет уравнение вида x = x0 и является прямой, параллельной оси Оy. Наклонная асимптота имеет уравнение вида y = k x + b. В частном случае при k = 0 асимптота называется горизонтальной, так как ее уравнение y = b есть прямая, параллельная оси Ох.
Вертикальные асимптоты.
Пусть дана кривая y = f (x). Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).
Если, например,
и ,
то прямая x = x0 ─ вертикальная асимптота кривой y = f (x) (рис. 1.8).
Наклонные и горизонтальные асимптоты.
Пусть задана кривая y = f (x).
Для нахождения наклонной асимптоты,
уравнение которой y = k x + b, находят коэффициенты k и b,
вычисляя пределы: 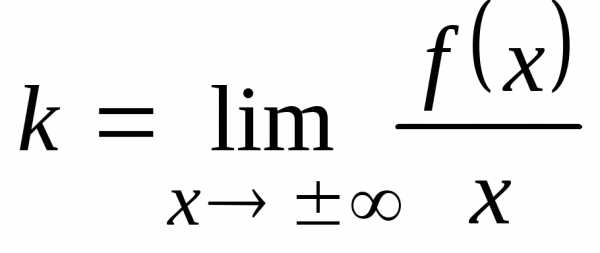 ,.
Эти пределы вычисляются отдельно для
случаеви.
Если хотя бы один из пределов для
вычисленияk и b равен ∞ или не существует, то кривая
наклонных и горизонтальных асимптот
не имеет.
,.
Эти пределы вычисляются отдельно для
случаеви.
Если хотя бы один из пределов для
вычисленияk и b равен ∞ или не существует, то кривая
наклонных и горизонтальных асимптот
не имеет.
В частном случае, когда k = 0, а b ─ конечное число, кривая имеет горизонтальную асимптоту, уравнение которой y = b.
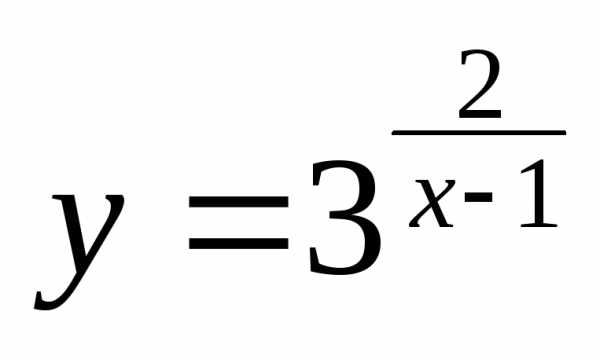 .
.
Решение. Функция 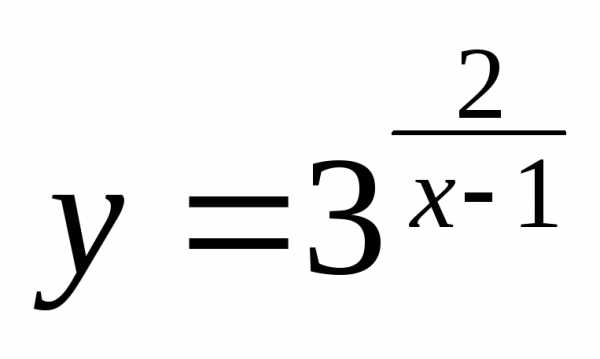 определена на всем множестве действительных
чиселR,
кроме точки x = 1. Определим характер разрыва, для чего
вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):
определена на всем множестве действительных
чиселR,
кроме точки x = 1. Определим характер разрыва, для чего
вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):
, .
Так как один из пределов бесконечен, то x = 1 является точкой разрыва второго рода, и, следовательно, кривая имеет вертикальную асимптоту x = 1.
Определим, имеет ли кривая наклонную или горизонтальную асимптоту. Для этого вычисляем соответствующие пределы:
, Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).
С
Рис. 1.9
хематический график функции представлен на рис. 1.9.1.14. Схема полного исследования функции и построение ее графика
Литература: [3], гл. V, § 11
[5], Ч.1, гл. 6, § 6.6
1. Находим область определения функции.
2. Устанавливаем четность, нечетность функции, периодичность. Находим характерные точки, например, точки пересечения с осями координат.
3.Находим точки разрыва функции, определяем их характер. При наличии точек разрыва второго рода (точек бесконечного разрыва) устанавливаем наличие вертикальных асимптот графика функции.
4. Находим производную функции, критические точки, промежутки монотонности, точки экстремума и значения функции в этих точках.
5. Находим вторую производную функции, интервалы выпуклости и вогнутости кривой и точки перегиба графика функции.
6.Устанавливаем наличие у исследуемой кривой наклонных и горизонтальных асимптот.
Замечание. Если функция является четной или нечетной, то исследование проводят не на всей числовой оси, а на промежутке [0, +∞). Затем график продолжают симметрично относительно оси ординат на промежуток (-∞, 0), если функция четная, и относительно центра системы координат, если функция нечетная.
Если функция периодическая, то ее график строят для одного периода, а затем периодически продолжают на всю числовую ось.
Пример.
Провести полное исследование функции 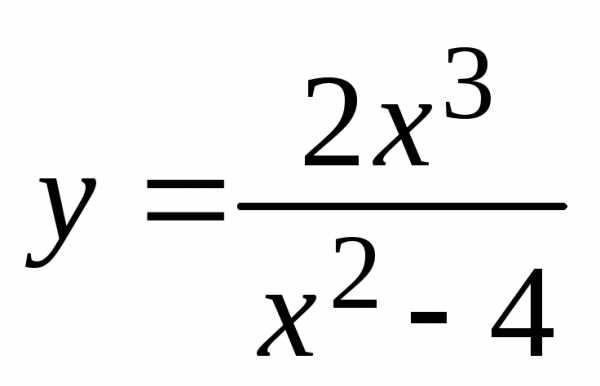 и построить ее график.
и построить ее график.
Решение.
1. Функция определена и непрерывна на всей числовой оси, кроме точек x = ± 2.
2. Функция нечетная, так как для нее выполняется условие . Поэтому достаточно провести исследование на промежутке [0, +∞).
3. В промежутке [0, +∞) имеется одна точка разрыва x = 2. Исследуем характер точки разрыва, для чего вычислим следующие пределы:
,
Так как односторонние пределы бесконечные, то прямая x = 2 является вертикальной асимптотой.
4. Находим первую производную:
.
Находим критические
точки на промежутке [0, +∞): 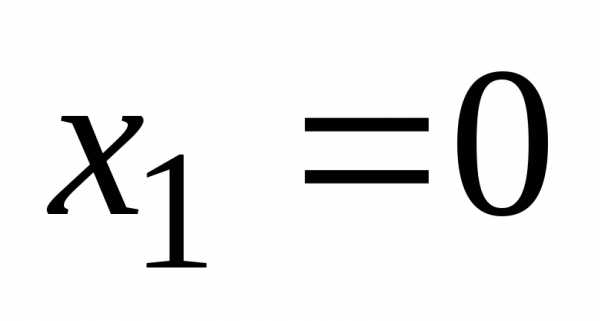 ,.
В точке
,.
В точке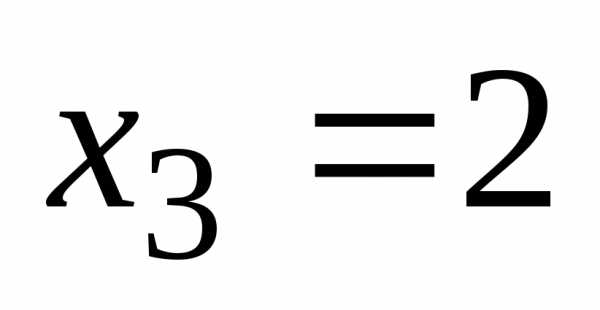 производная не существует, но эта точка
не является критической, так как функция
в ней не определена.
производная не существует, но эта точка
не является критической, так как функция
в ней не определена.
5. Находим вторую производную:
.
Вторая производная на промежутке [0, +∞) обращается в ноль в точке x1 = 0 и не существует в точке x3 = 2, которая не входит в область определения функции.
По полученным данным строим таблицу:
x | 0 | (0, 2) | 2 | (2, |
|
|
| 0 | − | Не существует | – | 0 | + |
| 0 | − | Не существует | + | + | + |
y | 0 | Не существует | min
|
В первой строке таблицы указаны интервалы, на которые критические точки и точки, где вторая производная равна нулю или не существует, разбивают промежуток [0, +∞). Во второй строке указан знак первой производной в этих интервалах, в третьей − знак второй производной. В четвертой строке условно изображено возрастание или убывание функции на промежутке (по знаку первой производной), и выпуклость или вогнутость кривой (по знаку второй производной).
6. Ищем наклонную асимптоту:
,
.
Кривая
на промежутке [0, +∞) имеет наклонную
асимптоту 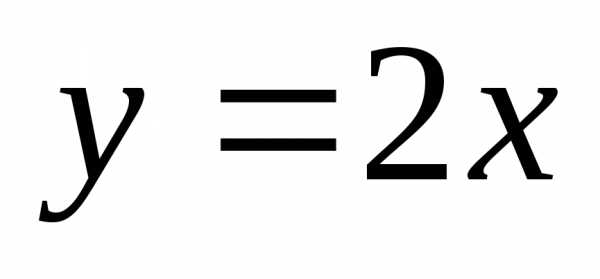 .
.
Строим вертикальную x = 2 и наклонную y = 2x асимптоты, а затем по данным таблицы строим график исследуемой функции на промежутке [0, +∞), который затем продолжаем на промежуток (-∞, 0) симметрично относительно центра системы координат.
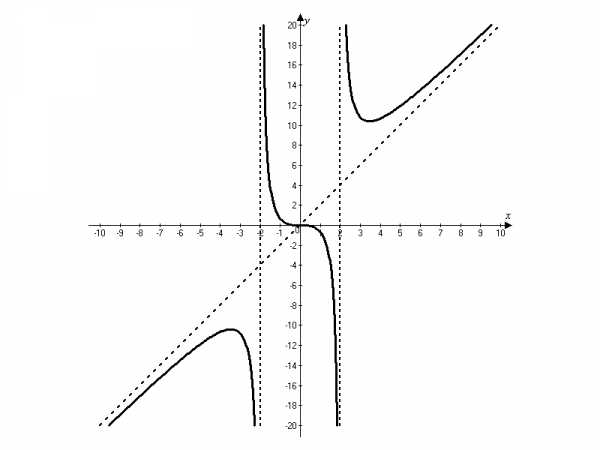
studfiles.net
Горизонтальные асимптоты — Мегаобучалка
Определение.
Если при ( ) функция имеет конечный предел, равный числу b:
,
то прямая есть горизонтальная асимптота графика функции .
Например, для функции имеем
, .
Соответственно, прямая − горизонтальная асимптота для правой ветви графика функции , а прямая − для левой ветви.
В том случае, если
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая называется наклонной асимптотой графика функции при ( ), если выполняется равенство
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы график функции имел при ( ) наклонную асимптоту , необходимо и достаточно, чтобы существовали конечные пределы
и .
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.
Замечания.
1. При отыскании асимптот следует отдельно рассматривать случаи и .
2. Если
и ,
то график функции имеет горизонтальную асимптоту .
3. Если
и ,
то прямая (ось Ох) является горизонтальной асимптотой графика функции .
Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при . Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
Найти асимптоты графика функции .
.
1) − точка разрыва второго рода:
, .
Прямая − вертикальная асимптота.
2) ,
,
.
Прямая − горизонтальная асимптота. Наклонной асимптоты нет.
Общая схема исследования функции и построение графика
В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.
Исследование функции целесообразно проводить по следующей схеме.
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Исследовать функцию на периодичность.
4. Найти точки пересечения графика функции с осями координат.
5. Найти интервалы знакопостоянства функции (интервалы, на которых или ).
6. Найти асимптоты графика функции.
7. Найти интервалы монотонности и точки экстремума функции.
8. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
9. Построить график функции.
Пример
Исследовать функцию и построить ее график.
1. Область определения функции .
2. Функция нечетная: . График функции симметричен относительно начала координат
3. Функция непериодическая.
4. Точки пересечения с осями координат:
С осью Оу: , точка .
С осью Ох: , , , .
5. Точки , и разбивают ось Ох на четыре интервала.
при ;
при ;
при ;
при .
6. Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.
.
Наклонной и горизонтальной асимптот нет.
7. ,
, , − критические точки.
для «↑»,
для «↓»,
для «↑».
Сведем данные в таблицу.
, ;
точка − максимум;
точка − минимум.
8. , , , .
при « »;
при « ».
Точка − точка перегиба.
9. График функции (рис.5.12)
 |
Рис. 5.12
Упражнения
Найти интервалы возрастания и убывания функций:
Найти экстремумы функций:
Найти наибольшее и наименьшее значения функции на указанных отрезках:
Найти интервалы выпуклости и вогнутости и точки перегиба графиков функций:
Найти асимптоты кривых:
Исследовать функции и построить их графики:
megaobuchalka.ru
Как найти горизонтальную асимптоту 🚩 горизонтальная асимптота 🚩 Математика
Автор КакПросто!
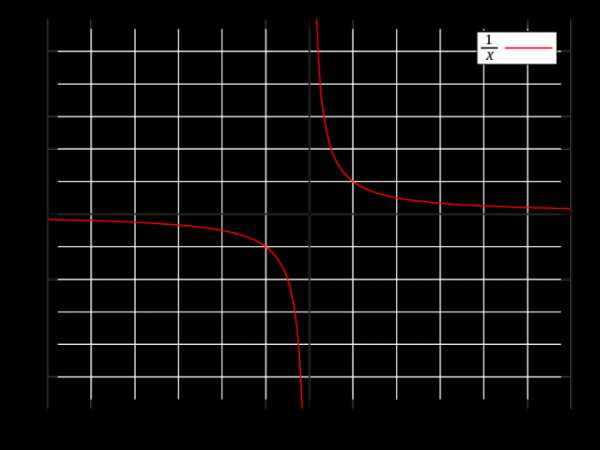
Что такое асимптота? Это такая прямая, к которой приближается график функции, но не пересекает её. Горизонтальная асимптота выражается уравнением y=A, где A — некоторое число. Геометрически горизонтальная асимптота изображается прямой, параллельной оси Ox и пересекающей ось Oy в точке A.
Статьи по теме:
Инструкция
Найдите предел функции при устремлении аргумента «x» к плюс бесконечности. Если этот предел равен некоторому числу A, то y=A — горизонтальная асимптота функции.Найдите предел функции при устремлении аргумента «x» к минус бесконечности. Опять же, если этот предел равен некоторому числу B, то y=B — горизонтальная асимптота функции. Пределы функции при стремлении аргумента к минус и плюс бесконечности могут совпадать, в этом случае имеем только одну горизонтальную асимптоту.
Отметьте на оси ординат Oy точки A и B (одну точку, если они совпадают). Проведите через каждую точку прямую параллельно оси абсцисс Ox. Это и будет горизонтальная асимптота функции.Используйте найденную горизонтальную асимптоту при построении графика функции. Помните, что при большом увеличении (уменьшении) аргумента он будет бесконечно приближаться к асимптоте, но никогда не пересечет её.
www.kakprosto.ru
Рассматривая рис. 3.14, приходим к очевидному выводу: если некоторая линия L с уравнением является невертикальной асимптотой графика функции при или при , то это значит, что при таком изменении X функция , то есть , а значит
, где при или при . (3.2)
И обратно, при выполнении (3.2) функция – асимптота функции . В частности, если
, где при или при , (3.3)
То соответственно при или при горизонтальная прямая будет асимптотой графика функции .
Пример 2. Найти невертикальные асимптоты графика функции
.
Решение. Для их нахождения нужно выяснить поведение функции Y При и при .
А) Если , то очевидно, что
; .
Поэтому при функция . А это значит, что линия L с уравнением является асимптотой графика нашей функции при .
Б) Если , то очевидно, что
; .
Поэтому при наша функция . А это значит, что при асимптотой графика нашей функции Y является горизонтальная прямая .
Пример 3. Определить все имеющиеся асимптоты графика функции и изобразить поведение этого графика возле его асимптот.
Решение. Начнем с нахождения области определения функции Y. Функция определена, а следовательно, и непрерывна для всех X, кроме . То есть – единственная точка разрыва нашей функции. А значит, вертикальная прямая , проходящая через эту точку – единственная возможная вертикальная асимптота графика нашей функции.
Проверим, действительно ли она – вертикальная асимптота. Для этого выясним, в соответствии с (3.1), поведение функции Y при и при :
;
То есть При и при . А это значит, что вертикальная прямая является асимптотой графика функции Y, причем и при , и при .
Теперь поищем возможные невертикальные асимптоты. Для этого рассмотрим поведение функции Y при и при .
А) Если , то
.
Учтем, что (это устанавливается делением на «в столбик»). То есть
, где , .
И так как при , а при к нулю не стремится, то при наша функция . А это, в соответствии с (3.2), означает, что линия с уравнением (прямая) является асимптотой графика нашей функции Y при .
Б) Если , то буквально повторяя (а), приходим к выводу, что прямая является асимптотой графика нашей функции и при .
Теперь изобразим график нашей функции вместе с его асимптотами. Для более качественного построения этого графика найдем еще точки его пересечения с осями координат.
1) С осью Ох:
.
2)  С осью Оу:
С осью Оу:
.
А теперь строим график (рис. 3.16).
Упражнения
Найти асимптоты графиков функций
А) ; б) ; в)

И построить эти графики вместе с их асимптотами.
Ответ: — см. рис. 3.17 (а) – (в).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
поиск асимптот — ПриМат
Напомним, что различают три вида асимптот: вертикальные, горизонтальные и наклонные, которые могут быть как односторонними так и двусторонними.
Определение 1. Пусть функция определена на отрезке . Прямая называется асимптотой (или наклонной асимптотой) графика функции при , если
По аналогии определяется (наклонная асимптота) при .
Итак, прямая является двусторонней вертикальной асимптотой графика функции .
Определение 2. Пусть функция определена на . Прямая называется асимптотой (или наклонной асимптотой) графика функции при если
Определение 3. Прямая называется вертикальной асимптотой графика функции , если хотя бы одна из границ или
равны бесконечности. Отсюда следует, что вертикальные асимптоты графика функции могут быть только при наличии граничных точек области определения функции или точек разрыва.
Что бы найти вертикальные асимптоты графика функции , надо найти такие значения, для которых выполняется одно или оба предыдущих условия.
Пример 1.Найдем вертикальные асимптоты графика функции . Ясно, что эта функция определена во всех точках числовой оси , кроме точки . Вычислим пределы:
и
Следовательно, прямая является односторонней вертикальной асимптотой графика рассматриваемой функции при .
Пример 2.Выясним существует ли вертикальные асимптоты у графика функции . Эта функция определена на множестве всех вещественных чисел кроме нуля причем
и
Иными словами, если мы имеем кривую, которая отдаляется в бесконечность, и если расстояние от точки кривой к некоторой прямой при отдалении точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой.
Из определения наклонной асимптоты следует следующее утверждение.
Для того, что бы График функции имел при наклонную асимптоту , необходимо и достаточно, что бы
Пример 3. Найти асимптоты графика
Функция определена на всей числовой оси кроме нуля. Вычислим пределы:
Следовательно, прямая — двухсторонняя вертикальная асимптота графика рассматриваемой функции.
Для нахождения наклонных асимптот графика представим эту функцию в виде
Так как при , то из определения наклонной асимптоты следует, что прямая является двухсторонней наклонной асимптотой графика указанной функции. Поскольку при и при , кривая графика лежит выше асимптоты при .
Литература
- Кудрявцев Л.Д. Курс математического анализа — М.: Высш.школа, 1981, т I — 687 с. ( с. 374- 375).
- Вартаняна Г.М. Конспект лекций по математическому анализу ч. 1.(с. 52-53).
- Лысенко З.М. Конспект лекций по математическому анализу.
- Исследование функций
Поделиться ссылкой:
ib.mazurok.com

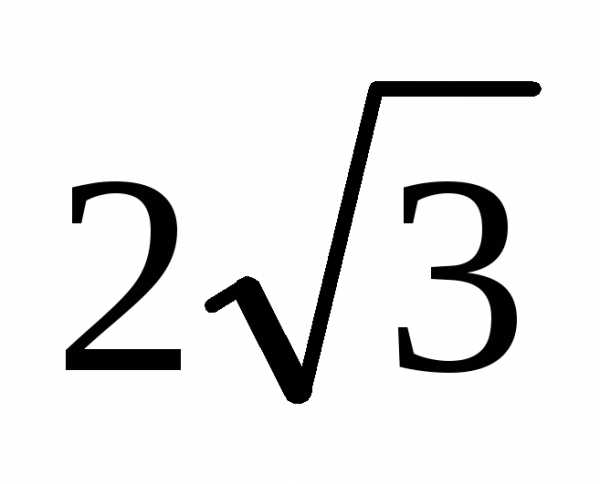 )
)