Решение СЛАУ и матрицы в Matlab
Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.
Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.
В традициях нашего сайта разберём на примере:
Решить систему линейных уравнений:
4*a + b - c = 6
a - b + c = 4
2*a - 3*b - 3*c = 4
Метод обратной матрицы в Matlab
Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.
В итоге у нас получится 2 матрицы:
A=[4 1 -1; 1 -1 1; 2 -3 -3]; % коэффициенты B=[6; 4; 4];
Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:
det(A)
Вывод: 30
После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv.
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:
x=inv(A)*B Вывод: 2 -1 1
Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть
Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.
Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.
Метод Гаусса
Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.(\) - левое деление.
При следующей записи:
x = A\B Вывод: 2 -1 1
Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.
Метод разложения матрицы
Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.
Возможны следующие разложения:
- разложение Холецкого
- LU разложение
- QR разложение
Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.
Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.
LU разложение
Решим выше предложенную задачу через LU разложение:[L, U] = lu(A);
Вывод:
L =
1 0 0
0.25 1 0
0.5 2.8 1
U =
4 1 -1
0 -1.25 1.25
0 0 -5
Затем:
y = L\B;
x = U\y
Вывод:
2
-1
1
QR разложение
И через QR разложение соответственно:
[Q, R] = qr(A); x = R\(Q'*B) Вывод: 2.0000 -1.0000 1.0000
Отметим, что апостроф ( ' ) после Q означает транспонирование.
Стандартные функции Matlab
Так же Matlab предлагает функцию linsolve, с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:
x = linsolve(A,B) Вывод: 2 -1 1
Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.
Повторение
Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:
Решить систему линейных уравнений:6*a - b - c = 0
a - 2*b + 3*d = 0
3*a - 4*b - 4*c = -1
A=[6 -1 -1; 1 -2 3; 3 -4 -4]; B=[0; 0; -1];
- Методом обратной матрицы:
x=inv(A)*B
Вывод:
0.0476
0.1810
0.1048
x = A\B
Вывод:
0.0476
0.1810
0.1048
[L, U] = lu(A);
y = L\B;
x = U\y
Вывод:
0.0476
0.1810
0.1048
[Q, R] = qr(A);
x = R\(Q'*B)
Вывод:
0.0476
0.1810
0.1048
На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.
Поделиться ссылкой:
Похожее
codetown.ru
3.6. Решение систем линейных уравнений средствами пакета matlab
Для решения систем линейных уравнений и связанных с ними матричных операций применяются операторы: сложения (+), вычитания (), умножения ( *), деления справа (/), деления слева (\), возведения в степень (^), транспонирования (), действие которых определяется правилами линейной алгебры.
Пусть задана система n линейных алгебраических уравнений с n неизвестными:
.
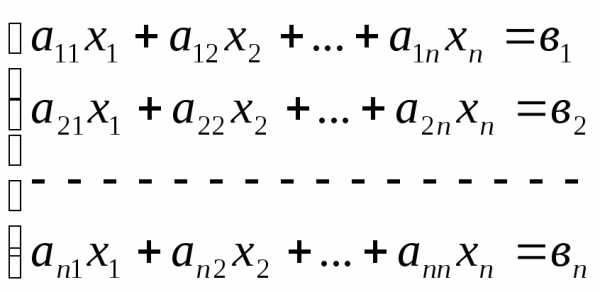(3.61)
Система уравнений (1) в матричной форме представляется следующим образом:
АХ = В, (3.62)
где А – квадратная матрица коэффициентов, размером n n строк и столбцов;
Х – вектор-столбец неизвестных;
В – вектор-столбец правых частей.
Систему уравнений (2) можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невырожденными матрицами, в противном случае метод Гаусса неприменим.
Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n100) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем. Если матрица А сильно разрежена, а ее определитель не близок к нулю, то метод Гаусса не пригоден для решения больших систем уравнений.
В MATLAB имеется обширный арсенал методов решения систем уравнений (2). Для этого применяются следующие операторы
/
правое деление;
\
левое деление;
— 1
возведение в степень –1;
inv(A)
обращение матрицы А.
Выражения
Х=В’/A’
Х=В’* (А^ 1)’
Х=В’* inv(A’)
Х=A\В
дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m n, В – матрица размером m к. Более сложные случаи решения систем уравнений (2) с плохо обусловленной матрицей А требуют применения специальных методов решения.
Для решения системы линейных уравнений вида
Ax=b,
где A матрица коэффициентов при неизвестных, x вектор-столбец неизвестных, b вектор-столбец свободных членов, в пакете MATLAB достаточно выполнить следующую команду:
>> A^-1*b
Пример 1.
Решить систему 4-х линейных уравнений:
Протокол программы (в скрипт-файле)
a= [1.1161 0.1397 0.1254 0.1490 ;
0.1582 0.1768 1.1675 0.1871 ;
0.1968 1.2168 0.2071 0.2271 ;
0.2368 0.2568 0.2471 1.2671] ;
b= [1.5471 ; 1.6471 ; 1.7471 ; 1.8471] ;
Х4 = а \ b
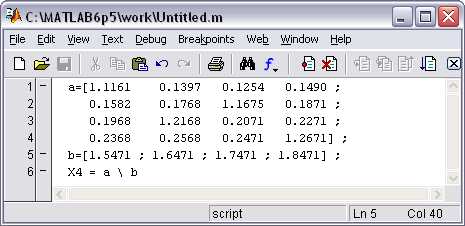
Рис.1 Скрипт-файл решения СЛАУ с помощью оператора Х=A\В
в окне редактора-отладчика
Эта программа выдает решение заданной системы с помощью четвертого оператора в виде матрицы – столбца
Х4=
1.0406
0.9351
0.9870
0.8813
X1 = b’/a’
X2 = b’*(a^-1)’
X3 = b’*inv(a’)
Результаты решения
X1 =
1.0406 0.9351 0.9870 0.8813
X2 =
1.0406 0.9351 0.9870 0.8813
X3 =
1.0406 0.9351 0.9870 0.8813
Отметим, что сравнение скорости решения системы линейных уравнений с помощью средств матричной алгебры пакета MATLAB и функции Zeidel( ), листинг которой приведен в предыдущем разделе свидетельствует о неоспоримом преимуществе первых.
Данное обстоятельство обусловлено тем, что в пакете MATLAB, который изначально разрабатывался для проведения матричных вычислений, используются специальные быстрые алгоритмы для выполнения арифметических операций с матрицами. Поэтому при решении каких-либо прикладных задач, в ходе которого возникает необходимость решения систем линейных уравнений, целесообразнее использовать встроенные возможности пакета MATLAB.
studfiles.net
Решение систем линейных алгебраических уравнений в пакете MATLAB
Решение систем линейных алгебраических уравнений в пакете MATLAB
Ранее » Возможности MATLAB ‣ левостороннее деление › x = Ab ‣ обратная матрица › x = inv(A)*b 2/13/2018 2
Небольшие системы уравнений » Небольшая система содержит, как привило, не более трех уравнений » Решение, чаще всего, может не требовать компьютера » Методы ‣ графический ‣ Крамера ‣ исключения неизвестных 2/13/2018 3
Графический метод » 2/13/2018 4
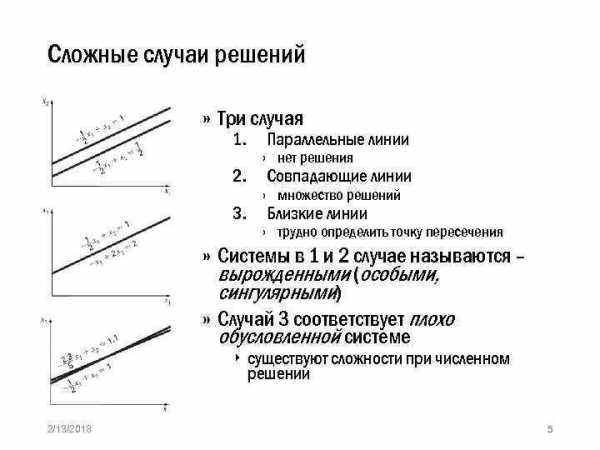Сложные случаи решений » Три случая 1. 2. 3. Параллельные линии › нет решения Совпадающие линии › множество решений Близкие линии › трудно определить точку пересечения » Системы в 1 и 2 случае называются – вырожденными (особыми, сингулярными) » Случай 3 соответствует плохо обусловленной системе ‣ существуют сложности при численном решении 2/13/2018 5
Метод Крамера » 2/13/2018 6
Метод Крамера » 2/13/2018 7
Исключение неизвестных » 2/13/2018 8
Исключение неизвестных » 2/13/2018 9
Метод Гаусса » 2/13/2018 10
Метод Гаусса – Прямой ход » 2/13/2018 11
Метод Гаусса – Прямой ход » 2/13/2018 12
Метод Гаусса – Прямой ход » 2/13/2018 13
Метод Гаусса – Прямой ход » 2/13/2018 14
Метод Гаусса – Обратный ход » 2/13/2018 15
Пример 2/13/2018 16
Метод Гаусса с обратной подстановкой » В рассмотренном варианте метода Гаусса могут возникнуть ситуации когда решение не может быть найдено или иметь существенную погрешность ‣ например, в случае если главный элемент равен 0, при нормализации возникает деление на 0 ‣ также существенно меньшее значение главного элемента по сравнению с остальными может привести к увеличению погрешности вычислений » Решение – выбор главного элемента ‣ частный › выбор максимального значения главного элемента с последующей перестановкой строк ‣ полный (применяется редко) › выбор максимального значения главного элемента с последующей перестановкой строк и столбцов 2/13/2018 17
Пример – Частный выбор главного элемента » 2/13/2018 18
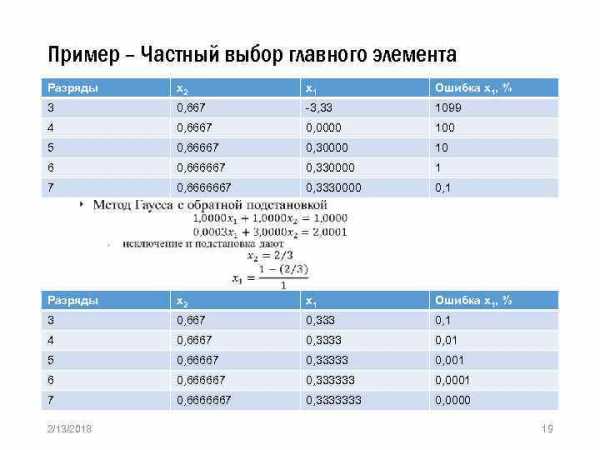Пример – Частный выбор главного элемента Разряды х2 х1 Ошибка х1, % 3 0, 667 -3, 33 1099 4 0, 6667 0, 0000 100 5 0, 66667 0, 30000 10 6 0, 666667 0, 330000 1 7 0, 6666667 0, 3330000 0, 1 Разряды х2 х1 Ошибка х1, % 3 0, 667 0, 333 0, 1 4 0, 6667 0, 3333 0, 01 5 0, 66667 0, 33333 0, 001 6 0, 666667 0, 333333 0, 0001 7 0, 6666667 0, 3333333 0, 0000 » 2/13/2018 19
Пример – MATLAB 2/13/2018 20
Факторизация матриц » В математике факторизация или факторинг — это декомпозиция объекта (например, числа, полинома или матрицы) в произведение других объектов или факторов, которые, будучи перемноженными, дают исходный объект » Целью факторизации является приведение объекта к «основным строительным блокам» ‣ Матрица может также быть факторизована на произведение матриц специального вида для приложений, в которых эта форма удобна » Виды факторизации матриц ‣ LU ‣ Холецкого ‣ QR 2/13/2018 22
LU факторизация » 2/13/2018 23
LU факторизация » 2/13/2018 24
‣ факторизация › выполняется декомпозиция матрицы А на верхнюю U и нижнюю L треугольные матрицы ‣ подстановка › прямая подстановка определяет промежуточный вектор d › обратная подстановка определяет вектор неизвестных x 2/13/2018 прямая обратная 25 подстановка » Два основных шага решения системы факторизация LU факторизация
Метод Гаусса как LU факторизация » 2/13/2018 26
Метод Гаусса как LU факторизация » 2/13/2018 27
Метод Гаусса как LU факторизация » 2/13/2018 28
Пример — Проверка » 2/13/2018 30
Пример — Проверка » 2/13/2018 31
Метод Гаусса как LU факторизация » 2/13/2018 32
Пример » 2/13/2018 33
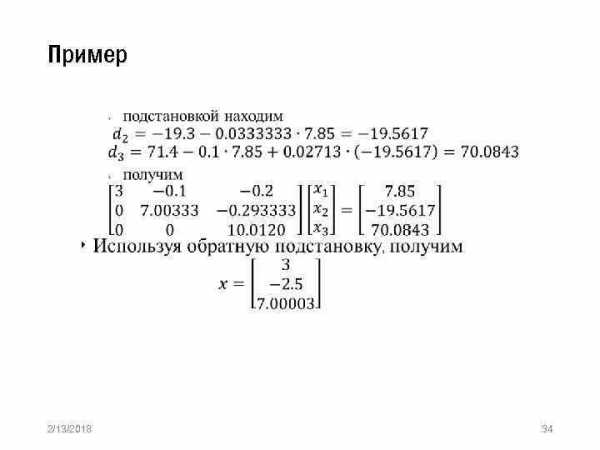Пример » 2/13/2018 34
LU факторизация с выбором главного элемента » Аналогично методу Гаусса для обеспечения надежности решения при использовании LU факторизации необходимо применять частный выбор главного элемента ‣ одним из способов является использование матрицы перестановки › единичная матрица для взаимной замены строк и столбцов 2/13/2018 35
LU факторизация с выбором главного элемента » 2/13/2018 36
Пример » 2/13/2018 37
Пример » 2/13/2018 38
LU факторизация – MATLAB функции » lu ‣ [L, U] = lu(A) – возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу L (то есть произведение нижней треугольной матрицы и матрицы перестановок), так что A=L*U ‣ [L, U, P] = lu(A) – возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок P, так что L*U =P*A 2/13/2018 39
Пример 2/13/2018 40
Факторизация Холецкого » 2/13/2018 41
Пример » 2/13/2018 42
Пример » 2/13/2018 43
Факторизация Холецкого » 2/13/2018 44
Пример 2/13/2018 46
Левостороннее деление MATLAB » При использовании левостороннего деления «» MATLAB выполняет оценку матрицы коэффициентов и применяет оптимальный метод для решения ‣ MATLAB проверяет вид матрицы коэффициентов при неизвестных для возможности нахождения решения без применения полного метода Гаусса › разреженная › треугольная › симметричная ‣ В противном случае применяется для квадратной матрицы применяется метод Гаусса с частным выбором главного элемента 2/13/2018 47
QR факторизация » 2/13/2018 48
QR факторизация – MATLAB функции » qr ‣ [Q, R] = qr(A) – вычисляет верхнюю треугольную матрицу R того же размера, как и у A, и унитарную матрицу Q, так что X=Q*R ‣ [Q, R, P] = qr(A) – вычисляет матрицу перестановок P, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что A*P=Q*R › Матрица перестановок P выбрана так, что abs(diag(R)) уменьшается ‣ [Q, R] = qr(A, 0) и [Q, R, P] = qr(A, 0) – вычисляют экономное разложение, в котором P – вектор перестановок, так что Q*R=A(: , P) › Матрица P выбрана так, что abs(diag(R)) уменьшается 2/13/2018 49
Пример 2/13/2018 50
Итерационные методы » Итерационные или аппроксимационные методы являются альтернативой ранее рассмотренным методам решения СЛАУ, основанным на исключении неизвестных » Можно выделить два основных этапа ‣ выбор начального приближения ‣ последующее систематическое уточнение » Методы ‣ ‣ ‣ 2/13/2018 Гаусса-Зейделя Якоби релаксации бисопряженных градиентов и др. 51
Метод Гаусса-Зейделя » 2/13/2018 52
Метод Гаусса-Зейделя » 2/13/2018 53
Пример » 2/13/2018 54
Пример » 2/13/2018 55
Пример » 2/13/2018 56
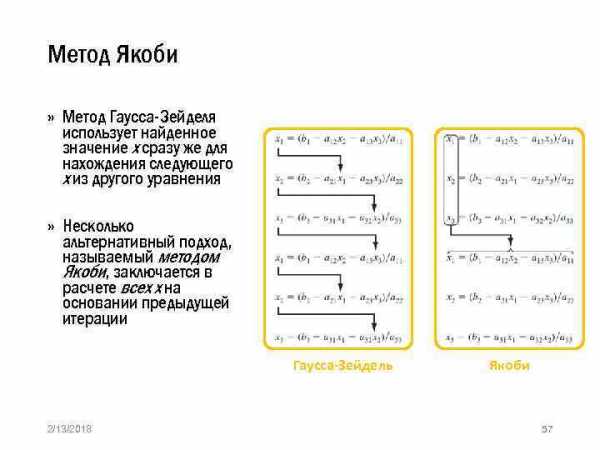Метод Якоби » Метод Гаусса-Зейделя использует найденное значение х сразу же для нахождения следующего х из другого уравнения » Несколько альтернативный подход, называемый методом Якоби, заключается в расчете всех х на основании предыдущей итерации Гаусса-Зейдель 2/13/2018 Якоби 57
Сходимость и диагональное преобладание » 2/13/2018 58
Пример » 2/13/2018 59
Метод релаксации » 2/13/2018 60
Метод релаксации » 2/13/2018 61
Пример » 2/13/2018 62
Пример » 2/13/2018 63
Пример » 2/13/2018 64
present5.com
1.11 Решение систем линейных уравнений
MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.
Яркий пример этому – решение систем линейных уравнений.
Пример:
Пусть дана система линейных уравнений
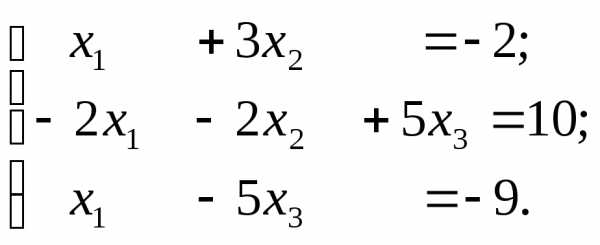
Решить систему с применением оператора обратного деления матриц < \ >.
Решение:
В матричной записи система имеет вид Ах = b, где
A = , b = , х =
– соответственно матрица из коэффициентов при незвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.
Введем матрицу А и вектор-столбец свободных членов b:
>> А=[1 3 0;-2 -2 5;1 0 -5]
А =
1 3 0
-2 -2 5
1 0 -5
>> b=[-2;10;-9]
b =
-2
10
-9
Известно, что система имеет единственное решение, если определитель матрицы А не равен нулю (│A│ = det(A) ≠ 0). Вычислим определитель матрицы А:
>> disp(det(A))
-5
Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:
>> x=А\b
x =
1
-1
2
Проверим полученное решение x1 = 1, x2 = -1, x3 = 2 подстановкой в систему уравнений:
>> disp(A*x)
-2.0000
10.0000
-9.0000
В результате проверки получен вектор-столбец свободных членов. Значит, система решена верно.
Найдем теперь решение системы х = A-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A-1:
>> A1=inv(A)
A1 =
-2.0000 -3.0000 -3.0000
1.0000 1.0000 1.0000
-0.4000 -0.6000 -0.8000
Находим решение системы:
>> A1*b
ans =
1.0000
-1.0000
2.0000
Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.
Пример:
Решить систему линейных уравнений
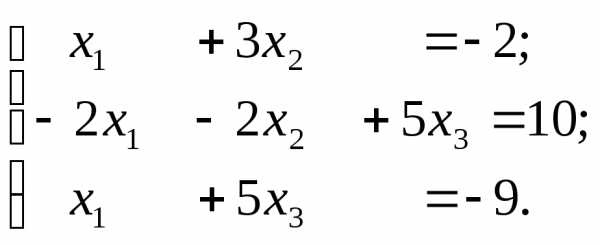
Решение:
>> A=[1 3 0;-2 -2 5;1 0 5]
A =
1 3 0
-2 -2 5
1 0 5
>> b=[-2 10 -9]
b =
-2 10 -9
>> disp(det(A))
35
Находим решение системы:
>> x=A\b’
x =
-7.5714
1.8571
-0.2857
Заметим, что обратное деление произведено на вектор-столбец b‘, поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A-1:
>> disp(inv(A))
-0.2857 -0.4286 0.4286
0.4286 0.1429 -0.1429
0.0571 0.0857 0.1143
Точное решение системы и точная обратная матрица выражаются через рациональные дроби:
>> format rat
>> x=A\b’
x =
-53/7
13/7
-2/7
>> disp(inv(A))
-2/7 -3/7 3/7
3/7 1/7 -1/7
2/35 3/35 4/35
Вопросы для самопроверки
1. Какие окна имеет интерфейс MATLAB и каково их назначение
2. Какова структура командного окна Command Window
3. Как называется отображение в командном окне сеанса работы с системой На какие зоны подразделяется текстовое поле окна Command Window
4. Для чего служат в MATLAB клавиши <↑> и <↓>
5. Для чего применяется команда disp
6. Как можно ввести слишком длинную команду в окне Command Window
7. Какая информация сохраняется в окнах Command History и Workspase после применения команды очистки экрана clc
8. Как получить справку по выбранной команде MATLAB
9. В каких форматах представляются в MATLAB вещественные числа
10. Какие форматы отображения вещественных чисел используются в MATLAB
11. Как в в MATLAB осуществляются операции с комплексными числами
12. В чем измеряются аргументы встроенных тригонометрических функций
13. Какая команда осуществляет векторизацию символьного выражения
14. Как MATLAB реагирует на ошибки ввода
15. Как обнаружить и устранить семантическую ошибку ввода
16. Как в MATLAB создаются векторы и матрицы
17. Как осуществляется просмотр и редактирование переменных в окне Workspase
18. Как в MATLAB осуществляются матричные и поэлементные операции над векторами и матрицами
19. Что вычисляют команды dot и cross
20. Как решается система линейных уравнений с помощью оператора обратного деления < \ >
studfiles.net
Решение систем линейных алгебраических уравнений в системе MATLAB
Решение систем линейных алгебраических уравнений методом Жордана-Гаусса
Метод Жордана — Гаусса является одной из модификаций метода Гаусса, в котором матрица коэффициентов при неизвестных последовательно приводится к единичной матрице, а на месте столбца свободных членов в расширенной матрице в результате располагается решение системы линейных алгебраических уравнений:
,
где — коэффициенты системы, — свободные члены, — неизвестные.
Сущность этого метода заключается в том, что, начиная со второго шага, зануляются все элементы в соответствующем столбце, кроме элемента, стоящего на главной диагонали. Это достигается с помощью алгебраических преобразований аналогичных классическому методу Гаусса. Если имеется система линейных алгебраических уравнений — го порядка, то на каждом шаге прямого хода метода Гаусса в каждом столбце матрицы коэффициентов зануляется ровно коэффициент.
Стандартной функцией, которая реализует метод Жордана-Гаусса в системе MATLAB , является функция rref(). Аргументом у этой функции является расширенная матрица коэффициентов.
Пример: решить с помощью метода Жордана –Гаусса систему линейных алгебраических уравнений
.
>> A=[3 2 -1;2 -1 3;1 -2 2]; B=[4;9;3];
>> AB=[A B]
AB =
3 2 -1 4
2 -1 3 9
1 -2 2 3
>> rref(AB)
ans =
1 0 0 1
0 1 0 2
0 0 1 3
Для решения систем линейных алгебраических уравнений с помощью MATLAB можно применять оператор «\», который самостоятельно выбирает лучший метод для решения заданной системы уравнений. При этом решение системы линейных алгебраических уравнений любого порядка достигается одной командой:
Индивидуальные задания
· Решить систему линейных алгебраических уравнений методом Гаусса,
· решить систему линейных алгебраических уравнений методом Жордана— Гаусса в системе MATLAВ.
Таблица 4
Продолжение табл. 4
Окончание табл. 4
Содержание соответствующего раздела
В пояснительной записке
Данный раздел должен содержать:
· краткие теоретические сведения,
· исследование системы линейных алгебраических уравнений на совместность,
· аналитическое решение системы линейных алгебраических уравнений методом Гаусса,
· решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB,
· сравнение полученных результатов, найденных разными способами.
infopedia.su
1.4. Решение системы алгебраических линейных уравнений MATLAB
r4=r1C41 | при C41 | = C21 C32 C43 | (1.28) |
r1=r4C14 | при C14 | = C΄43 C΄32 C΄21 |
|
Матрицу C14 можно также получить из C41 путем формального изменения знаков: ϕ →−ϕ, ψ →−ψ, θ →−θ , ввиду изменения направления отсче-
та углов.
Перепроецирование тензоров
Наряду с векторами (являющимися тензорами первого ранга), в механике встречаются также тензоры второго ранга – физические величины, которые определяются шестью скалярами в исходной системе, заполняющими симмметрическую 3×3-матрицу и определенной формулой перепроецирования на повернутые системы. К тензорам второго ранга относятся тензор инерции в точке абсолютно твердого тела, тензоры деформаций и напряжений в точке твердого деформированного тела.
Пусть в “нулевой” системе Oxyz задан тензор второго ранга симметрической (3×3) матрицей J. Тензор в повернутой системе Ox1y1z1 определяются симметрической матрицей J1, элементы которой вычисляются через исходные элементы по матричной формуле:
J1= C΄10 J C10 = C01 J C10 (1.29)
где C10 — матрица поворота первой системы Ox1 y1z1 от исходной системы Oxyz . Очевидно, что элементы матрицы (1.29) содержат вторые степени и
произведения направляющих косинусов.
Формула обратного перепроектирования из первой системы в исходную (нулевую):
Выражение (1.29) отличается по форме от выражения для вектора (1.26) дополнительным множителем – транспонированной матрицей поворота новой системы от исходной системы отсчета.
За геометрический образ тензора инерции второго ранга обычно принимают трехосный эллипсоид с центром в точке O, осями Ox,Oy,Oz занимающими в теле определенное угловое положение.
Рассмотрим систему линейных неоднородных алгебраических уравне-
ний, представленных в виде матричного уравнения | (1.31) |
* | |
V A + B = zeros(1, n), |
|
Здесь А — заданная неособая (т.е. det(A) ≠ 0 ) квадратная (n×n)-матрица, V и
B— вектор-строки размера (1×n), B — заданная вектор-строка. Здесь все члены уравнения перенесены в левую часть.
В MATLAB решение системы (1.31) возвращается функциями правого или левого деления матриц, в виде
V=–B/A | или | V=–(A΄\B΄)΄, | (1.32) |
|
|
| 12 |
studfiles.net
Решение систем линейных уравнений
В общем случае не требуется, чтобы матрица коэффициентов A была бы квадратной. ЕслиA имеет размер mхn, то возможны три случая:
1.m = n Квадратная система. Ищется точное решение.
2.m > n Переопределенная система. Ищется решение методом наименьших квадратов.
3.m < n Недоопределенная система. Находится базовое решение с самым большим
числом m ненулевых компонент.
Оператор \ использует различные алгоритмы для решения систем линейных уравнений с разными типами матриц коэффициентов. Различные случаи, которые диагностируются автоматически по типу матрицы коэффициентов, включают:
•Перестановки треугольных матриц
•Симметричные, положительно определенные матрицы
•Квадратные невырожденные матрицы
•Прямоугольные, переопределенные системы
•Прямоугольные, недоопределенные системы
Квадратные системы
Наиболее часто встречающейся ситуацией является квадратная матрица коэффициентовA и одномерныйвектор-столбецb справа, т.е.Ax = b. Решениеx = A\b имеет при этом тот же размер, что и векторb. Например,
x = A\u
x =
10 -125
где матрица А есть приведенная выше матрица Паскаля. Легко удостовериться, чтоA*x в точности равно векторуu (численные значения этого вектора даны выше).
Если A иB являются квадратными и имеют одинаковый размер, тоX = A\B имеет тот же размер, например
X = A\B
Легко убедиться, что A*X в точности равноB.
Оба этих примера имеют точное решение в виде целых чисел. Это связано с тем, что в качестве матрицы коэффициентов была выбрана матрица Паскаляpascal(3), чей детерминант равен единице. Далее будут рассмотрены примеры влияния ошибок округления, возникающих в более реальных системах.
Квадратная матрица A являетсясингулярной, если ее столбцы не являются линейно независимыми. ЕслиA – сингулярна, то решениеAX = B или не существует, или не является единственным. Оператор \ ,A\B, выдает предупреждающее сообщение, если матрицаA близка к сингулярной и сообщение об ошибке, если определено равенство нулю детерминанта матрицыА.
studfiles.net