Отрицательно определённая матрица — это… Что такое Отрицательно определённая матрица?
В линейной алгебре, положи́тельно определённая ма́трица — это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или полуторалинейной формой в случае с комплексными числами).
Формулировки
Пусть M будет эрмитовой матрицей размерности . Обозначим транспонированный вектор a посредством aT, а сопряжённый транспонированный вектор — посредством a * .
Матрица M является положительно определённой, если она удовлетворяет любому из следующих равнозначных критериев:
| 1. | Для всех ненулевых комплексных векторов , Отметим, что величина z *Mz всегда вещественна, поскольку M — эрмитова матрица. |
| 2. | Все собственные значения M, , положительны. Вспомним, что любая эрмитова матрица по теореме о спектральном разложении может быть представлена как вещественная диагональная матрица D, переведённая в другую систему координат (то есть M = P − 1DP, где P — унитарная матрица, строками которой являются ортонормальные собственные векторы M, образующие базис). По этому определению M — положительно определённая матрица, если все элементы главной диагонали D (или, другими словами, собственные значения M) положительны. То есть в базисе, состоящем из собственных векторов M, действие M на вектор равносильно покомпонентному умножению z на положительный вектор. |
| 3. | Полуторалинейная форма определяет внутреннее произведение в . Обобщая сказанное, любое внутреннее произведение в образуется из эрмитовой положительно определённой матрицы. |
| 4. | M — матрица Грама, образованная из множества линейно независимых векторов для какого-то k. Другими словами, элементы M определены следующим образом Таким образом, M = A *A, где A инъективная, но не обязательно квадратная матрица. |
| 5. | Определители всех угловых миноров матриц положительны (критерий Сильвестра). В соответствии с этим критерием у положительно полуопределённых матриц все угловые миноры неотрицательны, что, тем не менее, не является достаточным условием для положительной полуопределённости матрицы, как видно из следующего примера |
Для вещественных симметричных матриц в вышеприведённых свойствах пространство может быть заменено на , а сопряжённые транспонированные векторы на транспонированные.
Квадратичные формы
Также можно сформулировать положительную определённость через квадратичные формы. Пусть K будет полем вещественных () или комплексных () чисел, а будет векторным пространством над K. Эрмитова форма
является двулинейным отображением, притом числом, сопряженным , будет . Такая функция B называется положительно определённой, когда для любого ненулевого .
Отрицательно определённая, полуопределённая и неопределённая матрицы
Эрмитова матрица M размерности будет называться отрицательно определённой, если
для всех ненулевых (или, эквивалентным образом, для всех ненулевых ).
M будет называться положительно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
M будет называться отрицательно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
Таким образом, матрица будет отрицательно определённой, если все её собственные значения отрицательны, положительно полуопределённой, если все её собственные значения неотрицательны, и отрицательно полуопределённой, если все её собственные значения неположительны.
Матрица M будет положительно полуопределённой тогда и только тогда, когда она является матрицей Грама какого-нибудь множества векторов. В отличие от положительно определённой матрицы данные векторы не обязательно линейно независимы.
Для любой матрицы A выполняется следующее: A *A — положительно полуопределённая, а . Обратное утверждение также верно: любая положительно полуопределённая матрица M может быть выражена как M = A *A (разложение Холеского).
Эрмитова матрица не являющаяся ни положительно, ни отрицательно полуопределённой называется неопределённой.
Дополнительные свойства
Введём обозначение для положительно полуопределённых матриц и — для положительно определённых матриц.
Для произвольных квадратных матриц M,N будем писать , если , то есть M − N положительно полуопределённая матрица. Таким образом, отношение определяет частичный порядок на множестве квадратных матриц. Подобным образом можно определить отношение полного порядка .
| 1. | Любая положительно определённая матрица обратима, а её обратная матрица также положительно определённая. Если , то . |
| 2. | Если M — положительно определённая матрица и , то положительно определённая матрица. Если M and N — положительно определённые матрицы, то их сумма M + N и произведения MNM и NMN тоже положительно определённые. Если MN = NM, то MN тоже положительно определённая. |
| 3. | Если M — положительно определённая матрица, то элементы главной диагонали mii положительны. Следовательно, . Более того,
|
| 4. | M — положительно определённая матрица тогда и только тогда, когда существует положительно определённая такая, что B2 = M. Обозначим . Такая матрица B единственна при условии, что . Если , то . |
| 5. | Если M and N — положительно определённые матрицы, то (где обозначает произведение Кронекера). |
| 6. | Если M and N — положительно определённые матрицы, то (где обозначает произведение Адамара). Когда M,N вещественные матрицы, выполняется также следующее неравенство (неравенство Оппенхейма): . |
| 7. | Если M — положительно определённая матрица, а |
| 8. | Если M and N — положительно полуопределённые вещественные матрицы, то . |
| 9. | Если M — положительно определённая вещественная матрица, то существует число δ > 0 такое, что , где I — единичная матрица. |
Неэрмитовы матрицы
Вещественные несимметрические матрицы тоже могут удовлетворять неравенству xTMx > 0 для всех ненулевых вещественных векторов x. Такой, к примеру, является матрица
поскольку для всех ненулевых вещественных векторов x = (x1,x2)T
Обобщая, xTMx > 0 для всех ненулевых вещественных векторов x тогда и только тогда, когда симметрическая часть положительно определённая.
Для комплексных матриц существет несколько обобщений неравенства x *Mx > 0. Если x *Mx > 0 для всех ненулевых комплексных векторов x, тогда матрица M эрмитова. То есть если x *Mx > 0, то M эрмитова. С другой стороны, для всех ненулевых комплексных векторов x тогда и только тогда, когда эрмитова часть положительно определённая.Литература
- R. A. Horn, C. R. Johnson. Matrix Analysis, Cambridge University Press, Ch. 7, 1985.
- R. Bhatia, Positive definite matrices, Princeton Series in Applied Mathematics, 2007.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
§ 3. Положительно и отрицательно определенные формы. Критерий Сильвестра.
Нетрудно
заметить, что положительно определённая
квадратичная форма в записи (1) принимает
положительное значение, если хотя бы
одна из переменных величин: 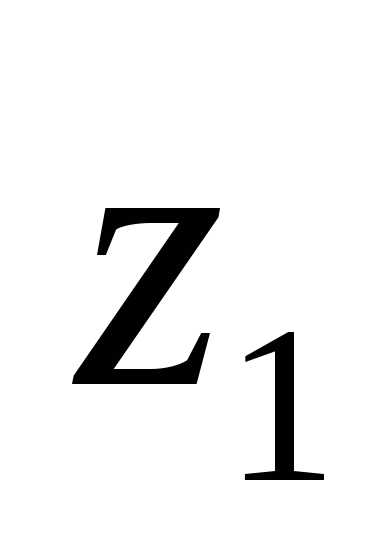 ,
,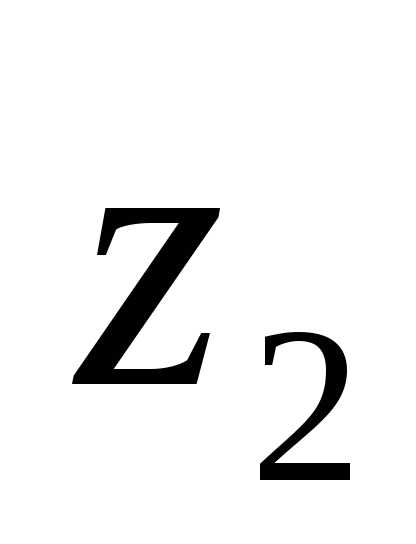 ,…,
,…,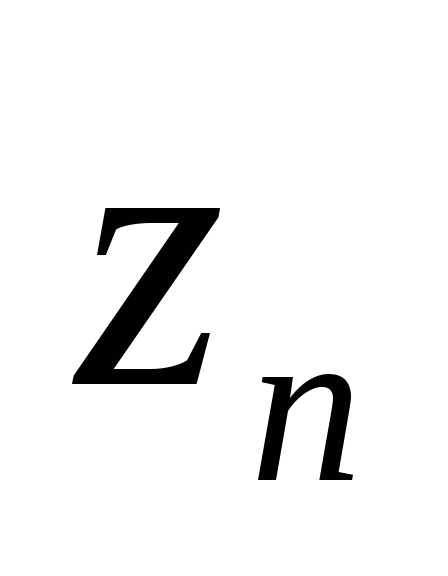 не равна нулю.
не равна нулю.
Нетрудно
заметить, что отрицательно определённая
квадратичная форма в записи (1) принимает
только отрицательные значение, если
хотя бы одна из переменных величин: 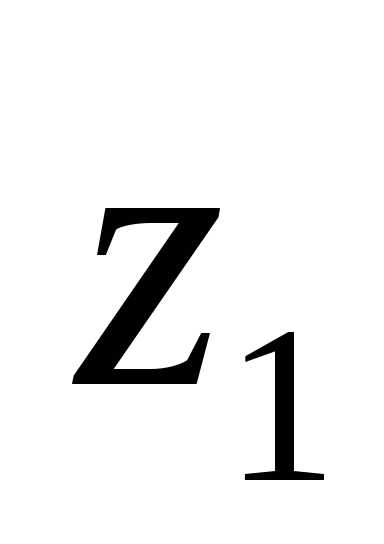
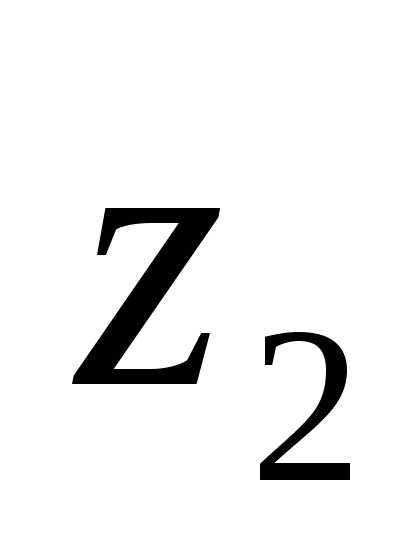 ,…,
,…,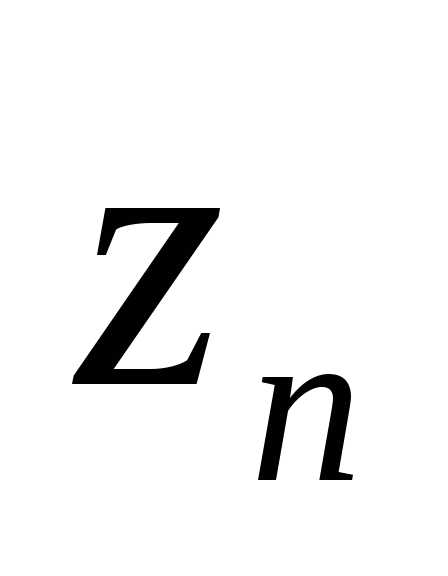 не равна нулю.
не равна нулю.Определение: (11.6) | Квадратичная
матрица с действительными коэффициентами
называется полуопределенной, если |
Нетрудно
заметить, что полуопределённая
квадратичная форма может принимать
нулевые значения, даже в случае, когда
не все переменные величины: 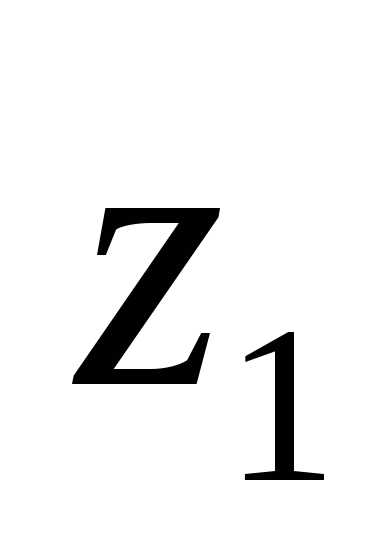
 ,…,
,…,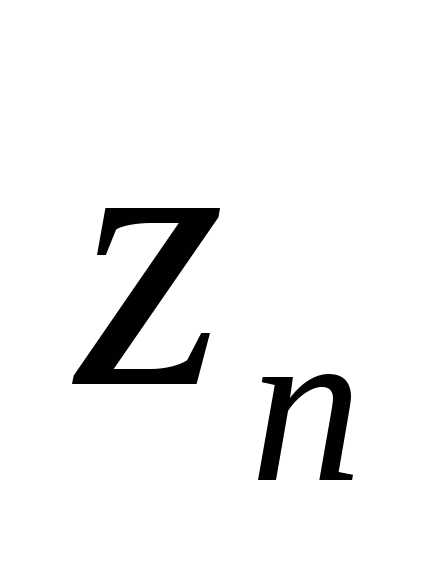 равны нулю.
равны нулю.Определение: (11.7) | Квадратичная матрица с действительными коэффициентами называется неопределенной, если она приводится к нормальному виду, в котором присутствуют как положительные, так и отрицательные слагаемые. |
Нетрудно заметить, что неопределённая квадратичная форма может принимать как положительные, так и отрицательные значения.
Когда квадратичная форма приведена к каноническому, или нормальному, виду, определить будет она положительно определённой или нет, несложно. Рассматривая примеры приведения квадратичной формы к каноническому и нормальному виду, мы могли убедиться в том, что процесс этот весьма трудоёмкий! Возникает вопрос, а нельзя ли, имея матрицу квадратичной формы, определить по ее коэффициентам будет она положительно определенной, или нет. На этот вопрос отвечает следующая теорема.
Теорема: (11.8) | Квадратичная
форма f от n неизвестных x=( |
►Пусть
положительно определенная квадратичная
форма невырожденным линейным
преобразованием  : y=(
: y=(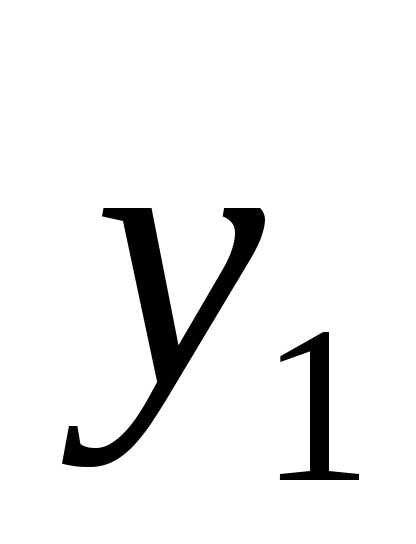 ,
,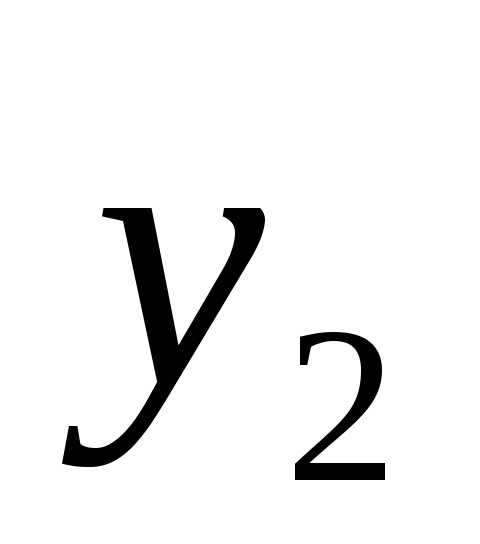 ,…,
,…,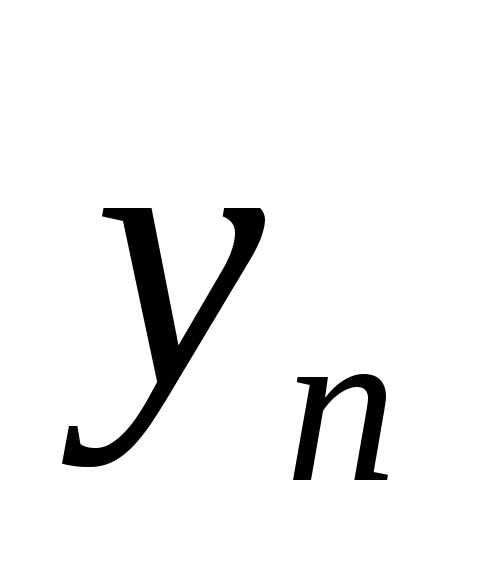 )=(
)=( ,
,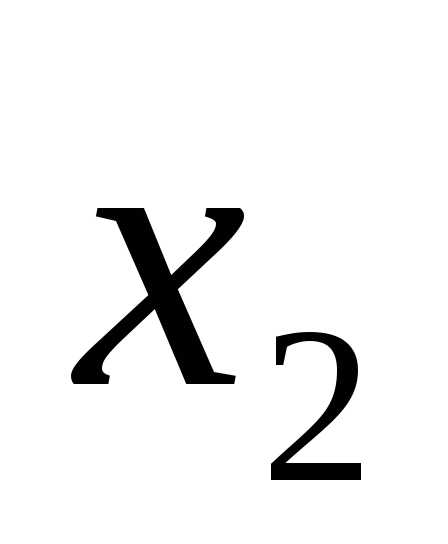 ,…,
,…,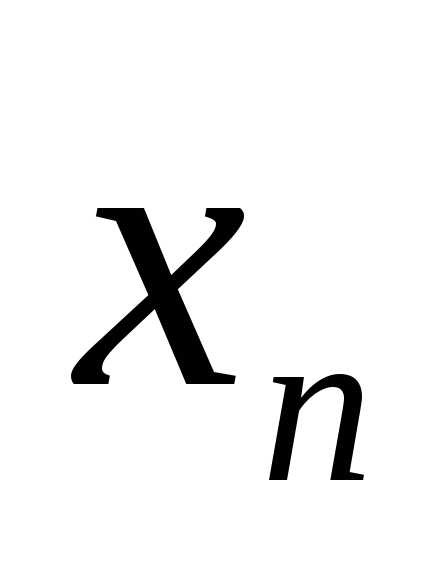 )·
)· приведена к нормальному виду:
приведена к нормальному виду:
f = 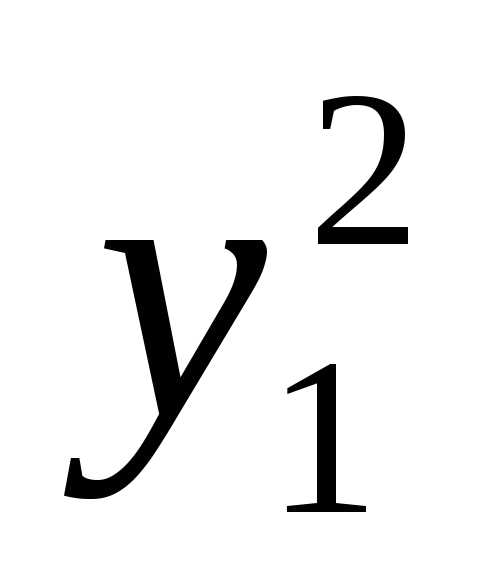 +
+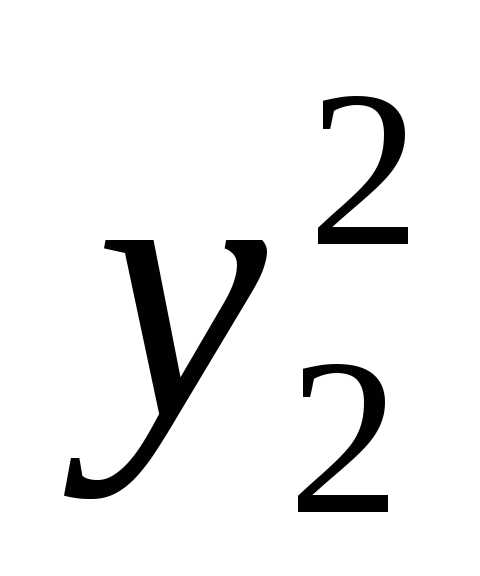 +…+
+…+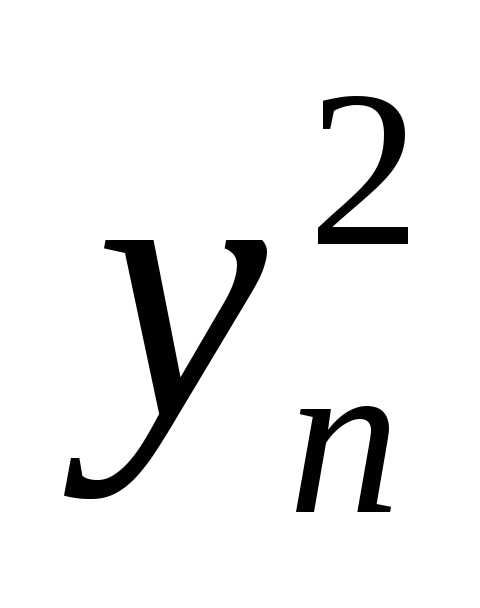 . (1)
. (1)
Если
рассматривать значения формы f при различных значениях x=(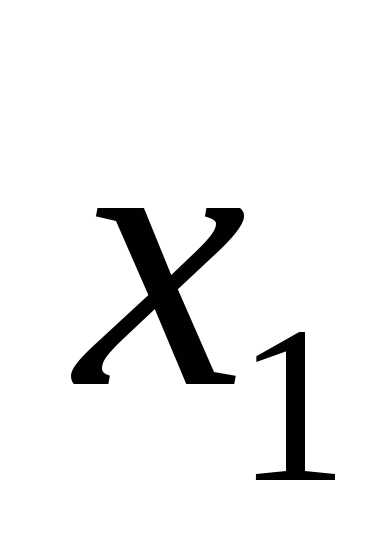 ,
,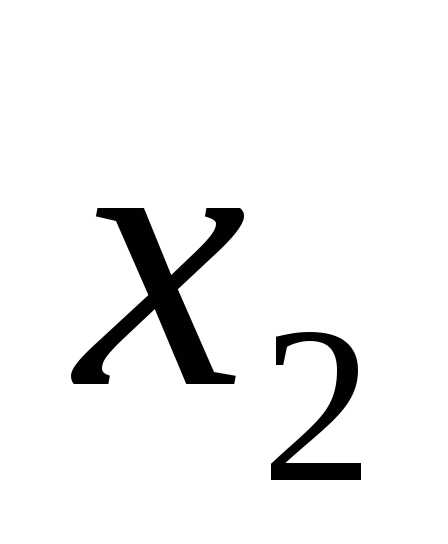 ,…,
,…,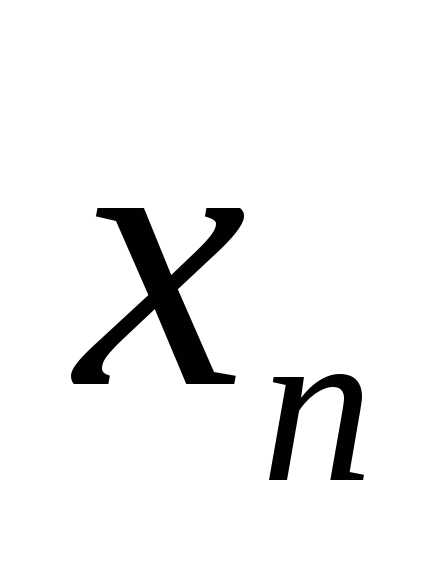 ),
причем хотя бы одно из них не равно нулю,
то необходимо сначала вычислить
),
причем хотя бы одно из них не равно нулю,
то необходимо сначала вычислить  =
=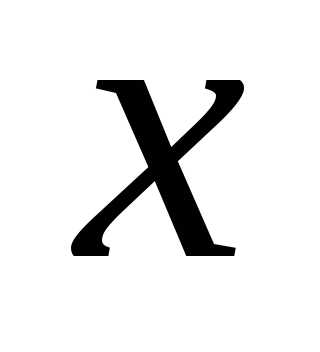 ·
· .
Значения переменных y:
(
.
Значения переменных y:
( ,
,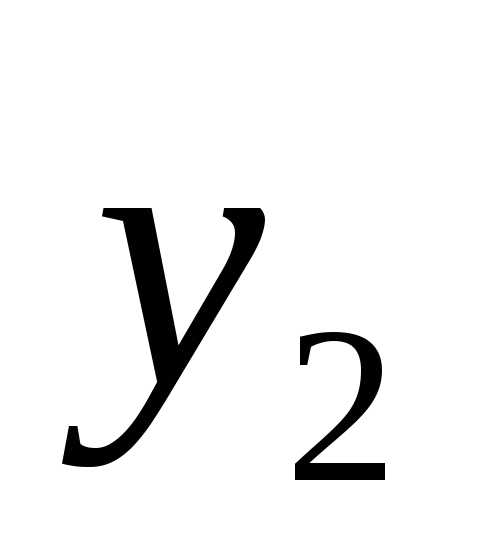 ,…,
,…,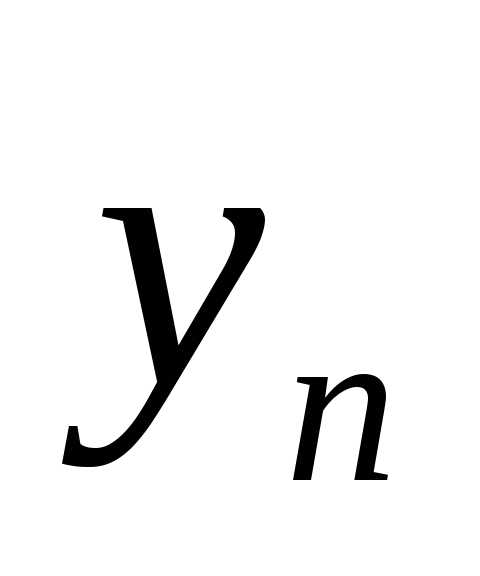 )
не могут все сразу обратиться в нуль,
так как в этом случае определитель
системы линейных однородных уравнений:
(
)
не могут все сразу обратиться в нуль,
так как в этом случае определитель
системы линейных однородных уравнений:
(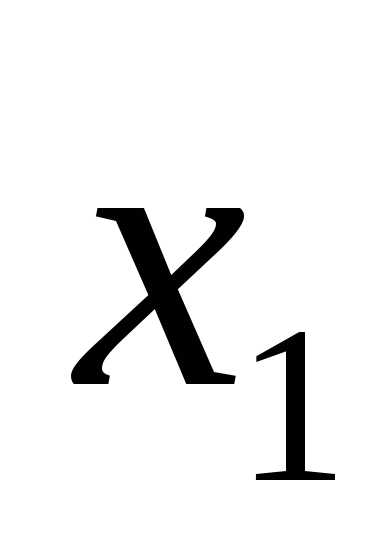 ,
,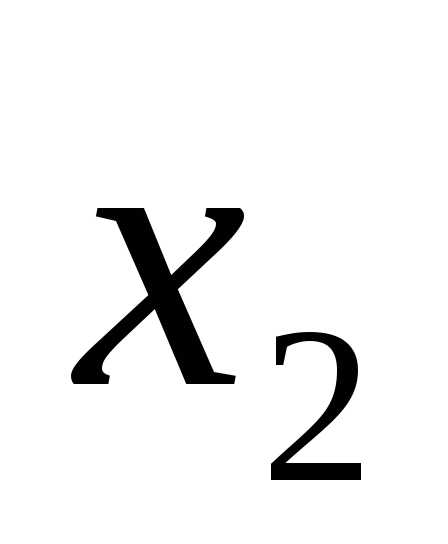 ,…,
,…,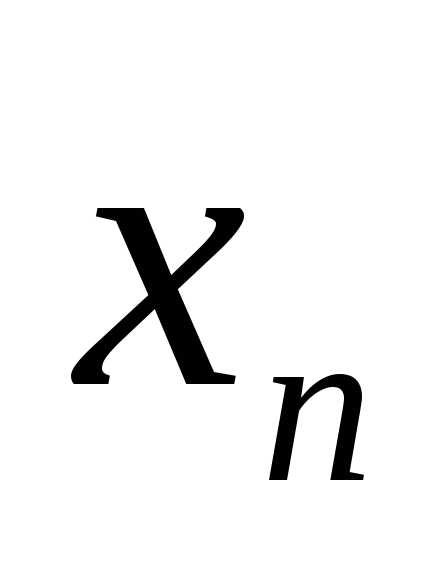 )·
)· =0
должен быть равным нулю. Но это значит:
|
=0
должен быть равным нулю. Но это значит:
| |=0.
Последнее невозможно: матрица
|=0.
Последнее невозможно: матрица  невырожденная!
невырожденная!
Итак,
если квадратичная форма положительно
определенная, она принимает положительное
значение при любом наборе значений
переменных x: (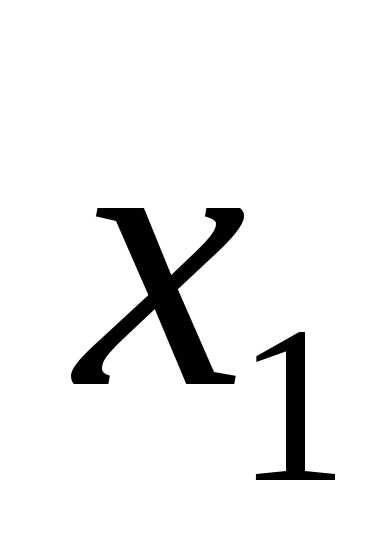 ,
,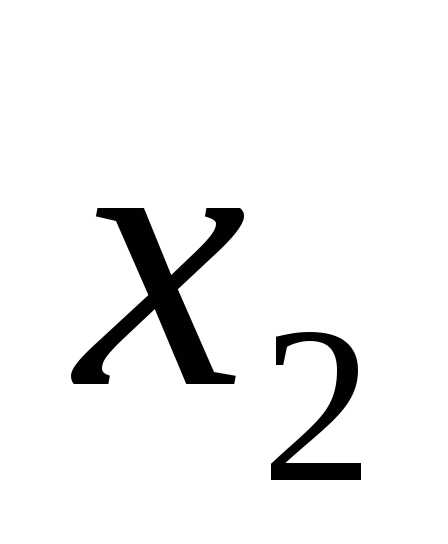 ,…,
,…,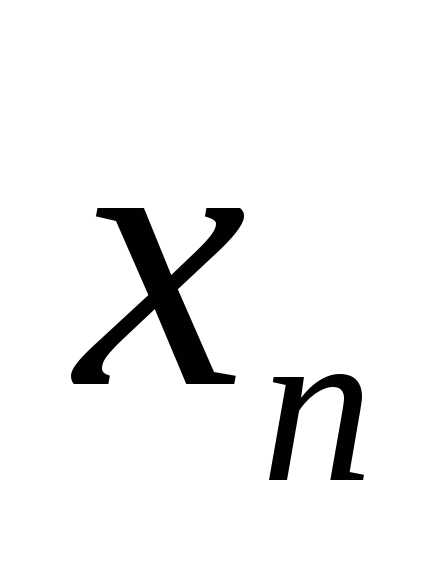 ),
хотя бы одно из которых не равно нулю.
),
хотя бы одно из которых не равно нулю.
Если квадратичная форма не является положительно определенной, то есть может быть приведена к виду:
f = 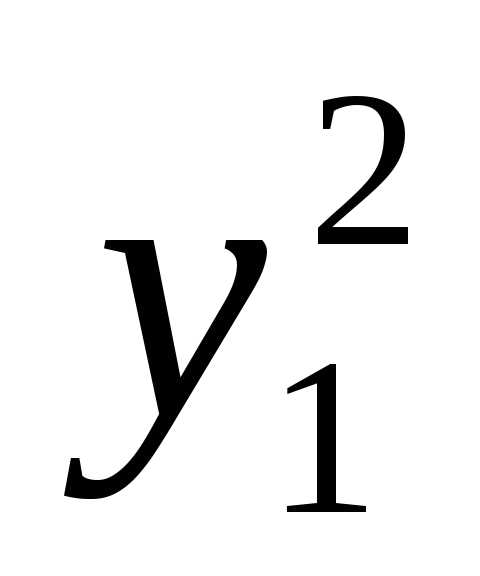 +
+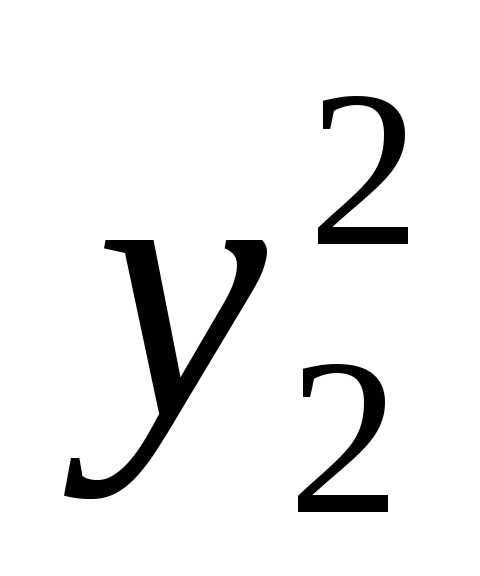 +…+
+…+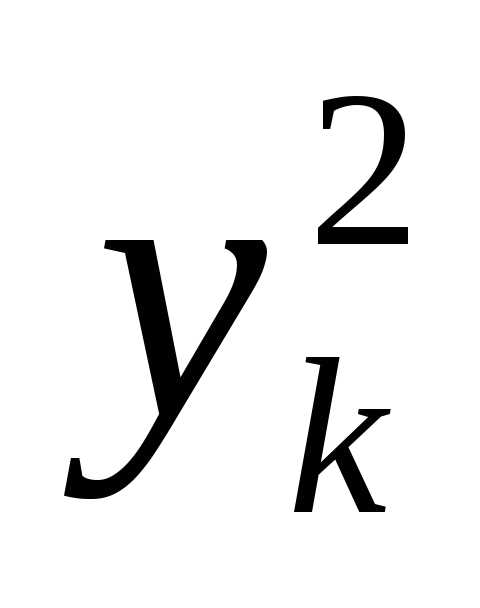 –
– –…–
–…– ,
,
то легко
подобрать такие значения переменных x: (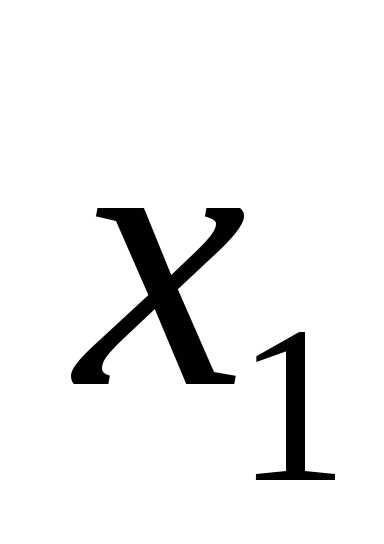 ,
, ,…,
,…,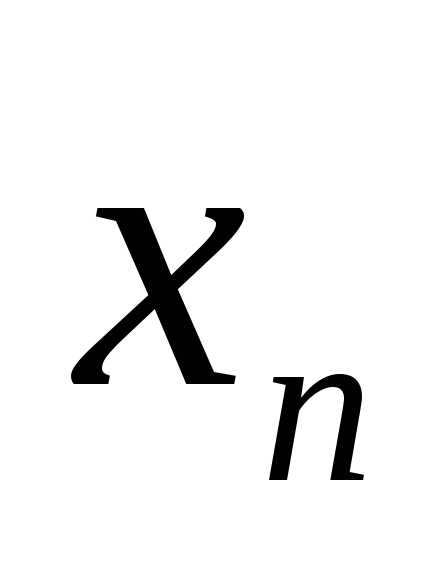 ),
причём хотя бы одно из них не равно нулю,
что форма будет принимать любое (наперед
заданное!) значение: как положительное,
так и отрицательное.
◄
),
причём хотя бы одно из них не равно нулю,
что форма будет принимать любое (наперед
заданное!) значение: как положительное,
так и отрицательное.
◄
Доказанная теорема (на первый взгляд!) не продвинула нас к реализации идеи (желания): определить по ее коэффициентам будет она положительно определенной, или нет.
Рассмотрим
последовательность миноров матрицы  ,
определяющей квадратичную форму f:
,
определяющей квадратичную форму f:
∆1 =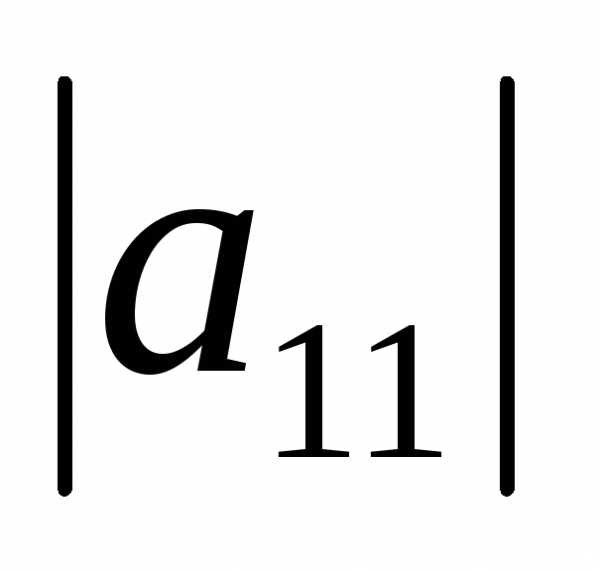 ,
∆2 =
,
∆2 =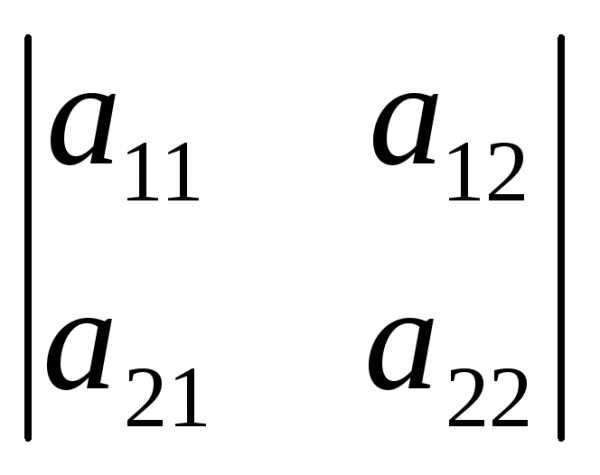 ,…,
∆k=
,…,
∆k= ,
… , ∆n=
,
… , ∆n= . (2)
. (2)
Определение: (11.8) | Последовательность
миноров (2) определителя матрицы |
Оказалось (!), при помощи главных миноров квадратичной формы, значит, при помощи коэффициентов формы, вопросы, связанные с положительно (и отрицательно) определенными формами, могут быть решены полностью. Это устанавливает следующая теорема.
Теорема: (11.9) | Квадратичная
форма f от n неизвестных x:
( |
►1).
Пусть квадратичная форма положительно
определенная. Это значит, что матрица  квадратичной формы, представленной в
нормальном виде, имеет определитель:
|
квадратичной формы, представленной в
нормальном виде, имеет определитель:
| |=1.
Докажем, что все главные миноры матрицы
|=1.
Докажем, что все главные миноры матрицы  строго положительны. Воспользуемся
методом индукции.
строго положительны. Воспользуемся
методом индукции.
♦ При 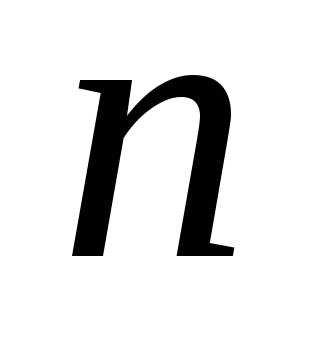 =1
форма:
=1
форма:  = a11
= a11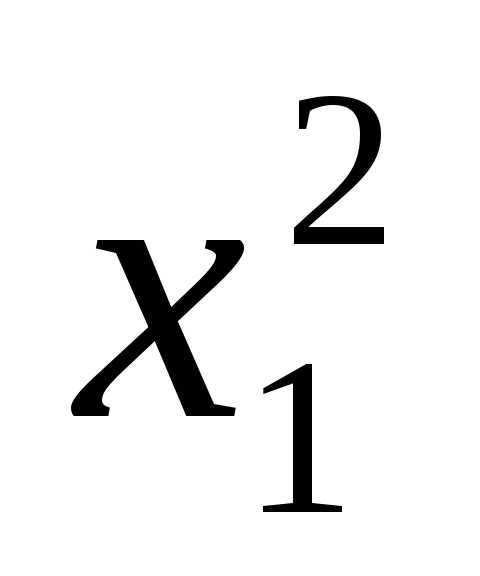 ,
ее матрица
,
ее матрица  =(a11),
единственный минор равен числу a11 . Форма положительно
определенная → число a11>0,
то есть главный минор строго положителен.
=(a11),
единственный минор равен числу a11 . Форма положительно
определенная → число a11>0,
то есть главный минор строго положителен.
♦ Пусть
утверждение верно для
(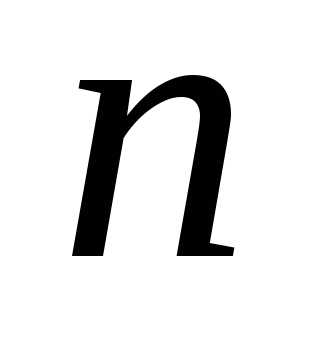 -1):
форма положительно определенная →
все главные миноры строго положительны.
-1):
форма положительно определенная →
все главные миноры строго положительны.
♦ Пусть
имеем форму: f =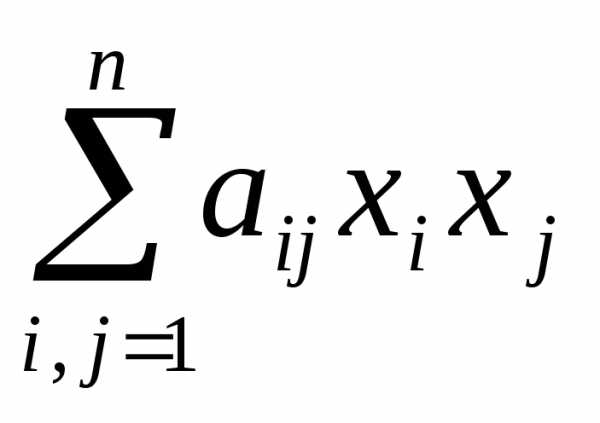 =
= (
(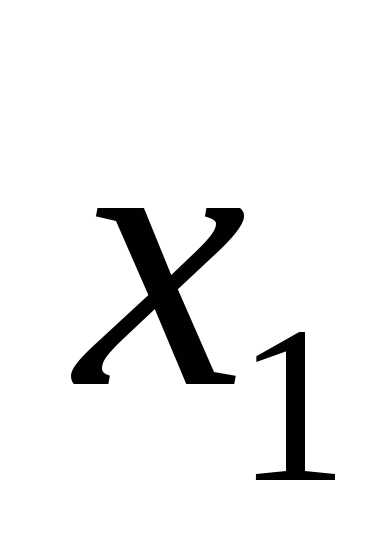 ,
,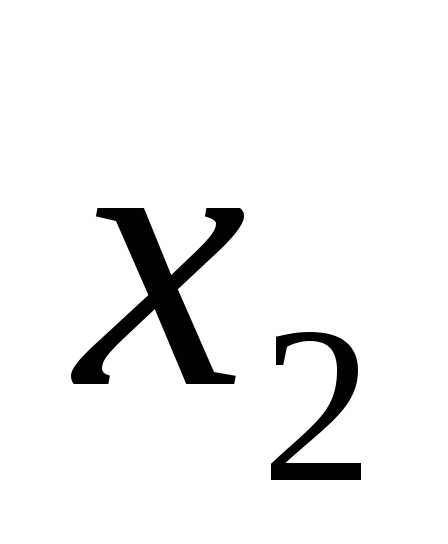 ,…,
,…,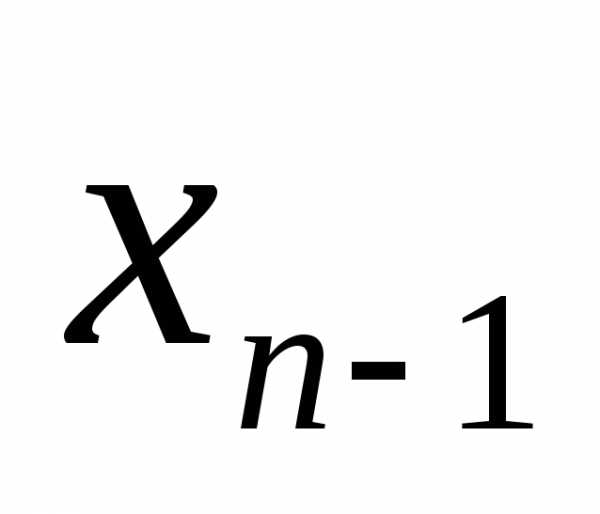 )+2
)+2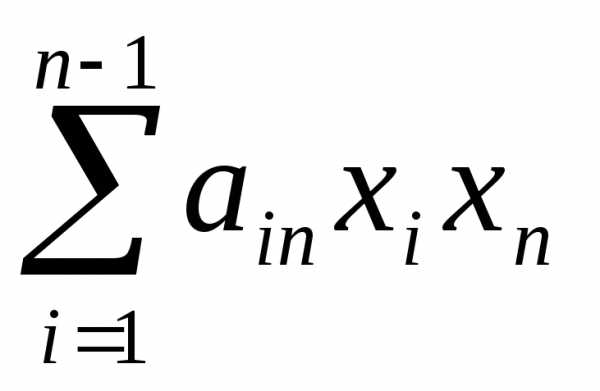 +
+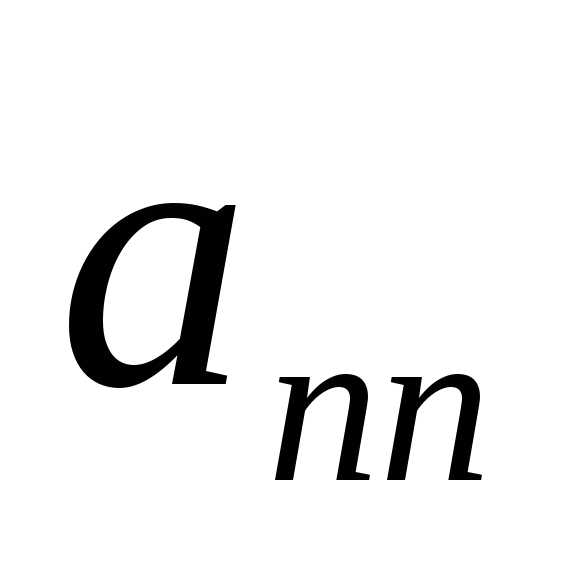 ·
·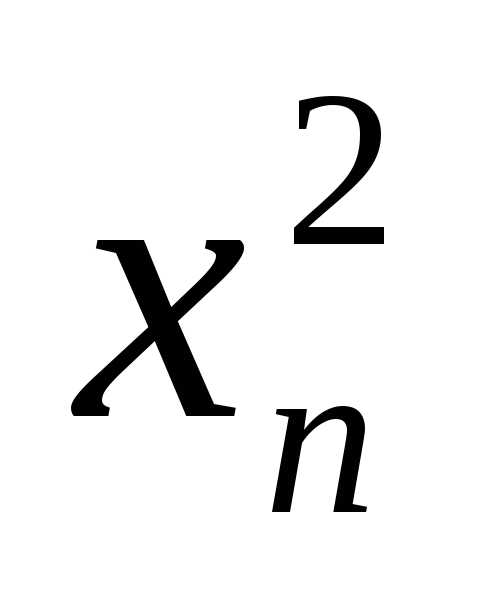 ,
,
где  – квадратичная форма
от (
– квадратичная форма
от (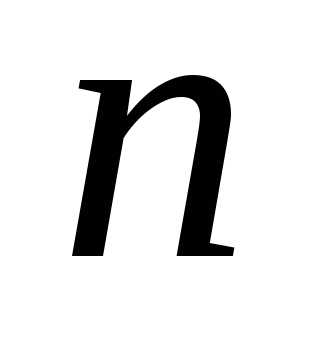 -1)
неизвестных переменных x:
(
-1)
неизвестных переменных x:
(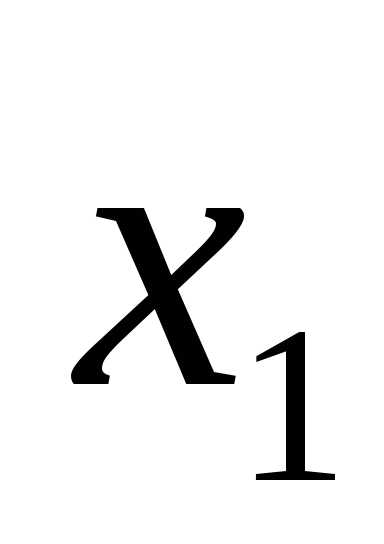 ,
,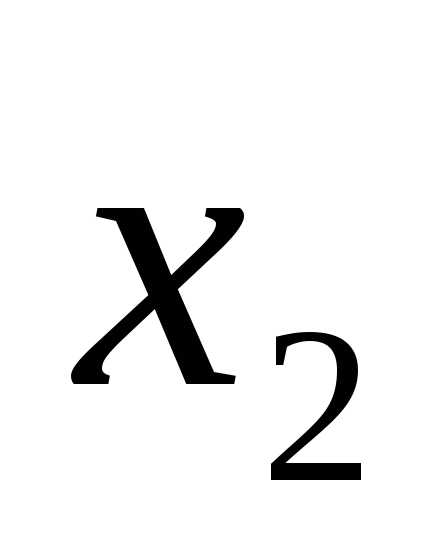 ,…,
,…,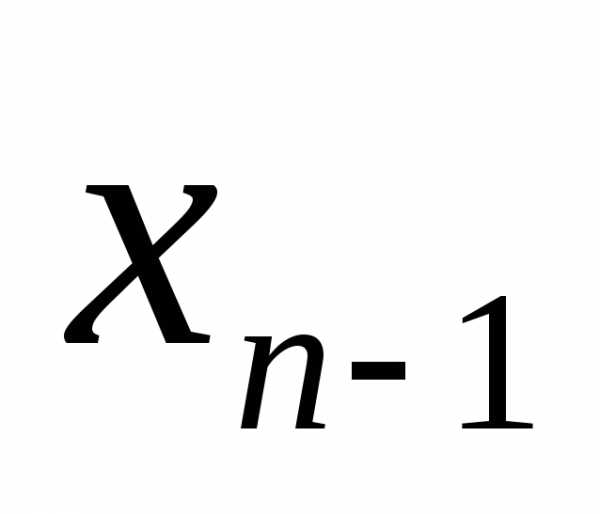 ),
без переменной
),
без переменной 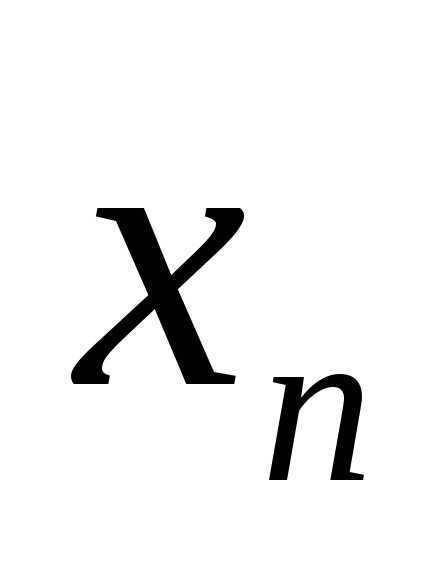 .
Главные миноры формы
.
Главные миноры формы  совпадают с главными минорами формы
совпадают с главными минорами формы  ,
кроме последнего. Так как форма f положительно определенная,
то
,
кроме последнего. Так как форма f положительно определенная,
то  тоже положительно определенная: если
она принимает значение ≤ 0, при
тоже положительно определенная: если
она принимает значение ≤ 0, при 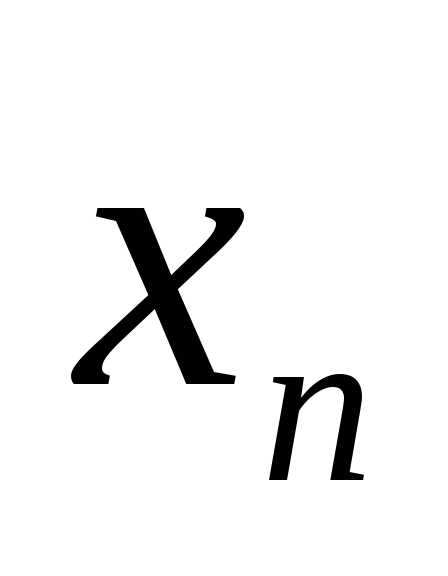 =0
и форма
=0
и форма  приняла бы это же значение, что противоречит
допущению.
приняла бы это же значение, что противоречит
допущению.
Что
касается последнего главного минора
формы  ,
то он строго положителен, так как
определитель матрицы
,
то он строго положителен, так как
определитель матрицы  формы нормального вида: |
формы нормального вида: | |>0.
Согласно Теореме 11.2 определитель матрицы
|>0.
Согласно Теореме 11.2 определитель матрицы  тоже >
0.
тоже >
0.
2).
Пусть теперь все главные миноры матрицы  строго положительны. Значит, строго
положительны все главные миноры формы
строго положительны. Значит, строго
положительны все главные миноры формы  .
Воспользуемся методом индукции.
.
Воспользуемся методом индукции.
♦ При 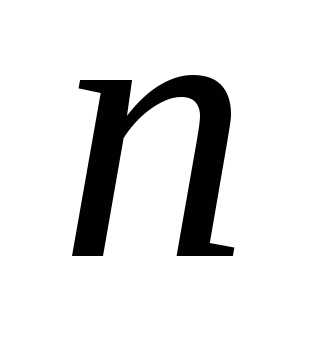 =1
единственный минор
(главный) равен числу a11>
0 →
форма
=1
единственный минор
(главный) равен числу a11>
0 →
форма  =a11
=a11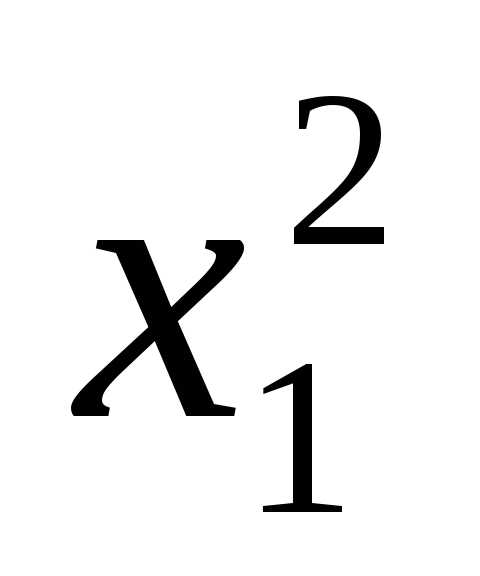 положительно определенная.
положительно определенная.
♦ Пусть
утверждение верно для
(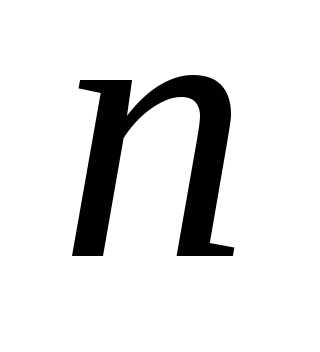 -1):
все главные миноры строго положительны
→ форма положительно определенная.
-1):
все главные миноры строго положительны
→ форма положительно определенная.
♦ Пусть
имеем форму: f =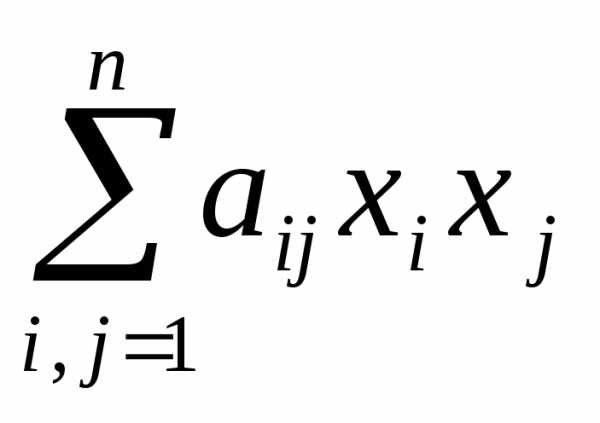 =
= (
(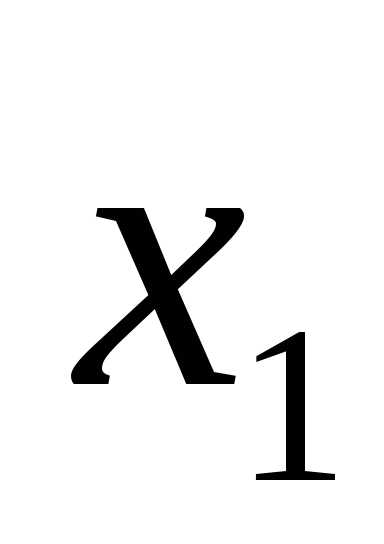 ,
,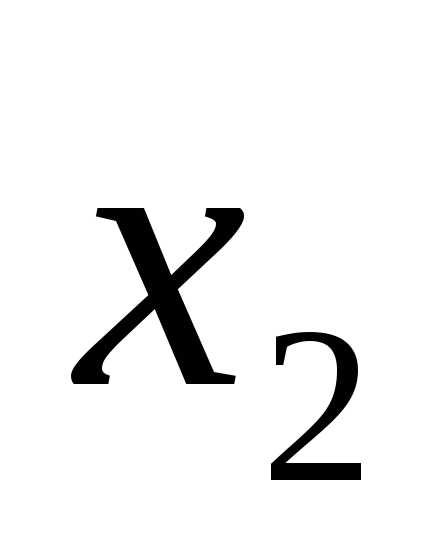 ,…,
,…,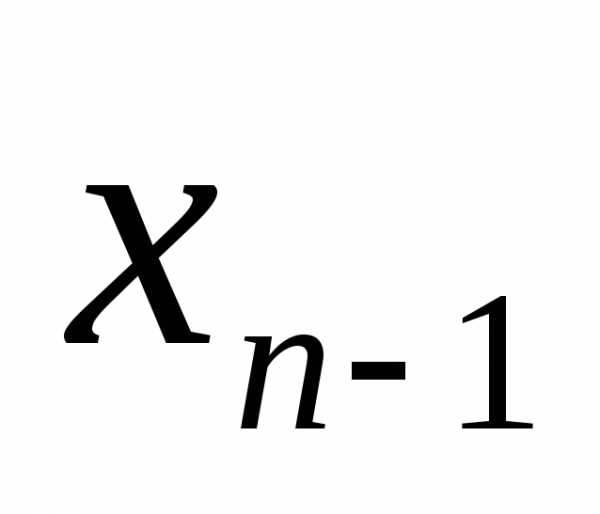 )+2
)+2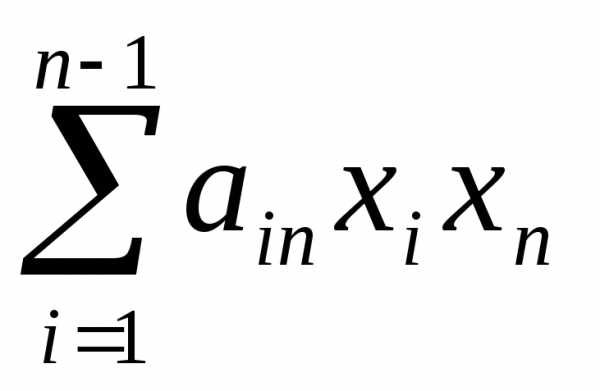 +
+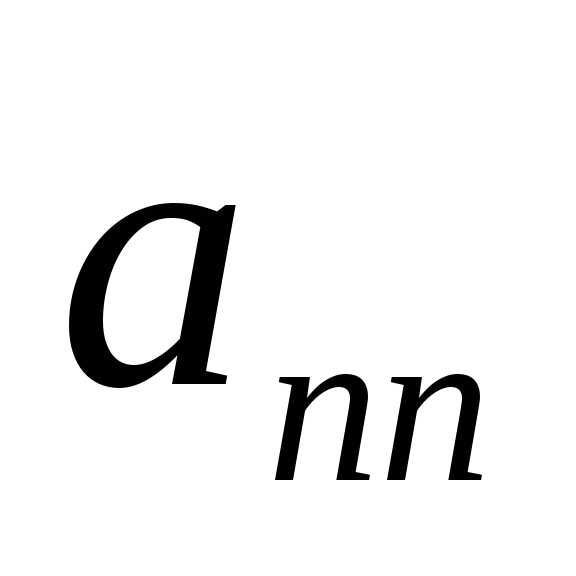 ·
·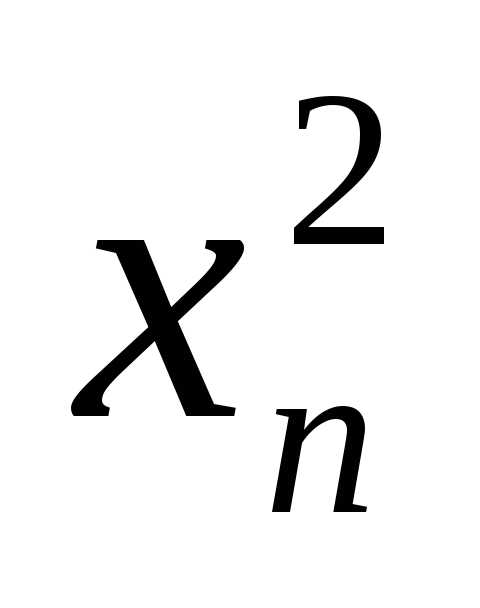 ,
,
где  – квадратичная форма
от (n-1) неизвестных
переменных x: (
– квадратичная форма
от (n-1) неизвестных
переменных x: (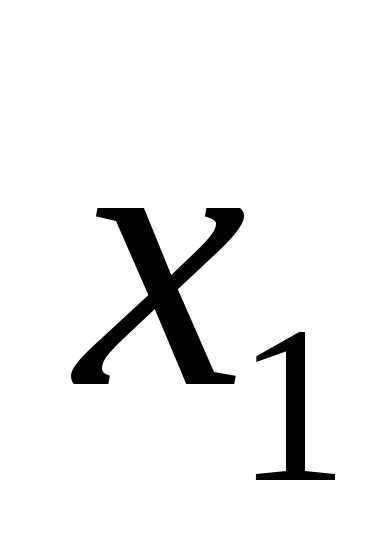 ,
,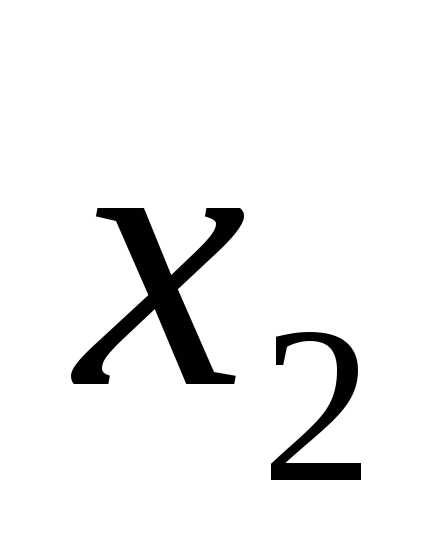 ,…,
,…,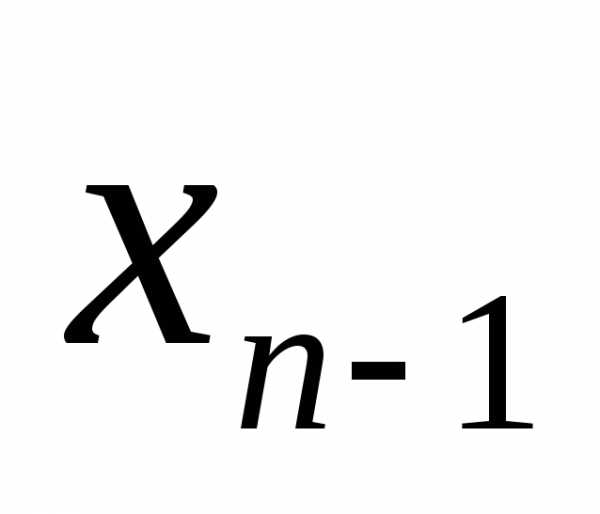 ),
без переменной
),
без переменной 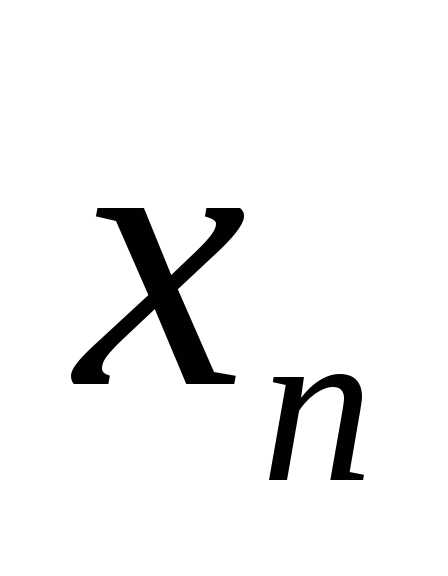 .
Главные миноры формы
.
Главные миноры формы  совпадают с главными минорами формы
совпадают с главными минорами формы  ,
кроме последнего. Пусть все главные
миноры строго положительны. По
предположению индукции форма
,
кроме последнего. Пусть все главные
миноры строго положительны. По
предположению индукции форма  положительно определенная и может быть
невырожденным линейным преобразованием
приведена к виду суммы (
положительно определенная и может быть
невырожденным линейным преобразованием
приведена к виду суммы (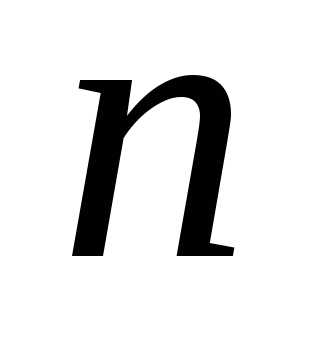 -1)
положительных квадратов от новых
неизвестных переменных y:
(
-1)
положительных квадратов от новых
неизвестных переменных y:
(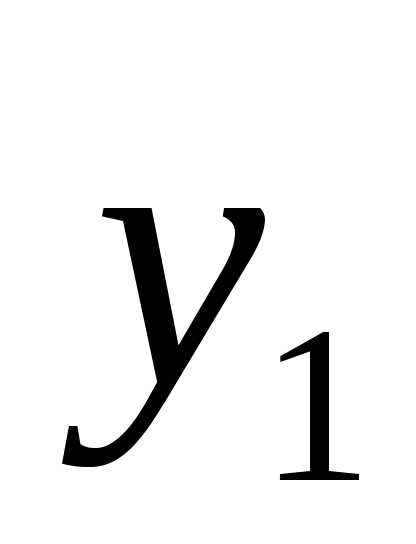 ,
,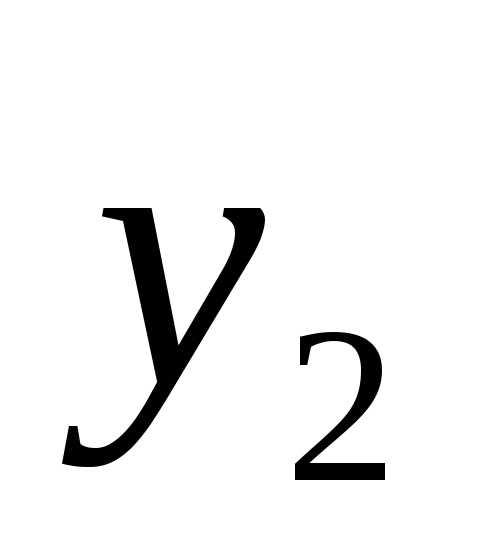 ,…,
,…,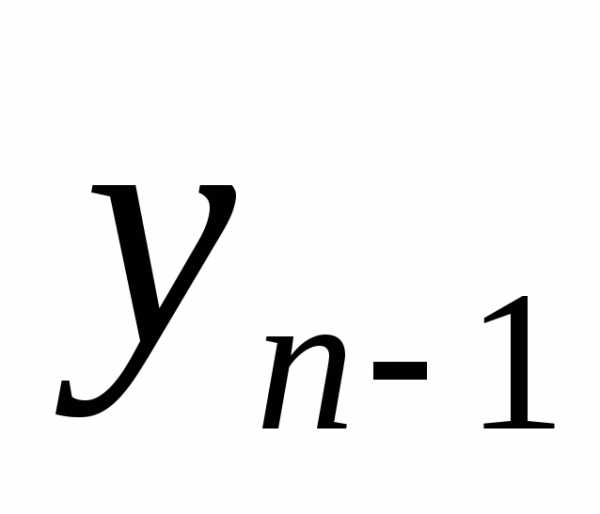 ).
Дополним это преобразование до линейного
(невырожденного) преобразования
неизвестных переменных x: (
).
Дополним это преобразование до линейного
(невырожденного) преобразования
неизвестных переменных x: (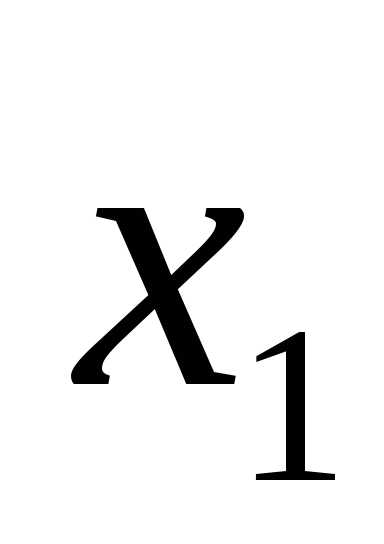 ,
,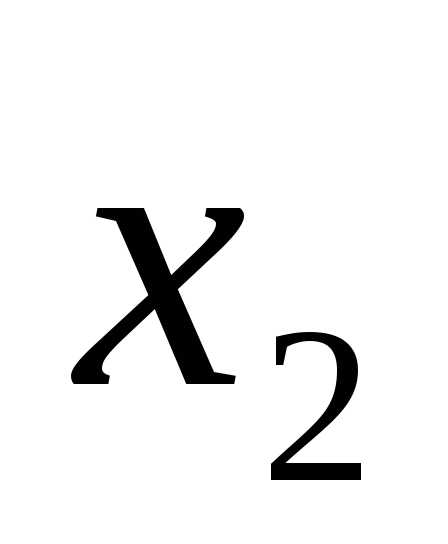 ,…,
,…,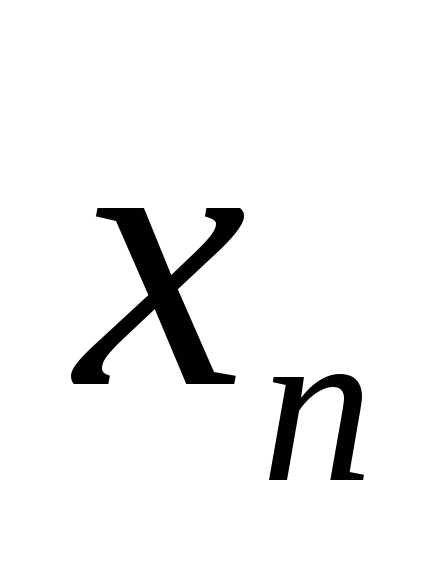 ),
полагая значение переменной:
),
полагая значение переменной: 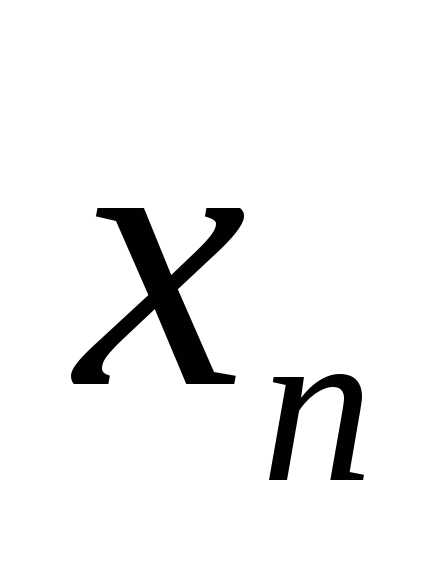 =
=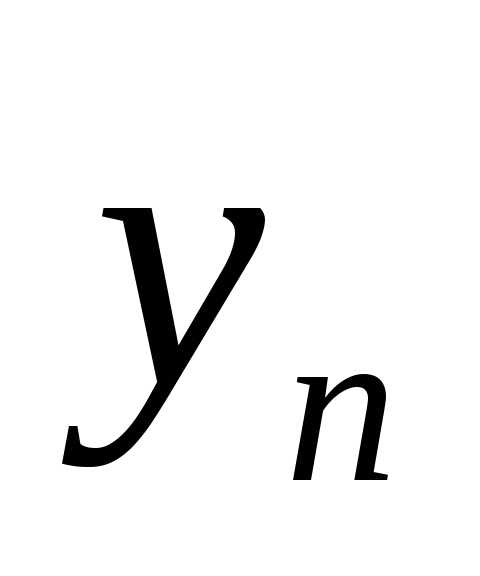 → получим:
→ получим:
f =  +2
+2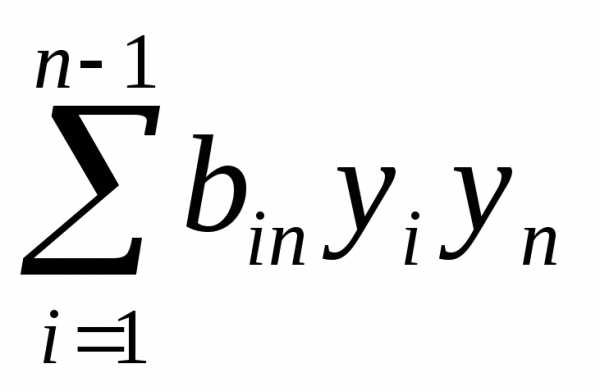 +
+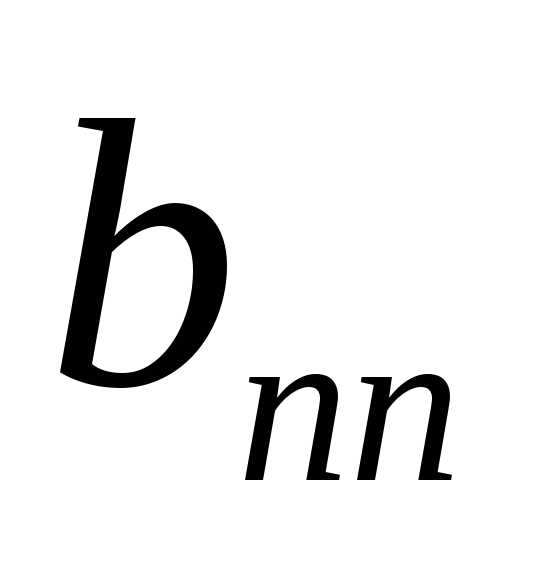 ·
·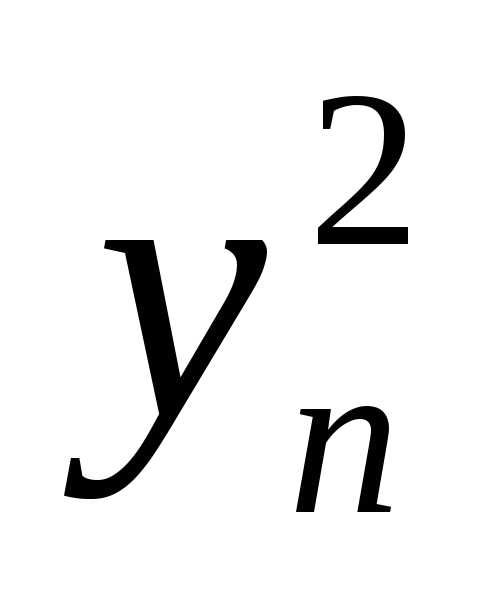 ,
(3)
,
(3)
причем точные выражения коэффициентов bin не требуются. Запишем тождество:
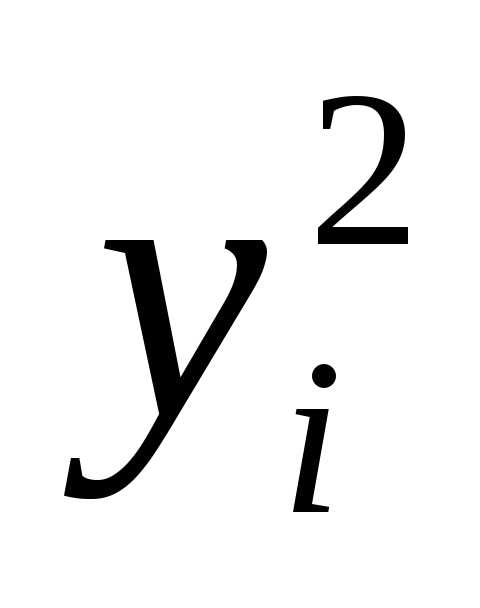 +2
+2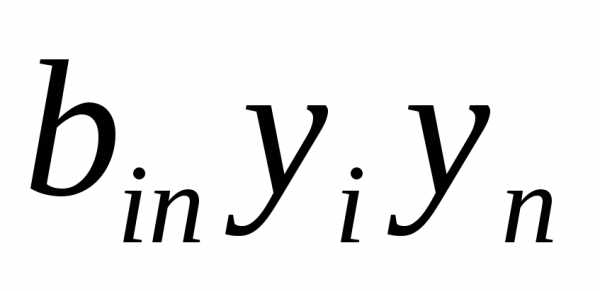 =–
=–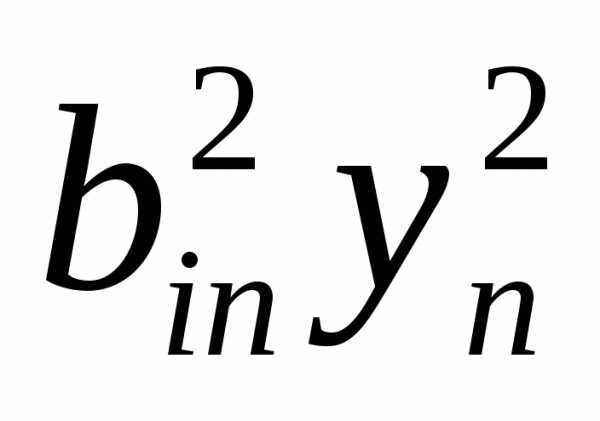 .
(4)
.
(4)
Далее применим невырожденное линейное преобразование переменных квадратичной формы (3):
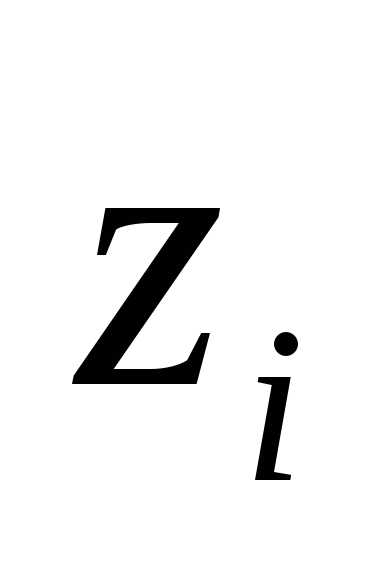 =
=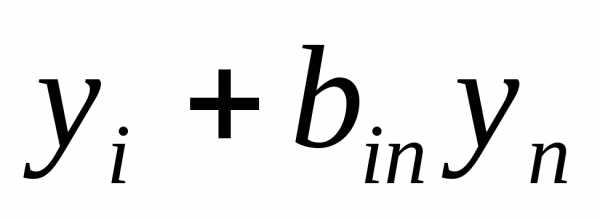 ,
, 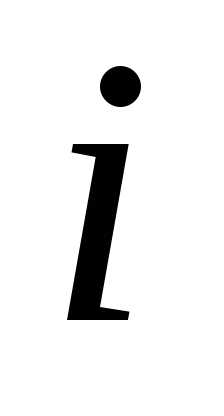 =,
=,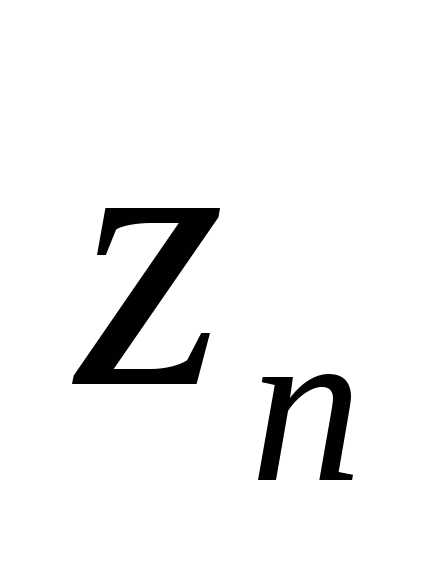 =
=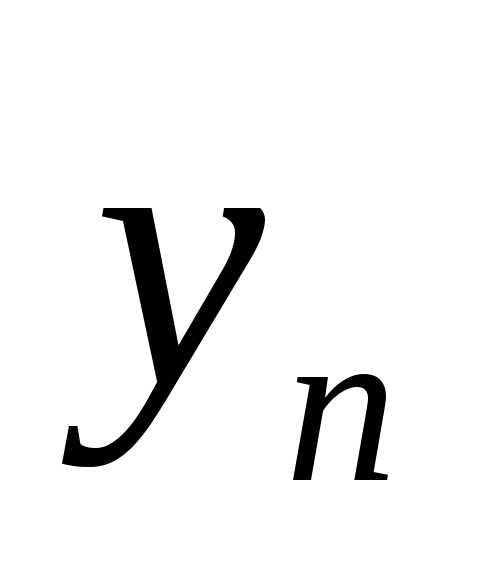 . (5)
. (5)
Легко
видеть, что преобразование переменных:
(4) приводит форму  к каноническому виду: f =
к каноническому виду: f =  +c
+c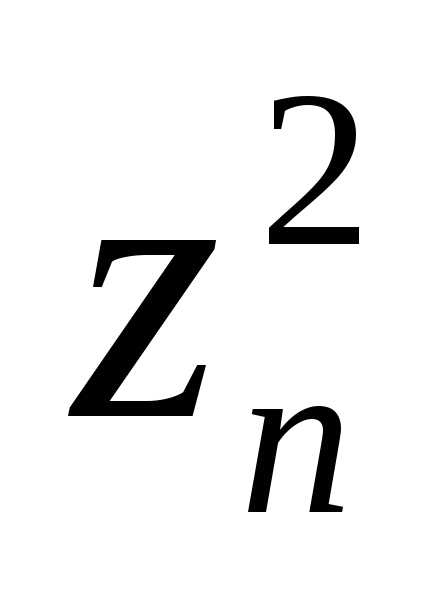 .
(6)
.
(6)
Матрица  квадратичной
формы (6) получена двумя невырожденными
преобразованиями переменных формы.
Значит матрица
квадратичной
формы (6) получена двумя невырожденными
преобразованиями переменных формы.
Значит матрица  —
невырожденная. Так как по
условию главный минор заданной
квадратичной формы: |
—
невырожденная. Так как по
условию главный минор заданной
квадратичной формы: | |>0,
то, в соответствии с
Теоремой 11.2, необходимо
|
|>0,
то, в соответствии с
Теоремой 11.2, необходимо
| |>0.
Из этого следует, что с –
положительное число. Следовательно,
форма положительно определенная.
◄
|>0.
Из этого следует, что с –
положительное число. Следовательно,
форма положительно определенная.
◄
Следствие: для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно выполнения неравенств: ∆1 < 0, ∆2 > 0,…, (–1)n∆n> 0.
►Приведем
отрицательно определенную форму к
положительно определенной форме
умножением ее на число (–1).
Это значит, что матрицей преобразованной
квадратичной формы будет матрица: – ,
то есть каждый элемент матрицы
,
то есть каждый элемент матрицы  умножается на число (–1).
В таком случае каждый главный минор
порядка k матрицы –
умножается на число (–1).
В таком случае каждый главный минор
порядка k матрицы – есть минор ∆k порядка k матрицы
есть минор ∆k порядка k матрицы  ,
умноженный на (–1)k (здесь используется свойство определителя:
из каждой строки (столбца) выносим (–1)
за знак определителя). Используем
утверждение Теоремы 11.9 и убеждаемся в
верности Следствия.
◄
,
умноженный на (–1)k (здесь используется свойство определителя:
из каждой строки (столбца) выносим (–1)
за знак определителя). Используем
утверждение Теоремы 11.9 и убеждаемся в
верности Следствия.
◄
Рассмотрим несколько примеров, иллюстрирующих принятые определения и доказанные теоремы о положительно и отрицательно определённых формах.
☺☺
Пример
11–07:Задана квадратичная
форма:  =.
Не приводя формук
каноническому виду, доказать, что форма
– положительно определённая.
=.
Не приводя формук
каноническому виду, доказать, что форма
– положительно определённая.
Решение:
1). Составим матрицу
заданной квадратичной формы:  =
= .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
 =5
→
=5
→ 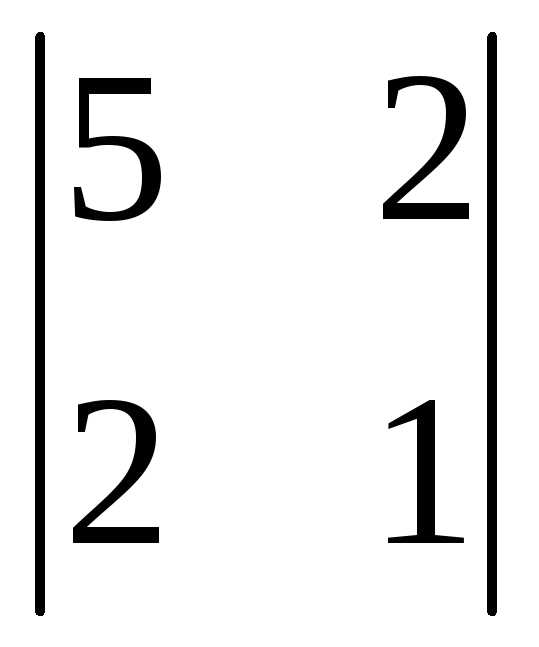 =1
→
=1
→ =1.
=1.
3). Так как все главные миноры квадратичной формы положительны, то заданная квадратичная форма – положительно определённая.
Ответ: доказано.
Пример
11–08:Задана квадратичная
форма:  =.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
=.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
Решение:
1). Составим матрицу
заданной квадратичной формы:  =
= .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
 =3
→
=3
→ 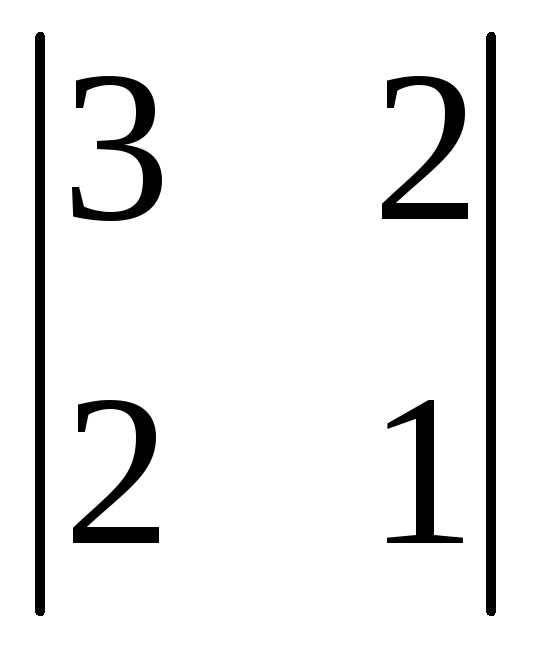 =–1
→
=–1
→ =–1.
=–1.
3). Значения главных миноров квадратичной формы соответствуют неопределённой квадратичной форме.
Ответ: квадратичная форма — неопределённая.
Пример
11–09:Задана квадратичная
форма:  =.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
=.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
Решение:
1). Составим матрицу
заданной квадратичной формы:  =
= .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
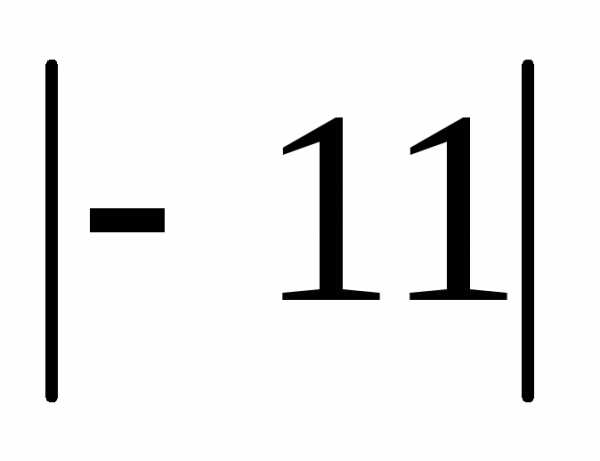 =–11<
0 →
=–11<
0 →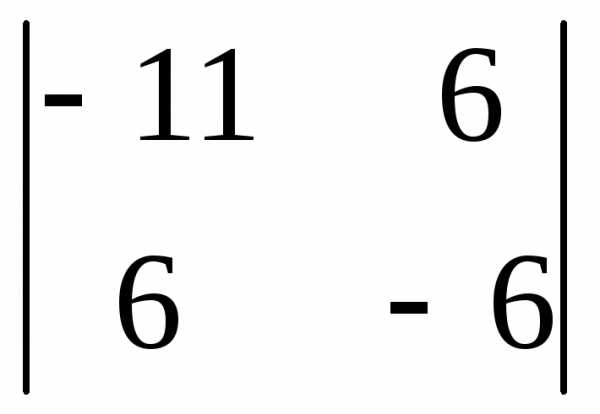 =30>
0→
=30>
0→  =–81<0.
=–81<0.
3). Значения главных миноров квадратичной формы соответствуют отрицательно определённой квадратичной форме.
Ответ: квадратичная форма – отрицательно определённая.
Пример
11–10:Задана квадратичная
форма:  =.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
=.
Не приводя формук
каноническому виду, определить тип
квадратичной формы.
Решение:
0). Чтобы не избежать
вычислений с дробями будем исследовать
квадратичную форму, тип которой совпадает
с типом заданной форм:  =2
=2 =.
=.
1). Составим матрицу
заданной квадратичной формы  :
: =
= .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
 =4→
=4→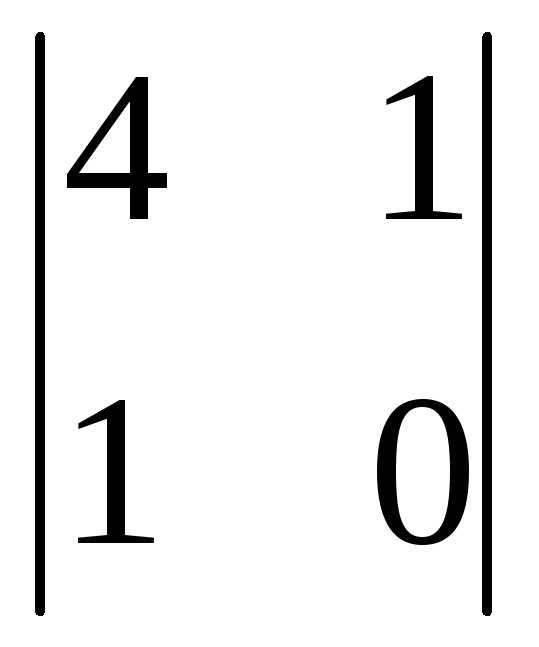 =–1<
0→
=–1<
0→ 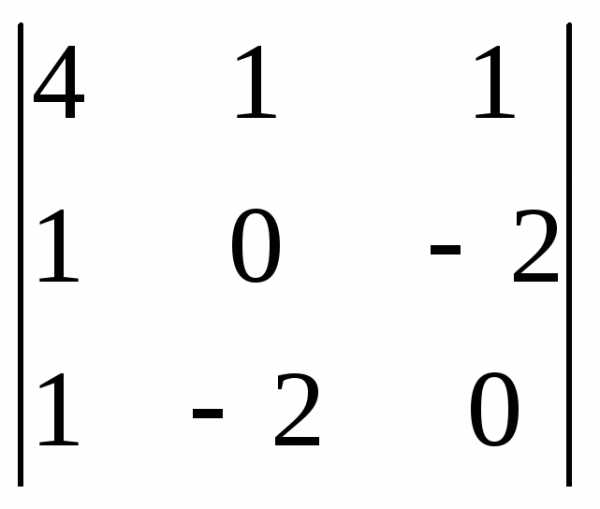 =–20<
0→
=–20<
0→  =
4 >
0.
=
4 >
0.
3). Значения главных миноров квадратичной формы соответствуют неопределённой квадратичной форме.
Ответ: квадратичная форма – неопределённая.
Пример
11–11:Задана квадратичная
форма:  =.
Найти все значения
=.
Найти все значения  ,
при которых квадратичная форма –
положительно определённая.
,
при которых квадратичная форма –
положительно определённая.
Решение:
1). Составим матрицу
заданной квадратичной формы:  =
=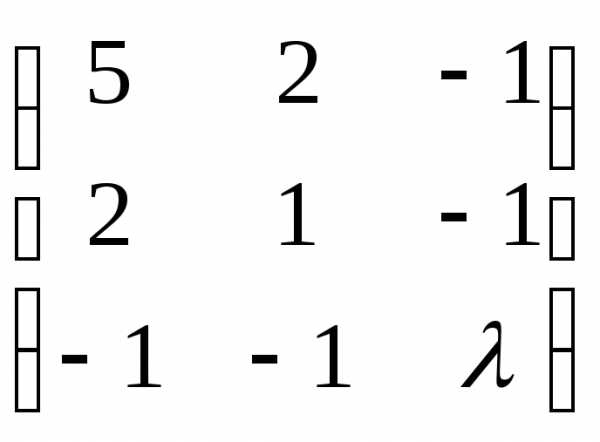 .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
 =5
→
=5
→ 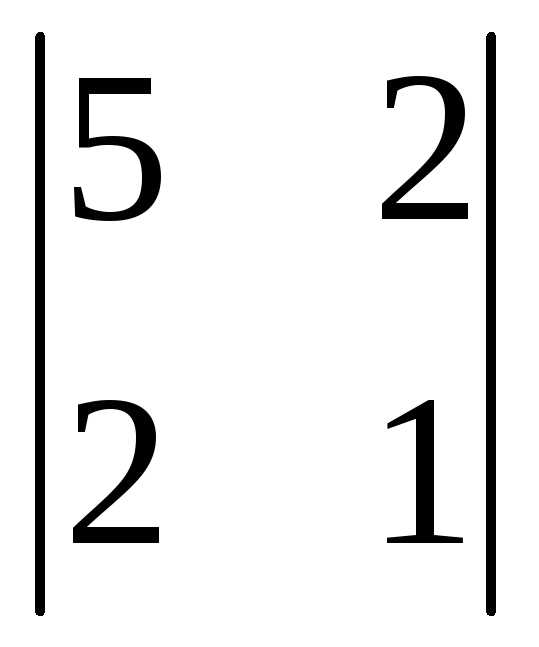 =1
→
=1
→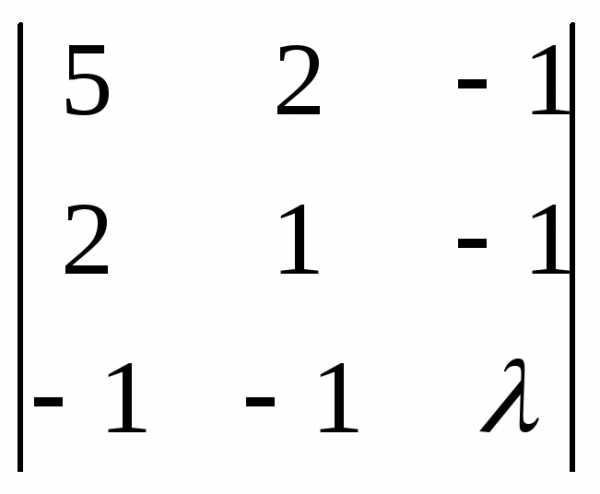 =
= –2.
–2.
3). Для того, чтобы
квадратичная форма была положительно
определённой, необходимо, чтобы
выполнялось условие:  –2>0.
–2>0.
Ответ:
квадратичная форма будет положительно
определённая при условии:  >2.
>2.
Пример
11–12:Задана квадратичная
форма:  =.
Найти все значения
=.
Найти все значения  ,
при которых квадратичная форма –
положительно определённая.
,
при которых квадратичная форма –
положительно определённая.
Решение:
1). Составим матрицу
заданной квадратичной формы:  =
=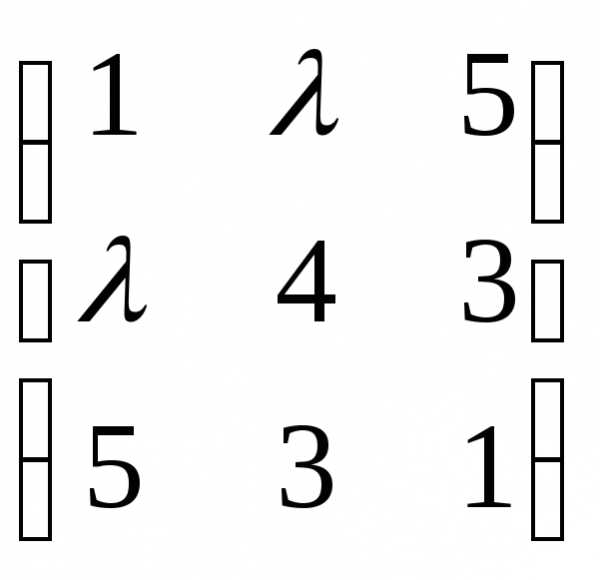 .
.
2). Вычислим главные
миноры заданной квадратичной формы,
учитывая матрицу  :
:
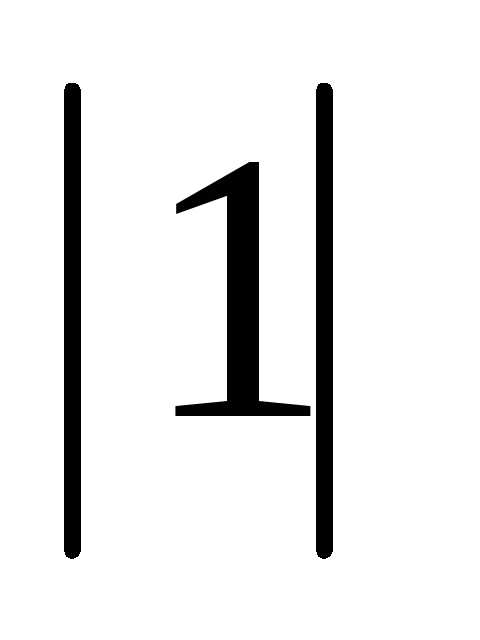 =1
→
=1
→ 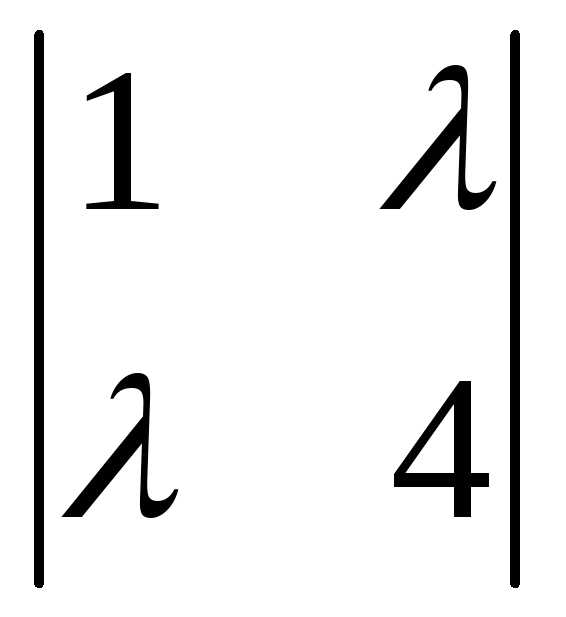 =4–
=4–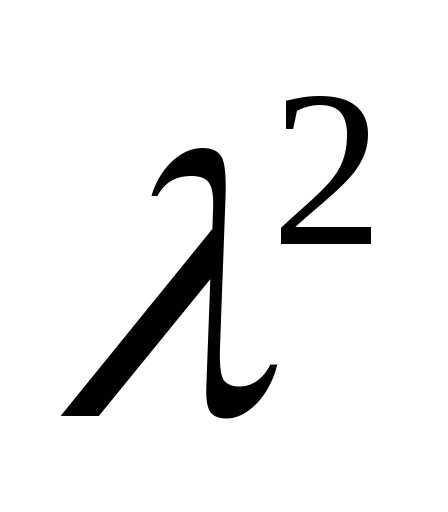 →
→ =
=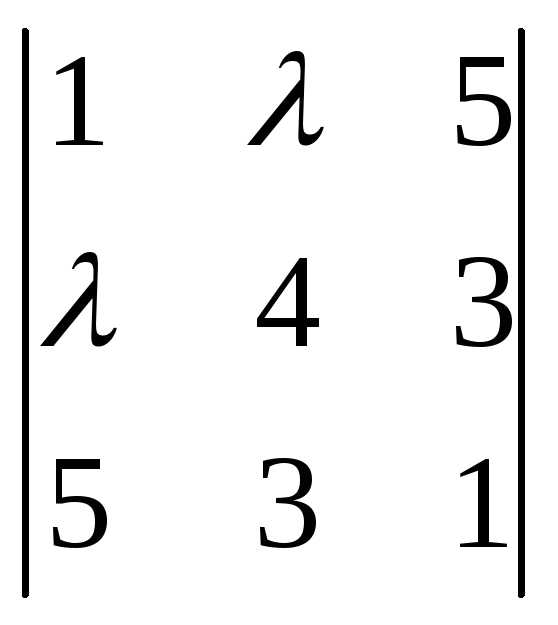 =–(
=–(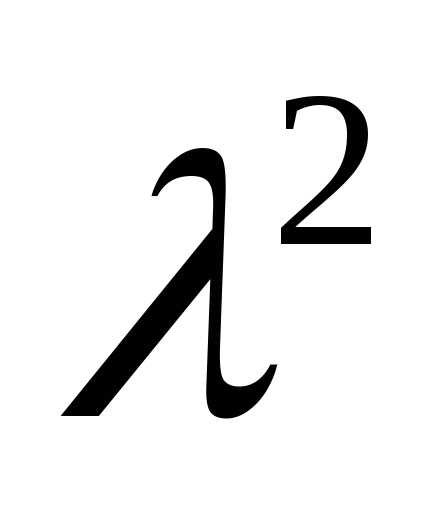 –30
–30 +105).
+105).
3). Решение системы
неравенств: 4–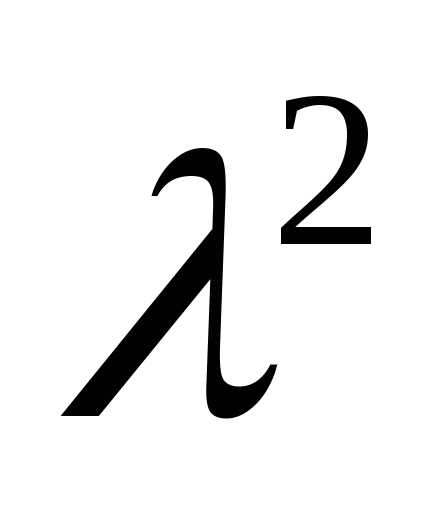 >0,
(
>0,
(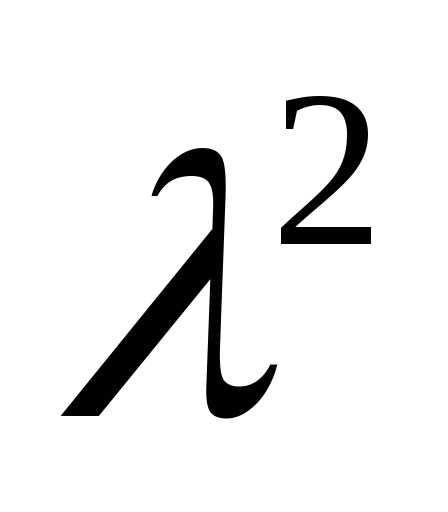 –30
–30 +105)<0
– пустое множество.Следует:
нет таких значений
+105)<0
– пустое множество.Следует:
нет таких значений  ,
при которых квадратичная форма могла
бы быть положительно определённой.
,
при которых квадратичная форма могла
бы быть положительно определённой.
Ответ:нет таких значений  ,
при которых квадратичная форма могла
бы быть положительно определённой.
,
при которых квадратичная форма могла
бы быть положительно определённой.
☻
Набор поясняющих примеров иллюстрирует наиболее сложные теоретические вопросы и предлагает рациональные схемы вычислений участвующих величин.
studfiles.net
Положительно определённая матрица — это… Что такое Положительно определённая матрица?
В линейной алгебре, положи́тельно определённая ма́трица — это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или полуторалинейной формой в случае с комплексными числами).
Формулировки
Пусть будет эрмитовой матрицей размерности . Обозначим транспонированный вектор посредством , а сопряжённый транспонированный вектор — посредством .
Матрица является положительно определённой, если она удовлетворяет любому из следующих равнозначных критериев:
| 1. | Для всех ненулевых комплексных векторов , Отметим, что величина всегда вещественна, поскольку — эрмитова матрица. |
| 2. | Все собственные значения , , положительны. Любая эрмитова матрица по теореме о спектральном разложении может быть представлена как вещественная диагональная матрица , переведённая в другую систему координат (то есть , где — унитарная матрица, строками которой являются ортонормальные собственные векторы , образующие базис). По этому определению — положительно определённая матрица, если все элементы главной диагонали (или, другими словами, собственные значения ) положительны. То есть в базисе, состоящем из собственных векторов , действие на вектор равносильно покомпонентному умножению на положительный вектор. |
| 3. | Полуторалинейная форма определяет внутреннее произведение в . Обобщая сказанное, любое внутреннее произведение в образуется из эрмитовой положительно определённой матрицы. |
| 4. | — матрица Грама, образованная из множества линейно независимых векторов для какого-то . Другими словами, элементы определены следующим образом Таким образом, , где инъективная, но не обязательно квадратная матрица. |
| 5. | Определители всех угловых миноров матриц положительны (критерий Сильвестра). В соответствии с этим критерием у положительно полуопределённых матриц все угловые миноры неотрицательны, что, тем не менее, не является достаточным условием для положительной полуопределённости матрицы, как видно из следующего примера |
Для вещественных симметричных матриц в вышеприведённых свойствах пространство может быть заменено на , а сопряжённые транспонированные векторы на транспонированные.
Квадратичные формы
Также можно сформулировать положительную определённость через квадратичные формы. Пусть будет полем вещественных () или комплексных () чисел, а будет векторным пространством над . Эрмитова форма
является билинейным отображением, притом числом, сопряженным , будет . Такая функция называется положительно определённой, когда для любого ненулевого .
Отрицательно определённая, полуопределённая и неопределённая матрицы
Эрмитова матрица размерности будет называться отрицательно определённой, если
для всех ненулевых (или, эквивалентным образом, для всех ненулевых ).
будет называться положительно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
будет называться отрицательно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
Таким образом, матрица будет отрицательно определённой, если все её собственные значения отрицательны, положительно полуопределённой, если все её собственные значения неотрицательны, и отрицательно полуопределённой, если все её собственные значения неположительны.
Матрица будет положительно полуопределённой тогда и только тогда, когда она является матрицей Грама какого-нибудь множества векторов. В отличие от положительно определённой матрицы данные векторы не обязательно линейно независимы.
Для любой матрицы выполняется следующее: — положительно полуопределённая, а . Обратное утверждение также верно: любая положительно полуопределённая матрица может быть выражена как (разложение Холецкого).
Эрмитова матрица не являющаяся ни положительно, ни отрицательно полуопределённой называется неопределённой.
Дополнительные свойства
Введём обозначение для положительно полуопределённых матриц и — для положительно определённых матриц.
Для произвольных квадратных матриц будем писать , если , то есть положительно полуопределённая матрица. Таким образом, отношение определяет частичный порядок на множестве квадратных матриц. Подобным образом можно определить отношение полного порядка .
| 1. | Любая положительно определённая матрица обратима, а её обратная матрица также положительно определённая. Если , то . |
| 2. | Если — положительно определённая матрица и , то положительно определённая матрица. Если and — положительно определённые матрицы, то произведения и тоже положительно определённые. Если , то тоже положительно определённая. |
| 3. | Если — положительно определённая матрица, то элементы главной диагонали положительны. Следовательно, . Более того,
|
| 4. | — положительно определённая матрица тогда и только тогда, когда существует положительно определённая такая, что . Обозначим . Такая матрица единственна при условии, что . Если , то . |
| 5. | Если and — положительно определённые матрицы, то (где обозначает произведение Кронекера). |
| 6. | Если and — положительно определённые матрицы, то (где обозначает произведение Адамара). Когда вещественные матрицы, выполняется также следующее неравенство (неравенство Оппенхейма): . |
| 7. | Если — положительно определённая матрица, а — эрмитова матрица и , то . |
| 8. | Если and — положительно полуопределённые вещественные матрицы, то . |
| 9. | Если — положительно определённая вещественная матрица, то существует число такое, что , где — единичная матрица. |
Неэрмитовы матрицы
Вещественные несимметрические матрицы тоже могут удовлетворять неравенству для всех ненулевых вещественных векторов . Такой, к примеру, является матрица
поскольку для всех ненулевых вещественных векторов
Обобщая, для всех ненулевых вещественных векторов тогда и только тогда, когда симметрическая часть положительно определённая.
Для комплексных матриц существует несколько обобщений неравенства . Если для всех ненулевых комплексных векторов , тогда матрица эрмитова. То есть если , то эрмитова. С другой стороны, для всех ненулевых комплексных векторов тогда и только тогда, когда эрмитова часть положительно определённая.
Литература
- R. A. Horn, C. R. Johnson. Matrix Analysis, Cambridge University Press, Ch. 7, 1985.
- R. Bhatia, Positive definite matrices, Princeton Series in Applied Mathematics, 2007.
См. также
dic.academic.ru
48. Положительно и отрицательно определенные квадратичные формы
Квадратичная форма Называется Положительно определенной, если значение на каждом ненулевом значении больше нуля, т. е.:
, если ,
Если же на каждом , то квадратичная форма называется Отрицательно определенной.
Теорема. Дана квадратичная форма , – ее канонический базис, а выражение , Канонический вид в базисе . Тогда справедливы следующие утверждения:
1. Квадратичная форма положительно определена тогда и только тогда, когда , ,…,.
2. Квадратичная форма отрицательно определена тогда и только тогда, когда , ,…,.
Доказательство:
Необходимость. Дано, что – положительно определенная форма. Так как , то и поэтому .
Достаточность. Дано, что в каноническом виде все коэффициенты , ,…,. Нужно доказать, что положительно определена. Рассмотрим произвольный ненулевой вектор и разложим его по базису :
Так как , то в разложении не все коэффициенты равны нулю. Следовательно , так как , ,…, и среди чисел хотя бы одно отлично от нуля.
Аналогично доказывается и второе утверждение.
Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.
Теорема. Дана квадратичная форма . Тогда справедливы следующие утверждения:
1. Квадратичная форма положительно определена тогда и только тогда, когда все собственные значения матрицы положительны.
2. Квадратичная форма отрицательно определена тогда и только тогда, когда все собственные значения матрицы отрицательны.
Доказательство:
Докажем первое утверждение. Рассмотрим ортонормированный базис пространства , состоящий из собственных векторов симметрической матрицы , и пусть , . Тогда – канонический базис квадратичной формы , а выражение – ее канонический вид в базисе . Теперь первое утверждение этой теоремы вытекает из первого предложения предыдущей теоремы.
Второе предложение доказывается аналогично.
Лемма. Если какой-нибудь угловой минор матрицы равен нулю, то найдется такой ненулевой вектор , что .
Теорема (Критерий Сильвестра). Справедливы следующие утверждения:
1. Квадратичная форма положительно определена тогда и только тогда, когда главные миноры матрицы положительны.
2. Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры матрицы четного порядка положительны, а главные миноры матрицы нечетного порядка отрицательны.
Доказательство: Докажем первое утверждение.
Необходимость. Дано, что положительно определена. Покажем, что все угловые миноры матрицы отличны от нуля. Допустим обратное, и пусть . Тогда согласно Лемме найдется такой ненулевой вектор , что . Однако это противоречит положительной определенности квадратичной формы.
Итак, матрица удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби , которая является каноническим базисом , причем выражение – Ее канонический вид в базисе . Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что , и значит, что .
Достаточность. Если , то угловые миноры матрицы отличны от нуля, и можно построить канонический базис квадратичной формы , в котором – Канонический вид квадратичной формы . Поскольку , то положительно определена.
Аналогично доказывается второе утверждение теоремы.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
отрицательная матрица — это… Что такое отрицательная матрица?
- отрицательная матрица
- мат. negative matrix
Большой англо-русский и русско-английский словарь. 2001.
- отрицательная логика
- отрицательная метрика
Смотреть что такое «отрицательная матрица» в других словарях:
Гессе матрица — [Hessian matrix] матрица вторых частных производных функций нескольких переменных: Определитель этой матрицы называется гессианом. Характеристика матрицы Гессе (ее отрицательная или положительная определенность и полуопределенность) служит… … Экономико-математический словарь
Гессе матрица — Матрица вторых частных производных функций нескольких переменных: Определитель этой матрицы называется гессианом. Характеристика матрицы Гессе (ее отрицательная или положительная определенность и полуопределенность) служит условием для… … Справочник технического переводчика
продуктивность матрицы МОБ — Требование, предъявляемое при анализе балансовых уравнений[1] AX + Y = X и состоящее в том, что для получения неотрицательного решения (вектора x) матрица А должна быть продуктивной. Продуктивной называется неотрицательная матрица A ? 0, если… … Справочник технического переводчика
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Метод узловых потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при… … Википедия
Метод контурных токов — Метод контурных токов метод сокращения размерности системы уравнений, описывающей электрическую цепь. Содержание 1 Основные принципы 2 Построение системы контуров … Википедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
Метод максимального правдоподобия — или метод наибольшего правдоподобия (ММП, ML, MLE Maximum Likelihood Estimation) в математической статистике это метод оценивания неизвестного параметра путём максимизации функции правдоподобия[1]. Основан на предположении о том, что… … Википедия
Список наиболее употребительных аббревиатур, встречающихся в научно-технической литературе по электронике — … Википедия
Насадочная линза — Насадочная линза дополнительное приспособление к объективу, служащее для изменения величины его фокусного расстояния (угла изображения). Она заключена в оправу и надевается непосредственно на объектив. Положительная линза уменьшает фокусное … Википедия
dic.academic.ru
Матрица отрицательно — Энциклопедия по экономике
Из модели диверсификации следует, что эффективность функционирования стабилизируется, когда использование продукта разбросано во времени и пространстве, в особенности когда изменения в эффективности каждого отрицательно коррелируют между собой или друг от друга. В матрице рост — доля рынка рующий эффект ожидается от продукта группы корова , однако существует возможность, что каждый про- [c.135]Чтобы квалифицированно ответить на этот вопрос, необходимо провести системный сравнительный анализ, выявить положительные и отрицательные моменты, а затем уже решать, в каком направлении вести поиски. В этой связи особую ценность представляют разработка модели федерального экономического пространства в системе товарно-денежных отношений и матрицы видов системно-экономической деятельности на федеральном, региональном и местном уровнях управления теоретическое осмысление технологии перехода к многоуровневой системе образования, оценка проводимых экспериментов и критический анализ происходящих революционных процессов в высшей школе. [c.70]
Но прежде чем переходить к проблемам планирования на основе межотраслевых балансов, необходимо выяснить, существует ли обратная матрица, используемая в формуле (2.4), а также не получим ли мы когда-нибудь отрицательные значения валовых выпусков отраслей Прежде чем ответить на этот вопрос, установим некоторые свойства коэффициентов прямых затрат. Во-первых, они неотрицательны, т. е. [c.136]
Выбору оптимального варианта методом итераций помогает составление положительно-отрицательной матрицы. В этом диалектическом сочетании противоположностей выражается как бы сама суть отбора оптимального решения. Набору всего положительного в избираемом варианте решения противопоставляется все отрицательное, могущее затруднить реализацию идеи и внедрение ее в практику. Теоретический анализ, доведенный до наивысшей степени объективности, позволяет выбрать действительно оптимальное решение. [c.218]
В формализованном виде отрицательный ответ о продолжении процедуры преобразования матрицы в формализованном виде выглядит так [c.50]
Решение подобных задач требует определенности в формулировании их условий установления количества игроков и правил игры, выявления возможных стратегий игроков, возможных выигрышей (отрицательный выигрыш понимается как проигрыш). Важным элементом в условии задач является стратегия, т. е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор данного игрока. Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. При исследовании конечной игры задаются матрицы выигрышей, а бесконечной — функции выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также сведение задачи к некоторой системе дифференциальных уравнений. [c.51]
Если матрица (10.12) имеет как положительные, так и отрицательные собственные значения, то вопрос не решается столь однозначно. Возможно, в этом случае имеет смысл предпочесть короткую модель (10.2), если след матрицы (10.12) положителен. [c.246]
В основе Бостонской матрицы, или матрицы роста/доли рынка лежит модель жизненного цикла товара, в соответствии с которой товар в своем развитии проходит четыре стадии выход на рынок (товар- проблема ), рост (товар- звезда ), зрелость (товар— дойная корова ) и спад (товар- собака>>). При этом денежные потоки и прибыль предприятия также меняются отрицательная прибыль сменяется ее ростом и затем постепенным снижением. Бостонская матрица концентрируется на положительных и отрицательных денежных потоках, которые ассоциируются с различными бизнес-единицами предприятия или его продуктами. [c.72]
На этот раз в четвертой ячейке столбца ответов мы получили отрицательный результат. Это означает, что нам следует инвестировать отрицательную сумму в размере 9,81% капитала в сберегательный счет. Чтобы решить проблему отрицательного X (т.е. когда значение на пересечении строки i и крайнего правого столбца меньшее или равно нулю), мы должны удалить из первоначальной расширенной матрицы строку i + 2 и столбец i и решить задачу для новой расширенной матрицы. Если значения последних двух строк крайнего правого столбца меньше или равны нулю, нам не о чем беспокоиться, поскольку они соответствуют множителям Лагранжа и могут принимать отрицательные значения. Так как отрицательное значение переменной соответствует отрицательному весу четвертого компонента, мы удалим из первоначальной расширенной матрицы четвертый столбец и шестую строку. Затем используем построчные операции для проведения элементарных преобразований, чтобы получить единичную матрицу [c.198]
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения [c.241]
Теперь, соединяя вместе анализ матрицы весов, учет положительных и отрицательных влияний и выходных значений кластеров, мы в состоянии оценить значимость вклада каждой из переменных. Б случае, если разные подходы приведут к разным выводам, следует, скорее, доверять результатам кластерного анализа в силу его многомерной природы. [c.110]
Очевидно, следует переместиться по стороне АВ как можно дальше от точки А, чтобы как можно больше уменьшить целевую функцию. Стало быть, можно взять в качестве координаты х, точки В ее максимальное возможное значение, допускаемое системой уравнений (3.5), соответствующей матрице (3.15), т.е. такое, при котором ни одна из переменных не становится отрицательной. [c.70]
Внутренние источники — это люди, работаю-щие в организации. В ряде стран, например Японии, при появлении вакансий в аппарате управления принято вначале объявлять внутренний конкурс на замещение должности из числа своих сотрудников и только затем, в случае отрицательных результатов, приглашать к участию в конкурсе специалистов со стороны. Считается, что это улучшает моральный климат в коллективе, укрепляет веру сотрудников в свою организацию. При работе с резервом во всех крупных фирмах существуют так называемые матрицы перемещений, в которых находит отражение настоящее положение каждого руководителя, его возможные перемещения и степень готовности к занятию следующей должности (гостов занять немедленно через год, через два года, но для этого необходимо повышение квалификации в определенных областях и т. д.)1. [c.222]
Кроме того, для отображения отрицательных значений изменения объема продаж используется более сложная форма рассмотренной матрицы (рис. 2.4). [c.38]
Поясните содержание, положительные и отрицательные стороны таких методов анализа продуктового портфеля, как матрица Бостонской консультационной группы и матрица корпорации Дженерал Электрик . [c.69]
О — безразличный выбор. Результаты опроса заносятся в групповую матрицу (табл. 7.2), которая позволяет наглядно представить первичную информацию и упростить математическую обработку собранных данных. Социометрическая матрица представляет собой таблицу, в которой по строкам помещены ответы каждого нз опрошенных членов группы (по дихотомическому критерию) + означает предпочтение (положительный выбор), — — отвергается (отрицательный выбор), О — фиксирует отсутствие выбора. [c.222]
Предполагается, что F x) является дважды непрерывно дифференцируемой и неоклассической, кроме того, ее матрица вторых производных отрицательно определена. [c.227]
Однако наличие второго слагаемого позволяет в ряде случаев добиться отрицательной определенности матрицы Г. Для этого диагональные элементы должны быть отрицательны и достаточно велики по модулю. Второе слагаемое в диагональных элементах имеет вид [c.348]
После того, как выбран вектор Xk, удовлетворяющий уравнению (9.137) и обеспечивающий отрицательную определенность матрицы Г, решение задачи (9.121) позволяет найти вектор xok = а (Л/с), а по нему ok = f(xok). Условия для пересчета коэффициентов аппроксимации /оа запишутся в виде [c.361]
Если исходная задача является задачей максимизации, то все элементы матрицы стоимостей следует умножить на (-1) и сложить их с достаточно большим числом так, чтобы матрица не содержала бы отрицательных элементов. Затем задачу следует решать как задачу минимизации. [c.504]
Аналогичное утверждение можно сформулировать и доказать для отрицательно (полу)определенных матриц заменой А на —А. (Примеч. пер.) [c.36]
Прежде чем переходить к проблемам планирования па основе межотраслевых балансов, необходимо выяснить, существует ли обратная матрица, используемая в формуле (2.4), а такж е не получим ли мы отрицательные значения валовых выпусков отраслей. [c.264]
Проверим целесообразность размещения грузов в клетках, в которых находятся вершины углов. Очевидно, более целесообразно переместить по 14 т груза (наименьшее значение груза в отрицательных клетках) из клетки Ь2а в клетку Ьгат, из клетки 65яз в клетку Ь5а2, из клетки 63а2 — в клетку Ьт,а. После перемещения матрица примет вид (матрица 7). Матрицу 7 постройте самостоятельно. Целевая функция, как это следует из матрицы 7, привела к последующему сокращению грузооборота (его величину определите самостоятельно). [c.49]
Один инструмент-матрица «Assessing Opportunities for Innovation», рассматривающая связанные риски под шестью заголовками (привлекательность рынка, деловая синергия, осуществимость идеи, требования к ресурсам, прибыль пользователя и защита идеи), привлекла наибольшее внимание. Путем последовательного перебора множества из двадцати шести положительных и отрицательных индикаторов пользователи могут выбрать идею, наиболее соответствующую их ситуации. Данная матрица может использоваться для проведения скрининга нескольких перспективных идей, однако наиболее эффективно использовать ее для выявления факторов риска, связанных с воплощением выбранной идеи. Это весьма важный момент. Несмотря на то что факт отказа от идеи -явление достаточно неприятное, фирмам следует знать заранее риски, которые их ожидают в случае обращения к той или другой идее Матрица помогает выбирать среднее между риском и потенциальным выигрышем. [c.25]
Далее обозначим рассматриваемую многотранспортную сеть как сеть G, матрицу соответствующей системы — как матрицу G. В системе уравнений (11 ) заменим все отрицательные коэффициенты их модулями. Получим систему уравнений, отображающую сеть Кенига. Назовем ее сетью G, а ее матрицу— матрицей G. Такое обозначение сетей и матриц не вызовет путаницы, так как из текста всегда будет ясно, что имеется в виду. Подчеркнем, что если некоторый. элемент g v матрицы G равен нулю, то соответствующий ему элемент ёцм матрицы G также равен нулю, а если элемент g матрицы G отличен от нуля,- то и соответствующий ему элемент g v матрицы G также отличен от нуля. [c.150]
Когда вы удаляете строки и столбцы, важно помнить, какие строки каким переменным соответствуют, особенно когда таких строк и столбцов несколько. Допустим, нам надо найти веса в портфеле при Е = 0,1965. Единичная матрица, которую мы сначала получим, будет содержать отрицательные значения для весов Toxi o (Xi) и сберегательного счета (ХД Поэтому вернемся к нашей первоначальной расширенной матрице [c.199]
Оказывается, что ответ на него в общем случае отрицательный. Имеются такие наборы образов, что какую бы матрицу синаптических связей и пороги нейронов, гарантирующие их стационарность, мы не выбрали, в сети с неизбежностью возникнут иные аттракторы. [c.100]
В столбце, обозначенном HIT/MISS, приведены отклонения от целевого значения того прогноза, который 6-3-1 сеть сделала по исходной входной матрице. Погрешность всюду была промасштабирова-на так, чтобы значения располагались от -100 до 100, при этом положительный знак соответствует превышению цели, а отрицательный — недобору. Малые по абсолютной величине числа означают точный прогноз (например, апрель 1984), а большие — значительную ошибку (август 1984). Если абсолютная величина ошибки велика, скажем, больше 40, то в этом случае определить вклад отдельной переменной затруднительно. Следующие 6 столбцов таблицы содержат отклонения выхода сети от целевого значения, соответствующие шести описанным выше входным матрицам. Здесь погрешности также промасштабированы и лежат от -100 до 100. По этим данным [c.146]
По мнению Бостонской консультативной группы, от того, в какой ячейке матрицы расположен товар, зависит показатель движения наличности. Обратите внимание на то, что движение наличности ( ash flow) — не одно и то же, что прибыльность (profitability). Прибыли увеличивают движение наличности, но значительные инвестиции в развитие производства, оборудование и маркетинг нередко приводят к тому, что компания может одновременно иметь прибыль и отрицательный показатель движения наличности. [c.230]
Первое уравнение (4.17) показывает, как изменится выпуск при увеличении цены на продукцию фирмы. Поскольку матрица Гесса Н отрицательно определена, то и матрица Н»1 также отрицательно определена, поэтому [c.234]
Определитель этой матрицы называется гессианом. Характеристика Г.м. (ее отрицательная или положительная определенность и полуопределенность) служит условием для определения вида стационарной точки является ли она соответственно максимумом, минимумом или седловой точкой в задаче оптимизации функции. [c.60]
Кроме того, матрица Гессе вторых производных этой функции по С должна быть при С = 0 отрицательно определенной. [c.342]
Чтобы функция FQ( ) была выпукла, достаточно, чтобы матрица Т = Tij была отрицательно определенной. Первые слагаемые в (9.108) отличаются от элементов 7 j матрицы Гессе исходной задачи неотрицательным множителем, так как функция FQ монотонно возрастающая. Если вторые слагаемые в этих выражениях равны нулю, то вогнутой функции достижимости исходной задачи будет соответствовать вогнутость и FQ( ). [c.348]
Первое из них представляет собой п уравнений относительно составляющих вектора А, а второе — условие отрицательной определенности квадратичной формы, которое проверяется по критерию Сильвестра применительно к матрице Гессе функции R . [c.357]
Здесь и ниже через R f0 и R i обозначены частные производные R по соответствующим переменным. Условиям отрицательной определенности должна удовлетворять матрица Гессе функции R с элементами (см. (9.125)) [c.360]
Желательно, чтобы эти условия выполнялись для всех С а не только для С = 0. Из условий Гершгорина отрицательной определенности матрицы Г [c.361]
Если прибыль рассматривать как отрицательные затраты, то исходная задача максимизации может быть сведена к минимизационной задаче о назначениях. Для того чтобы матрица стоимостей не содержала отрицательных элементов, сложим каждый элемент матрицы с числом 5760 и введем два вида фиктивной продукции (4 и 5), которой соответствует нулевая прибыль. В результате будут получены следующие матрицы [c.508]
Очевидно, что матрицы В В и В В являются неотрицательно определенными /Б, а А — отрицательно (неположительно) определенная матрица тогда и только тогда, когда —А — положительно (полу) определенная матрица. Квадратная нулевая матрица является одновременно неположительно и неотрицательно определенной. [c.27]
Если матрица Гессе Н0(с) не является ни положительно, ни отрицательно определенной, но тем не менее не вырождена, то точка с не может быть точкой локального экстремума (см. теорему 2). Значит, точка с — седловая. [c.169]
economy-ru.info
Отрицательно полуопределённая матрица — это… Что такое Отрицательно полуопределённая матрица?
В линейной алгебре, положи́тельно определённая ма́трица — это эрмитова матрица, которая во многом аналогична положительному вещественному числу. Это понятие тесно связано с положительно определённой симметрической двулинейной формой (или полуторалинейной формой в случае с комплексными числами).
Формулировки
Пусть M будет эрмитовой матрицей размерности . Обозначим транспонированный вектор a посредством aT, а сопряжённый транспонированный вектор — посредством a * .
Матрица M является положительно определённой, если она удовлетворяет любому из следующих равнозначных критериев:
| 1. | Для всех ненулевых комплексных векторов , Отметим, что величина z *Mz всегда вещественна, поскольку M — эрмитова матрица. |
| 2. | Все собственные значения M, , положительны. Вспомним, что любая эрмитова матрица по теореме о спектральном разложении может быть представлена как вещественная диагональная матрица D, переведённая в другую систему координат (то есть M = P − 1DP, где P — унитарная матрица, строками которой являются ортонормальные собственные векторы M, образующие базис). По этому определению M — положительно определённая матрица, если все элементы главной диагонали D (или, другими словами, собственные значения M) положительны. То есть в базисе, состоящем из собственных векторов M, действие M на вектор равносильно покомпонентному умножению z на положительный вектор. |
| 3. | Полуторалинейная форма определяет внутреннее произведение в . Обобщая сказанное, любое внутреннее произведение в образуется из эрмитовой положительно определённой матрицы. |
| 4. | M — матрица Грама, образованная из множества линейно независимых векторов для какого-то k. Другими словами, элементы M определены следующим образом Таким образом, M = A *A, где A инъективная, но не обязательно квадратная матрица. |
| 5. | Определители всех угловых миноров матриц положительны (критерий Сильвестра). В соответствии с этим критерием у положительно полуопределённых матриц все угловые миноры неотрицательны, что, тем не менее, не является достаточным условием для положительной полуопределённости матрицы, как видно из следующего примера |
Для вещественных симметричных матриц в вышеприведённых свойствах пространство может быть заменено на , а сопряжённые транспонированные векторы на транспонированные.
Квадратичные формы
Также можно сформулировать положительную определённость через квадратичные формы. Пусть K будет полем вещественных () или комплексных () чисел, а будет векторным пространством над K. Эрмитова форма
является двулинейным отображением, притом числом, сопряженным , будет . Такая функция B называется положительно определённой, когда для любого ненулевого .
Отрицательно определённая, полуопределённая и неопределённая матрицы
Эрмитова матрица M размерности будет называться отрицательно определённой, если
для всех ненулевых (или, эквивалентным образом, для всех ненулевых ).
M будет называться положительно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
M будет называться отрицательно полуопределённой, если
для всех (или, эквивалентным образом, для всех ).
Таким образом, матрица будет отрицательно определённой, если все её собственные значения отрицательны, положительно полуопределённой, если все её собственные значения неотрицательны, и отрицательно полуопределённой, если все её собственные значения неположительны.
Матрица M будет положительно полуопределённой тогда и только тогда, когда она является матрицей Грама какого-нибудь множества векторов. В отличие от положительно определённой матрицы данные векторы не обязательно линейно независимы.
Для любой матрицы A выполняется следующее: A *A — положительно полуопределённая, а . Обратное утверждение также верно: любая положительно полуопределённая матрица M может быть выражена как M = A *A (разложение Холеского).
Эрмитова матрица не являющаяся ни положительно, ни отрицательно полуопределённой называется неопределённой.
Дополнительные свойства
Введём обозначение для положительно полуопределённых матриц и — для положительно определённых матриц.
Для произвольных квадратных матриц M,N будем писать , если , то есть M − N положительно полуопределённая матрица. Таким образом, отношение определяет частичный порядок на множестве квадратных матриц. Подобным образом можно определить отношение полного порядка .
| 1. | Любая положительно определённая матрица обратима, а её обратная матрица также положительно определённая. Если , то . |
| 2. | Если M — положительно определённая матрица и , то положительно определённая матрица. Если M and N — положительно определённые матрицы, то их сумма M + N и произведения MNM и NMN тоже положительно определённые. Если MN = NM, то MN тоже положительно определённая. |
| 3. | Если M — положительно определённая матрица, то элементы главной диагонали mii положительны. Следовательно, . Более того,
|
| 4. | M — положительно определённая матрица тогда и только тогда, когда существует положительно определённая такая, что B2 = M. Обозначим . Такая матрица B единственна при условии, что . Если , то . |
| 5. | Если M and N — положительно определённые матрицы, то (где обозначает произведение Кронекера). |
| 6. | Если M and N — положительно определённые матрицы, то (где обозначает произведение Адамара). Когда M,N вещественные матрицы, выполняется также следующее неравенство (неравенство Оппенхейма): . |
| 7. | Если M — положительно определённая матрица, а N — эрмитова матрица и , то . |
| 8. | Если M and N — положительно полуопределённые вещественные матрицы, то . |
| 9. | Если M — положительно определённая вещественная матрица, то существует число δ > 0 такое, что , где I — единичная матрица. |
Неэрмитовы матрицы
Вещественные несимметрические матрицы тоже могут удовлетворять неравенству xTMx > 0 для всех ненулевых вещественных векторов x. Такой, к примеру, является матрица
поскольку для всех ненулевых вещественных векторов x = (x1,x2)T
Обобщая, xTMx > 0 для всех ненулевых вещественных векторов x тогда и только тогда, когда симметрическая часть положительно определённая.
Для комплексных матриц существет несколько обобщений неравенства x *Mx > 0. Если x *Mx > 0 для всех ненулевых комплексных векторов x, тогда матрица M эрмитова. То есть если x *Mx > 0, то M эрмитова. С другой стороны, для всех ненулевых комплексных векторов x тогда и только тогда, когда эрмитова часть положительно определённая.
Литература
- R. A. Horn, C. R. Johnson. Matrix Analysis, Cambridge University Press, Ch. 7, 1985.
- R. Bhatia, Positive definite matrices, Princeton Series in Applied Mathematics, 2007.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru

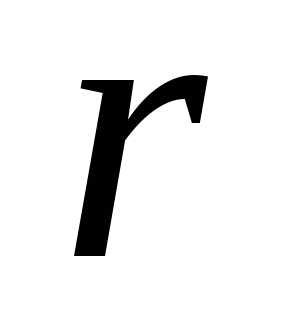 <
< и она приводится к нормальному виду, в
котором присутствуют слагаемые одного
знака.
и она приводится к нормальному виду, в
котором присутствуют слагаемые одного
знака.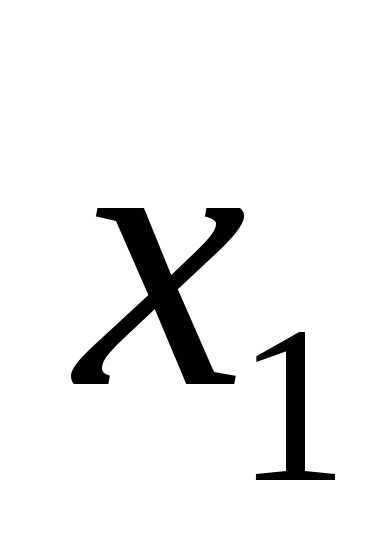 ,
,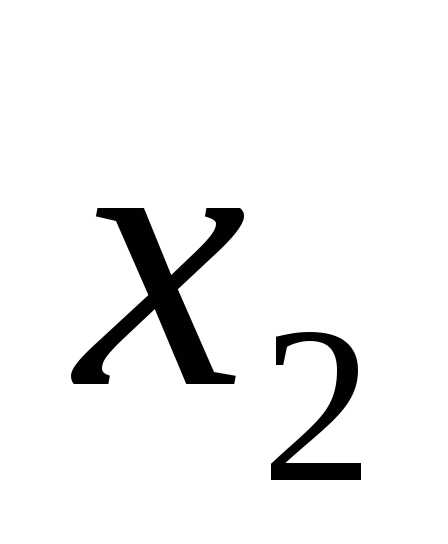 ,…,
,…,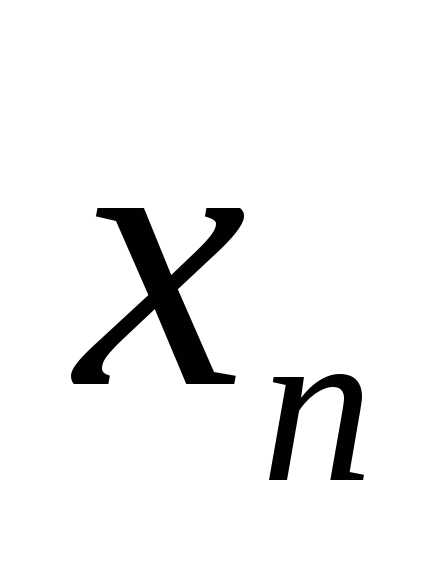 )
с действительными
коэффициентами тогда и только тогда
будет положительно определенной, если
при всяких действительных значениях
этих неизвестных, хотя бы одно из
которых отлично от нуля, эта форма
получает положительные значения.
)
с действительными
коэффициентами тогда и только тогда
будет положительно определенной, если
при всяких действительных значениях
этих неизвестных, хотя бы одно из
которых отлично от нуля, эта форма
получает положительные значения. называется последовательностью главных
миноров формы f.
называется последовательностью главных
миноров формы f.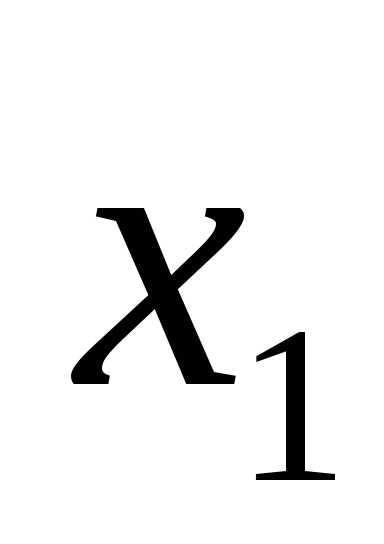 ,
,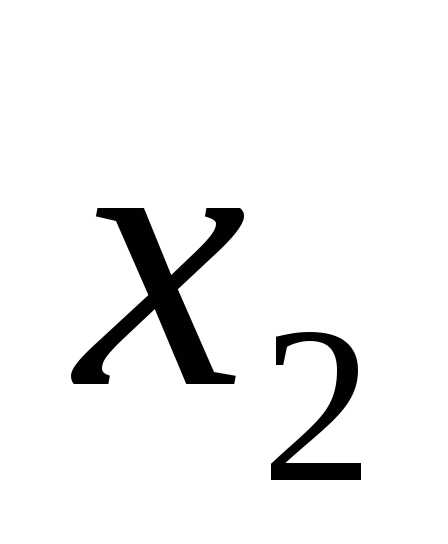 ,…,
,…, )
с действительными
коэффициентами тогда и только тогда
будет положительно определенной, если
все ее главные миноры строго положительны.
)
с действительными
коэффициентами тогда и только тогда
будет положительно определенной, если
все ее главные миноры строго положительны.