1.2.1. Метод простой итерации (метод Якоби)
Метод простой итерации [2], [5] рассмотрим на примере системы трех линейных алгебраических уравнений:
(2)
Которую коротко можно записать в виде матричного уравнения:
Ах=b.
В исходной системе выделим диагональные коэффициенты аii ¹0 (где i =1, 2, 3).Предположим, что диагональные коэффициенты удовлетворяют условиям:
Если хотя бы одно из этих условий не выполняется, то следует провести элементарные преобразования матрицы (см. п.4).
Разрешим первое уравнение системы (2) относительно х1, второе –относительно х2, третье – относительно х3.
В результате получим эквивалентную систему:
(3)
Где при i¹j (i, j=1,2,…,n).
Систему (3) можем записать в матричной форме:.
Систему (3) будем решать методом простой итерации. В качестве нулевого приближения x(0) примем элементы столбца свободных членов:
X(0)=b, т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3.
Далее, находим первое приближение х(1), подставляя найденные значения нулевого приближения в систему (3):
Подставляя значения приближения х(1) в правую часть системы (3), получим:
– второе приближение.
Продолжая этот процесс далее, получим последовательность х(0), x(1), x(2),…, x(k),… приближений, вычисляемых по рабочим формулам:
В общем виде рабочие формулы для системы n-уравнений:
(4)
Если последовательность приближений имеет предел:
То этот предел является решением системы. Таким образом, с увеличением числа итераций растет точность получаемых корней. Однако можно не производить огромное количество итераций, а задать определенную точность e решения, при достижении которой итерационный процесс завершается. Условие окончания итерационного процесса можно записать в виде:
где i= 1,2,3,…, n.
Пример № 1. Методом простой итерации решить систему с точностью e= =10-3.
Решение.
1. Приведем систему к виду (3) . Для этого необходимо все диагональные элементы системы оставить в левой части уравнения, а остальные элементы перенести с противоположным знаком в правую часть. Разделим каждое из уравнений системы на соответствующий коэффициент, стоящий в левой части уравнения:
2. В качестве начального вектора x(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:
3. Вычисления будем вести до тех пор, пока не будет выполнено условие
где e = 10-3, i = 1,2,3,4.
Последовательно вычисляем: при k = 1:
Сравнивая полученные xi(1) с xi(0) , видим, что условия сходимости не выполняются. При k = 2:
Сравнивая полученные xi(2) с xi(1), видим, что условия сходимости не выполняются. При k = 3
Сравнивая полученные xi(3) с xi(2) видим, что условия сходимости не выполняются. При k = 4:
Для сравнения xi(4) с xi(3), найдем модули разностей значений
Так как все найденные значения модулей больше заданного числа
e = 10-3, продолжаем итерации. Получаем при k = 5:
Находим модули разностей значений
Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,7999, x2 = 0,9999, x3 = 1,1999, x4 = 1,3999.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Метод простой итерации для решения уравнения онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Метод итерации или, как его еще принято называть метод последовательных приближений, используется в математике для отыскания корней функциональных уравнений следующего вида:
\[x =F(x)\]
Метод довольно простой и заключается в выборе некоторого начального приближения \[x_0,\] после чего строится итерационная последовательность такого вида:
\[x_{n+1} = F(x_n)\]
С учетом определенных условий данная итерационная последовательность сводится к корню уравнения \[х = F(x),\] благодаря чему ее элементы могут быть взяты за приближенные значения этого корня. В случаях, когда операция, задаваемая функцией \[F,\] удовлетворяет этим условиям, данная операция называется сжатием.
Так же читайте нашу статью «Решить уравнения методом подстановки онлайн»
Этапы решения уравнений методом простой итерации:
— отделение корней. По сути, необходимо найти интервалы их области определителя \[f(x),\] в каждом из которых находится только один корень уравнения \[f(x)=0;\]
— уточнения корней по заданной точности.
Где можно решить уравнение методом простой итерации онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Метод Якоби (простых итераций) — Мегаобучалка
Задана система линейных алгебраических уравнений
или в матричной форме
Для сходимости итерационного процесса, необходимо выполнения условия «преобладания диагональных элементов», т.е. диагональные элементы матрицы А должны удовлетворять условию:
Преобразуем систему (3.10) к эквивалентной, выражая неизвестное из каждого i-го уравнения:
Система (3.13) называется системой, приведенной к нормальному виду.
Вводя обозначения
систему (3.13) можно записать в матричной форме
где
Используя выражение (3.14), строим последовательность приближений (итераций), выбрав в качестве нулевого приближения, например, нулевой вектор или столбец свободных членов:
Таким образом, получили последовательность приближений (итераций):
Если эта последовательность имеет предел
то он является точным решением системы (3.11).
На практике итерационный процесс продолжается до тех пор, пока два соседних приближения не станут достаточно близкими.
Критерий близости двух приближений может быть определен следующим образом:
Если условие (3.18) выполнено, то итерационный процесс прекращается. За приближенное решение системы (3.11) с заданной точностью e принимается (k)-е приближение, т.е.
.
Если условие (3.18) не выполняется, то итерационный процесс (3.17) необходимо продолжить до тех пор, пока условие не выполнится.
G За м е ч а н и я:
1. Начальный вектор может быть взят произвольным, так как сходимость итерационного процесса зависит только от свойств матрицы a, и если процесс сходится при каком-нибудь начальном приближении, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения.
2. Сходящийся процесс итерации обладает важным свойством самоисправляемости, т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так что ошибочное приближение можно рассматривать как новый начальный вектор.
n Пример 3.2.Методом Якоби решить систему линейных алгебраических уравнений:
Решение: Условие преобладания диагональных коэффициентов матрицы системы выполнено. Приведем эту систему к нормальному виду:
В матричной форме систему (3.20) можно записать так:
За начальное (нулевое) приближение решения системы примем нулевой вектор, т.е.
Подставляя эти значения в правые части уравнения (3.20), получим первое приближение решения системы (первую итерацию):
Далее, подставляя это найденное приближение в систему (3.20), получим 2-ое приближение решения системы:
После новой подстановки будем иметь 3-е приближение:
Аналогично получим 4-ую итерацию:
Проверим выполнение условия «близости» двух итераций, т.е. условие (3.18):
Таким образом, за приближенное решение системы (3.19) с точностью ε=0,1 принимаем 4-ю итерацию
Чтобы получить решение СЛАУ (3.19) с точностью ε=0,001 , потребуется 8 итераций. Точное решение: х1=1; х2=2; х3=1.
Решение данного примера с использованием электронных таблиц Excel приведено в разделе 3.6.3.
megaobuchalka.ru
Лекция №5. Итерационные методы решения СЛАУ
Лекция Итерационные методы решения системы алгебраических линейных уравнений.
Условие сходимости итерационного процесса.Метод Якоби.Метод Зейделя
Метод простой итерации
Рассматривается система линейных алгебраических уравнений
Ax = b
Для применения итерационных методов система должна быть приведена к эквивалентному виду
x=Bx+d.
Затем выбирается начальное приближение к решению системы уравненийи находится последовательность приближений к корню.
Для сходимости итерационного процесса
достаточно, чтобы было выполнено условие
(норма матрицы). Критерий окончания
итераций зависит от применяемого
итерационного метода.
Метод Якоби.
Самый простой способ приведения системы к виду, удобному для итерации, состоит в следующем:
Из первого уравнения системы выразим неизвестное x1, из второго уравнения системы выразимx2, и т. д.
В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:
Компоненты вектора d вычисляются по формулам:
Расчетная формула метода простой итерации имеет вид:
или в покоординатной форме записи выглядит так:
Критерий окончания итераций в методе Якоби имеет вид:
Если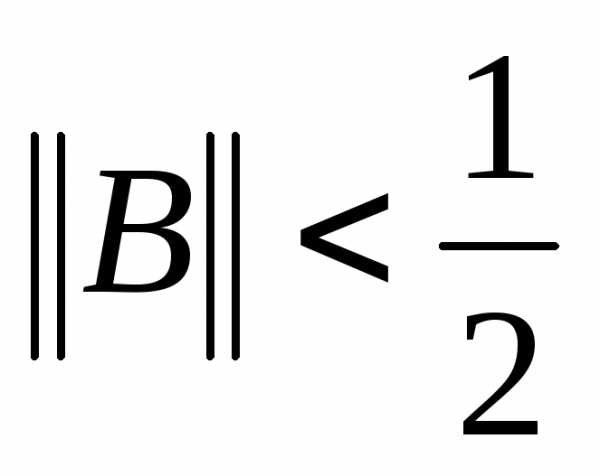 
,
то можно применять более простой критерий
окончания итераций
Пример 1. Решение системы линейных уравнений методом Якоби.
Пусть дана система уравнений:
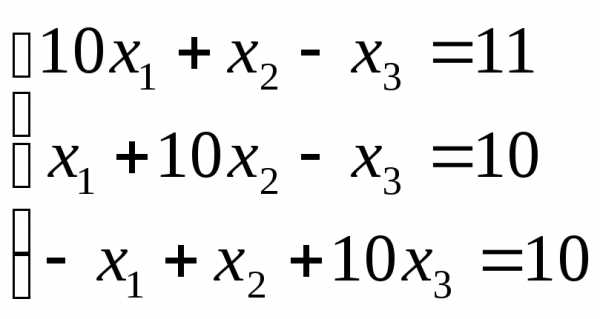
Требуется найти решение системы с
точностью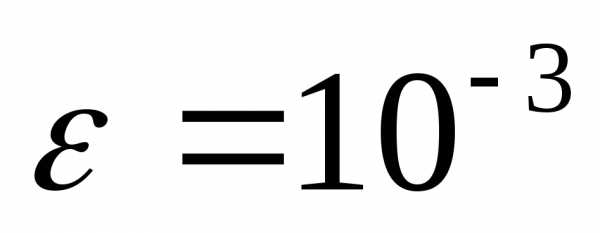 
Приведем систему к виду удобному для итерации:
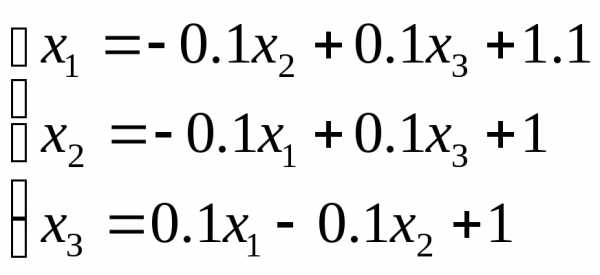
Выберем начальное приближение, например,
— вектор правой части.
Тогда первая итерация получается так:
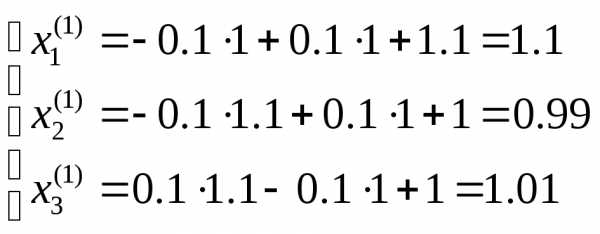
Аналогично получаются следующие приближения к решению.
Найдем норму матрицы B.
Будем использовать норму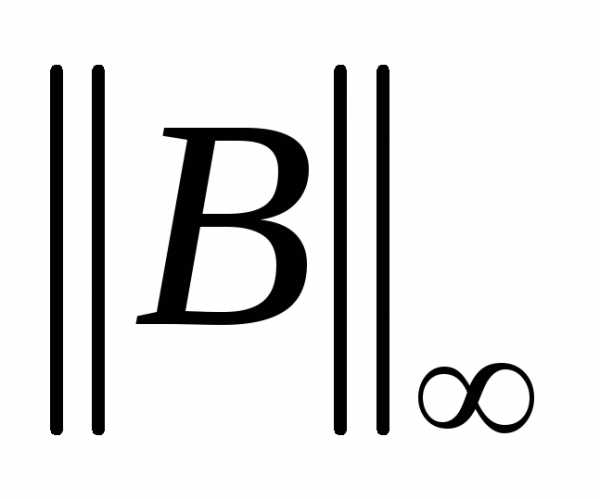 
Так как сумма модулей элементов в каждой строке равна 0.2, то , поэтому критерий окончания итераций в этой задаче
Вычислим нормы разностей векторов:
Так как заданная точность достигнута на четвертой итерации.
Ответ: x1 = 1.102, x2 = 0.991, x3 = 1.011
Метод Зейделя.
Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестномуxiприi >1используют уже найденные(n+1)-е приближения к неизвестнымx1,x2, …,xi — 1, а неn-ое приближение, как в методе Якоби.
Расчетная формула метода в покоординатной форме записи выглядит так:
Условия сходимости и критерий окончания итераций можно взять такими же, как в методе Якоби.
Пример 2.Решение систем линейных уравнений методом Зейделя.
Рассмотрим параллельно решение 3-х систем уравнений:
Приведем системы к виду удобному для итераций:
Заметим, что условие сходимости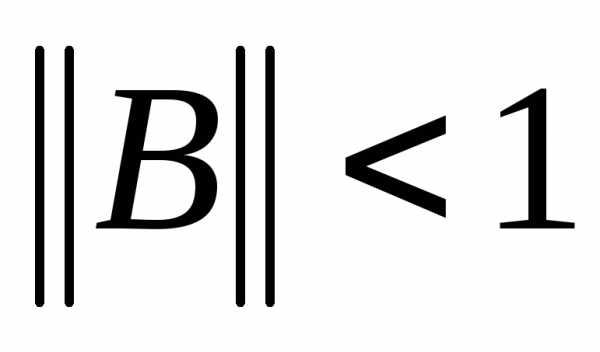 
выполнено только для первой системы.
Вычислим 3 первых приближения к решению
в каждом случае.
1-ая система:
Точным решением будут значения: x1 = 1.4, x2 = 0.2. Итерационный процесс сходится.
2-ая система:
Видно, что итерационный процесс расходится.
Точное решение x 1 = 1, x 2 = 0.2.
3-я система:
Видно, что итерационный процесс зациклился.
Точное решение x 1 = 1, x 2 = 2.
Пусть матрица системы уравнений A – симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.
Метод простой итерации.
Если A – симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду:
x=x-τ (Ax— b), τ – итерационный параметр.
Расчетная формула метода простой итерации в этом случае имеет вид:
x (n+1)=xn— τ (Ax (n)— b).
Здесь
B = E — τ A
и параметр τ > 0 выбирают так, чтобы по
возможности сделать минимальной величину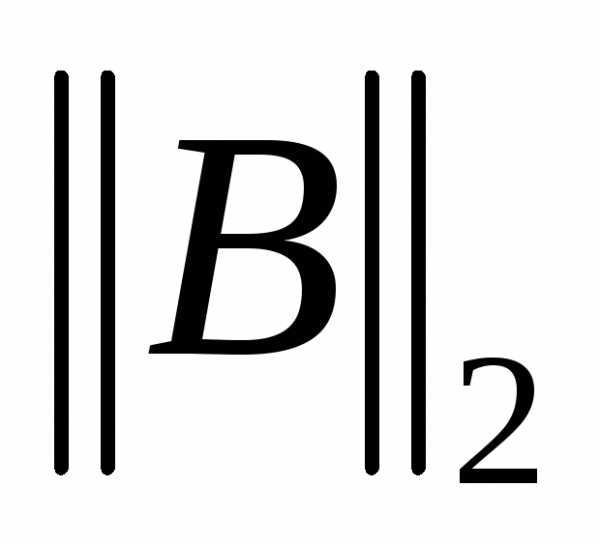 
Пусть λmin и λmax – минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра
В этом случае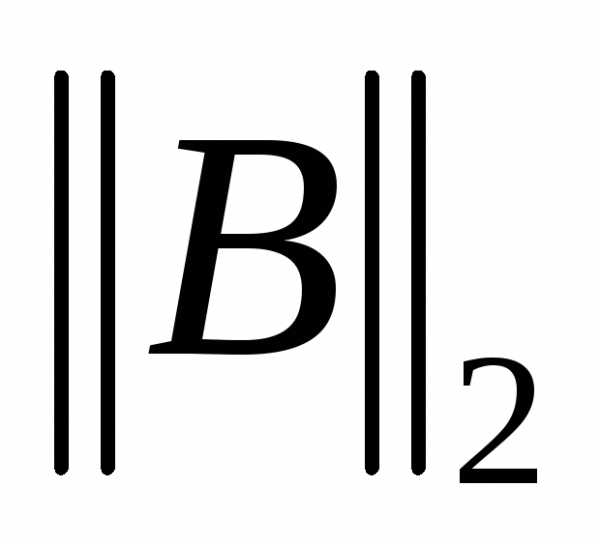 
принимает минимальное значение равное:
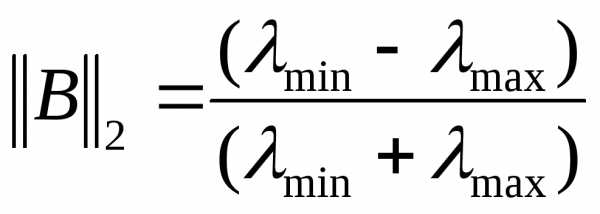
Пример 3.Решение систем линейных уравнений методом простой итерации. (вMathCAD)
Пусть дана система уравнений Ax = b
Для построения итерационного процесса найдем собственные числа матрицы A:
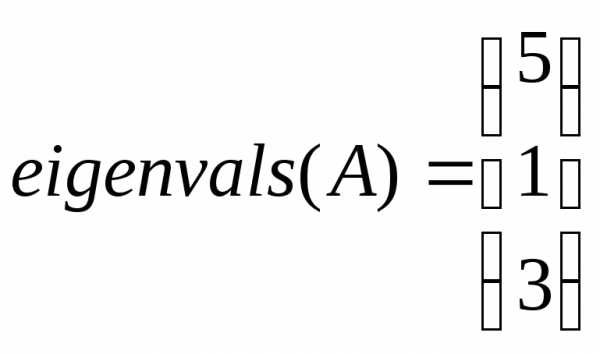— используется встроенная функция для
нахождения собственных чисел.
Вычислим итерационный параметр и проверим условие сходимости
— условие сходимости выполнено.
Возьмем начальное приближение — вектор x0, зададим точность 0.001 и найдем начальные приближения по приведенной ниже программе:
Точное решение
Замечание. Если в программе возвращать матрицу rez, то можно просмотреть все найденные итерации.
6
studfiles.net
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравненийЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
2. Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ:
Метод Крамера
Метод обратной матрицы
Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
Метод простой итерации или метод Якоби
Метод Гаусса – Зейделя
К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где , , .
A – матрица системы, – вектор правых частей, – вектор неизвестных.
При известных A и требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Прямые методы решения СЛАУ
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.
Например, для системы двух линейных уравнений
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
Метод обратной матрицы
Если det A ≠ 0, то существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
.
Из нее в обратном порядке находим все значения xi:
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:
Исключим из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
Обратный ход: .
Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.
Итерационные методы решения линейных алгебраических систем
Метод простой итерации или метод Якоби
Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:
,
где , , .
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
(1),
Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
(2)Аналогично находятся следующие приближения , где в (2) вместо необходимо подставить .
Или в общем случае:
. (3)
или
Условие окончания итерационного процесса .
Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .
Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.
Пример.
Решить систему линейных уравнений с точностью :
|
|
8 |
4 |
2 |
|
10 |
|
x1 |
|
|
= |
3 |
5 |
1 |
= |
5 |
= |
x2 |
|
|
|
3 |
–2 |
10 |
|
4 |
|
x3 |
|
Решение прямыми методами, например, обратной матрицей, даёт решение:
.
Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .
Приводим систему уравнений к виду (1):
.
Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1.250 |
1.000 |
0.400 |
1.2500 |
|
2 |
0.650 |
0.170 |
0.225 |
0.8300 |
|
3 |
1.109 |
0.565 |
0.239 |
0.4588 |
|
……… |
||||
|
4 |
0.908 |
0.287 |
0.180 |
0.2781 |
|
5 |
1.061 |
0.419 |
0.185 |
0.1537 |
|
6 |
0.994 |
0.326 |
0.165 |
0.0931 |
|
7 |
1.046 |
0.370 |
0.167 |
0.0515 |
|
8 |
1.023 |
0.594 |
0.160 |
0.2235 |
|
9 |
0.913 |
0.582 |
0.212 |
0.1101 |
|
10 |
0.906 |
0.505 |
0.242 |
0.0764 |
|
11 |
0.937 |
0.495 |
0.229 |
0.0305 |
|
12 |
0.945 |
0.516 |
0.218 |
0.0210 |
|
…… |
||||
|
13 |
0.937 |
0.523 |
0.220 |
0.0077 |
Здесь
,
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.
Следовательно, приближенное решение имеет вид:
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:
Начальное приближение:
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
Расчетные формулы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1.250 |
0.250 |
0.075 |
1.2500 |
|
2 |
1.106 |
0.321 |
0.132 |
0.1438 |
|
3 |
1.056 |
0.340 |
0.151 |
0.0500 |
|
4 |
1.042 |
0.344 |
0.156 |
0.0139 |
|
5 |
1.039 |
0.346 |
0.157 |
0.0036 |
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.
pers.narod.ru
Метод Якоби
Этот метод можно отнести к методам простой итерации.
В основе методов простой итерации лежит преобразование уравнения
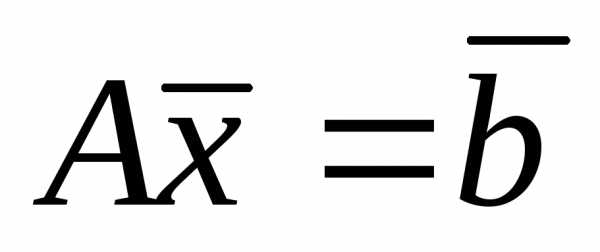(21)
к виду:
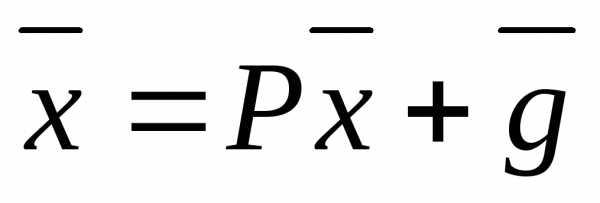(22)
и использование итерационной процедуры
, (23)
где Р– может быть произвольной функцией.
Теорема о достаточном условии
сходимости метода простой итерации. Если
< 1, то система уравнений (22) имеет
единственное решение и итерационный
процесс сходится к решению со скоростью
геометрической прогрессии.
Теорема о достаточном и необходимом условии сходимости метода простой итерации. Итерационный процесс сходится к решению при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы Р по модулю меньше единицы.
Метод Якоби:
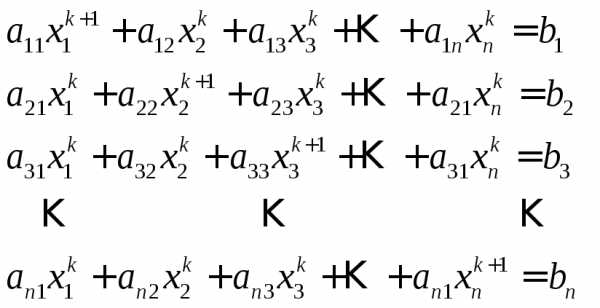(24)
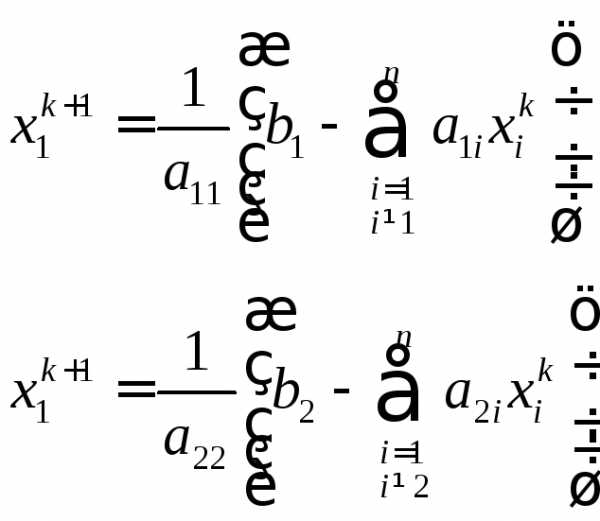
и т.д.
В общем случае
.
Для нелинейного случая
(25)
Метод Гаусса – Зейделя
В основе метода лежит уравнение вида:
, (26)
где L, U– нижнее и верхнее треугольное разложение матрицыА,D– диагональная матрица.
Без данного преобразования метод Гаусса-Зейделя выглядит следующим образом:
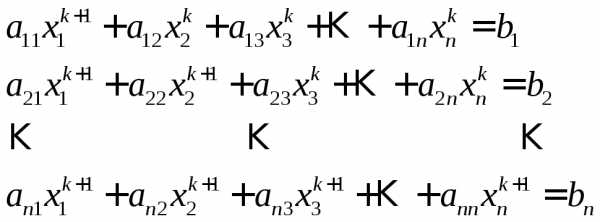(27)
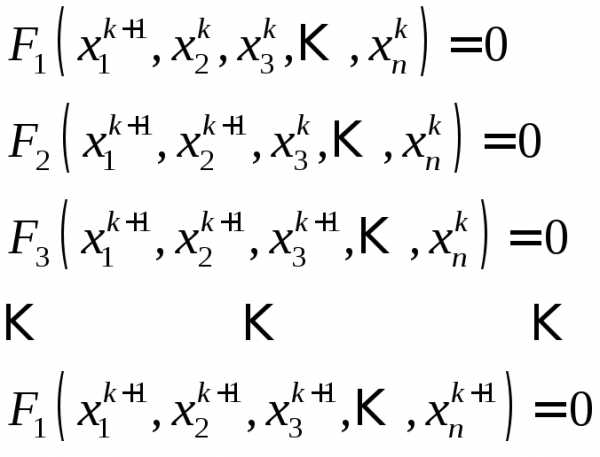(28)
Метод поверхностной верхней релаксации
Идея метода состоит в том, что приращение, полученное в результате одной итерации по методу Гаусса-Зейделя, умножается на некоторый релаксационный множитель и прибавляется к текущему значению.
(29)
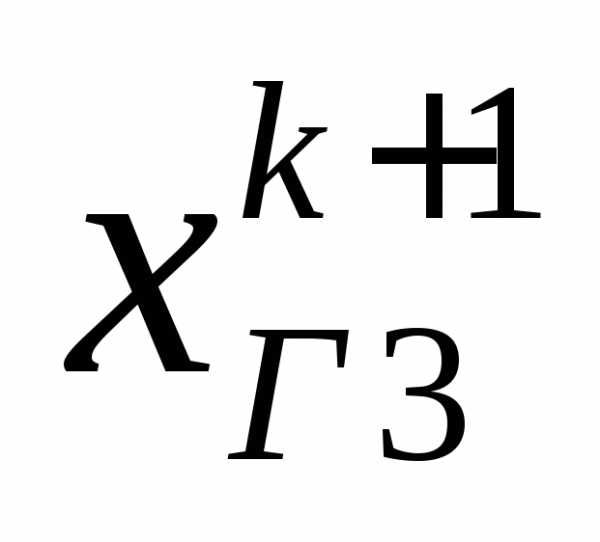— приращение, полученное по методу
Гаусса-Зейделя,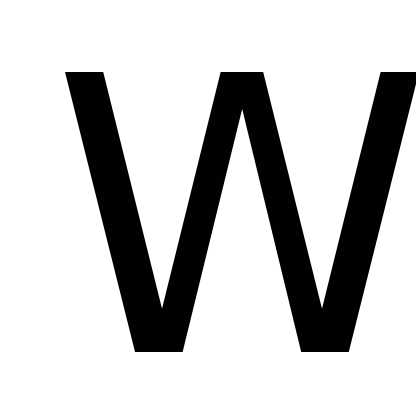
— диагональная матрица параметров
релаксации.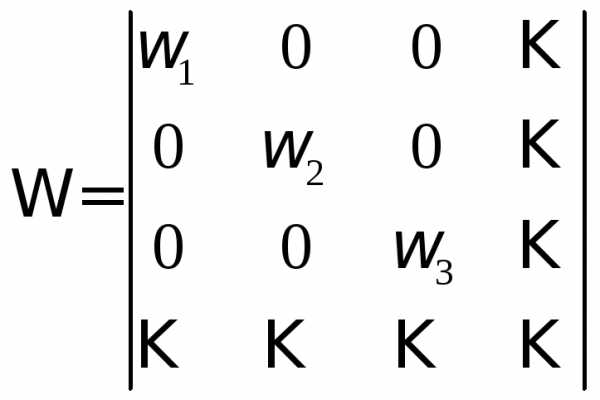
Общее условие сходимости:все собственные значения матрицы по модулю < 1.
Анализируя эти условие можно предположить, что для сходимости метода Якоби матрица Ауравнения (21), должна быть близка к диагональной, а для сходимости метода Гаусса-Зейделя – почти нижней треугольной формы, т.е. условием сходимости обоих методов является преобладание диагональных элементов.
Рис.4 Иллюстрация метода Гаусса-Зейделя:а) сходится; б) расходится ;в) цикл.
На рисунках показаны случаи, когда метод Гаусса сходится (рис.4а), расходится (рис.4б) и имеет цикл (рис.4в).
Сравнивая рисунки 4а и 4б видно, что сходимость метода Гаусса-Зейделя может изменять характер при перестановке уравнений.
В случае, если матрица А симметрична, выполняется теорема.
Пусть А – вещественная симметричная положительно определенная матрица, тогда метод Гаусса-Зейделя сходится. Рассмотрим решение ММС методом Гаусса-Зейделя для схемы, представленной на рис.
Представим математическую модель схемы в виде:
Решим ее точным методом и методом Гаусса-Зейделя
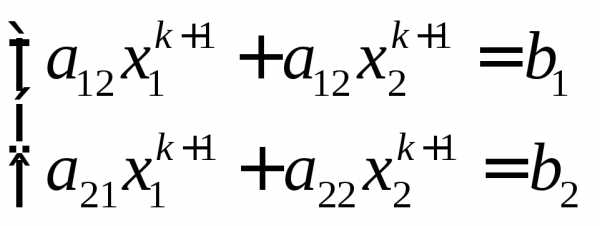(30)
Рис. 5 Эквивалентная схема.
Из системы (30) получим следующие уравнения:
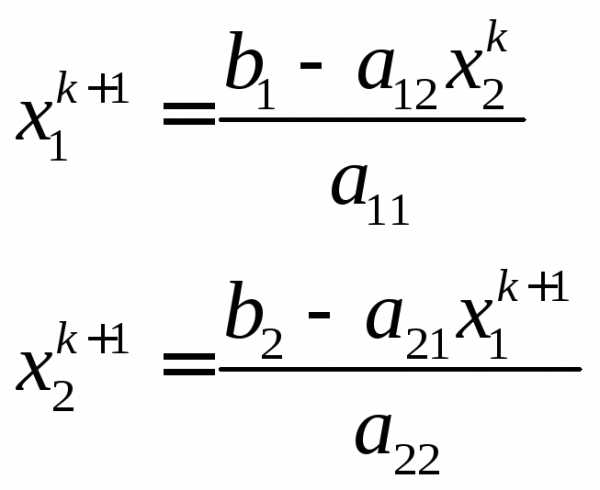(31)
Рассмотрим итерационную процедуру:
Из уравнения (31):
Введем погрешность:
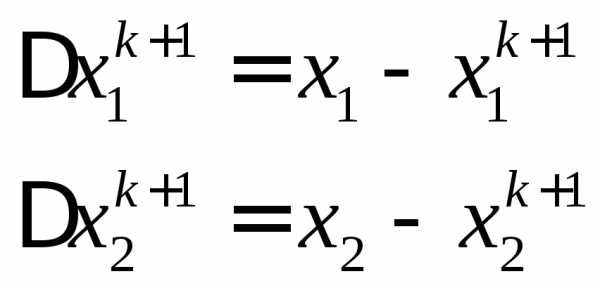
Подставим в формулы погрешности уравнения (31) в преобразованном виде:
Таким образом, выражения для погрешностей примут вид:
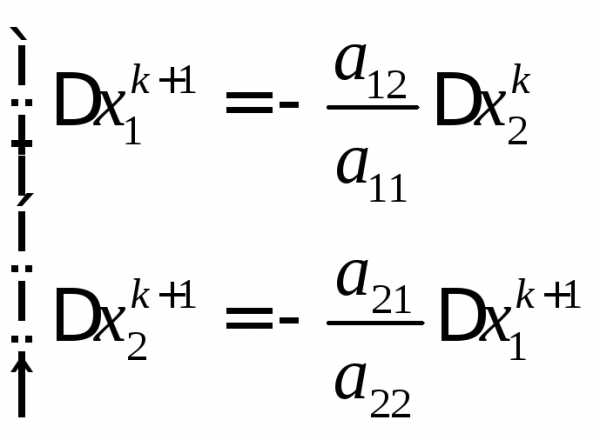
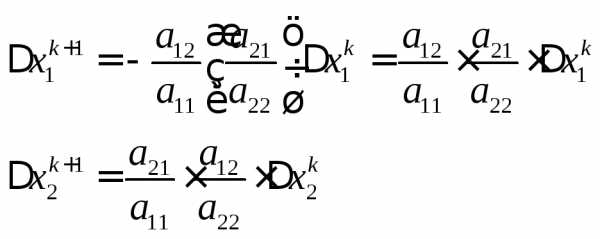
Можно показать, что:
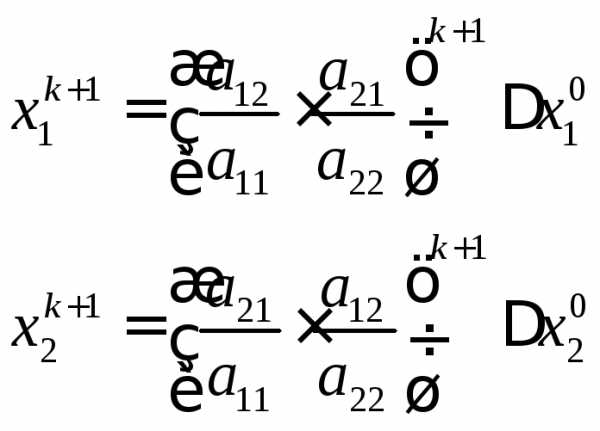
Условие сходимости к решению: 
Нетрудно видеть, что сходимость уравнений гарантируется при
Для приведенного примера
при,
то есть скорость сходимости к решению
.
Отметим, что при использовании МУП
формируется структурно-симметричная
матрица. Следовательно, при перестановке
уравнений в полученной системе характер
сходимости не меняется.
studfiles.net
6.5. Итерационные методы (метод Якоби, метод Зейделя, метод релаксации)
Итерационные методы решения СЛАУ позволяют найти решение лишь с заданной точностью. Пусть требуется решить систему Ax=F. Представим матрицу A в виде A=L+D+U, Где L — Нижнетреугольная матрица, D — Диагональная матрица, U — Верхнетреугольная матрица.
Запишем систему (6.1) в развернутом виде:
Где ( I=1,2,…,N ), и приведем к виду
Обозначим
В векторно-матричном виде система запишется в виде:
x=B x+C,
Где B={Bij}I, j=1,…,n , C={Ci}I=1,…,n, X=(x1,x2,…,xn)Т.
Построим Итерационный процесс по формуле
X(K+1)=B X(K)+C,
Где X0 — Задано, K — Номер итерации, X(K)=(X1K,X2K,…,Xnk)Т.
В качестве условия остановки итерационного процесса, можно использовать условие
,
Где E — заданная точность вычисления.
Достаточным условием сходимости метода простой итерации является:
Или условие диагонального преобладания матрицы A, т. е.
Необходимым и достаточным условием сходимости итерационных методов является условие Max|LI(B)| < 1. Оценка погрешности итерационного процесса запишется в виде:
,
Где X*— точное решение. Определяя необходимое число итераций для достижений заданной точности из формулы, получим
Итерационная формула Метода Якоби имеет вид:
,
Где
Для Метода Зейделя каждый вычисленный элемент вектора X на (K+1) — й итерации используется при вычислении следующего элемента:
В общем виде получим:
.
Для метода релаксации введем числовой параметр w так, что
При w > 1 будет Метод верхней релаксации,
При w = 1 — Метод полной релаксации (метод Зейделя),
При w < 1 — Метод нижней релаксации.
Если A=A* > 0, a w такое, что 0< w <2, то метод релаксации сходится. Параметр w выбирается из условия минимума спектрального радиуса оператора перехода от итерации к итерации.
| < Предыдущая | Следующая > |
|---|
matica.org.ua