Вычислить определитель матрицы онлайн с решением подробно: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Содержание

Определитель матрицы. Онлайн калькулятор

Для матрицы размерности n × n значение определителя вычисляется по формуле M_1j — дополнительный минор к элементу a_1j, получаемый из исходной матрицы А путем вычеркивания первой строки и j-го столбца

Значение n = 4, поэтому необходимо найти 4 дополнительных минора путем вычеркивания первой строки и j-го столбца

M₁₁ =

-3	12	0	4
31	5	7	2
0	0	-0.45	34.67
1	6	27	13

= ^{= -3248.16
M₁₂ =
-3 12 0 4
31 5 7 2
0 0 -0.45 34.67
1 6 27 13} = ^{= -28956.55
M₁₃ =
-3 12 0 4
31 5 7 2
0 0 -0.45 34.67
1 6 27 13} = ^{= -6275.27
M₁₄ =
-3 12 0 4
31 5 7 2
0 0 -0.45 34.67
1 6 27 13} = ^{= 81.45
Исходя из приведенной выше формулы, распишем сумму
det A = (-1)¹ ⋅ a₁₁ ⋅ M₁₁ + (-1)² ⋅ a
12 ⋅ M₁₂ + (-1)³ ⋅ a₁₃ ⋅ M₁₃ + (-1)⁴ ⋅ a₁₄ ⋅ M₁₄
det A = (-1)¹ ⋅ (-3) ⋅ det^{+ (-1)² ⋅ 12 ⋅ det^{+ (-1)³ ⋅ 0 ⋅ det + (-1)⁴ ⋅ 4 ⋅ det^{= (-1)¹ ⋅ (-3) ⋅ (-3248.16) + (-1)² ⋅ 12 ⋅ (-28956.55) + (-1)³ ⋅ 0 ⋅ (-6275.27) + (-1)⁴ ⋅ 4 ⋅ 81.45 = 356897.28}}}
Определитель матрицы, онлайн калькулятор с решением
Наш онлайн калькулятор помогает найти определитель матрицы всего в несколько кликов. Для вычисления определителя матрицы выберите ее размер (матрица обязательно должна быть квадратной), заполните все элементы матрицы и нажмите кнопку «Вычислить», калькулятор выдаст детальное решение и ответ! Каждый шаг будет подробно расписан, это поможет вам проверить свое решение и понять, как был получен ответ.
Заполните элементы матрицы

Решили сегодня: раз, всего раз
Понравился сайт? Расскажи друзьям!

Как найти определитель матрицы онлайн
Определитель рассчитывается только для квадратных матриц и является сумой слагаемых n-ого порядка. Подробный алгоритм его вычисления будет описан в готовом решении, которое вы сможете получить сразу после ввода условия в данный онлайн калькулятор. Это доступная и простая возможность получить детальную теорию, поскольку решение будет представлено с подробной расшифровкой каждого шага.
Инструкция пользования данным калькулятором проста. Чтобы найти определитель матрицы онлайн сначала вам нужно определиться с размером матрицы и выбрать количество столбцов и, соответственно, строк в ней. Для этого кликните на иконку «+» или «-». Далее остаётся только ввести нужные числа и нажать «Вычислить». Можно вводить как целые, так и дробные числа. Калькулятор сделает всю требуемую работу и выдаст вам готовый результат.
Чтобы стать экспертом в математике, нужно много и упорно тренироваться. A ещё никогда не помешает дополнительный раз себя перепроверить. Поэтому, когда перед вами поставлена задача вычислить определитель матрицы, целесообразно воспользоваться онлайн калькулятором. Он справится очень быстро, и в течение нескольких секунд на мониторе появится, готовое решение. Это не предполагает, что онлайн калькулятор должен заменять вам традиционные расчёты. Но он является превосходным помощником, если вам интересно понять алгоритм вычисления определителя матрицы. K тому же, это превосходная возможность проверить, правильно ли выполнена контрольная, подстраховаться от неудачной оценки.
Определитель матрицы онлайн
Определителем
называется число, которое по определённому правилу можно поставить в соответствие любой квадратной матрице.

Существует большое количество способов вычисления определителя квадратной матрицы. Наш онлайн калькулятор вычисляет определитель с использованием метода Гаусса или путем разложения определителя по элементам любой строки или столбца.

Для
вычисления определителя
методом Гаусса исходную матрицу путем элементарных преобразований приводят к
верхнетреугольному виду, при этом определитель исходной матрицы не меняется и равен произведению элементов на главной диагонали верхнетреугольной матрицы.

Определитель матрицы
A
вычисляется по формуле:

| A | = a_1,1 ∙ a_2,2 ∙ … ∙ a_n−1,n−1 ∙ a_n,n

Для вычисления определителя путем его разложения по элементам строки или столбца, сначала выбирают строку или столбец по которой будут осуществлять разложение определителя. Наиболее удобно, раскладывать определитель по строке (или столбцу) с максимальным количеством нулевых элементов. Если таких строк (или столбцов) в исходной матрице нет, тогда можно выбрать любую строку (или столбец).

Ниже представлено вычисление определителя матрицы
B,
при помощи его разложения по элементам первой строки:

Полученное разложение представляет собой линейную комбинацию определителей, порядок которых на единицу меньше исходного. Каждый из таких определителей вычисляется снова, путем разложения по выбранной строке или столбцу. Таким образом, рассматриваемый метод вычисления определителя представляет собой рекурсивный процесс.
Определитель матрицы онлайн
Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
Этот онлайн калькулятор позволит вам определитель (детерминант) матрицы.
Для того чтобы вычислить определитель (детерминант) матрицы онлайн, выберите необходимый вам размер матрицы:
Размер матрицы:

2×2
3×3
4×4
5×5
6×6
7×7

Введите значения Матрицы:
Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Найти определительСмотрите также:
Нахождение обратной матрицы
Определитель матрицы онлайн
Определитель матрицы
Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите
определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн. Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение
определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн!
Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных — возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение.
Похожие сервисы:
Вычислить детерминант матрицы
Matrix problem solverОнлайн калькулятор: Определитель (детерминант) матрицы
В движке сайта было сделано небольшое улучшение, касающееся поля для ввода длинного текста, и благодаря ему стало возможным делать калькуляторы для работы с матрицами. Начну я с азов — с расчета определителя матрицы. Сам калькулятор ниже, а ликбез про определители, как водится, под ним (для тех кто подзабыл).
Калькулятор считает определитель прямо по его определению, то есть рекурсивно, за что Википедия обещает всяческие кары в виде вычислительной сложности O(n!). Но я думаю, для интернет-целей, а-ля проверить пример, посчитанный вручную, производительности хватит (если не хватит, то можно использовать этот калькулятор Определитель матрицы методом Гаусса).
Определитель (детерминант) матрицы
Точность вычисленияЗнаков после запятой: 2
Определитель (детерминант) матрицы

save Сохранить extension Виджет
Итак детерминант.
Ну подробно можно почитать по ссылке в Википедии, приведенной выше, а я только напомню некоторые формулы:

— детерминант матрицы размерности 1 на 1

— детерминант матрицы размерности 2 на 2

— детерминант матрицы размерности n на n, где n > 2
— дополнительный минор к элементу .
Дополнительный минор к элементу — это детерминант матрицы, получаемой из исходной вычеркиванием 1-ой строки и j-го столбца. Собственно, поэтому определение и рекурсивное.
Для иллюстрации вот формула детерминанта для матрицы размером 3 на 3:
На этом можно и закончить.
Найти определитель матрицы онлайн
Определитель (детерминант) матрицы

Понятие «определитель» применимо только к квадратным матрицам.

Квадратная матрица размером 2 х 2 также называется матрицей 2-го порядка.

А в общем случаем квадратная матрица размером n x n называется матрицей n-го порядка.

В соответствии с этим есть определители 2-го порядка, определители 3-го порядка, определители 4-го порядка и так далее.

Допустим дана квадратная матрица A, тогда определитель матрицы A обозначается |A|, либо det(A), либо ΔA.
Определитель 1-го порядка
Определитель матрицы первого порядка (когда матрица состоит всего из одного элемента a₁₁)
равен её единственному элементу:
Определитель 2-го порядка Чтобы вычислить определитель матрицы второго порядка нужно взять произведение элементов главной диагонали матрицы
(диагонали, идущий из верхнего левого угла в нижний правый) и вычесть из него произвдение элементов,
расположенных на второй диагонали.
Определитель 3-го, 4-го и более высоких порядков
Для вычисления определителя матрицы 3-го и более высокого порядка применяется формула:

где
j — номер столбца матрицы,
M_j¹ — определитель матрицы, получившейся из исходной вычеркиванием 1-ой строки и j-го столбца.Вы также можете

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).

Полный список доступных функций можно найти в справке.
Калькулятор определителя матрицы
Определитель матрицы 2 × 2
Правило:
Для матрицы 2 × 2 определитель равен разности значений произведений элементов главной диагонали и антидиагонали: ∆ = = а ₁₁ · а ₂₂ — а ₁₂ · а ₂₁
Правило треугольника для определителя матрицы 3 × 3
Правило:
Значение определителя равно сумме произведений элементов главной диагонали и произведений элементов, лежащих на треугольниках со стороной, параллельной главной диагонали, из которой вычитается произведение антидиагональных элементов и произведений элементов. лежащих на треугольниках, сторона которых параллельна антидиагонали.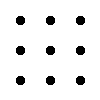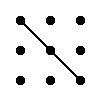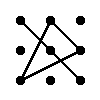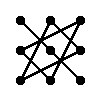
+ –

∆ = а ₁₁ а ₁₂ а ₁₃
а ₂₁ а ₂₂ а ₂₃
а ₃₁ а ₃₂ а ₃₃ =
=
а ₁₁ · а ₂₂ · а ₃₃ +
а ₁₂ · а ₂₃ · а ₃₁ +
а ₁₃ · а ₂₁ · а ₃₂ —
а ₁₃ · а ₂₂ · а ₃₁ —
а ₁₁ · а ₂₃ · а ₃₂ —
а ₁₂ · а ₂₁ · а ₃₃
. Калькулятор определяющей матрицы 2×2 3×3 4×4 NxN
Поиск инструмента
Определитель матрицы
Инструмент для вычисления определителя матрицы. Определитель квадратной матрицы M — это полезное значение, вычисляемое из ее внутренних элементов и обозначаемое det (M) или | M |.
Результаты
Определитель матрицы — dCode
Тег (-ы): Matrix
Поделиться
dCode и вы
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Рекламные объявления
Калькулятор определителя матрицы 2×2
Погрузка…
(если это сообщение не исчезает, попробуйте обновить страницу)
Рассчитать Калькулятор определителя матрицы 3×3
Загрузка …
(если это сообщение не исчезает, попробуйте обновить страницу)
Рассчитать Калькулятор определителя Matrix 4×4
Загрузка …
(если это сообщение не исчезает, попробуйте обновить страницу)
Рассчитать Калькулятор определителя матрицы NxN
Инструмент для вычисления определителя матрицы.Определитель квадратной матрицы M — это полезное значение, вычисляемое из ее внутренних элементов и обозначаемое det (M) или | M |.
Ответы на вопросы
Как вычислить определитель матрицы?
Для матрицы 2×2 расчет выглядит следующим образом:
$$ \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} = ad — bc $$
Пример: $$ \ begin {vmatrix } 1 & 2 \\ 3 & 4 \ end {vmatrix} = 1 \ times 4 — 2 \ times 3 = -2 $$
Для матрицы большего размера, такой как 3×3, вычислите:
$$ \ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} = a \ begin {vmatrix} e & f \\ h & i \ end {vmatrix} — b \ begin {vmatrix} d & f \\ g & i \ end {vmatrix} + c \ begin {vmatrix} d & e \\ g & h \ end {vmatrix} \\ = aei-afh + bfg-bdi + cdh-ceg $$
Идея та же для матриц большего размера:
Для матрицы 4×4
$$ \ begin {vmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \ end {vmatrix} = a \ begin {vmatrix} f & g & h \\ j & k & l \\ n & o & p \ end {vmatrix} — b \ begin {vmatrix} e & g & h \\ i & k & l \\ m & o & p \ end {vmatrix} + c \ begin {vmatrix} e & f & h \\ i & j & l \\ m & n & p \ end {vmatrix} — d \ begin {vmatrix} e & f & g \\ i & j & k \\ m & n & o \ end {vmatrix} \\ = \\ a (fkp — flo — gjp + gln + hjo — hkn) — b (ekp — elo — gip + glm + hio — hkm) + c (ejp — eln — fip + flm + hin — hjm) — d (ejo — ekn — fio + fkm + gin — gjm) \\ = \\ afkp — aflo — agjp + agln + ahjo — ahkn — bekp + belo + bgip — bglm — bhio + bhkm + cejp — celn — cfip + cflm + chin — chjm — dejo + dekn + dfio — dfkm — dgin + dgjm $$
Как вычислить определитель для неквадратной матрицы?
Определитель неквадратной матрицы не определен, он не существует согласно определению определителя.
По какой формуле вычисляется определитель матрицы порядка n?
Нет другой формулы, кроме приведенного выше объяснения для общего случая матрицы порядка n.
Как вычислить определитель матрицы 1х1?
Для матрицы 1×1 определитель является единственным элементом матрицы.
Пример: $$ | 1 | = 1 $$
Что является определителем единичной матрицы?
Определитель единичной матрицы равен 1.
Пример: $$ \ begin {vmatrix} 1 & 0 \\ 0 & 1 \ end {vmatrix} = 1 \ times 1 — 0 \ times 0 $$
Пример: $$ \ begin {vmatrix } 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {vmatrix} = (1 \ times 1 \ times 1) — (1 \ times 0 \ times 0) + (0 \ times 0 \ раз 0) — (0 \ раз 0 \ раз 1) + (0 \ раз 0 \ раз 0) — (0 \ раз 1 \ раз 0) = 1 $$
Только член, соответствующий умножению диагональ будет равна 1, а остальные члены будут нулевыми.
Задайте новый вопрос Исходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Определитель матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) доступ к данным, скриптам или API не будет бесплатным, то же самое касается загрузки Определителя матрицы для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Рекламные объявления
Ключевые слова
определитель, матрица, дет, квадрат, тождество
Ссылки

Источник: https: // www.dcode.fr/matrix-determinant
© 2020 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. . Калькулятор определителя матрицы nxn
Как найти определитель матрицы?
Рассмотрим матрицу $ A = \ left [
\ begin {array} {cc}
а & б \\
CD \\
\ end {массив}
\ right] $ размером $ 2 \ times2 $. Реальное число
$$ \ left | \ begin {array} {cc}
а & б \\
CD \\
\ end {массив}
\ right | = ad-cb $$
— определитель матрицы $ A $. Точнее, чтобы найти определитель матрицы $ 2 \ times 2 $, нам нужно выполнить следующие шаги:
Умножьте элемент в первой строке и первом столбце на элементы во второй строке и втором столбце;
Умножить элемент в первой строке и втором столбце на элемент во второй строке и первом столбце;
Определитель матрицы $ 2 \ times 2 $ — это разница между вторым и первым произведением. Минор элемента любого определителя матрицы $ n \ times n $ является определителем матрицы $ (n-1) \ times (n-1) $. Если мы удалим строку и столбец, содержащие элемент, то получим соответствующий минор.
Например, минор элемента $ a $, элемента в первой строке и первом столбце определителя Чтобы вычислить определитель матрицы $ n \ times n $, нам нужно разложить определитель на миноры.
Сначала выбираем строку в матрице. В каждой позиции в строке мы умножаем элемент на
его незначительный знак, умноженный на его позицию, и сложить все суммы для всей строки.Знаки позиции в матрице — плюс или минус в зависимости от позиции элемента. Например, знаки положения в матрице $ 3 \ times 3 $:
$$ \ left [
\ begin {array} {ccc}
+ & — & + \\
— & + & — \\
+ & — & + \\
\ end {массив}
\ right] $$
Это означает, что $$ \ begin {align} det (A) = | A | & = \ left |
\ begin {array} {ccc}
а & b & c \\
d & e & f \\
г & ч & я \\
\ end {массив}
\ право | \\ & = a \ left |
\ begin {array} {cc}
е & е \\
Здравствуй \\
\ end {массив}
\ right | -b \ left |
\ begin {array} {cc}
д & е \\
г & я \\
\ end {массив}
\ right | + c \ left |
\ begin {array} {cc}
d & e \\
г & ч \\
\ end {массив}
\ right | \ end {align} $$
Если мы применим этот метод для вычисления определителя $ 4 \ times 4 $, мы получим
$$ \ begin {align} det (A) = | A | & = \ left |
\ begin {array} {cccc}
а & b & c & d \\
e & f & g & h \\
я & j & k & l \\
m & n & o & p \\
\ end {массив}
\ право |
\\ & = a \ left |
\ begin {array} {ccc}
f & g & h \\
j & k & l \\
n & o & p \\
\ end {массив}
\ right | -b \ left |
\ begin {array} {ccc}
e & g & h \\
я & к & л \\
м & о & п \\
\ end {массив}
\ right | + c \ left |
\ begin {array} {ccc}
e & f & h \\
я & j & l \\
m & n & p \\
\ end {массив}
\ right | -d \ left |
\ begin {array} {ccc}
e & f & g \\
я & j & k \\
м & н & о \\
\ end {массив}
\ право |
\ end {align} $$
Для каждого элемента исходной матрицы его минор является определителем $ 3 \ times 3 $. Существует другой способ вычисления определителя $ 3 \ times 3 $, хорошо известный как правило Сарруса или схема Сарруса.
Расширить определитель, переписав первые два столбца чисел:
Сложите произведения красных диагоналей и вычтите произведения синих диагоналей, т. Е.
$$ det (A) = aei + bfg + cdh-ceg-afh-bdi $$
Это правило можно запомнить, вспомнив о диагоналях расширенного определителя
читать диагонали означает плюс $ (aei + bfg + cdh) $, а синие диагонали означают минус $ (- ceg-afh-bdi) $. Правило Сарруса не применимо для вычисления определителя $ 4 \ times 4 $, оно требует некоторых изменений. Например, найдем определитель матрицы $ 3 \ times 3 $
$$ \ left | \ begin {array} {ccc}
10 и 20 и 10 \\
4 и 5 и 6 \\
2 и 3 и 5 \\
\ end {массив}
\ right | $$ Используя правило Сарруса, получаем
$$ \ left | \ begin {array} {ccc | cc}
10 и 20 и 10 и 10 и 20 \\
4 и 5 и 6 и 4 и 5 \\
2 и 3 и 5 и 2 и 3 \\
\ end {массив}
\право.= 10 \ cdot5 \ cdot5 + 20 \ cdot6 \ cdot2 + 10 \ cdot4 \ cdot 3-10 \ cdot5 \ cdot2-10 \ cdot6 \ cdot3-20 \ cdot4 \ cdot5 = -70 $$
Работа с определителем матрицы $ n \ times n $ с шагами показывает полный пошаговый расчет для
нахождение определителя $ 3 \ times 3 $ матрицы $ A $ по формуле определителя. Для
любые другие матрицы, просто укажите действительные числа как элементы матрицы и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы и люди, изучающие математику, используют этот калькулятор определителя матрицы nxn для создания
работать, проверять результаты определителя матрицы, полученные вручную, или эффективно выполнять домашние задания.Ученики начальной школы также могут использовать этот калькулятор для решения системы линейных уравнений. . Определитель матрицы онлайн калькулятор
Определитель матрицы — это число, которое по окончательному правилу может быть установлено во взаимно однозначном соответствии любой квадратной матрице.
Есть много способов найти определитель матрицы. Этот онлайн-калькулятор поддерживает метод Гаусса и метод разложения определителя по выбранной строке или столбцу.
Чтобы определитель нахождения по методу Гаусса начальная матрица элементарными преобразованиями упрощена до
ряд уменьшенной формы.Элементарные преобразования не меняют значения определителя. На завершающем этапе метода Гаусса определитель вычисляется как произведение элементов главной диагонали строковой приведенной матрицы.

Определитель матрицы
А
рассчитывается по формуле:
| А | = a _1,1 ∙ a _2,2 ∙ … ∙ a _{n − 1, n − 1} ∙ a _{n, n}
Чтобы найти определитель матрицы с помощью разложения по строкам или столбцам, нужно сначала выбрать строку или столбец для разложения.Удобнее всего выбрать строку (или столбец), в которой максимум элементов равен нулю. Если таких строк или столбцов нет, можно выбрать любую строку или столбец.

Ниже представлен расчет матрицы
B,
определитель путем разложения по элементам первой строки:

Такое разложение состоит из линейной комбинации определителей младших порядков по сравнению с исходным.Каждый из таких определителей можно снова вычислить с помощью разложения. Следовательно, задействованный метод представляет собой рекурсивный процесс.
.No related posts.}