Метод наименьших квадратов
Программа МНК
Введите данные
Данные и аппроксимация y = a + b·x
i – номер экспериментальной точки;
xi – значение фиксированного параметра в точке i;
yi – значение измеряемого параметра в точке i;
ωi – вес измерения в точке i;
yi, расч. – разница между измеренным и вычисленным по регрессии значением y в точке i;
Sxi(xi) – оценка погрешности xi при измерении y в точке i.
Кликните по графику,
чтобы добавить значения в таблицу
Данные и аппроксимация y = k·x
| i | xi | yi | ωi | yi, расч. | Δyi | Sxi(xi) |
|---|
чтобы добавить значения в таблицу
Инструкция пользователя онлайн-программы МНК.
В поле данных введите на каждой отдельной строке значения `x` и `y` в одной экспериментальной точке. Значения должны отделяться пробельным символом (пробелом или знаком табуляции).
Третьим значением может быть вес точки `w`. Если вес точки не указан, то он приравнивается единице. В подавляющем большинстве случаев веса экспериментальных точек неизвестны или не вычисляются, т.е. все экспериментальные данные считаются равнозначными. Иногда веса в исследуемом интервале значений совершенно точно не равнозначны и даже могут быть вычислены теоретически. Например, в спектрофотометрии веса можно вычислить по простым формулам, правда в основном этим все пренебрегают для уменьшения трудозатрат.
Данные можно вставить через буфер обмена из электронной таблицы офисных пакетов, например Excel из Майкрософт Офиса или Calc из Оупен Офиса. Для этого в электронной таблице выделите диапазон копируемых данных, скопируйте в буфер обмена и вставьте данные в поле данных на этой странице.
Для расчета по методу наименьших квадратов необходимо не менее двух точек для определения двух коэффициентов `b` – тангенса угла наклона прямой и `a` – значения, отсекаемого прямой на оси `y`.
Для оценки погрешности расчитываемых коэффициентов регресии нужно задать количество экспериментальных точек больше двух. Чем больше количество экспериментальных точек, тем более точна статистическая оценка коэффицинетов (за счет снижения коэффицинета Стьюдента) и тем более близка оценка к оценке генеральной выборки.
Получение значений в каждой экспериментальной точке часто сопряжено со значительными трудозатратами, поэтому часто проводят компромиссное число экспериментов, которые дает удобоваримую оценку и не привеодит к чрезмерным трудо затратам. Как правило число экспериментах точек для линейной МНК зависимости с двумя коэффицинетами выбирает в районе 5-7 точек.
Краткая теория метода наименьших квадратов для линейной зависимости
Допустим у нас имеется набор экспериментальных данных в виде пар значений [`y_i`, `x_i`], где `i` – номер одного эксперементального измерения от 1 до `n`; `y_i` – значение измеренной величины в точке `i`; `x_i` – значение задаваемого нами параметра в точке `i`.
В качестве примера можно рассмотреть действие закона Ома. Изменяя напряжение (разность потенциалов) между участками электрической цепи, мы замеряем величину тока, проходящего по этому участку. Физика нам дает зависимость, найденную экспериментально:
`I = U / R`,
где `I` – сила тока; `R` – сопротивление; `U` – напряжение.
В этом случае `y_i` у нас имеряемая величина тока, а `x_i` – значение напряжения.
В качестве другого примера рассмотрим поглощение света раствором вещества в растворе. Химия дает нам формулу:
`A = ε l C`,
где `A` – оптическая плотность раствора;
`ε` – коэффициент пропускания растворенного вещества;
`l` – длина пути при прохождении света через кювету с раствором;
`C` – концентрация растворенного вещества.
В этом случае `y_i` у нас имеряемая величина отптической плотности `A`, а `x_i` – значение концентрации вещества, которое мы задаем.
Мы будем рассматривать случай, когда относительная погрешность в задании `x_i` значительно меньше, относительной погрешности измерения `y_i`. Так же мы будем предполагать, что все измеренные величины `y_i` случайные и нормально распределенные, т.е. подчиняются нормальному закону распределения.
В случае линейной зависимости `y` от `x`, мы можем написать теоретическую зависимость:
`y = a + b x`.
С геометрической точки зрения, коэффициент `b` обозначает тангенс угла наклона линии к оси `x`, а коэффициент `a` – значение `y` в точке пересечения линии с осью `y` (при `x = 0`).
Нахождение параметров линии регресии.
`y_i = a + b x_i + ε_i` (1),
где `ε_i` – неизвестная ошибка измерения `y` в `i`-ом эксперименте.
Зависимость (1) так же называют регрессией, т.е. зависимостью двух величин друг от друга со статистической значимостью.
Задачей восстановления зависимости является нахождение коэффициентов `a` и `b` по экспериментальным точкам [`y_i`, `x_i`].
Для нахождения коэффициентов `a` и `b` обычно используется метод наименьших квадратов (МНК). Он является частным случаем принципа максимального правдоподобия.
Перепишем (1) в виде `ε_i = y_i — a — b x_i`.
Тогда сумма квадратов ошибок будет
`Φ = sum_(i=1)^(n) ε_i^2 = sum_(i=1)^(n) (y_i — a — b x_i)^2`. (2)
Принципом МНК (метода наименьших квадратов) является минимизация суммы (2) относительно параметров `a` и `b`.
Минимум достигается, когда частные производные от суммы (2) по коэффициентам `a` и `b` равны нулю:
`frac(partial Φ)(partial a) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial a) = 0`
`frac(partial Φ)(partial b) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial b) = 0`
Раскрывая производные, получаем систему из двух уравнений с двумя неизвестными:
`sum_(i=1)^(n) (2a + 2bx_i — 2y_i) = sum_(i=1)^(n) (a + bx_i — y_i) = 0`
`sum_(i=1)^(n) (2bx_i^2 + 2ax_i — 2x_iy_i) = sum_(i=1)^(n) (bx_i^2 + ax_i — x_iy_i) = 0`
Раскрываем скобки и переносим независящие от искомых коэффициентов суммы в другую половину, получим систему линейных уравнений:
`sum_(i=1)^(n) y_i = a n + b sum_(i=1)^(n) bx_i`
`sum_(i=1)^(n) x_iy_i = a sum_(i=1)^(n) x_i + b sum_(i=1)^(n) x_i^2`
Решая, полученную систему, находим формулы для коэффициентов `a` и `b`:
`a = frac(sum_(i=1)^(n) y_i sum_(i=1)^(n) x_i^2 — sum_(i=1)^(n) x_i sum_(i=1)^(n) x_iy_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.1)
`b = frac(n sum_(i=1)^(n) x_iy_i — sum_(i=1)^(n) x_i sum_(i=1)^(n) y_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.2)
Эти формулы имеют решения, когда `n > 1` (линию можно построить не менее чем по 2-м точкам) и когда детерминант `D = n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2 != 0`, т.е. когда точки `x_i` в эксперименте различаются (т.е. когда линия не вертикальна).
Оценка погрешностей коэффициентов линии регресии
Для более точной оценки погрешности вычисления коэффициентов `a` и `b` желательно большое количество экспериментальных точек. При `n = 2`, оценить погрешность коэффициентов невозможно, т.к. аппроксимирующая линия будет однозначно проходить через две точки.
Погрешность случайной величины `V` определяется законом накопления ошибок
`S_V^2 = sum_(i=1)^p (frac(partial f)(partial z_i))^2 S_(z_i)^2`,
где `p` – число параметров `z_i` с погрешностью `S_(z_i)`, которые влияют на погрешность `S_V`;
`f` – функция зависимости `V` от `z_i`.
Распишем закон накопления ошибок для погрешности коэффициентов `a` и `b`
`S_a^2 = sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial a)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 `
,`S_b^2 = sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial b)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 `
,т.к. `S_(x_i)^2 = 0` (мы ранее сделали оговорку, что погрешность `x` пренебрежительно мала).
`S_y^2 = S_(y_i)^2` – погрешность (дисперсия, квадрат стандартного отклонения) в измерении `y` в предположении, что погрешность однородна для всех значений `y`.
Подставляя в полученные выражения формулы для расчета `a` и `b` получим
`S_a^2 = S_y^2 frac(sum_(i=1)^(n) ( sum_(i=1)^(n) x_i^2 — x_i sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2) sum_(i=1)^(n) x_i^2 ) (D^2) = S_y^2 frac(sum_(i=1)^(n) x_i^2) (D)` (4.1)
`S_b^2 = S_y^2 frac(sum_(i=1)^(n) ( n x_i — sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(n ( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 frac(n) (D)` (4.2)
В большинстве реальных экспериментов значение `Sy` не измеряется. Для этого нужно проводить несколько паралельных измерений (опытов) в одной или нескольких точках плана, что увеличивает время (и возможно стоимость) эксперимента. Поэтому обычно полагают, что отклонение `y` от линии регрессии можно считать случайным. Оценку дисперсии `y` в этом случае, считают по формуле.
`S_y^2 = S_(y, ост)^2 = frac(sum_(i=1)^n (y_i — a — b x_i )^2) (n-2)`
.Делитель `n-2` появляется потому, что у нас снизилось число степеней свободы из-за расчета двух коэффициентов по этой же выборке экспериментальных данных.
Такую оценку еще называют остаточной дисперсией относительно линии регрессии `S_(y, ост)^2`.
Оценка значимости коэффициентов проводится по критерию Стьюдента
`t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)`
Если рассчитанные критерии `t_a`, `t_b` меньше табличных критериев `t(P, n-2)`, то считается, что соответсвующий коэффициент не значимо отличается от нуля с заданной вероятностью `P`.
Если `t_a
Если `t_b
Для оценки качества описания линейной зависимости, можно сравнить `S_(y, ост)^2` и `S_(bar y)` относительно среднего с использованием критерия Фишера.
`S_(bar y) = frac(sum_(i=1)^n (y_i — bar y)^2) (n-1) = frac(sum_(i=1)^n (y_i — (sum_(i=1)^n y_i) /n )^2) (n-1)`
– выборочная оценка дисперсии `y` относительно среднего.
Для оценки эффективности уравнения регресии для описания зависимости расчитывают коэффициент Фишера
`F = S_(bar y) / S_(y, ост)^2`,
который сравнивают с табличным коэффициентом Фишера `F(p, n-1, n-2)`.
Если `F > F(P, n-1, n-2)`, считается статистически значимым с вероятностью `P` различие между описанием зависимости `y = f(x)` с помощью уравенения регресии и описанием с помощью среднего. Т.е. регрессия лучше описывает зависимость, чем разброс `y` относительно среднего.
xn——7kcbakcjfdd9ab3avfoelp4b2ar8dzd9e.xn--p1ai
Метод наименьших квадратов при решении экспериментальных задач по физике
При решении экспериментальных задач по физике часто возникает необходимость измерения физических величин, находящихся в функциональной зависимости. Как правило, после измерений информация о физическом явлении извлекается из графиков, построенных по данным, полученным экспериментальным путем, а зависимость между двумя физическими величинами — xи yпредставляется в виде таблицы 1.
Таблица 1
|
x |
x1 |
x2 |
x3 |
… |
xn |
|
y |
y1 |
y2 |
y3 |
… |
yn |
В связи с тем, что значения величин xи y измеряются с погрешностью, нанесенные на координатную плоскость точки будут разбросаны относительно предполагаемой кривой.
Если график y = f (x) строить, непосредственно соединяя экспериментально полученные точки, то он будет иметь вид ломаной. Однако в большинстве случаев функции, описывающие процессы в природе, являются гладкими. Значит, необходимо подобрать такую функцию y = f (x), которая наилучшим образом выражала бы экспериментальную зависимость y от x.
Наиболее простым видом функциональной зависимости является прямо пропорциональная зависимость между физическими величинами вида.
Необходимо отыскать такой коэффициент k, а значит, прямую, наилучшим образом согласованную с экспериментальными точками, нанесенными на плоскость (x, y), при котором общее отклонение
минимально (рисунок 1). Для этого необходимо решить уравнение:
или ,
где xi, yi — измеренные значения величин; N — количество пар значений измеренных величин.
Естественно, что для отыскания экстремума дифференцирование ведется по параметру, от которого зависит, как пройдет график. Воспользовавшись правилами дифференцирования суммы и сложной функции, получим
Полученное значение параметра k позволяет наиболее близко к экспериментальным точкам провести прямую, выходящую из начала координат.
Рис. 1. Экспериментальные точки при измерении величин
Погрешность при определении параметра k:
Экспериментальная задача. Измерить сопротивление проводника при помощи амперметра и вольтметра. Оценить погрешность измерений.
Для решения поставленной задачи необходимо собрать электрическую цепь, изображенную на рисунке 2.
Рис. 2. Экспериментальная установка для измерения сопротивления проводника при помощи амперметра и вольтметра
Изменения силы тока и напряжения на резисторе, полученные в результате измерений приведены в таблице 2.
Таблица 2
|
I, А |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
U, В |
0,27 |
0,56 |
0,9 |
1,18 |
1,49 |
1,79 |
2,05 |
2,42 |
2,68 |
3,01 |
|
I, А |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2 |
|
U, В |
3,35 |
3,56 |
3,85 |
4,18 |
4,48 |
4,79 |
5,12 |
5,45 |
5,68 |
5,9 |
Необходимо подобрать такую формулу U = f (I), чтобы она наиболее удачно отражала зависимость между силой тока I и напряжением U. Закон Ома устанавливает эту зависимость в виде U=RI. Это линейная зависимость. Определим величину сопротивления
Способ № 1.
- Определим значение сопротивления R каждого из N измерений:
.
- Определим среднее значение сопротивления по формуле:
(Ом).
Погрешность такого косвенного измерения сопротивления можно найти по правилам обработки результатов прямых измерений, рассматривая набор значений Ri как статистический набор данных. Пренебрегая инструментальной погрешностью, получим:
(Ом).
Итак,Ом.
Это самый простой, но не лучший способ выбора коэффициента k в случае, когда сглаживающая зависимость между величинами xи y линейная и имеет вид: y = kx.
Способ № 2 (Метод наименьших квадратов)
- Значение сопротивления R можно найти по формуле:
(Ом).
- Погрешность вычислим по формуле:
(Ом).
В результате получим: (Ом).
Видно, что наиболее вероятные значения сопротивлений, вычисленные двумя рассмотренными способами, попадают в доверительные интервалы друг друга и, следовательно, оба имеют право на существование. Однако погрешность расчета сопротивления при использовании метода наименьших квадратов оказалась вдвое меньше по сравнению с первым способом. Таким образом, результат, полученный методом наименьших квадратов, более точен.
Литература:
- Тейлор Дж. Введение в теорию ошибок / Дж. Тейлор; Пер. с англ. М.: Мир, 1985. 272 с.
- Исаков В. А. Физика колебаний. Лабораторный практикум: Методические указания к лабораторным работам по физике / В. А. Исаков, В. П. Нестеров / Омский гос. ун-т путей сообщения. Омск, 2001. 22 с.
- Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений / Ю. В. Линник. Л.: Физматгиз, 1962. 352 с.
yun.moluch.ru
Метод наименьших квадратов
Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x. В результате измерений получается ряд значений:
;
.
По данным такого
эксперимента можно построить график
зависимости 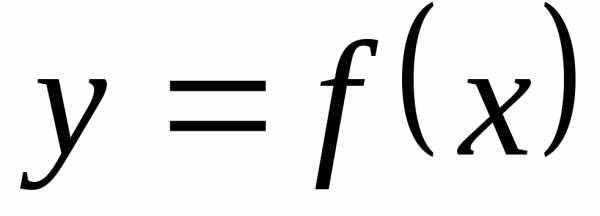 .
Полученная кривая дает возможность
судить о виде функции
.
Полученная кривая дает возможность
судить о виде функции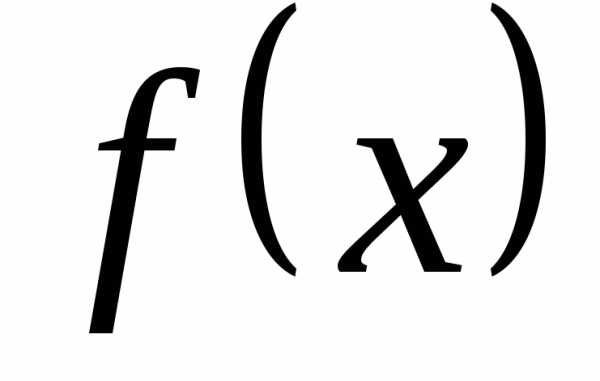 .
Однако постоянные коэффициенты, которые
входят в эту функцию, остаются неизвестными.
Оптимальный подход к решению подобных
задач возможен на основе применения
метода наименьших квадратов.
.
Однако постоянные коэффициенты, которые
входят в эту функцию, остаются неизвестными.
Оптимальный подход к решению подобных
задач возможен на основе применения
метода наименьших квадратов.
Суть метода
наименьших квадратов состоит в том, что
наивероятнейшими значениями аргументов
искомой аналитической зависимости
будут те, при которых сумма квадратов
отклонений экспериментальных значений
функции  от значений самой функцииy,
т.е.
от значений самой функцииy,
т.е. 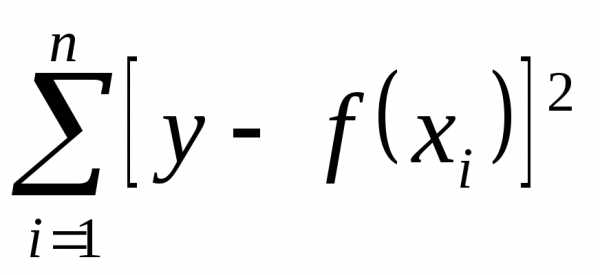 является наименьшей.
является наименьшей.
На
практике этот метод наиболее часто (и
наиболее просто) используется в случае
линейной зависимости, т.е. когда 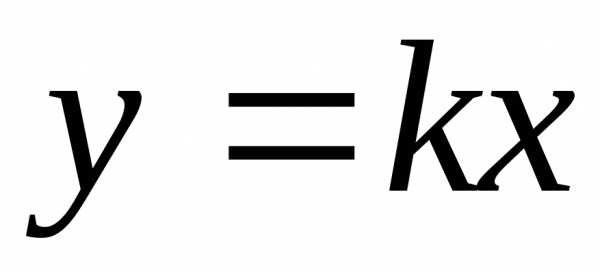 или.
или.
Линейная
зависимость очень широко распространена
в физике. И даже когда зависимость
нелинейная, обычно стараются строить
график так, чтобы получить прямую линию.
Например, если предполагают, что
показатель преломления стекла n связан с длиной λ световой волны
соотношением
,
то на графике строят зависимостьn от 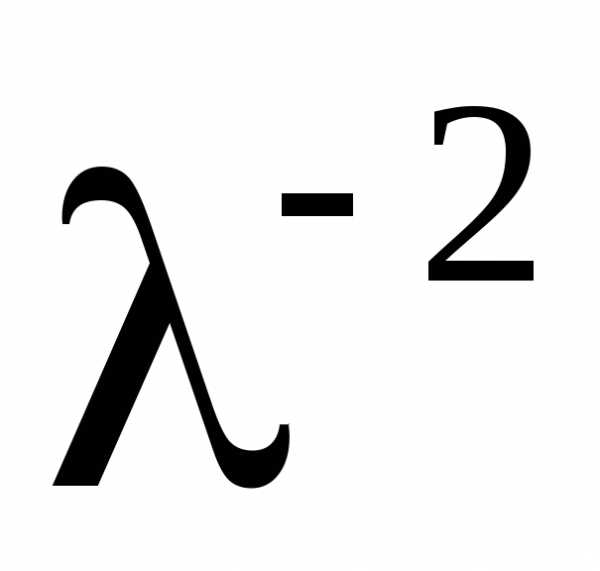 .
.
Для
начала рассмотрим зависимость 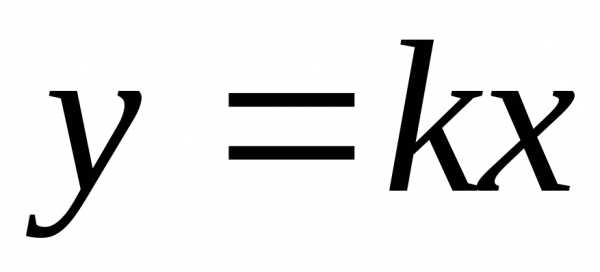 (прямая, проходящая через начало
координат). Составим величину
(прямая, проходящая через начало
координат). Составим величину – сумму квадратов отклонений
экспериментальных точек от прямой
– сумму квадратов отклонений
экспериментальных точек от прямой
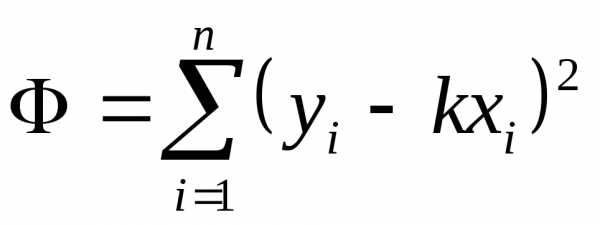 .
.
Величина  всегда положительна и оказывается тем
меньше, чем ближе к прямой лежат
экспериментальные точки. Метод наименьших
квадратов утверждает, что дляk следует выбирать такое значение, при
котором
всегда положительна и оказывается тем
меньше, чем ближе к прямой лежат
экспериментальные точки. Метод наименьших
квадратов утверждает, что дляk следует выбирать такое значение, при
котором  имеет минимум
имеет минимум
или
| (16) |
Вычисление показывает, что среднеквадратичная ошибка определения величины k при этом равна
| (17) |
Теперь можно рассмотреть более трудный случай, когда точки должны удовлетворить формуле .
Задача
состоит в том, чтобы по имеющемуся набору
значений 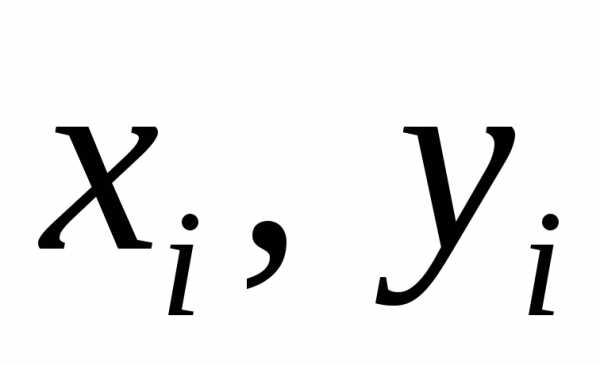 найти наилучшие значенияa и b.
найти наилучшие значенияa и b.
Составляя
квадратичную форму  ,
равную сумме квадратов отклонений точек
,
равную сумме квадратов отклонений точек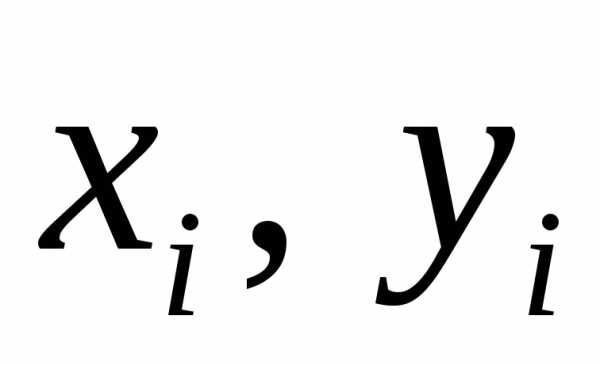 от прямой
от прямой
определяют
значения a и b,
при которых  имеет минимум
имеет минимум
,
.
Совместное решение этих уравнений дает
| (18) |
. | (19) |
Среднеквадратичные ошибки определения a и b равны
| (20) |
. | (21) |
При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (16) – (21). Формы этих таблиц приведены в рассматриваемых ниже примерах.
Пример 1. Исследовалось основное уравнение динамики вращательного движения (прямая, проходящая через начало координат). При различных значениях моментаM измерялось угловое ускорение ε некоторого тела. Требуется определить момент инерции этого тела. Результаты измерений момента силы и углового ускорения занесены во второй и третий столбцы таблицы 2.
Таблица 2. Результаты эксперимента
n |
|
|
| |||
1 | 1.44 | 0.52 | 2.0736 | 0.7488 | 0.039432 | 0.001555 |
2 | 3.12 | 1.06 | 9.7344 | 3.3072 | 0.018768 | 0.000352 |
3 | 4.59 | 1.45 | 21.0681 | 6.6555 | 0.006693 | |
4 | 5.90 | 1.92 | 34.8100 | 11.3280 | 0.002401 | |
5 | 7.45 | 2.56 | 55.5025 | 19.0720 | 0.073725 | 0.005435 |
| – | – | 123.1886 | 41.1115 | – | 0.016436 |
Используя линейную зависимость
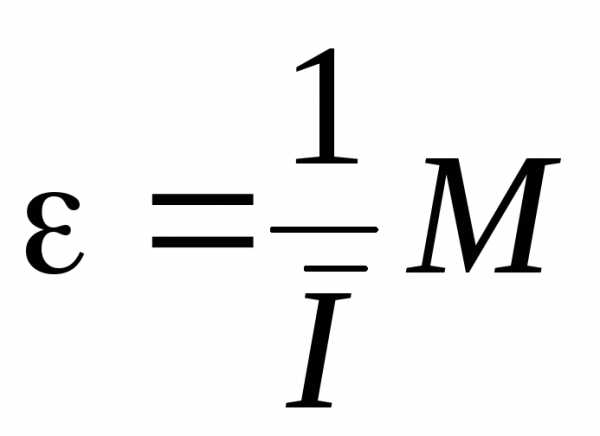 ,
,
по формуле (16) определяем
,
откуда .
Для определения среднеквадратичной ошибки воспользуемся формулой (17)
.
По формуле (14) имеем
.
Задавшись надежностью
,
по таблице коэффициентов Стьюдента для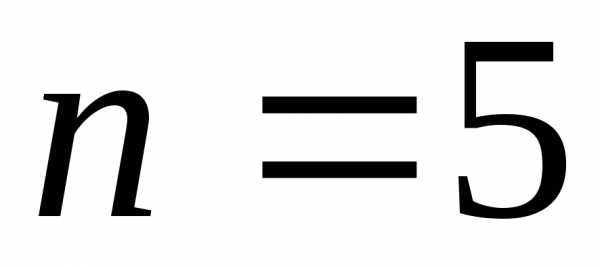 ,
находим
,
находим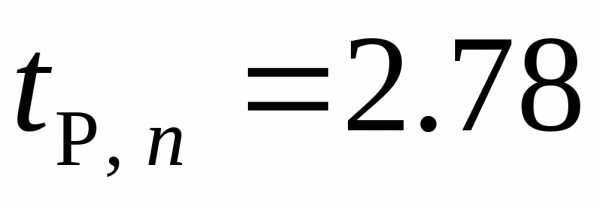 и определяем абсолютную ошибку
и определяем абсолютную ошибку
.
Относительная погрешность
.
Окончательно результат можно записать в виде:
при ,.
Пример 2. Вычислить коэффициент линейного расширения металлического стержня по методу наименьших квадратов. Длина металлического стержня от температуры зависит по линейному закону
.
Свободный
член 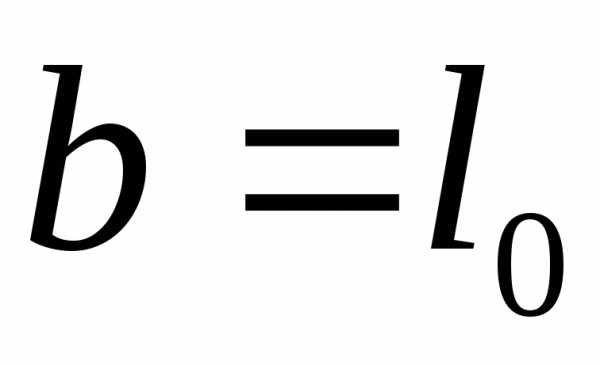 определяет первоначальную длину
определяет первоначальную длину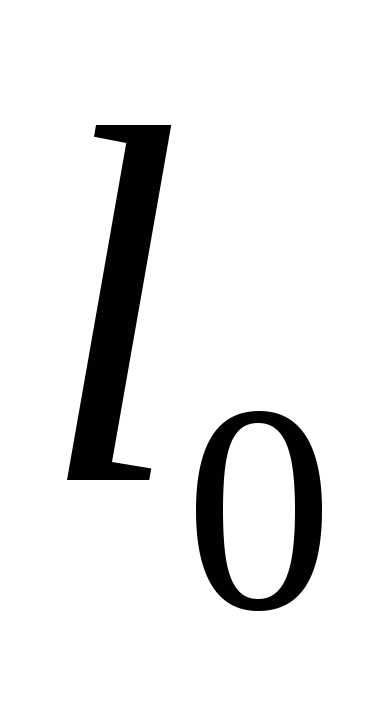 при температуре 0° C, а угловой
коэффициент
при температуре 0° C, а угловой
коэффициент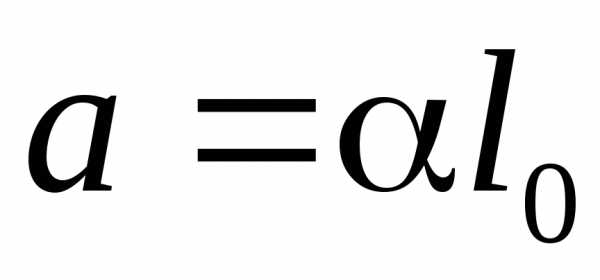 – произведение коэффициента линейного
расширения
– произведение коэффициента линейного
расширения на первоначальную длину
на первоначальную длину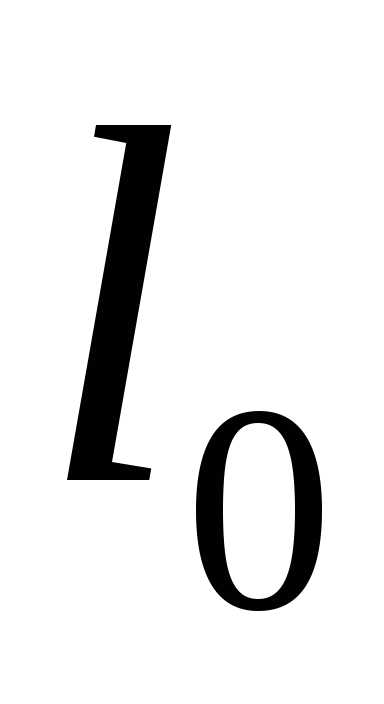 .
.
Результаты измерений и расчетов приведены в таблице 3.
Таблица 3.Результаты эксперимента
n | | l, мм | | | | ||
1 | 23 | 150.005 | | 2500 | 0.0001429 | 2.041 | |
2 | 43 | 150.040 | | 900 | 0 | 0.0003143 | 9.878 |
3 | 63 | 150.074 | | 100 | 1500.74 | 0.0002286 | 5.224 |
4 | 83 | 150.109 | 10 | 100 | 1501.09 | 0.0002286 | 5.226 |
5 | 103 | 150.143 | 30 | 900 | 4504.29 | 0.0003143 | 9.878 |
6 | 123 | 150.178 | 50 | 2500 | 7508.90 | 0.0001429 | 2.041 |
| 438 | 900.549 | 0 | 7000 | 12.09 | – | 34.286 |
| 73 | 150.091 | – | – | – | – | – |
По формулам (18), (19) определяем
,
.
Отсюда:
.
Найдем
ошибку в определении  .
Так как
.
Так как 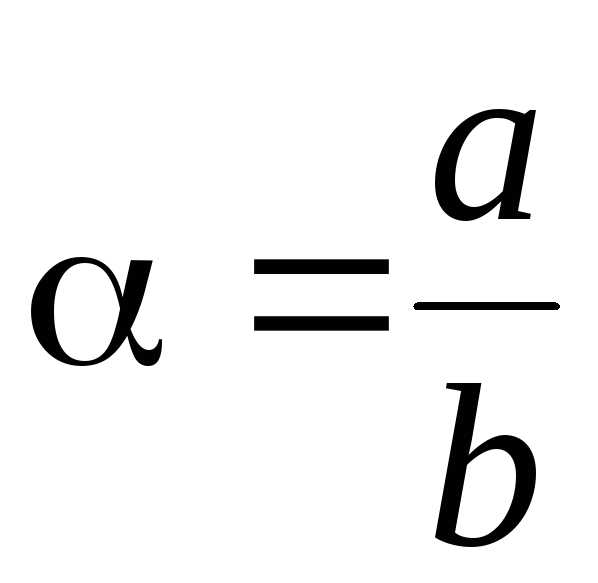 ,
то по формуле (14) имеем:
,
то по формуле (14) имеем:
.
Пользуясь формулами (20), (21) имеем
,
.
Тогда
.
Задавшись
надежностью
,
по таблице коэффициентов Стьюдента для 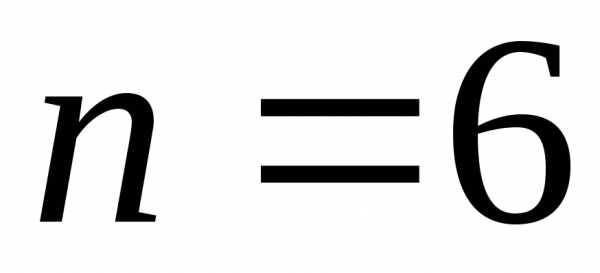 ,
находим
,
находим 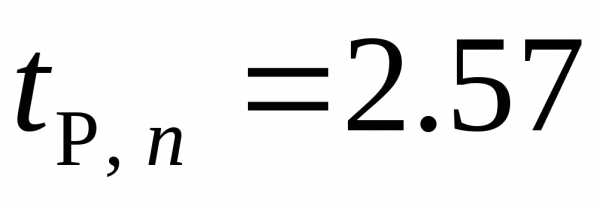 и определяем абсолютную ошибку
и определяем абсолютную ошибку
.
Тогда результат вычисления равен
.
Относительная погрешность
.
Окончательно результат можно записать в виде:
при
, 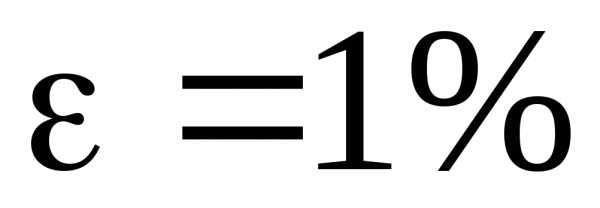 .
.
studfiles.net
§ 5 Метод наименьших квадратов (мнк).
Помимо двух вышеописанных способов оценки погрешности результата при косвенных измерениях, иногда применяют еще так называемый «метод наименьших квадратов» или сокращенно МНК. Этот метод можно использовать, если известен вид функциональной зависимостимежду измеряемыми физическими величинами, а требуется определитькоэффициенты, входящие в эту функцию. В наших лабораторных работах предлагается применять этот метод для определения параметров линейной зависимости.
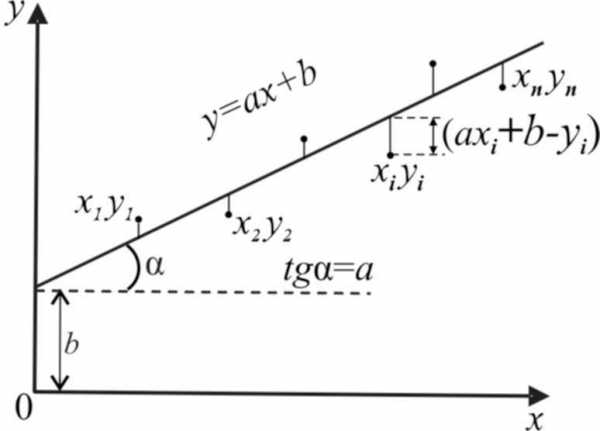
Пусть в эксперименте можно измерить ряд значений некоторой величины xи, соответствующие им значения, величиныy. И пусть при этомизвестно, что между ними справедлива зависимость вида: y = ax + b.Как известно, такая зависимость графически представляется прямой линией (рис.4). Однако измеренные значенияxi и yi включают в себя погрешность и, в результате, не лягут идеально на прямую линию.
Как по данным экспериментальных наблюдений наилучшим образом найти коэффициенты aиb? Графически эта задача сводится к построению прямой, ближе всего лежащей ко всем экспериментальным токам, так как прямая однозначно задается этими коэффициентами (рис.4.).
| Для аналитического выражения коэффициентов применяется метод наименьших квадратов. Утверждается, что наилучшей будет та прямая, сумма квадратов расстояний до которой, от всех экспериментальных точек будет минимальной. Расстояние (вдоль оси y) от точки с координатамиxi,yi до искомой прямой определяется выражением: (axi +b yi), |
Рис.4 |
тогда сумма квадратов расстояний будет равна:
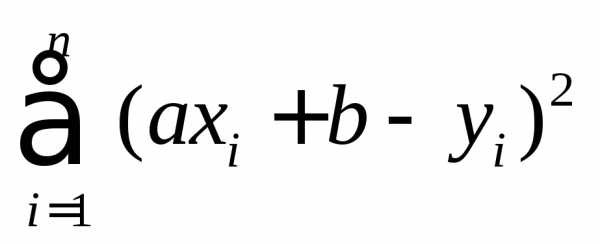
Решение задачи на нахождение минимума этого выражения (см. приложение, §8) приводит к следующим выражениям для коэффициентовaиb.
| (25) |
| (26) |
Дисперсию отклонения экспериментальных точек от прямой S02и дисперсию коэффициентовaиb Sa2 иSb2 можно вычислить по формулам:
S02 = | (27) |
| (28) |
Sb2= | (29) |
Доверительные интервалы для коэффициентов aиb определяются как обычно:
ap = 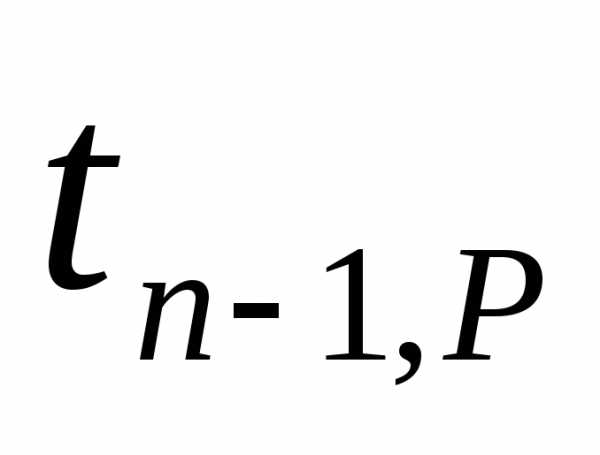 Sabp =
Sabp = 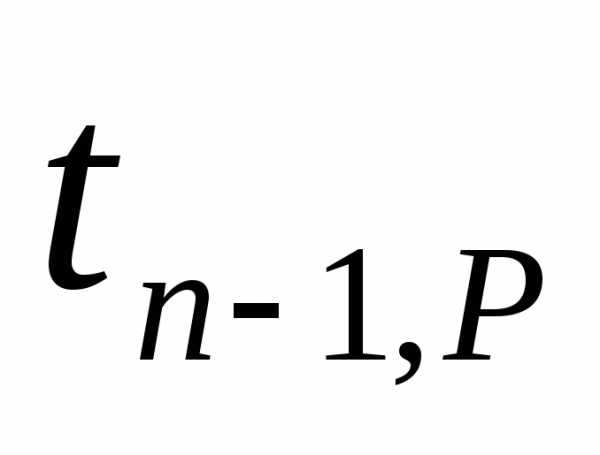 Sb
Sb
Если график исследуемой зависимости проходит через начало координат, то есть b=0, формулы 25, 27 и 28 существенно упрощаются. В этом случае коэффициентaи его дисперсию можно рассчитать по следующим формулам:
Однако следует иметь в виду, что формулы 25-28 включают разности больших величин, мало отличающихся друг от друга, что легко может привести к ошибкам при вычислениях, если их проводить с недостаточным числом значащих цифр. Поэтому все промежуточные вычисления следует выполнять с большим числом значащих цифр, без округления. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, а результаты измерений имеют более трех верных знаков, то велика вероятность получить неправильный результат вычислений. В этом случае рекомендуется для вычисления коэффициентовaиb,а также доверительных границ их погрешности вместо вышеуказанных формул использовать выражения, преобразованные к другому виду:
Во всех случаях проведения расчетов по МНК для определения коэффициентов линейной зависимости и их погрешностей необходимо вычислить некоторые суммы.Для этого удобно воспользоваться следующими таблицами – алгоритмами вычислений. Подсчитав суммы в каждом столбце и подставив их в соответствующие формулы, легко определить и значенияa,b,a иb
Таблица 5
xi | yi | xi2 | yi2 | xi yi |
x1 | y1 | x12 | y12 | x1 y1 |
x2 | y2 | x22 | y22 | x2 y2 |
… | … | … | … | … |
xn | yn | xn2 | yn2 | xn yn |
xi | yi | xi2 | yi2 | x1 y1 |
Или в случае использования формул 33 -37
Таблица 6
xi | yi | xi | (xi | (xi | xi2 | (axi +b yi)2 |
x1 | y1 | x1 | (x1 | (x1 | x12 | (ax1 +b y1)2 |
x2 | y2 | x2 | (x2 | (x2 | x22 | (ax2 +b y2)2 |
… | … | … | … | |||
xn | yn | xn | (xn | (xn | xn2 | (axn +b yn)2 |
xi | yi | (xi | (xi | (xi | xi2 | (axi +b yi)2 |
studfiles.net
Метод наименьших квадратов
Метод наименьших квадратов
Пусть требуется установить функциональную зависимость между переменными х, упо результатам экспериментальных исследований, приведенных в таблице:
Нужно подобрать функцию 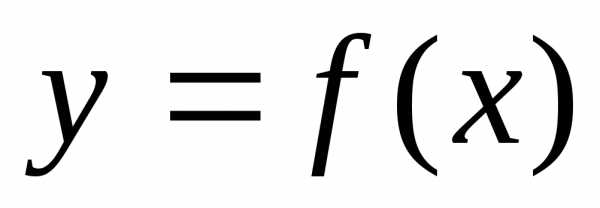 так, чтобы ее значения были как можно
более близкими к экспериментальным
значениям. Выбор функции
так, чтобы ее значения были как можно
более близкими к экспериментальным
значениям. Выбор функции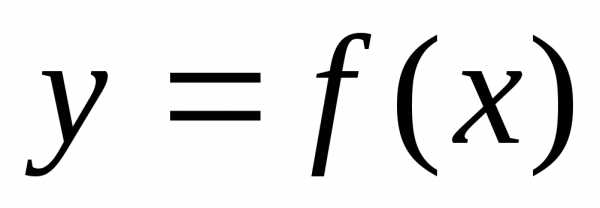 зависит от характера расположенных на
плоскости экспериментальных точек.
зависит от характера расположенных на
плоскости экспериментальных точек.
Пример:
Погрешность, возникающая при замене
экспериментальных значений  на значения функции,
равна в каждой точке.
на значения функции,
равна в каждой точке.
В МНК коэффициенты функции f(x)подбираются из следующего условия:сумма квадратов погрешностей по всей совокупности экспериментов принимает минимальное значение:
.
Обычно рассматривают несколько видов функций f(x) выбирают ту функцию, для которой суммарная погрешность окажется наименьшей.
Рассмотрим основные виды функций 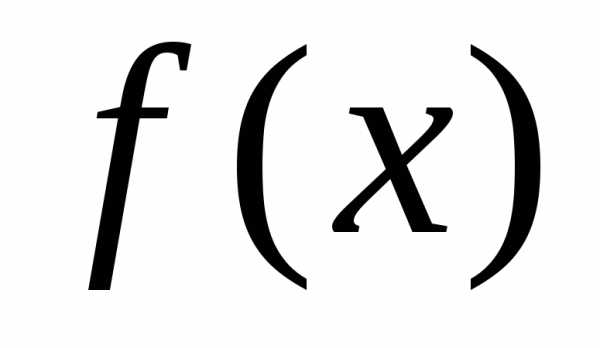 ,
используемые в МНК.
,
используемые в МНК.
Линейная зависимость.
Пусть , тогда необходимо найтиminфункции двух переменных:.
По необходимому условию экстремума обе частные производные этой функции двух переменных должны быть равны нулю:
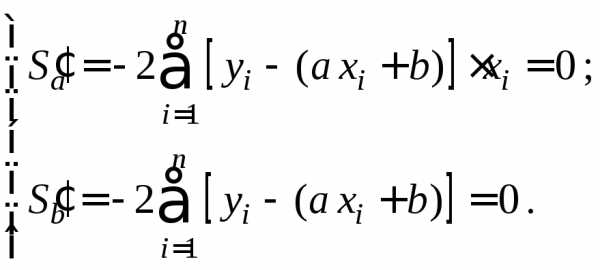 .
.
Раскрывая скобки, получим систему для определения неизвестных параметров aиb:
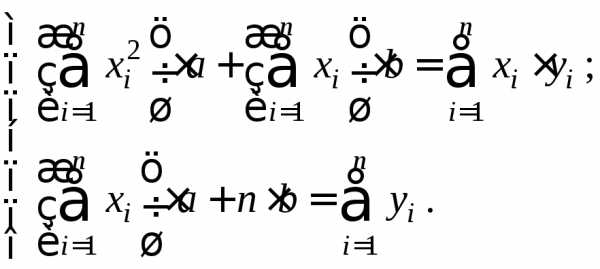 .
.
Значения коэффициентов при неизвестных a и b определяем из первоначальной таблицы как соответствующие суммы значений переменных х, у .
Решая эту систему относительно коэффициентов aиb:, получим:
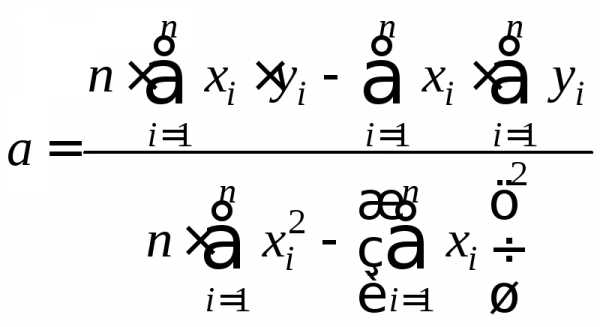 ,
,
.
Убедимся, что в точке функцияS(a,b)имеет минимум.
Составим матрицу Гессе и найдем ее главные миноры:
,
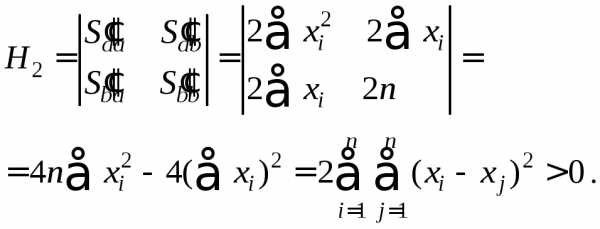
Так как главные миноры матрицы Гессе
положительны, то по критерию Сильвестра
матрица положительно определена и
квадратичная форма второго дифференциала 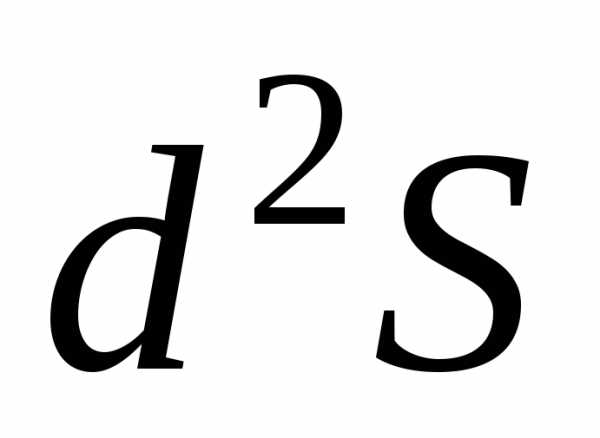 ,
соответствующая этой матрице, принимает
только положительные значения.
,
соответствующая этой матрице, принимает
только положительные значения.
Из условия 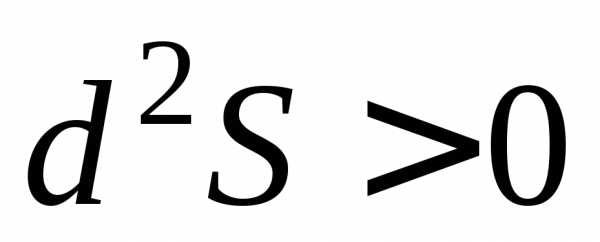 следует, что- точка минимума.
следует, что- точка минимума.
Если коэффициенты линейной функции найдены, можно вычислить суммарную погрешность: .
II. Показательная функция.
Сведем этот случай к линейной функции.
Логарифмируем уравнение: .
Логарифмируем таблицу:
Обозначим 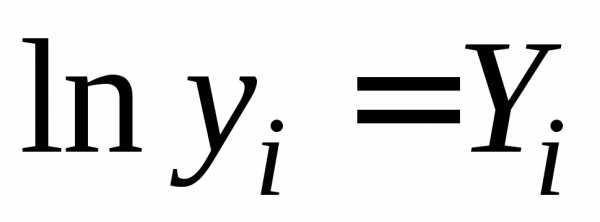 ,,
тогда
,,
тогда
Найдем коэффициенты Аиbаналогично первому случаю линейной функции:
.
Дальнейшие вычисления провести
самостоятельно аналогично первому
пункту. Окончательное значение
коэффициента аопределить по формуле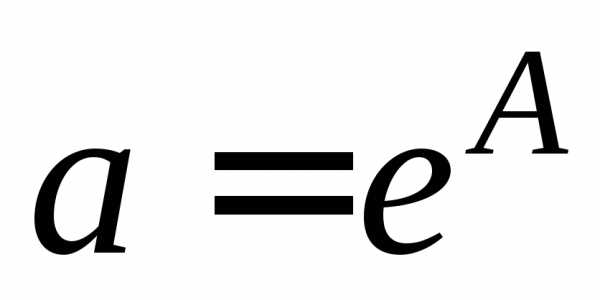 .
.
Суммарная погрешность равна .
III. Степенная функция 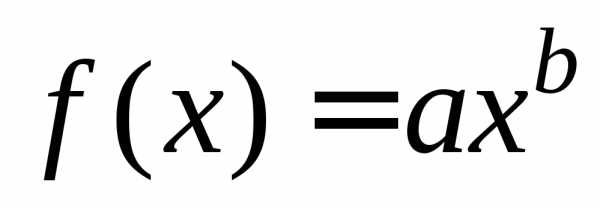 .
.
Поступим аналогично показательной функции.
Логарифмируем уравнение: , получим— линейную функцию.
Логарифмируем таблицу:
3. Обозначим . Тогда .
Найдем коэффициенты иb аналогично первому случаю:
.
Дальнейшие вычисления провести
самостоятельно аналогично первому
пункту. Окончательное значение
коэффициента аопределить по формуле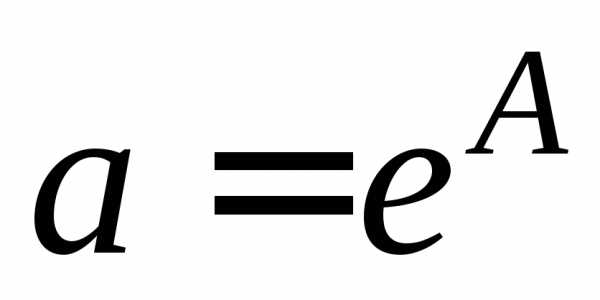 .
.
Суммарная погрешность равна .
IV. Квадратичная функция .
Условие метода наименьших квадратов имеет вид:
.
Аналогично линейной функции составляется система трех уравнений , из которой находятся коэффициентыa, bис:
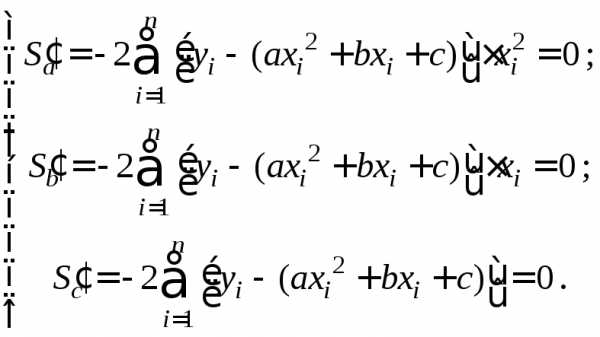
Запишем систему в развернутом виде:
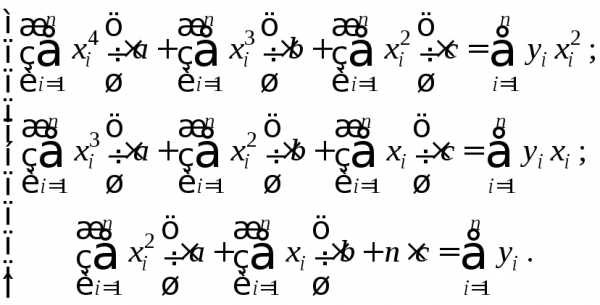
Эта система имеет единственное решение.
Кроме того, можно доказать, что
коэффициенты, получаемые методом
наименьших квадратов, всегда определяют
именно минимум функции 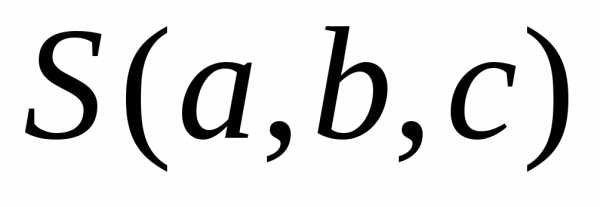 .
.
Суммарная погрешность .
studfiles.net
Метод наименьших квадратов

Метод наименьших квадратов (МНК).
Пример.
Экспериментальные данные о значениях переменных х иу приведены в таблице.
В результате их выравнивания получена функция
Используя метод наименьших квадратов , аппроксимировать эти данные линейной зависимостьюy=ax+b (найти параметрыа иb). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Суть метода наименьших квадратов (МНК).
Задача заключается в нахождении коэффициентов линейной зависимости, при
которых функция двух переменных а иb принимает наименьшее значение. То есть, при данныха иb сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
Вывод формул для нахождения коэффициентов.
Составляется и решается система из двух уравнений с двумя неизвестными.
Находим частные производные функции по переменныма иb, приравниваем эти производные к нулю.
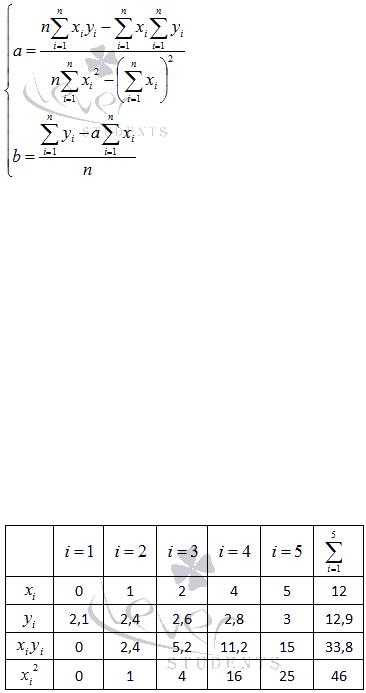
Решаем полученную систему уравнений любым методом (например методом подстановки илиметодом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).
При данных а иb функцияпринимает наименьшее значение. Доказательство этого факта приведенониже по тексту в конце страницы .
Вот и весь метод наименьших квадратов. Формула для нахождения
параметра a содержит суммы,,,и параметрn — количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициентb находится после вычисленияa.
Пришло время вспомнить про исходый пример.
Решение.
В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.
Значения в четвертой строке таблицы получены умножением значений 2-ойстроки на значения3-ейстроки для каждого номераi .
Значения в пятой строке таблицы получены возведением в квадрат значений 2- ой строки для каждого номера i .
Значения последнего столбца таблицы – это суммы значений по строкам.
Используем формулы метода наименьших квадратов для нахождения коэффициентов а иb. Подставляем в них соответствующие значения из
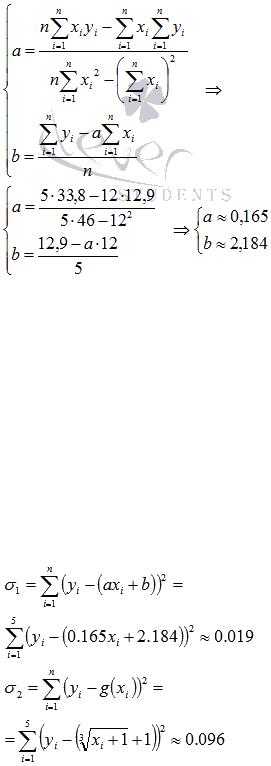
последнего столбца таблицы:
Следовательно, y = 0.165x+2.184 — искомая аппроксимирующая прямая.
Осталось выяснить какая из линий y = 0.165x+2.184 илилучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.
Оценка погрешности метода наименьших квадратов.
Для этого требуется вычислить суммы квадратов отклонений исходных данных
от этих линий и, меньшее значение соответствует линии, которая лучше в смысле метода наименьших квадратов аппроксимирует исходные данные.
Так как , то прямаяy = 0.165x+2.184 лучше приближает исходные данные.
Графическая иллюстрация метода наименьших квадратов
(мнк).
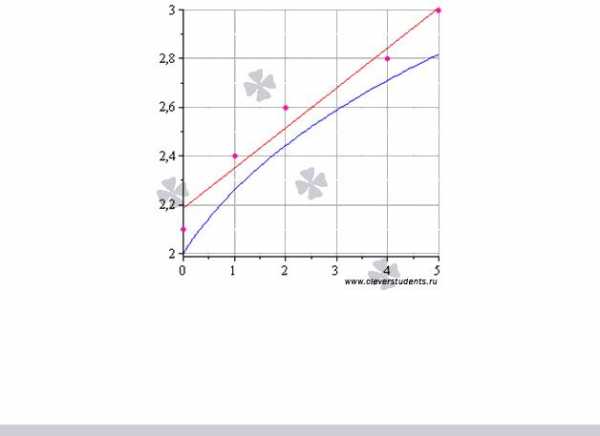
На графиках все прекрасно видно. Красная линия – это найденная прямая y =
0.165x+2.184, синяя линия – это, розовые точки – это исходные данные.
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y приx=3 или приx=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
К началу страницы
Доказательство.
Чтобы при найденных а иb функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала
второго порядка для функции была положительно определенной. Покажем это.

Дифференциал второго порядка имеет вид:
То есть
Следовательно, матрица квадратичной формы имеет вид
причем значения элементов не зависят от а иb .
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка . Неравенство строгое, так как точкинесовпадающие. В дальнейшем это будем подразумевать.

Угловой минор второго порядка
Докажем, что методом математической индукции.
1.Проверим справедливость неравенства для любого значения n, например дляn=2.
Получили верное неравенство для любых несовпадающих значений
и.
2.Предполагаем, что неравенство верное для n.
— верное.
3.Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что исходя из предположения что- верное.

Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значенияа иb соответствуют наименьшему значению
функции , следовательно, являются искомыми параметрами для метода наименьших квадратов.
studfiles.net
Л. А. Литневский, с. А. Минабудинова
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
В ЛАБОРАТОРНОМ ПРАКТИКУМЕ ПО ФИЗИКЕ
ОМСК 2004
Министерство путей сообщения Российской Федерации
Омский государственный университет путей сообщения
___________________
Л. А. Литневский, С. А. Минабудинова
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
В ЛАБОРАТОРНОМ ПРАКТИКУМЕ ПО ФИЗИКЕ
Утверждено редакционно-издательским советом университета
в качестве методических указаний к лабораторным работам по физике
для студентов 1-го, 2-го курсов дневного обучения
Омск 2004
УДК 530.1 (076.5)
ББК 22.3я73
Л64
Метод наименьших квадратов в лабораторном практикуме по физике: Методические указания к выполнению лабораторных работ; Л. А. Литневский, С. А. Минабудинова / Омский гос. ун-т путей сообщения. Омск, 2004. 32 с.
В методических указаниях подробно рассмотрен метод наименьших квадратов, приведены примеры его применения и расчет погрешности при обработке результатов измерений функциональных зависимостей между физическими величинами.
Методические указания по физике предназначены для студентов 1-го и 2-го курсов всех факультетов, могут быть использованы при выполнении лабораторных работ и дополнительных заданий к лабораторным работам.
Библиогр.: 3 назв. Табл. 7. Рис. 2.
Рецензенты: доктор техн. наук, профессор В. Н. Зажирко;
канд. физ.-мат. наук Г. И. Косенко.
________________________
© Омский гос. университет
путей сообщения, 2004
ОГЛАВЛЕНИЕ
Введение 5
Обработка результатов измерений функциональных зависимостей 6
Метод наименьших квадратов 6
Погрешность параметров a, b, … 7
Критерий качества аппроксимации 9
Аппроксимация экспериментальной зависимости линейной функцией вида y = k x 10
Вычисление параметра k 10
Вычисление погрешности параметра k 12
Пример: зависимость силы тока от напряжения на резисторе 13
Аппроксимация экспериментальной зависимости линейной функцией вида y = p x + q 15
Вычисление параметров p и q 15
Вычисление погрешности параметров p и q 16
Пример: зависимость сопротивления проводника от температуры 17
Аппроксимация экспериментальной зависимости параболической функцией 19
Вычисление параметров a и b функции y = a x2 + bx 19
Вычисление погрешности параметров a и b функции y = a x2 + bx 20
Вычисление параметра с функции y = c x2 и его погрешности 21
Другие виды экспериментальной зависимости 22
Общий подход 22
Экспоненциальная зависимость между величинами вида y = α e βx 22
Экспоненциальная зависимость между величинами вида y = α e β/x 22
Использование прикладных программ 23
Метод наименьших квадратов в работе «Затухающие электрические колебания» 24
Постановка задачи 24
Вычисление логарифмического декремента затухания и его погрешности с помощью прикладных программ 25
Вычисление логарифмического декремента затухания и его погрешности аппроксимацией линейной функцией 26
Вычисление сопротивления контура и его погрешности 28
Библиографический список 30
ВВЕДЕНИЕ
При проведении экспериментов часто возникает необходимость измерения физических величин, находящихся в функциональной зависимости. Как правило, после измерений информация о физическом явлении извлекается из графиков, построенных по данным, полученным экспериментальным путем, а зависимость между двумя физическими величинами – X и Y – представляется в виде табл. 1.
Таблица 1
Зависимость физических величин X и Y
X
x1
x2
x3
…
xN
Y
y1
y2
y3
…
yN
Обработка результатов таких измерений не может быть выполнена по известным правилам обработки результатов прямых и косвенных измерений, поскольку наборы чисел (x1, x2, …, xN) и (y1, y2, …, yN) не являются значениями многократного измерения одной и той же величины. В связи с тем, что значения величин X и Y измеряются с погрешностью, нанесенные на координатную плоскость точки будут разбросаны относительно предполагаемой кривой. Как тогда построить кривую, чтобы она наилучшим образом соответствовала проведенным измерениям?
Если график y = f (x) строить, непосредственно соединяя экспериментально полученные точки, то он будет иметь вид ломаной. Однако в большинстве случаев функции, описывающие процессы в природе, являются гладкими. Значит, необходимо подобрать такую функцию y = f (x), которая наилучшим образом выражала бы экспериментальную зависимость Y от X. Другими словами, требуется сгладить построенную по точкам ломаную линию. Эту задачу называют задачей о сглаживании экспериментальных зависимостей. Она решается при помощи метода наименьших квадратов.
Подбор формул по экспериментальным данным называют подбором эмпирических формул. На самом деле, формула тем точнее, чем больше теоретических представлений вложено в нее и чем в меньшей степени она является эмпирической. В действительности необходимо сначала задаться видом функции, а затем, пользуясь результатами эксперимента, определить значения различных параметров (постоянных величин), входящих в нее.
Перед тем как приступить к подбору формулы, полезно нанести экспериментальные данные на график и от руки провести через полученные точки наиболее правдоподобную гладкую кривую. При этом сразу выявляются те данные, в которых можно предполагать существенные ошибки. Очень важно при проведении кривой по экспериментальным точкам знать, как должна вести себя кривая при значениях аргумента, весьма близких к нулю, при больших значениях аргумента, проходит ли кривая через начало координат, пересекает ли координатные оси и т. п.
Итак, допустим, что эта предварительная работа выполнена, подобрана формула, и требуется определить значения входящих в формулу постоянных величин. Как это сделать?
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
studfiles.net

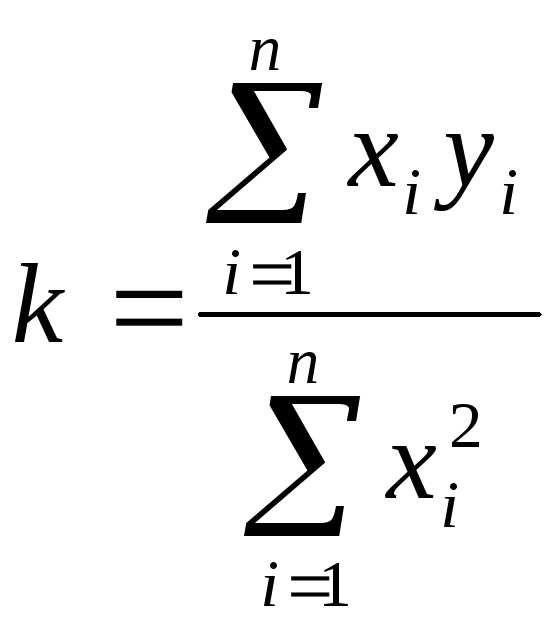 .
.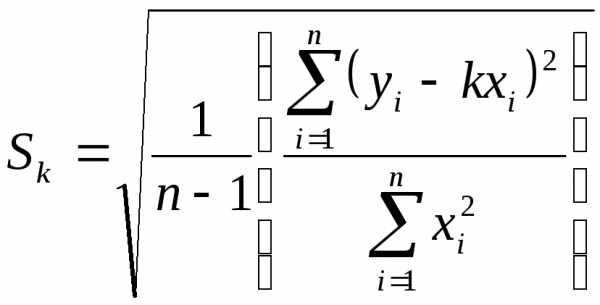 .
.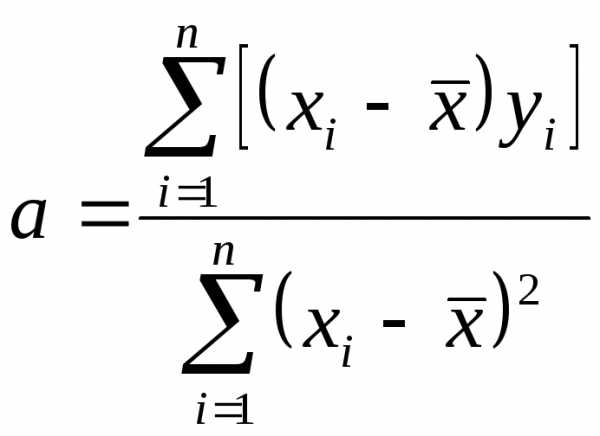 ,
,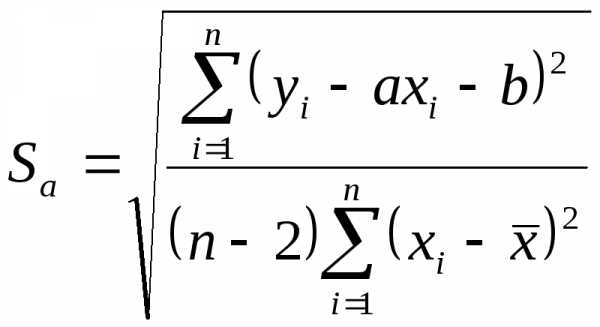 ,
,
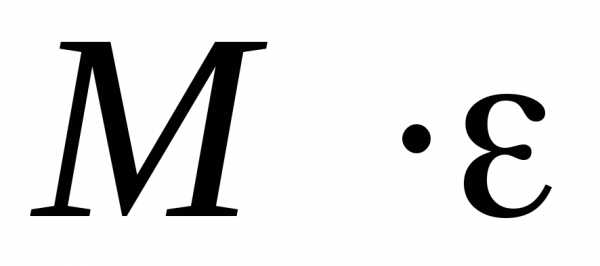

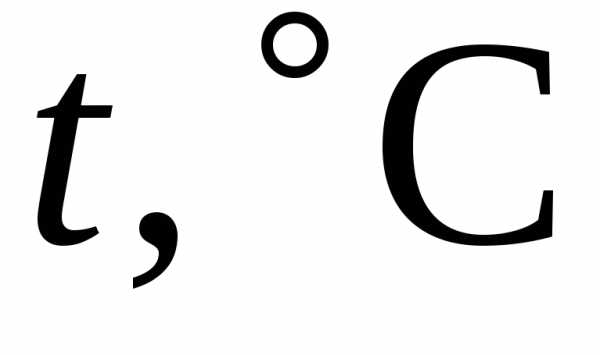



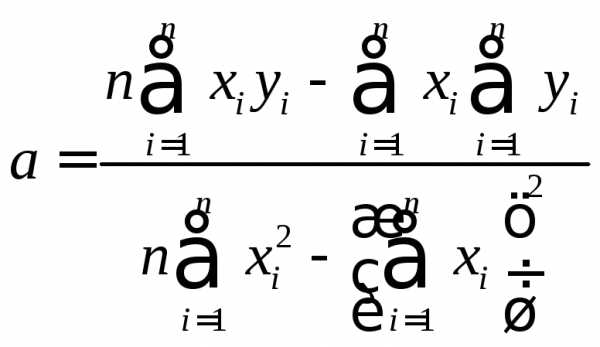
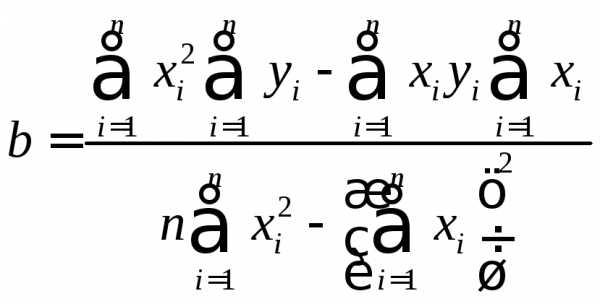
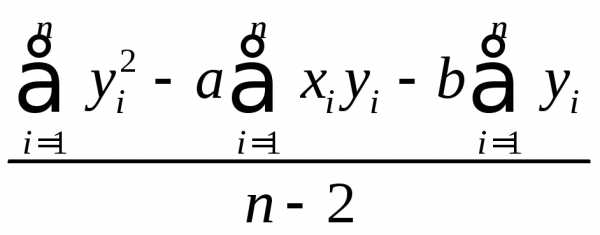
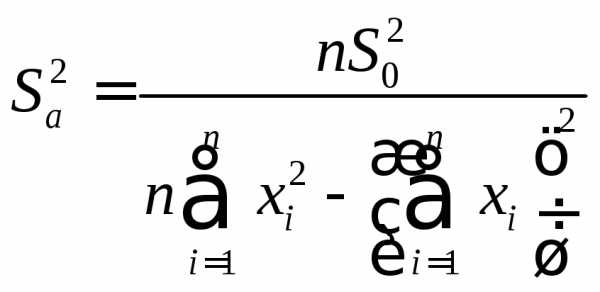
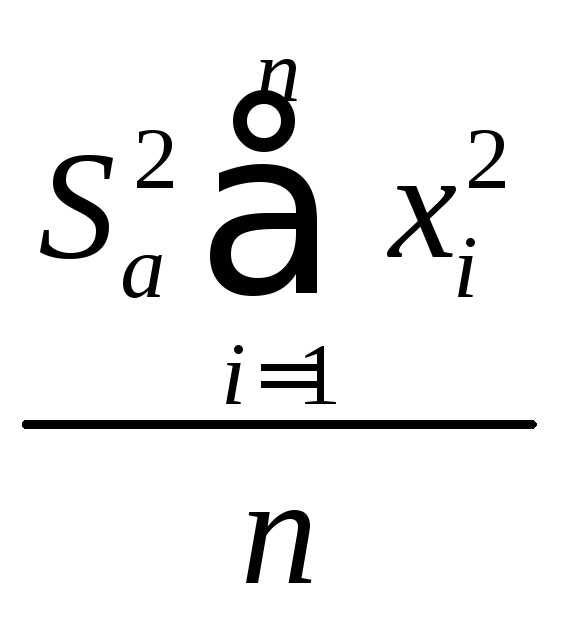
 )2
)2 )yi
)yi
 )2
)2 )y1
)y1
 )2
)2 )y2
)y2
 )2
)2 )yn
)yn )
) )2
)2 )yi
)yi