Математический анализ. Множества и функции Понятие множества. Операции над множествами
14
Понятие множества является первичным, не определяемым через более простые.
Множество – это совокупность некоторых объектов. Эти объекты, называют элементами, или точками, этого множества.
Это может быть множество точек окружности, множество предприятий отрасли, множество студентов в аудитории и т.п. Примеры множеств:
А = {Иванов, Смирнов, Петров, Сидоров}
B = {k, m, n}
C = {5; -7; 0,9; 100; 8}
D — множество чисел от 5 до 10
E = {Иванов}
F — множество чисел от 7 до 100
G = {Соколов, Кузнецов}
N – множество натуральных чисел
Множества могут включать любое количество элементов – один (Е), другое конечное число (A, B, C, E, G), бесконечное число (D, F, N) либо ноль, т.е. вообще ни одного элемента. В последнем случае множество называют пустым и обозначают .
Говорят, что элемент множества принадлежит этому множеству. Для обозначения принадлежности используется символ «» (если элемент не принадлежит множеству, это обозначают символом «»). Например, Иванов А; 5 С; 10 С.
Операции над множествами
Если одно множество состоит из части элементов другого или совпадает с ним, то первое из них называют подмножеством второго и записывают это с помощью символа «». Например, Е – подмножество А, т.е. Е А.
Два множества называются равными, если они состоят из одних и тех же элементов.
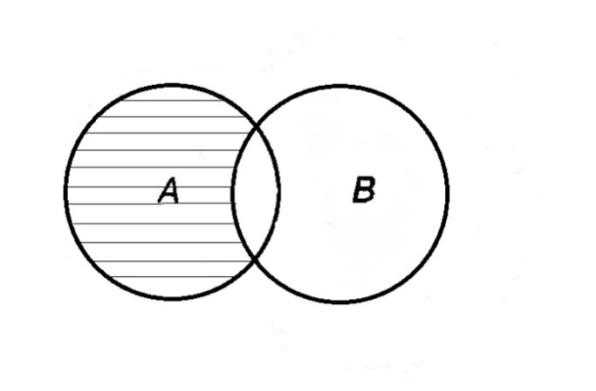
Объединением двух множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Оно обозначается символом «». Например, DF — множество чисел от 5 до 100.
Пересечением двух множеств называется множество, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств. Оно обозначается символом «». Например, DF — множество чисел от 7 до 10; CD = {5; 8}; АЕ = {Иванов}; АG = .
Разностью множеств называется множество, состоящее из всех элементов, принадлежащих первому из них, которые не принадлежат второму. Она обозначается символом «\». Например, {Смирнов, Петров, Сидоров}; С\D = {-7; 0,9; 100}.
Дополнением множества, которое является подмножеством другого множества, называют множество, состоящее из всех элементов второго множества, не принадлежащих первому. Например, для Е А дополнением Е до А будет множество {Смирнов, Петров, Сидоров} =А\Е.
Множества,
элементами которых являются действительные
Из школьного курса алгебры известны числовые множества: R — действительных чисел, Q — рациональных, I — иррациональных, Z — целых, N — натуральных чисел. Очевидно, что NZQR, IR, R=QI.
Множество действительных чисел R изображается точками числовой прямой (или числовой оси), т.е. прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба. Между множеством действительных чисел и точками этой прямой существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой — определенное действительное число (см. рис. 1.1). Поэтому часто вместо «число х» говорят «точка х».
Множество, элементы которого удовлетворяют неравенству a x b, называется отрезком (или сегментом) [а; b]; неравенству а < х < b — интервалом ]а; b[ 2; неравенствам ах<b или а<хЬ, называются полуинтервалами соответственно [а; b[ и ]а; b]. Наряду с этим рассматриваются бесконечные интервалы и полуинтервалы ]-; а[, ]b; +[, ]-, +[, ]-; а] и [b; +[. В дальнейшем все указанные множества объединbм термином промежуток.
studfiles.net
Множества и их свойства. Функции. — МегаЛекции
ГЛАВА 1. МНОЖЕСТВА. ЧИСЛОВЫЕ МНОЖЕСТВА.
В математике все понятия делятся на первичные и определяемые через первичные или уже известные. Основным первичным понятием математики, ее фундаментом является понятие множество. Слова «совокупность», «семейство», «система», «набор», «объединение» являются синонимами слова «множество». Под множеством понимается некоторая совокупность объектов, которые объединены в одну группу по некоторым признакам. Примеры множеств: множество учащихся в аудитории; совокупность тех из них, кто получает по математике только отличные оценки; семейство звезд Большой Медведицы; множество страниц книги; множество всех целых положительных чисел и т. д. Из приведенных примеров следует, что множество может содержать конечное или бесконечное число объектов произвольной природы. Первичными понятиями являются также
Объекты, образующие множества называются элементами или точками множества. Множества будем обозначать: А, В,…, X, Y…, а соответствующие элементы: а,b …,x, y… Если а есть элемент множества А, то пишут . Если a не является элементом множества А, то пишут .
Два множества А и В называются равными, если они состоят из одних и тех же элементов и пишут .
Элементы множества записываются в скобках, например: .Если множество А состоит из элементов , то записывают , или . Например, — множество целых положительных чисел, которые называются натуральными числами.
Имеет место понятие пустого множества, т.е. множества, не содержащего ни одного элемента, и его обозначают Ø.
Определение 1. Множество А называется подмножеством множества В, если все элементы множества А являются элементами множества В. Обозначается: .
.
Пустое множество содержится в любом множестве, т.е. Ø А. Из определения также следует, что .
Рассмотрим операции над множествами. Пусть А и В два множества.
Определение 2.Объединением (суммой) множеств А и В называется такое множество S, каждый элемент которого принадлежит хотя бы одному множеству
Объединение конечного числа множеств есть: , т.е. x принадлежит хотя бы одному из множеств. Можно говорить об объединении бесконечного числа множеств.
.
Определение 3.Пересечением (произведением) двух множеств А и В называется такое множество P, которое состоит из элементов множества А и элементов множества В.
.
Пересечение конечного числа множеств есть .
Определение 4.Разностью двух множеств А и В называется множество D, которое состоит из элементов множества А, но не принадлежащих множеству В.
Если , то множество называется дополнением множества В до множества А.
Определение 5.Симметрической разностью двух множеств А и В называется множество С= . Обозначается: С=А ∆ В.
Свойства операций над множествами:
1.
2.Если
3. Если
4. Ø
5.
6.
7.
8.
9.
10.
11.
12.
Доказательство этих свойств весьма просто. Например, для доказательства равенства двух множеств надо доказать, что элемент принадлежащий левой части равенства принадлежит и правой.
Пусть заданы два множества и . Два элемента, записанные в виде , где и будем называть упорядоченной парой элементов или просто парой.
Определение 6.Декартовым произведением множеств Х и Y называется множество всех упорядоченных пар , где , и обозначается , т.е.
.
Определение 7.Подмножество F декартового произведения называется отображением множества Х в множество Y, если выполняется следующее условие: существует единственная пара . Обозначения:
Из определения следует, что не всякое подмножество является отображением Х в Y. Например, если , а , то — отображение, но — не отображение. То есть, первые элементы в F должны быть все различные. Синонимами термина «отображение» являются следующие: функция, преобразование, соответствие, морфизм. Они отличаются буквенной символикой и сферами (разделами математики) употребления. В математическом анализе обычно используют термин «функция». Часто дают и другое определение функции, не используя термин «отображение».
Определение 8.Функцией F заданной на множестве Х и принимающей значение на множестве Y называется правило, по которому элементу ставится в соответствие строго один элемент . При этом пишут: . Обозначение функции: F, Ф, f, g, и др.
Множество Х называется областью определения , а множество y: называется множеством значений функции. Каждый элемент называется аргументом или независимой переменной, а элемент или — значением функции или зависимой переменной.
Иногда говорят, что элемент у является образом элемента x при отображении F, а элемент х называют прообразом (одним из возможных) элемента у при отображении F.
Множество всех элементов называется образом множества X при отображении F, т.е. .
Пусть существует также отображение , как множество упорядоченных пар . Такое отображение называется обратной функцией и это обозначают следующим образом: .
Очевидны следующие тождества:
Если существуют отображения и одновременно, то отображение называется взаимно-однозначным.
Определение 9.Пусть . Тогда отображение , определенное равенством называется суперпозицией
Теперь дадим определение очень важного в математическом анализе понятия.
Определение 10.Функция определения на множестве натуральных чисел и принимающая значения из некоторого множества А называется последовательностью.
Пусть . Соответствующее значение последовательности будем обозначать . Последовательность будем обозначать или , где – члены последовательности. Таким образом, значения этой функции можно занумеровать.
Определение 11.Множества А и В называются эквивалентными, если существует взаимно-однозначное отображение этих множеств.
Обозначение: ~B.
Пример. Пусть — множество натуральных чисел. Обозначим множество целых чисел . Ясно . Однако покажем, что эти множества эквивалентны. Установим следующее взаимно-однозначное соответствие между N иZ. Нечетному числу поставим в соответствие положительное число . Четному числу поставим в соответствие отрицательное .
Полученная функция отображает множество N на множество взаимно-однозначно, т.е. N~Z. Здесь и т.д.
Определение 12.Пусть . Множество А называется конечным, если существует такой номер n, что А ~ . В противном случае множество А называется бесконечным.
Определение 13.Бесконечное множество А называется счетным, если А~N, в противном случае бесконечное множество называется несчетным.
Говорят, что множество А не более чем счетное, если оно либо конечно, либо счетное. Элементы такого множества можно занумеровать: .
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Лекция 1.Множества Элементы теории множеств. Операции над множествами.
Определение 1.Множеством называется совокупность некоторых объектов, объединенных в одно целое по какому ‒ либо признаку.
Объекты, из которых состоит множество, называются его элементами.
Обозначаются заглавными буквами латинского алфавита A, B, …, X, Y, …, а их элементы обозначаются малыми буквами a, b, …, x, y.
Определение 1.1.Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø.
Множество можно задать пересечением и описанием.
Пример:; .
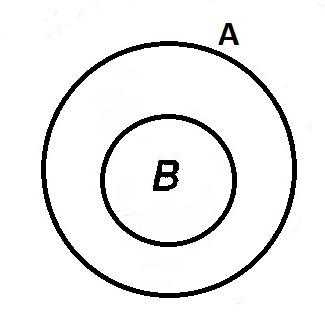
Определение 1.2.Множеством A называется подмножеством B, если каждый элемент множества A является элементом множестваB. Символически это обозначают так: AB (A содержится вB).
Определение 1.3.Два множества A иB называются равными, если они состоят из одних и тех же элементов (A =B).
Операции над множествами.
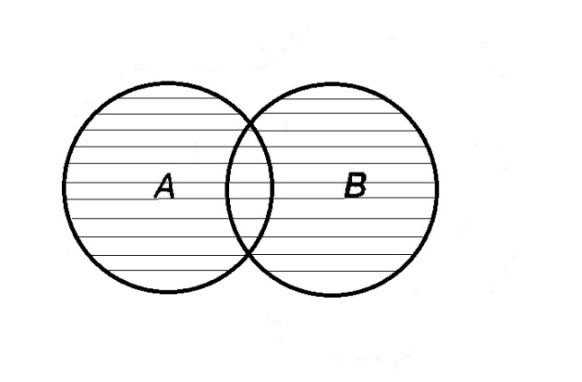
Определение 1.4.Объединением или суммой множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.
Объединение множеств обозначают AB (или A +B). Кратко можно записать AB = .
AB= A +B
Если BA, то A +B=A
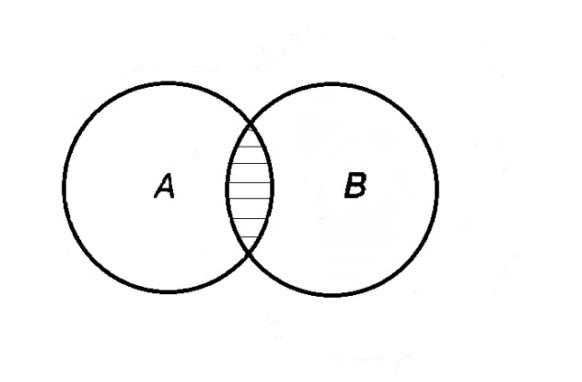
Определение 1.5.Пересечением или произведением множеств A иB называется множество, состоящее из элементов, каждый из которых принадлежит множеству A и множествуBодновременно. Пересечение множеств обозначают AB (илиA·B). Кратко можно записать:
AB =.
AB =A ·B
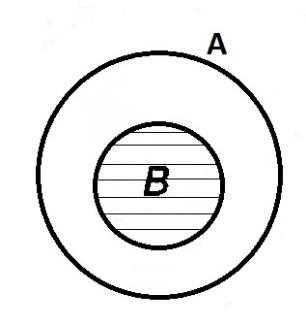
ЕслиBA, тоA · B= B
Определение 1.6. Разностью множеств A и B называется множество, каждый элемент которого является элементом множества Aи не является элементом множества B. Разность множеств обозначают A/B. По определению A/B = .
A/B =A–B
Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
N = — множество натуральных чисел.
Z= — множество целых чисел.
Q= — множество рациональных чисел.
R‒ множество действительных чисел.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ;… ‒ рациональные числа.
Иррациональное число выражается бесконечной непериодической десятичной дробью. Так, = 1,41421356…; = 3,14159265…. – иррациональное число.
K– множество комплексных чисел (вида Z=a+bi)
RK
Определение 1.7. Ɛ ‒ окрестностью точки x0 называется симметричный интервал (x0 – Ɛ; x0 + Ɛ), содержащий точку x0.
В частности, если интервал (x0 –Ɛ; x0 +Ɛ), то выполнятся неравенство x0 –Ɛ<x<x0 +Ɛ, или, что то же, │x– x0 │<Ɛ. Выполнение последнего означает попадание точки x в Ɛ – окрестность точки x0.
Пример 1:
= 2, Ɛ = 0,1.
(2 – 0,1; 2 + 0,1) или (1,9; 2,1) – Ɛ– окрестность.
│x– 2│< 0,1
–0,1<x – 2<0,1
2 –0,1<x< 2 + 0,1
1,9<x< 2,1
Пример 2:
A– множество делителей 24;
B– множество делителей 18.
A=.
B=.
AB= A +B =
AB =A ·B =
A /B =A –B =
Лекция 2. Функция Понятие функции. Основные свойства функции.
Определение 1. Пусть даны два непустых множестваХ и Y.Соответствие f, при котором каждому элементу xХсоответствует один единственный элемент уY, называется функцией и записывается у = f(x),
xХили f:x→ у (x → у).
x— аргумент функции; у — значение функции.
Пример:
y = 2 x – 1
Множество Хназывается областью определения функцииfи обозначается D(f). Множество всех уYназывается множеством значений функцииfи обозначается E(f).
Если элементами множеств Х и Yявляются действительные числа, то функцию fназывают числовой функцией.
studfiles.net
Функции множества — это… Что такое Функции множества?
функции, сопоставляющие каждому множеству из некоторого класса множеств определённое число. Например, длина отрезка является Ф. м., определённой на классе всех отрезков на прямой (функцией отрезка).
Интеграл x) также является функцией отрезка — интервала интегрирования [α, β]. Рассматривают также функции от областей на плоскости или в пространстве. Например, при заданном распределении плотностей масса, заключённая в данной области Ω, является функцией этой области. Понятие функции области — более гибкий аппарат для описания физических явлений, чем понятие функции точки, т.к. позволяет учитывать случаи, когда плотность физических величин в отдельных точках бесконечна (точечные источники и т.д.). Кроме того, это понятие более отвечает условиям физического эксперимента (при котором наблюдается не функция точки, а среднее от этой функции по некоторой малой области). Понятие Ф. м. получило развитие в связи с построением теории интеграла Лебега, в которой приходится рассматривать не только функции от областей, но и функции от произвольных измеримых множеств. Одним из первых примеров такой Ф. м. является мера Лебега μ(Е) измеримого множества Е (см. Мера множества). Эта Ф. м. вполне аддитивна, т. е. мера суммы любой конечной или счётной совокупности непересекающихся измеримых множеств есть сумма мер этих множеств. Наряду с лебеговской мерой множеств рассматривают др. меры, являющиеся неотрицательными вполне аддитивными Ф. м., определёнными на соответствующем классе множеств. Такие Ф. м. встречаются в общей теории интеграла. Ф. м. f (E) называют абсолютно непрерывной относительно некоторой меры μ, если f (E) = 0 при μ(Е) = 0. Так, интеграл Лебега x) по множеству М является вполне аддитивной абсолютно непрерывной (относительно меры Лебега) функцией от М. Обратно, всякая вполне аддитивная абсолютно непрерывная Ф. м. может быть представлена в качестве интеграла Лебега от некоторой суммируемой функции φ(x). Важным примером Ф. м. являются Распределения вероятностей.Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976; Халмош П., Теория меры, пер. с англ., М., 1953
dic.academic.ru
Глава I. Множества, отображения и функции
О Г Л А В Л Е Н И Е
Стр.
Множества. Общие понятия. . . . . . . . . . . . . 5
Числовые множества . . . . . . . . . . . . . . . 8
Отображения . . . . . . . . . . . . . . . . . . 10
Композиция отображений. Обратные отображения . . . . . 12
Глава II. Введение в теорию векторных пространств.
Векторная алгебра.
Геометрические векторы. Основные определения. . . . . . 12
Простейшие операции над векторами
Числовые матрицы
Операции над матрицами
Перестановки и подстановки из n символов
Определитель матрицы. Понятие определителя
Правило Сарруса для квадратных матриц 3 порядка
Свойства определителей
Линейное свойство определителя
СЛАУ
Метод Гаусса
1. Множества, отображения и функции
Понятие множества пронизывает все современное естество-знание и, в особенности, математику. Оно приобретает все возра-стающее значение во многих сферах производственной деятельно-сти и – даже – в быту. Это относится также к понятию отображе-ния множеств, частным случаем которого является (числовая) фун-кция. В учебной литературе по высшей математике этим понятиям уделяется недостаточное внимание. Настоящее учебное пособие восполняет пробел. Оно содержит минимальные сведения о множествах и их отображениях. В связи с этим работа может заинтересовать не только студентов но и начинающих преподавателей.
1.1. Множества. Общие понятия
Множество – набор, совокупность, собрание каких-либо объ-ектов, называемых его элементами, или точками, обладающих об-щим для них характеристическим свойством. При введении его в рассмотрение постулируется, что понятие множества является пер-вичным и не определяется с помощью иных, если можно так выра-зиться, более первичных и простых понятий. К другим терминам – синонимам понятия множества относятся, например, слова: семей-ство, группа, класс, геометрическое место точек (ГМТ).
При этом множество задаётся либо перечислением его элемен-тов, либо с помощью правила, позволяющего определить принадле-жит или нет данный объект рассматриваемому множеству.
Первый способ годится теоретически для любых конечных мно-жеств, т.е. множеств, состоящих из конечного числа элементов.
В математике (и не только в ней) приходится иметь дело также с множествами бесконечными; например, множеством всех нату-ральных чисел, всех чётных чисел, всех целых чисел, всех прямых на плоскости и т.д.
Если х есть элемент множества А,
то пишут:
или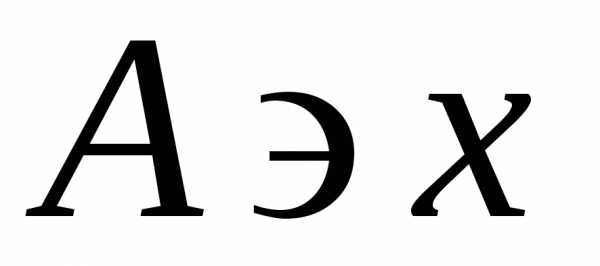 .
.
Если
каждый элемент множества А является в то же время элементом множества В,
то А называется частью или подмно-жеством множества В.
Записывают это так:  или
или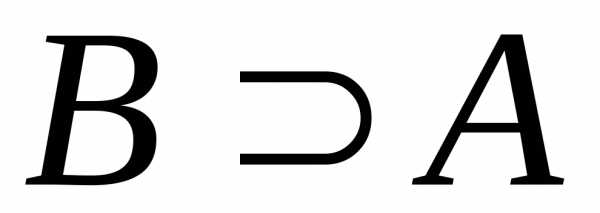 .
.
Равенство А=В означает, что  и, одновременно
и, одновременно .
.
Всякое
множество А есть подмножество самого себя:  (точнееА=А). Пустое
множество Ø (т.е.
множество не имеющее элементов) также
является частью всякого множества А:
Ø
(точнееА=А). Пустое
множество Ø (т.е.
множество не имеющее элементов) также
является частью всякого множества А:
Ø 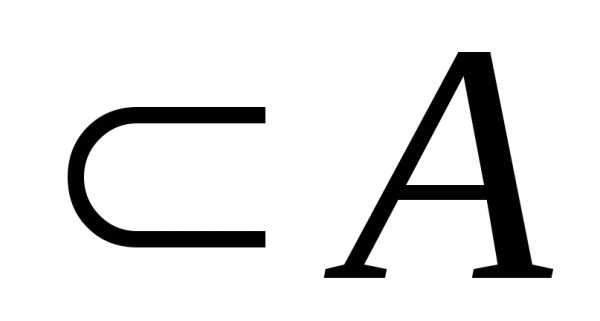 .Множества А и Ø называют несобственными подмножествами множества
А; все
остальные подмножества – собственные.
.Множества А и Ø называют несобственными подмножествами множества
А; все
остальные подмножества – собственные.
Подмножество
множества А,
состоящее из всех элементов, удовлетворяющих
данному условию S,
обозначается через 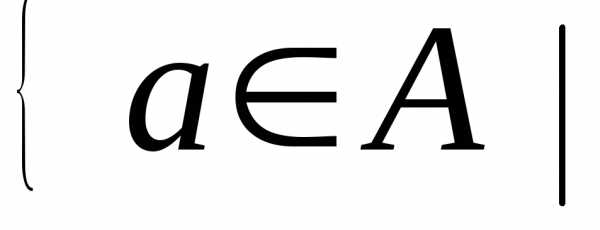 а удовлетворяет
а удовлетворяет  .
Например, двухэлементное множество
.
Например, двухэлементное множество 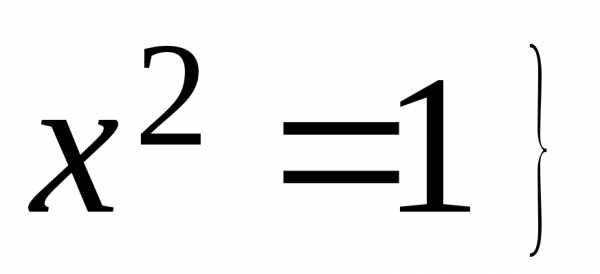 .
.
Условие S здесь означает, что х удовлетворяет уравнению х2 =1; А – есть множество решений этого уравнения.
Объединением двух множеств А и В называется множество элементов, каждый из которых принадлежит хотя бы одному из множеств А и В.
На этом рисунке слева множества А и В
изображены кругами; их объединение —
заштрихованная часть плоскости, покрыва-
А В емая обоими кругами.
Обозначение
объединения:  .
.
Пересечением
(общей
частью) множеств А
и В
называется множество всех тех элементов,
каждый из которых содержится в обоих
множества А
и В.
Пересечение
обозначается через  .
.
На рисунке слева кругами обозначают-
ся множества А и В; их пересечение
 —
заштрихованная часть плоско-
—
заштрихованная часть плоско-
сти (общая часть кругов А и В).
А В
Разностьюдвух множеств А и В (второе не обязательно со-держится в первом) называется множество тех элементов мно- жеств которые не суть элементы множества В.
Разность А и В обозначается через
А \ В. На этом рисунке слева множе-
ства А и изображены кругами; их
разность А\В – заштрихованная
А В часть круга А.
Приведём некоторые свойства операций над множествами.
Коммутативность
Ассоциативность
Дистрибутивность пересечения относительно объединения
Дистрибутивность объединения относительно пересечения
5)
6) Законы двойственности де Моргана
X
\
(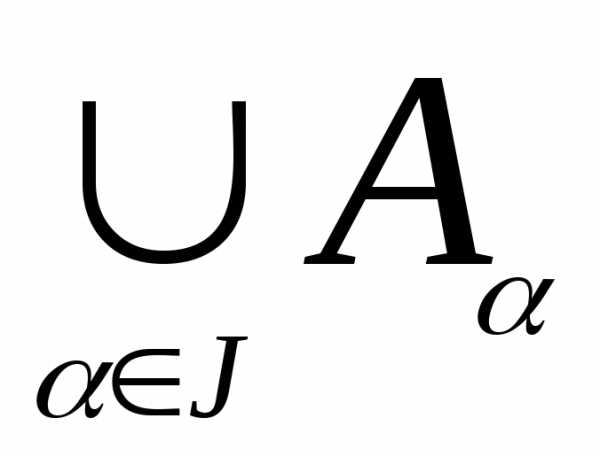 )
=
)
= 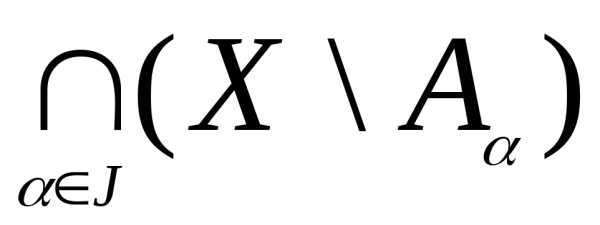 ,
X
\ (
,
X
\ (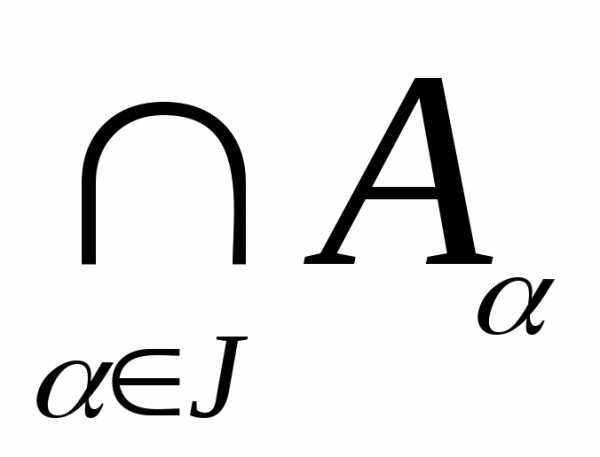 )
=
)
= 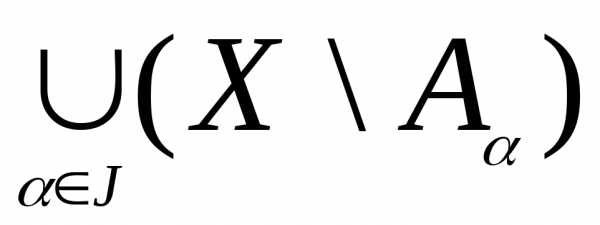 ,
,
J – некоторое множество индексов.
studfiles.net
Выпуклые множества и функции
При исследовании экономических явлений математическими методами весьма значительным оказывается такое свойство многих множеств и функций, как выпуклость. Характер поведения многих экономических объектов связан с тем, что определенные зависимости, описывающие эти объекты, являются выпуклыми.
С выпуклостью функций и множеств часто связано существование или единственность решения экономических задач: на этом же свойстве основаны многие вычислительные алгоритмы.
Справедливость многих утверждений, относящихся к выпуклым множествам и функциям, совершенно ясна, они почти очевидны. В то же время их доказательство зачастую очень сложно. Поэтому здесь будут изложены некоторые основные факты, связанные с выпуклостью, без доказательств, в расчете на их интуитивную убедительность.
Выпуклые множества на плоскости.
Любая геометрическая фигура на плоскости может рассматриваться как множество точек, принадлежащих этой фигуре. Одни множества (например, круг, прямоугольник, полоса между параллельными прямыми) содержат и внутренние, и граничные точки; другие (например, отрезок, окружность) состоят только из граничных точек.
Множество точек на плоскости называется выпуклым, если оно обладает следующим свойством: отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве.
Примерами выпуклых множеств являются: треугольник, отрезок, полуплоскость (часть плоскости, лежащая по одну сторону от какой-либо прямой), вся плоскость.
Множество, состоящее из одной-единственной точки, и пустое множество, не содержащее ни одной точки, по принятому соглашению, также считаются выпуклыми. Во всяком случае, в этих множествах невозможно провести отрезок, соединяющий какие-то точки этих множеств и не принадлежащий этим множествам целиком, — в них вообще невозможно выбрать две точки. Поэтому их включение в число выпуклых множеств не приведет к противоречию с определением, а для математических рассуждений этого достаточно.
Пересечение, т. е. общая часть двух выпуклых множеств, всегда выпукло: взяв любые две точки пересечения (а они — общие, т. е. принадлежат каждому из пересекающихся множеств) и соединив их отрезком, мы легко убеждаемся в том, что все точки отрезка являются общими для обоих множеств, так как каждое из них выпукло. Выпуклым будет и пересечение любого числа выпуклых множеств.
Важным свойством выпуклых множеств является их отделимость: если два выпуклых множества не имеют общих внутренних точек, то плоскость можно разрезать по прямой таким образом, что одно из множеств будет целиком лежать в одной полуплоскости, а другое — в другой (на линии разреза могут располагаться точки обоих множеств). Отделяющая их прямая в одних случаях оказывается единственно возможной, в других — нет.
Граничная точка любого выпуклого множества сама может рассматриваться как выпуклое множество, не имеющее с исходным множеством общих внутренних точек, следовательно, она может быть отделена от него некоторой прямой. Прямая, отделяющая от выпуклого множества его граничную точку, называется опорной прямой этого множества в данной точке. Опорные прямые в одних точках контура могут быть единственными, в других — не единственными.
Введем на плоскости систему декартовых координат х, у. Теперь у нас появилась возможность рассматривать различные фигуры как множества таких точек, координаты которых удовлетворяют тем или иным уравнениям или неравенствам (если координаты точки удовлетворяют какому-либо условию, будем для краткости говорить, что сама точка удовлетворяет этому условию).
worldofscience.ru
1. Выпуклые множества и функции
Выпуклые множества и функции — определения, критерии. Теорема о пересечении выпуклых множеств. (только формулировки).
1. Выпуклые множества и функции — определения, критерии. Теорема о пересечении выпуклых множеств. (только формулировки).
Определение 1. Пусть заданы
точки 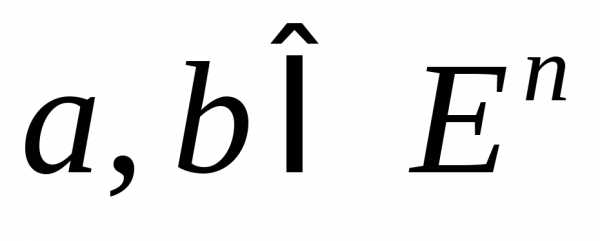 и любое
и любое .
Линейная комбинацияназываетсявыпуклой комбинацией точек
.
Линейная комбинацияназываетсявыпуклой комбинацией точек  и
и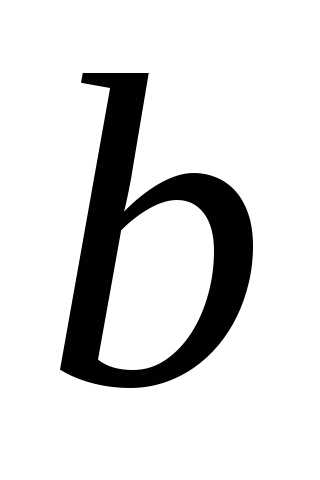 .
.
Часто выпуклую комбинацию записывают в виде или .
Легко увидеть, что эти формы записи эквивалентны.
Определение 2. Множество 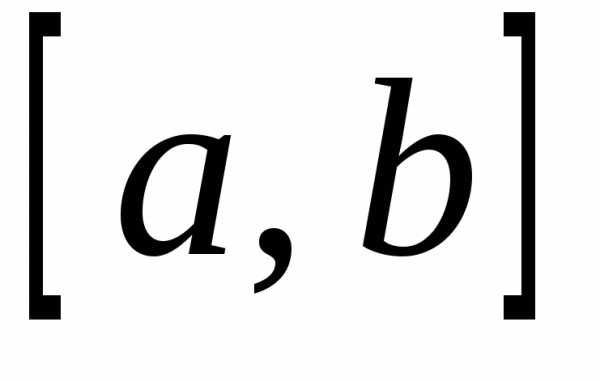 всехвыпуклых комбинаций точек
всехвыпуклых комбинаций точек 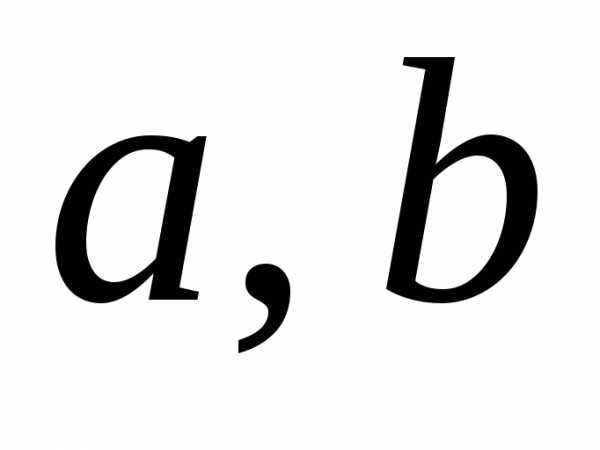 называетсяотрезком прямой,
соединяющим эти точки.
называетсяотрезком прямой,
соединяющим эти точки.
Определение 3. Множество 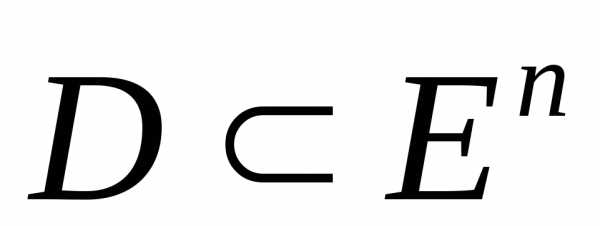 называетсявыпуклым, если
отрезок
называетсявыпуклым, если
отрезок 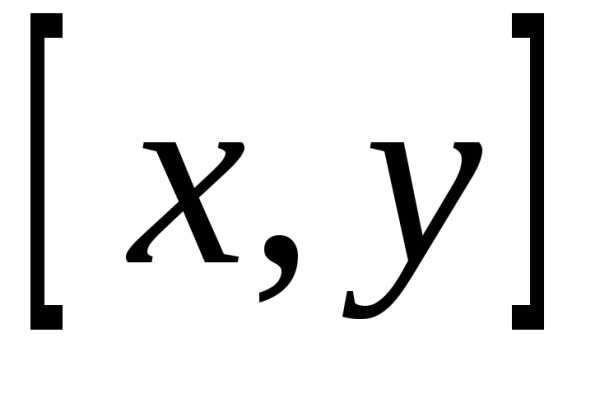 включается в
включается в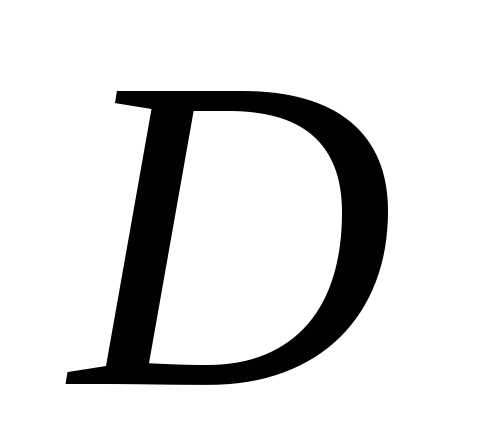 для любых
для любых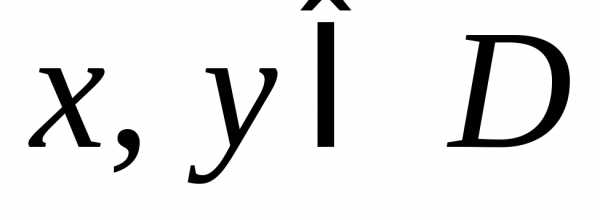 .
.
Теорема 1. Пусть имеется
семейство выпуклых множеств  .
Тогда множество
.
Тогда множество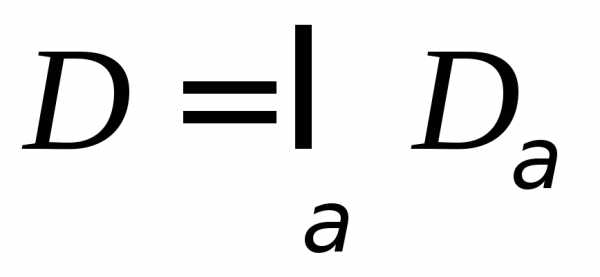 является выпуклым.
является выпуклым.
Теорема 2. Пусть для всех
множества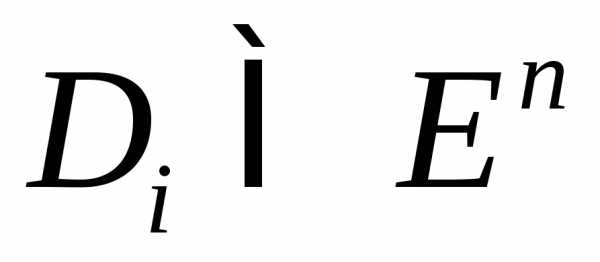 – выпуклые,
– выпуклые,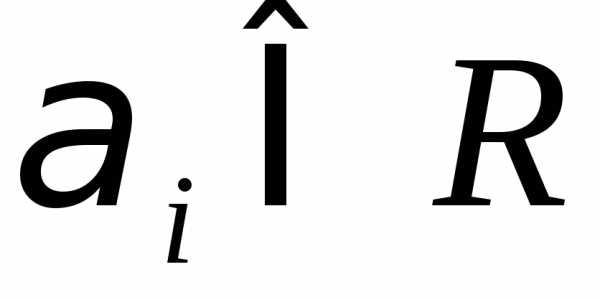 .
Тогда выпукло и множество
.
Тогда выпукло и множество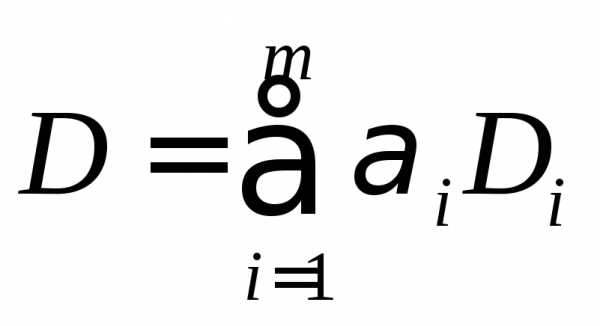 .
.
Теорема 3. Пусть 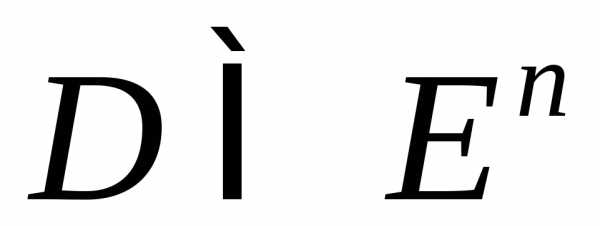 – выпуклое множество, тогда его
замыкание
– выпуклое множество, тогда его
замыкание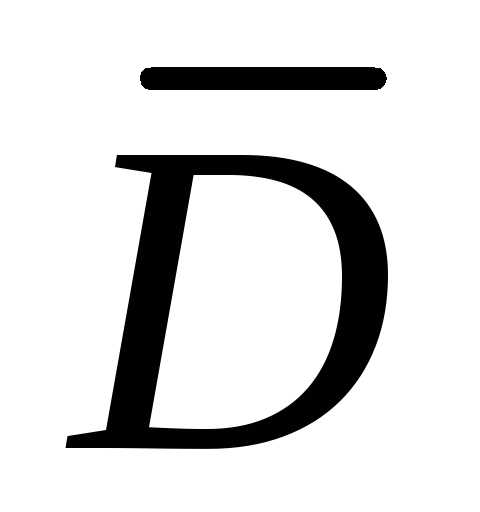 также выпукло.
также выпукло.
Теорема 4. Пусть 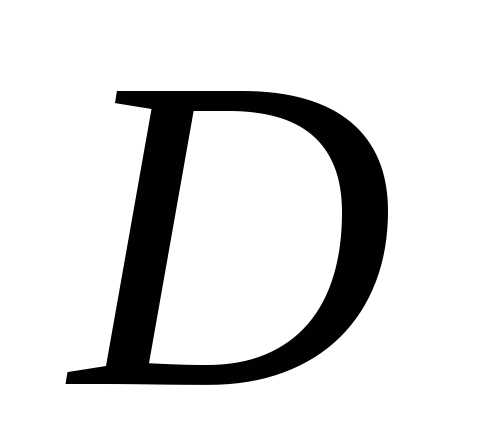 – выпуклое множество, тогда его
внутренность
– выпуклое множество, тогда его
внутренность также выпукла.
также выпукла.
Выше было приведено определение выпуклой
комбинации двух векторов. Обобщим это понятие на
случай произвольного конечного числа векторов.
Определение 3. Линейная
комбинация 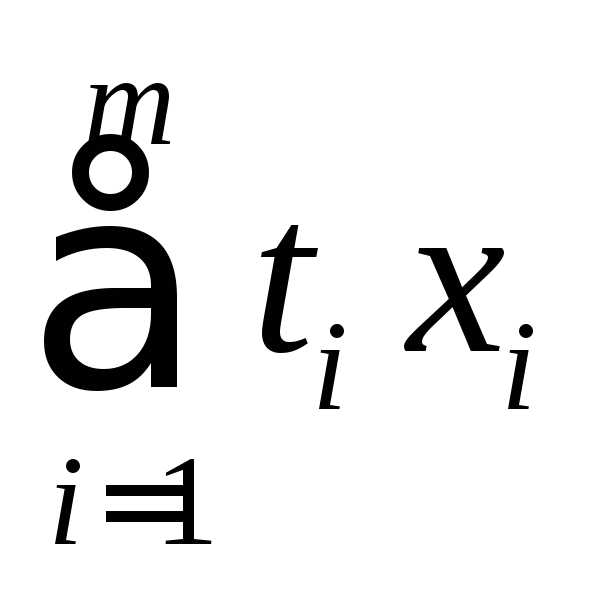 векторовназываетсявыпуклой комбинацией,
если
векторовназываетсявыпуклой комбинацией,
если 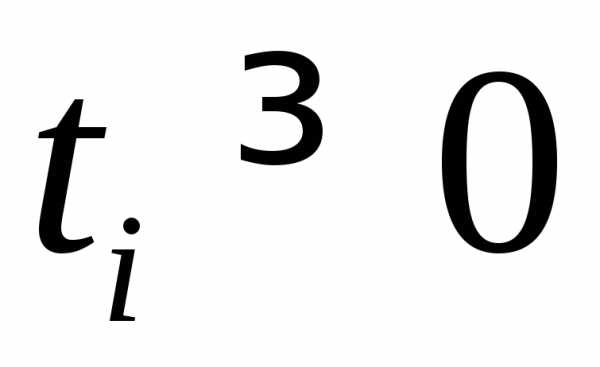 , и
, и 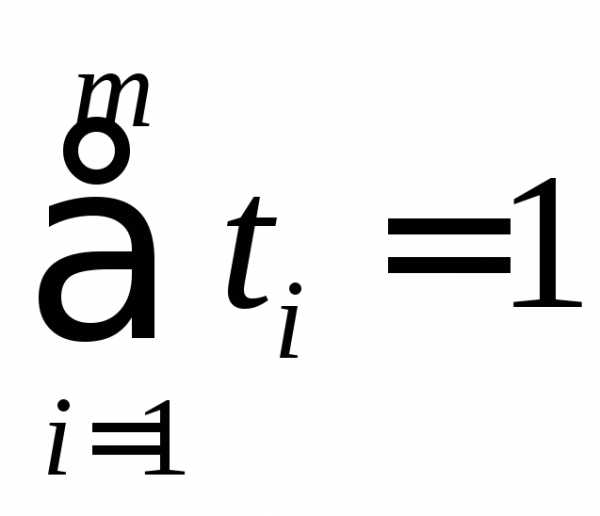 .
.
Определение 4. Множество
всевозможных выпуклых комбинаций любого
конечного числа векторов из множества 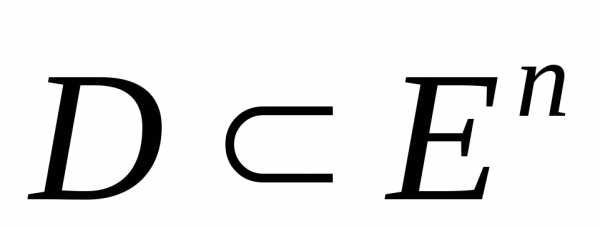 называетсявыпуклой оболочкой множества
называетсявыпуклой оболочкой множества 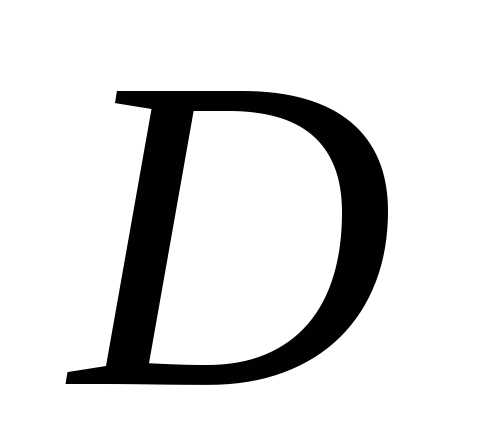 и обозначается
и обозначается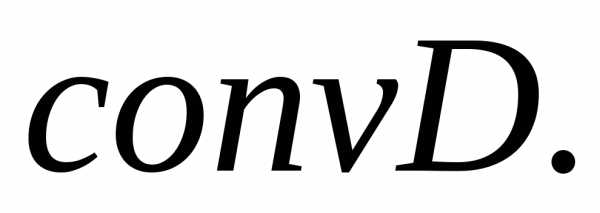
Очевидно, что для всякого 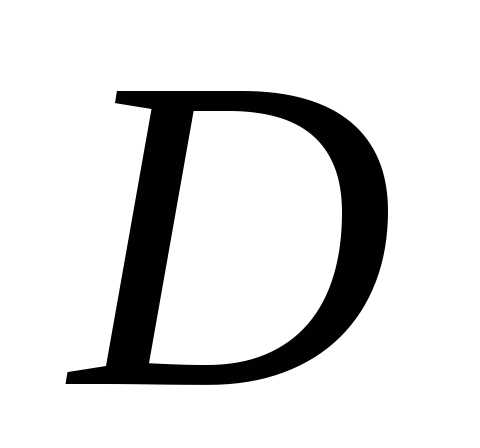 множество
множество 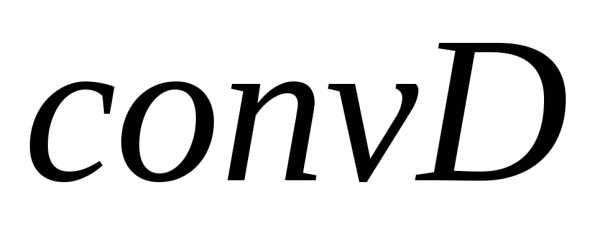 является выпуклым. Нетрудно показать,
что множество
является выпуклым. Нетрудно показать,
что множество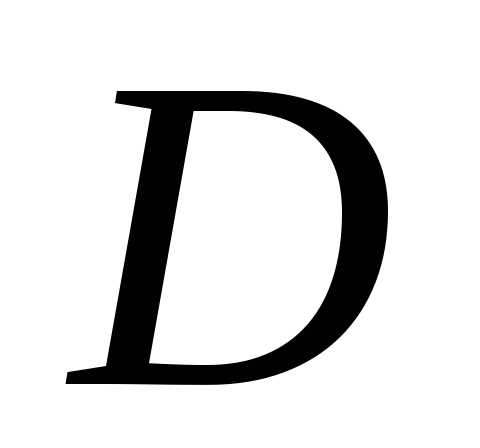 является выпуклым тогда и только
тогда, когда
является выпуклым тогда и только
тогда, когда
Возможен и другой подход к определению
выпуклой оболочки множества. Выпуклой
оболочкой множества 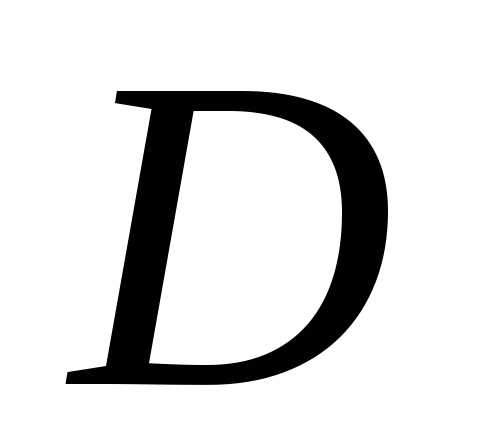 называется наименьшее выпуклое множество,
содержащее
называется наименьшее выпуклое множество,
содержащее 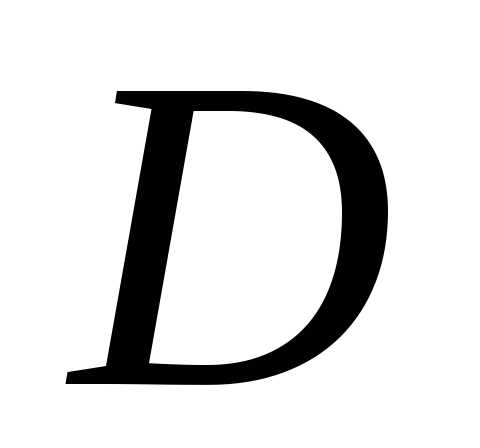 ,
то есть пересечение всех выпуклых
множеств, содержащих
,
то есть пересечение всех выпуклых
множеств, содержащих 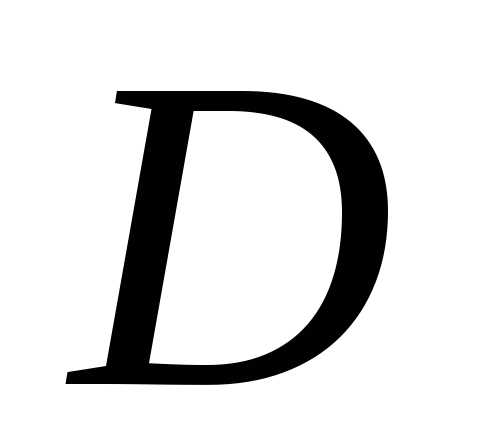 .Эти определения выпуклой оболочки
эквивалентны.
.Эти определения выпуклой оболочки
эквивалентны.
Определение 5. Вектор 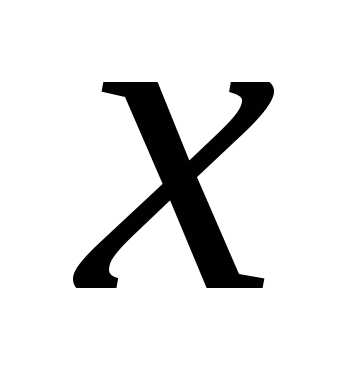 из выпуклого множества
из выпуклого множества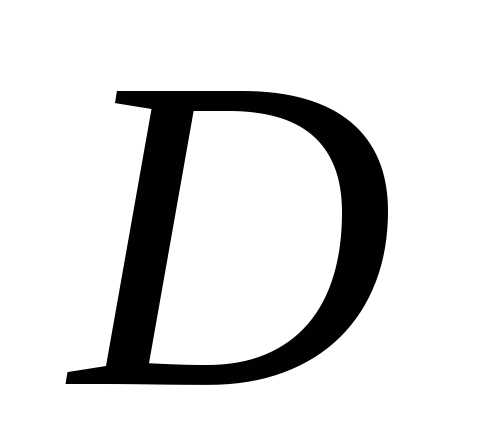 называетсякрайней точкой множе-ства
называетсякрайней точкой множе-ства 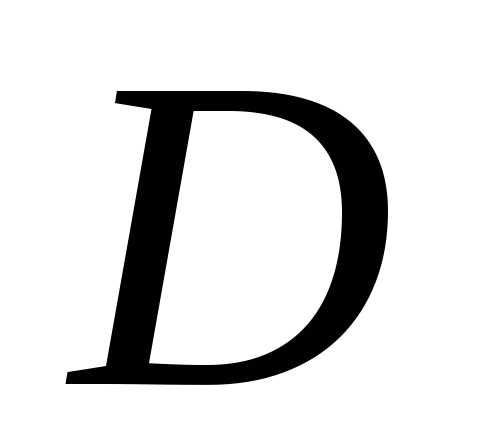 ,
если он не является выпуклой комбинацией
никаких двух других векторов из
,
если он не является выпуклой комбинацией
никаких двух других векторов из .
.
Легко увидеть, что любая крайняя точка выпуклого множества является его граничной точкой, но не всякая граничная точка является крайней.
Определение 1. Функция  ,
определенная на
,
определенная на ,
называется выпуклой, если для любых
,
называется выпуклой, если для любых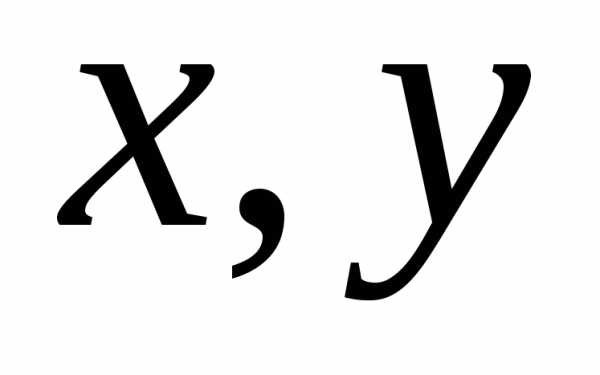 и любого
и любого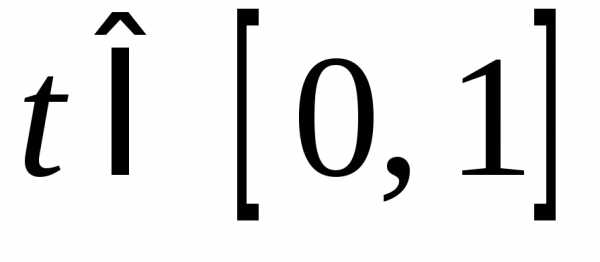 выполняется неравенство
выполняется неравенство
. (1)
Если при 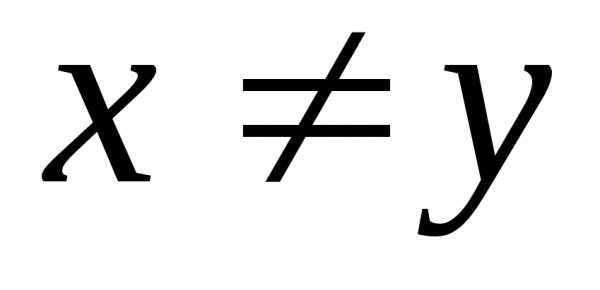 и
и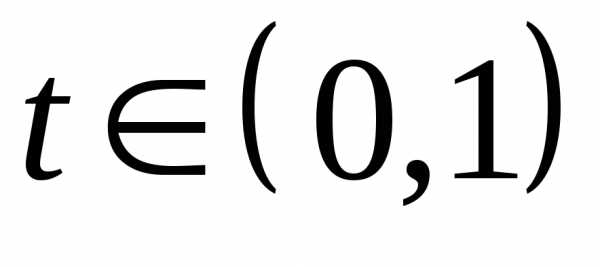 неравенство (1) выполняется как строгое,
то функция
неравенство (1) выполняется как строгое,
то функция называется строго выпуклой.
называется строго выпуклой.
Определение 2. Функция  ,
определенная на
,
определенная на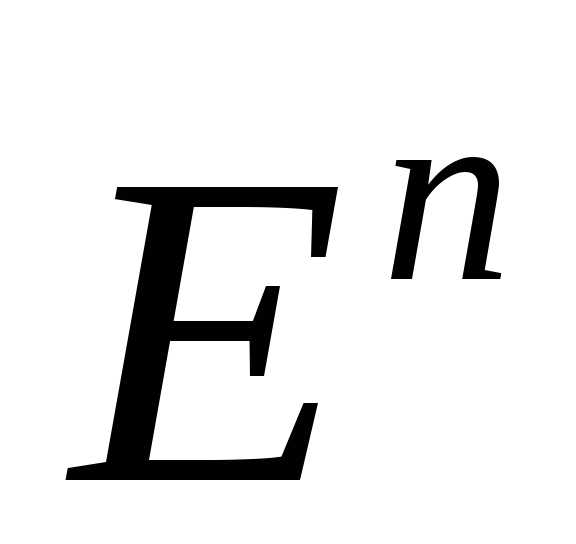 ,
называется вогнутой (строго вогнутой),
если функция
,
называется вогнутой (строго вогнутой),
если функция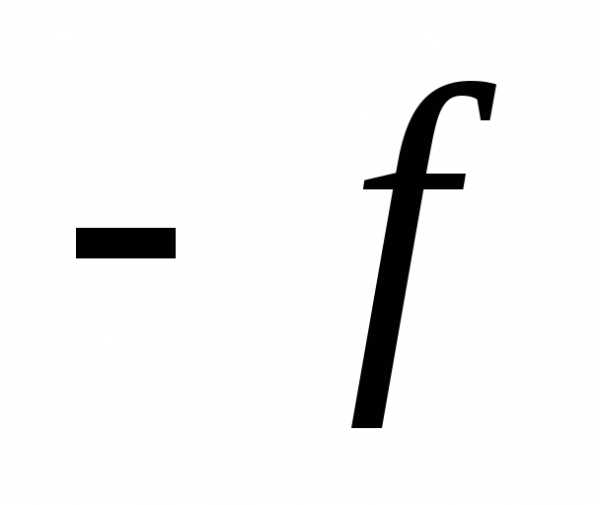 является выпуклой (строго выпуклой).
является выпуклой (строго выпуклой).
Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.
Приведем некоторые операции допустимые в классе выпуклых функций.
Теорема 1. Пусть все функции 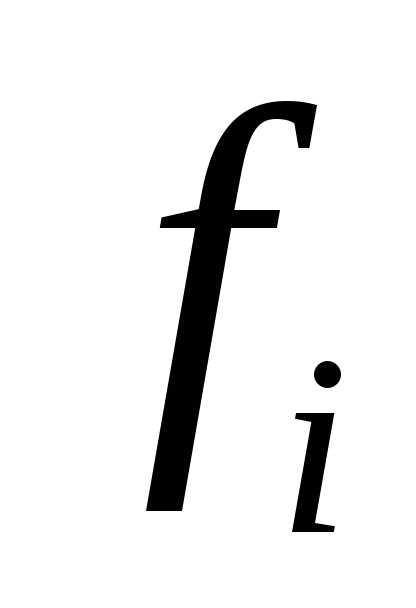 ,,
,,
выпуклы на 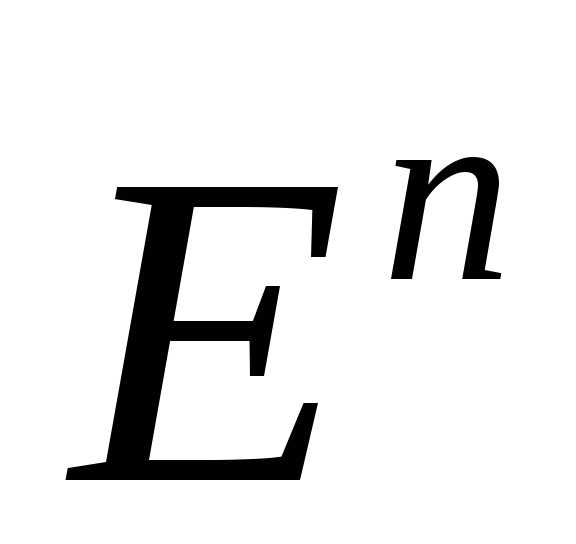 ,
числа
,
числа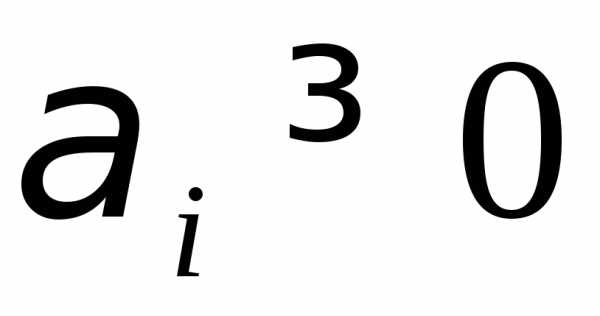 .
Тогда функция
.
Тогда функция также выпукла.
также выпукла.
Доказательство. Пусть заданы векторы 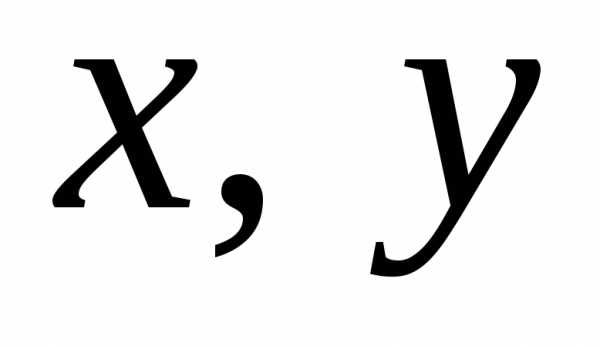 и число
и число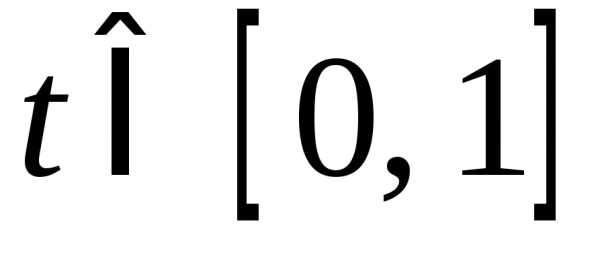 .
Так как функции,
выпуклы, то для всех
.
Так как функции,
выпуклы, то для всех выполняются неравенства
выполняются неравенства
.
Умножая эти неравенства на неотрицательные
величины и суммируя их по
и суммируя их по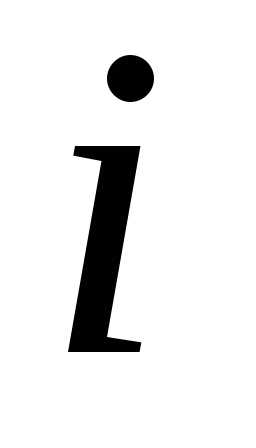 ,
получим неравенство
,
получим неравенство
.
Следовательно, . Что и требовалось.
Теорема 2. Пусть на 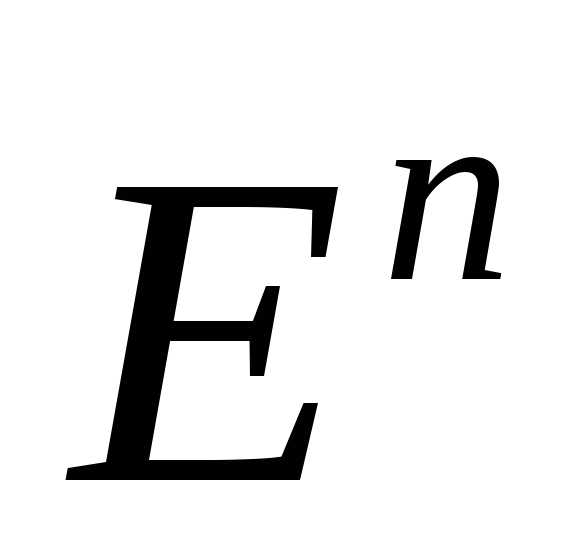 определены функции
определены функции
,.
Если все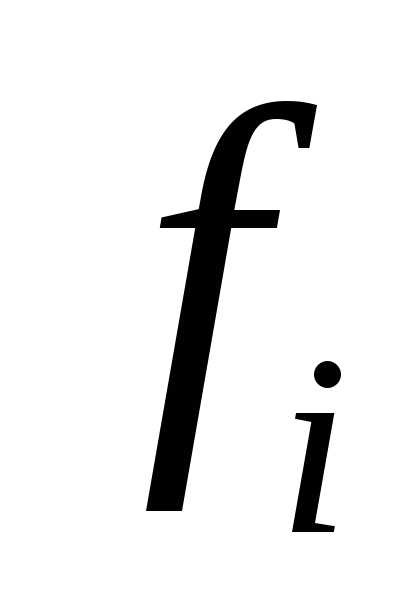 – выпуклые, то функция
– выпуклые, то функция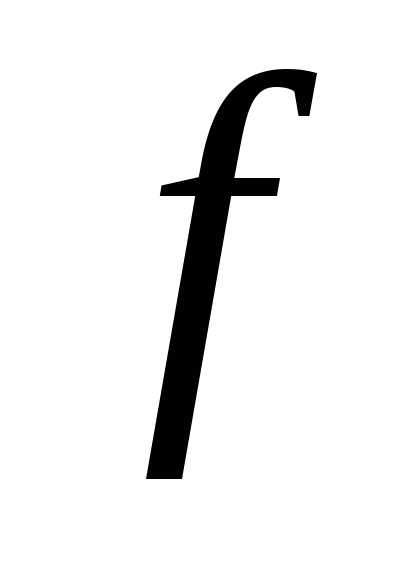 также выпуклая.
также выпуклая.
Приведем теоремы о суперпозициях выпуклых функций.
Теорема 3. Пусть функция  определена на отрезке
определена на отрезке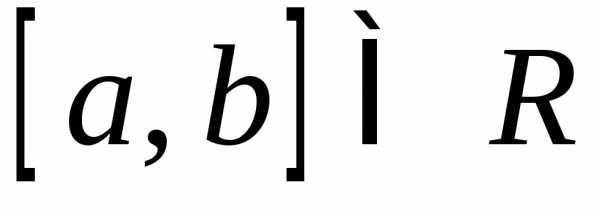 и является на нем выпуклой и
неубывающей; функция
и является на нем выпуклой и
неубывающей; функция выпукла на выпуклом множестве
выпукла на выпуклом множестве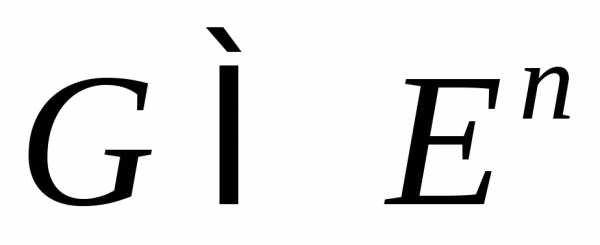 ,,для всех
,,для всех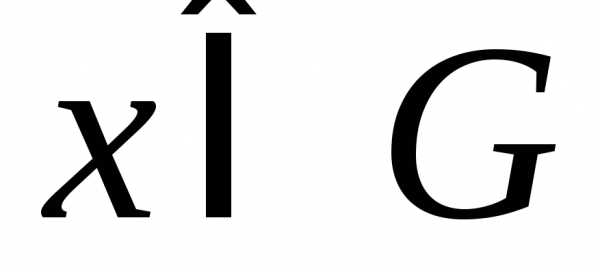 .
Тогда функция
.
Тогда функция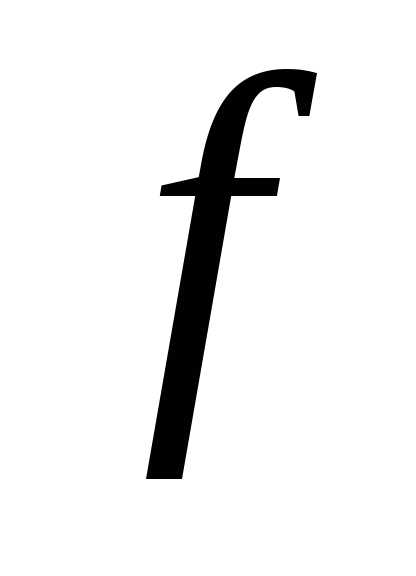 выпукла на
выпукла на .
.
Теорема 4. Пусть  – матрица размерности
– матрица размерности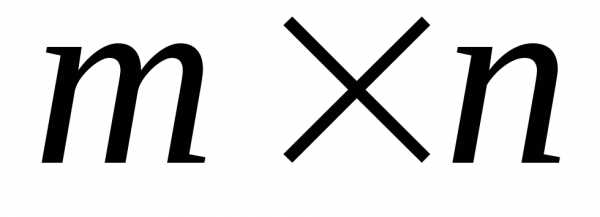 ,
, – вектор размерности
– вектор размерности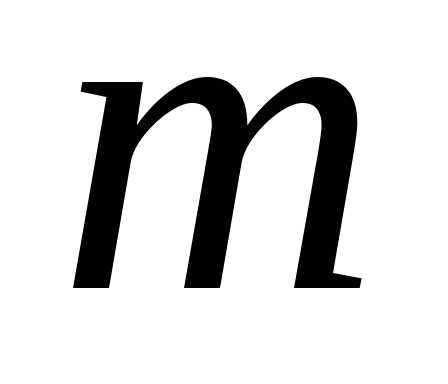 ,
, – функция, определенная и выпуклая
на многообразии
– функция, определенная и выпуклая
на многообразии
,.
Тогда функция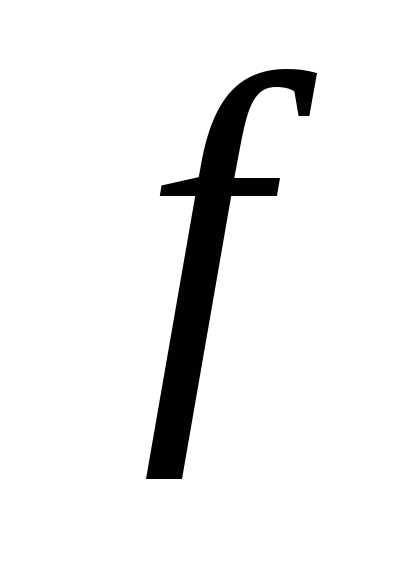 выпукла на
выпукла на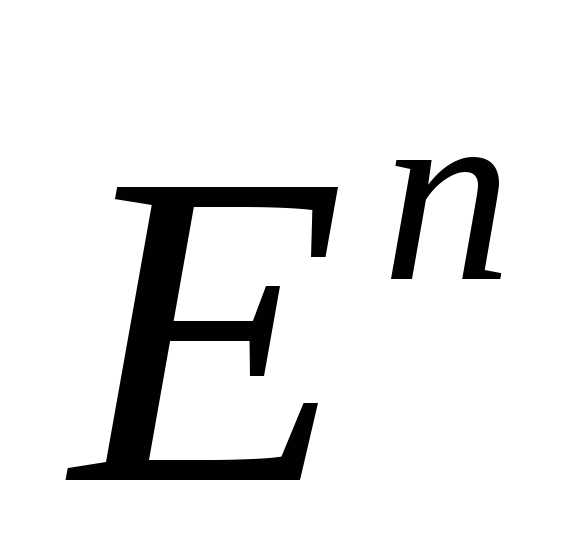 .
.
Далее покажем, что выпуклость функции
многих переменных можно установить,
исследуя на выпуклость ее сужения на
всевозможные прямые в 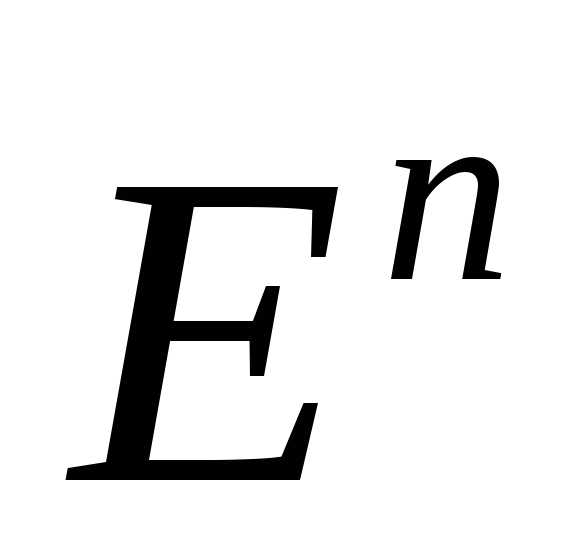 .
Выпуклость функции одной переменной
установить зачастую значительно проще,
чем выпуклость функции многих
переменных.
.
Выпуклость функции одной переменной
установить зачастую значительно проще,
чем выпуклость функции многих
переменных.
Пусть заданы функция 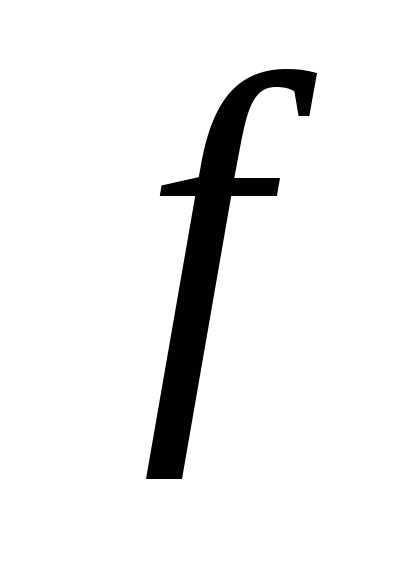 и векторы
и векторы .
Сужение
.
Сужение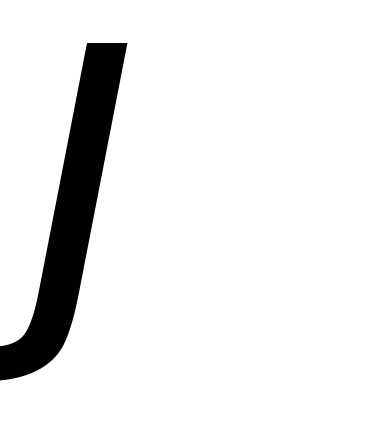 функции
функции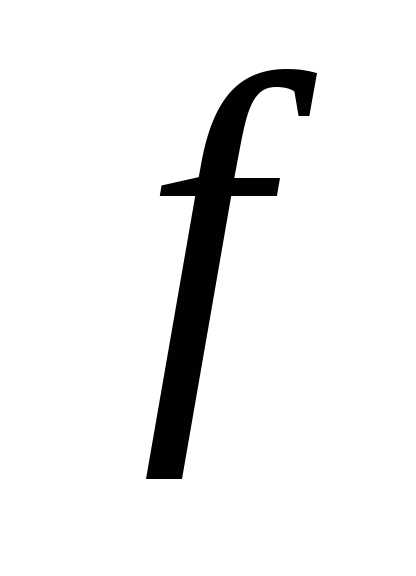 на прямую
на прямую определим следующим образом:
определим следующим образом:
. (2)
Теорема 5. Функция 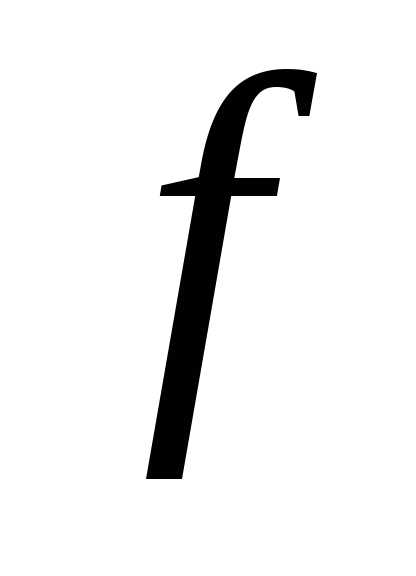 является выпуклой тогда и только
тогда, когда выпуклой является и
функция
является выпуклой тогда и только
тогда, когда выпуклой является и
функция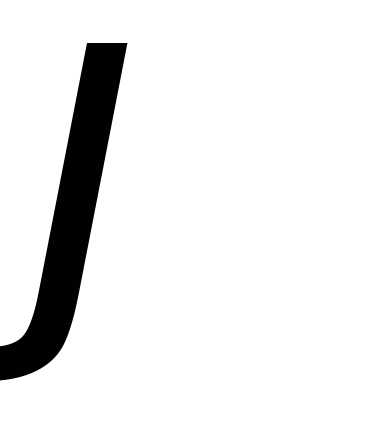 ,
определенная по формуле (2) при любых
,
определенная по формуле (2) при любых .
.
Теорема 6. Пусть функция 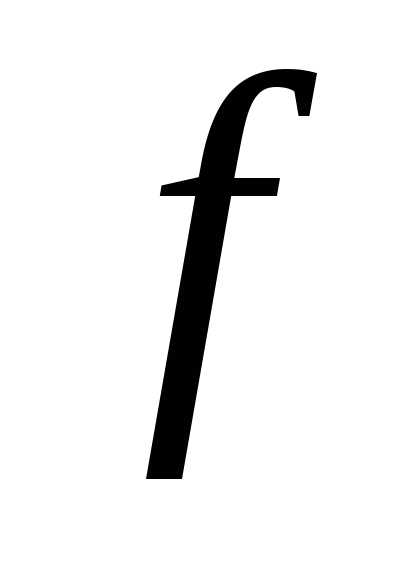 выпукла на
выпукла на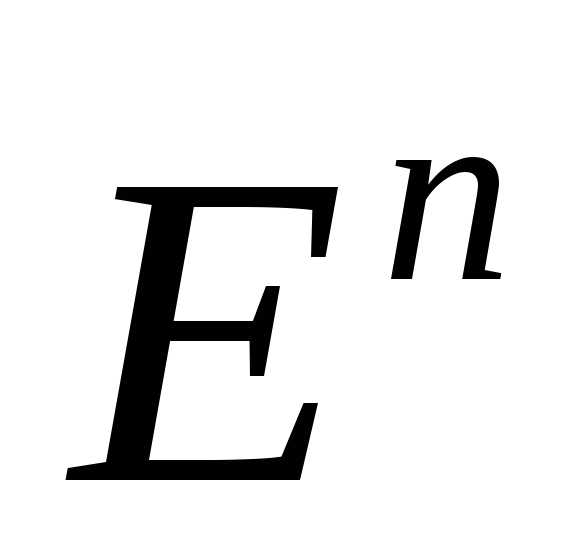 .
Тогда любое ее лебегово множество
выпукло.
.
Тогда любое ее лебегово множество
выпукло.
Эта теорема устанавливает одностороннюю связь между выпуклыми множествами и выпуклыми
функциями. Утверждение, обратное теореме 6, не имеет места.
studfiles.net
