Модули тема – CGI script error

Модули

Модуль — больная тема для многих учеников. И дело вовсе не в каких-то особо сложных теоремах и выкладках. Просто учителя зачастую сами не умеют работать с этой функцией.

Добавьте к этому крайне непродуманную школьную программу, когда в 8—9 классах учителя говорят: «Модули — это для старших классов. Еще успеете изучить», а в 10—11 классах — «Чем вы занимались раньше? Вы должны уже все это знать!». Ну и как в таких условиях учиться?

Так вот, знайте: модули — один из самых простых и понятных разделов математики. Посмотрите видеоуроки — и убедитесь в этом сами. Решайте задачи, практикуйтесь — и не верьте школьным сказкам про «должны знать».

Глава 1.

Модуль числа

§ 4.

Графики функций, содержащих модуль, и их свойства

Глава 2.

Уравнения с модулем

§ 1.

Как решать уравнения с модулем

§ 2.

Простейшие уравнения с модулем

§ 3.

Уравнение с двумя модулями

§ 4.

Дробно-рациональные уравнения с модулем

§ 5.

Уравнения с модулем: учет области значений

§ 6.

Нестандартные уравнения с модулем

§ 12.

Уравнения с модулем в модуле — как их решать с помощью разных приёмов

Глава 3.

Неравенства с модулем

§ 1.

Неравенства с модулем: графическое решение

§ 2.

Решение неравенств с модулем: 4 способа

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

www.berdov.com

Модули — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Базовые сведения о модуле

К оглавлению…

Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:

Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.

Основные свойства модуля:

 

Некоторые методы решения уравнений с модулями

К оглавлению…

Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:

Предпочтительным способом решения будет переход к совокупности:

А для уравнений вида:

Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:

Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:

Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:

• Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.
• Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять.
• Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.

educon.by

Тема урока: «Модуль числа» (6 класс)

1. Модуль числа. Иллюстрирующий пример. Определение. Примеры

Рассмотрим чертеж. Координата точки М – . Знак минус указывает, что точка М лежит левее начала отсчета. Число шесть говорит о том, что расстояние от точки О до точки М равно шесть единичных отрезков.

Число 6 называют модулем числа . Записывают это так: 

 

Определение.

Модулем числа a называют расстояние от начала координат до точки с координатой a.

Мы помним, что расстояние на координатной прямой измеряется в единичных отрезках.

Примеры.

Модуль числа 5 равен 5, так как точка с координатой пять удалена от точки начала отсчета на пять единичных отрезков.

Модуль 0 равен 0, так как точка с координатой ноль – это и есть начало отсчета.

2. Модуль противоположных чисел

Модуль числа – это расстояние. Поэтому он не может быть отрицательным. Для положительного числа его модуль равен самому числу, а для отрицательного – противоположному.

Примеры:

Заметим, что противоположные числа имеют равные модули. В общем виде это можно записать так:

 

 

3. Задание 1

Найдите значение выражения    , если   .

Решение.

Сначала подставим значения переменных.

  – число отрицательное. Его модуль равен противоположному числу   .

Модуль числа  равен 3,6.

Выполним вычитание. Получим: 10,9.

4. Задание 2

Отметьте на координатной прямой числа, модуль которых равен 2.

Решение.

Начертим координатную прямую. Для этого на прямой выберем начало отсчета, единичный отрезок и направление.

Поставим точки на расстоянии 2 единичных отрезка от начала отсчета.

Таких точки две. Одной соответствует число  , а другой число 2.

5. Задание 3

Найдите значение выражений:

        ;            4 

Решение.

1)      

Модуль числа  равен 8. Модуль числа 5 равен 5.

2)          

Модуль числа 10 равен 10. Модуль числа  равен 15.

3)      .

  Раскрыв модули, получим сумму чисел 2,3 и 3,7

4)      

Модули данных чисел равны соответственно 24 и 80.

6.

infourok.ru

Технология модульного обучения

Модульное обучение – обучение, при котором учебный материал разбит на информационные блоки-модули. Технология построена на самостоятельной деятельности обучающихся, которые осваивают модули в соответствии с поставленной целью обучения.

Особенности модульного обучения

Ключевой элемент структуры в данной технологии – информационный модуль.

Модуль – это отдельный блок, включающий теоретический материал, тренировочные задания, методические рекомендации для учащихся. Составной элемент модуля – контрольные вопросы и тесты, а также ключи для самопроверки или взаимопроверки. Благодаря изучению модуля учащиеся достигают определенной дидактической или педагогической цели.

Содержание учебного занятия конструируется из нескольких логически связанных между собой модулей, каждый из которых решает конкретную учебную задачу. На выполнение модуля дается фиксированное время. Вместе все модульные блоки направлены на достижение предметных и личностных результатов.

Технология основана на деятельностном подходе, ориентирована на личность каждого ученика. Предполагается самостоятельная деятельность обучающихся в освоении материала. Минимальная продолжительность занятия – 2 академических часа. Учащиеся должны быть психологически готовы к самостоятельной деятельности с высокой степенью интенсивности. Поэтому возраст школьников, которые эффективно смогут работать в технологии модульного обучения, – 13-14 лет.

Виды модульного обучения

• Модульная программа. Планирование курса модульных уроков, которые связаны между собой целью, обеспечивающей достижение предметных, личностных и регулятивных результатов. Это программа деятельности учащихся.

• Модульный урок. Это элемент модульной программы.

• Планирование в формате модуля. Использование технологических карт – особой формы структурирования учебного материала.

Цели использования модульного обучения в средней школе

• Освоение учебного материала в процессе активной деятельности учеников.

• Развитие навыков самостоятельности и самоконтроля.

• Повышения познавательного интереса обучающихся.

• Развитие у обучающихся умения планировать свою деятельность.

Принципы

• Модульность. Учебный материал разбивается на отдельные законченные блоки, логически связанные между собой и объединенные одной дидактической целью.

• Динамичность. Модули можно свободно дополнять, заменять в зависимости от изменений в программах, по которым строится обучение.

• Гибкость. Адаптация содержания модуля к индивидуальным запросам обучающихся.

• Осознанная перспектива. Перед учащимся ставятся ближние и дальние цели. Обучение строится на осознанном отношении к процессу освоения знаний.

• Индивидуальные консультации и инструкции для каждого обучающегося.

Роль преподавателя

Учитель разбивает учебный материал на блоки, составляет модульную программу, разрабатывает модульные уроки.

Главная цель – организация самостоятельной деятельности учащихся при работе с модулем. Для этого в продолжение занятия преподаватель контролирует учебный процесс, оказывает консультационную помощь. Следит за временем выполнения каждого учебного элемента и сообщает обучающимся о лимите времени.

Преимущество для учащихся

• Самостоятельное освоение учебного материала.

• Психологическая комфортность на занятиях.

• Работа с модулями осуществляется в индивидуальном темпе.

• Индивидуальная траектория работы на каждом модульном уроке.

Преимущество для учителя

• На уроке освобождается время для индивидуального консультирования учащихся.

Основные трудности для учащихся

• Временной дефицит при выполнении заданий.

• Высокий темп выполнения заданий.

• Не все учащиеся умеют работать самостоятельно. Низкое и фрагментарное качество освоения учебных тем.

Основные трудности для учителя

• Разработка материалов для модуля (комплект заданий, тестов, инструкций) требует больших затрат времени и сил.

• Необходим высокий уровень профессиональной компетенции.

• Материальные затраты на копирование комплектов заданий для каждого учащегося.

Структура модульного урока

1. Мотивационный этап. Беседа, настраивающая на самостоятельную деятельность на уроке. Инструкции к последующей работе.

2. Работа с модульными блоками – учебными элементами (УЭ), которые структурируются в определенном порядке, нумеруются и предлагаются учащимся в индивидуальных комплектах. Ограничения: количество УЭ на уроке должно быть не более семи.

3. Рефлексия. Самооценка уровня продуктивности работы на уроке. Дифференцированное задание для работы дома, выбор которого зависит от результата работы с модулем.

Содержание учебных элементов в модуле:

• УЭ 0 – для учащегося определяется цель, которая будет достигнута в результате освоения модуля по теме урока.

• УЭ 1 – входная диагностика, проверяющая сформированность необходимых умений для освоения модуля. Дается ключ для самопроверки или взаимопроверки, если предполагается парная или групповая работа.

• УЭ 2 – УЭ 6 – обучающие модули, которые включают теоретические и практические задания.

• УЭ 7 – выходная диагностика, оценивающая степень усвоения темы. Ключ к заданию может быть у учителя или также проводится самопроверка.

В печатных комплектах для учащихся обязательно размещается технологическая карта, которая включает следующие элементы:

• Номер УЭ. Время на выполнение каждого учебного блока.

• Учебный материал.

• Инструкции для выполнения каждого учебного элемента.

• Ключи (если предусмотрена самопроверка).

Перспективы развития

Для активного внедрения технологии модульного обучения необходимо повышение мотивации ученика. У школьников должно быть хорошо развито умение самостоятельной познавательной деятельности. Важно, чтобы материальная база учебного заведения позволяла обеспечить учащихся индивидуальными комплектами для работы на модульных уроках.

aujc.ru

Модуль числа. Видеоурок. Математика 6 Класс

Положительные числа, натуральные, а затем и дробные мы ввели для указания количества:  дерева,  литра молока (рис. 1).

Рис. 1. Пример использования положительных чисел

Затем мы ввели отрицательные числа: например, . Теперь число, кроме количества, содержит еще и знак, который указывает, что нужно делать с этим количеством – добавить или отнять. То есть после того, как были введены отрицательные числа, мы можем сказать, что любое число состоит из количества (реально существующего) и знака (придуманного нами для упрощения записи арифметических действий).

Но иногда бывает важна только одна характеристика – количество, а знак нас не интересует.

Рассмотрим такой пример. Для таксиста важно, какой длины путь он преодолевает с пассажиром (рис. 2).

Рис. 2. Километраж

Ведь, если в конце поездки пассажира привозят обратно домой, это не означает, что он ничего таксисту не должен, так как он проехал какое-то расстояние с начала поездки (рис. 3).

Рис 3. Путь, проделанный такси

Пусть теперь такси может ездить только вдоль прямой (вправо или влево). У нас уже есть подходящая модель – координатная прямая (рис. 4).

Рис. 4. Аналогия с координатной прямой

Предположим, клиенты проехали  км влево, затем  км вправо, затем ещё  км вправо, затем ещё  км влево. В результате автомобиль отъехал на  км влево от исходной точки:  (рис. 5).

Рис. 5. Сколько проехала машина (считаем с помощью числовой прямой)

Но ведь путь, который проделало такси, значительно больше:  км.

Для подсчёта пути мы складывали только количества, без учёта знака.

Ту часть числа, которая указывает на количество, называют абсолютным значением (или модулем числа). То есть можно сказать и так: любое число состоит из знака и абсолютного значения (модуля). Если знак плюс, то для краткости его обычно не пишут.

Например, у числа  знак минус и модуль , у числа , знак плюс и модуль  (рис. 6).

Рис. 6. Из чего состоят противоположные числа

Пример: машина проехала  км по дороге. Используем для этой ситуации математическую модель – числовую прямую. Машина из точки  могла двигаться вправо или влево. Можно так и говорить: перемещение на  км вправо, перемещение на  км влево. Но у нас есть удобный инструмент, отрицательные числа. Поэтому короче мы можем говорить так: перемещение  или перемещение  (рис. 7).

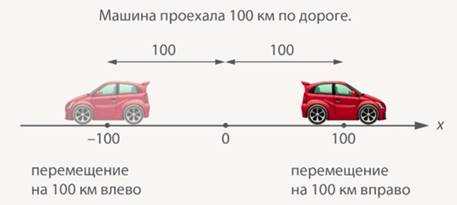
Рис. 7. Возможные движения машины

Перемещение было разное, но удалился автомобиль от начальной точки (от ) на одно и то же расстояние – на  км. Но  – это и есть модуль (как для числа , так и для ).

То есть про модуль числа можно сказать и так: модуль – это расстояние от числа до нуля (на самом деле это определение более универсальное, но об этом вы узнаете в старших классах).

В физике два этих понятия так и называют:

• перемещение: для него важен результат – где были и где оказались в итоге;
• путь: здесь важно расстояние, которое мы прошли, и не важно, где мы оказались в итоге.

Так, если машина, двигалась из точки  вправо  км, а потом влево  км, то она вернется в начальную точку. Перемещение равно , но путь равен  км (рис. 8).

Рис. 8. Перемещение и путь

Перемещение от одной точки до другой изображают отрезком со стрелкой. Называют его вектором (рис. 1).

Рис. 9. Вектор

Здесь ситуация как с числами: есть количественная часть (длина) и есть направление (у числа их было всего два ( и ), а здесь направлений может быть бесконечно много).

Сам вектор обозначают со стрелкой сверху. Длину вектора называют модулем (помните, как и у числа: модуль – это количественная часть) и обозначают с прямыми скобками или просто как отрезок (рис. 2).

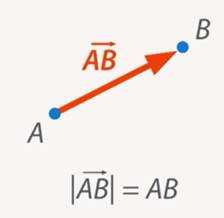
Рис. 10. Обозначение вектора и его длины

Если нам нужно попасть из одной точки в другую, мы не всегда можем пройти по прямой. Например, из точки  мы движемся в точку , обходя газон, по которому ходить запрещено. То есть мы переместились два раза и. Итоговое перемещение  (рис. 3).

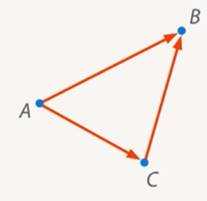
Рис. 11. Перемещение

Перемещение  – это сумма двух перемещений : . Для путей это не верно. Длина отрезка  меньше суммы длин отрезков  и : . Путь по прямой короче, чем в обход.

Все это можно записать одним неравенством: . Оно означает вот что: сумма двух перемещений – это итоговое перемещение. Его длина меньше, чем сумма длин каждого перемещения по отдельности: .

Подумайте, может ли здесь быть равенство, если по-другому будут расположены векторы перемещения? А противоположный знак, то есть знак ?

Рассмотрим такой пример. Человек гуляет с собакой, он движется из точки  в точку  по прямой, при этом собака движется еще из стороны в сторону, насколько позволяет поводок (рис. 4).

Рис. 12. Иллюстрация к примеру

Перемещение человека  (рис. 5).

Рис. 13. Перемещение человека

Перемещение собаки складывается из кусочков и тоже в итоге равно  (рис. 6).

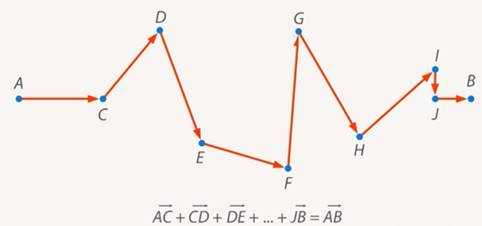
Рис. 14. Перемещение собаки

Но если складывать не перемещения, а пути, т.е. не векторы, а их модули, то окажется, что собака пробежала путь, в два или три раза больший. Собака, совершая одинаковое перемещение с хозяином, могла пробежать и в , и в  раз больший путь, все ограничивается ее активностью.

Есть такая задача: измерение длины береговой линии. С перемещением от точки  до точки  вдоль берега все понятно. Это вектор  (рис. 7).

Рис. 15. Перемещение

А вот путь складывается из кусочков (рис. 8). Тут вроде бы как с собакой: нужно сложить модули таких перемещений, векторов.

Рис. 16. Кусочки пути

Но если смотреть более точно, каждое такое перемещение складывается из еще более мелких перемещений. Путь сильно возрастает (рис. 9).

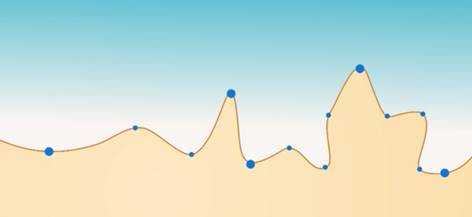
Рис. 17. Возрастание пути

Но это еще не все: если смотреть еще более точно, то и они делятся на маленькие перемещения. Береговая линия все более и более изрезана (рис. 10). И это никогда не заканчивается.

Рис. 18. Изрезанная береговая линия

То есть длину береговой линии не получается точно измерить таким образом.

Вот так получается, что, не отходя далеко от общего вектора перемещения, можно получить очень большой (как путь собаки) или даже бесконечный путь (как береговая линия).

Модуль числа договорились обозначать вертикальными скобками. Итак, модуль положительного числа  равен самому числу , модуль отрицательного числа  тоже равен , то есть противоположному числу: , .

Остался вопрос: чему равен модуль нуля? Расстояние от нуля до нуля равно нулю. Поэтому модуль нуля считать равным нулю: .

Итак, мы уже все знаем, чтобы дать более точное определение, что такое модуль числа.

Модуль числа – это число, равное ему самому, если число положительное, противоположному числу, если оно отрицательное, и все равно какому (самому или противоположному), если число равно нулю. Пусть будет самому: .

Чтобы запись была короче, объединим первую и третью строчки. И определение теперь звучит так: модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное: .

Это определение не объясняет суть, что такое модуль. Но мы про суть уже поговорили раньше. Оно является удобным инструментом для выполнения арифметических действий. Особенно пригодится это определение, когда мы будем решать уравнения с модулем.

Если отвлечься от задач про путь и перемещение, то нахождения модуля интересно еще вот чем. Раньше мы выполняли операции с двумя или несколькими числами. Например, брали два числа, складывали их, получали новое число, сумму: . Или сравнивали два числа: .

Модуль же – это операция с одним числом. Берем одно число и находим для него другое число – модуль: . Сходная ситуация была при округлении чисел, хотя сам смысл процедуры там был совсем другой: .

Итак, мы обсудили, что такое модуль, для чего он нужен, дали ему точное определение. Теперь перейдем к технике вычислений. Потренируемся этот модуль находить.

Для того чтобы найти модуль числа, необязательно изображать число на координатной прямой и измерять расстояние до нуля. Чтобы найти модуль числа, нужно просто не обращать внимания на знак числа: . То есть даже определение модуля нам пока не очень понадобится. Нужно просто записывать число без знака. Таким образом, у противоположных чисел модули равны: .

Решим несколько примеров на нахождение модуля.

Как быть с модулем переменной величины? Про нее мы можем не знать, отрицательная она или положительная. Она может быть равна и нулю. Что нам известно про её модуль в такой ситуации? Мы не можем утверждать, что модуль  равен самому числу . Ведь может оказаться, что  отрицательно, но модуль не может быть отрицательным.

Рассмотрим противоположное число . Знак минус перед  не означает, что оно отрицательно. Поэтому с модулем этого числа тоже нет определенности.

Что мы знаем наверняка, так это, что модули этих двух чисел равны друг другу. И этот модуль равен одному из этих чисел, тому, которое неотрицательно: или .

Итак, подведем итог.

• Модуль числа – это расстояние от числа до нуля (рис. 9).

Рис. 19. Модуль числа

• Чтобы найти модуль числа, нужно записать это число без учета знака (рис. 10).

Рис. 20. Как найти модули

• Модули противоположных чисел равны (рис. 11).

Рис. 21. Модули противоположных чисел

• Точное определение модуля выглядит так:модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное (рис. 12).

Рис. 22. Определение модуля

 

Список рекомендованной литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
2. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. Ч. 2. М.: «Просвещение».
3. Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Yaklass.ru (Источник). 
2. Math-prosto.ru (Источник).
3. Cleverstudents.ru (Источник).

 

Домашнее задание

1. Точка  лежит на  единицы от начала отсчета влево, а точка  – вправо на  единицы. Найдите координаты точек и модули этих координат.
2. Найдите значение выражения: .
3. Какое из предложенных чисел имеет наибольший модуль: ?

interneturok.ru

Тема «Модули»

Во вводной части лекции следует объяснить учащимся, что только с появлением модулей Паскаль стал средством разработки больших профессиональных программных комплексов. Модуль, как и процедуры, служит реализации идеи модульности — выделения подзадач внутри большой задачи. Отличие модуля от набора «внутренних» процедур — возможность отдельной трансляции и отдельного от программы хранения; к модулю может обращаться не °Дна программа, а много разных программ. Благодаря модулям в Паскале возможно организовывать внешние библиотеки программ По различным проблемам.

Целью школьного спецкурса не может быть самостоятельная Разработка учащимися модулей. Такое задание возможно в качестве проекта для некоторых учащихся, а для большинства эта тема является ознакомительной. Вполне достаточно привести примеры двух-трех несложных модулей и разобрать как их внутреннее устройство, так и механизм взаимодействия с обращающимися к ним программами.

Описав общую структуру модуля и объяснив назначение основных его разделов (заголовок, интерфейсная часть, раздел реализации, раздел инициализации), приведите пример модуля. Допустим, мы хотим дополнить’Паскаль средствами работы с комплексными числами (хотя бы на уровне четырех арифметических действий). В школе, в которой углубленно изучается программирование, учащиеся скорее всего с комплексными числами знакомы. Возможны два подхода к реализации этой задачи.

1. Комплексное число представляется парой действительных (а, Ь). Конструируют четыре процедуры — действия над комплексными числами; у каждой из них по 4 параметра-значения и по 2 параметра-переменных. Сводят их в модуль, в интерфейсной части которого находятся заголовки этих процедур. Показывают, как обращается к нему внешняя программа, объясняют смысл наличия в ней инструкции uses <список модулей.

2. Комплексное число представляется одним идентификатором, т.е. мы хотим иметь возможность записывать присваивания вида А := В + ЕС, где А, В и С — комплексные числа. Эта задача потруднее. Путь к ее решению — создать тип (назвав его Complex), элементы которого — двухполевые записи; первое поле — действительная часть числа, второе — коэффициент при мнимой части.

Всякий раз, разбирая примеры модулей, подчеркните, что разработчику внешней программы, использующему модули, нет никакой необходимости знать устройство процедур, составляющих раздел реализации. Вполне достаточно иметь детальное описание интерфейсной части и назначения модуля.

Более детально учащиеся знакомятся с модулями и приходят, в частности, к пониманию сформулированного выше утверждения на примерах стандартных модулей, входящих обычно в комплект программ Турбо Паскаля. Наиболее доступны из них два модуля — Crt (доступ к экрану дисплея в текстовом режиме, работа с клавиатурой, звуком) и Graph (управление графическим режимом работы дисплея).

Тема «Графические возможности Турбо Паскаля»

Изучение изобразительных (графических) возможностей — традиционно популярная тема при изучении языков программирования. Приходится удивляться, с каким старанием учащиеся программируют построение изображений, хотя прекрасно знают, что большинство из этих изображений можно гораздо проще реализовать с помощью специализированных программ.

Во вводной беседе уместно напомнить учащимся об основных способах формирования изображений — растровом и векторном, напомнить, что такое пиксел, как пикселы отражаются в видеопамяти.

Рассказ о процедурах модуля Graph начните с процедуры перехода в графический режим InitGraph. Надо заметить, что поскольку в модуле Graph более 50 графических процедур и функций, то целесообразно подготовить к занятиям короткий, на одной странице, справочник по основным из них. Поскольку уроки по этой теме ограничатся скорее всего построением простых геометрических примитивов, то именно с этой точки зрения и надо отобрать те процедуры, с которыми следует в первую очередь познакомить учащихся. Все остальные можно всему классу не приводить, а тем учащимся, которые получат задания на разработку соответствующих проектов, предоставить возможность самостоятельного изучения необходимых изобразительных средств.

Приведем список этих основных процедур (их назначение, списки параметров и др. — в любом учебнике по Паскалю, в котором разобран состав модуля Graph):

Arc Bar	CloseGraph Circle
Ellipse FillEllipse	FloodFill InitGraph
Rectangle OutTextXY	OutText PiesLice
PutPixel SetFillStyle	Sector SetLine
StileLine SetTextStyle

Для описания действия этих процедур желателен лекционный режим. Он может при наличии соответствующего оборудования сопровождаться экранными проекциями — демонстрациями действия процедур.

Традиционно первые практические занятия по этой теме проводят в «свободном полете»: рисование несложных изображений, закрашивание их частей, эксперименты с цветами и т.д. Нарисовать домик, снежную бабу и т.д. — вполне подходящие задания.

Освоив простейшие приемы графики Паскаля, целесообразно научиться строить графики функций. Это реализует связь с математикой, позволяет освоить масштабирование, формирует навыки пользования «экранной» системой координат. Поскольку эта система направлена нетрадиционно (начало координат — верхний левый угол экрана, ось ординат направлена вниз, а не вверх), то встает задача научиться простым аффинным преобразованиям Координат. Поставленная задача будет полностью выполнена, если Написанная учащимися программа может выполнить следующую Работу: построить на экране график произвольной функции (задаваемой внутри программы в строке function) на произвольном отрезке, координаты которого вводятся в диалоге. График должен включать оси координат, ориентированные традиционным образом, их разметку, кривую, изображающую функцию. Такая программа достаточно сложна; промежуточным этапом может быть построение графика одной хорошо знакомой учащимся функции на фиксированном отрезке (например: построить график функции у = sin(x) на отрезке от 0 до 2).

Разумеется, с наиболее подготовленными учащимися можно идти дальше и осваивать такие приемы графики, как управление видеостраницами и покадровая мультипликация, но в целом это следует признать для данного этапа обучения чрезмерным.

studfiles.net

Тема «Модули»

Во вводной части лекции следует объяснить учащимся, что только с появлением модулей Паскаль стал средством разработки больших профессиональных программных комплексов. Модуль, как и процедуры, служит реализации идеи модульности — выделения подзадач внутри большой задачи. Отличие модуля от набора «внутренних» процедур — возможность отдельной трансляции и отдельного от программы хранения; к модулю может обращаться не °Дна программа, а много разных программ. Благодаря модулям в Паскале возможно организовывать внешние библиотеки программ По различным проблемам.

Целью школьного спецкурса не может быть самостоятельная Разработка учащимися модулей. Такое задание возможно в качестве проекта для некоторых учащихся, а для большинства эта тема является ознакомительной. Вполне достаточно привести примеры двух-трех несложных модулей и разобрать как их внутреннее устройство, так и механизм взаимодействия с обращающимися к ним программами.

Описав общую структуру модуля и объяснив назначение основных его разделов (заголовок, интерфейсная часть, раздел реализации, раздел инициализации), приведите пример модуля. Допустим, мы хотим дополнить’Паскаль средствами работы с комплексными числами (хотя бы на уровне четырех арифметических действий). В школе, в которой углубленно изучается программирование, учащиеся скорее всего с комплексными числами знакомы. Возможны два подхода к реализации этой задачи.

1. Комплексное число представляется парой действительных (а, Ь). Конструируют четыре процедуры — действия над комплексными числами; у каждой из них по 4 параметра-значения и по 2 параметра-переменных. Сводят их в модуль, в интерфейсной части которого находятся заголовки этих процедур. Показывают, как обращается к нему внешняя программа, объясняют смысл наличия в ней инструкции uses <список модулей.

2. Комплексное число представляется одним идентификатором, т.е. мы хотим иметь возможность записывать присваивания вида А := В + ЕС, где А, В и С — комплексные числа. Эта задача потруднее. Путь к ее решению — создать тип (назвав его Complex), элементы которого — двухполевые записи; первое поле — действительная часть числа, второе — коэффициент при мнимой части.

Всякий раз, разбирая примеры модулей, подчеркните, что разработчику внешней программы, использующему модули, нет никакой необходимости знать устройство процедур, составляющих раздел реализации. Вполне достаточно иметь детальное описание интерфейсной части и назначения модуля.

Более детально учащиеся знакомятся с модулями и приходят, в частности, к пониманию сформулированного выше утверждения на примерах стандартных модулей, входящих обычно в комплект программ Турбо Паскаля. Наиболее доступны из них два модуля — Crt (доступ к экрану дисплея в текстовом режиме, работа с клавиатурой, звуком) и Graph (управление графическим режимом работы дисплея).

Тема «Графические возможности Турбо Паскаля»

Изучение изобразительных (графических) возможностей — традиционно популярная тема при изучении языков программирования. Приходится удивляться, с каким старанием учащиеся программируют построение изображений, хотя прекрасно знают, что большинство из этих изображений можно гораздо проще реализовать с помощью специализированных программ.

Во вводной беседе уместно напомнить учащимся об основных способах формирования изображений — растровом и векторном, напомнить, что такое пиксел, как пикселы отражаются в видеопамяти.

Рассказ о процедурах модуля Graph начните с процедуры перехода в графический режим InitGraph. Надо заметить, что поскольку в модуле Graph более 50 графических процедур и функций, то целесообразно подготовить к занятиям короткий, на одной странице, справочник по основным из них. Поскольку уроки по этой теме ограничатся скорее всего построением простых геометрических примитивов, то именно с этой точки зрения и надо отобрать те процедуры, с которыми следует в первую очередь познакомить учащихся. Все остальные можно всему классу не приводить, а тем учащимся, которые получат задания на разработку соответствующих проектов, предоставить возможность самостоятельного изучения необходимых изобразительных средств.

Приведем список этих основных процедур (их назначение, списки параметров и др. — в любом учебнике по Паскалю, в котором разобран состав модуля Graph):

Arc Bar	CloseGraph Circle
Ellipse FillEllipse	FloodFill InitGraph
Rectangle OutTextXY	OutText PiesLice
PutPixel SetFillStyle	Sector SetLine
StileLine SetTextStyle

Для описания действия этих процедур желателен лекционный режим. Он может при наличии соответствующего оборудования сопровождаться экранными проекциями — демонстрациями действия процедур.

Традиционно первые практические занятия по этой теме проводят в «свободном полете»: рисование несложных изображений, закрашивание их частей, эксперименты с цветами и т.д. Нарисовать домик, снежную бабу и т.д. — вполне подходящие задания.

Освоив простейшие приемы графики Паскаля, целесообразно научиться строить графики функций. Это реализует связь с математикой, позволяет освоить масштабирование, формирует навыки пользования «экранной» системой координат. Поскольку эта система направлена нетрадиционно (начало координат — верхний левый угол экрана, ось ординат направлена вниз, а не вверх), то встает задача научиться простым аффинным преобразованиям Координат. Поставленная задача будет полностью выполнена, если Написанная учащимися программа может выполнить следующую Работу: построить на экране график произвольной функции (задаваемой внутри программы в строке function) на произвольном отрезке, координаты которого вводятся в диалоге. График должен включать оси координат, ориентированные традиционным образом, их разметку, кривую, изображающую функцию. Такая программа достаточно сложна; промежуточным этапом может быть построение графика одной хорошо знакомой учащимся функции на фиксированном отрезке (например: построить график функции у = sin(x) на отрезке от 0 до 2).

Разумеется, с наиболее подготовленными учащимися можно идти дальше и осваивать такие приемы графики, как управление видеостраницами и покадровая мультипликация, но в целом это следует признать для данного этапа обучения чрезмерным.

studfiles.net