Степенные ряды. Сходимость степенного ряда. Область сходимости ряда.
Степенные ряды на Math34.biz для практических занятий с целью закрепления пройденного материала. И оттачивания навыков студентов для того, чтобы научиться однозначно определять сходимость степенного ряда. Практические занятия в полной мере дают желаемый результат, если в курсе по изучению выделено достаточное количество занятий. Это в полной мере обеспечит высококлассную подготовку учащихся. Но что делать, когда их нет? В этом случае решить степенные ряды онлайн поможет как раз наш сайт, или аналогичный ресурс. Однако не всегда подобные калькуляторы смогут предоставить правильный ответ на поставленную задачу. Как раз для этого на примере одного условия нужно сравнить полученные ответы между решениями подобных сайтов. Можно заметить, что область сходимости ряда вычисляется порой по разным теоремам и ответ, хоть он и правильный, но может быть выражен отличными формами записи. Конечно, такое не будет считаться ошибкой, все дело в том, как именно вам будет удобнее его воспринимать. Короче говоря, найти сходимость степенного ряда с помощью того или иного сайта, решать вам, то есть как будет вам удобно для дальнейших применений ответа. Иногда само решение степенного ряда выражают через записи со знаками неравенств, а чаще всего через знак модуля. Это не случайно, поскольку на практике используют наиболее чаще приемы сравнений общих членов ряда с использованием модулей. Через ряд преобразований выделяют переменную, заключенную в модуль, и остается краткая запись, которая нормально воспринимается для понимания решения. Для наглядного представления радиус сходимости ряда можно представить на числовой оси с указанием граничных точек, это, кстати, тоже приветствуется в ряде случаев. Не нужно загонять себя в какие-то определенные рамки, которые сузят ваш кругозор. Вообще-то говоря, степенные ряды важная тема в математике, поскольку сложная и для того, чтобы её понять, вам придется изучить несколько курсов. Например, теорию предельного перехода и интегральное исчисление, поскольку для доказательства сходимости степенного ряда часто используют именно такие приемы, в которых присутствуют эти действия. Для вас мы предлагаем пройти практические занятия, и проверит свои знаний по изучению степенных рядов онлайн прямо на Math34.biz, поскольку мы даем гарантию, что все решаемые задачи выдаются с точным ответом, в считанные секунды и абсолютно бесплатно в режиме реального времени. Помимо области сходимости ряда, или как её еще называют радиус сходимости ряда, мы предлагаем вашему вниманию много других сопутствующих калькуляторов, которые вы, безусловно, оцените на высочайшем уровне. Если требуется найти сходимость степенного ряда, то предоставьте это сделать за вас именно нам, поскольку Math34.biz есть залог точности и гарантия безупречного качественного ответа. Многие студенты не редко задаются таким вопросом как быстрая подготовка в решении степенного ряда, но не просто решение, а качественное и правильное. Во все времена степенные ряды носили более обширный смысл, чем об этом сейчас рассказывают ученикам. Оно и понятно, потому что объясняется это тем, что нет времени в связи с необходимостью глубокого изучения более важные тем. С одной стороны — ДА, но тогда означает ли это, что можно пренебрегать сходимостью степенного ряда? Скорее всего, нет, так как, не изучив должным образом степенные ряды онлайн, вы попросту не сможете грамотно ответить на очевидные вопросы на защите курсовой или дипломной работы. Допустим, ваша предметная область включает такую дисциплину как механика сплошных сред или строительная механика. Очевидно, что устойчивость систем важна при проектировании стратегических объектов, тем более, если это напрямую касается охраны жизнедеятельности людей. Казалось бы, что можно вынести полезного, если научиться или хотя бы понять суть как находить область сходимости ряда? Трудно в одном предложении передать важность этого определения. Но поверьте на слово, найти сходимость степенного ряда такая же важная и необходимая процедура, как, к примеру, знать теорему Пифагора. Если решение степенного ряда будет выполнено с ошибкой, то в дальнейших расчетах обязательно это сыграет злую шутку со студентом. Бывает порой, что из-за досадной неточности в ошибке происходит крушение летательного аппарата уже на первых испытаниях. Согласитесь, это обидно после проделанных работ и колоссального вклада времени. Поэтому учитесь и еще раз учитесь находить радиус сходимости ряда, прививая тем самым с самого начала правильность т строгость в решении задач. Вернемся к теме степенные ряды и расскажем немного об этом разделе подробнее. В практике множество степенных рядов начинаются именно с первого члена, хотя встречаются такие ряды, в условии которых первый член может начаться и со второго, и с третьего члена. Во многом это связано с тем, что, например, начиная с первого члена, сразу обращается в бесконечность вся сумма ряда, что конечно тривиально, по сути. Сходимость степенного ряда как предмет изучения области его сходимости, на практике применяется не часто, особенно студентами, если они не проходят её на кафедре математического анализа. Суть ясна и задачи все расставлены. Наш калькулятор вычисляет степенные ряды онлайн, а также говорит о сходимости ряда, по какому признаку числовой ряд сходится, короче говоря, умеет определять сходимость степенных рядов. Попасть в область сходимости ряда переменная может, если удовлетворяет конкретному единственному условию, то есть чтобы соответствующий получившийся при этом числовой ряд сходился к конечному действительному числовому значению. Пожалуй, это не одно условие, нужно также, чтобы все члены ряда при любом порядковом натуральном значении параметра n существовал и однозначно определялся. Найти сходимость степенного ряда означает определить область его сходимости на числовой оси абсцисс, если речь идет о декартовой системе координат. Такое сделать представляется возможным по признаку Даламбера, однако, нужно понимать, что лишь по признаку, так как сам принцип устанавливает лишь интервал, в который попадет переменная. Помните, для функциональных рядов признак Даламбера не применим, он только для числовых рядов. Решение степенного ряда напрямую связано с нахождением радиуса сходимости этого ряда, но для краткости выражаются именно так. Мы тоже будем применять этот термин, дабы не отставать от тенденции в научном мире. Степенные ряды в граничных точках изучаются отдельно. Разумеется, это есть часть общей задачи по исследованию на сходимость степенного ряда. В этих граничных точках ряд исследуется как числовой — знакопостоянный или знакопеременный, в зависимости от вида общего члена ряда. Ряды, членами которых являются степенные функции, называются степенными рядами, а калькулятор может решать их онлайн. Когда так говорят, сразу приходит на ум следующее предположение, а если членами ряда будут являться периодические функции, то такой ряд наверно должен называться функциональным периодическим рядом! Забавное дело получается, но все очень серьезно. Когда мы определили область сходимости ряда, необходимо после этого проделать завершающие вычисления, а именно исследовать числовые ряды на сходимость, которые получаются путем подстановок границ определенного интервала вместо переменной x степенного ряда. Дальше сможете написать полноценный ответ с решением. Рассмотрим пример, как можно найти сходимость степенного ряда без применения основных теорем, а лишь сравнительным способом. При этом нужно грамотно составлять сравнения двух функциональных рядов до тех пор, пока не упростим исходный ряд до давно изученного элементарного. По этому принципу возьмем за ответ как раз результат давно известный всем наперед. По решению степенного ряда еще не однозначно можно предположить, какой же точно будет радиус сходимости ряда, поскольку перед этим еще надо произвести исследование как минимум двух числовых рядов на каждой из границ интервала. Однако это второстепенно и в этом вам сможет помочь калькулятор онлайн Math34.biz совершенно бесплатно. По виду все степенные ряды одинаковы тем, что их общий член представляет собой обычную функцию от аргумента. Суть изучения состоит как раз в том, чтобы определить допустимые значения этого аргумента для сходимости ряда (условной или безусловной), а также на каких интервалах соответствующий ему уже числовой ряд будет расходиться. Исследование степенного ряда на сходимость отнимает у вас уйму времени, и мы рекомендуем вам использовать готовый калькулятор Math34.biz. Нужно исследовать и границы интервала тоже, в противном случае задачу будет выполнена не полностью, а значит, гарантировано снимут два балла. На нашем сайте вы можете вычислить сумму степенных рядов онлайн. Всегда быстро, надежно, а главное бесплатно! Удобный интерфейс и понятный запрос данных. Разложение функций в степенные ряды очень просто только с нами на Math34.biz. По праву область сходимости ряда есть конкретное условие существования суммы ряда числового. Если значение на границе интервала дает расхождение полученного знакопеременного ряда. то говорят, что ряд сходится условно, то есть он конечно сходится в этой области, но при определенных условиях, что немаловажно в любом случае. Если абстрагироваться от понятия степенного ряда, и на миг просто представить себе сумму степенного ряда как некую функцию по переменной x, то речь уже пойдет не о том, чтобы найти сходимость степенного ряда, а об определении таких условий, при которых будет существовать значение функции при разных значениях её аргумента x. Короче говоря, задачу сведем к простейшему нахождению области определения функции. Правда ведь очень просто и понятно! Любое решение степенного ряда всегда говорит о радиусе сходимости такого степенного ряда и обычно определяется через признак Даламбера, но не напрямую, а лишь с условием. После этого раскрывают модуль полученного неравенства и исследуют числовые ряды на абсолютную или условную сходимость. Потом делают вывод. Очень интересно, когда степенные ряды в первоначальном виде интегрируются или дифференцируются, а потом уже вычисляется сумма ряда от нового степенного ряда. Отсюда следуют много вариантов как себя ведет ряд при тех или иных условиях. Найденная сумма степенного ряда от проинтегрированных членов исходного ряда, есть, по сути, проинтегрированная сумма исходного степенного ряда. Интересно и познавательно, не правда ли? Если грамотно сформулировать текст задачи, то он выглядит примерно так: найти интервал сходимости степенного ряда и исследовать его на границах найденного интервала. Отсюда ряд может сходиться или расходиться абсолютно, что не требует дополнительных исследований. Равномерная сходимость показывает степенные ряды в онлайн вычислении, складывая поочередно все члены исходного ряда, записанного в классическом виде, как в университете. Полагаясь только на свое чутье, студент рискует по неопытности попасть в ловушку своей самоуверенности, когда проще простого взять и воспользоваться калькулятором Math34.biz в самом начале учебы. Из области сходимости ряда делают выводы о сходимости функционального, а точнее степенного ряда, а именно устанавливают сходиться он либо условно, либо абсолютно. Все это необходимо для завершающей записи конечного ответа. Не усложняя ситуацию и не применяя названия сложных теорем, скажем, что найти сходимость степенного ряда будет проще для понимания, если представить в качестве суммы ряда некую функцию и уже исследовать именно ее. А это всем давно ясно и понятно как делать! Радиус сходимости ряда и решение степенного ряда понятия тождественные, так как означают одно и то же, точнее определяют однозначно ту область, значения переменной из которой дает сходимость соответственного числового ряда.
math24.biz
∑ Сумма ряда онлайн
Введите данные для подчета суммы ряда
Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Сходимость ряда
Данный калькулятор умеет определять — сходится ли ряд, также показывает — какие признаки сходимости срабатывают, а какие — нет.
Также умеет определять сходимость степенных рядов.
Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
www.kontrolnaya-rabota.ru
Сходимость степенного ряда — радиус и область сходимости. Решение задач по высшей математике
Функциональным рядом называется ряд вида:
где – функции, определенные на некотором множестве .
Множество всех точек сходимости ряда (*) называется его областью сходимости.
В области сходимости определены функции:
( n-я частичная сумма ряда)
(сумма ряда)
(остаток ряда)
Ряд
называется абсолютно сходящимся, если сходится ряд
Из всех функциональных рядов наиболее часто применяют степенные ряды, которыми называют ряды вида
Действительные числа называют коэффициентами ряда.
Неотрицательное число , такое, что ряд (**) сходится в интервале и расходится вне этого интервала, называется радиусом сходимости этого ряда, а интервал – интервалом сходимости ряда.
Радиус сходимости степенного ряда можно найти по формулам:
или
Свойства степенных рядов
1. Сумма степенного ряда при всех значениях из интервала сходимости есть непрерывная функция.
2. Степенной ряд в его интервале сходимости можно почленно дифференцировать, то есть:
3. Степенной ряд можно интегрировать по любому отрезку, содержащемуся в интервале сходимости, причем:
100task.ru
Степенные ряды, их сходимость, разложение функций в степенные ряды
Среди функциональных рядов наиболее важное место занимают степенные ряды.
Степенным рядом называют ряд
члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x, а c0, c1, c2, cn — постоянные величины. Числа c1, c2, cn — коэффициенты членов ряда, c0 — свободный член. Члены степенного ряда определены на всей числовой прямой.
Ознакомимся с понятием области сходимости степенного ряда. Это множество значений переменной x, для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox.
При подстановке в степенной ряд значения x = 0 получится числовой ряд
c0+0+0+…+0+…,
который сходится.
Следовательно, при x = 0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы.
Теорема 1 (теорема Абеля). Если степенной ряд сходится при некотором значении x = x0, отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x| < |x0|. Обратите внимание: и отправное значение «икс нулевое» и любое значение «икса», которое сравнивается с отправным, взяты по модулю — без учёта знака.
Следствие. Если степенной ряд расходится при некотором значении x = x1, то он расходится и при всех значениях |x| > |x1|.
Как мы уже выяснили ранее, любой степенной ряд сходится при значении x = 0. Есть степенные ряды, которые сходятся только при x = 0 и расходятся при остальных значениях х. Исключая из рассмотрения этот случай, предположим, что степенной ряд сходится при некотором значении x = x0, отличном от нуля. Тогда, по теореме Абеля, он сходится во всех точках интервала ]-|x0|, |x0|[ (интервала, левой и правой границами которого являются значения икса, при котором степенной ряд сходится, взятые соответственно со знаком минус и со знаком плюс), симметричного относительно начала координат.
Если же степенной ряд расходится при некотором значении x = x1, то на основании следствия из теоремы Абеля он расходится и во всех точках вне отрезка [-|x1|, |x1|]. Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости, в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда.
В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x = 0 и считается, что R = 0) или представлять собой всю числовую прямую (тогда ряд сходится во всех точках числовой прямой и считается, что ).
Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при ).
Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, т.е..
(28)
Пример 1. Найти область сходимости степенного ряда
Решение. Здесь
т.е.
Используя формулу (28), найдём радиус сходимости данного ряда:
Исследуем сходимость ряда на концах интервала сходимости . В примере 13 показано, что данный ряд сходится при x = 1 и расходится при x = -1. Следовательно, областью сходимости служит полуинтервал .
Пример 2. Найти область сходимости степенного ряда
Решение. Коэффициенты ряда положительны, причём
Имеем
Найдём предел этого отношения, т.е. радиус сходимости степенного ряда:
Исследуем сходимость ряда на концах интервала . Подстановка значений x = -1/5 и x = 1/5 в данный ряд даёт:
Первый из этих рядов сходится (см. пример 5). Но тогда в силу теоремы параграфа «Абсолютная сходимость» сходится и второй ряд, а область его сходимости – отрезок
Пример 3. Найти область сходимости степенного ряда
Решение. Здесь
По формуле (28) находим радиус сходимости ряда:
Исследуем сходимость ряда при значениях . Подставив их в данный ряд, соответственно получим
Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал .
Пример 4. Найти область сходимости степенного ряда
Решение. Здесь , а
Найдём отношение
Следовательно, радиус сходимости ряда
то есть ряд сходится при любом конечном значении x. Область его сходимости – бесконечный интервал .
Пример 5. Найти область сходимости степенного ряда
Решение. Находимо отношение , где , а :
Согласно формуле (28) радиус сходимости данного ряда
,
то есть ряд сходится только при x = 0 и расходится при остальных значениях х.
Примеры показывают, что на концах интервала сходимости ряды ведут себя различно. В примере 1 на одном конце интервала сходимости ряд сходится, а на другом – расходится, в примере 2 – на обоих концах сходится, в примере 3 – на обоих концах расходится.
Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера, или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.
Пусть для степенного ряда
(29)
радиус сходимости R > 0, т.е. этот ряд сходится на интервале .
Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство
(30)
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f(x) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f(x) на интервале сходимости.
Вне интервала сходимости равенство (30) не имеет смысла.
Можно доказать, что сумма степенного ряда f(x) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.
Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.
Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .
Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
Пусть дана функция f(x), которую требуется разложить в степенной ряд, т.е. представить в виде (30):
Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:
……………………………………………….. (31)
Полагая в равенствах (30) и (31) х = 0, находим
Тогда
Подставляя найденные выражения в равенство (30), получим
(32)
Это разложение функции f(x) в ряд называется рядом Маклорена.
Найдём разложение в ряд Маклорена некоторых элементарных функций.
Пример 8. Разложить в ряд Маклорена функцию
Решение. Производные этой функции совпадают с самой функцией:
Поэтому при х = 0 имеем
Подставляя эти значения в формулу (32), получим искомое разложение:
(33)
Этот ряд сходится на всей числовой прямой (его радиус сходимости ).
Пример 9. Разложить в ряд Маклорена функции: 1) f(x) = sin x; 2) f(x) = cos x.
Решение.
1)Находим производные функции f(x) = sin x; имеем
Так как производная четвёртого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдём значения функции и её производных при х = 0:
Поэтому ряд Маклорена для f(x) = sin x имеет вид
(34)
2) Находим
производные следующих порядков повторяются в той же последовательности. Далее, имеем
В результате получаем следующее разложение функции f(x) = cos x в ряд Маклорена:
Разложить функцию в ряд Маклорена самостоятельно, а затем посмотреть решение
Пример 11. Разложить в ряд Маклорена функцию
Решение. Находим производные данной функции:
…………………………………….……..
(при n < m). Необходимо различать две возможности для показателя степени m. Если m – целое положительное число, то при n = m получим
т.е. постоянную величину, а потому производные следующих порядков равны нулю. Найдём значения функции и её производных при x = 0:
Подставляя эти значения в формулу (32), после упрощений получим
Это не ряд, а сумма, состоящая из конечного числа слагаемых и представляющая собой известное разложение бинома Ньютона.
Если же показатель m не является целым положительным числом, то производные в нуль не обратятся. Найденное выше выражение для производной n-го порядка справедливо для любого . При х = 0 получаем
Подстановка значений функции и её производных в равенство (32) в этом случае даёт
(35)
Полученный ряд называется биномиальным. Найдём его интервал сходимости. Так как коэффициенты этого ряда
то их отношение после упрощения принимает вид
Находим предел абсолютной величины этого отношения при :
Итак, радиус сходимости биномиального ряда R = 1, а — его интервал сходимости.Всё по теме «Ряды»
function-x.ru
Радиус и область сходимости ряда
Степенные и функциональные ряды могут быть сходящимися на множестве действительных чисел, на определенном интервале, или быть расходящимися. Установка радиуса сходимости и области сходимости ряда является важным при исследовании рядов. Радиус сходимости равный половине ширины области сходимости. На практике обе характеристики найти не трудно и Вы в этом скоро убедитесь.
Пример: 3.6 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Для оценки сходимости ряда составим ряд с модулей членов заданного ряда, то есть ряд с последующим общим членом
Далее, исходя с того что полученный ряд имеет положительные члены — исследовать его на сходимость будем с помощью признака Даламбера:
Для этого выписываем следующий после общего член ряда
и подставляем в формулу предела. Вид членов ряда непрост, поэтому будьте внимательны при упрощении предела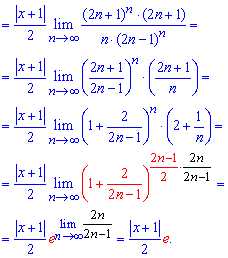
Наконец приходим к экспоненте и функциональному множителю.
Если граница меньше единицы
то ряд сходится по теореме Даламбера, причем абсолютно.
Отсюда составляем ограничения на допустимые «иксы»
— область сходимости ряда.
Итак, ми нашли — радиус сходимости и
— область сходимости ряда в виде интервала.
Для себя запомните, что радиус сходимости функционального ряда равен половине расстояния между крайними точками области сходимости.
б)
Вычисления: Составим ряд из модулей членов заданного ряда, то есть с общим членом
Нетрудно видеть что такой прием позволяет получить ряд с положительными членами и при этом исследовать его на сходимость с помощью признака Даламбера.
Для предела нам еще нужен следующий член ряда
Подставляем члены ряда в предел и вычисляем
При пределе меньшей единицы — ряд убывает за Даламбером.
Из этого условия находим
— область сходимости в виде ограничений переменной.
В итоге мы нашли R=4 — радиус сходимости ряда и его область сходимости
Пример: 3.11 Найти радиус сходимости и область сходимости степенного ряда:
а)
Вычисления: Члены заданного функционального ряда
определены на всей действительной оси, то есть область определения следующая
Составляем ряд из модулей членов заданного ряда
Его общий член может бить выражен формулой
Поскольку новый ряд имеет положительные члены — исследуем на сходимость по Даламберу: 
При — ряд совпадает по теореме Даламбера, то есть необходимо, чтобы выполнялись условия
Отсюда находим R = 2 — радиус сходимости ряда и (0; 4) — область сходимости.
б)
Вычисления: Члены заданного функционального ряда
определены для всех действительных переменных то есть область определения следующая
Составим ряд из модулей членов заданного ряда
Снова применяем признак Даламбера для исследования ряда на сходимость
За Даламбером при пределе меньше единицы — ряд убывает.
Отсюда находим область сходимости
и R=1/3 радиус сходимости. Из приведенных примеров
Вы могли увидеть такую закономерность что значение которое ограничивает модуль с переменной и является радиусом сходимости ряда.
Область сходимости имеет в два раза большую длину и определяется раскрытием модуля.
Пример: 3.17 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Члены функционального ряда
определены при то есть
Составим ряд из модулей членов заданного ряда
то есть
Исследуем его на сходимость по признаку Даламбера. Выписываем следующий после общего члена ряда
и подставляем в предел
При 3|x|<1 — ряд убывает,
отсюда находим
– область сходимости ряда.
Все что находится справа от модуля это R = 1/3 — радиус сходимости ряда, а ограничения на «икс»
– это область сходимости.
б)
Вычисления: Члены функционального ряда
определены на всей действительной прямой , их область определения имеет вид .
По схеме составляем ряд из модулей членов заданного ряда
и получаем ряд со следующим общим членом
Образованный ряд будем анализировать на сходимость по признаку Даламбера
Выписываем следующий член ряда
и подставляем в предел
При 2|x|<1- ряд будет сходящимся.
Раскрываем модуль и находим
— область сходимости и R=1/2 – радиус сходимости.
В виде интервала записываем область сходимости ряда
Пример: 3.27 Найти радиус сходимости и область сходимости степенного ряда
а)
Вычисления: Члены функционального ряда определены на действительной оси
Сначала составим ряд из модулей членов этого ряда
Общий член задается формулой
Исследуем ряд с модулей на сходимость по признаку Даламбера:
Находим предел отношения следующего члена ряда общему
Поскольку A=0<1 то ряд сходится при всех действительных переменных, то есть имеет неограниченную — область сходимости.
Ряд имеет бесконечный радиус сходимости.
б)
Вычисления: Члены ряда определены на множестве действительных чисел
Построим ряд с модулей членов ряда:
Далее записываем общий и следующий после него члены ряда
и подставляем в предел
По теореме Даламбера ряд сходится при
3|x|<1. Из этого условия определяем
— область сходимости ряда
и R=1/3 – радиус сходимости.
В виде интервала записываем в ответ область сходимости
Теперь Вы знаете как найти область сходимости и радиус сходимости ряда. Пользуйтесь приведенными формулами и успешной Вам сдачи сессии.
yukhym.com
Область сходимости степенного ряда. Примеры решения задач
Область сходимости степенного ряда
Задача Найти область сходимости степенного ряда Решение Заданный ряд является степенным рядом.
Согласно признаку Даламбера, для абсолютной сходимости ряда достаточно, чтобы .
Для решаемой задачи , .
Так как , то ряд будет абсолютно сходиться при значениях , удовлетворяющих неравенству .
Решением этого неравенства является интервал , следовательно, при исследуемый степенной ряд будет абсолютно сходиться.
Исследуем поведение ряда на концах интервала, то есть при и .
При получаем числовой ряд . Это знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница: , . Поэтому ряд сходится, и граница интервала принадлежит области сходимости. В область абсолютной сходимости ряда эта граница не входит, так как ряд расходится.
При получаем числовой ряд . Это гармонический ряд, и он расходится. Следовательно, граница интервала не принадлежит области сходимости степенного ряда.
Итак, областью сходимости степенного ряда является полуинтервал
, а областью абсолютной сходимости степенного ряда является интервал
.
www.matem96.ru
Найти интервал сходимости степенного ряда — 6 Мая 2013 — Примеры решений задач
Пример на сходимость степенного ряда
Найти интервал сходимости степенного ряда
Решение. Применяя признак Даламбера
Согласно признака Даламбера, на данном интервале ряд сходится абсолютно.
При x=-√2/3,
Согласно принципа Лейбница, ряд сходится условно.
При x=√2/3
Ряд расходится.
И так, получаем, интервал сходимости
www.reshim.su
