Математическое ожидание. Вычисление
Одной из часто используемых на практике характеристик при анализе случайных величин является математическое ожидание. Под данным термином часто употребляют «среднее значение» случайной величины . Рассчитывать его не так трудно, особенно если имеем дискретную величину с небольшим количеством точек.
Математическим ожиданием случайной величины определенной на дискретном множестве значений называется величина, равная сумме попарных произведений величин на их вероятности появления
Если множество ограничено, то нужно искать сумму числа слагаемых
Если множество является непрерывным, то математическое ожидание случайной величины определяется интегрированием по формуле
Если , то
Если то
Свойства математического ожидания
1. Математическое ожидание от постоянной величины равно постоянной
2. Постоянный множитель при случайной величине можно выносить за скобки
Для дискретной случайной величины справедлива зависимость
Для непрерывной следующая:
3. Если и являются постоянными величинами, то справедливая зависимость
Для дискретной случайной величины:
Для непрерывной случайной величины:
————————-
Приведем решения распространенных на практике задач.
Пример 1. Закон распределения дискретной случайной величины задан таблично:
Вычислить математическое ожидание.
Решение. Согласно приведенной выше формулы, вычисляем
Таким образом, найдено математическое ожидание равное 0,5.
————————-
Пример 2. По заданной функцией плотности вероятностей
вычислить математическое ожидание.
Решение. Согласно формулы для непрерывной случайной величины проводим интегрирование
Найдем интегралы по очереди, для первого выполним замену переменных
————————-
Пример 3. Плотность вероятностей задано тригонометрической формулой
Найти математическое ожидание.
Решение. Проводим интегрирования по частям
Найдено математическое ожидание равно
————————-
Пример 4. По заданной функцией распределения вероятностей
вычислить математическое ожидание.
Решение. Для вычисления необходимо сначала найти плотность вероятностей. Для этого осуществляем дифференцирования функции распределения
После этого проводим интегрирование по уже формуле:
—————————
Для проверки правильности вычислений запомните, что если случайная величина принадлежит промежутку , то математическое ожидание также должно находиться внутри , выполняя роль центра распределения этой величины. В случаях когда найдено математическое ожидание выходит за пределы промежутка нужно проанализировать предварительные вычисления и исправить ошибки. Будьте внимательны при интегрировании функций и замене переменных, именно в этом скрыта львиная доля Ваших ошибок.
yukhym.com
Примеры решения задач
Задача 1. Вероятность всхожести семян пшеницы равна 0,9. Какова вероятность того, что из четырех посеянных семян взойдут не менее трех?
Решение. Пусть событие А – из 4 семян взойдут не менее 3 семян; событие В – из 4 семян взойдут 3 семени; событие С – из 4 семян взойдут 4 семени. По теореме сложения вероятностей
.
Вероятности 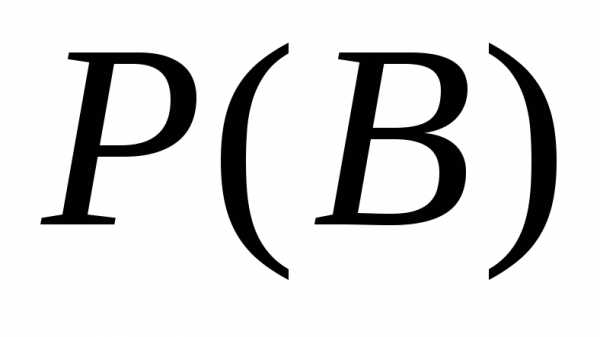 и
и 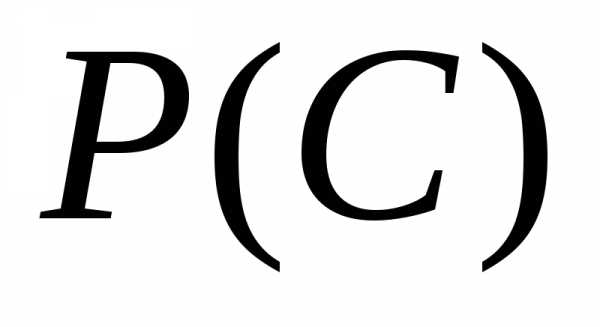 определим по формуле Бернулли, применяемой
в следующем случае. Пусть проводится
серия п независимых испытаний, при каждом из
которых вероятность наступления события
постоянна и равна р,
а вероятность ненаступления этого
события равна
определим по формуле Бернулли, применяемой
в следующем случае. Пусть проводится
серия п независимых испытаний, при каждом из
которых вероятность наступления события
постоянна и равна р,
а вероятность ненаступления этого
события равна 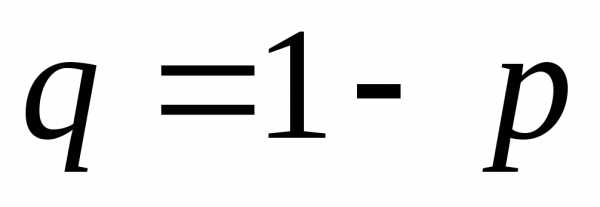
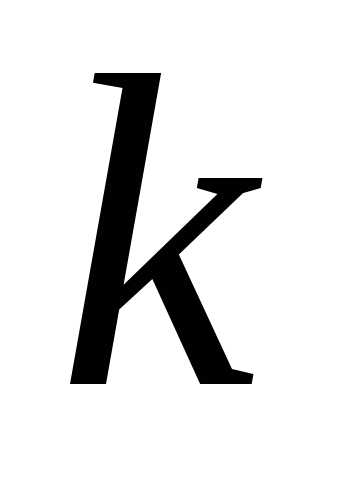 раз, вычисляется по формуле Бернулли
раз, вычисляется по формуле Бернулли,
где 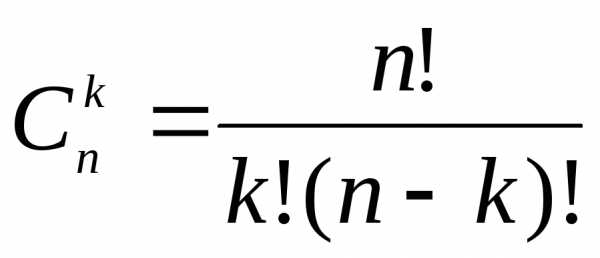 – число сочетаний из п элементов по
– число сочетаний из п элементов по 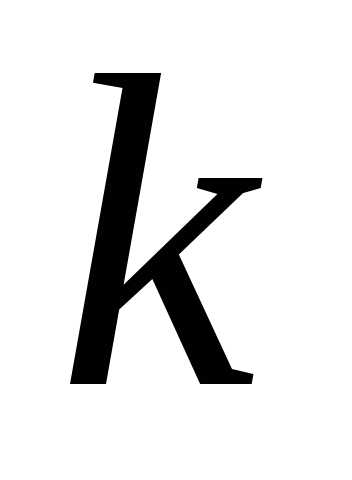 .
Тогда
.
Тогда
Искомая вероятность
.
Задача 2. Вероятность всхожести семян пшеницы равна 0,9. Найти вероятность того, что из 400 посеянных семян взойдут 350 семян.
Решение. Вычислить
искомую вероятность 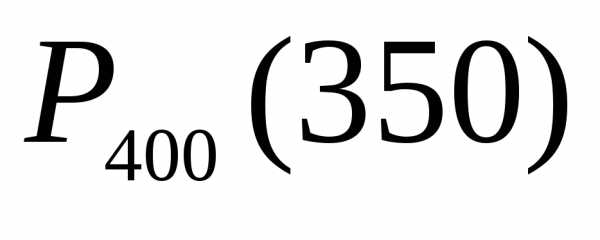 по формуле Бернулли затруднительно
из-за громоздкости вычислений. Поэтому
применим приближенную формулу, выражающую
локальную теорему Лапласа:
по формуле Бернулли затруднительно
из-за громоздкости вычислений. Поэтому
применим приближенную формулу, выражающую
локальную теорему Лапласа:
 ,
, где 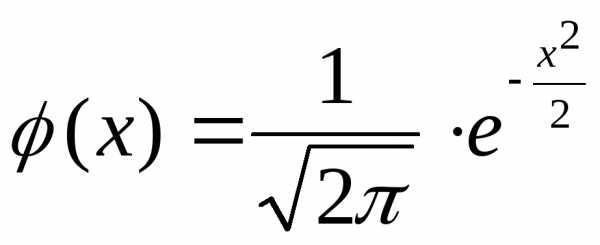 и
и 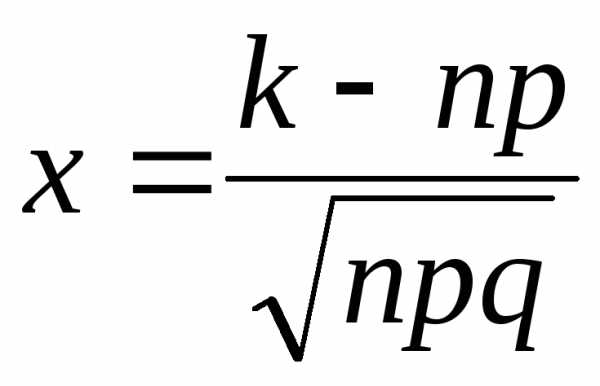 .
.
Из условия задачи . Тогда
.
Из таблицы 1 приложений находим . Искомая вероятность равна
.
Задача 3. Среди семян пшеницы 0,02% сорняков. Какова вероятность того, что при случайном отборе 10000 семян будет обнаружено 6 семян сорняков?
Решение. Применение
локальной теоремы Лапласа из-за малой
вероятности
приводит к значительному отклонению
вероятности от точного значения  .
Поэтому при малых значениях р для вычисления
.
Поэтому при малых значениях р для вычисления 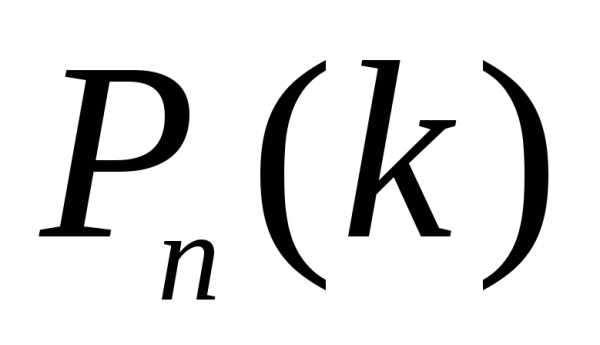 применяют асимптотическую формулу
Пуассона
применяют асимптотическую формулу
Пуассона
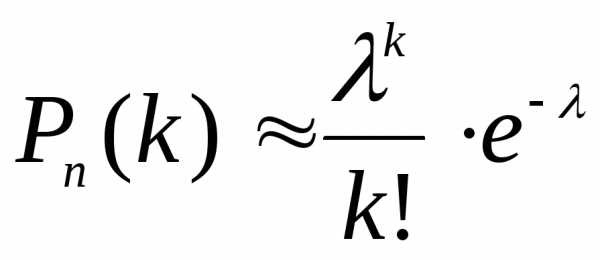 ,
где .
,
где .
Эта формула
используется при 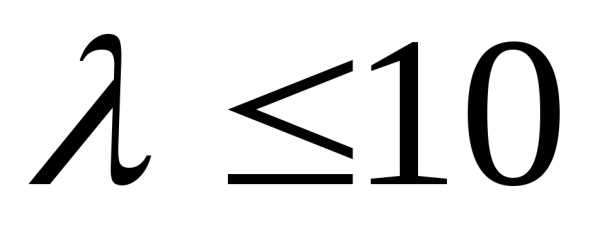 ,
причем чем меньше р и больше п,
тем результат точнее.
,
причем чем меньше р и больше п,
тем результат точнее.
По условию задачи ; . Тогда
и
.
Задача 4. Процент всхожести семян пшеницы равен 90%. Найти вероятность того, что из 500 посеянных семян взойдут от 400 до 440 семян.
Решение. Если
вероятность наступления события А в каждом из п испытаний постоянна и равна р,
то вероятность
того, что событие А в таких испытаниях наступит не менее 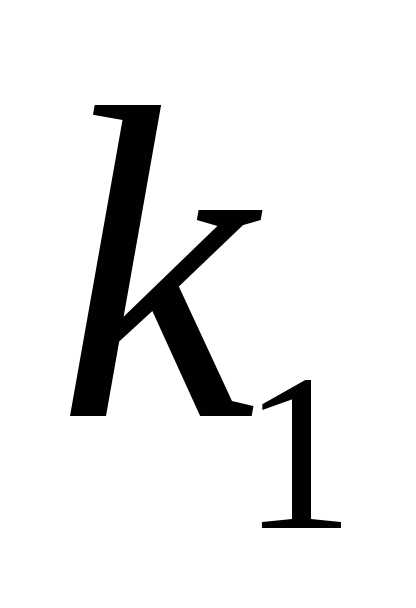 раз и не более
раз и не более 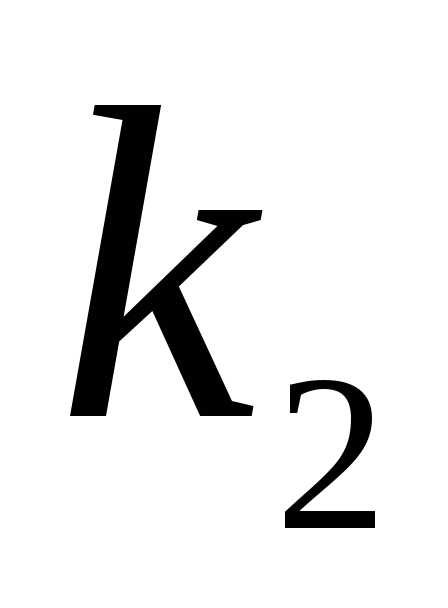 раз определяется по интегральной теореме
Лапласа следующей формулой:
раз определяется по интегральной теореме
Лапласа следующей формулой:
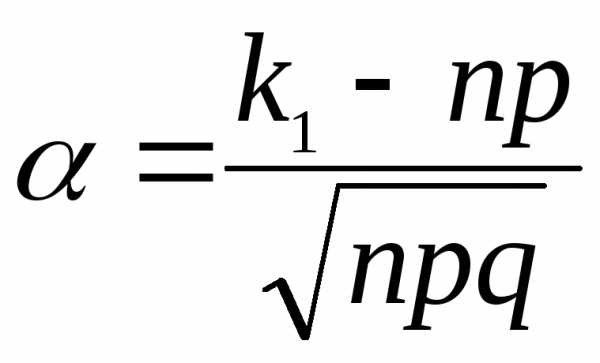 ,
, 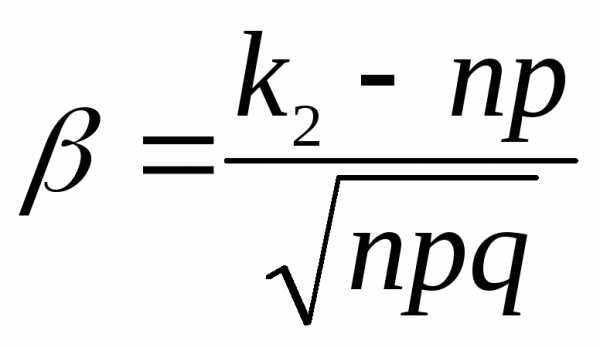 .
.
Функция  называется функцией Лапласа. В приложениях
(табл. 2) даны значения этой функции для
.
При
называется функцией Лапласа. В приложениях
(табл. 2) даны значения этой функции для
.
При  функция .
При отрицательных значениях х в силу нечетности функции Лапласа .
Используя функцию Лапласа, имеем:
функция .
При отрицательных значениях х в силу нечетности функции Лапласа .
Используя функцию Лапласа, имеем:
.
По условию задачи
.
По приведенным выше формулам находим  и
и  :
:
.
Тогда
Задача 5. Задан закон распределения дискретной случайной величины Х:
Х | 40 | 42 | 41 | 44 | ||
р | 0,1 | 0,3 | 0,2 | 0,4 |
Найти: 1) математическое ожидание ; 2) дисперсию ; 3) среднее квадратическое отклонение .
Решение. 1) Если закон распределения дискретной случайной величины задан таблицей
Х |
| х2 | х3 | х4 | ||
р | р1 | р2 | р3 | р4, |
Где в первой строке даны значения случайной величины х, а во второй – вероятности этих значений, то математическое ожидание вычисляется по формуле
.
Тогда .
2) Дисперсия 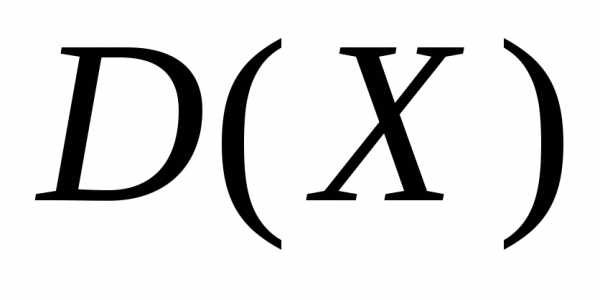 дискретной
случайной величины Х называется математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания, т.е.
дискретной
случайной величины Х называется математическое ожидание
квадрата отклонения случайной величины
от ее математического ожидания, т.е.
.
Эта величина
характеризует среднее ожидаемое значение
квадрата отклонения 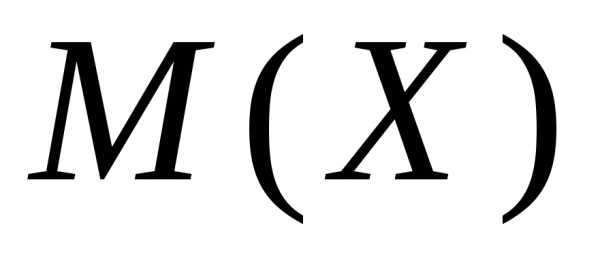 .
Из последней формулы имеем
.
Из последней формулы имеем
Дисперсию 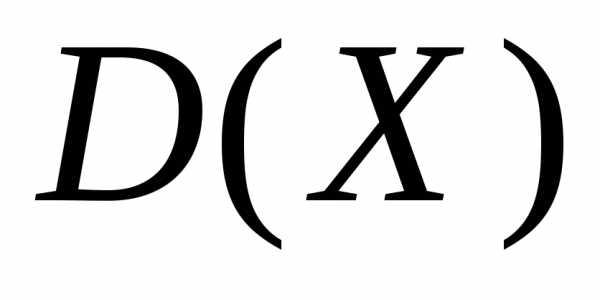 можно найти другим способом, исходя из
следующего ее свойства: дисперсия
можно найти другим способом, исходя из
следующего ее свойства: дисперсия 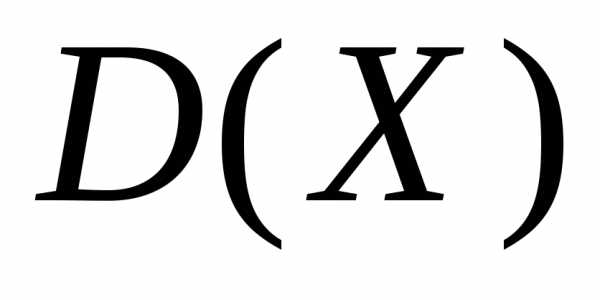 равна разности между математическим
ожиданием квадрата случайной величины Х и квадратом ее математического ожидания
равна разности между математическим
ожиданием квадрата случайной величины Х и квадратом ее математического ожидания 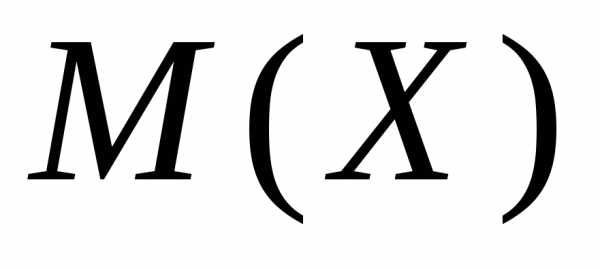 ,
то есть
,
то есть
.
Для вычисления 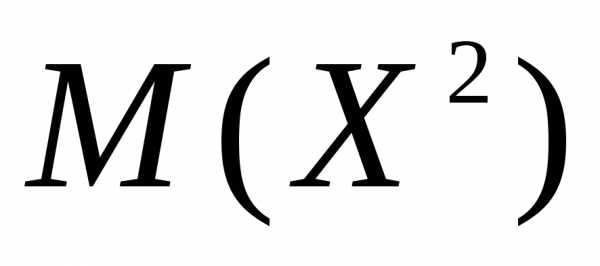 составим следующий закон распределения
величины
составим следующий закон распределения
величины  :
:
Х2 | 402 | 422 | 412 | 442 | ||
р | 0,1 | 0,3 | 0,2 | 0,4 |
Тогда
3) Для характеристики
рассеяния возможных значений случайной
величины вокруг ее среднего значения
вводится среднее квадратическое
отклонение 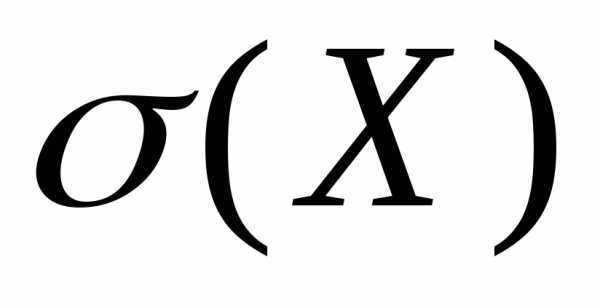 случайной величины Х,
равное квадратному корню из дисперсии
случайной величины Х,
равное квадратному корню из дисперсии 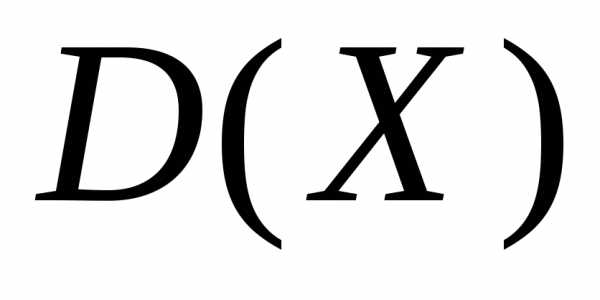 ,
то есть
,
то есть
.
Из этой формулы имеем:
Задача 6. Непрерывная случайная величина Х задана интегральной функцией распределения

Найти: 1)
дифференциальную функцию распределения 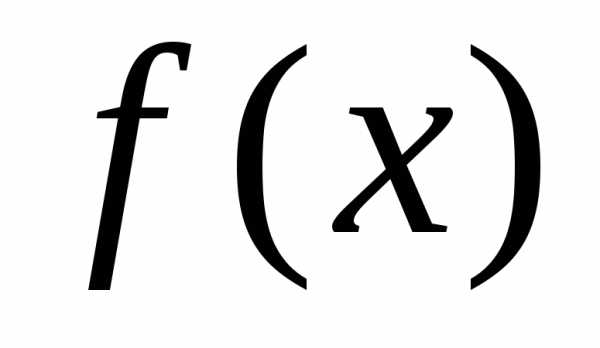 ;
2) математическое ожидание
;
2) математическое ожидание 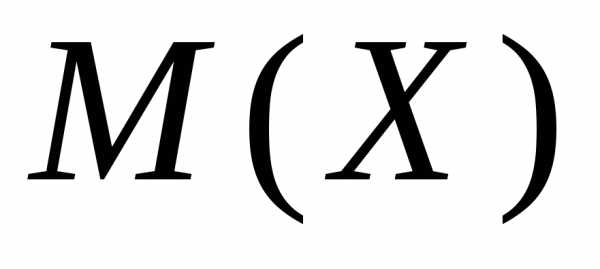 ;
3) дисперсию
;
3) дисперсию 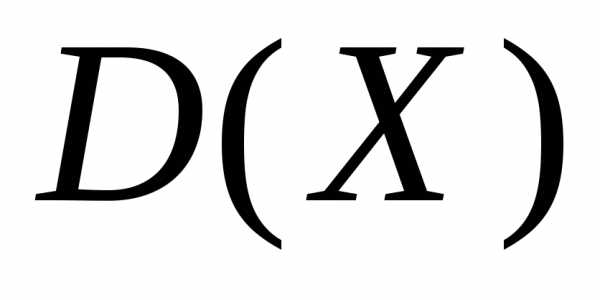 .
.
Решение. 1)
Дифференциальной функцией распределения 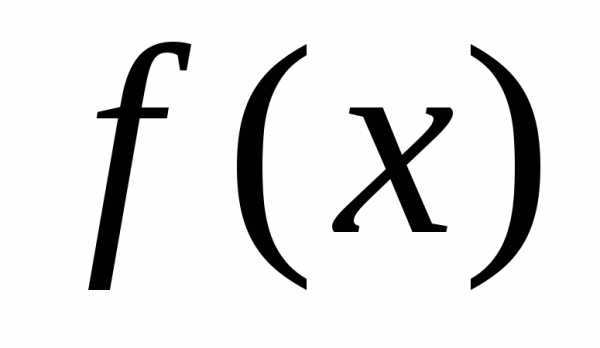 непрерывной случайной величины Х называется производная от интегральной
функции распределения
непрерывной случайной величины Х называется производная от интегральной
функции распределения 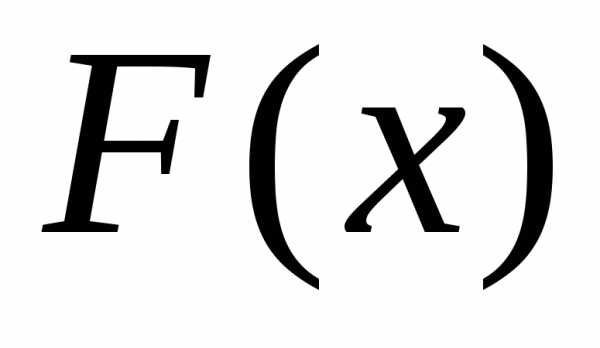 ,
то есть
,
то есть
.
Искомая дифференциальная функция имеет следующий вид:
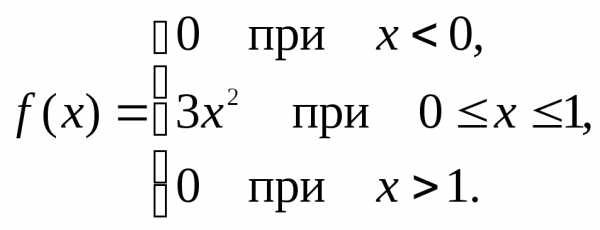
2) Если непрерывная
случайная величина Х задана функцией 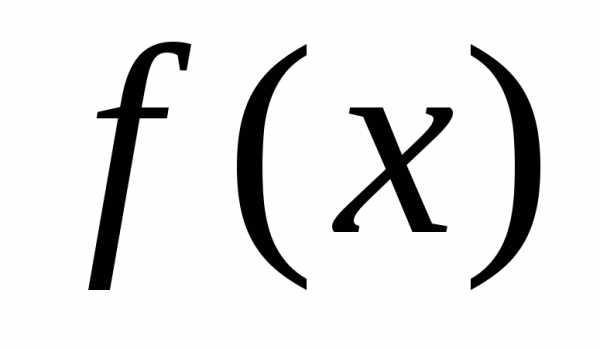 ,
то ее математическое ожидание определяется
формулой
,
то ее математическое ожидание определяется
формулой
Так как функция 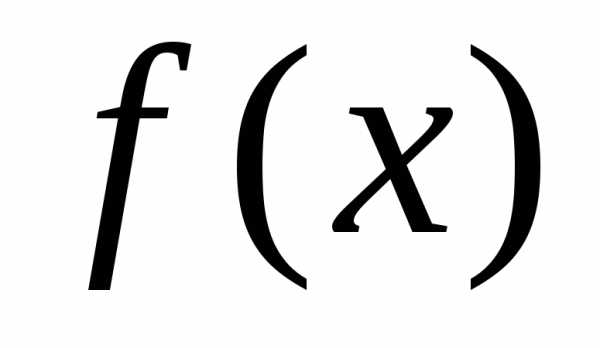 при
при  и при
и при 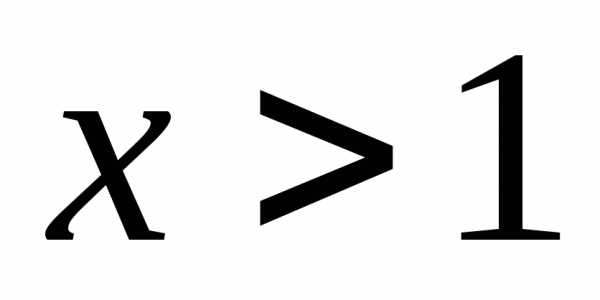 равна нулю, то из последней формулы
имеем
равна нулю, то из последней формулы
имеем
.
3) Дисперсию  определим по формуле
определим по формуле
Тогда
Задача 7. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40 мм и средним квадратическим отклонением 3 мм. Найти: 1) вероятность того, что длина произвольно взятой детали будет больше 34 мм и меньше 43 мм; 2) вероятность того, что длина детали отклонится от ее математического ожидания не более чем на 1,5 мм.
Решение. 1) Пусть Х – длина детали. Если случайная величина Х задана дифференциальной функцией  ,
то вероятность того, что Х примет значения, принадлежащие отрезку
,
то вероятность того, что Х примет значения, принадлежащие отрезку 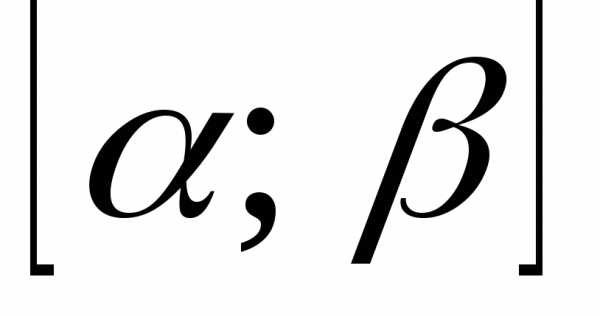 ,
определяется по формуле
,
определяется по формуле
.
Вероятность выполнения строгих неравенств определяется той же формулой. Если случайная величина Х распределена по нормальному закону, то
, (1)
где 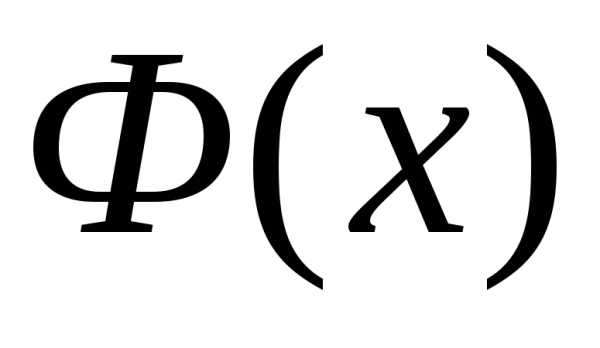 – функция Лапласа, .
– функция Лапласа, .
В задаче . Тогда
2) По условию задачи , где . Подставив в (1) , имеем
то есть
. (2)
Из формулы (2) имеем:
.
studfiles.net
ТеорВер-Онлайн: 2.3 Математическое ожидание
Так как случайная величина может принимать различные значения , в зависимости от того, какой исход «виртуального» эксперимента ( 1.3) будет разыгран, то с разных точек зрения удобно иметь числовую характеристику, имеющую смысл «среднего значения» случайной величины.
Определение 2.3 Математическим ожиданием случайной величины называется число Математическое ожидание существует в том и только в том случае, когда этот ряд сходится абсолютно. Лемма 2.1 Математическое ожидание может быть вычислено по формуле| (7) |
Доказательство. Мы будем использовать следующий факт из курса математического анализа (см., например, [9, § 25, Теорема 1]). Пусть дан абсолютно сходящийся ряд. Тогда его члены можно произвольным образом переставлять и группировать, полученные в результате этого ряды будут сходиться к одному и тому же значению.
Пример 2.4 Случайная величина из Примера 2.1: Пример 2.5 — число очков, выпавших на игральной кости. Распределение этой случайной величины: Упражнение 2.1 Найти математическое ожидание пуассоновской случайной величины .
teorver-online.narod.ru

