Косинус квадрат и синус квадрат
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α)
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
квадрат, куб, в 4 степени
Ниже представлены таблицы с формулами степеней (квадрат, куб, в 4-ой степени) прямых и обратных тригонометрических функций: синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы квадратов
Формулы кубов
| Степень | Формула |
| Синус в кубе | 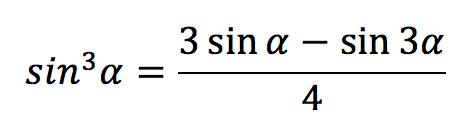 |
| Косинус в кубе | 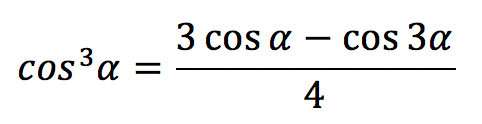 |
| Тангенс в кубе | 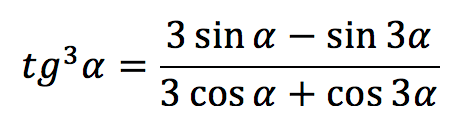 |
| Котангенс в кубе | 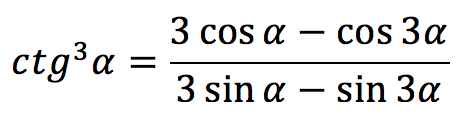 |
microexcel.ru
Формулы функций в 4-ой степени
| Степень | Формула |
| Синус в 4-ой степени | 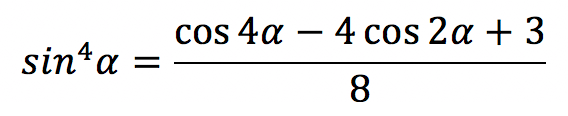 |
| Косинус в 4-ой степени | 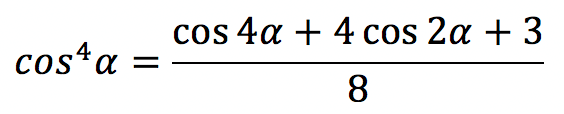 |
| Тангенс в 4-ой степени | 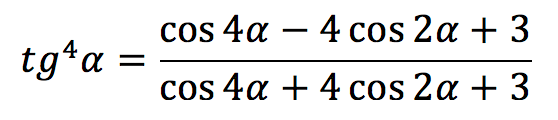 |
| Котангенс в 4-ой степени | 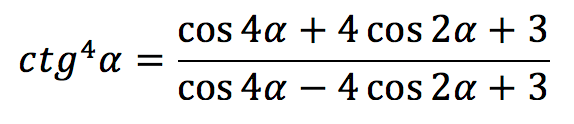 |
microexcel.ru
Формулы понижения степени являются одним из видов основных тригонометрических формул. Они выражают степени (2, 3, …) тригонометрических функций синус, косинус, тангенс, котангенс через синус и косинус первой степени, но кратного угла (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).
Содержание статьи:
Список всех тригонометрических формул понижения степени
Запишем данные тождества для тригонометрических функций от 2-й по 4-ю степень угла `\alpha`, а также для угла `\frac \alpha 2` и для произведения синус на косинус. Для удобства разделим их на группы.
Для квадрата
Формулы этой группы, особенно две первые, наиболее нужны. Они применяются при решении тригонометрических уравнений, интегралов и т. д.
`sin^2 \alpha=\frac{1-cos \ 2\alpha}2`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2`
`tg^2 \alpha=\frac{1-cos \ 2\alpha}{1+cos \ 2\alpha}`
`ctg^2 \alpha=\frac{1+cos \ 2\alpha}{1-cos \ 2\alpha}`
Для куба
Тождества этой группы и следующих встречаются гораздо реже, но это не повод их не знать.
`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`
`tg^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}{3cos \ \alpha+cos \ 3\alpha}`
`ctg^3 \alpha=\frac{3sin \ \alpha+sin \ 3\alpha}{3cos \ \alpha-cos \ 3\alpha}`
Для 4-й степени
`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Для функций половинного угла
Это формулы половинного угла. Но когда они записаны именно в таком виде, то их можно отнести и к тодествам понижения степени.
` sin^2 \frac \alpha 2=\frac{1-cos \alpha}2`
` cos^2 \frac \alpha 2=\frac{1+cos \alpha}2`
`tg^2 \frac \alpha 2=\frac{1-cos \alpha}{1+cos \alpha}`
`ctg^2 \frac \alpha 2=\frac{1+cos \alpha}{1-cos \alpha}`
Для произведения синус на косинус
`sin^2 \alpha \cdot cos^2 \alpha=\frac{1-cos \ 4\alpha}8`
`sin^3 \alpha \cdot cos^3 \alpha=\frac{3sin \ 2\alpha-sin \ 6\alpha}32`
`sin^4 \alpha \cdot cos^4 \alpha=\frac{3-4cos \ 4\alpha+cos \ 8\alpha}128`
`sin^5 \alpha \cdot cos^5 \alpha=\frac{10sin \ 2\alpha-5sin \ 6\alpha+sin \ 10\alpha}512`
Доказательство
Теперь перейдем непосредственно к выводу формул понижения степени тригонометрических функций.
Чтобы доказать их для квадрата, нам понадобятся фождества двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`.
Формулу понижения степени синуса в квадрате получим, разрешив первое равенство относительно ` sin^2 \alpha`: `sin^2 \alpha=\frac{1-cos \ 2\alpha}2`.
Аналогично и с косинусом в квадрате, получим тождество, разрешив второе равенство относительно ` cos^2 \alpha`: `cos^2 \alpha=\frac{1+cos \ 2\alpha}2`.
Формула понижения степени тангенса и котангенса автоматически выводится из определений этих функций. Поскольку `tg \alpha=\frac {sin \alpha}{cos \alpha}`, то `tg^2 \alpha=\frac {sin^2 \alpha}{cos^2 \alpha}=` `\frac {\frac{1-cos \ 2\alpha}2}{\frac{1+cos \ 2\alpha}2}=\frac{1-cos \ 2\alpha}{1+cos \ 2\alpha}`. Аналогично получим `ctg^2 \alpha=\frac {cos^2 \alpha}{sin^2 \alpha}=` `\frac {\frac{1+cos \ 2\alpha}2}{\frac{1-cos \ 2\alpha}2}=\frac{1+cos \ 2\alpha}{1-cos \ 2\alpha}`.
Для лучшего усвоения теоретического материала рекомендуем посмотреть видео, где подробно описывается процесс доказательстве первых двух формул:
Если формулы тройного угла `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha` и
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha` разрешить относительно `sin \ 3\alpha` и `cos \ 3\alpha`, то получим формулы понижения степени для синуса и косинуса в кубе: `sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4` и `cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`.
Доказать данной равности для синуса и косинуса можно, воспользовавшись два раза формулами понижения квадратов:
`sin^4 \alpha=(sin^2 \alpha)^2=(\frac{1-cos \ 2\alpha}2)^2=` `\frac{1-2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1-2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`;
`cos^4 \alpha=(cos^2 \alpha)^2=(\frac{1+cos \ 2\alpha}2)^2=` `\frac{1+2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1+2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`.
Общий вид формул понижения степени
Для четных показателей степени (n=1, 2, 3,…):
`sin^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} (-1)^{\frac n 2 -k} \cdot C_k^n \cdot cos((n-2k) \alpha)` и `cos^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} C_k^n \cdot cos((n-2k) \alpha)`.
Для нечетных показателей степени (n=3, 5, 7,…):
`sin^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} (-1)^{\frac {n-1} 2 -k} \cdot C_k^n \cdot sin((n-2k) \alpha)` и `cos^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} C_k^n \cdot cos((n-2k) \alpha)`.
Примеры решения задач с применением формул понижения степени
Пример 1. Воспользуйтесь формулой понижения степени для `cos^2 4\alpha`.
Решение. Применив формулу `cos^2 \alpha=\frac{1+cos \ 2\alpha}2`, получим `cos^2 4\alpha=\frac{1+cos 2\cdot\ 4\alpha}2=\frac{1+cos 8\alpha}2`.
Ответ. `cos^2 4\alpha=\frac{1+cos 8\alpha}2`.
Пример 2. Используя выше указанные тождества, вычислить `sin^2 \frac \pi 8`.
Решение. Согласно формуле `sin^2 \alpha=\frac{1-cos \ 2\alpha}2`, понизим степень синуса. Получим `sin^2 \frac \pi 8=\frac{1-cos \ 2\frac \pi 8}2=\frac{1-cos \frac \pi 4}2`. Поскольку `cos \frac \pi 4=\frac {\sqrt 2}2`, то `sin^2 \frac \pi 8=\frac{1-cos \frac \pi 4}2=\frac{1-\frac {\sqrt 2}2}2=\frac{\frac {2-\sqrt 2}2}2=\frac {2-\sqrt 2}4`.
Ответ. `sin^2 \frac \pi 8=\frac {2-\sqrt 2}4`.
Отметим, что формулы понижения степени в тригонометрии чаще всего используются при решении уравнений и преобразовании выражений.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…Квадрат — синус
Cтраница 1
Квадраты синусов определяют на выходе вторую гармонику. [1]
Преобразуя квадрат синуса, находим. [2]
Сумма квадратов синуса и косинуса одного угла равна единице. [3]
Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине. [4]
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения. [5]
Для исследования суммы квадратов синусов этих углов воспользуйтесь теоремой косинусов. [6]
Доказать, что сумма квадратов синусов трех углов, образуемых произвольным лучом с ребрами прямого трехгранного угла, равна двум. [7]
Так как в выражении (5.21) присутствует квадрат синуса, то мгновенная мощность всегда является положительной величиной. Положительный знак мгновенной мощности отражает тот факт, что происходит, односторонний процесс поглощения энергии в цепи переменного тока. [9]
Эту теорему можно сформулировать так: квадрат синуса любого угла плюс квадрат косинуса того же угла равен единице. [10]
Для получения подобного ряда следует взять отношения квадрата синуса 6 — каждой из линий Кка дифракционной картины рент-генограммы к квадрату синуса 9i первой линии. [11]
Для получения подобного ряда следует взять отношения квадрата синуса в — каждой из линий ХЛа дифракционной картины рентгенограммы к квадрату синуса 0Г первой линии. [13]
Формула или закон, известный обычно как закон квадрата синуса сопротивления воздуха Ньютона, относится к силе, действующей на наклонную плоскую пластину, омываемую равномерным воздушным потоком. [14]
Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла. [15]
Страницы: 1 2 3 4
1. Формула стороны квадрата через диагональ

a — сторона квадрата
d — диагональ квадрата
Формула стороны квадрата, (a):

2. Формула стороны квадрата через радиус вписанной окружности

a — сторона квадрата
R — радиус вписанной окружности
D — диаметр вписанной окружности
Формула стороны квадрата, (a):

3. Формула стороны квадрата через радиус описанной окружности

a — сторона квадрата
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула стороны квадрата, (a):

4. Формула стороны квадрата через площадь и периметр

a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
Формула стороны квадрата, (a):

5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата

a — сторона квадрата
C — линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):

Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.

d — диагональ прямоугольника
a, b — стороны
α, β — углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):

Формулы диагонали через сторону и угол, (d):


Формулы величины углов через диагональ и стороны, (α, β):


2. Формулы углов между диагоналями в прямоугольнике.

d — диагонали прямоугольника
a, b — стороны
α, β — углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):


1. Формулы диагонали квадрата через стороны, площадь, периметр

a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
d — диагональ квадрата
Формулы диагонали квадрата, (d ):



2. Формула диагонали квадрата через радиус вписанной окружности

R — радиус вписанной окружности
D — диаметр вписанной окружности
d — диагональ квадрата
Формула диагонали квадрата, (d ):

3. Формула диагонали квадрата через радиус описанной окружности

R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула диагонали квадрата, (d ):

4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата

C — линия выходящая из угла на середину стороны квадрата
d — диагональ
Формула диагонали квадрата, (d ):

Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
02=0 12=1 22=4 32=9 42=16 52=25 62=36 72=49 82=64 92=81 | 102=100 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 | 202=400 212=441 222=484 232=529 242=576 252=625 262=676 272=729 282=784 292=841 | 302=900 312=961 322=1024 332=1089 342=1156 352=1225 362=1296 372=1369 382=1444 392=1521 | 402=1600 412=1681 422=1764 432=1849 442=1936 452=2025 462=2116 472=2209 482=2304 492=2401 |
502=2500 512=2601 522=2704 532=2809 542=2916 552=3025 562=3136 572=3249 582=3364 592=3481 | 602=3600 612=3721 622=3844 632=3969 642=4096 652=4225 662=4356 672=4489 682=4624 692=4761 | 702=4900 712=5041 722=5184 732=5329 742=5476 752=5625 762=5776 772=5929 782=6084 792=6241 | 802=6400 812=6561 822=6724 832=6889 842=7056 852=7225 862=7396 872=7569 882=7744 892=7921 | 902=8100 912=8281 922=8464 932=8649 942=8836 952=9025 962=9216 972=9409 982=9604 992=9801 |
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
62 = 6 × 6 = 36
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».
Скачать таблицу квадратов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
Косинус в квадрате, формула и примеры
ОПРЕДЕЛЕНИЕ Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом:
и
Тогда
Полученное выражение представляет собой правую часть формулы произведения синусов, т.е.
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Синусоидальная функция — исчисление
Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена информация о функции, включая ее область, диапазон и ключевые данные, касающиеся построения графиков, дифференцирования и интеграции.
Просмотрите полный список определенных функций на этой вики
Определение
Эта функция, обозначаемая  , определяется как составная функция квадрата и функции синуса.Явно это карта:
, определяется как составная функция квадрата и функции синуса.Явно это карта:
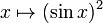
Для краткости мы пишем 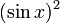 как
как 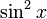 .
.
Ключевые данные
| пункт | Значение|
|---|---|
| Домен по умолчанию | все действительные числа, то есть все 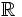 |
| диапазон | ![[0,1]](/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т.е. , т.е. 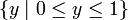 абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | 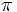 , то есть , то есть 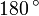 |
| локальное максимальное значение и очки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых числах, кратных 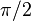 . . |
| местное минимальное значение и очки достижения | Все локальные минимальные значения равны 0 и достигаются при целых числах, кратных 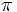 . . |
| точек перегиба (обе координаты) | нечетных кратных 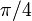 , со значением 1/2 в каждой точке. , со значением 1/2 в каждой точке. |
| производных | 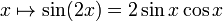 , то есть функция синусоидального угла. , то есть функция синусоидального угла. |
| вторая производная | 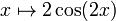 |
 производная производная | 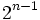 раз выражение, которое составляет раз выражение, которое составляет 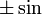 или или 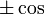 из из 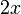 , в зависимости от остатка , в зависимости от остатка 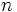 мод мод 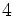 |
| антипроизводных |  |
| среднее значение за период | 1/2 |
| выражение в виде синусоидальной функции плюс постоянная функция | 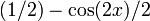 |
| важных симметрий | Четная функция (следует из составной части четной функции с нечетной функцией четного, квадратная функция четная, а синус-функция нечетная) в более общем случае зеркально симметрично относительно любой вертикальной линии формы 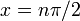 , , 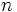 целое число. целое число.Кроме того, половина поворота симметрии вокруг всех точек формы 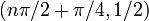 . . |
| описание интервала на основе увеличения / уменьшения и вогнутого вверх / вниз | Для каждого целого числа 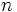 интервал от интервал от 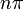 до до 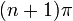 подразделяется на четыре части: подразделяется на четыре части: 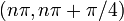 : увеличивается и вогнут до : увеличивается и вогнут до  : увеличивается и вогнут : увеличивается и вогнут 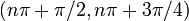 : уменьшается и вогнут, : уменьшается и вогнут, 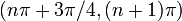 : уменьшается и вогнут до : уменьшается и вогнут до |
| и серия Тейлор | Степенной ряд около 0 (что, следовательно, также ряд Тейлора) равен 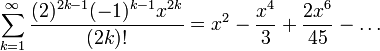 Это глобально сходящийся степенной ряд. |
Персоны
У нас есть следующие важные личности, связанные с  :
:
График
Вот график на интервале ![[-2\pi,2\pi]](/800/600/https/calculus.subwiki.org/w/images/math/f/c/d/fcd3f9b324e7bfa715240a4c3fb40b9a.png) , нарисованный в масштабе:
, нарисованный в масштабе:

Вот крупным планом график между 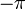 и
и 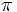 . Пунктирная горизонтальная линия показывает среднее значение
. Пунктирная горизонтальная линия показывает среднее значение 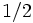 :
:
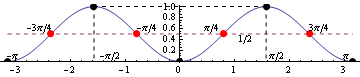
Красные пунктирные точки указывают точки перегиба, а черные пунктирные точки указывают локальные экстремальные значения.
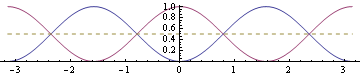
Вот изображение, показывающее функцию (синяя) и функцию квадрата косинуса (фиолетовая) с пунктирной линией 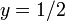 . На рисунке показано, что
. На рисунке показано, что 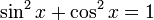 :
:
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного угла косинуса
У нас есть:
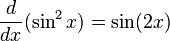
Мы можем сделать это двумя способами.
Используя цепное правило для дифференциации, мы имеем:
![\! \frac{d}{dx}[(\sin x)^2] = 2\sin x \frac{d}{dx} (\sin x) = 2\sin x \cos x](/800/600/https/calculus.subwiki.org/w/images/math/2/b/2/2b2cc43fe01f388596699dd016369c93.png)
По формуле синусоидального угла это то же самое, что и 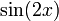 .
.
В качестве альтернативы, используя формулу косинуса двойного угла, мы переписываем:
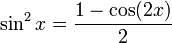
В отличии мы получаем:
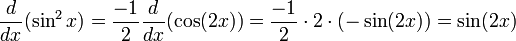
Вторая производная
Снова дифференцируя производную, получаем:
![\frac{d^2}{dx^2}(\sin^2x) = \frac{d}{dx}[\sin(2x)] = \frac{d}{d(2x)}[\sin(2x)]\frac{d(2x)}{dx} = 2\cos(2x)](/800/600/https/calculus.subwiki.org/w/images/math/d/e/e/deec58ad406891f9ceb48cb74697b6ca.png)
График функции с производной
Заполните это позже
точек и интервалов интереса
Критические очки
Рассмотрим 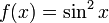 .Как было вычислено ранее, мы имеем:
.Как было вычислено ранее, мы имеем:
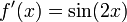
Это равно нулю точно в точках 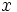 , где
, где 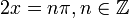 , то есть
, то есть 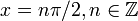 . Другими словами, критические точки встречаются при целых числах, кратных
. Другими словами, критические точки встречаются при целых числах, кратных 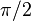 .
.
Интервалы увеличения и уменьшения
Функция 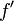 положительна для
положительна для 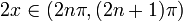 с
с  и отрицательна для
и отрицательна для 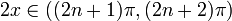 с
с  . Разделив на 2, получим:
. Разделив на 2, получим:
Местные экстремальные значения
Из информации о интервалах увеличения и уменьшения мы заключаем, что:
Интервалы вогнутой вверх и вогнутой вниз
Вторая производная 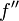 — это функция
— это функция 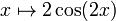 .Это положительно для
.Это положительно для  и отрицательно для
и отрицательно для 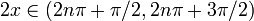 , где
, где  . Таким образом, мы получаем:
. Таким образом, мы получаем:
точек перегиба
Из определения интервалов, когда  является вогнутой вверх и вогнутой вниз, мы обнаруживаем, что точки перегиба — это точки с
является вогнутой вверх и вогнутой вниз, мы обнаруживаем, что точки перегиба — это точки с 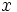 -координатом, нечетным кратным
-координатом, нечетным кратным 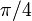 Значение функции во всех этих точках равно
Значение функции во всех этих точках равно 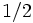 .
.
- В точках с
 функция переходит от вогнутой вверх (слева) к вогнутой вниз (справа).
функция переходит от вогнутой вверх (слева) к вогнутой вниз (справа). - В точках с
 функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интеграция
Первый антидериватив
ЧТО МЫ ИСПОЛЬЗУЕМ : формула двойного угла косинуса, рекурсивный вариант интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
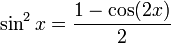
Теперь мы можем сделать интеграцию:

Чтобы интегрировать 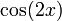 , мы используем метод интегрирования линейного преобразования функции, чтобы получить
, мы используем метод интегрирования линейного преобразования функции, чтобы получить 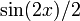 .Подключив это, мы получаем:
.Подключив это, мы получаем:
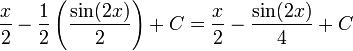
Использование интеграции по частям
Мы переписываем 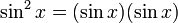 и используем интеграцию по частям в его рекурсивной версии:
и используем интеграцию по частям в его рекурсивной версии:
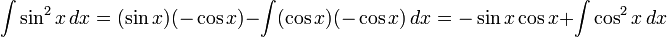
Теперь мы переписываем  и получаем:
и получаем:
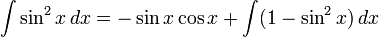
Если установить  как выбор антидериватива, так что вышеупомянутое выполняется без каких-либо свободно плавающих констант, мы получим:
как выбор антидериватива, так что вышеупомянутое выполняется без каких-либо свободно плавающих констант, мы получим:

Переставляя, получаем:
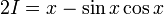
Это дает:
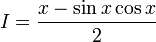
Итак, общее антидеривативное выражение:
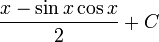
Используя формулу двойного угла синуса 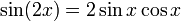 , мы можем убедиться, что это соответствует предыдущему ответу.
, мы можем убедиться, что это соответствует предыдущему ответу.
Для заданной непрерывной функции на связном множестве антипроизводные, полученные разными методами, должны отличаться на константу . В некоторых случаях антипроизводные могут быть в точности равны, но это , вообще не обязательно .
См нулевой производной подразумевает локально постоянную
График функции с антидеривативным
На рисунке ниже мы изображаем  (синий) и функцию
(синий) и функцию 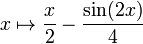 (фиолетовый). Это уникальный анти-производный, который принимает значение 0 в 0.Другие антипроизводные могут быть получены путем вертикального смещения фиолетового графика:
(фиолетовый). Это уникальный анти-производный, который принимает значение 0 в 0.Другие антипроизводные могут быть получены путем вертикального смещения фиолетового графика:
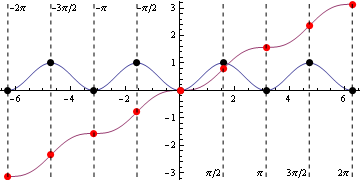
Черные точки соответствуют локальным крайним значениям для  , а красные точки соответствуют точкам перегиба для антипроизводных. Как и следовало ожидать, каждая черная точка находится в той же вертикальной линии, что и красная точка, поскольку точки перегиба для антидериватива соответствуют локальным экстремальным значениям для исходной функции. Дальше:
, а красные точки соответствуют точкам перегиба для антипроизводных. Как и следовало ожидать, каждая черная точка находится в той же вертикальной линии, что и красная точка, поскольку точки перегиба для антидериватива соответствуют локальным экстремальным значениям для исходной функции. Дальше:
Определенные интегралы
Часть 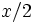 в антидеривативе означает, что линейная часть антипроизводного
в антидеривативе означает, что линейная часть антипроизводного  имеет наклон
имеет наклон 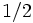 , и это связано с тем фактом, что
, и это связано с тем фактом, что  имеет среднее значение
имеет среднее значение 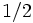 на любом интервале длины, равном периоду.Фактически ясно, что функция является синусоидальной функцией около
на любом интервале длины, равном периоду.Фактически ясно, что функция является синусоидальной функцией около 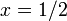 .
.
Таким образом, имеем:
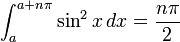
, где 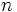 — целое число.
— целое число.
Среднее значение для  за интервал длины, кратный периоду, составляет
за интервал длины, кратный периоду, составляет 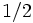 . Таким образом, для очень больших интервалов среднее значение
. Таким образом, для очень больших интервалов среднее значение  очень близко к 1/2, даже если оно не должно быть точно 1/2. В частности:
очень близко к 1/2, даже если оно не должно быть точно 1/2. В частности:
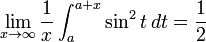
Преобразованные версии
На основе интегрирования  мы также можем интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:
мы также можем интегрировать квадрат любой синусоидальной функции, используя интегрирование линейного преобразования функции:

Таким образом, мы видим, что среднее значение этой функции также составляет 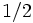 для любого интервала длины, кратного периоду
для любого интервала длины, кратного периоду  .Кроме того, в течение достаточно длительного интервала среднее значение близко к 1/2:
.Кроме того, в течение достаточно длительного интервала среднее значение близко к 1/2:
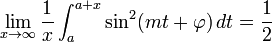
Высшее антипроизводное
Антидифференцировать  можно более одного раза. Антипроизводное
можно более одного раза. Антипроизводное  представляет собой сумму полинома степени
представляет собой сумму полинома степени 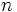 и тригонометрической функции с периодом
и тригонометрической функции с периодом 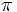 .
.
Силовая серия и серия Тейлор
Вычисление степенных рядов
Мы можем использовать личность:
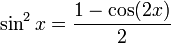
вместе с степенным рядом для функции косинуса, чтобы найти степенной ряд для  .
.
Степенной ряд для функции косинуса сходится к функции везде и имеет вид:

Силовая серия для 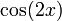 это:
это:
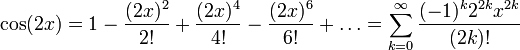
Силовая серия для 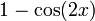 это:
это:

Разделив на 2, мы получим степенной ряд за 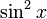 :
:

Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
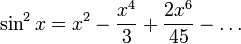
полиномов Тейлора как приближения
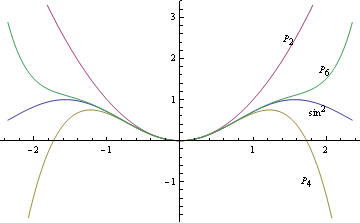
Обратите внимание, что, поскольку  является четной функцией, все ее полиномы Тейлора также являются четными полиномами.На рисунке ниже мы рассматриваем графики
является четной функцией, все ее полиномы Тейлора также являются четными полиномами.На рисунке ниже мы рассматриваем графики  и его второго, четвертого и шестого приближений Тейлора.
и его второго, четвертого и шестого приближений Тейлора.
Предельные вычисления
Ноль порядка
Из степенных рядов получаем следующий предел:
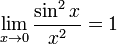
Таким образом, порядок нуля  в нуле равен 2, а остаток равен 1.
в нуле равен 2, а остаток равен 1.
Этот предел может быть рассчитан многими способами:
Пределы высшего порядка
У нас есть предел:
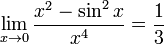
Этот предел может быть рассчитан многими способами:
,диагоналей, отношений и свойств квадрата
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Класс 11 бизнес-дисциплин Syllabus
- Класс 11 Экономика Syllabus
- Класс 12 Бухгалтерский учебный план
- класс 12 бизнес-исследований S
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы по CBSE 8 класса
- Дополнительные вопросы по CBSE 8 по естествознанию
- CBSE 9 Дополнительные вопросы по математике
- CBSE 9 по дополнительным вопросам по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8

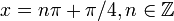 функция переходит от вогнутой вверх (слева) к вогнутой вниз (справа).
функция переходит от вогнутой вверх (слева) к вогнутой вниз (справа).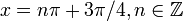 функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).