Найти объем фигуры ограниченной линиями онлайн – Объем тела вращения | Онлайн калькулятор

∫∫∫ Тройной интеграл — Калькулятор Он-лайн

Введите подинтегральную функцию, для которой необходимо вычислить тройной интеграл

Найдём решение тройного интеграла от функции f(x, y, z)

Введите вверхние и нижние пределы для области интегрирования и подинтегральную функцию для тройного интеграла.
Если подинтегральной функции нету, то укажите 1

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

e

e число, которое примерно равно 2.7

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

pi

Число — «Пи», которое примерно равно 3.14

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7.5, не 7,5

2*x

— умножение

3/x

— деление

x^3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

www.kontrolnaya-rabota.ru

Объем тела вращения — 9 Октября 2015 — Примеры решений задач

Вычисление объема тела вращения вокруг оси Ох

Пусть график функции y = f(x) вращается вокруг оси Ox, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями x = a, x = b.

Объем тела вращения, образованного вращением графика y=f(x) вокруг оси Ox, может быть вычислен по формуле

Пример 1. Вычислить объем тела, образованного вращением дуги кривой y=x², x∈[1,3] вокруг оси Оx.

Решение. Данные a=1, b=3,  f(x)=x², подставляем в формулу, получаем

С помощью калькулятора проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

 

Вычисление объема тела вращения вокруг оси Оy

Пусть график функции x=φ(y) вращается вокруг оси Oy, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями y = c, y = d.

Объем тела вращения, образованного вращением графика x=φ(y) вокруг оси Oy, может быть вычислен по формуле

Пример 2. Вычислить объем тела, образованного вращением дуги кривой x=3y-y², x∈[1,2] вокруг оси Оx.

Решение. Данные c=1, d=2,  φ(y)=3y-y², подставляем в формулу, получаем

В калькулятор вставляем функцию x=3y-y²,  x меняем на y, границы  от 1 до 2, проверяем правильность вычисления объема , а также получаем рисунок тела вращения.

Следующая тема: Вычислить длину кривой

 

www.reshim.su

вычислить объем тела вращения онлайн калькулятор

Расчет площади и объема геометрических фигур

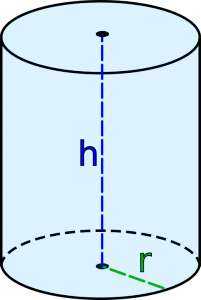
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон. Другое определение: цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.

объем цилиндра формула

Если вы хотите знать, как вычислить объем цилиндра,то все, что вам нужно сделать — найти высоту (h) и радиус (r) и и подставить их в формулу:

Если внимательно посмотреть на эту формулу, то можно заметить, что {\pi r^2} — это формула площади круга, а в нашем случае — площадь основания.

Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Произвести расчет объема цилиндра вам поможет наш калькулятор онлайн. Просто введите указанные параметры цилиндра и получите его объем.

Ваша оценка

[Оценок: 168 Средняя: 3.4]

Объем цилиндра Автор mnogof средний рейтинг 3.4/5 — 168 рейтинги пользователей

Просмотров страницы: 45 055

Объем цилиндра формула (через радиус основания и высоту)

{V=\pi r^2 h}, где

r — радиус основания цилиндра,

h — высота цилиндра

Объем цилиндра формула (через площадь основания и высоту)

{V=S h}, где

S — площадь основания цилиндра,

h — высота цилиндра

Объем цилиндра калькулятор онлайн

Как найти объём тела вращения с помощью интеграла

С помощью определённого интеграла можно вычислять не только площади плоских фигур, но и объёмы тел, образованных вращением этих фигур вокруг осей координат.

Тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y= f(x), имеет объём

.

(1)

Аналогично объём v тела, полученного вращением вокруг оси ординат (Oy) криволинейной трапеции выражается формулой

. (2)

При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.

Пример 1.

Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, ограниченной гиперболой , осью абсцисс и прямыми , .

Решение. Объём тела вращения найдём по формуле (1), в которой , а пределы интегрирования a = 1, b = 4:

Пример 2.

Найти объём шара радиуса R.

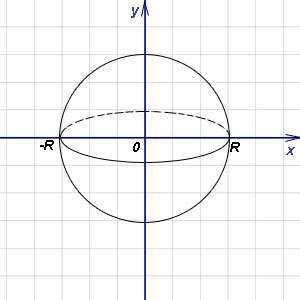
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция запишется в виде , а пределами интегрирования служат -R и R. Следовательно,

Нет времени вникать в решение?

Можно заказать работу!

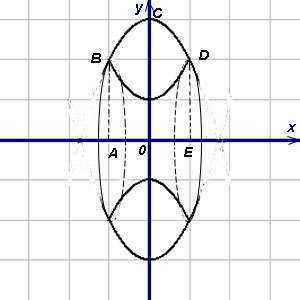
Пример 3. Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, заключённой между параболами и .

Решение.

Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси абсцисс криволинейных трапеций ABCDE и ABFDE. Объёмы этих тел найдём по формуле (1), в которой пределы интегрирования равны и — абсциссам точек B и D пересечения парабол. Теперь можем найти объём тела:

Пример 4.

Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга ().

Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис.

Формулы площадей и объёмов геометрических фигур

20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD

Используя разность объёмов тел, получаем для объёма тора v выражение

Пример 5.

Найти объём тела, образованного вращением вокруг оси ординат (Oy) фигуры, ограниченной линиями и .

Решение.

Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси ординат треугольника OBA и криволинейной трапеции OnBA.

Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат и — ординаты точек O и B пересечения параболы и прямой.

Таким образом, получаем объём тела:

К началу страницы

Пройти тест по теме Интеграл

Начало темы «Интеграл»

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Метод замены переменной в неопределённом интеграле

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Интегрирование дробей

Интегрирование рациональных функций и метод неопределённых коэффициентов

Интегрирование некоторых иррациональных функций

Интегрирование тригонометрических функций

Определённый интеграл

Площадь плоской фигуры с помощью интеграла

Несобственные интегралы

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

Лучшая кроватка в математике. Качественный. Ничего лишнего.

Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объем тела или емкости судна определяется его формой и линейными размерами.

Объем куба

Объем куба равна кубу длины ее лица.

Формула Куб

где — объем куба,
— длина куба.

Область призмы

Область призмы равна произведению поверхности дна призмы на высоту.

Формула объема призмы

где — степень призмы,

так

— основание призмы,

час

— высота призмы.

Объем паралелепипедов

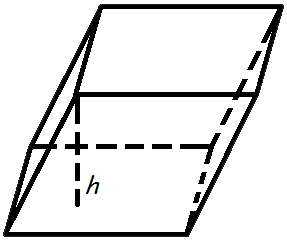
Объем паралелепипедов равна произведению поверхности основания относительно высоты.

Объем формулы паралелепипеда

где — объем паралелепипедов,

так

— базовая площадь,

час

— высота высота.

Объем прямоугольного параллелепипеда

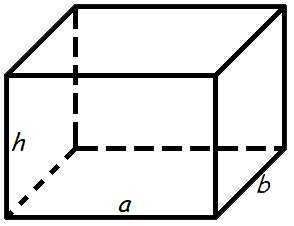
Объем прямоугольного параллелепипеда это то же самое, что и произведение его длины, ширины и высоты.

Формула для объема прямоугольного параллелепипеда

где — объем прямоугольного параллелепипеда,
— длина,

б

— ширина

час

— высота.

Объем пирамиды

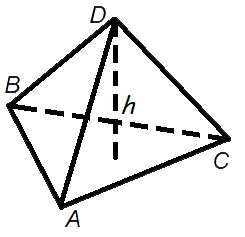
Объем пирамиды составляет одну треть продукта в базовой области по высоте.

Формула объема пирамиды

где — объем пирамиды,

так

— основание основания пирамиды,

час

— длина пирамиды.

Объем правильного тетраэдра

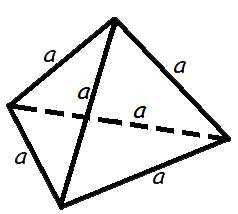
Формула для объема правильного тетраэдра

vipstylelife.ru

Как вычислить объем тела вращения?

Объем тела вращения можно вычислить по формуле:

В формуле перед интегралом обязательно присутствует число . Так повелось – всё, что в жизни крутится, связано с этой константой.

Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.

Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболысверху. Это и есть та функция, которая подразумевается в формуле.

В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:, таким образоминтеграл всегда неотрицателен, что весьма логично.

Вычислим объем тела вращения, используя данную формулу:

Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.

Ответ: 

В ответе нужно обязательно указать размерность – кубические единицы . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубическиеединицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.

Пример 2

Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями,,

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Рассмотрим две более сложные задачи, которые тоже часто встречаются на практике.

Пример 3

Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями ,,и

Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями ,,,, не забывая при этом, что уравнениезадает ось:

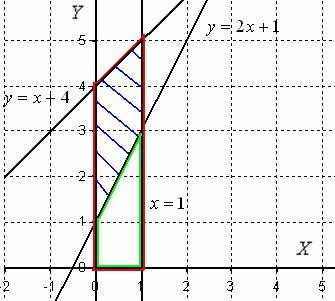
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами.

Объем тела вращения вычислим как 

разность объемов тел.

Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси получается усеченный конус. Обозначим объем этого усеченного конуса через.

Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через.

И, очевидно, разность объемов – в точности объем нашего «бублика».

Используем стандартную формулу для нахождения объема тела вращения: 

1) Фигура, обведенная красным цветом ограничена сверху прямой , поэтому:

2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:

3) Объем искомого тела вращения: 

Ответ: 

Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.

Само решение чаще оформляют короче, примерно в таком духе:

Теперь немного отдохнем, и расскажу о геометрических иллюзиях.

У людей часто возникают иллюзии, связанная с объемами, которую подметил еще Перельман (другой) в книге Занимательная геометрия. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составляет чуть более 50 кубических единиц, что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.

Вообще, система образования в СССР действительно была самой лучшей. Та же книга Перельмана, изданная ещё в 1950 году, очень хорошо развивает, как сказал юморист, соображаловку и учит искать оригинальные нестандартные решения проблем. Недавно с большим интересом перечитал некоторые главы, рекомендую, доступно даже для гуманитариев. Нет, не нужно улыбаться, что я предложил беспонтовое времяпровождение, эрудиция и широкий кругозор в общении – отличная штука.

После лирического отступления как раз уместно решить творческое задание:

Пример 4

Вычислить объем тела, образованного вращением относительно оси плоской фигуры, ограниченной линиями,, где.

Это пример для самостоятельного решения. Обратите внимание, что все дела происходят в полосе , иными словами, фактически даны готовые пределы интегрирования.  Правильно начертите графики тригонометрических функций, напомню материал урока огеометрических преобразованиях графиков: если аргумент делится на два: , то графики растягиваются по осив два раза. Желательно найти хотя бы 3-4 точкипо тригонометрическим таблицам, чтобы точнее выполнить чертеж. Полное решение и ответ в конце урока. Кстати, задание можно решить рационально и не очень рационально.

studfiles.net

Как найти объём тела вращения с помощью интеграла

С помощью определённого интеграла можно вычислять не только площади плоских фигур, но и объёмы тел, образованных вращением этих фигур вокруг осей координат.

Тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y = f(x), имеет объём

. (1)

Примеры таких тел — на рисунке ниже.

Аналогично объём v тела, полученного вращением вокруг оси ординат (Oy) криволинейной трапеции выражается формулой

. (2)

При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.

Пример 2. Найти объём шара радиуса R.

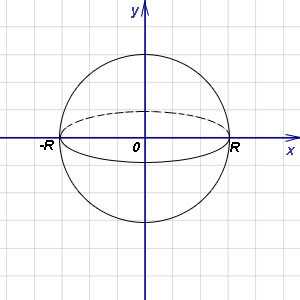
Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция запишется в виде , а пределами интегрирования служат —R и R. Следовательно,

Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD

 

Используя разность объёмов тел, получаем для объёма тора v выражение

Начало темы «Интеграл»

function-x.ru

Вычислить площадь фигуры ПРИМЕРЫ

Вычислить площадь фигуры, ограниченной линиями .

Решение.

Находим точки пересечения заданных линий. Для этого решаем систему уравнений:

Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:

    или    .

Находим: x₁ = -2, x₂ = 4.

Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).

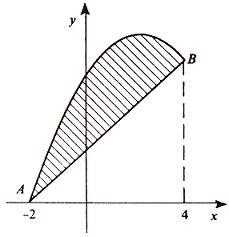
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:

По формуле Ньютона-Лейбница находим:

Найти площадь области, ограниченной эллипсом .

Решение.

Из уравнения эллипса для I квадранта имеем . Отсюда по формуле получаем

Применим подстановку x = a sin t, dx = a cos t dt. Новые пределы интегрирования t = α и t = β определяются из уравнений 0 = a sin t, a = a sin t. Можно положить α = 0 и β = π/2.

Находим одну четвертую искомой площади

Отсюда S = πab.

Найти площадь фигуры, ограниченной линиями y = —x² + x + 4 и y = —x + 1.

Решение.

Найдем точки пересечения линий y = —x² + x + 4, y = —x + 1, приравнивая ординаты линий: —x² + x + 4 = —x + 1 или x² — 2x — 3 = 0. Находим корни x₁ = -1, x₂ = 3 и соответствующие им ординаты y₁ = 2, y₂ = -2.

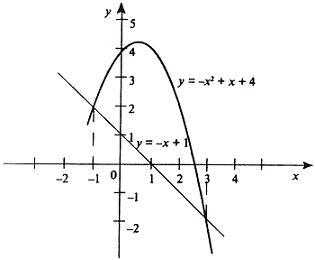
По формуле площади фигуры получаем

Определить площадь, ограниченную параболой y = x² + 1 и прямой x + y = 3.

Решение.

Решая систему уравнений

находим абсциссы точек пересечения x₁ = -2 и x₂ = 1.

Полагая y₂ = 3 — x и y₁ = x² + 1, на основании формулы получаем

Вычислить площадь, заключенную внутри лемнискаты Бернулли r² = a²cos 2φ.

Решение.

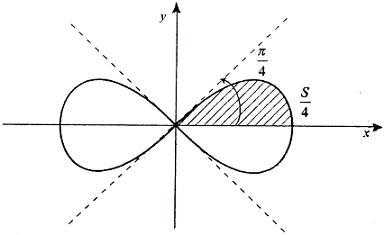
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ₁ = ʅ и φ₂ = ʆ, выразится интегралом

В силу симметрии кривой определяем сначала одну четвертую искомой площади

Следовательно, вся площадь равна S = a².

Вычислить длину дуги астроиды x^2/3 + y^2/3 = a^2/3.

Решение.

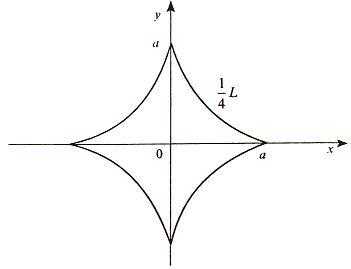
Запишем уравнение астроиды в виде

(x^1/3)² + (y^1/3)² = (a^1/3)².

Положим x^1/3 = a^1/3cos t, y^1/3 = a^1/3sin t.

Отсюда получаем параметрические уравнения астроиды

x = a cos³t,     y = a sin³t,     (*)

где 0 ≤ t ≤ 2π.

Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π/2.

Получаем

dx = -3a cos²t sin t dt,     dy = 3a sin²t cos t dt.

Отсюда находим

Интегрируя полученное выражение в пределах от 0 до π/2, получаем

Отсюда L = 6a.

Найти площадь, ограниченную спиралью Архимеда r = aφ и двумя радиусами-векторами, которые соответствуют полярным углам φ₁и φ₂ (φ₁ < φ₂).

Решение.

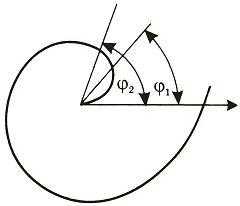
Площадь, ограниченная кривой r = f(φ) вычисляется по формуле , где α и β — пределы изменения полярного угла.

Таким образом, получаем

     (*)

Из (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ₁ = 0; φ₂ = 2π):

Аналогичным образом находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда (φ₁ = 2π; φ₂ = 4π):

Искомая площадь равна разности этих площадей

Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x² и x = y².

Решение.

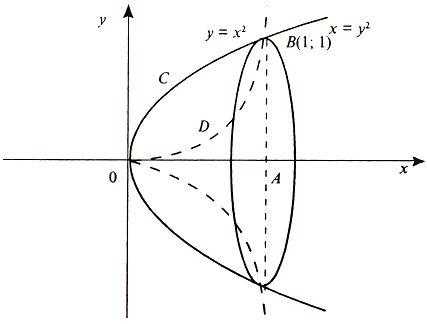
Решим систему уравнений

и получим x₁ = 0, x₂ = 1, y₁ = 0, y₂ = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:

Вычислить площадь, ограниченную осью Ox и синусоидой y = sin x на отрезках: а) [0, π]; б) [0, 2π].

Решение.

а) На отрезке [0, π] функция sin x сохраняет знак, и поэтому по формуле , полагая y = sin x, находим

б) На отрезке [0, 2π], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2π] разделить на два [0, π] и [π, 2π], в каждом из которых функция сохраняет знак.

По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус.

В итоге, искомая площадь равна

Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг большой оси a.

Решение.

Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Oxплощади OAB, равной одной четверти площади эллипса, и полученный результат удвоить.

Обозначим объем тела вращения через V_x; тогда на основании формулы имеем , где 0 и a — абсциссы точек B и A. Из уравнения эллипса находим . Отсюда

Таким образом, искомый объем равен . (При вращении эллипса вокруг малой оси b, объем тела равен )

Найти площадь, ограниченную параболами y² = 2px и x² = 2py.

Решение.

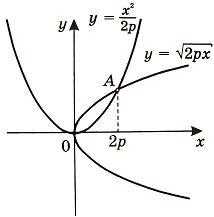
Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем и . Приравнивая эти значения, получим или x⁴ — 8p³x = 0.

Отсюда

x⁴ — 8p³x = x(x³ — 8p³) = x(x — 2p)(x² + 2px + 4p²) = 0.

Находим корни уравнений:

Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2p.

Искомую площадь находим по формуле

studfiles.net

Найти площадь фигуры ограниченной кривыми онлайн

Как найти площадь фигуры ограниченной линиями онлайн

Предлагаем Вашему вниманию онлайн калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор находит площадь криволинейной трапеции.

1). Как найти площадь криволинейной трапеции онлайн.

Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x)≥0], прямыми x=a, x=b и отрезком [a,b] оси Ox находим по формуле

Пример. Найти площадь криволинейной трапеции ограниченной кривой y=2x^2+1 и прямыми x=1,x=2.

Решение. Вставляем в калькулятор функции в виде y=2x^2+1,x=1,x=2, нажимаем «Ok», получаем ответ.

2). Как найти площадь фигуры ограниченной линиями онлайн
Площадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x)  [f₁(x) ≤  f₂(x)] и прямыми x=a, x=b вычисляется по формуле  y=f₁(x) и y=f₂(x)  [f₁(x) ≤  f₂(x)] и прямыми x=a, x=b вычисляется по формуле

 

 

Пример. Найти площадь фигуры ограниченной линиями y=4x-x^2, y=4-x

Решение. Вставляем функции y=4x-x^2, y=4-x в калькулятор, нажимаем «Ok», получаем ответ.

27,454 просмотров всего, 49 просмотров сегодня

otvet-prost.ru

No related posts.