Онлайн решить показательные уравнения – Решения показательных уравнений | Онлайн калькулятор

Решение показательных уравнений онлайн с подробным решением

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Степенные или показательные уравнения называют уравнения, в которых переменные находятся в степенях, а основанием является число. Например:

\[10^2=36\]

Решение показательного уравнения сводится к 2 довольно простым действиям:

1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания неодинаковые, ищем варианты для решения данного примера.

2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.

Так же читайте нашу статью «Решить функцию уравнение онлайн решателем»

Допустим, дано показательное уравнение следующего вида:

\[2^{2x+4} — 10 \cdot 4^x = 2^4\]

Начинать решение данного уравнения стоит с анализа основания. Основаниея разные — 2 и 4, а для решения нам нужно, чтобы были одинаковые, поэтому преобразуем 4 по такой формуле -\[ (a^n)^m = a^{nm}:\]

\[4^x = (2^2)^x = 2^{2x}\]

Далее для преобразования используем формулу \[a^n \cdot a^m = a ^{n+m}:\]

\[2^{2x+4} = 2^{2x} \cdot 2^4\]

Прибавляем к исходному уравнению:

\[2^{2x} (2^4 — 10) = 24\]

Вынесем за скобки \[2^{2x}:\]

\[2^{2x}(2^4-10)=24\]

\[2^4 — 10 = 16 — 10 = 6\]

\[6 \cdot 2^{2x} = 24\]

\[2^{2x} = 4\]

Выразим \[4 = 2^2:\]

\[2^{2x} = 2^2\]

Поскольку степени одинаковые, отбрасываем их:

\[2x = 2\]

\[x = 1\]

Ответ: \[x = 1.\]

Где можно решить показательное уравнение онлайн решателем?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Калькулятор онлайн — Решение показательных уравнений. Описание

Знак умножения нужно вводить только между числами, во всех остальных случаях его можно не вводить.

При решении этой задачи используется большой и дорогой модуль одного «забугорного» сервиса. Решение он выдает в виде изображения и только на английском языке. Изменить это, к сожалению, нельзя. Ничего лучше мы найти не смогли. Зато он выводит подробное и очень качественное решение в том виде в котором оно принято в высших учебных заведениях. Единственное неудобство — на английском языке, но это не большая цена за качество.

Если вам что-то осталось не понятно обязательно напишите об этом в Обранной связи и мы дополним эту таблицу.

Функция	Описание	Пример ввода	Результат ввода
pi	Число \(\pi\)	pi	$$ \pi $$
e	Число \(e\)	e	$$ e $$
e^x	Степень числа \(e\)	e^(2x)	$$ e^{2x} $$
exp(x)	Степень числа \(e\)	exp(1/3)	$$ \sqrt[3]{e} $$
|x| abs(x)	Модуль (абсолютное значение) числа \(x\)	|x-1| abs(cos(x))	\( |x-1| \) \( |\cos(x)| \)
sin(x)	Синус	sin(x-1)	$$ sin(x-1) $$
cos(x)	Косинус	1/(cos(x))^2	$$ \frac{1}{cos^2(x)} $$
tg(x)	Тангенс	x*tg(x)	$$ x \cdot tg(x) $$
ctg(x)	Котангенс	3ctg(1/x)	$$ 3 ctg \left( \frac{1}{x} \right) $$
arcsin(x)	Арксинус	arcsin(x)	$$ arcsin(x) $$
arccos(x)	Арккосинус	arccos(x)	$$ arccos(x) $$
arctg(x)	Арктангенс	arctg(x)	$$ arctg(x) $$
arcctg(x)	Арккотангенс	arcctg(x)	$$ arcctg(x) $$
sqrt(x)	Квадратный корень	sqrt(1/x)	$$ \sqrt{\frac{1}{x}} $$
x^(1/n)	Корень произвольной числовой целой степени >= 2 x^(1/2) эквивалентно sqrt(x)	(cos(x))^(1/3)	$$ \sqrt[\Large 3 \normalsize]{cos(x)} $$
ln(x)	Натуральный логарифм (основание — число e)	1/ln(3-x)	$$ \frac{1}{ln(3-x)} $$
log(a,x)	Логарифм x по основанию a	log(3,cos(x))	$$ log_3(cos(x)) $$
sh(x)	Гиперболический синус	sh(x-1)	$$ sh(x-1) $$
ch(x)	Гиперболический косинус	ch(x)	$$ ch(x) $$
th(x)	Гиперболический тангенс	th(x)	$$ th(x) $$
cth(x)	Гиперболический котангенс	cth(x)	$$ cth(x) $$
Вывод	Перевод, пояснение
Solve for x over the real numbers	Решить относительно х в действительных числах (бывают ещё комплексные)
Multiply both sides by …	Умножаем обе части на …
Equate exponents of … on both sides	Приравниваем степени … в обоих частях (с обоих сторон)
Simplify and substitute …	Упрощаем и делаем подстановку …
Bring … together using the commom denominator …	Приводим … к общему знаменателю …
The left hand side factors into a product with two terms	Левая часть разбивается на множители как два многочлена
Split into two equations	Разделяем на два уравнения
Take the square root of both sides	Извлекаем квадратный корень из обоих частей
Subtract … from both sides	Вычитаем … из обеих частей уравнения
Add … to both sides	Прибавляем … к обоим частям уравнения
Multiply both sides by …	Умножаем обе части уравнения на …
Divide both sides by …	Делим обе части уравнения на …
Substitute back for …	Обратная подстановка для …
… has no solution since for all …	… не имеет решения для всех …
Simplify the expression	Упрощаем выражение
Answer	Ответ
\(log(x)\)	Натуральный логарифм, основание — число e. У нас пишут \(ln(x)\)
\(arccos(x)\) или \(cos^{-1}(x)\)	Арккосинус. У нас пишут \( arccos(x) \)
\(arcsin(x)\) или \(sin^{-1}(x)\)	Арксинус. У нас пишут \( arcsin(x) \)
\(tan(x)\)	Тангенс. У нас пишут \(tg(x) = \frac{sin(x)}{cos(x)}\)
\(arctan(x)\) или \(tan^{-1}(x)\)	Арктангенс. У нас пишут \(arctg(x)\)
\(cot(x)\)	Котангенс. У нас пишут \(ctg(x) = \frac{cos(x)}{sin(x)}\)
\(arccot(x)\) или \(cot^{-1}(x)\)	Арккотангенс. У нас пишут \(arcctg(x)\)
\(sec(x)\)	Секанс. У нас пишут также \(sec(x) = \frac{1}{cos(x)}\)
\(csc(x)\)	Косеканс. У нас пишут \(cosec(x) = \frac{1}{sin(x)}\)
\(cosh(x)\)	Гиперболический косинус. У нас пишут \(ch(x) = \frac{e^x+e^{-x}}{2} \)
\(sinh(x)\)	Гиперболический синус. У нас пишут \(sh(x) = \frac{e^x-e^{-x}}{2} \)
\(tanh(x)\)	Гиперболический тангенс. У нас пишут \(th(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \)
\(coth(x)\)	Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \)

www.math-solution.ru

Решение показательных неравенств онлайн · Как пользоваться Контрольная Работа РУ

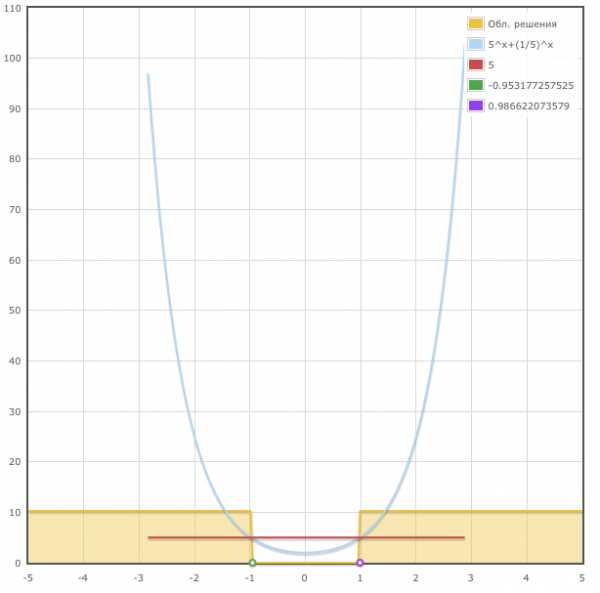
Решим показательное неравенство 5^x + (1/5)^x > 5 с помощью онлайн сервиса, который находится по ссылке

>>решение неравенств онлайн <<

Введём указанное неравенство в данный калькулятор:

Вы получите следующее подробное решение для неравенства:

Дано неравенство: $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ Решаем:
Дано уравнение: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ или $$5^{x} + \left(\frac{1}{5}\right)^{x} — 5 = 0$$ Сделаем замену $$v = \left(\frac{1}{5}\right)^{x}$$ получим $$v — 5 + \frac{1}{v} = 0$$ или $$v — 5 + \frac{1}{v} = 0$$ делаем обратную замену $$\left(\frac{1}{5}\right)^{x} = v$$ или $$x = — \frac{\log{\left (v \right )}}{\log{\left (5 \right )}}$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ Данные корни $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{2}$$ Возьмём например точку $$x_{0} = x_{2} — 1$$ =

             /      ____\    
-log(2) + log\5 - \/ 21 /    
------------------------- - 1
            1                
         log (5)             

= $$-1 + \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ подставляем в выражение $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$

              /      ____\                       /      ____\        
 -log(2) + log\5 - \/ 21 /          -log(2) + log\5 - \/ 21 /        
 ------------------------- - 1    - ------------------------- + 1    
             1                                  1                    
          log (5)                            log (5)                 
5                              + 5                                > 5


                   /      ____\                     /      ____\    
      -log(2) + log\5 - \/ 21 /        -log(2) + log\5 - \/ 21 /    
 -1 + -------------------------    1 - ------------------------- > 5
                log(5)                           log(5)             
5                               + 5                                 

значит одно из решений нашего неравенства будет при:
$$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$

 _____           _____          
      \         /
-------ο-------ο-------
       x2      x1

Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ: $$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x > \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$

Также вы будете иметь графическое решение показательного неравенства:

www.kontrolnaya-rabota.ru

Решение уравнений онлайн

Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Math34.biz поможет решить любое уравнение онлайн. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн. Пошаговое решение уравнений онлайн на сайте Math34.biz. Уравнения онлайн. Решить уравнение онлайн на сайте Math34.biz

math24.biz

Показательные уравнения, формулы и примеры

Простейшие показательные уравнения

   

В зависимости от знака такое уравнение имеет различное количество корней:

1. если , то уравнение (1) решений не имеет, то есть

      

2. если , то

      

Уравнения вида

1. Если .
2. Если .

Уравнения вида

   

Уравнения такого типа равносильны уравнению

   

Уравнения вида

1. Если , то обе части такого уравнения равны для любых .
2. Если , то уравнение эквивалентно уравнению .
3. В случае, если , то уравнение эквивалентно системе

Решение показательных уравнений сведением к общему основанию

Если левая и правая части заданного показательного уравнения содержат только произведения, частные, корни или степени, то рациональнее при помощи основных формул для степеней привести обе части равенства к одному основанию, то есть к уравнению вида (2).

Решение показательных уравнений вынесением общего множителя

Если показательное уравнение содержит выражение вида , причем показатели степени отличаются только свободным коэффициентом, то для решения необходимо вынести за скобки наименьшую степень .

Приведение показательных уравнений к квадратным

К показательным уравнениям, которые можно привести к квадратным, относятся следующие уравнения.

   

где — некоторые числа, .

В этом случае выполняется замена

   

   

где — некоторые ненулевые числа, причем , — произвольное действительное число. Для сведения к квадратному обе части уравнения необходимо умножить на :

   

Далее заменой получаем квадратное уравнение

   

Однородные показательные уравнения

Делением обеих его частей на (или ), сводим уравнение к показательному вида :

   

Схема решения таких уравнений следующая:

1) Делим обе части уравнения или на , или на , в результате получаем:

   

или

;

2) заменой последнее уравнение сводится к квадратному:

   

ru.solverbook.com

Методы решения показательных уравнений

Разделы: Математика

---

Методы решения показательных уравнений

1. Простейшие показательные уравнения

Примеры.

Пример 1. Решите уравнение: 3^4x-5 = 3^x+4

.

Решение.

3^4x-5 = 3^x+4 <=> 4x 5 = x+4 <=> 3x=9<=> x = 3 .

Ответ:3

Пример 2. Решите уравнение: 2^x-4 = 3 .

Решение.

2^x-4 = 3 <=> x- 4 = x = + 4 <=> x = + <=> x = .

Ответ:.

Пример 3. Решите уравнение:^-3x = -7 .

Решение.

^-3x = -7 , решений нет, так как ^-3x > 0 для x R .

Ответ: ^.

2. Методы преобразования показательных уравнений к простейшим.

A. Метод уравнивания оснований.

Примеры.

Пример 1. Решите уравнение: 27- = 0 .

Решение.

27- = 0 <=> 3³3^4x-9— (3²)^x+1 = 0 <=> 3^{3+ (4x-9)}— 3^2(x+1) = 0<=> 3^4x-6-3^2x+2 = 0 <=> 3^4x-6 = 3^2x+2<=> 4x-6=2x+2 <=> 2x = 8 <=> x=4.

Ответ: 4.

Пример 2. Решите уравнение: .

Решение.

0 <=> (2²)^x3^x5^x = 60^4x-15 <=> 4^x3^x5^x = 60^4x-15 <=> (4^x = 60^4x-15 <=> 60^x=60^4x-15 <=> <=>x=4x-15 <=> 3x=15 <=> x=5.

Ответ: 5.

В. Уравнения, решаемые разложением на множители.

Примеры.

Пример 1. Решите уравнение: x2^x = 22^x + 8x-16.

Решение.

x2^x = 22^x + 8x-16 <=> x2^x — 22^x = 8x-2) <=> 2^x(x-2) — 8^{<=> (x-2) x — 8) = 0 <=> <=> <=> <=> .}

Ответ:

Пример 2 . Решите уравнение:

Решение.

5^2x — 7^x — 5^2x35 +7^x = 0 <=> (5^2x — 7^x)((

Ответ: 0.

С. Уравнения, которые с помощью подстановки ^f(x) = t, t>0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).

Пусть , где А, В, С — некоторые числа. Сделаем замену: >0, тогда A² + B + C = 0

Решаем полученное уравнение, находим значения t, учитываем условие t >0 , возвращаемся к простейшему показательному уравнению ^f(x) = t, решаем его и записываем ответ.

Примеры.

Пример 1 . Решите уравнение: 2^2+x — 2^2-x = 5.

Решение.

2^2+x — 2^2-x = 5 <=> 2²2^x — = 15 <=> 4(2^x)² — 4 = 15^x

Делаем замену t = 2^x, t > 0. Получаем уравнение 4² — 4 = 15t <=> 4t² — 15t — 4=0

<=> , t = не удовлетворяет условию t > 0.

Вернемся к переменной х:

2^х = 4<=> 2^x = 2² <=> x=2.

Ответ: 2

Пример 2. Решите уравнение:

Решение.

5

Делаем замену: , тогда Получаем уравнение:

5 , t = не удовлетворяет условию t

Вернемся к переменной Х:

Ответ: 2.

D. Уравнения, левая часть которых имеет вид A ^nx + B ^kx b^mx + С b^nx, где k, m N, k + m = n

Для решения уравнения такого типа необходимо обе части уравнения разделить либо на ^nx, либо на ^nx и получится уравнение типа С).

Примеры.

Пример 1. Решите уравнение: 22^2x — 5^x + 33^2x = 0.

Решение.

22^2x — 5^x + 33^2x = 0 <=> 2^2x — 5^x3^x + 33^2x = 0 <=> 2 — + 3 = 0 <=>

<=> 2^2x — 5^x + 3 = 0

Пусть t = ^x, t>0 , тогда 2t- 5t + 3 = 0 <=> , оба значения t удовлетворяют условию t Вернемся к переменной х:

<=> <=> .

Ответ:

Пример 2. Решите уравнение: 8^x + 18^x — 227^x = 0 .

Решение.

8^x + 18^x — 227^x = 0 <=> + — 2 = 0 <=> 2^3x + 2^x 3^2x — 23^3x = 0<=>

<=> + — 2 = 0 <=> + — 2 = 0.

Пусть = t, t>0 , тогда t³ + t — 2 = 0<=> (t³ — 1) + (t -1 )= 0 <=> (t-1) (t² +t +1) + (t — 1) <=> (t — 1) (t² + t +2) = 0 <=> <=> t - 1= 0 <=> t=1. (t>0)

Вернемся к переменной х: = 1 <=> = x = 0 .

Ответ: 0.

К данному типу уравнений относятся уравнения , левая часть которых имеет вид , где А, В, С -некоторые числа, причем .

Уравнения такого типа решаются с помощью подстановки :

= t , тогда = .

Пример 3. Решите уравнение:

Решение.

Заметим, что произведение оснований степени равно единице:

(. Поэтому можно ввести новую переменную: , причем . Получим уравнение:

t ,оба корня удовлетворяют условию :.

Вернемся к переменной х:

.

Ответ: .

Е. Уравнения, имеющие вид Aa^m = Bb^m.

Для решения необходимо обе части уравнения разделить либо на a^m, либо на b^m. В результате получается простейшее уравнение.

Примеры.

Пример 1. Решите уравнение: 7^х = 5^х.

Решение.

7^х = 5^х <=> = 1 <=> = <=> x = 0.

Ответ: 0.

Пример 2. Решите уравнение: .

Решение.

.

Ответ: 2.

F. Метод, основанный на использовании свойства монотонности показательной функции .

Примеры.

Пример 1. Решите уравнение: ^.

Решение.

Заметим, что при х=1 уравнение обращается в тождество. Следовательно, х=1 — корень уравнения. Перепишем уравнение в виде

^(*)

Так как при основании, меньшем единицы, показательная функция убывает на R, то при х^{левая часть уравнения (*) больше единицы, то есть}

Если то левая часть уравнения меньше единицы, то есть

Поэтому, других корней, кроме х=1, уравнение не имеет.

Ответ: 1.

Пример 2. Решите уравнение: .

Решение.

Это уравнение также обращается в тождество при х=1.

Перепишем уравнение в виде:

.

При основании, меньшем единицы, показательная функция убывает на R.

Поэтому при ха при х: . Таким образом, других корней, кроме х=1 , уравнение не имеет.

Ответ: 1.

G. Графический способ решения уравнений вида f(x).

Чтобы графически решить уравнение такого вида, необходимо построить графики функций y=f(x) в одной системе координат и найти (точно или приближенно) абсциссы точек (если они есть) пересечения этих графиков. Абсциссы этих точек — корни данного уравнения (точность результатов определяем только после подстановки в уравнение ).

Примеры.

Пример 1. Решите уравнение: .

Решение.

1.Рассмотрим две функции: f(x) = и g(x) = x+1.

2.Графиком функции f(x) = является кривая, расположенная в верхней полуплоскости, графиком функции g(x) = x+1 является прямая.

3. Зададим таблицы значений этих функций:

х		-1		0	1	2	3
f(x) =					1	2	4
х	0		3
g(x)= x+1	1		4

4. Из рисунка видно, что прямая и кривая пересекаются в двух точках- в точке А и в точке В. По графику определяем абсциссы этих точек: . Значит, уравнение имеет два корня: х=3 и х= . Число х=3 — точный корень заданного уравнения, так как при подстановке в это уравнение получается верное числовое равенство:

Ответ: 3; .

Пример 2. Решите уравнение: .

Решение.

1. Рассмотрим две функции f(x) = и g(x) = .Используем свойства степени и преобразуем выражение :

= , тогда вторую формулу можно переписать в виде: f(x) = .

2. Функция f(x) = — показательная по основанию и ее графиком является кривая, расположенная в верхней полуплоскости.

Функция g(x) =- прямая пропорциональность и ее график - прямая, проходящая через точку .

3. Зададим таблицы значений этих функций и затем построим их графики в одной системе координат.

4. Графики пересекаются в одной точке — в точке А, ее абсцисса равна единице.Значит, х=1 — корень заданного уравнения.

Примечание:

Если одна часть уравнения содержит убывающую функцию f(x) , а другая часть -возрастающую функцию g(x), и уравнение имеет корень х=, то он -единственный.

В примере 2. : f(x) = убывающая на R функция, а g(x = - возрастающая на R функция, х=1- корень уравнения и он единственный.

Ответ: 1.

Приложени

xn--i1abbnckbmcl9fb.xn--p1ai

Решение показательных уравнений

Показательные уравнения – это уравнения вида

где

x -неизвестный показатель степени,

a и b– некоторые числа.

Примеры показательного уравнения:

А уравнения:

уже не будут являться показательными.

 

Рассмотрим примеры решения показательных уравнений:

Пример 1.
Найдите корень уравнения:

Приведем степени к одинаковому основанию, чтобы воспользоваться свойством степени с действительным показателем

 

Тогда можно будет убрать основание степени и перейти к равенству показателей.

Преобразуем левую часть уравнения:

Далее используем свойство степени 

Преобразуем правую часть уравнения:

Используем свойство степени 

Ответ: 4,5.

Пример 2.
Решите неравенство:

Разделим обе части уравнения на 

Замена:

Обратная замена:

Число обращается в 1, если его показатель равен 0

Ответ: x=0.

 

Пример 3.

Решите уравнение и найдите корни на заданном промежутке:

Приводим все слагаемые к одинаковому основанию:

Замена:

Ищем корни уравнения, путём подбора кратных свободному члену:

 – подходит, т.к. равенство выполняется.
 – подходит, т.к. равенство выполняется.
– подходит, т.к. равенство выполняется.
– не подходит, т.к. равенство не выполняется.

Обратная замена:

1) 

Число обращается в 1, если его показатель равен 0

2)

Не подходит, т.к. 

3)

Логарифмируем обе части по основанию 2:

Правая часть равна 1, т.к.

Показатель степени встаёт перед выражение, т.к. 

Отсюда:

 

Пример 4.

Решите уравнение:

Замена: , тогда

Обратная замена:

1 уравнение:

если основания чисел равны, то их показатели будут равны, то

2 уравнение:

Логарифмируем обе части по основанию 2:

Показатель степени встаёт перед выражение, т.к. 

Левая часть равна 2x, т.к. 

Отсюда:

 

Пример 5.

Решите уравнение:

Преобразуем левую часть:

Перемножаем степени по формуле: 

Упростим:  по формуле: 

Представим  в виде :

Замена:

Переведём дробь в неправильную:

Вычисляем корень из дискриминанта:

a₂ -не подходит, т.к. а не принимает отрицательные значения

Обратная замена:

Приводим к общему основанию:

Если 

Ответ: x=20.

Пример 6.

Решите уравнение:

О.Д.З.

Преобразуем левую часть по формуле: 

Замена:

Вычисляем корень из дискриминанта:

a₂-не подходит, т.к. а не принимает отрицательные значения

Приводим к общему основанию:

Если 

Возводим в квадрат обе части:

Ответ: x=9.

Автор статьи: Дьяков Александр Дмитриевич

Редакторы статьи: Гаврилина Анна Викторовна, Агеева Любовь Александровна

www.teslalab.ru

No related posts.