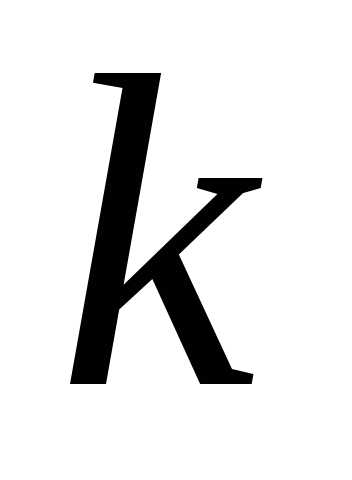Решением дифференциального уравнения — Решение
Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную искомой функции.
Символически дифференциальное уравнение можно написать так
или
.
Неизвестной здесь является функция y, входящая под знак производных (или дифференциалов).
Если искомая функция y(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным. В этой главе мы будем рассматривать только обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение есть уравнение первого порядка,
а уравнение — уравнение второго порядка.
Решением дифференциального уравнения называется всякая функция y(x), которая будучи подставленной в уравнение, обращает его в тождество. Решение еще называется интегралом дифференциального уравнения.
Пример
Рассмотрим уравнение .
Функция является решением этого уравнения.
Действительно,
и
уравнение обращается в тождество:
.
Решением рассматриваемого уравнения
будут и функции
и
вообще функции
,
где
и
—
произвольные постоянные.
В самом
деле
и
уравнение обращается в тождество
.
Заметим, что рассматриваемое уравнение имеет бесчисленное множество решений вида: .
Решение дифференциальных уравнений первого порядка
Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную первого порядка искомой функции.
Дифференциальное уравнение первого порядка имеет вид .
Общее и частное решение
Общим решением дифференциального уравнения первого порядка называется решение , зависящее от одной произвольной постоянной C, придавая конкретное значение которой , можно получить решение , удовлетворяющее любому заданному начальному условию .
Равенство вида
,
неявно задающее общее решение,
называется общим интегралом дифференциального уравнения.
Заметим,
что в практике чаще всего бывает
нужным не общее решение, а так называемое частное решение,отвечающее
определенным начальным условиям,
вытекающим из условия данной конкретной
задачи.
Частным решением называется
любая функция
,
которая получается из общего решения
,если
в последнем произвольной постоянной C придать определенное значение
.
Соотношение
называется
в этом случае частным интегралом.
Задача отыскания решения
дифференциального уравнения y I = f(x,y) , удовлетворяющего
заданным начальным условиям y(xo ) = yo,
называется задачей Коши.
Теорема Коши
Если
функция f(x,y) — правая часть дифференциального
уравнения y I = f(x,y) —
непрерывна в некоторой замкнутой
области D плоскости xOy и имеет в этой
области ограниченную частную
производную f Iy (x,y),
то каждой внутренней точке области
D соответствует, и притом единственное,
решение, удовлетворяющее начальным
условиям.
Пример
Рассмотрим
уравнение
.
Общим решением
этого уравнения является семейство
функций
.
Действительно,
при любом значении C эта функция
удовлетворяет уравнению:
.
Кроме того, всегда можно найти такое
значение C, что соответствующее частное
решение будет удовлетворять заданному
начальному условию.
Найдем,
например, частное решение, удовлетворяющее
начальному условию y(1)=-2. Подставляя
эти значения в уравнение
,
получим
.
Решая это уравнение относительно
C получим C = — 3.
Следовательно, искомым
частным решением будет функция: Y = X2 — 3.
Это решение можно получить, используя нижеприведенный апплет для построения поля направлений и интегральных кривых для уравнения первого порядка.
Интегральные кривые
С геометрической точки зрения общее
решение уравнения первого порядка
представляет собой семейство кривых
на плоскости xOy, зависящее от одной
произвольной постоянной C. Эти
кривые называются интегральными
кривыми данного дифференциального
уравнения.
Частному решению
соответствует одна интегральная
кривая, проходящая через некоторую
заданную точку. Так, в последнем
примере общее решение геометрически
изобразится семейством парабол,
причем каждому значению параметра C будет соответствовать вполне
определенная кривая. Частное решение
изобразится параболой (рис. 1.
)
проходящей через точку
Заметим,
что задать начальное условие для
уравнения первого порядка с
геометрической точки зрения означает
задать точку
,
через которую должна пройти
соответствующая интегральная кривая.
Решить или проинтегрировать данное дифференциальное уравнение это значит:
а) найти его общее решение или общий интеграл, если не заданы начальные условия,
или
б) найти частное решение, удовлетворяющее заданным начальным условиям.
gigabaza.ru
Примеры решения дифференциальных уравнений
Методы решения дифференциальных уравнений здесь.
Пример. Частное решение дифференциального уравнения (ДУ)
Дано: ДУ y′′ + y = 0.
Найти: решение ДУ.
Решение:
Так как (sinx)′′ = −sinx, (cosx)′′ = −cosx, функция вида будет удовлетворять уравнению.
Если c1 = 1, c2 = 3, то
если c1 = 0, c2 = -2, то
Пример. Решение ДУ с разделяющимися переменными.
Дано: ДУ
Найти: решение ДУ.
Решение:
Данное в задаче уравнение удобно записать в виде:
Перепишем уравнение в виде равенства дифференциалов двух функций одного аргумента:
Умножим правую и левую часть уравнения на .
Получим: .
Если дифференциалы функций равны, то сами функции отличаются на константу. Тогда общий интеграл этого ДУ имеет вид:
ln|y| = ln|x| + ln|c|, где постоянная интегрирования представлена в логарифмической форме.
Отсюда следует: ln|y| = ln|с×x|, |y| = |с×x|, x ≠ 0.
Пример. Решение однородного ДУ первого порядка.
Дано: ДУ
Найти: решение ДУ.
Решение:
Правая часть уравнения есть функция только отношения значит ДУ однородное.
Принимаем: . Значит .
Наше уравнение приобретает вид:
ln|lnu| = ln|x| + ln|c|, lnu=c×x, отсюда .
В итоге, получаем:
Пример. Решение линейного ДУ первого порядка.
Дано:
Найти: решение ДУ.
Решение:
Принимаем: .
Получаем: ,
,
.
Определяем v из ДУ:
ln|v| = 2×ln|x+1|, отсюда .
Находим u из ДУ:
.
Запишем общее решение ДУ: .
Пример. Уравнение Бернулли.
Дано: ДУ .
Найти: решение ДУ.
Решение:
Уравнение Бернулли — это ДУ вида где P(x), Q(x) – непрерывные функции или постоянные.
При n = 0 оно линейное, при n = 1 с разделяющимися переменными.
В нашем случае
Умножаем обе части, данного в условии задачи, уравнения на .
Получаем:
Заменим:
Получим:
Принимаем:
Получаем линейное ДУ для v:
Отсюда ln|v| = x2, .
Запишем уравнение для u
:Тогда
Сразу заменив , можно было решить уравнение Бернулли как линейное.
matematika.electrichelp.ru
Контрольная работа № 4
Пример 1. Найти общее решение уравнения
Решение. Сначала определим вид дифференциального уравнения. Данное уравнение не является уравнением с разделенными переменными, так как коэффициенты при и зависят каждый от двух переменных. Но, разделив обе части уравнения на произведение (считая, что ), приведем его к виду
Это уравнение с разделенными переменными.
Находим общее решение
Или
.
Умножив обе части на (-1), включим знак “-“ в постоянную С. Решение примет вид
.
Таким образом, нами получено общее решение заданного уравнения.
3. Однородные уравнения первого порядка
[2, гл. ХIII, § 5, упр. 39-46].
Пример 2. Найти общее решение уравнения
. (1)
Решение. Определим вид этого уравнения. Это – однородное уравнение, поскольку его правая часть есть .
Поделив почленно правую часть на , получим
Делаем подстановку или . Тогда и уравнение примет вид
. (2)
Разделяем переменные
И интегрируем
Или после потенцирования
.
Нами получено общее решение уравнения (2).
Чтобы найти общее решение уравнения (1), вернемся к старой переменной Y. Подставим , тогда будем иметь
или .
4. Линейные уравнения первого порядка
[2, гл. ХIII, § 7, упр. 57-65].
Пример 3. Найти общее решение уравнения первого порядка
Решение. Определим вид этого уравнения. Уравнение вида Называется линейным. Полагаем ; и подставляем это в данное уравнение
Группируем члены
И полагаем
(3)
Остается
. (4)
Находим сначала V из (3)
Заметим, что V не содержит никаких произвольных постоянных.
Подставляем V в (4) и получаем
Окончательно получаем искомое общее решение
.
5. Дифференциальные уравнения высших порядков. Основные понятия.
[2, гл. ХIII, § 16, 17, упр. 118-124].
6.Линейные однородные уравнения второго порядка
Пример 4. Найти общее решение уравнения .
Решение. Ищем решение уравнения в виде тогда и, подставляя в исходное уравнение получим Так как то на него можно сократить и мы получим
Находим его корни
Корни характеристического уравнения вещественные, различные, значит, общее решение дифференциального уравнения имеет вид
Или
Пример 5. Найти общее решение уравнения
Решение. Составляем характеристическое уравнение (см. пример 9)
Решаем его
Корни характеристического уравнения вещественные равные. Общее решение дифференциального уравнения имеет вид
Или
Пример 6. Найти общее решение уравнения
Решение. Составляем характеристическое уравнение (см. пример 9)
Корни характеристического уравнения комплексные сопряженные, значит, общее решение дифференциального уравнения имеет вид
Или
7. Линейные, неоднородные уравнения второго порядка
Пример 7. Найти общее решение уравнения
Решение. Находим сначала общее решение соответствующего однородного уравнения
Характеристическое уравнение Его корни
Общее решение однородного уравнения
Теперь следует найти частное решение неоднородного уравнения. Правая часть значит ищем в форме , т. к. не является корнем характеристического уравнения.
Требуется найти неизвестные коэффициенты А и В. Для определения А и В дифференцируем дважды
И подставляем это в данное неоднородное уравнение:
Так как то сократив , получим тождественное равенство двух полиномов
Значения А и В найдем, приравнивая коэффициенты при одинаковых степенях в левой и правой частях
При Х :
При Х0:
Подставляем найденные А и В в
Общее решение неоднородного уравнения
Пример 8. Найти общее решение уравнения
Решение. Соответствующее однородное уравнение
Решаем его
Правая часть данного неоднородного уравнения
Следовательно, частное решение разыскиваем в виде
,
Т. к. не является решением характеристического уравнения.
Дифференцируем и подставляем это решение в неоднородное уравнение
Приравниваем коэффициенты при одинаковых тригонометрических функциях в левой и правой частях тождества
При
При
Из этой системы находим А и В
Общее решение
Пример 9. Найти частное решение уравнения удовлетворяющее начальным условиям
Решение. Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, необходимо получить сначала общее решение данного неоднородного уравнения. Находим его (см. пример 8)
Подставляем в уравнение
Искомое частное решение будем находить из общего. Общее решение неоднородного уравнения
Подставляем начальные условия. При имеем
Найденные постоянные подставляем в общее решение неоднородного уравнения
• искомое частное решение.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Решение типового варианта контрольной работы. Дифференциальные уравнения.
Задание 1. Найти общее решение дифференциальных уравнений.
А) .
Решение. Попытаемся разделить переменные интегрирования. Для этого вынесем за скобки общий множитель:, разнесем слагаемые: ; выражая из полученного уравнения убедимся в том, что и, значит, наше уравнение является дифференциальным уравнением в разделяющихся переменных. Разделим переменные. .
Проинтегрируем получившееся выражение по соответствующим переменным: .
Получим , .
Таким образом, мы убедились в том, что — общий интеграл заданного уравнения.
Ответ: .
Б).
Решение. Убедимся в том, что переменные разделить не удается. Поэтому поделим обе части уравнения на X.
— Убедимся в том, что производная в представленном уравнении зависит только от отношения , то есть и, значит, это однородное дифференциальное уравнение 1-го порядка. Будем решать его с помощью соответствующей замены.
Введем новую переменную .
;
;
; проинтегрируем выражение
;
;
;
;
— общее решение уравнения.
Ответ: .
В).
Решение. Начинаем вновь с проверки не разделятся ли переменные интегрирования. Убеждаемся, что это не так, и, кроме того, однородным оно тоже не является. Это линейное дифференциальное уравнение 1-го порядка, так как имеет структуру вида: . Будем решать его с помощью стандартной в этом случае, замены: .
;
;
;
;
;
;
;
;
;
— общее решение уравнения.
Ответ: .
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям .
Решение. — неоднородное линейное дифференциальное уравнение с постоянными коэффициентами 2-ого порядка. Решение будем искать в виде суммы решений: общего решения однородного уравнения и частного решения неоднородного уравнения , которое будем искать по виду правой части. Начнем с отыскания .
Составим характеристическое уравнение: .
Следовательно, общее решение однородного уравнения: .
будем искать в виде . — частное решение уравнения, поэтому оно превращает его в верное числовое тождество. Подставим его в уравнение и вычислим А. .
. Значит . Таким образом, общее решение неоднородного уравнения . Для вычисления частного решения определим значения констант исходя из начальных условий:
; ;
;
Ответ: .
Задание 3. Найти общее решение системы дифференциальных уравнений.
Решение. Сведем предложенную систему к одному дифференциальному уравнению с постоянными коэффициентами второго порядка. Для этого продифференцируем первое уравнение системы по T:
и заменим воспользовавшись для этого вторым уравнением системы:
. Окончательно .
— однородное линейное дифференциальное уравнение с постоянными коэффициентами. Составим характеристическое уравнение: .
Следовательно, решение: . Из первого уравнения , поэтому ;
.
Ответ: ; .
Задание 4. Записать уравнение кривой, проходящей через точку, для которой треугольник, образованный осью Оу, касательной к кривой в произвольной её точке и радиус-вектором точки касания, равнобедренный (причем основанием его служит отрезок касательной от точки касания до оси Оу).
Решение. Пусть искомое уравнение кривой. Проведем касательную MN в произвольной точке M(X;Y) кривой до пересечения с осью Оу В точке N. Согласно условию, должно выполняться равенство, но , а найдем из уравнения , полагая X=0, то есть.
Итак, приходим к однородному уравнению .
Полагая Y=Tx (Y’=T’X+T), получим или , откуда – данное решение представляет собой семейство парабол, осью которых является ось Оу.
Определим значение константы С исходя из того, что кривая проходит через точку . Подставляя координаты заданной точки в вышенайденное общее решение, получим ; из двух значений С=0 И С=2 Нас устраивает лишь второе, так как при С=0 Парабола оказывается вырожденной. Итак, искомое решение , или .
Ответ: .
Задание 5.
А) Найти общее решение дифференциального уравнения .
Решение. Так как производная в данном случае является функцией, зависящей только от переменной X, то его решение может быть получено в результате последовательного интегрирования: .
Ответ. .
Б) Найти общее решение дифференциального уравнения .
Решение. Поскольку данное уравнение не содержит в явном виде переменной , то замена позволяет преобразовать его в уравнение первого порядка с разделяющимися переменными .
;
. Учтя, что – произвольная постоянная, то полученное решение можно упростить: .
Ответ. .
В) Найти общее решение дифференциального уравнения .
Решение. Так как решаемое уравнение не содержит явно переменной , будем получать его решение с помощью введения новой переменной , откуда , так как в этом случае мы вычисляем производную сложной функции. Заданное уравнение в результате такой замены будет иметь вид: . Решение является особым, и, делая обратную замену в этой ситуации, запишем: . Оставшееся уравнение является уравнением в разделяющихся переменных: . Интегрируя последнее равенство, получим . Выразим теперь функцию : . Делая вновь обратную замену , получим: . В данном уравнении можно разделить переменные: . Интегрируя последнее выражение, получим . Получившаяся неявная функция также является решением заданного дифференциального уравнения.
Ответ. ; .
Задание 6. Решить уравнение .
Решение. Правая часть уравнения представляет собой дифференциальное уравнение с постоянными коэффициентами. Выпишем общее решение однородного дифференциального уравнения второго порядка . Так как корнями соответствующего характеристического уравнения являются числа , то общее решение данного уравнения, как известно, имеет вид . Правая часть исходного уравнения не позволяет найти частное решение неоднородного уравнения методом подбора (или неопределенных коэффициентов) поэтому воспользуемся для его нахождения методом вариации произвольных постоянных. Поэтому будем искать частное решение в виде: , предполагая, что здесь и (мы воспользовались видом найденной фундаментальной системы решений однородного уравнения), а и Решения следующей системы дифференциальных уравнений:
таким образом .
Из второго уравнения выпишем . Проинтегрировав, получим (постоянную интегрирования будем полагать равной нулю). Теперь, подставляя значение в первое уравнение системы, получим дифференциальное уравнение для функции : . Вновь интегрируя, запишем: .
Таким образом, частное решение исходного уравнения имеет вид , выпишем общее решение неоднородного дифференциального уравнения
Ответ. .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Решением дифференциального уравнения — Решение
Рассмотрим линейное однородное уравнение второго порядка, т.е. уравнение
и установим некоторые свойства его решений.
Свойство 1
Если
является
решением линейного однородного
уравнения, то C,
где C — произвольная постоянная,
является решением того же
уравнения.
Доказательство.
Подставляя
в левую часть рассматриваемого
уравнения C,
получим:
,
но
,
т.к.
является
решением исходного уравнения.
Следовательно,
и
справедливость указанного свойства
доказана.
Свойство 2
Сумма двух решений
линейного однородного уравнения
является решением того же уравнения.
Доказательство.
Пусть
и
являются
решениями рассматриваемого уравнения,
тогда
и
.
Подставляя теперь
+
в рассматриваемое уравнение будем
иметь:
,
т.е.
+
есть решение исходного уравнения.
Из доказанных свойств следует, что,
зная два частных решения
и
линейного
однородного уравнения второго порядка,
мы можем получить решение
,
зависящее от двух произвольных
постоянных, т.е. от такого количества
постоянных, какое должно содержать
общее решение уравнение второго
порядка. Но будет ли это решение общим,
т.е. можно ли путем выбора произвольных
постоянных
и
удовлетворить
произвольно заданным начальным
условиям?
При ответе на этот вопрос
будет использовано понятие линейной
независимости функций, которую можно
определить следующим образом.
Две функции
и
называются линейно независимыми на некотором
интервале, если их отношение на этом
интервале не является постоянным,
т.е. если
.
В противном случае функции называются линейно зависимыми .
Иными
словами, две функции
и
называются
линейно зависимыми на некотором
интервале, если
на
всем интервале.
Примеры
1. Функции y1 = e x и
y2 =
e —
x линейно
независимы при всех значениях x , т.к.
.
2. Функции y1 = e x и
y2 =
5 e x линейно
зависимы, т.к.
.
Теорема 1.
Если функции и линейно зависимы на некотором интервале, то определитель , называемый определителем Вронского данных функций, тождественно равен нулю на этом интервале.
Доказательство.
Если
,
где
,
то
и
.
Следовательно,
.
Теорема доказана.
Замечание.
Определитель Вронского,
фигурирующий в рассмотренной теореме,
обычно обозначается буквой W или
символами
.
Если функции
и
являются
решениями линейного однородного
уравнения второго порядка, то для них
справедлива следующая обратная и
притом более сильная теорема.
Теорема 2.
Если определитель Вронского, составленный для решений и линейного однородного уравнения второго порядка, обращается в ноль хотя бы в одной точке, то эти решения линейно зависимы.
Доказательство.
Пусть определитель Вронского обращается
в ноль в точке
,
т.е.
=0,
и пусть
и
.
Рассмотрим линейную однородную
систему
относительно
неизвестных
и
.
Определитель этой системы
совпадает
со значением определителя Вронского
при
x= ,
т.е. совпадает с
,
и, следовательно, равен нулю. Поэтому
система имеет ненулевое решение
и
(
и
не
равны нулю). Используя эти значения
и
,
рассмотрим функцию
.
Эта функция является решением того
же уравнения, что и функции
и
.
Кроме того, эта функция удовлетворяет
нулевым начальным условиям:
,
т.к.
и
.
С другой стороны, очевидно, что
решением уравнения
,
удовлетворяющим нулевым начальным
условиям, является функция y =0.
В
силу единственности решения, имеем:
.
Откуда следует, что
,
т.е. функции
и
линейно
зависимы. Теорема доказана.
Следствия.
1. Если определитель Вронского, фигурирующий в теоремах, равен нулю при каком-нибудь значении x=, то он равен нулю при любом значении x из рассматриваемого интервала.
2. Если решения и линейно независимы, то определитель Вронского не обращается в ноль ни в одной точке рассматриваемого интервала.
3. Если определитель Вронского отличен от нуля хотя бы в одной точке, то решения и линейно независимы.
Теорема 3.
Если и — два линейно независимых решения однородного уравнения второго порядка , то функция , где и — произвольные постоянные, является общим решением этого уравнения.
Доказательство.
Как известно, функция
является
решением рассматриваемого уравнения
при любых значениях
и
.
Докажем теперь, что каковы бы ни были
начальные условия
и
,
можно так подобрать значения
произвольных постоянных
и
,
чтобы соответствующее частное решение
удовлетворяло заданным начальным
условиям.
Подставляя начальные
условия в равенства, получим систему
уравнений
.
Из этой системы можно определить
и
,
т.к. определитель этой системы
есть
определитель Вронского при x= и,
следовательно, не равен нулю (в силу
линейной независимости решений
и
).
;
.
Частное решение при полученных значениях и удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.
Примеры
Пример 1.
Общим решением
уравнения
является
решение
.
Действительно,
.
Следовательно, функции sinx и cosx линейно независимы. В этом можно убедиться, рассмотрев отношение этих функций:
.
Пример 2.
Решение y = C1 e x + C2 e — x уравнения является общим, т.к. .
Пример 3.
Уравнение
,
коэффициенты которого
и
непрерывны
на любом интервале, не содержащем
точки x = 0, допускает частные решения
(легко
проверить подстановкой). Следовательно,
его общее решение имеет вид:
.
Замечание
Мы установили, что общее решение линейного однородного уравнения второго порядка можно получить зная два каких-либо линейно независимых частных решения этого уравнения. Однако, не существует общих методов для нахождения таких частных решений в конечном виде для уравнений с переменными коэффициентами. Для уравнений с постоянными коэффициентами такой метод существует и будет рассмотрен нами позднее.
gigabaza.ru
§ 2. Дифференциальные уравнения второго порядка
Линейное
однородное дифференциальное уравнение
второго порядка с постоянными
коэффициентами имеет общее решение,
где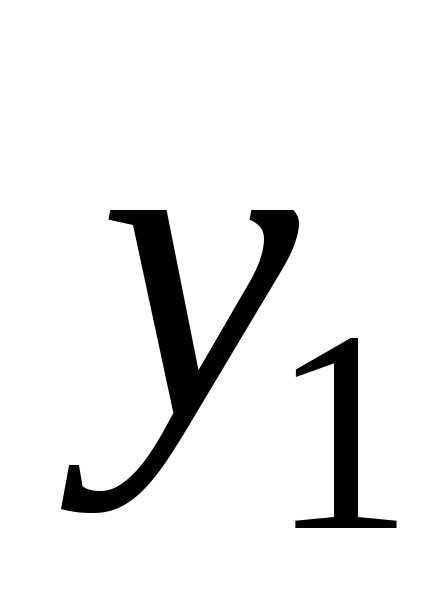 и
и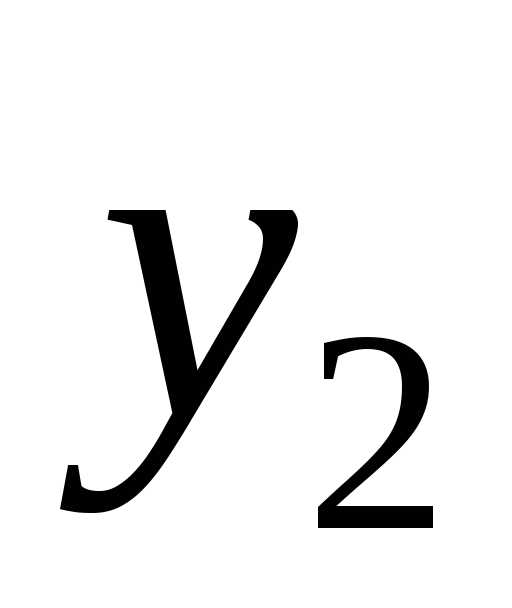 линейно-независимые частные решения
этого уравнения.
линейно-независимые частные решения
этого уравнения.
Общий вид решений однородного дифференциального уравнения второго порядка с постоянными коэффициентами , зависит от корней характеристического уравнения.
Корни характеристического уравнения | Вид общего решения |
Корни | |
Корни действительные и одинаковые | |
Корни комплексные , |
Пример
Найти общее решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
1)
Решение: Составим характеристическое уравнение: .
Решив его, найдем
корни 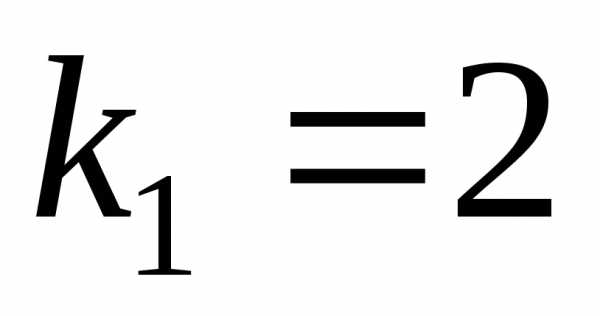 ,
,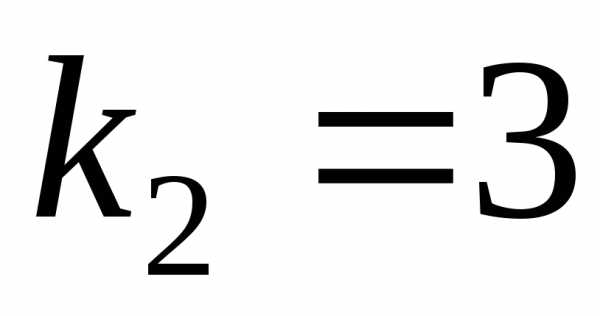 действительные и различные. Следовательно,
общее решение имеет вид:.
действительные и различные. Следовательно,
общее решение имеет вид:.
2)
Решение: Составим характеристическое уравнение: .
Решив его, найдем
корни 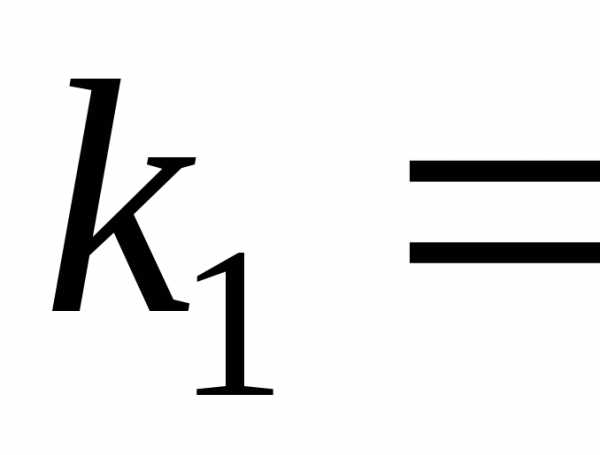
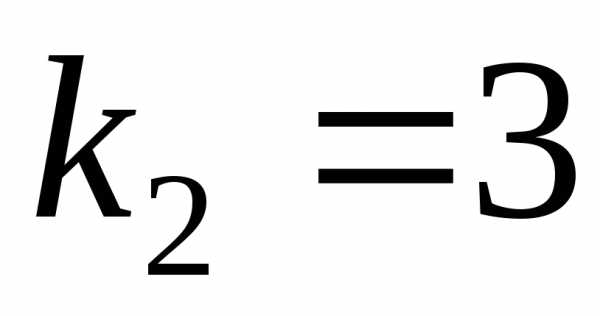 действительные и одинаковые. Следовательно,
общее решение имеет вид:.
действительные и одинаковые. Следовательно,
общее решение имеет вид:.
3)
Решение: Составим характеристическое уравнение: .
Решив его, найдем корни комплексные. Следовательно, общее решение имеет вид:.
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
,
где 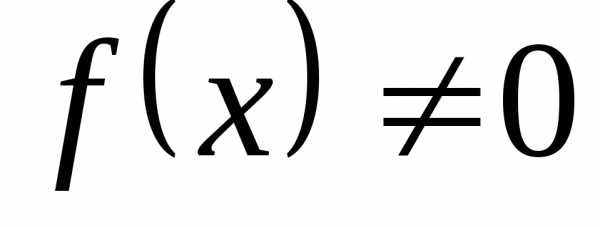 . (1)
. (1)
Общее решение
линейного неоднородного дифференциального
уравнения второго порядка
имеет вид,
где – частное решение этого уравнения,– общее решение соответствующего
однородного уравнения, т.е. уравнения.
– частное решение этого уравнения,– общее решение соответствующего
однородного уравнения, т.е. уравнения.
Вид частного
решения  неоднородного уравнения (1) в зависимости
от правой части
неоднородного уравнения (1) в зависимости
от правой части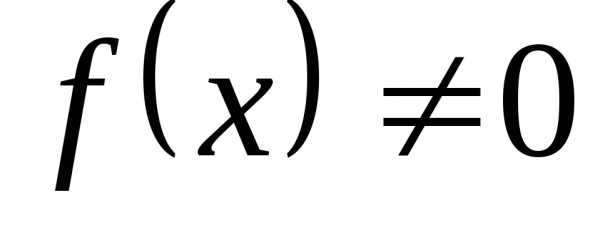 :
:
Рассмотрим различные виды правых частей линейного неоднородного дифференциального уравнения :
1. Пусть правая часть имеет вид
,
где– многочлен степени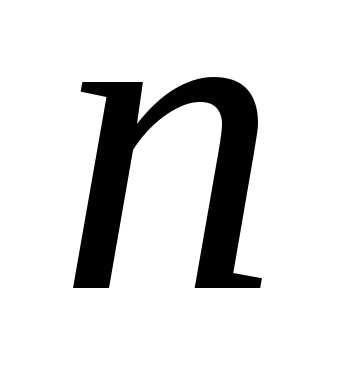 .
Тогда частное решениеможно искать в виде,
где
.
Тогда частное решениеможно искать в виде,
где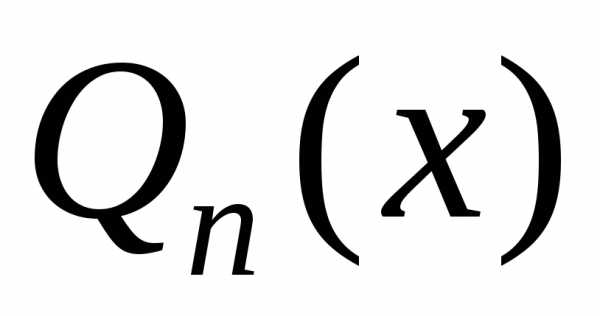 – многочлен той же степени, что и
– многочлен той же степени, что и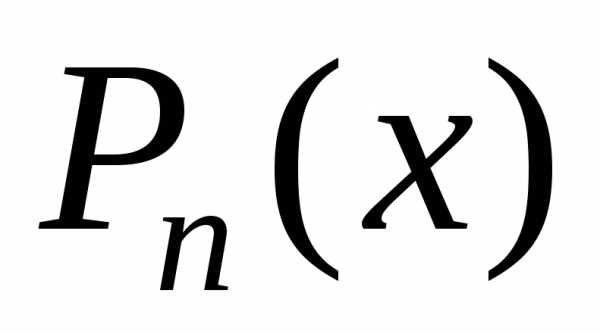 ,
а
,
а – число корней характеристического
уравнения, равных нулю.
– число корней характеристического
уравнения, равных нулю.
Пример
Найти общее решение .
Решение:
А) Найдем общее решение соответствующего однородного уравнения . Для этого запишем характеристическое уравнение. Найдем корни последнего уравнения. Следовательно, общее решение однородного уравнения имеет вид.
Б) Так как правая
часть уравнения является многочленом
первой степени и ни один из корней
характеристического уравнения
не равен нулю (),
то частное решение ищем в виде,
где и
и – неизвестные коэффициенты. Дифференцируя
дваждыи подставляя
– неизвестные коэффициенты. Дифференцируя
дваждыи подставляя ,
, и
и в исходное уравнение, находим.
в исходное уравнение, находим.
Приравнивая
коэффициенты при одинаковых степенях 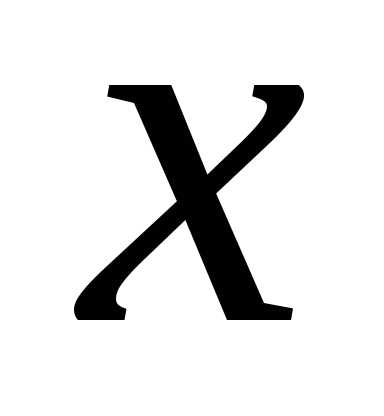 в обеих частях равенства
в обеих частях равенства ,,
находим
,,
находим ,
,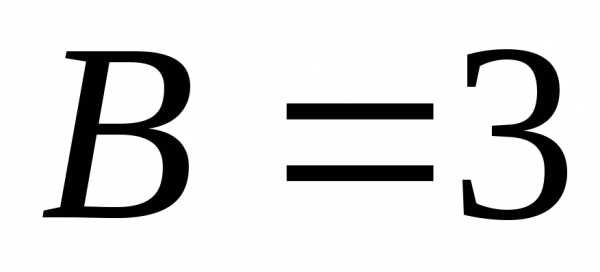 .
Итак, частное решение данного уравнения
имеет вид,
а его общее решение.
.
Итак, частное решение данного уравнения
имеет вид,
а его общее решение.
2. Пусть правая часть имеет вид
,
где– многочлен степени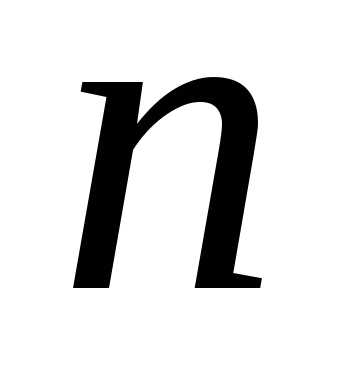 .
Тогда частное решение
.
Тогда частное решение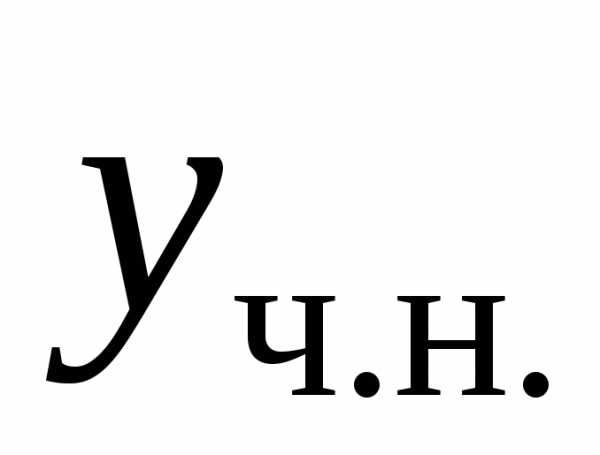 можно искать в виде,
где
можно искать в виде,
где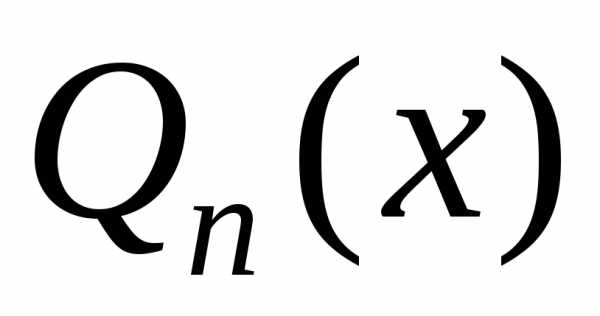 – многочлен той же степени, что и
– многочлен той же степени, что и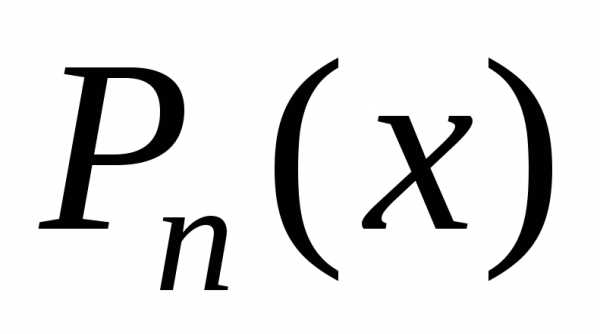 ,
а
,
а – число, показывающее, сколько раз
– число, показывающее, сколько раз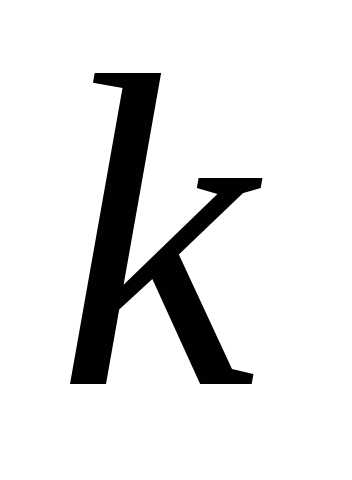 является корнем характеристического
уравнения.
является корнем характеристического
уравнения.
Пример
Найти общее решение .
Решение:
А) Найдем общее решение соответствующего однородного уравнения . Для этого запишем характеристическое уравнение. Найдем корни последнего уравнения. Следовательно, общее решение однородного уравнения имеет вид.
Б) Так как правая
часть уравнения есть функция 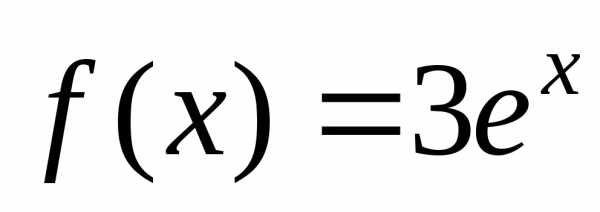 ,
то контрольное число данного уравнения,
оно не совпадает с корнямихарактеристического уравнения.
Тогда частное решение ищем в виде,
где
,
то контрольное число данного уравнения,
оно не совпадает с корнямихарактеристического уравнения.
Тогда частное решение ищем в виде,
где – неизвестный коэффициент. Дифференцируя
дваждыи подставляя
– неизвестный коэффициент. Дифференцируя
дваждыи подставляя ,
, и
и в исходное уравнение, находим.
Откуда,
то есть
в исходное уравнение, находим.
Откуда,
то есть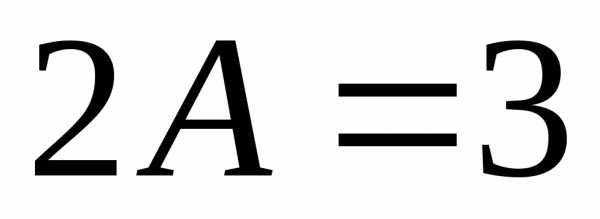 или
или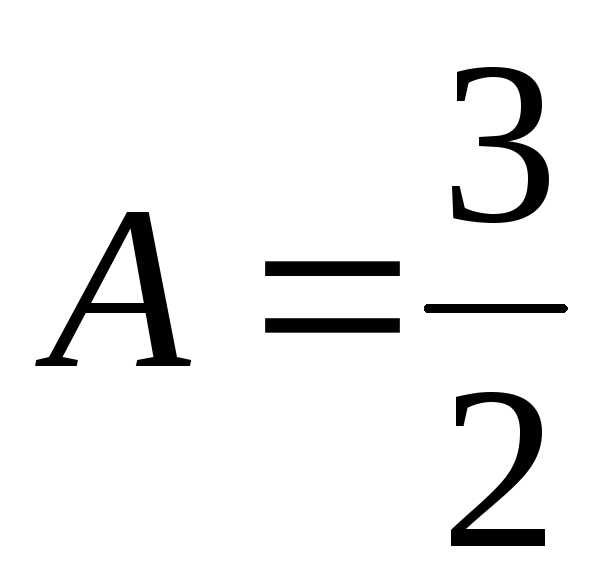 .
.
Итак, частное
решение данного уравнения имеет вид 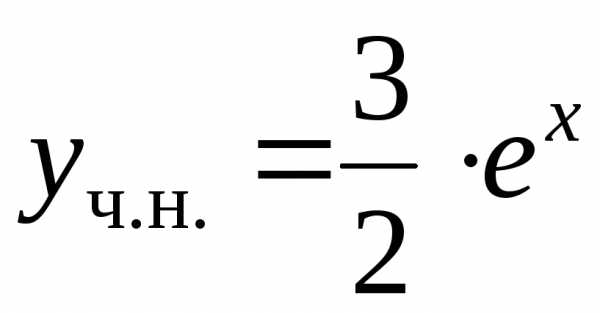 ,
а его общее решение.
,
а его общее решение.
3. Пусть правая часть имеет вид
,
где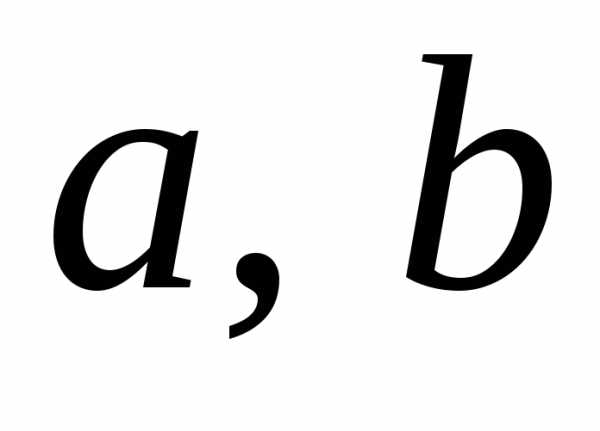 и
и – данные числа. Тогда частное решение
– данные числа. Тогда частное решение можно искать в виде,
где
можно искать в виде,
где и
и – неизвестные коэффициенты, а
– неизвестные коэффициенты, а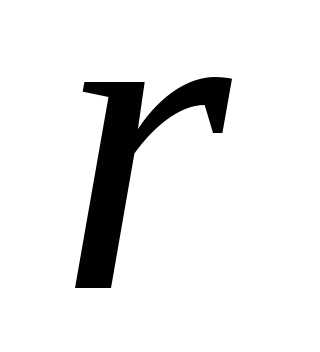 – число, равное числу корней
характеристического уравнения,
совпадающих с
– число, равное числу корней
характеристического уравнения,
совпадающих с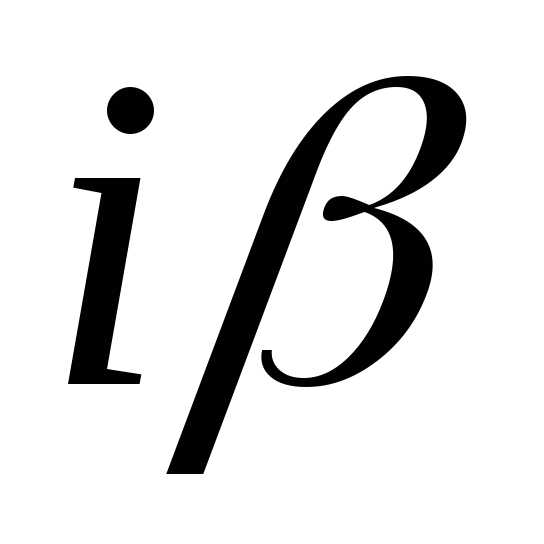 .
Если в выражение функции
.
Если в выражение функции входит хотя бы одна из функций
входит хотя бы одна из функций или
или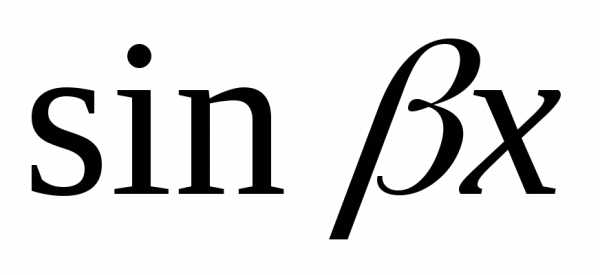 ,
то в
,
то в надо всегда вводитьобе функции.
надо всегда вводитьобе функции.
Пример
Найти общее решение .
Решение:
А) Найдем общее решение соответствующего однородного уравнения . Для этого запишем характеристическое уравнение. Найдем корни последнего уравнения. Следовательно, общее решение однородного уравнения имеет вид.
Б) Так как правая часть уравнения есть функция , то контрольное число данного уравнения, оно не совпадает с корнямихарактеристического уравнения. Тогда частное решение ищем в виде
,
где  и
и – неизвестные коэффициенты. Дифференцируя
дважды,
получими.
Подставляя
– неизвестные коэффициенты. Дифференцируя
дважды,
получими.
Подставляя ,
,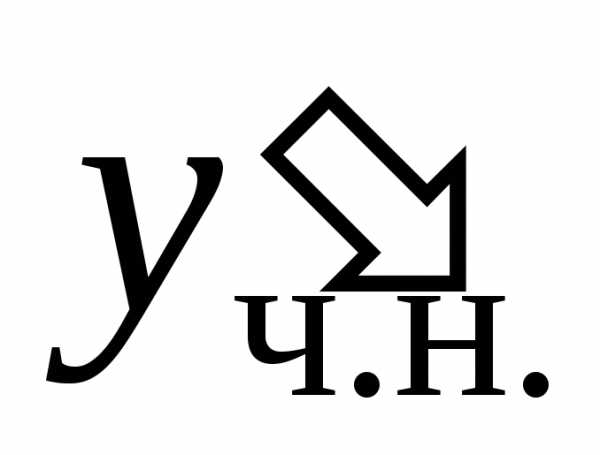 и
и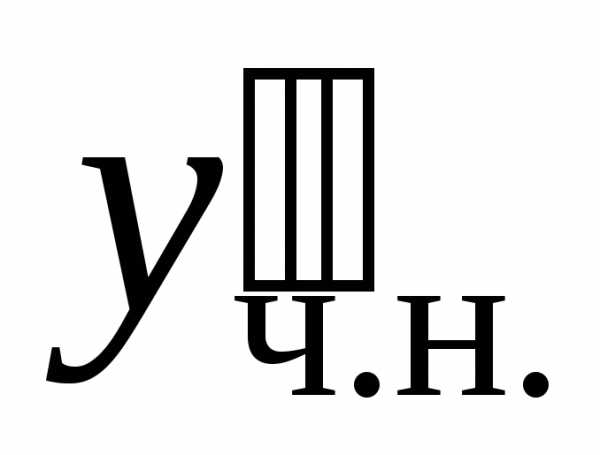 в исходное уравнение, находим
в исходное уравнение, находим
.
Приводя подобные слагаемые, получим
.
Приравниваем
коэффициенты при  и
и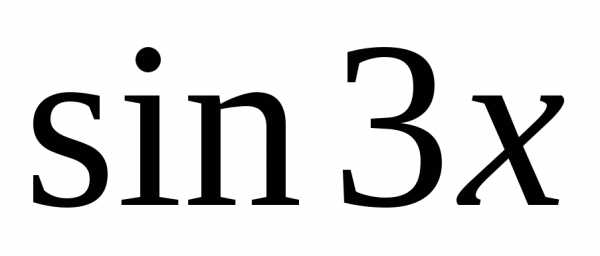 в правой и левой частях уравнения
соответственно. Получаем систему
в правой и левой частях уравнения
соответственно. Получаем систему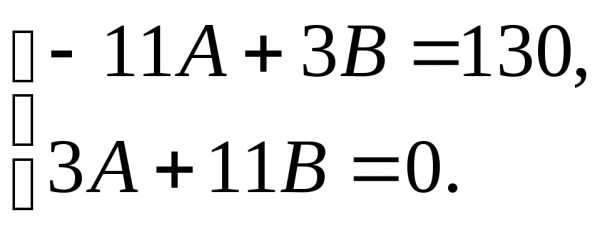 .
Решая ее, находим,
.
Решая ее, находим,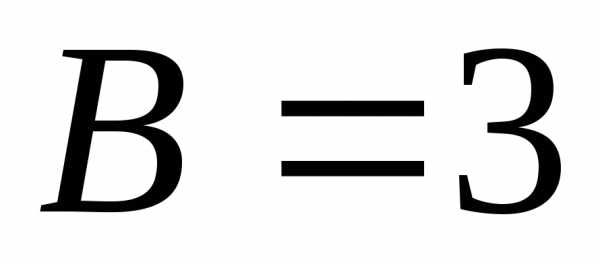 .
.
Итак, частное решение исходного дифференциального уравнения имеет вид .
Общее решение исходного дифференциального уравнения имеет вид .
studfiles.net
Дифференциальные уравнения первого порядка. Задача Коши. Общее, частное и особое решения дифференциального уравнения
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
Определение. Задачей Коши(Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
Теперь интегрируем:
— это общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
Определение. Интегральной кривойназывается график y = j(x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решениемдифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
— это так называемая дифференциальная формауравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
23.Теорема Коши существования и единственности решения дифференциального уравнения первого порядка (без доказательства).
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х0, у0) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
24.Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные, линейные.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
— это так называемая дифференциальная формауравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
megaobuchalka.ru

 и
и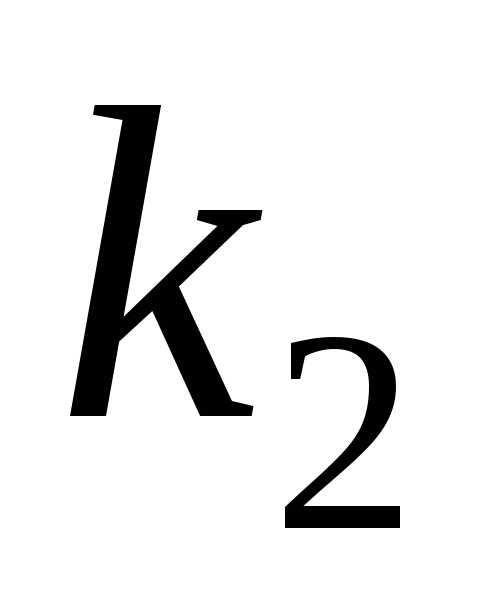 действительные и различные
действительные и различные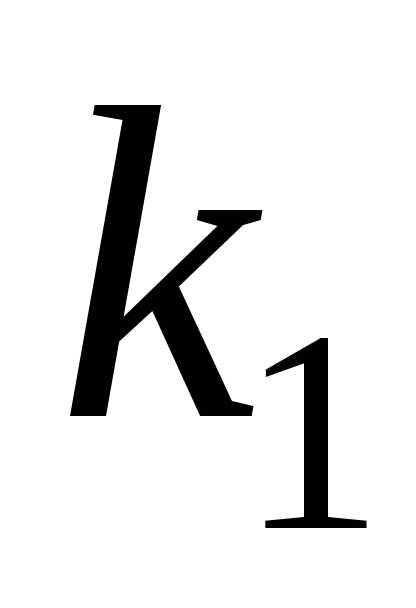 =
=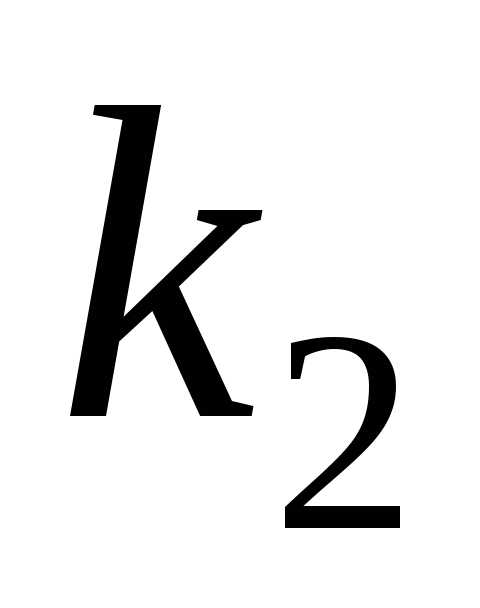 =
=