Площадь параллелограмма построенного на векторах
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье площадь параллелограмма. Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a(x1;y1;z1), а вектора b(x3;y3;z3).
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
2mb.ru
Найти площадь параллелограмма построенного на вектора
Площадь параллелограмма, который построен на векторах, можно найти как произведение длин этих векторов на синус угла между ними
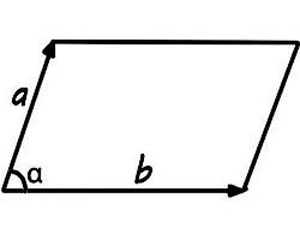
Если в условии задачи заданы длины этих векторов, то найти площадь является простой задачей.
Если же длины векторов не заданы, то их нужно найти с помощью координат этих векторов.
Рассмотрим пример вычисления площади параллелограмма по векторам.
Пример 1.
Найти площадь параллелограмма, построенного на векторах a + 3b и 3a + b. Известно, что длины векторов а и b равны единице, а угол между ними составляет 30 градусов.
Решение.
Найдем произведение векторов, на которых построен параллелограмм:
(a + 3b)(3a + b) = 3a * a + a * b + 9a * b +3b * b.
Поскольку для векторов произведение а * а или b * b равно 0, то запишем:
3a * a + a * b + 9a * b +3b * b = 3 * 0 + a * b + 9b * a + 3 * 0 = a * b — 9a * b = —8a * b.
Найдем площадь параллелограмма:
Ответ. Площадь параллелограмма равна 4.
Если же вектора заданы своими координатами, то сначала нужно найти их длины, используя формулу, согласно которой длина вектора равна квадратному корню из суммы квадратов его координат.
Например, если координаты вектора равны (7; 11; 17), то его длина будет найдена по формуле:
ru.solverbook.com
Примеры решения задач по векторной алгебре
. Примеры решения задач по векторной алгебре
Пример 1. Найти длину вектора и его направляющие косинусы.
Решение:
 =
=
Решение: Находим
Так как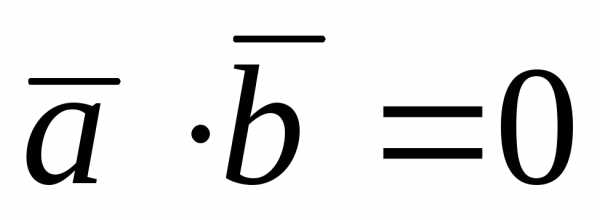 и,
то
и,
то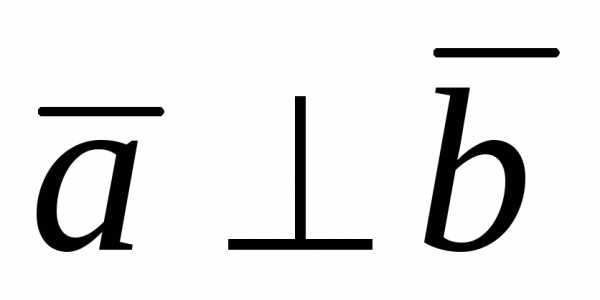 .
.
Пример 3. Определить,
при каком значении m векторы 3 + m
+ m 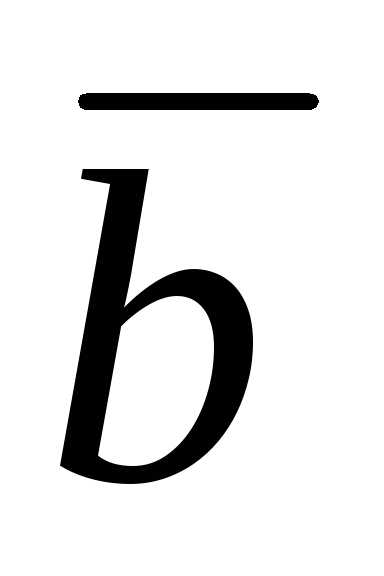 и
и  –
2
–
2 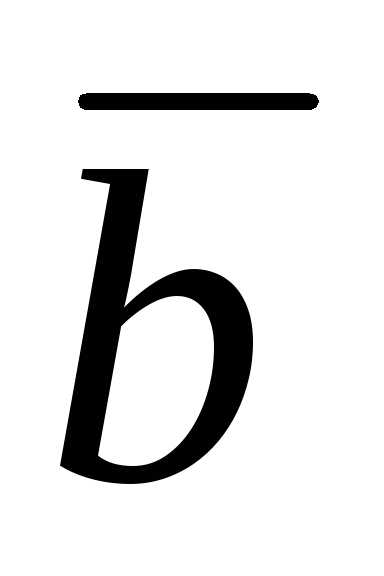 будут взаимно перпендикулярны, если
будут взаимно перпендикулярны, если
 = 7
= 7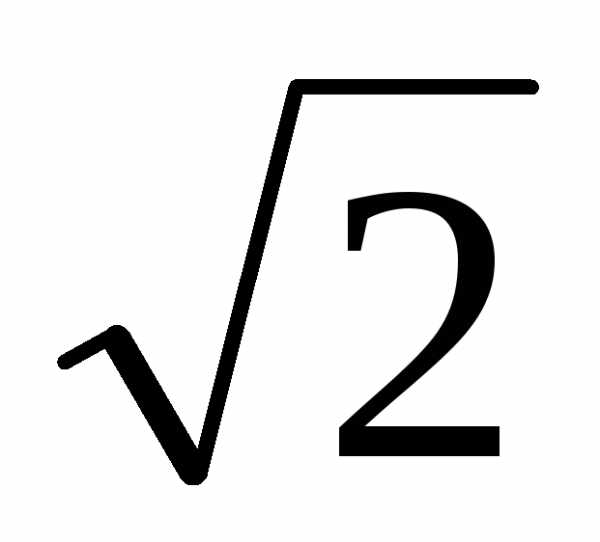
 = 4;
(
= 4;
(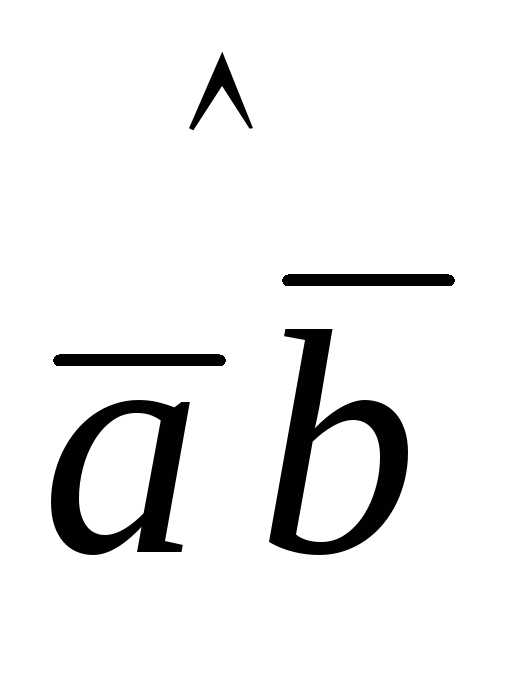 ) =
) =  .
.Решение:
Если два вектора взаимно перпендикулярны, то их скалярное произведение равно нулю.
Возьмем скалярное
произведение векторов 3 + m
+ m 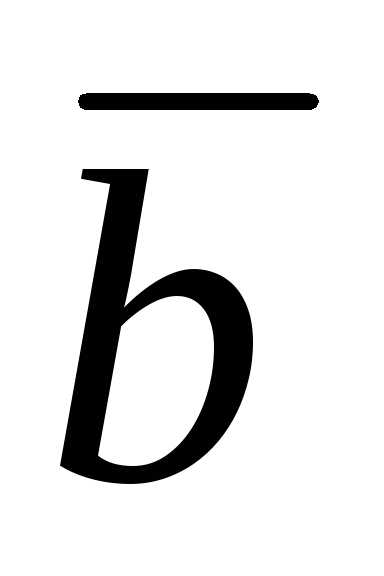 и
и  – 2
– 2 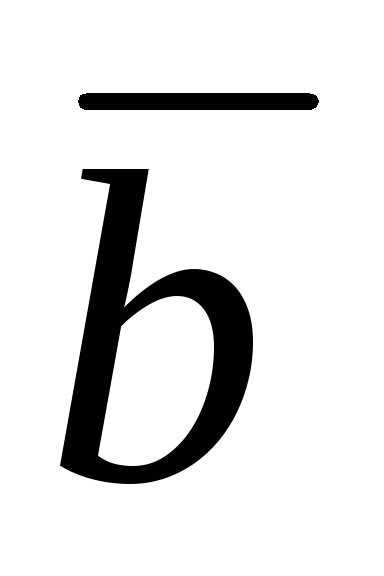 и, приравняв его нулю, найдем m:
и, приравняв его нулю, найдем m:
(3 + m
+ m 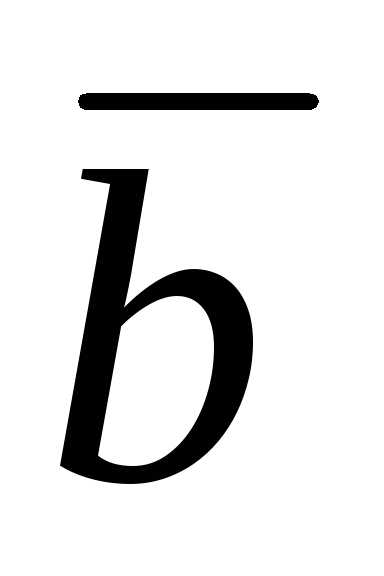 )(
)( – 2
– 2 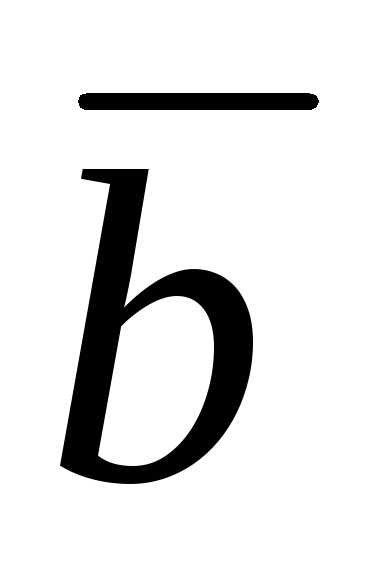 ) = 0;
) = 0;
3  2– 6
2– 6 
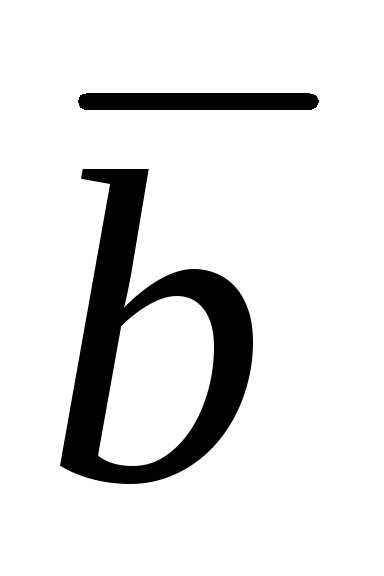 cos +m
cos +m
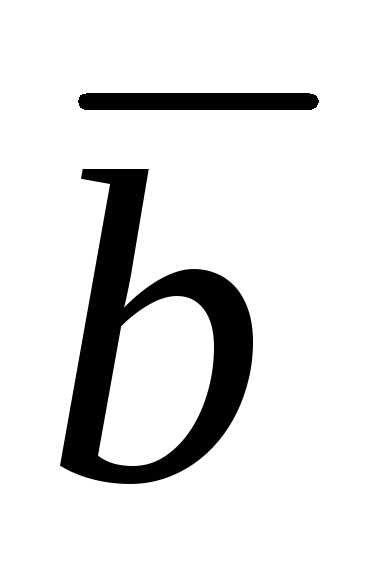
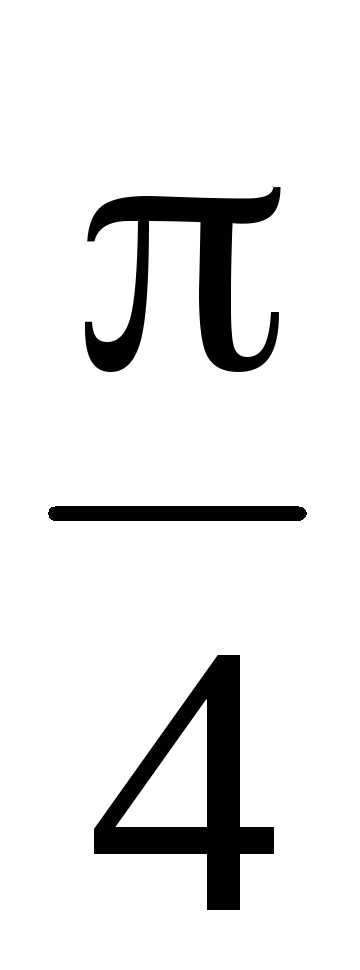 – 2m
– 2m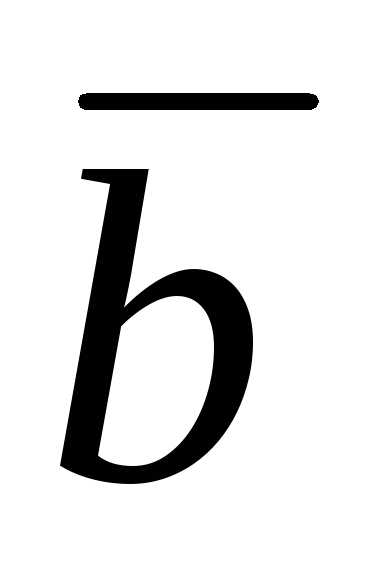 2 = 0;
2 = 0;
3 49 2 – 6 7 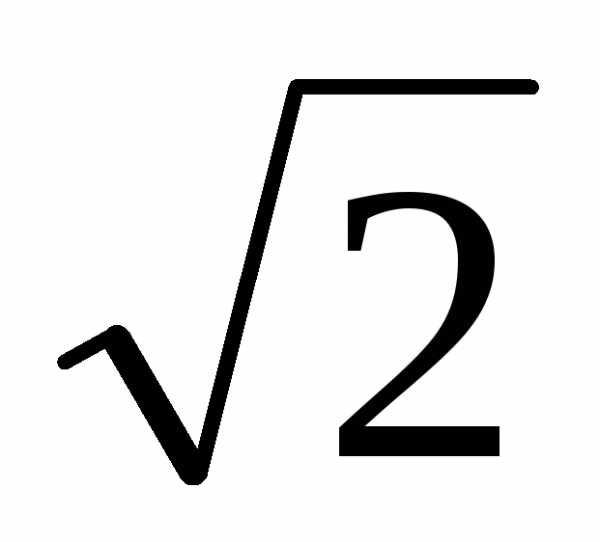 4
4  +m 7
+m 7 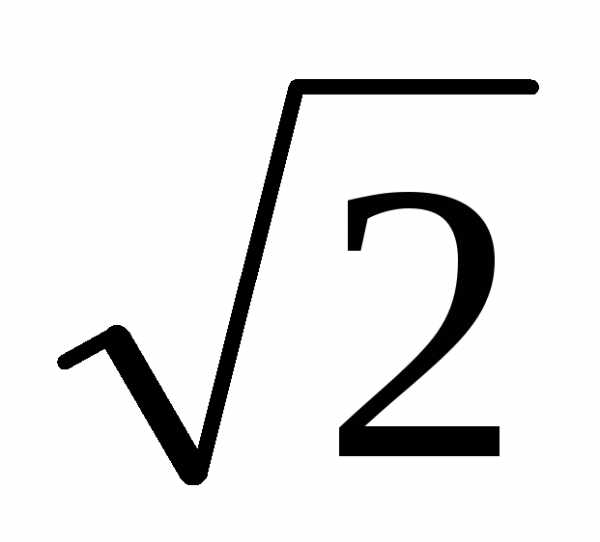 4
4 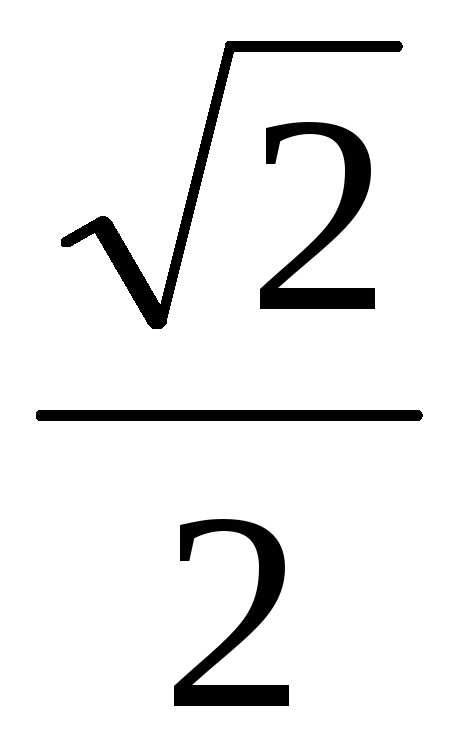 –
2 m 16 = 0;
–
2 m 16 = 0;
294 –
168 + 28 m – 32 m = 0,
4 m =126, m =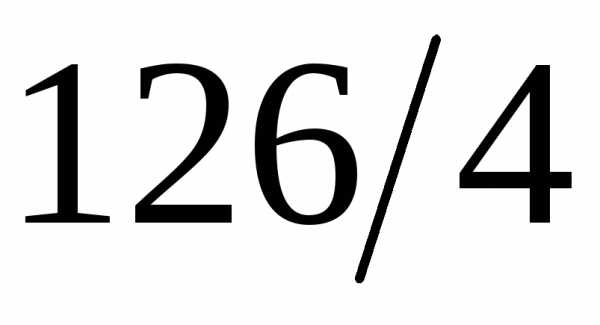 = 31,5.
= 31,5.
Пример 4. Определить угол между векторами и.
Решение:
Так как 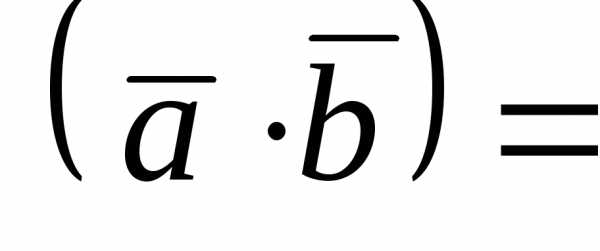

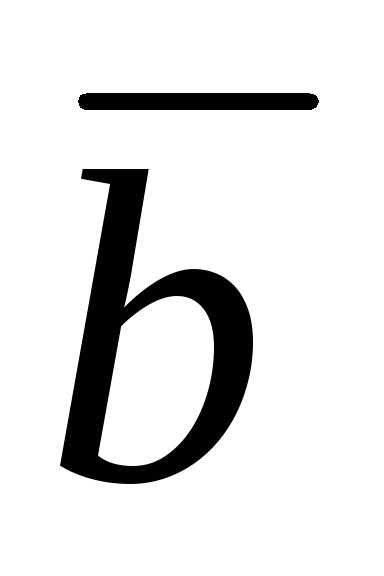 cos ,
то cos =
cos ,
то cos = 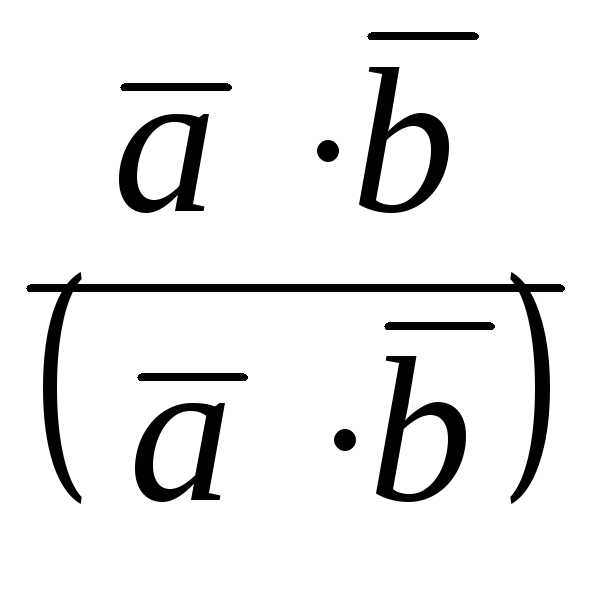 .
Имеем
.
Имеем
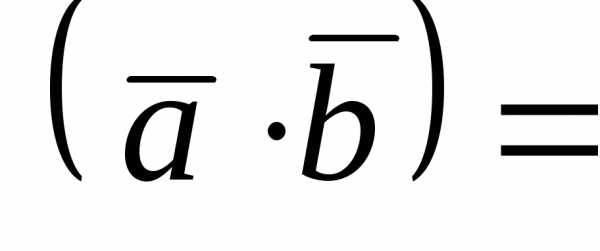 2 4 + 1 6 – 3 7
= –7;
2 4 + 1 6 – 3 7
= –7;
 =;
=;
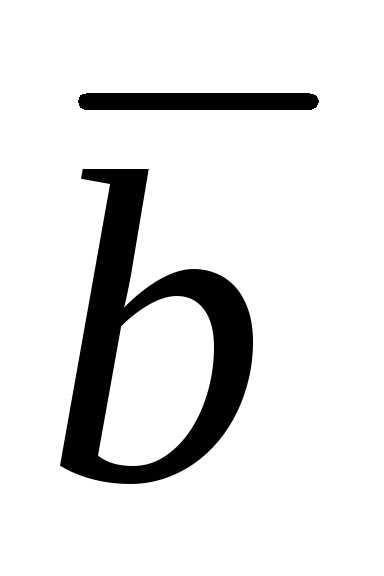
Следовательно,
cos = , = arccos  .
.
Пример 5. Найти векторное произведение векторов и.
Решение:
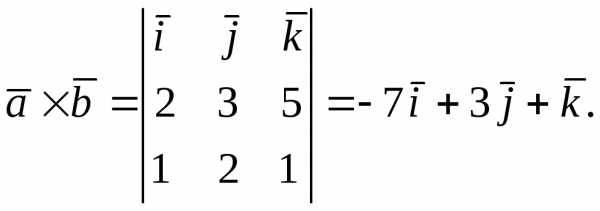
Пример 6. Вычислить площадь параллелограмма, построенного на векторах и
Решение:
Находим векторное
произведение  на
на 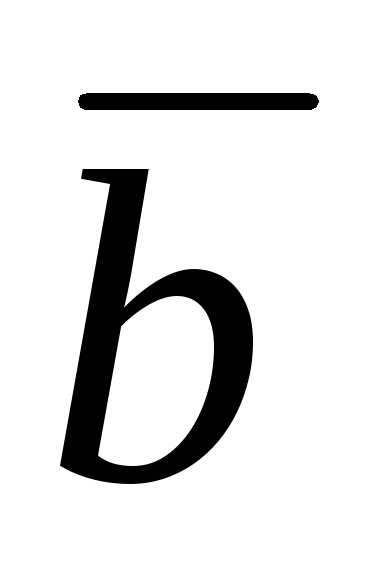 :
:
Так
как модуль векторного произведения
двух векторов равен площади построенного
на них параллелограмма, то S =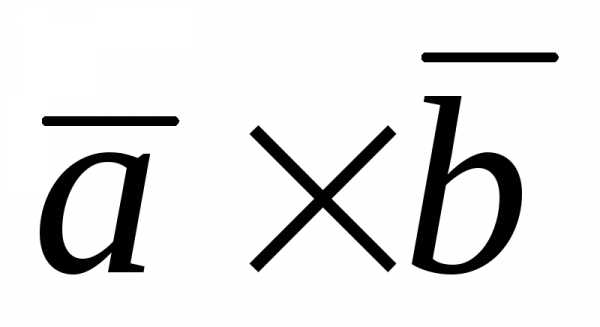 ==
49 (кв. ед.).
==
49 (кв. ед.).
Пример 7. Найти площадь треугольника ABC с вершинами A (1, 2, 0), B (3, 0, –3) и C (5, 2, 6).
Решение:
Площадь треугольника ABC равна половине площади параллелограмма,
построенного на векторах 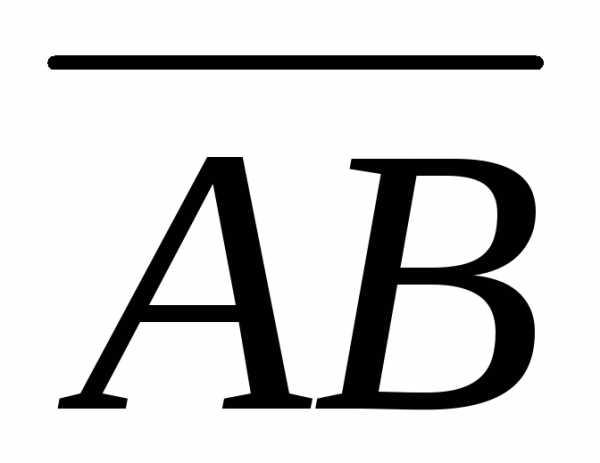 и
и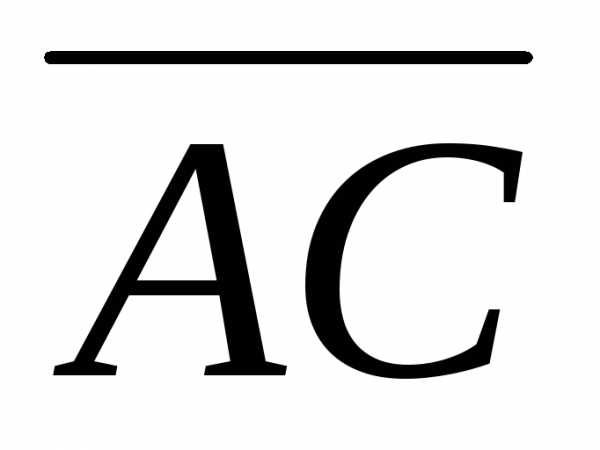 :S =
:S = 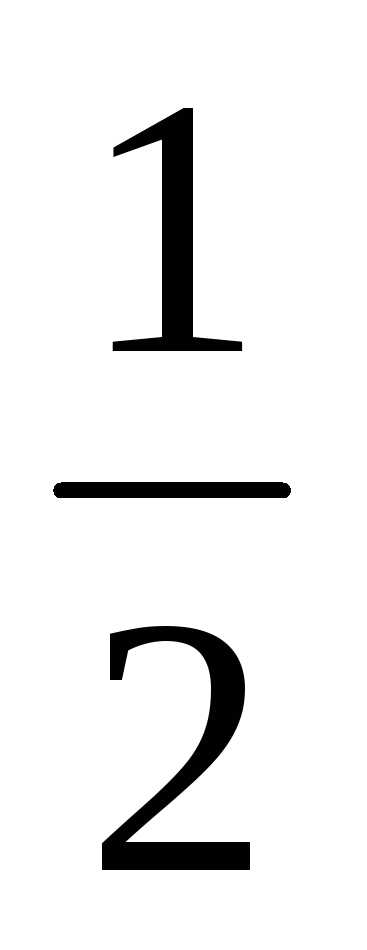
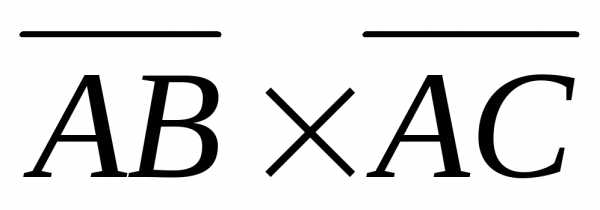
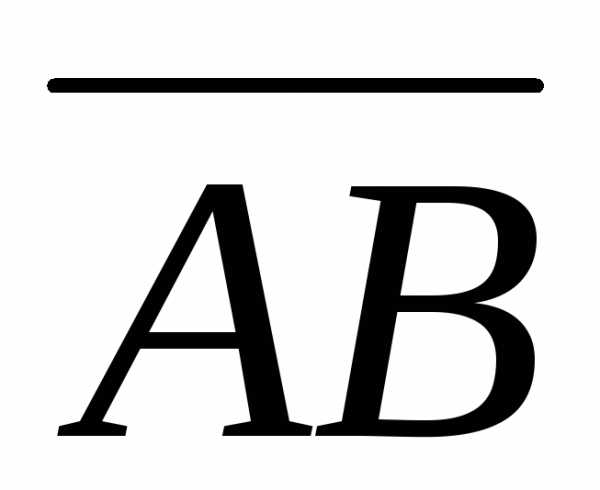 и
и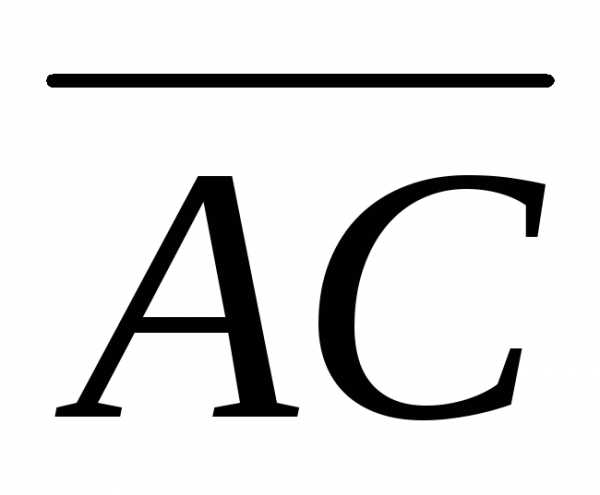 :
: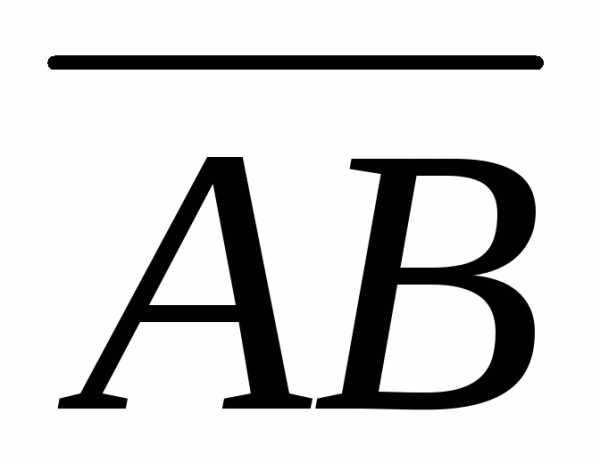 =;=
=;=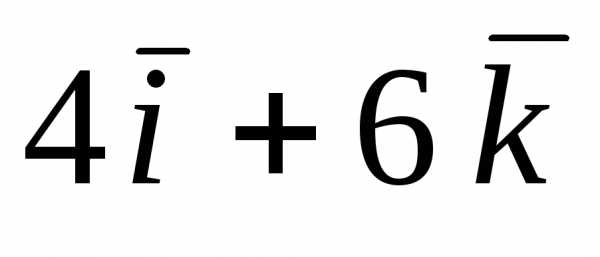 .
.Их векторное произведение
,
поэтому
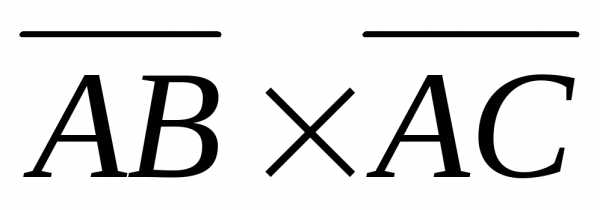 = 4 = 4 = 28,
и следовательно, S = 14 (кв.
ед.)
= 4 = 4 = 28,
и следовательно, S = 14 (кв.
ед.)
Пример 8. Вычислить
площадь параллелограмма, построенного
на векторах  =
6
=
6 – 3
– 3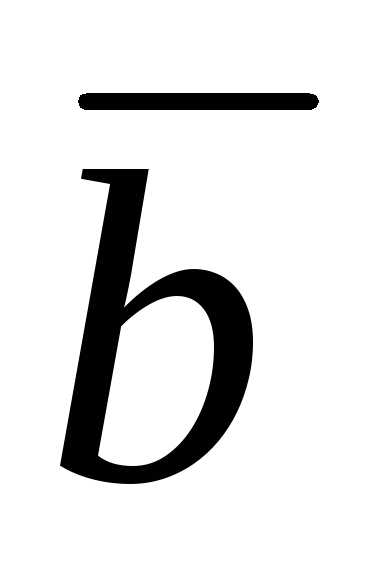 и
и  = 3
= 3  + 2
+ 2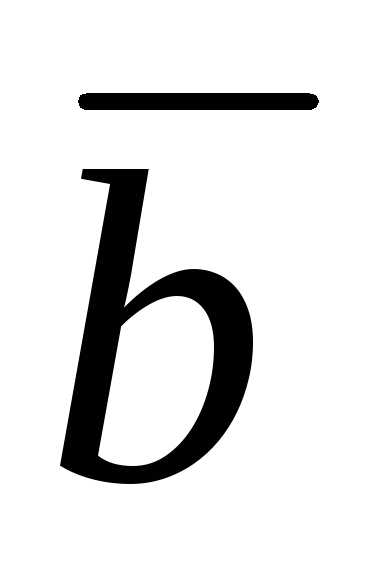 , если
, если  = 3;
= 3;
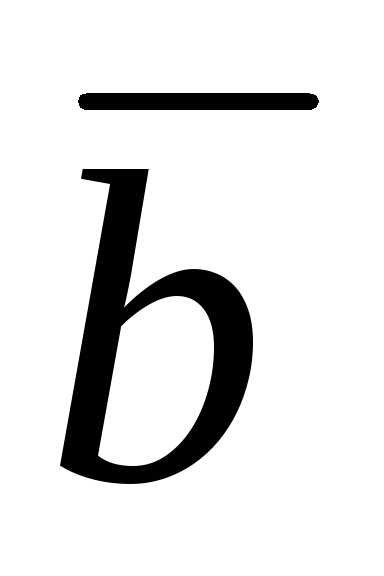 = 5;
(
= 5;
( )=
)= 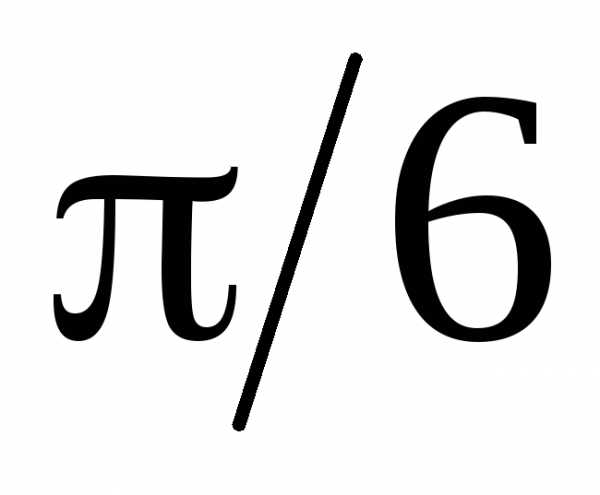 .
.
Решение:
Имеем 18 (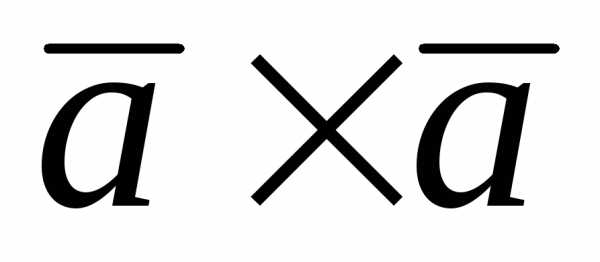 )
–9 (
)
–9 (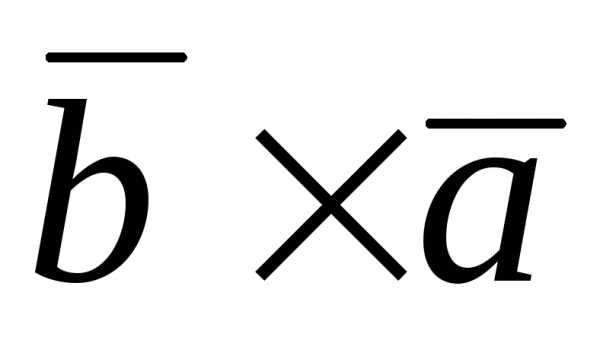 ) +12 (
) +12 (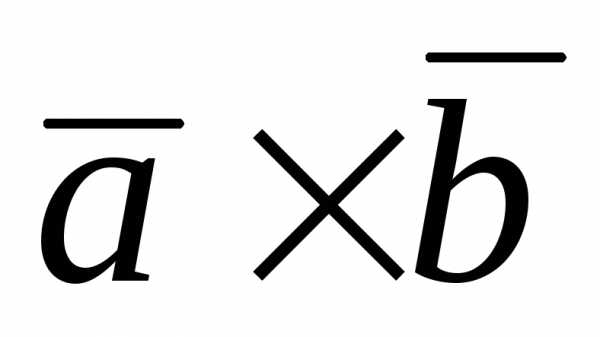 ) – 6 (
) – 6 (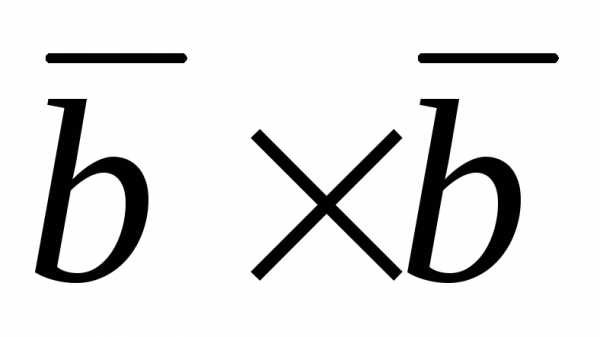 ) = 21(
) = 21(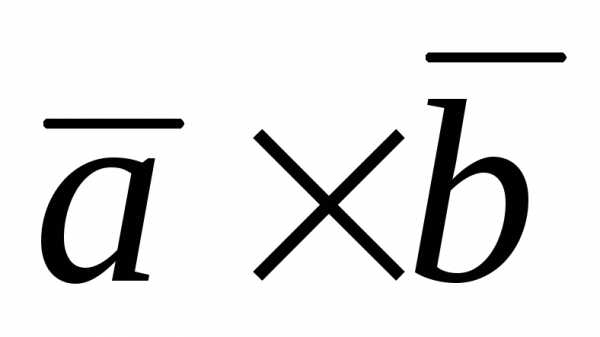 ),
где
),
где
.
Итак, S =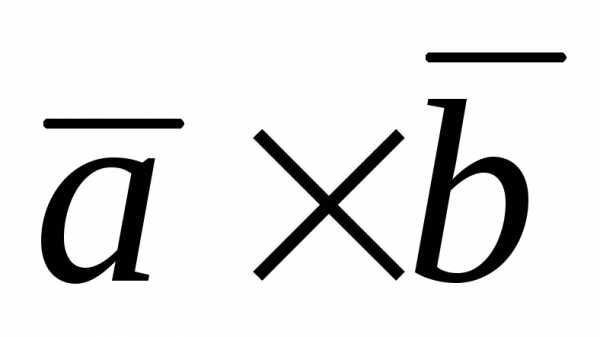 = 21 3 5
= 21 3 5 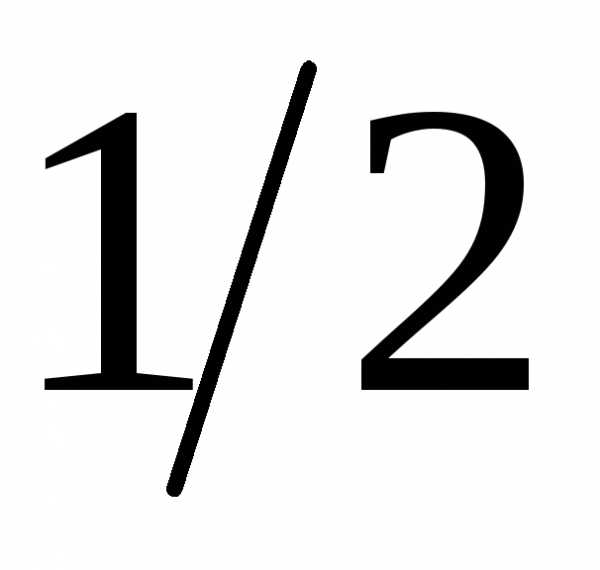 = 157,5
(кв. ед.)
= 157,5
(кв. ед.)
Пример 9. Найти смешанное произведение векторов ,и.
Решение:
Пример 10. Показать, что векторы ,икомпланарны.
Решение:
Так как 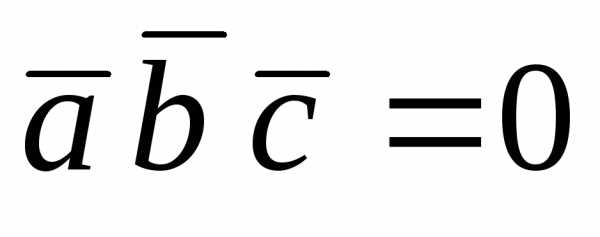 ,
то заданные векторы компланарны.
,
то заданные векторы компланарны.
Пример 11. Найти объем треугольной пирамиды с вершинами A (2, 2, 2), B (4, 3, 3), C (4, 5, 4) и D (5, 5, 6).
Решение:
Найдем векторы  и
и ,
совпадающие с ребрами пирамиды,
сходящимися в вершинеA:
,,.
,
совпадающие с ребрами пирамиды,
сходящимися в вершинеA:
,,.
Находим смешанное произведение этих векторов:
Так как объем
пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах 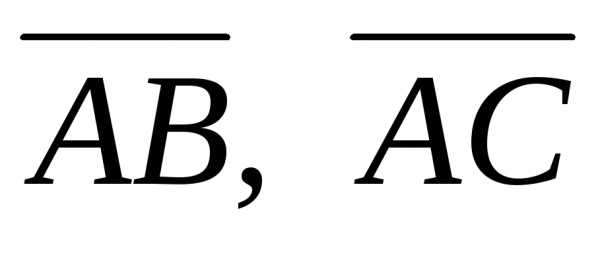 и
и ,
тоVпир =
,
тоVпир =  (куб. ед.).
(куб. ед.).
studfiles.net
