Умножение обычных дробей: Умножение дробей
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь .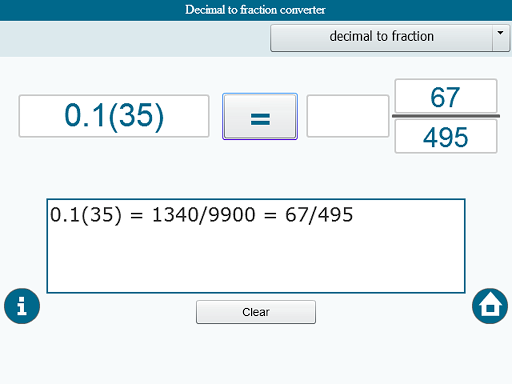 Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5.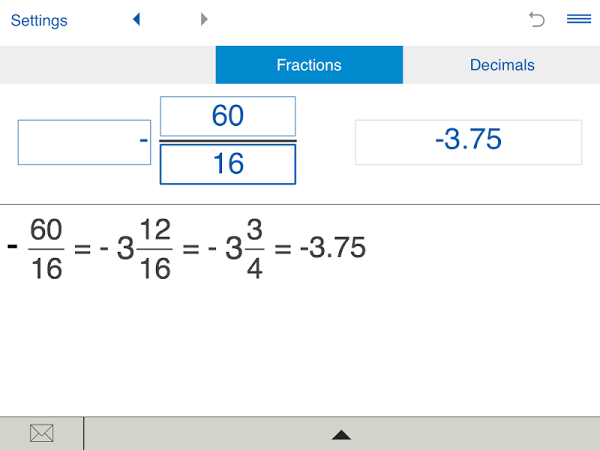 Наименьшее общее кратное этих чисел равно 30
Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.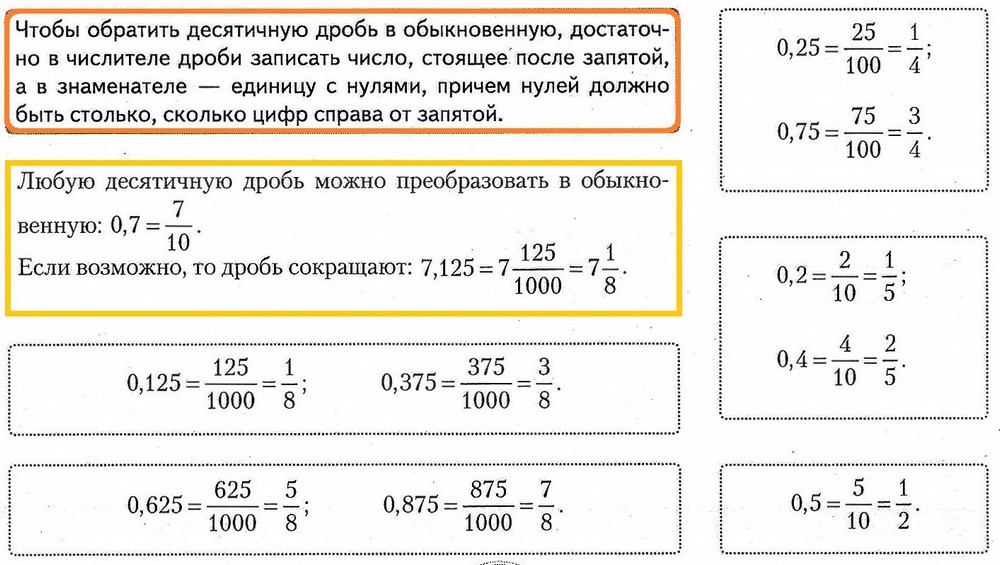
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2.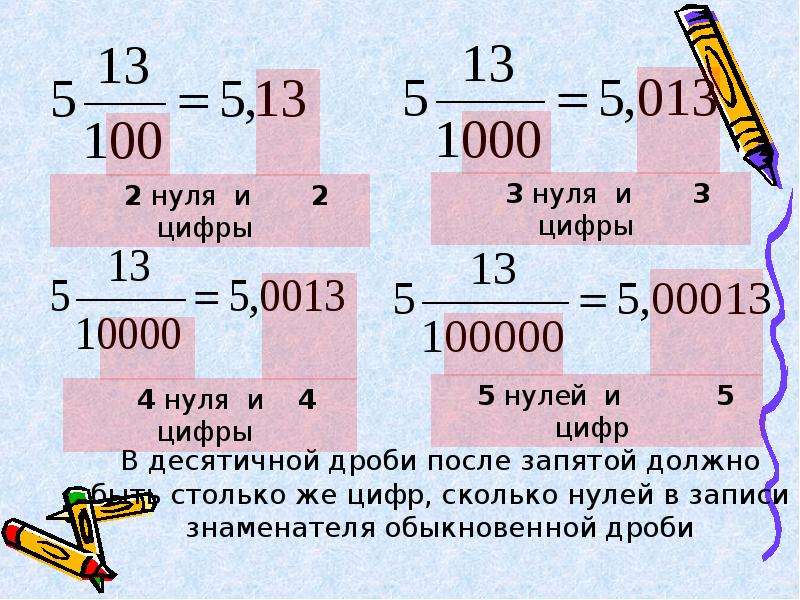 Действительно, четверть пиццы содержится в половине пиццы два раза:
Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как умножить обыкновенную дробь на десятичную дробь
В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную. Также разберем примеры для закрепления теоретического материала.
Произведение обыкновенной и десятичной дробей
Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой.
Примечания:
1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой.
2. Смешанные обыкновенные дроби сперва необходимо превратить в неправильные.
Примеры
Пример 1
Давайте найдем результат произведения дроби
3/20
и 2,19.
Решение 1
Переведем обыкновенную дробь в десятичную:
3/20
=
3⋅5/20⋅5
=
15/100
= 0,15
Теперь выполним умножение десятичных дробей:
0,15 ⋅ 2,19 = 0,3285.
Решение 2
Преобразуем десятичную дробь в обыкновенную:
2,19 = 2
19/100
=
2 ⋅ 100 + 19/100
=
219/100
Остается только найти произведение двух обыкновенных дробей:
219/100
⋅
3/20
=
219 ⋅ 3/100 ⋅ 20
=
657/2000
Пример 2
Умножим 6,24 на дробь 2
4/9
.
Решение
Преобразуем заданную смешанную дробь в неправильную:
2
4/9
=
2 ⋅ 9 + 4/9
=
22/9
Далее у нас есть выбор: либо мы переводим десятичную дробь в обыкновенную, либо наоборот. Выберем первый вариант.
6,24 = 6
24/100
=
6 ⋅ 100 + 24/100
=
624/100
Теперь разделим одну простую дробь на другую:
624/100
:
22/9
=
624/100
⋅
9/22
=
624 ⋅ 9/100 ⋅ 22
=
5616/2200
= 2
1216/2200
= 2
152/275
≈ 2,5528
Умножение обыкновенных и десятичных дробей
Умножение обыкновенных и десятичных дробей сводится к умножению либо обыкновенных дробей, либо десятичных дробей.
Чтобы умножить обыкновенную дробь на десятичную, надо обе дроби привести к одному виду.
Любую десятичную дробь можно перевести в обыкновенную (как слышим, так и пишем).
Например,
Если возможно, полученную дробь следует сократить.
Например,
Обыкновенную дробь перевести в десятичную (речь идёт о несократимой дроби) можно только в том случае, когда её знаменатель равен 2, 5 или числу, которое можно разложить на множители, состоящие только из двоек и пятёрок.
Например,
40=2∙2∙2∙5.
Разложение числа состоит только из двоек и пятёрок, значит, любое число можно разделить на 40. Делим 7 на 40 и получает представление обыкновенной дроби в виде десятичной.
Перейдём к примерам умножения обыкновенных и десятичных дробей.
Примеры.
1-й способ
Так как знаменатель обыкновенной дроби равен 5, эту дробь можно перевести в десятичную и выполнить умножение десятичных дробей:
2-й способ
Переведём десятичную дробь в обыкновенную, сократим полученную дробь и выполним умножение обыкновенных дробей:
то есть при любом способе получаем одинаковый ответ, отличается только форма записи.
Знаменатель обыкновенной дроби равен 14. 14=2∙7. Такую дробь перевести в десятичную перевести не получится. Значит, десятичную дробь представим в виде обыкновенной:
Здесь ответ может быть записан как в виде обыкновенной, так и в виде десятичной дроби.
Дробь со знаменателем 11 не можем представить в виде десятичной. Поэтому переводим десятичную дробь в обыкновенную:
1-й способ
Раскладываем знаменатель на простые множители: 4=2∙2.
Переводим обыкновенную дробь в десятичную:
2-й способ:
Сведём умножение десятичной и обыкновенной дробей к умножению обыкновенных дробей:
Я рекомендую при возможности выбора стараться работать как с обыкновенными, так и с десятичными дробями. Важно освоить навыки счёта на уроках математики в 5-6 классах, а старших классах вам предстоит решать другие задачи.
Вычисления с обыкновенными и десятичными дробями
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php on line 93
lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai. lt/public_html/trupmena-1-ru.php on line 112
lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Как рассчитать проценты, процент от числа
Квадратное уравнение — Калькулятор
Другие полезные темы:
| Делимся | знаниями |
Если думаешь, что Это интересно для друга, напиши
Умножение дробей и смешанных чисел.
 Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)Умножение дробей и смешанных чисел.
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Главное замечание по теме от проекта dpva.ru: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части).
Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть.
Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей. 2) первое произведение записать числителем, второе — знаменателем.
2) первое произведение записать числителем, второе — знаменателем.
Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.
Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят.
Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю.
Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
Умножение и деление десятичных дробей
С десятичными дробями намного проще производить разные действия, чем с обычными, но здесь также есть свои недостатки. Например, необходимо очень тщательно следить за положением десятичной запятой.
Например, рассмотрим пример умножения: 0,2х0,2.
Вы можете попробовать решить этот пример по аналогии со сложением: 2+2=4, также 2×2=4, тогда, поскольку 0,2+0,2=0,4. Возможно, и 0,2х0,2=0,4? Нет, этого не может быть, и я сейчас докажу вам это.
Перейдем обратно к обыкновенным дробям, с которыми мы научились так хорошо обращаться: $0,2=\frac{2}{10}$. Теперь перемножим дроби по старой методике: $\frac{2}{10} \times \frac{2}{10}=\frac{4}{100}$ (числитель умножаем на числитель, знаменатель на знаменатель). А в десятичных дробях — это 0,04. Следовательно, 0,2 х 0,2 отнюдь не равно 0,4. 0,2х0,2=0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82х0,21=0,1772, а 0,82х2,1=1,772. (Это можно проверить следующим образом: $\frac{82}{100} \times \frac{21}{100}=\frac{1772}{10000}$, а $\frac{82}{100} \times \frac{21}{10}=\frac{1772}{1000}$.)
Следовательно, 0,2 х 0,2 отнюдь не равно 0,4. 0,2х0,2=0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82х0,21=0,1772, а 0,82х2,1=1,772. (Это можно проверить следующим образом: $\frac{82}{100} \times \frac{21}{100}=\frac{1772}{10000}$, а $\frac{82}{100} \times \frac{21}{10}=\frac{1772}{1000}$.)
Теперь мы можем сформулировать общее правило:
При умножении десятичных дробей количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Так, при умножении 0,2х0,2 общее количество цифр справа от десятичной запятой в перемножаемых числах равно 2, и это означает, что 0,2х0,2=0,04 (ноль справа от десятичной запятой также является значащей цифрой).
Естественно, что если один из сомножителей является целым числом, то он не влияет на положение десятичной запятой. Положение десятичной запятой в произведении будет таким же, как и в том сомножителе, который является десятичной дробью.
То есть 0,2х2=0,4; 1,5х5=7,5; а 1,1х154=169,4.
Эти результаты соответствуют правилу умножения, и в любом случае количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Определить положение запятой в случае деления десятичных дробей можно по аналогичной методике, действуя в обратном порядке. Но обычно при делении процедуру стараются упростить и приводят делитель или знаменатель (если деление проводят с помощью обычных дробей) к виду целого числа, не содержащего значащих чисел справа после запятой.
Предположим, нам надо 1,82 разделить на 0,2. Это выражение можно записать как $\frac{1,82}{0,2}$. Не изменяя величины дроби, умножаем числитель и знаменатель на 10. Тогда 1,82х10 (в соответствии с правилом определения положения десятичного знака) равно 18,20, или 18,2, поскольку ноль, стоящий справа после последней значащей цифры, не изменяет величины числа и, следовательно, его можно опустить. Точно так же 0,2х10=2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2).
Точно так же 0,2х10=2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2).
Следовательно, дробь можно записать как $\frac{18,2}{2}$ – и теперь знаменатель является целым числом, следовательно, при делении положение десятичного знака после запятой не меняется, так же как и в случае деления. Раз в числителе одна значащая цифра справа после запятой, то и результат должен иметь одну значащую цифру справа после запятой, то есть — $\frac{18,2}{2}=9,1$.
Освоив деление десятичных дробей, мы сможем переводить обычные дроби в десятичные. Предположим, нам нужно найти десятичный эквивалент для $\frac{1}{40}$. Мы можем представить эту дробь в виде $\frac{1,000}{40}$, а затем произвести деление. Поскольку мы делим на целое число, то положение десятичной запятой не меняется. Проведем деление:
Таким образом, мы показали, что десятичный эквивалент $\frac{1}{40}$ равен 0,025. Это можно проверить, переведя 0,025 в обычную дробь: $0,025=\frac{2}{100}+\frac{5}{1000}$, или $\frac{20}{1000}+\frac{5}{1000}$, или $\frac{25}{1000}$, или если произвести деление, то получим $\frac{1}{40}$.
Ну, а если вы все-таки допустили ошибку при исчислении находясь заграницей, то что бы не выглядеть глупо в глазах иностранцев, обязательно надо исправится и извинится. Для тех, которые, как и я, не знаю, как извиниться по-английски, рекомендую почитать статью на сайте e-english.ru. Это значительно улучшит ваши познания и даст возможность не делать ошибок, хотя бы в этом.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Умножение и деление дробей. Тест — тренажер 6 класс — Kid-mama
Умножение и деление обыкновенных дробей
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните умножение или деление и введите ответ. Сократите дробь, если это возможно. Неправильную дробь переведите в смешанное число, иначе будет засчитана ошибка.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
С ответом
С отметкой о просмотре
Если вы не знаете, как умножать и делить обыкновенные дроби, читайте статью:
Тест можно использовать как тренажер, проходя его несколько раз. Каждый раз задания выпадают разные.
Умножение дроби на целое число
Чтобы умножить дробь на целое число, помните, что умножение — это повторное сложение.
Пример 1:
Умножить
1
7
⋅
3
.
Запишите умножение в виде сложения. Добавлять
1
7
три раза.
1
7
⋅
3
знак равно
1
7
+
1
7
+
1
7
Теперь нам просто нужно
добавить дроби
с одинаковыми знаменателями.Знаменатели оставьте неизменными, а числители сложите.
знак равно
(
1
+
1
+
1
)
7
знак равно
3
7
Пример 2:
Умножить
5
⋅
3
16
.
5
⋅
3
16
знак равно
3
16
+
3
16
+
3
16
+
3
16
+
3
16
знак равно
5
⋅
3
16
знак равно
15
16
Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем
1
.
5
⋅
3
16
знак равно
5
1
⋅
3
16
Затем умножьте
числители
а также
знаменатели
, согласно обычным правилам для
умножение дробей
.
знак равно
5
⋅
3
1
⋅
16
знак равно
15
16
В некоторых случаях ваш ответ может быть больше, чем
1
, поэтому вы захотите переписать его как
смешанное число
.Возможно, вам также придется
уменьшить фракцию
чтобы получить его в простейшем виде.
Пример 3:
Умножить
1
4
⋅
10
.
1
4
⋅
10
знак равно
10
4
И числитель, и знаменатель имеют общий множитель:
2
. Разделите оба на
2
.
знак равно
5
2
Перепишите эту неправильную дробь как смешанное число.
знак равно
2
1
2
Рабочий лист умножения дробей с общими знаменателями
Ричард Вильялонundefined undefined / Getty Images
Обновлено 21 февраля 2019 г.
Рабочий лист № 1 (Ответы на 2-й странице PDF)
Д. Рассел
Рассел
Распечатать PDF-файл: Рабочий лист № 1
Каждый рабочий лист содержит множество дробей с общим (одинаковым) знаменателем.При умножении дробей просто умножьте числитель (верхнее число), затем умножьте знаменатель (нижнее число) и при необходимости уменьшите до наименьшего члена.
- Пример 1: 1/4 x 3/4 = 3/16 (1 x 3 вверху и 3 x 4 внизу) в этом примере дробь не может быть уменьшена дальше.
- Пример 2: 1/3 x 2/3 = 2/9 Это не может быть уменьшено дальше.
- Пример 3: 1/6 x 2/6 = 2/36 В этом случае дробь может быть дополнительно уменьшена. Оба числа можно разделить на 2, что дает нам 1/18, что является сокращенным ответом.
Подобные рабочие листы содержат упражнения для учащихся, чтобы улучшить их понимание.
Рабочий лист № 2 (ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 2
Умножение неправильных дробей, Рабочий лист № 3 (ответы на 2-й странице PDF)
Д. Рассел
Рассел
Распечатать PDF-файл: Рабочий лист № 3
Рабочий лист № 4 (ответы на 2-й странице PDF)
Д.Рассел
Распечатать PDF: Рабочий лист № 4
Рабочий лист № 5 (Ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 5
Рабочий лист № 6 (ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 6
Рабочий лист № 7 (ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 7
Рабочий лист № 8 (ответы на 2-й странице PDF)
Д.Рассел
Распечатать PDF-файл: Рабочий лист № 8
Рабочий лист № 9 (ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 9
Рабочий лист № 10 (Ответы на 2-й странице PDF)
Д. Рассел
Распечатать PDF-файл: Рабочий лист № 10
Умножение и деление дробей, Урок 2
Mathscene — Умножение и деление дробей, Урок 2
| 2006 Rasmus ehf | Фракции | Печать |
Урок 2.
Умножение дробей и целых
номера:
| Изменить целое число в фракция | |
| Тогда умножить. |
Только числитель умножается на целое
числа.
Умножение дроби на
дробь: (общий знаменатель не обязателен)
| Первый умножить числители | ||
| Тогда умножаем знаменатели | ||
2 | 2 1 = 2 | Вы можно упростить, прежде чем умножить, и мы можем отменить обычное коэффициент 2 |
| 2 4 = 8 | ||
Замена смешанных чисел на
неправильные дроби:
Пример:
Умножьте целое число (2)
на знаменатель (3)
и прибавляем к числителю (1)
| Вы так это 2 3 + 1 = 7 | |
| В знаменатель остается прежним.  |
Смешанные числа заменены на
неправильные дроби перед умножением.
| Изменить смешанные числа в неправильные дроби | |
| Look для исключения общих факторов | |
| ср может отбросить множитель 4 из | |
| Тогда упростить, чтобы получить правильный ответ |
Сначала изменяются смешанные числа
на неправильные дроби, а затем упрощается.
Иногда переменные
(буквы) используются.
Применяются те же правила: первый
уменьшить, а затем упростить.
На дроби
Чтобы разделить дроби, инвертируйте
делитель (вторая дробь) и умножаем.
| инвертировать делитель (второй дробь) и умножаем | |
| Тогда упростить, исключив общие множители, умножить и упростить. |
Целые числа необходимо заменить на
фракции.
| Изменить целое число в дробь | |
| инвертировать делитель (вторая дробь) и умножаем |
Смешанные числа необходимо заменить на
неправильные дроби.
| Изменить смешать число в неправильную дробь | |
| инвертировать делитель (вторая дробь) и умножаем | |
| Затем продажа общие факторы и упростить |
Иногда алгебраические переменные
использовал.
| инвертировать делитель (вторая дробь) и умножаем | |
| Тогда исключая общие факторы и упрощая |
Те же правила применяются для номеров и
буквы.
Попробовать тест 2 на
Умножение и деление дробей.
Не забудьте использовать свой
Контрольный список.
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения окончательной неправильной дроби. |
| Умножить | Показывает последний шаг умножения. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД, чтобы уменьшить дробь. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей в дроби
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих указанное целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной.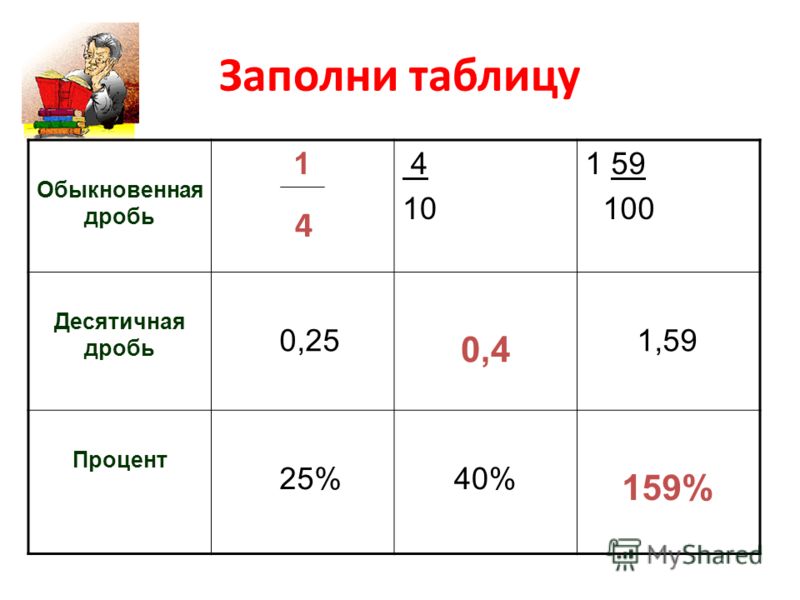 Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Отдел:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , равно
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.
Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздко, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.
Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.
Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Преобразование общей инженерной дроби в десятичную дробь
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 th | 32 nd | 16 th | 8 th | 4 th | 2 nd | (десятичное) | ||||||||||
| 1/64 | 0,015625 | 0,396875 | ||||||||||||||
| 2/64 | 1/32 | 03125 | 0,79375 | |||||||||||||
| 3/64 | 0,046875 | 1,1 | ||||||||||||||
| 4/64 2/64 | 0,0625 | 1,5875 | ||||||||||||||
| 5/64 | 0,078125 | 1,984375 | 0. 09375 09375 | 2.38125 | ||||||||||||
| 7/64 | 0.109375 | 2.778125 | 8/64 | 8/64 | 0,125 | 3,175 | ||||||||||
| 9/64 | 0,140625 | 3,571855 | 3,571875 | 0.15625 | 3.96875 | |||||||||||
| 11/64 | 0.171875 | 4.365625 | ||||||||||||||
| 0,1875 | 4,7625 | |||||||||||||||
| 13/64 | 0.203125 | 5,159375 | 0.21875 | 5.55625 | ||||||||||||
| 15/64 | 0,234375 | 5.953125 | 1/4 | 0,25 | 6,35 | |||||||||||
| 17/64 | 0,265625 | 0. 28125 28125 | 7,14375 | |||||||||||||
| 19/64 | 0,296875 | 7,540625 | ||||||||||||||
| 20/64 10/64 | ||||||||||||||||
| 20/64 10/64 | ||||||||||||||||
| 20/64 10/64 | 0,3125 | 7,9375 | ||||||||||||||
| 21/64 | 0,328125 | 8,334375 | ||||||||||||||
| 0.34375 | 8,73125 | |||||||||||||||
| 23/64 | 0,359375 | 9.128125 | ||||||||||||||
| 24/50 | ||||||||||||||||
| 24/50 9015 | 0,375 | 9,525 | ||||||||||||||
| 25/64 | 0,3 | 9.9218875 | 9.921875 | 0.40625 | 10.31875 | |||||||||||
| 27/64 | 0,421875 | 10. 715625 715625 | 10.715625 | |||||||||||||
| 1450 9015 9015 9015 9015 7/64 | 0,4375 | 11,1125 | ||||||||||||||
| 29/64 | 0,453125 | |||||||||||||||
| 0.46875 | 11. | |||||||||||||||
| 31/64 | 0,484375 | 12.303125 | ||||||||||||||
| 2/4 | 1/2 | 0,5 | 12,7 | |||||||||||||
| 33/64 | 0,515625 | 13166875 | 13166875 | 0.53125 | 13.49375 | |||||||||||
| 35/64 | 0,546875 | 13.8 | 36/64 9015 9015 9015 9015 | 0.5625 | 14.2875 | |||||||||||
| 37/64 | 0.578125 | 14.684375 | 0. 59375 59375 | 15.08125 | ||||||||||||
| 39/64 | 0.609375 | 15.478125 | 0,625 | 15.875 | ||||||||||||
| 41/64 | 0,640625 | 16.2161875 9015 9015 9015 9015 9015 9015 9015 9015 9015 | 0.65625 | 16.66875 | ||||||||||||
| 43/64 | 0,671875 | 17,065625 | 17.065625 | |||||||||||||
| 44/64 9015 9015 | 0,6875 | 17,4625 | ||||||||||||||
| 45/64 | 0,703125 | 17.859375 | 0.71875 | 18.25625 | ||||||||||||
| 47/64 | 0,734375 | 18.653125 | 48/64 | 1250/64 | 3/4 | 0,75 | 19,05 | |||||||||
| 49/64 | 0,765625 | 0. 78125 78125 | 19.84375 | |||||||||||||
| 51/64 | 0,796875 | 20.240625 | ||||||||||||||
| 9015/64/64 9015 9015 9015 9016 52/64 9015 | 0,8125 | 20,6375 | ||||||||||||||
| 53/64 | 0,828125 | 21,034375 | 0.84375 | 21,43125 | ||||||||||||
| 55/64 | 0,859375 | 21,828125 | ||||||||||||||
| 0,875 | 22,225 | |||||||||||||||
| 57/64 | 0,8 | 22.621875 9015 9015 9015 9015 9015 9015 | 0. | 23,01875 | ||||||||||||
| 59/64 | 0,921875 | 23,415625 | 60/64 9015 9015 9015 9015 | 0,9375 | 23,8125 | |||||||||||
| 61/64 | 0,953125 | 24. 2093151 9015 625 9015 625 9015 9015 9015 625 2093151 9015 625 9015 625 9015 9015 9015 625 | 0.96875 | 24.60625 | ||||||||||||
| 63/64 | 0,984375 | 25,003125 | 64/64 | 64/64 9015 | 4/4 | 2/2 | 1 | 25,4 |
Как рассчитать дроби
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь состоит из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, — это числитель . Второе число, расположенное под чертой, — это знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-либо делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из».Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Как можно представить дроби?
Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби.
- Правильная дробь — это дробь, в которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
- У неправильной дроби числитель больше знаменателя. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
- Смешанное число объединяет целое число и дробь. Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).
Упрощение дробей
Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.
Есть два способа упростить дробь.
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54
- Разделите еще раз на 2, чтобы получить 6/27
- Разделите на 3, чтобы получить 2/9
Сложение дробей
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить дробь ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½).
Дополнение: Пример 2
Допустим, вы хотите сложить дроби ⅓ и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей
Вычитание дробей работает аналогично:
- Шаг 1. Убедитесь, что знаменатели совпадают.
- Шаг 2. Вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: Пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей
Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
На дроби
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и у вас останется 3/2.
Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции.
Распространенные ошибки и на что следует обращать внимание
При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам нужно умножить дробь.
Возьмем для примера сложение ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Прочие типичных ошибок включают:
- При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы у них был общий знаменатель.
- Изменение знаменателя дроби без внесения необходимых изменений в числитель.
- Непонимание вопроса полностью; например, деление вместо вычитания или умножение вместо сложения.
- Знаменатель остается неизменным при ответах на вопросы, касающиеся умножения или сложения.
Понимание взаимосвязи между смешанными числами и неправильными дробями, а также того, как переводить одно в другое, имеет решающее значение при работе с дробями.
Дроби и десятичные дроби: умножение дробей и смешанных чисел Учебное пособие
Умножение дробей и смешанных чисел
Умножение дробей довольно просто по сравнению со сложением и вычитанием.И угадай что? Нам не нужно искать общий знаменатель. Мы, и , должны убедиться, что каждое число является дробной частью: смешанные числа или целые числа недопустимы. Это клуб элитной фракции.
Просто выполните следующие четыре простых шага:
- Преобразуйте все смешанные числа или целые числа в неправильные дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Уменьшите окончательный ответ и при необходимости преобразуйте его обратно в смешанное число.
Пример умножения 1
| Умножьте числители, затем умножьте знаменатели. | |
| Уменьшить дробь. 12 и 72 имеют GCF 12, поэтому разделите верхнюю и нижнюю на 12. | |
Стрела, вот и наш ответ. |
Пример умножения 2
Сокращение: перекрестное сокращение
Вместо уменьшения дроби в конце задачи мы можем перекрестно сократить перед умножением .Это не обязательно, но это сэкономит несколько шагов.
Перекрестное сокращение означает, что при умножении дробей мы можем уменьшить любой числитель с любым знаменателем . В этом примере 5 и 10 можно разделить на 5, даже если они не принадлежат к одной и той же дроби.
Давайте еще раз посмотрим на пример 1 и посмотрим, как использовать этот метод.
Обращение десятичной дроби в простую и обратно. Калькулятор онлайн.Перевод десятичной дроби в обыкновенную
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными .
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \). Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят,
что из неправильной дроби
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Зачастую дети, которые учатся в школе, интересуются, для чего в им в реальной жизни может понадобится математика, в особенности те разделы, которые уже заходят намного дальше, чем простой счет, умножение, деление, суммирование и отнимание. Многие взрослые также задаются данным вопросом, если их профессиональная деятельность очень далека от математики и разнообразных вычислений. Однако стоит понимать, что ситуации бывают всякие, и порой никак не обойтись без той самой, пресловутой школьной программы, от которой мы так пренебрежительно отказывались в детстве. К примеру, вовсе не все знают, как перевести дробь в десятичную дробь, а такие знания могут чрезвычайно пригодится, для удобства счета. Для начала, нужно полностью убедиться, что нужная вам дробь может быть преобразована в конечную десятичную. То же самое касается и процентов, которые также можно легко перевести в десятичные дроби.
Проверка обычной дроби на возможность перевода ее в десятичную
Прежде, чем что-либо считать, необходимо убедиться, что полученная в итоге десятичная дробь будет конечной, иначе она окажется бесконечной и высчитать окончательный вариант будет попросту невозможно. Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.
Причем бесконечные дроби также могут быть периодическими и простыми, но это уже тема для отдельного раздела.
Перевести обыкновенную дробь в ее конечный, десятичный вариант можно только в том случае, если ее уникальный знаменатель способен раскладываться только на множители 5 и 2 (простые множители). Причем даже в том случае, если они повторяются произвольное количество раз.
Уточним, что оба эти числа являются простыми, так в итоге разделить без остатка их можно только на самих себя, или же, на единицу. Таблицу простых чисел можно отыскать без проблем в сети интернет, это вовсе не сложно, хотя непосредственного отношения к нашему счету она и не имеет.
Рассмотрим примеры:
Дробь 7/40 поддается преобразованию из обычной дроби в ее десятичный эквивалент, потому что ее знаменатель можно без труда разложить на множители 2 и 5.
Однако, если первый вариант даст в результате конечную десятичную дробь, то, к примеру, 7/60 уже никак не даст подобного результата, так как ее знаменатель не будет уже раскладываться на искомые нами числа, а будет иметь в числе множителей знаменателя тройку.
Перевести обычную дробь в десятичную возможно несколькими способами
После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.
Как переводить дроби в десятичные: наиболее простой метод
Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.
Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.
Рассмотрим примеры:
Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.
Можно рассмотреть дополнительный пример, для наглядности:
Второй и боле популярный способ
переводить дроби в десятичныеВторой вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.
Стоит запомнить
Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.
По сути, дробь – это и есть деление, с этим не поспоришь.
Рассмотрим действие на примере:
Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.
Как перевести проценты в десятичную дробь : нет ничего прощеВот наконец дошел ход и до процентов, которые, оказывается, как гласит все та же, школьная программа, можно перевести в десятичную дробь. Причем тут все будет еще гораздо проще, и пугаться не стоит. Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.
Справятся с задачей даже те, кто не заканчивал университеты, а пятый класс школы вовсе прогулял и ничего не смыслит в математике.
Начать, пожалуй, нужно с определения, то есть разобраться, что такое, собственно, проценты. Процент – это одна сотая часть от какого-либо числа, то есть, абсолютно произвольно. От сотни, к примеру, это будет единица и так далее.
Таким образом, чтобы перевести проценты в десятичную дробь, нужно попросту убрать значок %, а потом разделить само число на сотню.
Рассмотрим примеры:
Причем, чтобы произвести обратную «конвертацию», нужно попросту сделать все наоборот, то есть, число нужно умножить на сотню и приписать к нему значок процента. Точно таким же образом, посредством применения полученных знаний, можно также и обычную дробь перевести в проценты. Для этого достаточно будет просто сперва преобразовать обычную дробь в десятичную, а потому уже ее перевести в проценты, а также легко можно произвести и обратное действие. Как видите, ничего сверхсложного нет, все это элементарные знания, которые просто необходимо держать в уме, в особенности, если имеете дело с цифрами.
Как видите, ничего сверхсложного нет, все это элементарные знания, которые просто необходимо держать в уме, в особенности, если имеете дело с цифрами.
Путь наименьшего сопротивления: удобные онлайн сервисы
Бывает и так, что считать совершенно не хочется, да и попросту нет времени. Именно для таких случаев, или же, особо ленивых пользователей, в сети интернет есть множество удобных и простых в применении сервисов, которые позволят перевести обычные дроби, а также проценты, в десятичные дроби. Это действительно дорога наименьшего сопротивления, потому пользоваться подобными ресурсами – одно удовольствие.
Полезный справочный портал «Калькулятор»
Для того, чтобы воспользоваться сервисом «Калькулятора», достаточно просто перейти по ссылке http://www.calc.ru/desyatichnyye-drobi.html , и ввести необходимые числа в нужные поля. Причем ресурс позволяет переводить в десятичные, как обычные, так и смешанные дроби.
После краткосрочного ожидания, приблизительно секунды в три, сервис выдаст конечный результат.
Точно таким же образом можно перевести в обычную дробь десятичную.
Онлайн-калькулятор на «Математическом ресурсе» Calcs.su
Еще одним, очень полезным сервисом можно назвать калькулятор дробей на «Математическом ресурсе. Тут также не придется ничего считать самостоятельно, просто выберите из предложенного списка то, что вам нужно и вперед, за орденами.
Далее, в отведенное специально для этого поле, нужно ввести искомое число процентов, которые и нужно преобразовать в обычную дробь. Причем если вам нужны десятичные дроби, то вы легко можете уже сами справиться с задачей перевода или же воспользоваться тем калькулятором, который для этого и предназначен.
В конечном итоге, стоит обязательно добавить, что сколько бы новомодных сервисов не было бы придумано, сколько ресурсов не предлагали бы вам свои услуги, но и голову тренировать периодически не помешает. Потому стоит обязательно применять полученные знания, тем более, что вы потом с гордостью сможете помогать делать уроки собственным детям, а затем и внукам. Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Для того же, кто страдает от вечной нехватки времени, подобные онлайн-калькуляторы на математических порталах окажутся как раз кстати и даже помогут понять, как перевести обычную дробь в десятичную.
Из курса алгебры школьной программы переходим к конкретике. В этой статье мы подробно изучим особый вид рациональных выражений – рациональные дроби , а также разберем, какие характерные тождественные преобразования рациональных дробей имеют место.
Сразу отметим, что рациональные дроби в том смысле, в котором мы их определим ниже, в некоторых учебниках алгебры называют алгебраическими дробями. То есть, в этой статье мы под рациональными и алгебраическими дробями будем понимать одно и то же.
По обыкновению начнем с определения и примеров. Дальше поговорим про приведение рациональной дроби к новому знаменателю и о перемене знаков у членов дроби. После этого разберем, как выполняется сокращение дробей. Наконец, остановимся на представлении рациональной дроби в виде суммы нескольких дробей. Всю информацию будем снабжать примерами с подробными описаниями решений.
Всю информацию будем снабжать примерами с подробными описаниями решений.
Навигация по странице.
Определение и примеры рациональных дробей
Рациональные дроби изучаются на уроках алгебры в 8 классе. Мы будем использовать определение рациональной дроби, которое дается в учебнике алгебры для 8 классов Ю. Н. Макарычева и др.
В данном определении не уточняется, должны ли многочлены в числителе и знаменателе рациональной дроби быть многочленами стандартного вида или нет. Поэтому, будем считать, что в записях рациональных дробей могут содержаться как многочлены стандартного вида, так и не стандартного.
Приведем несколько примеров рациональных дробей . Так , x/8 и — рациональные дроби. А дроби и не подходят под озвученное определение рациональной дроби, так как в первой из них в числителе стоит не многочлен, а во второй и в числителе и в знаменателе находятся выражения, не являющиеся многочленами.
Преобразование числителя и знаменателя рациональной дроби
Числитель и знаменатель любой дроби представляют собой самодостаточные математические выражения, в случае рациональных дробей – это многочлены, в частном случае – одночлены и числа. Поэтому, с числителем и знаменателем рациональной дроби, как и с любым выражением, можно проводить тождественные преобразования. Иными словами, выражение в числителе рациональной дроби можно заменять тождественно равным ему выражением, как и знаменатель.
Поэтому, с числителем и знаменателем рациональной дроби, как и с любым выражением, можно проводить тождественные преобразования. Иными словами, выражение в числителе рациональной дроби можно заменять тождественно равным ему выражением, как и знаменатель.
В числителе и знаменателе рациональной дроби можно выполнять тождественные преобразования . Например, в числителе можно провести группировку и приведение подобных слагаемых, а в знаменателе – произведение нескольких чисел заменить его значением. А так как числитель и знаменатель рациональной дроби есть многочлены, то с ними можно выполнять и характерные для многочленов преобразования, например, приведение к стандартному виду или представление в виде произведения.
Для наглядности рассмотрим решения нескольких примеров.
Пример.
Преобразуйте рациональную дробь так, чтобы в числителе оказался многочлен стандартного вида, а в знаменателе – произведение многочленов.
Решение.
Приведение рациональных дробей к новому знаменателю в основном применяется при сложении и вычитании рациональных дробей .
Изменение знаков перед дробью, а также в ее числителе и знаменателе
Основное свойство дроби можно использовать для смены знаков у членов дроби. Действительно, умножение числителя и знаменателя рациональной дроби на -1 равносильно смене их знаков, а в результате получится дробь, тождественно равная данной. К такому преобразованию приходится достаточно часто обращаться при работе с рациональными дробями.
Таким образом, если одновременно изменить знаки у числителя и знаменателя дроби, то получится дробь, равная исходной. Этому утверждению отвечает равенство .
Приведем пример. Рациональную дробь можно заменить тождественно равной ей дробью с измененными знаками числителя и знаменателя вида .
С дробями можно провести еще одно тождественное преобразование, при котором меняется знак либо в числителе, либо в знаменателе. Озвучим соответствующее правило. Если заменить знак дроби вместе со знаком числителя или знаменателя, то получится дробь, тождественно равная исходной. Записанному утверждению соответствуют равенства и .
Записанному утверждению соответствуют равенства и .
Доказать эти равенства не составляет труда. В основе доказательства лежат свойства умножения чисел. Докажем первое из них: . С помощью аналогичных преобразований доказывается и равенство .
Например, дробь можно заменить выражением или .
В заключение этого пункта приведем еще два полезных равенства и . То есть, если изменить знак только у числителя или только у знаменателя, то дробь изменит свой знак. Например, и .
Рассмотренные преобразования, позволяющие изменять знак у членов дроби, часто применяются при преобразовании дробно рациональных выражений.
Сокращение рациональных дробей
В основе следующего преобразования рациональных дробей, имеющего название сокращение рациональных дробей, лежит все тоже основное свойство дроби. Этому преобразованию соответствует равенство , где a , b и c – некоторые многочлены, причем b и c — ненулевые.
Из приведенного равенства становится понятно, что сокращение рациональной дроби подразумевает избавление от общего множителя в ее числителе и знаменателе.
Пример.
Сократите рациональную дробь .
Решение.
Сразу виден общий множитель 2 , выполним сокращение на него (при записи общие множители, на которые сокращают, удобно зачеркивать). Имеем . Так как x 2 =x·x и y 7 =y 3 ·y 4 (при необходимости смотрите ), то понятно, что x является общим множителем числителя и знаменателя полученной дроби, как и y 3 . Проведем сокращение на эти множители: . На этом сокращение завершено.
Выше мы выполняли сокращение рациональной дроби последовательно. А можно было выполнить сокращение в один шаг, сразу сократив дробь на 2·x·y 3 . В этом случае решение выглядело бы так: .
Ответ:
.
При сокращении рациональных дробей основная проблема заключается в том, что общий множитель числителя и знаменателя далеко не всегда виден. Более того, он не всегда существует. Для того, чтобы найти общий множитель или убедиться в его отсутствии нужно числитель и знаменатель рациональной дроби разложить на множители. Если общего множителя нет, то исходная рациональная дробь не нуждается в сокращении, в противном случае – проводится сокращение.
Если общего множителя нет, то исходная рациональная дробь не нуждается в сокращении, в противном случае – проводится сокращение.
В процессе сокращения рациональных дробей могут возникать различные нюансы. Основные тонкости на примерах и в деталях разобраны в статье сокращение алгебраических дробей .
Завершая разговор о сокращении рациональных дробей, отметим, что это преобразование является тождественным, а основная сложность в его проведении заключается в разложении на множители многочленов в числителе и знаменателе.
Представление рациональной дроби в виде суммы дробей
Достаточно специфическим, но в некоторых случаях очень полезным, оказывается преобразование рациональной дроби, заключающееся в ее представлении в виде суммы нескольких дробей, либо сумме целого выражения и дроби.
Рациональную дробь, в числителе которой находится многочлен, представляющий собой сумму нескольких одночленов, всегда можно записать как сумму дробей с одинаковыми знаменателями, в числителях которых находятся соответствующие одночлены. Например, . Такое представление объясняется правилом сложения и вычитания алгебраических дробей с одинаковыми знаменателями .
Например, . Такое представление объясняется правилом сложения и вычитания алгебраических дробей с одинаковыми знаменателями .
Вообще, любую рациональную дробь можно представить в виде суммы дробей множеством различных способов. Например, дробь a/b можно представить как сумму двух дробей – произвольной дроби c/d и дроби, равной разности дробей a/b и c/d . Это утверждение справедливо, так как имеет место равенство . К примеру, рациональную дробь можно представить в виде суммы дробей различными способами: Представим исходную дробь в виде суммы целого выражения и дроби. Выполнив деление числителя на знаменатель столбиком, мы получим равенство . Значение выражение n 3 +4 при любом целом n является целым числом. А значение дроби является целым числом тогда и только тогда, когда ее знаменатель равен 1 , −1 , 3 или −3 . Этим значениям отвечают значения n=3 , n=1 , n=5 и n=−1 соответственно.
Ответ:
−1 , 1 , 3 , 5 .
Список литературы.
- Алгебра: учеб.
 для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9. - Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да
логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.
До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да
логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.
Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?
Виды дробей. Преобразования.
Дроби бывают трёх видов.
1. Обыкновенные дроби , например:
Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.
И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.
Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.
32/8 = 32: 8 = 4
Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.
2. Десятичные дроби , например:
Именно в таком виде нужно будет записывать ответы на задания «В».
3. Смешанные числа , например:
Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.
Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !
С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !
Основное свойство дроби.
Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:
Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.
А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но. .. человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
.. человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .
Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.
Например, надо упростить выражение:
Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:
Все правильно. Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении
и получить снова
Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!
Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!
Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё… пока сокращается, короче. Получим 3/8! Куда приятнее, правда?
Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?
Как переводить дроби из одного вида в другой.
С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.
А если целых — не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .
Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .
А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.
Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…
Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.
На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.
Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000… Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.
А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333… Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
Кстати, это полезная информация для самопроверки. В разделе «В» в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.
Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками… Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.
Пусть в задачке вы с ужасом увидели число:
Спокойно, без паники соображаем.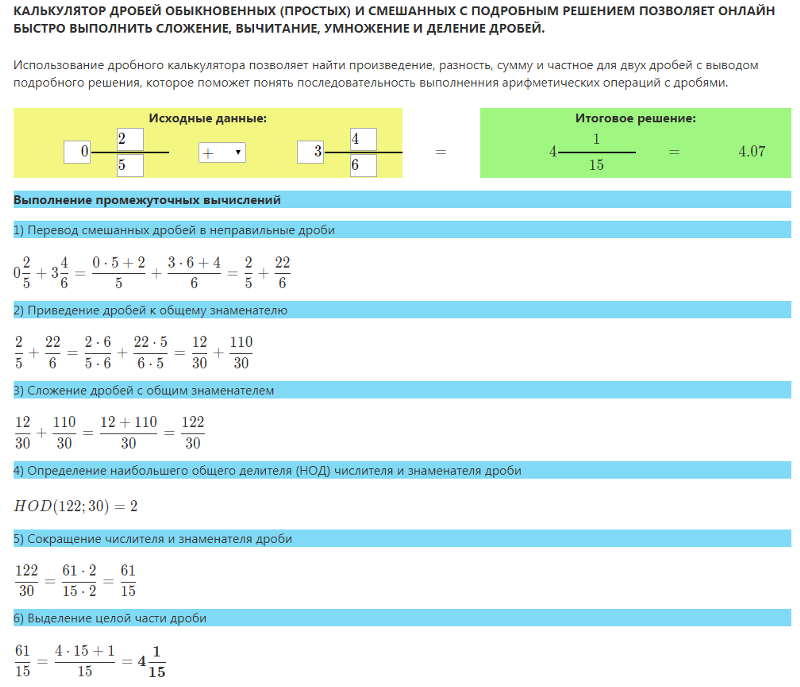 Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:
Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:
Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.
Обратная операция — перевод неправильной дроби в смешанное число — в старших классах редко требуется. Ну если уж… И если Вы — не в старших классах — можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.
Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?
Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Если в задании сплошь десятичные дроби, но гм… злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?
0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Подведём итоги этого урока.
1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.
Обыкновенные, десятичные и смешанные числа.
2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.
3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное — перейти к обыкновенным дробям.
Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
Должны получиться вот такие ответы (в беспорядке!):
На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего…) Если уж кто совсем крепко забыл, или ещё не освоил… Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас. )
)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В этой статье мы разберем, как осуществляется перевод обыкновенных дробей в десятичные дроби , а также рассмотрим обратный процесс – перевод десятичных дробей в обыкновенные дроби. Здесь мы озвучим правила обращения дробей и приведем подробные решения характерных примеров.
Навигация по странице.
Перевод обыкновенных дробей в десятичные дроби
Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби .
Сначала мы рассмотрим, как обыкновенные дроби со знаменателями 10, 100, 1 000, … представить в виде десятичных дробей . Это объясняется тем, что десятичные дроби по сути являются компактной формой записи обыкновенных дробей со знаменателями 10, 100, … .
После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, …
) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.
При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.
Теперь обо всем по порядку.
Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби
Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.
«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь после дописывания нулей будет иметь вид .
После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.
Дадим правило перевода правильной обыкновенной дроби со знаменателем 10, или 100, или 1 000, … в десятичную дробь . Оно состоит из трех шагов:
- записываем 0 ;
- после него ставим десятичную запятую;
- записываем число из числителя (вместе с дописанными нулями, если мы их дописывали).
Рассмотрим применение этого правила при решении примеров.
Пример.
Переведите правильную обыкновенную дробь 37/100 в десятичную.
Решение.
В знаменателе находится число 100 , в записи которого два нуля. В числителе находится число 37 , в его записи две цифры, следовательно, эта дробь не нуждается в подготовке к переводу в десятичную дробь.
Теперь записываем 0 , ставим десятичную запятую, и записываем число 37 из числителя, при этом получаем десятичную дробь 0,37 .
Ответ:
0,37 .
Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, …
в десятичные дроби разберем решение еще одного примера.
Пример.
Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.
Решение.
Количество цифр в числителе равно 3 , а количество нулей в знаменателе равно 7 , поэтому данная обыкновенная дробь нуждается в подготовке к переводу в десятичную. Нам нужно дописать 7-3=4 нуля слева в числителе, чтобы общее количество цифр там стало равно количеству нулей в знаменателе. Получаем .
Осталось составить нужную десятичную дробь. Для этого, во-первых, записываем 0 , во-вторых, ставим запятую, в-третьих, записываем число из числителя вместе с нулями 0000107 , в итоге имеем десятичную дробь 0,0000107 .
Ответ:
0,0000107 .
Неправильные обыкновенные дроби не нуждаются в подготовке при переводе в десятичные дроби. Следует придерживаться следующего правила перевода неправильных обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби :
- записываем число из числителя;
- отделяем десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.

Разберем применение этого правила при решении примера.
Пример.
Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.
Решение.
Во-первых, записываем число из числителя 56888038009, во-вторых, отделяем десятичной запятой 5 цифр справа, так как в знаменателе исходной дроби 5 нулей. В итоге имеем десятичную дробь 568 880,38009 .
Ответ:
568 880,38009 .
Для обращения в десятичную дробь смешанного числа , знаменателем дробной части которого является число 10 , или 100 , или 1 000, … , можно выполнить перевод смешанного числа в неправильную обыкновенную дробь, после чего полученную дробь обратить в десятичную дробь. Но можно пользоваться и следующим правилом перевода смешанных чисел со знаменателем дробной части 10, или 100, или 1 000, … в десятичные дроби :
- при необходимости выполняем «предварительную подготовку» дробной части исходного смешанного числа, дописав необходимое количество нулей слева в числителе;
- записываем целую часть исходного смешанного числа;
- ставим десятичную запятую;
- записываем число из числителя вместе с дописанными нулями.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.
Пример.
Переведите смешанное число в десятичную дробь.
Решение.
В знаменателе дробной части 4 нуля, в числителе же находится число 17 , состоящее из 2 цифр, поэтому, нам нужно дописать два нуля слева в числителе, чтобы там число знаков стало равно числу нулей в знаменателе. Выполнив это, в числителе окажется 0017 .
Теперь записываем целую часть исходного числа, то есть, число 23 , ставим десятичную запятую, после которой записываем число из числителя вместе с дописанными нулями, то есть, 0017 , при этом получаем искомую десятичную дробь 23,0017 .
Запишем все решение кратко: .
Несомненно, можно было сначала представить смешанное число в виде неправильной дроби, после чего перевести ее в десятичную дробь. При таком подходе решение выглядит так: .
Ответ:
23,0017 .
Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби
В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями 10, 100, …
, но обыкновенные дроби с другими знаменателями. Сейчас мы разберемся, как это делается.
Сейчас мы разберемся, как это делается.
В некоторых случаях исходная обыкновенная дробь легко приводится к одному из знаменателей 10 , или 100 , или 1 000, … (смотрите приведение обыкновенной дроби к новому знаменателю), после чего не составляет труда полученную дробь представить в виде десятичной дроби. Например, очевидно, что дробь 2/5 можно привести к дроби со знаменателем 10 , для этого нужно числитель и знаменатель умножить на 2 , что даст дробь 4/10 , которая по правилам, разобранным в предыдущем пункте, легко переводится в десятичную дробь 0,4 .
В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.
Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел , а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.
При этом деление выполняется так же, как деление столбиком натуральных чисел , а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.
Пример.
Переведите обыкновенную дробь 621/4 в десятичную дробь.
Решение.
Число в числителе 621 представим в виде десятичной дроби, добавив десятичную запятую и несколько нулей после нее. Для начала допишем 2 цифры 0 , позже, при необходимости, мы всегда можем добавить еще нулей. Итак, имеем 621,00 .
Теперь выполним деление столбиком числа 621,000
на 4
. Первые три шага ничем не отличаются от деления столбиком натуральных чисел, после них приходим к следующей картине:
Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:
На этом деление закончено, а в результате мы получили десятичную дробь 155,25
, которая соответствует исходной обыкновенной дроби.
Ответ:
155,25 .
Для закрепления материала рассмотрим решение еще одного примера.
Пример.
Переведите обыкновенную дробь 21/800 в десятичную дробь.
Решение.
Для перевода данной обыкновенной дроби в десятичную, выполним деление столбиком десятичной дроби 21,000…
на 800
. Нам после первого же шага придется поставить десятичную запятую в частном, после чего продолжить деление:
Наконец-то мы получили остаток 0 , на этом перевод обыкновенной дроби 21/400 в десятичную дробь закончен, и мы пришли к десятичной дроби 0,02625 .
Ответ:
0,02625 .
Может случиться, что при делении числителя на знаменатель обыкновенной дроби мы так и не получим в остатке 0
. В этих случаях деление можно продолжать сколь угодно долго. Однако, начиная с некоторого шага, остатки начитают периодически повторяться, при этом повторяются и цифры в частном. Это означает, что исходная обыкновенная дробь переводится в бесконечную периодическую десятичную дробь . Покажем это на примере.
Покажем это на примере.
Пример.
Запишите обыкновенную дробь 19/44 в виде десятичной дроби.
Решение.
Для перевода обыкновенной дроби в десятичную выполним деление столбиком:
Уже сейчас видно, что при делении начали повторяться остатки 8 и 36 , при этом в частном повторяются цифры 1 и 8 . Таким образом, исходная обыкновенная дробь 19/44 переводится в периодическую десятичную дробь 0,43181818…=0,43(18) .
Ответ:
0,43(18) .
В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.
Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.
Понятно, что если обыкновенную дробь можно привести к одному из знаменателей 10, 100, 1 000, …
, то полученную дробь легко перевести в конечную десятичную дробь по правилам, разобранным в предыдущем пункте. Но к знаменателям 10, 100, 1 000
и т.д. приводятся далеко не все обыкновенные дроби. К таким знаменателям можно привести лишь дроби, знаменатели которых являются хотя бы одного из чисел 10, 100, …
А какие числа могут быть делителями 10, 100, …
? Ответить на этот вопрос нам позволят чисел 10, 100, …
, а они таковы: 10=2·5
, 100=2·2·5·5
, 1 000=2·2·2·5·5·5, …
. Отсюда следует, что делителями 10, 100, 1 000
и т.д. могут быть лишь числа, разложения которых на простые множители содержат лишь числа 2
и (или) 5
.
Но к знаменателям 10, 100, 1 000
и т.д. приводятся далеко не все обыкновенные дроби. К таким знаменателям можно привести лишь дроби, знаменатели которых являются хотя бы одного из чисел 10, 100, …
А какие числа могут быть делителями 10, 100, …
? Ответить на этот вопрос нам позволят чисел 10, 100, …
, а они таковы: 10=2·5
, 100=2·2·5·5
, 1 000=2·2·2·5·5·5, …
. Отсюда следует, что делителями 10, 100, 1 000
и т.д. могут быть лишь числа, разложения которых на простые множители содержат лишь числа 2
и (или) 5
.
Теперь мы можем сделать общий вывод о переводе обыкновенных дробей в десятичные дроби:
- если в разложении знаменателя на простые множители присутствуют лишь числа 2 и (или) 5 , то эту дробь можно перевести в конечную десятичную дробь;
- если кроме двое и пятерок в разложении знаменателя присутствуют другие простые числа, то эта дробь переводится к бесконечную десятичную периодическую дробь.
Пример.
Не выполняя перевод обыкновенных дробей в десятичные, скажите, какие из дробей 47/20
, 7/12
, 21/56
, 31/17
можно перевести в конечную десятичную дробь, а какие — только в периодическую.
Решение.
Разложение на простые множители знаменателя дроби 47/20 имеет вид 20=2·2·5 . В этом разложении присутствуют лишь двойки и пятерки, поэтому эта дробь может быть приведена к одному из знаменателей 10, 100, 1 000, … (в этом примере к знаменателю 100 ), следовательно, может быть переведена в конечную десятичную дробь.
Разложение на простые множители знаменателя дроби 7/12 имеет вид 12=2·2·3 . Так как оно содержит простой множитель 3 , отличный от 2 и 5 , то эта дробь не может быть представлена в виде конечной десятичной дроби, но может быть переведена в периодическую десятичную дробь.
Дробь 21/56 – сократимая, после сокращения она принимает вид 3/8 . Разложение знаменателя на простые множители содержит три множителя, равных 2 , следовательно, обыкновенная дробь 3/8 , а значит и равная ей дробь 21/56 , может быть переведена в конечную десятичную дробь.
Наконец, разложение знаменателя дроби 31/17
представляет собой само 17
, следовательно, эту дробь нельзя обратить в конечную десятичную дробь, но можно обратить в бесконечную периодическую.
Ответ:
47/20 и 21/56 можно перевести в конечную десятичную дробь, а 7/12 и 31/17 — только в периодическую.
Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби
Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?
Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.
Из теоремы о делимости с остатком ясно, что остаток всегда меньше делителя, то есть, если мы выполняем деление некоторого целого числа на целое число q , то остатком может быть лишь одно из чисел 0, 1, 2, …, q−1 . Отсюда следует, что после завершения деления столбиком целой части числителя обыкновенной дроби на знаменатель q , не более чем через q шагов возникнет одна из двух следующих ситуаций:
- либо мы получим остаток 0 , на этом деление закончится, и мы получим конечную десятичную дробь;
- либо мы получим остаток, который уже появлялся ранее, после этого остатки начнут повторяться как в предыдущем примере (так как при делении равных чисел на q
получаются равные остатки, что следует из уже упомянутой теоремы о делимости), так будет получена бесконечная периодическая десятичная дробь.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.
Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь разберемся, как перевести десятичную дробь в обыкновенную. Начнем с перевода конечных десятичных дробей в обыкновенные дроби. После этого рассмотрим метод обращения бесконечных периодических десятичных дробей. В заключение скажем о невозможности перевода бесконечных непериодических десятичных дробей в обыкновенные дроби.
Перевод конечных десятичных дробей в обыкновенные дроби
Получить обыкновенную дробь, которая записана в виде конечной десятичной дроби, достаточно просто. Правило перевода конечной десятичной дроби в обыкновенную дробь состоит из трех шагов:
- во-первых, записать данную десятичную дробь в числитель, предварительно отбросив десятичную запятую и все нули слева, если они есть;
- во-вторых, в знаменатель записать единицу и к ней дописать столько нулей, сколько цифр находится после запятой в исходной десятичной дроби;
- в-третьих, при необходимости выполнить сокращение полученной дроби.

Рассмотрим решения примеров.
Пример.
Обратите десятичную дробь 3,025 в обыкновенную дробь.
Решение.
Если в исходной десятичной дроби убрать десятичную запятую, то мы получим число 3 025 . В нем нет нулей слева, которые бы мы отбросили. Итак, в числитель искомой дроби записываем 3 025 .
В знаменатель записываем цифру 1 и справа к ней дописываем 3 нуля, так как в исходной десятичной дроби после запятой находятся 3 цифры.
Так мы получили обыкновенную дробь 3 025/1 000 . Эту дробь можно сократить на 25 , получаем .
Ответ:
.
Пример.
Выполните перевод десятичной дроби 0,0017 в обыкновенную дробь.
Решение.
Без десятичной запятой исходная десятичная дробь имеет вид 00017 , отбросив нули слева получаем число 17 , которое и является числителем искомой обыкновенной дроби.
В знаменатель записываем единицу с четырьмя нулями, так как в исходной десятичной дроби после запятой 4
цифры.
В итоге имеем обыкновенную дробь 17/10 000 . Эта дробь несократима, и перевод десятичной дроби в обыкновенную закончен.
Ответ:
.
Когда целая часть исходной конечной десятичной дроби отлична от нуля, то ее можно сразу перевести в смешанное число, минуя обыкновенную дробь. Дадим правило перевода конечной десятичной дроби в смешанное число :
- число до десятичной запятой надо записать как целую часть искомого смешанного числа;
- в числитель дробной части нужно записать число, полученное из дробной части исходной десятичной дроби после отбрасывания в ней всех нулей слева;
- в знаменателе дробной части нужно записать цифру 1 , к которой справа дописать столько нулей, сколько цифр находится в записи исходной десятичной дроби после запятой;
- при необходимости выполнить сокращение дробной части полученного смешанного числа.
Рассмотрим пример перевода десятичной дроби в смешанное число.
Пример.
Представьте десятичную дробь 152,06005 в виде смешанного числа
Перевод десятичных чисел в дробь: онлайн калькулятор
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/103 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/106 = 625/1000000.
По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Десятичные дроби, формулы и онлайн калькуляторы
Содержание:
Определение
Десятичная дробь — это дробь, полученная в результате деления единицы на десять, сто, тысячу и т.д. частей.
При записи десятичных дробей нет необходимости указывать знаменатель, он определяется местом, которое занимает соответствующая цифра. Слева от десятичной точки/запятой записывается целая часть заданного числа, а первая цифра справа от нее означает число десятых, вторая — число сотых, третья — число тысячных и так далее. Цифры, стоящие справа от запятой, называются десятичными знаками. Пример:
Десятичную дробь достаточно просто представить в виде обыкновенной дроби. Число целых обыкновенной дроби равно числу целых десятичной дроби. Далее в числителе пишем цифры, стоящие после запятой, а в знаменателе записываем 1 с таким количеством нулей, сколько цифр стоит после запятой.
Пример. Представить десятичную дробь 2,345678 в виде обыкновенной дроби.
Свойства десятичных дробей
Если справа к десятичной дроби добавить нули, то значение дроби не меняется.
Пример. $3,45 = 3,450 = 3,4500$
Десятичная дробь не изменится, если убрать нули, стоящие в конце дроби.
Пример. $3,4500 = 3,45$
- Если десятичную запятую перенести на одну, две и т.д. позиций вправо, то значение дроби увеличится в 10, 100 и т.д. раз.
- Если десятичную запятую перенести на одну, две и т.д. позиций влево, то значение дроби уменьшится в 10, 100 и т.д. раз.
Десятичная дробь, после десятичной запятой которой стоит конечное число цифр, называется конечной, и дробь называется бесконечной в противном случае.
Бесконечная десятичная дробь, в которой одна или несколько цифр неизменно повторяются в одной и той же последовательности, называется периодической десятичной дробью. Повторяющиеся цифры называются периодом. Для сокращения записи период берут в скобки.
Пример
$4,234567567567567 \ldots=4,234(567)$
Периодическая дробь называется чистой, если период начинается сразу после запятой; смешанной, если между запятой и периодом есть одна или более неповторяющихся цифр.
Слишком сложно?
Десятичные дроби не по зубам? Тебе ответит эксперт через 10 минут!
Пример
$23,(91)$ — чистая периодическая дробь; $23,45(91)$ — смешанная периодическая дробь.
Читать следующую тему: иррациональные числа.
Онлайн-калькулятор для деления в столбик десятичных дробей
Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения.
Читайте также: Конвертеры величин онлайн
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга. Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.
Способ 1: OnlineMSchool
Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так:
Перейти на сайт OnlineMSchool
- Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
- Внизу вы найдете сервисы для теории чисел. Выберите там «Деление в столбик» или «Деление в столбик с остатком».
- В первую очередь обратите внимание на инструкцию по использованию, представленную в соответствующей вкладке. Рекомендуем с ней ознакомиться.
- Теперь вернитесь в «Калькулятор». Здесь вам следует еще раз убедиться, что выбрана правильная операция. Если нет, измените ее, воспользовавшись всплывающим меню.
- Введите два числа, используя точку для обозначения целой части дроби, а также отметьте галочкой пункт, если необходимо делить остаток.
- Для получения решения щелкните левой кнопкой мыши на знаке равно.
- Вам будет предоставлен ответ, где подробно расписан каждый шаг получения конечного числа. Ознакомьтесь с ним и можете переходить к следующим вычислениям.
Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным.
Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool.
Способ 2: Rytex
Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом:
Перейти на сайт Rytex
- Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи «Онлайн калькуляторы».
- Опуститесь в самый низ вкладки и на панели слева отыщите «Деление столбиком».
- Перед началом выполнения основного процесса прочтите правила использования инструмента.
- Теперь в соответствующие поля введите первое и второе число, а затем укажите, нужно ли делить остаток, отметив галочкой необходимый пункт.
- Для получения решения нажмите на кнопку «Вывести результат».
- Теперь вы можете узнать, как было получено итоговое число. Поднимитесь выше по вкладке, чтобы перейти к вводу новых значений для дальнейшей работы с примерами.
Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру.
Читайте также:
Сложение систем счисления онлайн
Перевод из восьмеричной в десятичную онлайн
Перевод из десятичной в шестнадцатеричную систему онлайн
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТДеление в столбик десятичных дробей с помощью онлайн-калькулятора
Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения.
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга. Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.
Способ 1: OnlineMSchool
Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так:
- Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
В первую очередь обратите внимание на инструкцию по использованию, представленную в соответствующей вкладке. Рекомендуем с ней ознакомиться.
Теперь вернитесь в «Калькулятор». Здесь вам следует еще раз убедиться, что выбрана правильная операция. Если нет, измените ее, воспользовавшись всплывающим меню.
Введите два числа, используя точку для обозначения целой части дроби, а также отметьте галочкой пункт, если необходимо делить остаток.
Вам будет предоставлен ответ, где подробно расписан каждый шаг получения конечного числа. Ознакомьтесь с ним и можете переходить к следующим вычислениям.
Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным.
Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool.
Способ 2: Rytex
Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом:
- Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи «Онлайн калькуляторы».
Опуститесь в самый низ вкладки и на панели слева отыщите «Деление столбиком».
Перед началом выполнения основного процесса прочтите правила использования инструмента.
Теперь в соответствующие поля введите первое и второе число, а затем укажите, нужно ли делить остаток, отметив галочкой необходимый пункт.
Для получения решения нажмите на кнопку «Вывести результат».
Теперь вы можете узнать, как было получено итоговое число. Поднимитесь выше по вкладке, чтобы перейти к вводу новых значений для дальнейшей работы с примерами.
Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Калькулятор дробей: решение уравнений с дробями
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Онлайн калькулятор уравнений с дробями
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.
- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление в столбик онлайн. Калькулятор наглядного деления.
Деление столбиком онлайн калькулятор может разделить столбиком два числа выдавая полностью расписанный процесс деления.
Калькулятор деления в столбик поддерживает целые числа, десятичные дроби,отрицательные числа и результат с остатком.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме
Для простоты вычислений умножим делимое 1.5 и делитель 9 на 10. Результат (частное) от этого не изменится. В результате пример сводится к делению следующих чисел:
| – | 1 | 5 | 9 | ||||||||||||
| 9 | . | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | ||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| – | 6 | ||||||||||||||
| 5 | 4 | ||||||||||||||
| 6 |
Просто введите делимое в поле 1 и делитель в поле 2 и нажмите кнопку “ВЫЧИСЛИТЬ”. Результат появится на экране.
Поддерживаются следующие виды чисел:
1. Целые(1,2,3. ). 2. Десятичное (1.1, 2,35). 3. Отрицательные (-7.35,-2). Дробные числа умножаются на 10 пока не станут целыми.
Разделить одно число на другое является самой сложной задачей арифметики. Данный калькулятор может помочь Вам разобраться как это сделать самостоятельно.
Самое важное запомните: Деление – это обратная операция умножения.
После проведения расчета нажмите на кнопочку “Расчет не верен” если Вы обнаружили ошибку. Или нажмите “расчет верный” если ошибок нет.
Этот калькулятор умеет умножать столбиком два числа.Можно умножать целые и дробные числа, положительные и отрицательные.
Сложение столбиком двух чисел. Можно сложить столбиком два любых числа. Показываются все переносы.
Калькулятор вычитает столбиком и показывает подробное решение.
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Деление в столбик десятичных дробей с помощью онлайн-калькулятора
Как работать с калькулятором обыкновенных дробей?
Калькулятор предназначен для решения простых дробей и дробей с целыми числами (смешанных). В будущем, планируется внедрение функции решения десятичных дробей, но в данный момент она отсутствует.
Для начала работы с дробным калькулятором необходимо понять очень простой принцип ввода данных. Все целые числа вводятся с помощью больших кнопок, расположенных слева. Все числители вводятся с помощью маленьких белых кнопок, расположенных в правом верхнем блоке цифр. Все знаменатели, соответственно, вводятся путем нажатия на кнопки в правом нижнем углу. Данный способ ввода данных является в некотором роде инновационным, поскольку четко разграничивает целое, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным.», после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
Теперь нажмите на кнопку равно и получите результат калькуляции. В примере выше проиллюстрирован практически весь арсенал возможностей калькулятора дробей. Точно таким же образом, вы можете осуществлять умножение, деление и вычитание дробей, как простых, так и алгебраических, с одинаковыми и разными знаменателями, целыми числами и т.д. Также, калькулятор может вычислить проценты от дробей, что требуется не так часто, но тем не менее очень важно для решения многих актуальных задач.
Если вам требуется сделать положительное число отрицательным, то сначала введите число, а потом нажмите на кнопку «+/-». После этого число или дробь автоматически обернется в скобки с отрицательным значением или наоборот (в зависимости от изначального статуса числа). Если необходимо удалить число, числитель или знаменатель, то воспользуйтесь соответствующей стрелкой Backspace, которая есть в блоке и числителя и знаменателя. Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Управление калькулятором дробей с клавиатуры.
Использовать калькулятор дробей онлайн можно не только с помощью компьютерной мыши, но и с помощью клавиатуры. Здесь логика очень проста:
- Все целые числа вводятся как обычно, нажатиями на клавиши чисел.
- Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1).
- Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).
Действия умножения, деления, сложения и вычитания так же инициируются соответствующими кнопками клавиатуры, если они есть (обычно располагаются в правой части, в так называемой области Numpad). Удаление производится нажатием на клавишу Backspace. Действие очистки (красная кнопка «C») вызывается нажатием на клавишу «C». Квадратный корень – нажатием на соседнюю клавишу «V» . Удаление производится нажатием на клавишу Backspace.
Зачем нужен калькулятор дробей онлайн?
Калькулятор дробей онлайн предназначен для решения обыкновенных и смешанных дробей (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно превосходит аналогичные онлайн приложения.
Калькулятор простых дробей онлайн поможет вам решить примеры с дробями и при этом вам не надо беспокоиться о том, как предварительно сократить дробь. Здесь это сделается автоматически, т.к. приложение само вычисляет общий знаменатель и выдает вам готовый результат на экран.
В чем преимущества такого способа решения дробей?
Калькулятор поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении алгебраических дробей или отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор обыкновенных дробей полностью бесплатный и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Работать можно с помощью мыши или прямо с клавиатуры (это касается как чисел, так и действий). Мы постарались реализовать максимально удобный интерфейс дробных вычислений, благодаря чему сложные математические калькуляции превратятся для вас в одно удовольствие! 🙂
Калькулятор дробей: сложение, вычитание, умножение, деление
С помощью онлайн калькулятора дробей вы легко сможете складывать, умножать, вычитать, делить и возводить в степень обыкновенные, смешанные и десятичные дроби, преобразовывать десятичные дроби в обыкновенные, неправильные дроби в смешанные и наоборот. Вам необходимо лишь ввести исходные данные, используя интерфейсные визуальные кнопки или клавиатуру. Дробный онлайн калькулятор очень простой и удобный в использовании.
Дробь — число, представляющее одну часть единицы или несколько равных ее частей. Записывается дробь в виде двух чисел, разделенных горизонтальной чертой. Над чертой располагается числитель, под чертой — знаменатель, показывающий на сколько одинаковых частей разделено целое. В числителе показано, сколько частей взято от целого. Когда числитель меньше знаменателя, дробь — правильная, если больше знаменателя — неправильная. Выделить целую часть из правильной дроби нельзя, т.к. результат от деления числителя на знаменатель меньше единицы. В неправильной дроби это возможно. Частное от деления числителя неправильной дроби на ее знаменатель покажет число целых единиц.
Смешанной называется дробь в виде целого числа и правильной дроби. Для преобразования неправильной дроби в смешанную, выделяется число целых единиц путем деления числителя на знаменатель. В смешанной дроби частное от деления — число целых единиц, остаток от деления заносим в числитель.
Дробь без целого числа — простая дробь. Десятичная дробь записывается без знаменателя, т.к. в знаменателе будет только единица с последующими нулями. Из двух десятичных дробей больше та, у которой больше число целых. Если число целых равно, больше число десятых и т.д.
В повседневной жизни мы постоянно сталкиваемся с необходимостью совершать математические действия. Это могут быть простые арифметические расчеты в виде сложения, вычитания, а возможны и более сложные финансовые, хозяйственные расчеты, где приходится сталкиваться с простыми и десятичными дробями, которые окружают нас повсюду, являются неотъемлемой частью нашей жизни. Слив содержимое двух пол-литровых банок (0,5 + О,5 или ½ + ½) в одну литровую мы складываем обыкновенные или десятичные дроби, поделив пирог на равные части по числу присутствующих, мы дробим целое число на доли, хотя совершенно не задумываемся об этом. И это лишь простейшие примеры из нашей обычной жизни. Представителям же естественно-научных, инженерно-технических специальностей постоянно приходится решать более сложные задачи, непосредственно связанные с дробными числами. Неточные инженерные расчеты могут повлечь за собой разрушение мостов, дорог, всевозможных сооружений. Физики с невероятной точностью определяют размеры и количество атомов, из которых состоят тела. Создание счетных машин непосредственно связано с десятичными дробями. Людям разных профессий необходимо знать правила дробей, уметь решать как простейшие, так и сложные задачи на дроби.
Калькулятор десятичной дроби в дробь
Добро пожаловать в наш калькулятор десятичной дроби в дробь — умный инструмент, который поможет вам преобразовать любую десятичную дробь в дробь в мгновение ока . Вы узнаете, как преобразовать десятичную дробь в дробь или даже как преобразовать повторяющиеся десятичные дроби в дроби. Основная идея этого конвертера дробей состоит в том, чтобы записать любое десятичное число в дробь — отношение двух целых чисел.
Почему полезно преобразовывать десятичную дробь в дробь?
В повседневной жизни мы используем числа, как десятичные, так и дробные.Хотя десятичные дроби могут казаться более естественными для записи, рано или поздно могут возникнуть некоторые проблемы.
Например, используя рациональные числа, мы иногда вынуждены округлять значения в какой-то момент, в зависимости от того, сколько значащих цифр нам нужно использовать. Запись того же числа в дробной форме дает нам точное значение .
Вычислить дробные показатели с дробями проще, чем с десятичными. Что такое 4 2,5 ? Что ж, на первый взгляд это не так очевидно.Но как насчет 4 5 / 2 ? Это проще представить как (√4) ⁵ = 2⁵ = 32 . Эта проблема становится еще более проблематичной, когда мы имеем дело с повторяющимися цифрами, поэтому стоит знать, как преобразовать повторяющуюся десятичную дробь в дробь.
Есть также более практичные способы использования дробей вместо десятичных. Представьте, что вы на вечеринке и хотите разделить торт или пиццу на равные части. Если есть группа из шести человек, сколько из общего числа получит каждый? Это либо около 0.166 или точно 1 / 6 — это ваш выбор.
С другой стороны, вы можете решить и наоборот, изменив любую дробь на десятичную или даже дробь на процент. Все зависит от контекста.
Как превратить десятичную дробь в дробь?
Наша цель — найти двух целых чисел , числителя и знаменателя, которые делятся сами на себя и составляют начальное значение. Допустим, мы хотим оценить, что 0.125 составляет в виде дроби:
Установите начальный числитель таким же, как начальное число (
0,125), а знаменатель установите как1.Переместите десятичную точку в конец числителя
0,125 → 1,25 → 12,5 → 125. Каждый скачок соответствует умножению числителя на 10.Поскольку мы переместили точку на три цифры, это означает, что мы должны умножить знаменатель на 1000, что составляет 10 в степени 3.
Найдите наибольший общий множитель
125и1000, который равен 125.Разделите оба значения на 125, в числителе будет
1, а в знаменателе —8.В результате этого конвертера дробей мы обнаружили, что
0,125в виде дроби составляет1 / 8.
Как преобразовать повторяющуюся десятичную дробь в дробь?
Преобразование повторяющейся десятичной дроби в дробь немного сложнее.Давайте посмотрим, как наш калькулятор десятичной дроби справится с этой задачей. Учтем 0,6252525… , то есть 0,625 с двумя повторяющимися цифрами. Мы также можем записать его как 0,625 или 0,6 (25) :
Пусть наше число будет
x, так чтоx = 0,6252525….Умножьте это на 100, что равно 10 в степени 2 (количество повторяющихся цифр).
100x = 62,5252525….Вычтите эти два значения:
100x - x = 99x = 62.5252525… - 0,6252525… = 61,9. Как видите, с помощью этого трюка завершающие цифры просто сокращают !Перемещайте десятичную точку, пока значение не станет целым числом:
61,9 → 619. Это эквивалентно умножению числа на 10, поэтому990x = 619.Разделим обе стороны на 990, получим
x = 619 / 990.Оцените наибольший общий делитель 619 и 990, чтобы узнать, можем ли мы упростить дробь.На самом деле gcd равен 1. Это означает, что 619 и 990 являются взаимно простыми числами , так что наша дробь уже представлена в простейшей форме.
0,625в виде дроби будет619 / 990.
Как использовать калькулятор десятичной дроби? — Конвертер дробей на практике
Теперь, когда мы знаем, как преобразовать десятичную дробь в дробь, давайте рассмотрим проблему. Есть ли разница между a = 1,83 и b = 1.833 ? Другими словами, имеет ли значение количество повторяющихся цифр для преобразования дроби, и если да, то каким образом? Начните с a :
- Одна повторяющаяся цифра означает, что нам нужно найти
9a, что составляет16,5. - Умножение на 10 дает
90a = 165, так чтоa = 165 / 90. - gcf 165 и 90 равно 15, поэтому мы можем записать дробь в ее простейшей форме:
a = 11 / 6.
Так как насчет того, чтобы превратить другую десятичную дробь в дробь, выполнив ту же процедуру?
- Две повторяющиеся цифры означают, что нам нужно найти
99b, что составляет181,5. - Умножение на 10 дает
990b = 1815, так чтоb = 1815 / 990. - Gcf 1815 и 990 равняется 165, поэтому мы можем записать дробь в ее простейшей форме:
b = 11 / 6.
Отлично! a и b абсолютно одинаковы. Вы можете проверить это с помощью этого калькулятора десятичной дроби, если вы еще не уверены! Вы можете записать десятичную дробь по-разному, и это не изменит результат преобразования ее в дробь.
Кроме того, вы можете преобразовать результат из неправильной дроби в смешанное число. Это можно сделать двумя способами:
Разделите числитель и знаменатель и возьмите целую часть результата.Для дробной части используйте оператор по модулю над числителем со знаменателем в качестве делителя.
… или переписать целую часть в начале и просто преобразовать десятичную часть в дробную. В конце соедините обе части.
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи с дробями в словах:
следующие математические задачи »
Калькулятор от десятичной дроби к дроби — онлайн-калькулятор от десятичной к дроби
Что такое калькулятор десятичной дроби?
Калькулятор десятичных дробей — это инструмент, преобразующий десятичные числа в их дробную форму.
Онлайн-калькуляторCuemath поможет вам преобразовать десятичные дроби в дроби за несколько секунд.
Как использовать калькулятор десятичных дробей?
Следуйте инструкциям ниже и попробуйте использовать калькулятор.
- Шаг 1: Введите десятичное число в поле.
- Шаг 2: Щелкните «Преобразовать» , чтобы получить дробное число.
- Шаг 3: Щелкните «Сбросить» , чтобы ввести новый номер.
Как преобразовать десятичную дробь в дробную?
Выполните следующие действия, чтобы преобразовать десятичную дробь в дробную.
Шаг 1: Запишите десятичное число в виде дроби, например: десятичное / 1
Шаг 2: Умножьте числитель и знаменатель на 10 для каждого числа после десятичной точки. (Например, если после десятичной точки стоят два числа, используйте 100, если их три, используйте 1000 и т. Д.)
Шаг 3: Упростите или уменьшите дробь
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример на калькуляторе десятичных дробей
Решенный пример 1:
Что такое 2,6 в виде дроби?
Решение:
Для десятичного числа 2.6 разрядным значением цифры после десятичной дроби является единица.
Итак, убрав десятичную дробь, в знаменателе запишем 10 = 26/10
При дальнейшем упрощении получаем 13/5
Аналогично
- 10.6 записывается как 106/10 или 53/5 в дробной форме.
- 48.02 записывается как 4802/100 или 2401/50 в дробной форме.
Теперь попробуйте калькулятор и преобразуйте следующие десятичные числа в дроби:
Десятичный калькулятор дробей — Дюймовый калькулятор
Преобразуйте десятичное число в дробь с помощью нашего калькулятора, введя десятичное значение ниже. Калькулятор показывает всю работу в решении, поэтому вы можете видеть каждый шаг.
Решенная фракция:
.75 = 34
Шаги для преобразования десятичной дроби в дробь
Преобразуйте десятичную дробь в дробную, поместив десятичную дробь над 1 в формате дроби
0,75 = 0,75 1
Умножьте числитель и знаменатель на 10, чтобы удалить десятичные разряды
0,75 × 101 × 10 = 7,510
Умножьте числитель и знаменатель на 10, чтобы удалить десятичные знаки
7.5 × 1010 × 10 = 75100
Уменьшите дробь, найдя наибольший общий делитель. Наибольший общий делитель 75 и 100 равен 25
Разделите числитель и знаменатель на наибольший общий делитель (25)
75 ÷ 25100 ÷ 25 = 34
Вы хотите преобразовать дробь в десятичную?
Как преобразовать десятичную дробь в дробную
Десятичные и дробные числа представляют собой число, не являющееся четным целым числом, или число, не являющееся целым числом.Каждое десятичное число можно преобразовать в дробь всего за три простых шага.
Обратите внимание, что процесс преобразования повторяющейся десятичной дроби отличается.
Шаг первый: создание начальной дроби
Первым шагом в преобразовании десятичной дроби в дробь является создание начальной дроби с десятичной дробью в качестве верхнего числа и 1 в качестве нижнего числа.
Например, , чтобы преобразовать 0,75 в дробь, начните с создания дроби с 0,75 в числителе и 1 в знаменателе.
0,75 = 0,751
Шаг второй: умножить на десять
Следующим шагом будет умножение числителя и знаменателя на 10, чтобы удалить десятичный знак. Продолжайте умножать оба числа на 10, пока числитель не станет целым числом.
Продолжая приведенный выше пример, давайте преобразуем 0,751 в 75100.
0,751 = (0,75 × 10) (1 × 10) = 7,510
7,510 = (7,5 × 10) (10 × 10) = 75100
Шаг третий: Уменьшите дробь
Последний шаг в преобразовании десятичной дроби в дробь — уменьшить или упростить дробь.Чтобы уменьшить, найдите наибольший общий делитель числителя и знаменателя. Затем разделите числитель и знаменатель на наибольший общий множитель.
Чтобы завершить приведенный выше пример, мы знаем, что наибольший общий делитель 75 и 100 равен 25. Итак, давайте разделим числитель и знаменатель на 25, чтобы найти уменьшенную дробь.
75100 = (75 ÷ 25) (100 ÷ 25)
75100 = 34
Совет: используйте наш упрощатель дробей, чтобы легко уменьшить дробь.
Для отрицательных чисел удалите отрицательный символ из начального десятичного разделителя, затем выполните указанные выше действия. После преобразования в дробную форму снова добавьте отрицательный знак.
Как преобразовать повторяющееся десятичное число в дробь
Повторяющиеся десятичные числа требуют немного другого процесса для преобразования в дробь. Повторяющееся десятичное число — это бесконечное десятичное число, например 1,1787878.
Эти числа обычно выражаются в округлой форме, например.788, или с такой перекладиной: 1.178.
Шаг первый: создание уравнения
Первым шагом в преобразовании повторяющейся десятичной дроби является создание алгебраического уравнения для представления десятичной дроби.
Например, преобразует десятичную дробь 1,178 в дробь. Начните с создания уравнения, чтобы присвоить x выражение 1.1787878.
х = 1,1787878
Шаг второй: умножьте на 10, пока десятичная дробь не окажется слева
Второй шаг — продолжить умножение обеих частей уравнения на 10, пока повторяющееся число не окажется слева от десятичной точки.
Если в шаблоне повторяется несколько повторяющихся чисел, умножьте их на 10, пока повторяющийся шаблон не окажется слева от десятичной точки.
Продолжая приведенный выше пример, давайте умножим обе части уравнения на 10, пока повторяющаяся часть десятичной дроби не окажется слева от десятичной точки.
x = 1,1787878
10 × x = 10 × 1,1787878
10x = 11,787878
10 × 10x = 10 × 11,787878
100x = 117,87878
10 × 100x = 10 × 117.87878
1000x = 1178,78
Шаг третий: умножьте на 10, пока десятичный знак не окажется справа
Третий шаг — создать новое уравнение для x и умножить до тех пор, пока повторяющаяся десятичная часть не окажется справа от десятичной точки.
Основываясь на нашем примере, умножайте обе части уравнения на 10 до тех пор, пока повторяющаяся часть десятичной дроби «78» не окажется справа от десятичной точки.
x = 1,1787878
10 × x = 10 × 1,1787878
10x = 11.78
Шаг четвертый: объедините уравнения
Следующим шагом является объединение уравнений и перемещение обеих переменных x влево и обоих десятичных значений вправо.
Давайте объединим уравнения и решим.
1000x — 10x = 1178,78 — 11,788
Шаг пятый: решить
Наконец, найдите x, чтобы преобразовать десятичное значение в дробь.
Давайте объединим уравнения и решим.
1000x — 10x = 1178,78 — 11,78
990x = 1167
990×990 = 1167990
x = 1167990
Таблица преобразования десятичных дробей в дробные
Альтернативный метод преобразования десятичной дроби в дробь — использовать таблицу преобразования, подобную этой.См. Дробные эквиваленты некоторых распространенных десятичных значений ниже. Таблица позволяет удобно увидеть соответствующую дробь для десятичного числа.
| Десятичное значение | Значение дроби |
|---|---|
| 0,0625 | 1/16 |
| 0,08333 | 1/12 |
| 0,1 | 1/10 |
| 0.111 | 1/9 |
| 0,125 | 1/8 |
| 0,1666 | 1/6 |
| 0,2 | 1/5 |
| 0,222 | 2/9 |
| 0,25 | 1/4 |
| 0,333 | 1/3 |
| 0,375 | 3/8 |
| 0,4 | 2/5 |
| 0,444 | 4/9 |
| 0.5 | 1/2 |
| 0,555 | 9/5 |
| 0,6 | 3/5 |
| 0,625 | 5/8 |
| 0,666 | 2/3 |
| 0,75 | 3/4 |
| 0,777 | 9/7 |
| 0,8 | 4/5 |
| 0,8333 | 5/6 |
| 0,875 | 7/8 |
| 0.888 | 9/8 |
См. Больше десятичных эквивалентов дробной части.
Калькулятор десятичных дробей в дробные со встроенным динамическим учебным курсом
Существует несколько различных методов преобразования десятичных дробей в дроби — в зависимости от того, имеет ли десятичное число цифры слева от десятичной точки. Я объясню каждый сценарий отдельно.
Нет цифр слева от десятичной точки
Если нет цифр слева от десятичной точки, можно просто пересчитать десятичное число как дробь.Это делается путем размещения числа справа от десятичной точки в качестве числителя, а знаменатель становится 1 , за которым следует количество нулей, равное количеству цифр в числителе, например:
Переформулируйте 0,625 как a ДробьЕсли возможно, просто дробь:
| 625 | = | 625 ÷ 125 | = | 5 | |||||||||||||||||||||||||||||||
| 1000 | 1000 ÷ 125 | 8 | С или Цифры слева от десятичной точки
| 3.625 * 1000 | = | 3625 |
| 1 * 1000 | 1000 |
Если возможно, просто дробь:
| 3625 | = | ÷ 12596 | = | 3 | 5 |
| 1000 | 1000 ÷ 125 | 8 | 8 |
Обратите внимание, что число, на которое вы умножаете верхнюю и нижнюю части, всегда равно 1 с одинаковым количеством нулей. добавляется как количество верхних цифр.Итак, если верхняя часть состоит из 2 цифр, вы умножите верхнюю и нижнюю на 100. Если верхняя часть состоит из 4 цифр, вы должны умножить верхнюю и нижнюю на 10000 и так далее.
с цифрами слева от десятичной точки
Если есть одна или несколько цифр слева от десятичной точки и их значение больше нуля, то десятичное число можно пересчитать как смешанное число, и, в свою очередь, это смешанное число. число можно преобразовать в дробь, например:
Преобразовать десятичное число как смешанное число, затем как дробноеПреобразовать смешанное число в дробное:
| 3 | 625 | = | 1000 * 3 + 625 | = | 3625 |
| 1000 | 1000 | 1000 |
Если возможно, просто дробь:
| 3625 | = | 362562 ÷ 125 | 3 | 5 |
| 1000 | 1000 ÷ 125 | 8 | 8 |
Надеюсь, я достаточно хорошо объяснил вам процесс преобразования следовать инструкциям.Если нет, дайте мне знать, заполнив форму обратной связи, расположенную под калькулятором.
Простой в использовании калькулятор дробей [для деления, умножения и упрощения дробей]
Калькулятор дробей складывает, вычитает, умножает и делит дроби с одинаковыми или разными знаменателями. Это также позволит нам упростить дроби, преобразовать дроби в десятичные и десятичные в дроби.
Сначала просто введите значения a, b, c, d для дробей \ (\ frac {a} {b} \) и \ (\ frac {c} {d} \), а затем математическую операцию по вашему желанию. выполнить (+, -, x, /).Калькулятор моментально и точно выполнит операцию и выдаст ответ в простейшей форме. Вы также можете использовать калькулятор, чтобы проверить свою работу, которую вы проделали вручную.
Сложение и вычитание дробей Подобные (общие) знаменателиСложите или вычтите числители, сохраняя знаменатели одинаковыми.
Пример: \ (\ frac {3} {5} + \ frac {4} {5} \)
Поскольку знаменатель равен 5 в обеих дробях, сложите 3 и 4, чтобы получить 7.Знаменатель остается равным 5, поэтому ответ равен 7/5.
\ (\ frac {7} {6} — \ frac {5} {6} \)Поскольку знаменатель равен 6 в обеих дробях, вычтите 5 из 7, чтобы получить 2. Тогда дробь будет \ (\ frac {2} {6} \).
Но теперь мы можем упростить \ (\ frac {2} {6} \). Чтобы упростить, поищите общий фактор. Обратите внимание, что 2 равномерно делится как на 2, так и на 6. Следовательно, разделите числитель и знаменатель на 2, чтобы получить \ (\ frac {1} {3} \). Теперь дробь упрощена.
В отличие от знаменателейЧтобы сложить и вычесть разные знаменатели, сначала вычислите общий знаменатель.Самый простой способ сделать это — умножить два знаменателя. Это не всегда дает наименьший общий знаменатель, но вы можете упростить его после сложения и вычитания.
Пример: \ (\ frac {2} {5} + \ frac {4} {7} \)
Общий знаменатель равен 5 (7) = 35. Поскольку знаменатель в первой дроби умножается на 7, числитель также нужно умножить на 7, чтобы получить \ (\ frac {14} {35} \). Поскольку знаменатель второй дроби умножается на 5, числитель должен быть таким же, чтобы получить \ (\ frac {20} {35} \).
Теперь добавьте \ (\ frac {14} {35} + \ frac {20} {35} = \ frac {34} {35} \)
Вычитание выполняется таким же образом, просто вычтите две дроби после перезаписи дроби с их общими знаменателями. Если вам нужно упростить, не забудьте разделить на наибольший общий множитель.
При умножении дробей просто умножайте их в числителях и знаменателях.Тогда упростите. Вы также можете сначала упростить, прежде чем умножать.
Пример: \ (\ frac {2} {9} \ times \ frac {4} {7} \)
Умножьте 2 и 4, чтобы получить 8. Затем умножьте 9 и 7, чтобы получить 63. Результат: \ ( \ frac {8} {63} \). Упрощения не требуется, поскольку наибольший общий делитель равен 1.
Теперь предположим, что мы хотим разделить \ (\ frac {2} {9} \ div \ frac {4} {7} \).
При делении дробей возьмите первую дробь и умножьте на обратную величину второй. Обратное просто меняет местами числитель и знаменатель.Проблема деления превращается в проблему умножения.
\ (\ frac {2} {9} \ times \ frac {7} {4} \) 2 × 7 = 14 и 9 × 4 = 36. Итак, ответ \ (\ frac {14} { 36} \). Но обратите внимание, что это не в простейшей форме. Наибольший общий делитель равен 2, поэтому деление обоих на 2 дает упрощенный ответ \ (\ frac {7} {18} \).
Калькулятор преобразования дробей в десятичные принимает любую дробь и преобразует ее в десятичную.
Метод преобразования дроби в десятичную довольно прост. Просто разделите числитель на знаменатель.
Замените \ (\ frac {14} {25} \) на десятичное число.
Разделите 14 на 25, чтобы получить 0,56. Вы можете сделать это на калькуляторе или вручную с помощью длинного деления. Некоторые фракции не так просто обрабатывать вручную, особенно те, которые не завершаются. На этом калькуляторе с ними работать намного проще.
Но если вы решите решить вручную, калькулятор станет отличным инструментом для мгновенной проверки вашей работы.
Преобразование десятичных знаков в дроби является обратным преобразованию дробей в десятичные. Калькулятор быстро выполнит это и даст точные результаты, просто введя десятичное значение.
Чтобы преобразовать вручную, возьмите десятичную дробь и преобразуйте ее в целое число, затем разделите на 10, возведенное в число десятичных знаков, перемещенных вправо для преобразования числа. Оттуда вы можете упростить дробь, если это необходимо.
Пример:
Преобразует 0,68 в дробь. Чтобы изменить 0,68 на целое число, переместите десятичную запятую на 2 разряда вправо, чтобы получить 68. Поскольку мы переместили 2 десятичных разряда, разделите 68 на 10 во второй степени, которая равна 100.
Это дает нам \ (\ гидроразрыв {68} {100} \). Теперь мы можем упростить дробь, найдя общий множитель. Если вы не знаете наибольшего общего множителя, вы можете начать с деления на любой общий множитель. Замечания 68 и 100 делятся на 2. Это уменьшает дробь до 34/50.Отсюда обратите внимание, что и 34, и 50 делятся на 2. Это сводится к \ (\ frac {17} {25} \), что является упрощенным ответом.
Вы можете проверить свои ручные вычисления с помощью этого калькулятора или просто ввести информацию для вашей конкретной проблемы, чтобы получить почти мгновенные и точные результаты!
Калькулятор дробей + десятичные знаки в App Store
Представляем первый в мире калькулятор дробей с дополнительными функциями, такими как сокращение или упрощение дробей, преобразование дробей в десятичные и калькулятор десятичных дробей.Все это в одном отличном приложении. Откройте для себя простой способ решения повседневных задач дроби. Складывайте, вычитайте, умножайте, делите и даже конвертируйте дроби быстро и четко. Калькулятор дробей Visual Math Interactive — отличный помощник по выполнению домашних заданий и справочный инструмент для бизнеса с красивыми чистыми клавиатурами и большим дисплеем для быстрых и простых вычислений.
ОСОБЕННОСТИ:
— Приложение для вычисления дробей и приложение для преобразования десятичных дробей в одно.
— Также автоматически выполняет обратное преобразование дробей в десятичные для вашей быстрой справки.
— Поддерживает неправильные и правильные дроби, смешанные числа и целые числа.
— Теперь вы можете пойти и в обратном порядке: тоже вычислить от десятичных дробей к дробям.
— Большие, четкие, не загроможденные клавиатуры для быстрых и простых вычислений каждый раз.
— Дополнительная помощь в домашнем задании: нужна дополнительная помощь в понимании дробей? Теперь вы также можете транслировать БЕСПЛАТНЫЕ визуально интерактивные видеоролики «Основы дроби», чтобы быстро изучить основы дробей.
ПОКУПКА В ПРИЛОЖЕНИИ ДЛЯ РАЗБЛОКИРОВКИ ПРЕМИАЛЬНЫХ ФУНКЦИЙ
► Конвертер десятичных дробей в дробные
► Конвертер неправильных дробей в смешанные
ИЛИ ПОЛУЧИТЕ
ZAPZAPMATH HOME ALL ACCESS PASS
► Разблокируйте премиум-функцию с помощью All Access Pass.
► Ваш All Access Pass открывает весь контент для Zapzapmath Home с K по 6!
УСЛОВИЯ ПОДПИСКИ ZAPZAPMATH
► До трех учетных записей на подписку
Ваша подписка будет автоматически продлена, если автоматическое продление не будет отключено по крайней мере за 24 часа до истечения срока подписки.
Стоимость продления равна стоимости исходной подписки, и оплата будет снята с вашей учетной записи iTunes после подтверждения продления.
Вы можете отключить автоматическое продление в любое время после покупки, перейдя в настройки своей учетной записи iTunes, но за неиспользованную часть срока возврат средств не производится.
Цена указана для клиентов из США. Цены в других странах могут отличаться, а оплата может быть конвертирована в вашу местную валюту. См. Наш:
► Условия использования (https://www.zapzapmath.com/terms)
► Политика конфиденциальности (https://www.zapzapmath.com/privacy)
ВАМ ТАКЖЕ МОЖЕТ ПОТРЕБОВАТЬСЯ:
Zap Zap Fractions
Интересный способ изучить основы дробей, дополненный интерактивной визуализацией, геймификацией и аналитикой производительности.
Основы работы с дробями
Комплексный курс повышения квалификации по дробям в 12 простых, наглядных, удобных для поиска анимационных видеороликах.Также называется: «Словарь дробей».
ПОСЕТИТЕ США — www.zapzapmath.com
НРАВИТСЯ НАС — facebook.com/ZapZapMathApp
ПОДПИШИТЕСЬ НА НАС — twitter.com/ZapZapMathApp
ЧИТАЙТЕ О НАС — blog.zapzapmath.com

 Он принимает правильные, неправильные, смешанные дроби и целые числа. Если они существуют, решения и ответы представлены в упрощенном виде,
Он принимает правильные, неправильные, смешанные дроби и целые числа. Если они существуют, решения и ответы представлены в упрощенном виде, для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.


