Разложение в степенной ряд бинома Ньютона
Одной из самых фундаментальных алгебраических функций, порождающих ряды, является бином Ньютона, выражение которого записывается в виде: (1)
В этом выражении коэффициенты при представляют собой число сочетаний из элементов по  и называются биномиальными коэффициентами . Таблица биномиальных коэффициентов для целых значений и
и называются биномиальными коэффициентами . Таблица биномиальных коэффициентов для целых значений и  в пределах имеет вид:
в пределах имеет вид:
Биномы целых положительных степеней
Если показатель степени является целым положительным числом, то выражение бинома состоит из конечного числа слагаемых равного (). К примеру,

Эти формулы широко применяются в элементарной математике. Для заданных конечных значений числа  эти формулы всегда дают однозначный ответ в форме конечного числа. Биномы целых положительных степеней были известны очень давно, и Ньютон не сказал бы ничего нового в этом отношении, если бы он не совершил исключительно оригинальный по тем временам шаг. Этот шаг состоял в переходе от целых значений числа в биномах к дробным и отрицательным значениям. Хотя правомерность такого перехода не была обоснована строго математически, она дала большой толчок развитию теории числовых и функциональных рядов. Спустя 150 лет Н. Абель доказал правомерность такого перехода строго математически.
эти формулы всегда дают однозначный ответ в форме конечного числа. Биномы целых положительных степеней были известны очень давно, и Ньютон не сказал бы ничего нового в этом отношении, если бы он не совершил исключительно оригинальный по тем временам шаг. Этот шаг состоял в переходе от целых значений числа в биномах к дробным и отрицательным значениям. Хотя правомерность такого перехода не была обоснована строго математически, она дала большой толчок развитию теории числовых и функциональных рядов. Спустя 150 лет Н. Абель доказал правомерность такого перехода строго математически.
Биномы целых отрицательных степеней
Биномы целых отрицательных степеней при помощи формулы (1) записываются в форме бесконечного ряда. К примеру,
(2)
Отметим в качестве указания на фундаментальность формулы бинома Ньютона, что бесконечная геометрическая прогрессия является его частным случаем (см. 1-ю формулу в выражениях (2)).
Любую из этих формул можно получить и без использования формул комбинаторики при помощи элементарной операции деления. Так, например, получается бином минус второй степени:
Точно так же можно получить ряд для бинома любой целой отрицательной степени. Все эти биномы имеют радиус сходимости R=1. За пределами этого интервала ряд не воспроизводит значение функции, из которой он получен. Биномы дробных положительных и отрицательных степеней
Биномы дробных положительных и отрицательных степеней раскладываются в ряд при помощи формулы (1), полагая в ней число равным дробному показателю степени бинома. В качестве примера можно представить следующие разложения:
(3)
Ограничения по использованию этих формул показывают, что при положительном показателе степени они применимы в интервале сходимости .
При отрицательных показателях степени они применимы в интервале сходимости  <1.
<1.
Таким образом, разложения биномов дробных и отрицательных степеней так же характеризуются радиусом сходимости  и за пределами этого радиуса не воспроизводят исходную функцию, хотя она существует за этими пределами вплоть до и до .
и за пределами этого радиуса не воспроизводят исходную функцию, хотя она существует за этими пределами вплоть до и до .
Все эти ряды можно тождественно преобразовать к виду, который обеспечивает сходимость за пределами интервала (, +1) в пределах от –1 до и от +1 до . Такое тождественное преобразование выглядит следующим образом: (4)
В преобразованном выражении 4 в скобках заключён тоже бином Ньютона, но уже в другой записи. Раскладывая новый бином в ряд, получим:
(5)
Бесконечный ряд в квадратных скобках последнего выражения сходится в пределах  >1, а при n<0 он сходится в пределах . На основании формулы 5 все выше приведённые разложения бинома Ньютона могут быть тождественно преобразованы к виду:
>1, а при n<0 он сходится в пределах . На основании формулы 5 все выше приведённые разложения бинома Ньютона могут быть тождественно преобразованы к виду:
(6)
Суть произведённых преобразований бинома Ньютона к ряду, сходящемуся в бесконечных пределах хорошо видна из последних формул 6. В квадратных скобках каждого разложения стоит ряд абсолютно того же содержания, что и соответствующий ряд в выражениях 4 за исключением того, что вместо аргумента (как было в выражениях 4) в выражениях 6 стоит обратная ему величина , что и делает последний ряд сходящимся. Перед квадратными скобками каждого ряда в выражениях 6 стоит множитель вида , который можно условно назвать масштабирующим множителем. Этот масштабирующий множитель как бы компенсирует влияние перехода в квадратных скобках от аргумента к его обратной величине.
В обобщённой форме эти действия можно записать как преобразование вида: 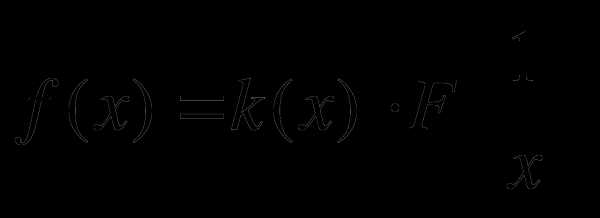 . Такая запись ориентирует на преобразование исходной функции к произведению двух функций
. Такая запись ориентирует на преобразование исходной функции к произведению двух функций 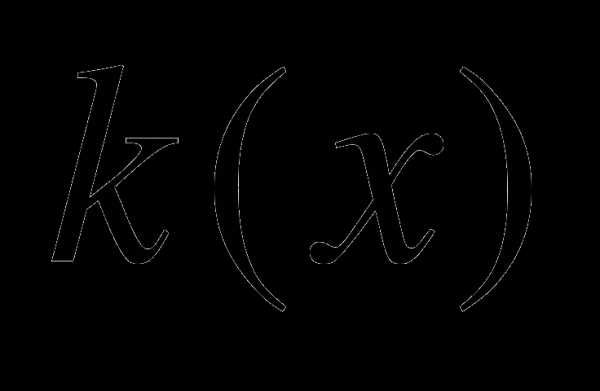 и
и  . Последняя функция
. Последняя функция  и позволяет путём разложения перейти к сходящемуся ряду-эквиваленту.
и позволяет путём разложения перейти к сходящемуся ряду-эквиваленту.
Биномы дробных положительных и отрицательных степеней воспроизводятся только в категориях комбинаторики (выражение 1). Никакие элементарные математические операции не позволяют непосредственным образом получить разложение в ряд бинома дробной степени, как это было в случае биномов целых отрицательных степеней.
Биномы и их разложения в ряд играют в математике исключительно важную роль, поскольку интегрирование этих функций и их разложений в ряд ведёт к алгебраическим, логарифмическим, обратным тригонометрическим и обратные гиперболическим функциям и их разложениям в ряд.
Литература:
1.Е.Е. Алексеева, Е.М. Лушников. Проблемы и решения в теории рядов. Калининград. Изд.„Янтарный сказ”. 2004. 256c.
2 Е.А. Власова. Ряды. Выпуск 9 М.: Изд. МГТУ им. Н.Э. Баумана, 2002. 612с.
3. Н.Н. Воробьёв, Теория рядов. 6-е издание, стереотипное. СПб.: Издательство «Лань», 2002. 408с.
infourok.ru
Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона») Литература
id_016
Курьякова Татьяна Сергеевна
учитель математики МОУ «СОШ №36», г. Ангарск
Бином Ньютона – одна из тем, рассмотрение которых способствует глубинному пониманию учащимися на только комбинаторных понятий, но и формул сокращенного умножения. В данной статье представлен один из вариантов лекции для старшеклассников по теме «Бином Ньютона».
Тема: «Бином Ньютона»
План лекции 1. Понятие бинома Ньютона
2. Свойства бинома и биномиальных коэффициентов
3. Типовые задачи по теме «Бином Ньютона»
4. Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона»)
Литература
1. Сборник конкурсных задач по математике для поступающих во втузы / Под ред. М.И.Сканави: Учеб. пособие. Санкт-Петербург, 1995. – с.84.
2. Супрун В.П. Избранные задачи повышенной сложности по математике. Мн.: Полымя, 1998. – 108с.
– 1 –
Понятие бинома Ньютона
Биномом Ньютона называют разложение вида:
Но, строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n
Цель изучения бинома Ньютона – упрощение вычислительных действий.
Компоненты формулы «бином Ньютона»:
правая часть формулы – разложение бинома;
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Например, четвертая строчка треугольника как раз наглядно демонстрирует биномиальные коэффициенты для бинома четвертой степени:
Альтернатива треугольнику Паскаля:
перемножить почленно четыре скобки:
;
вспомнить разложение бинома Ньютона четвертой степени:
где Т – член разложения; – порядковый номер члена разложения.
– 2 –
Свойства бинома и биномиальных коэффициентов
Число всех членов разложения на единицу больше показателя степени бинома, то есть равно

Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома, то есть n
Доказательство
Рассмотрим -й член разложения:
Сумма показателей степеней a и b:
Ч.т.д.
Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой: (правило симметрии)
Сумма биномиальных коэффициентов всех членов разложения равна

Доказательство
Пусть , тогда:
Тогда: 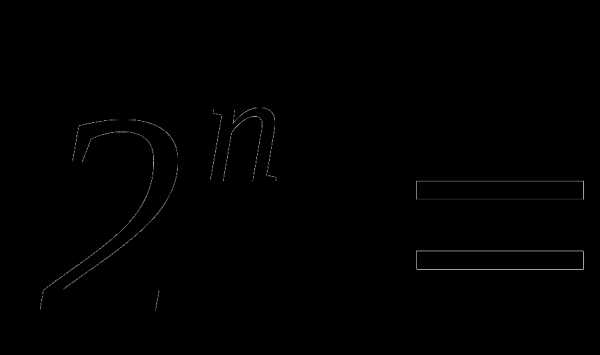
Ч.т.д.
Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна

Правило Паскаля:
Доказательство – самостоятельно
Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби

Доказательство – самостоятельно
– 3 –
Типовые задачи по теме «Бином Ньютона»
К типовым (стандартным) заданиям по данной теме можно отнести задачи на вычисление, среди которых:
Найти член (номер члена) разложения бинома
Вывести бином по известным членам разложения (по известной сумме)
Вычислить сумму биномиальных коэффициентов разложения бинома
и другие.
Продемонстрируем на примерах (их решение несложное, поэтому большинство предлагаем решить самостоятельно).
Пример 1
Разложить по формуле бином 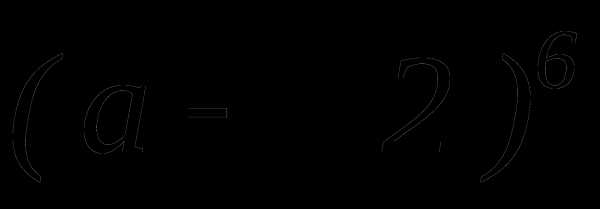
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знакочередование!
Пример 2
Найти шестой член разложения 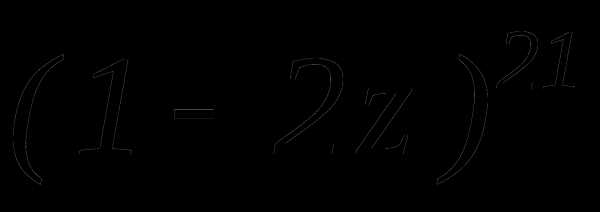
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знак!
Лучше начинать рассуждения со следующего:
Пример 3
Найдите два средних члена разложения
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на то, что эти члены равноотстоят от конца, поэтому их биномиальные коэффициенты будут равны.
НЕ ЗАБУДЬТЕ в процессе решения проводить преобразования степеней с одинаковыми основаниями (то есть упрощать).
Пример 4
В биномиальном разложении 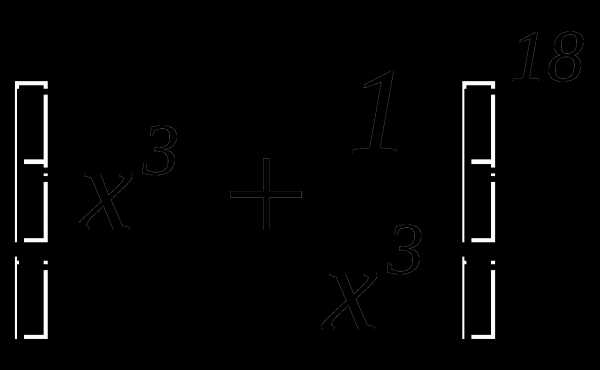 найти член разложения, не содержащий х
найти член разложения, не содержащий х
Решение
Так как в разложении мы ищем член
не содержащий
Тогда
Ответ: 
– 4 –
Задачи, сводящиеся к использованию формулы бинома Ньютона
(нестандартные задачи по теме «Бином Ньютона»)
К нестандартным заданиям по данной теме можно отнести такие, в которых нет явного намека на необходимость использования бинома. Однако в итоге, решение сводится к нему и выглядит очень интересным.
Пример 5
Доказать, что для любых и для любых  верно неравенство Бернулли:
верно неравенство Бернулли:
Доказательство
Пусть
Так как , то
Переформулируем требование: Доказать, что , гдеТак как , значит в разложении как минимум три члена разложения, тогда:
Это означает, что
Ч.т.д.
Пример 6
Доказать, что 
Доказательство – самостоятельно
(Подсказка: используйте неравенство Бернулли)
Пример 7
Доказать, что при любом натуральном n число делится на 9
Доказательство
1 способ:
Ч.т.д.
2 способ:
Начнем рассматривать бином в общем виде:
Ч.т.д.
Пример 8
Решить уравнение
Решение
Осуществим замену:
Тогда уравнение перепишем:
Применим формулу бинома к левой части уравнения:
В итоге
Ответ:
Дополнительные задания для самостоятельного выполнения
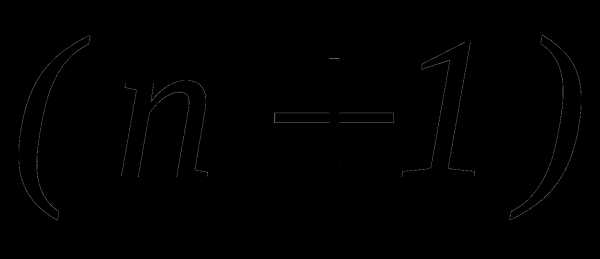
Найти номер члена разложения бинома
 ,
не содержащего х.
,
не содержащего х.Найти пятый член разложения бинома
 .
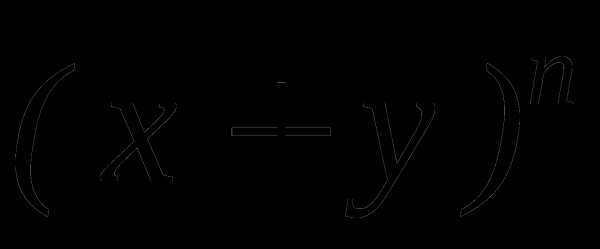
.Найти сумму биномиальных коэффициентов членов, стоящих на нечетных местах в разложении бинома
, если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
Найти седьмой член разложения бинома
 ,
если биномиальный коэффициент третьего
члена равен 36.
,
если биномиальный коэффициент третьего
члена равен 36.Сколько членов разложения бинома являются целыми числами?
Вычислить сумму .
Найти алгебраическую сумму коэффициентов многочлена относительно х, получаемого в разложении бинома
 .
.Сумма нечетных биномиальных коэффициентов разложения
 равна 512. Найти слагаемое, не содержащее
равна 512. Найти слагаемое, не содержащее При каких значениях х четвертое слагаемое разложения
 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых?При каком значении х четвертое слагаемое разложения в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?
В какую наибольшую степень следует возвести бином
 чтобы отношение четвертого слагаемого
разложения к третьему было равно
чтобы отношение четвертого слагаемого
разложения к третьему было равно  ?
?
gigabaza.ru
Название биномиальных коэффициентов следует из теоремы, известной в математике как Формула Бинома Ньютона.
Теорема 11.1. .
Теорема 11.2. .
Доказательство. По формуле бинома с использованием тождественных преобразований алгебраических выражений.
.■
Последнее равенство также называется формулой бинома Ньютона, его правая часть называется разложением степени бинома.
Теорема 11.3.
Доказательство следует из формулы бинома Ньютона при
Теорема 11.4.
Доказательство следует из формулы бинома Ньютона при .
Формулы сокращённого умножения являются частными случаями формулы бинома Ньютона.
1) квадрат суммы при :
;
Заменив в формуле квадрата суммы B на (–B), получаем формулу квадрата разности:
2) куб суммы при :
заменив в формуле куба суммы B на (–B), получаем формулу куба разности:
Задачи и упражнения.
11.1. Найдите разложение бинома.
11.2. Найдите член разложения бинома , не содержащий Х.
11.3. Найдите наибольший коэффициент разложения бинома , если сумма всех коэффициентов равна 4096.
11.4. Найдите Х в , если отношение седьмого слагаемого от начала в разложении бинома к седьмому слагаемому от конца равно .
11.5. Докажите, что сумма квадратов коэффициентов разложения бинома равна .
12. Треугольник Паскаля.
Для вычисления биномиальных коэффициентов используется специальная таблица.
Таблица 2
Вычисление биномиальных коэффициентов

Биномиальные коэффициенты удобно выстроить в Треугольник Паскаля – равнобедренный треугольник, обладающий следующими закономерностями:
1) в строке треугольника записываются биномиальные коэффициенты -й степени бинома;
2) число располагается в строке на месте;
3) боковые стороны треугольника состоят только из единиц;
4) каждое внутреннее число строки равно сумме двух последовательных чисел предыдущей строки, стоящих над ним слева и справа.
На рисунке 7 представлен треугольник Паскаля, выстроенный для коэффициентов разложения бинома -й степени.

Рис. 1
Треугольник Паскаля
Например, при треугольник Паскаля имеет вид:
Значит, .
Задачи и упражнения.
12.1. Найдите разложение бинома.
12.2. Докажите, что .
12.3. Проверьте выполнение равенства задачи 3.27 для 8 и 10 строк треугольника Паскаля.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
4. Cочетания, бином Ньютона
Пусть
множество,
состоящее из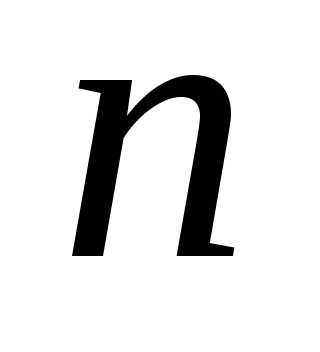 элементов. Любое подмножество
элементов. Любое подмножество (включая и пустое подмножество), содержащее
(включая и пустое подмножество), содержащее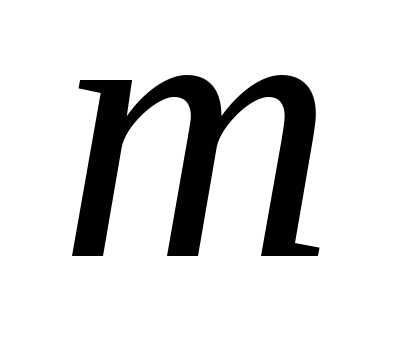 элементов, называетсясочетаниемпо
элементов, называетсясочетаниемпо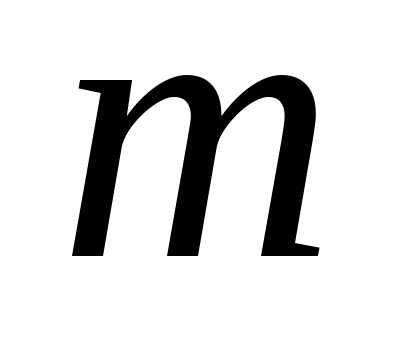 элементов из
элементов из 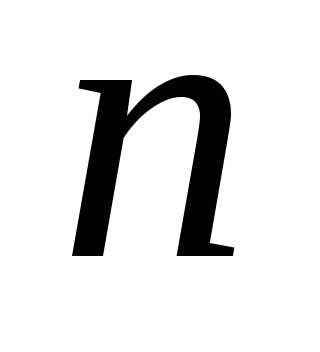 (или комбинацией по
(или комбинацией по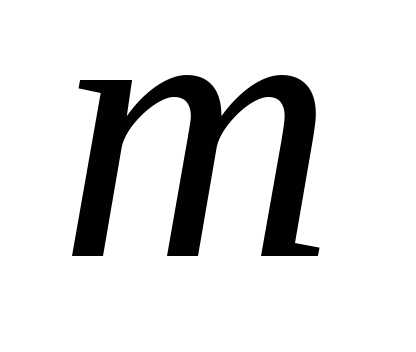 элементов из
элементов из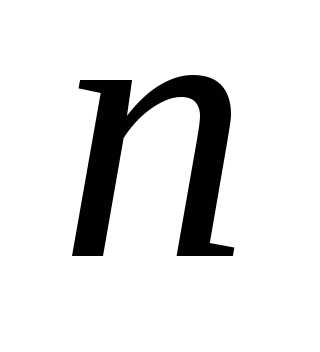 ),
при этом, разумеется,,
т.е.
),
при этом, разумеется,,
т.е.
сочетанияминазывают комбинации, составленные изnразличных элементов поmэлементам. Сочетания считаются различными, если их состав отличаются друг от друга хотя бы одним элементом.
Теорема 2. Число сочетаний из n элементов по m определяется равенством:
(3) .
Доказательство.Пусть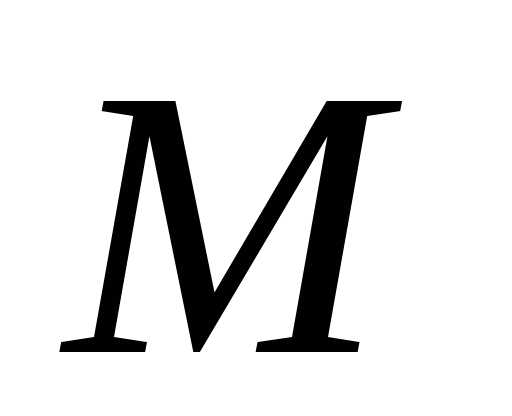 заданное
множество, состоящее из
заданное
множество, состоящее из элементов,
элементов, —
какое либо подмножество
—
какое либо подмножество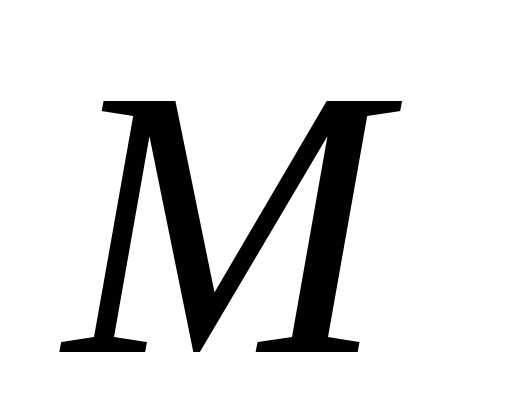 ,
содержащее
,
содержащее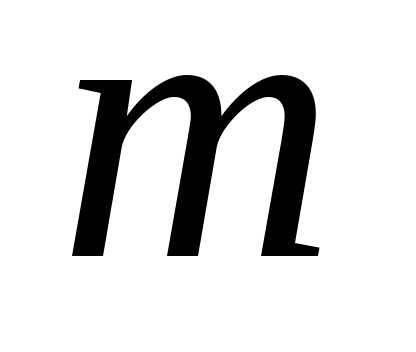 элементов. Составим всевозможные
перестановки из элементов
элементов. Составим всевозможные
перестановки из элементов ,
получим
,
получим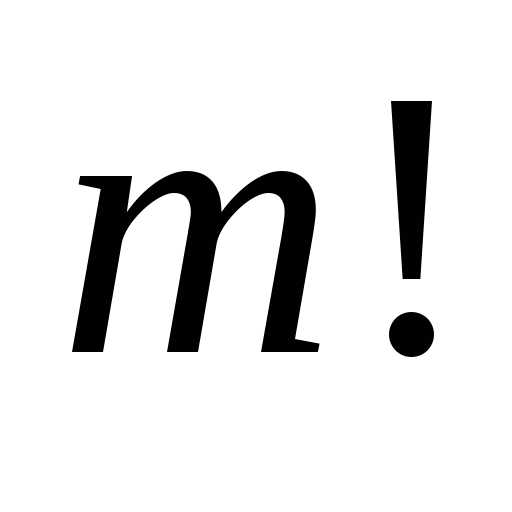 различных строк длиной
различных строк длиной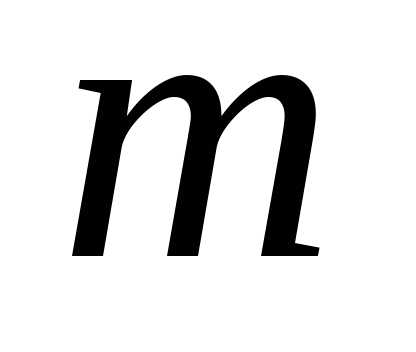 .
Если указанную операцию произвести с
каждым
.
Если указанную операцию произвести с
каждым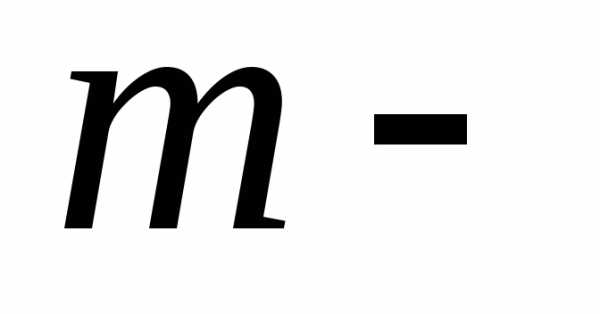 элементным
подмножеством множества
элементным
подмножеством множества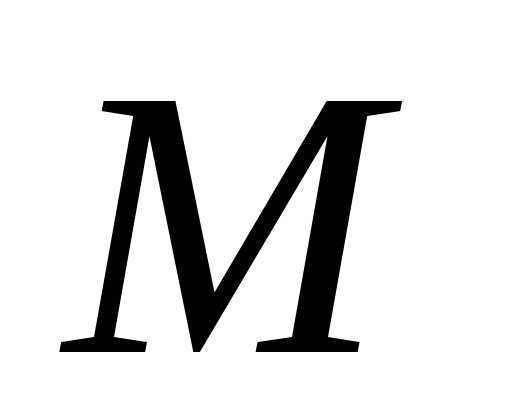 ,
то получим всего
,
то получим всего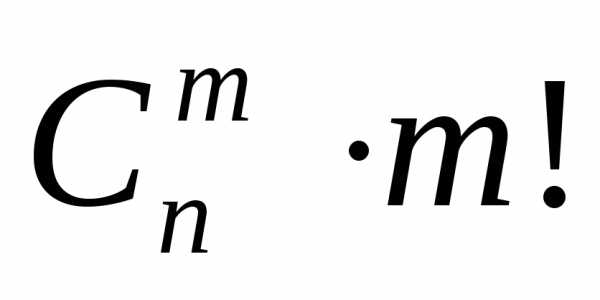 различных строк длиной
различных строк длиной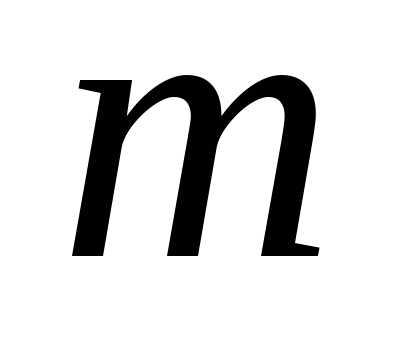 .
Естественно, таким способом должны
получиться без исключения все строки
.
Естественно, таким способом должны
получиться без исключения все строки
длиной  без
повторений, которые можно составить из
элементов множества
без
повторений, которые можно составить из
элементов множества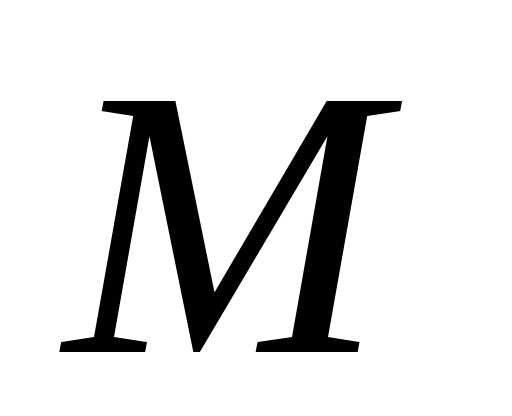 .
Поскольку, по теореме 1, число таких
строк
.
Поскольку, по теореме 1, число таких
строк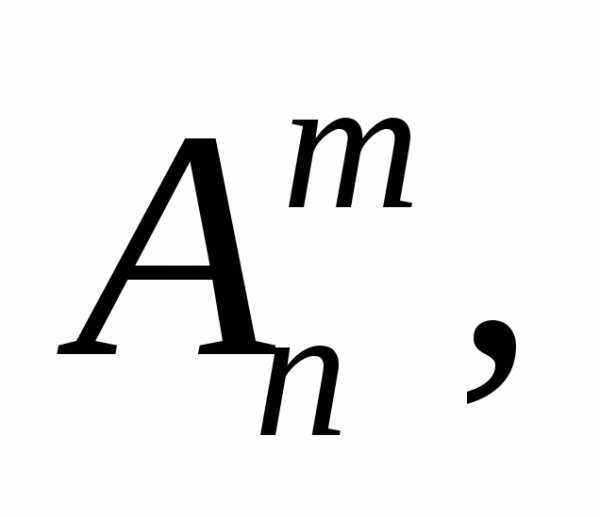 то имеем равенство
то имеем равенство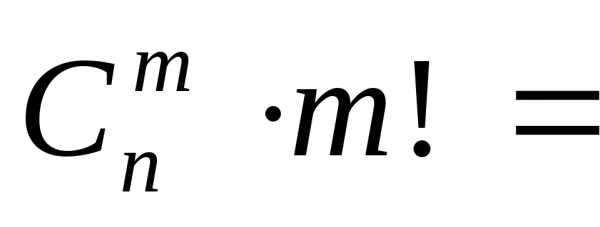
 ,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами
,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами
.
т.е. с учетом равенство (2) получаем (3). В частности,
.
Далее, рассмотрим несколько примеров на применение комбинаторных понятий.
Пример 7. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Решение: Искомое число трехзначных чисел:
.
Выпишите самостоятельно эти наборы чисел.
Пример 8. Сколько можно составить сигналов из 6 флажков различного цвета, взятых
по 2?
Решение: Искомое число сигналов
.
Пример 9. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение: Искомое число способов.
Пример 10. Какое количество партий сыграли 8 шахматистов, встречаясь с каждым партнером только один раз.
Решение. В данной задаче набор пар несущественен.
Двухэлементное
множество можно упорядочить только
2!=2 способами (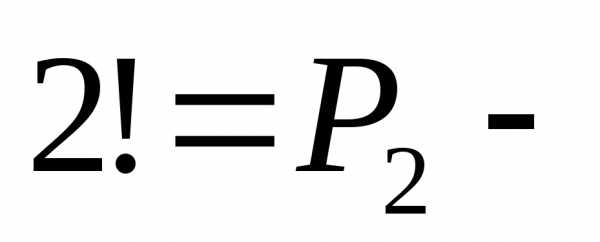 число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.
число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.
Решение этой задачи можно изящно
иллюстрировать геометрически (см.
Рис.4). Рассмотрим выпуклый восьмиугольник
.
С каждой любой вершины восьмиугольника
можно провести к другим вершинам семь
отрезков, т.е. количество встреч партий
шахматистов с другими партнерами равно
числу отрезков, соединяющих с остальными.
Общее число вершин (шахматистов) равно
8, а так как отрезкиАВиВАи т.д.
являются равными, то различных отрезков
(партий) будет равно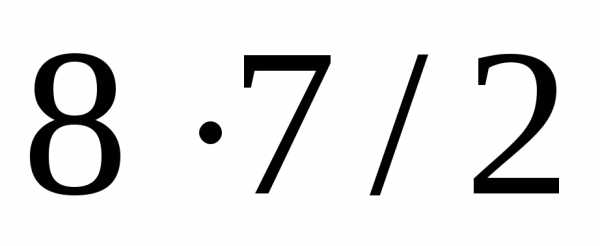 .
.
Задания. 1.Эту же задачу решите, с помощью турнирной таблицу встреч.
Бином Ньютона. Пусть и
и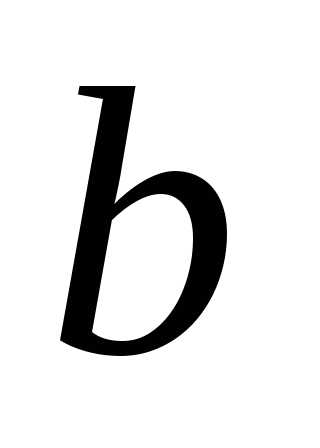 такие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества:
такие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества:
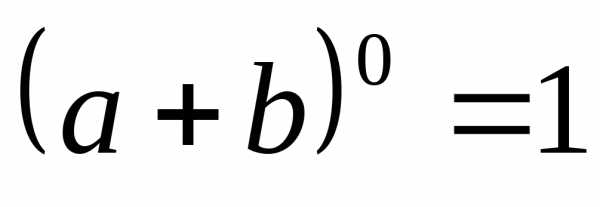 ,
,
,
,
,
.
Продолжая, этот процесс, т.е. пользуясь равенствами можно написать следующее равенство:
Данное равенство называется
формулой бинома Ньютона. При этом мы
воспользовались равенствами: 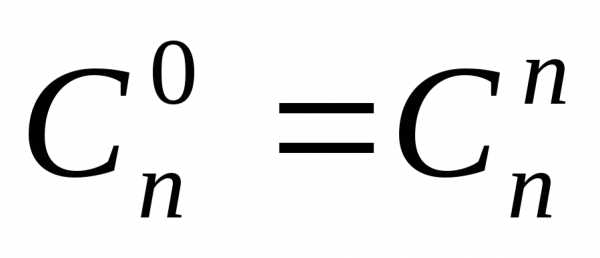 =1.
Неотрицательные целые числа
=1.
Неотрицательные целые числа (обычно называют их биномиальными
коэффициентами) определены равенствами:
(обычно называют их биномиальными
коэффициентами) определены равенствами:
,
если
и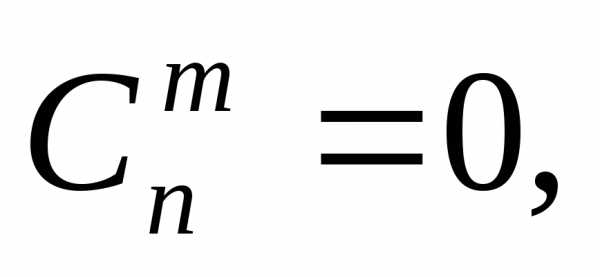 при остальных значениях
при остальных значениях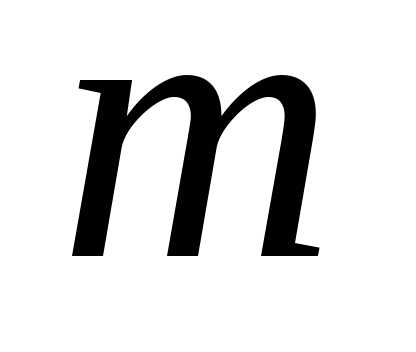 .
Напомним, что принято 0!=1.
.
Напомним, что принято 0!=1.
В частности, имеют место равенства:
,
Обычно формула бинома Ньютона доказывается методом математической индукции с учетом равенств:
;.
Основные свойства бинома Ньютона.
1. В разложении  содержится
содержится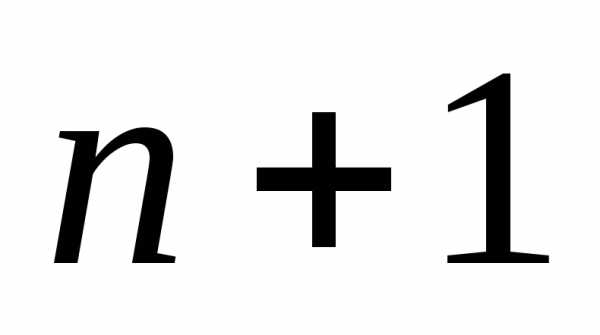 слагаемых.
слагаемых.
2. Показатель степени параметра  убывает отnдо 0,
напротив, показатель степени
убывает отnдо 0,
напротив, показатель степени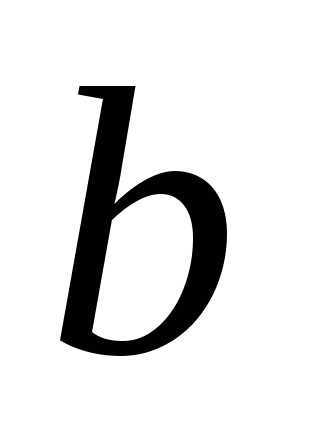 возрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров)
возрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров) и
и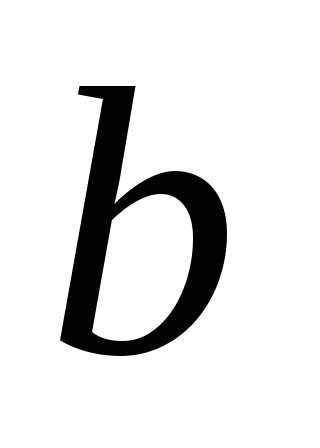 равнаn – показателю
степени бинома.
равнаn – показателю
степени бинома.
3. Биномиальные коэффициенты, равноудаленные от концов разложения, равны между собой, т.е. А также верно и другое разложение
(1)
4. Для биномиальных коэффициентов 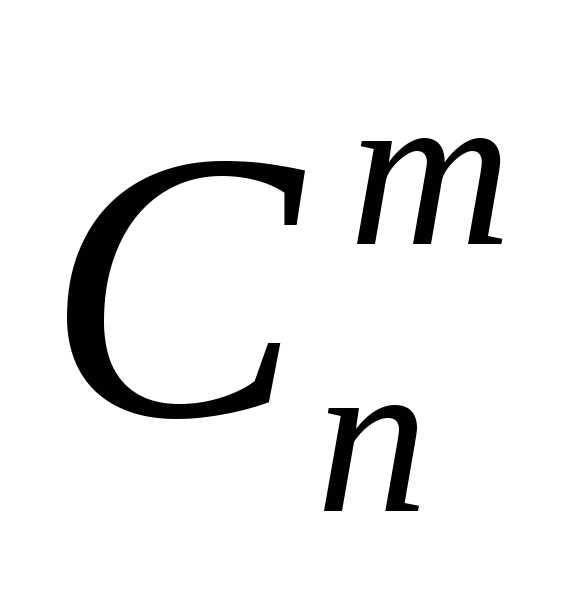 верно равенство
верно равенство
Некоторые непосредственные выводы.
5. Из общей формулы (1) непосредственно выводятся следующие равенства:
а. Если сумма чисел, то имеет место равенство
В дальнейшем это равенство играет важную роль в теории вероятностей.
в. Если
,
то сумма биномиальных коэффициентов
равно ,
т.е. верна формула
,
т.е. верна формула
с. Если , то сумма биномиальных коэффициентов всегда равна нулю.
.
В частности, полагая  ,
получим равенство
,
получим равенство
.
Формулу (1) можно переписать в виде:
6. Биномиальные коэффициенты сначала возрастают, а затем, убывают. При этом:
— если показатель степени бинома четный, то биномиальный коэффициент среднего слагаемого разложения наибольший;
— если же показатель степени бинома нечетный, то биномиальные коэффициенты двух средних слагаемых равны между собой и являются наибольшими;
— на основании свойства 4.биномиальные
коэффициенты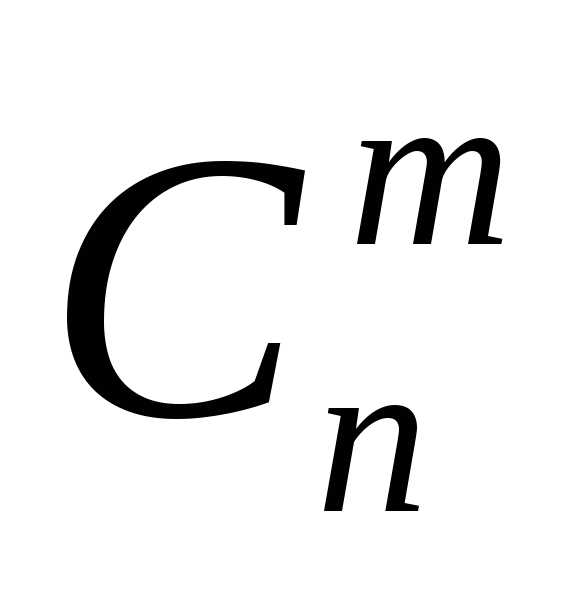 могут быть вычислены с помощью так
называемого «треугольника Паскаля»
могут быть вычислены с помощью так
называемого «треугольника Паскаля»
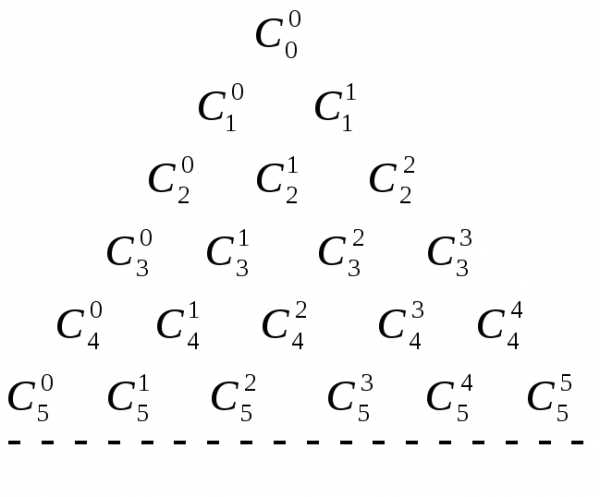
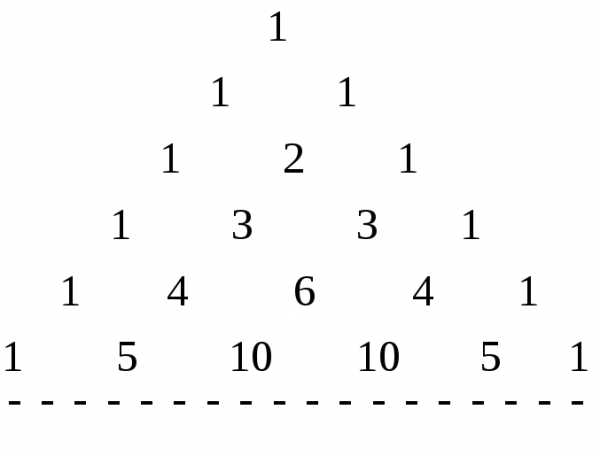
В этих «треугольных» таблицах легко заметить, что каждое число, кроме крайних единиц, является суммой двух вышерасположенных чисел.
7. Поскольку биномиальный коэффициент
начинается с нулевого члена, то в общем
виде принято (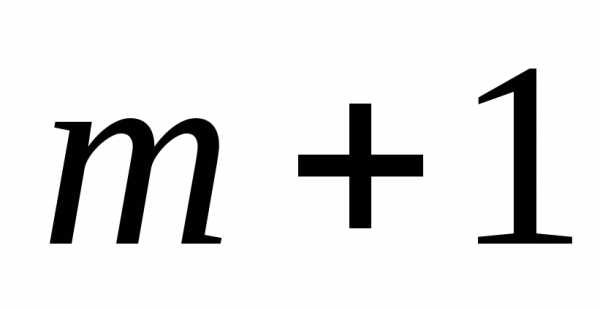 )
– ое слагаемое
)
– ое слагаемое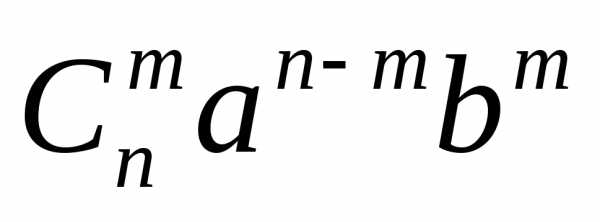 считать
считать  – им членом разложения, и обозначается:
– им членом разложения, и обозначается:
Задача 1. Для выражения найти
шестое слагаемое.
найти
шестое слагаемое.
Решение.Нужно воспользоваться биномиальной формулой, когда.
Ответ. .
Задача 2..Найдите наибольший член
разложения
Решение.Для решения этой задачи
необходимо выяснить для каких  выполняется неравенства:
выполняется неравенства:
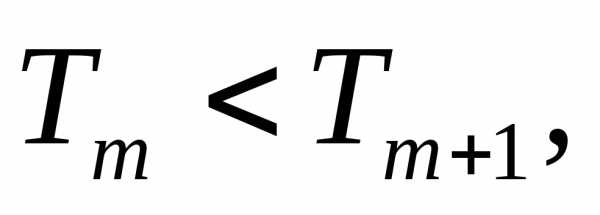
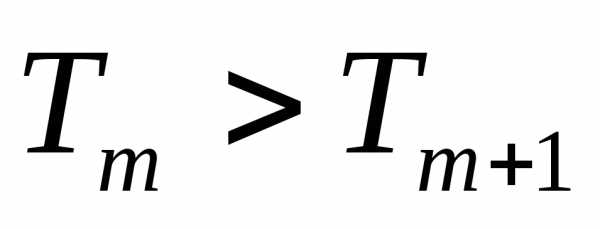 .
.
Рассмотрим отношение
.
Отсюда следует, что при
,
т.е.,
при 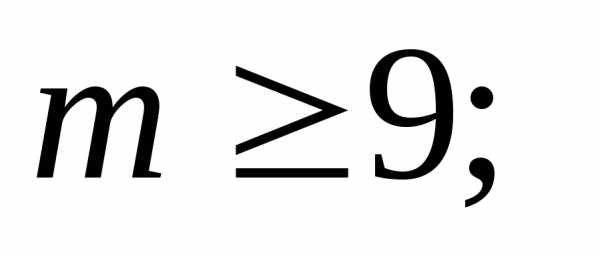 коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым
коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым
.
Задача 3. Найти член разложения,
не содержащий положительной степени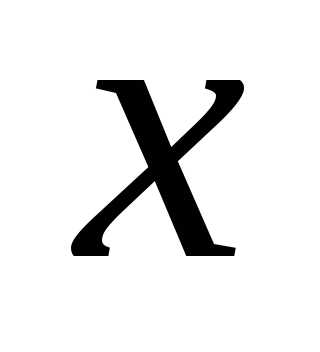 (т.е. найти слагаемое содержащее
(т.е. найти слагаемое содержащее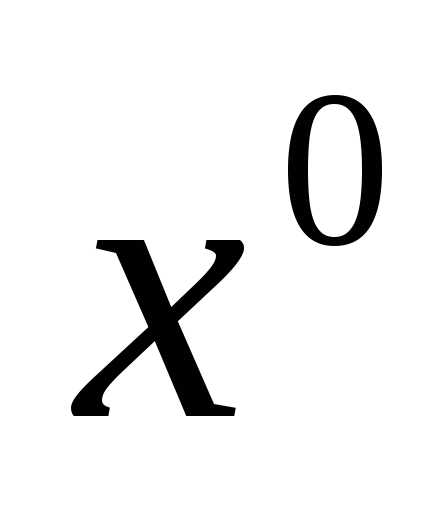 ).
).
Решение. Так как,тогда выписывая показатель степени ,
после несложных упрощений получим:
,
после несложных упрощений получим:
Следовательно, четвёртый член разложения (он же пятое слагаемое) является решением задачи.
Ниже предложим некоторые сведения из теории арифметических функций.
Упражнения: А. Докажите, что
1. При
любом простом 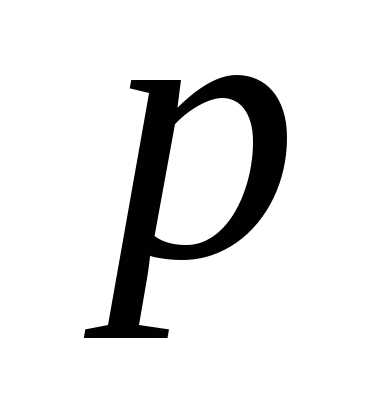 биномиальные
коэффициенты
биномиальные
коэффициенты  делятся
на число
.
делятся
на число
.
2. Докажите тождества:
3.  ,
еслилюбое
нечётное простое число..
,
еслилюбое
нечётное простое число..
В.
Дополнительные сведения. Пусть
—
каноническое представление натурального
числа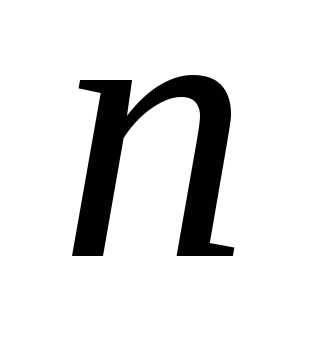 ,
определим классическую функцию Мебиуса
,
определим классическую функцию Мебиуса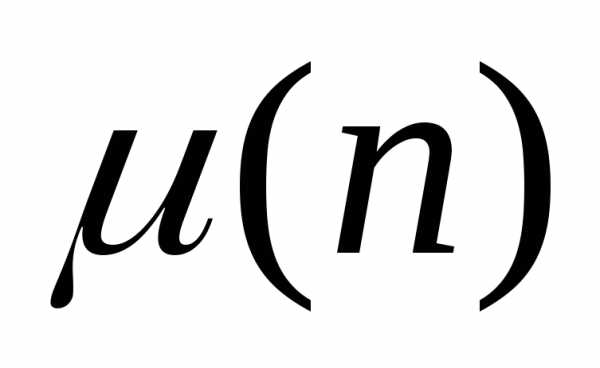 с помощью комбинаторных коэффициентов
с помощью комбинаторных коэффициентов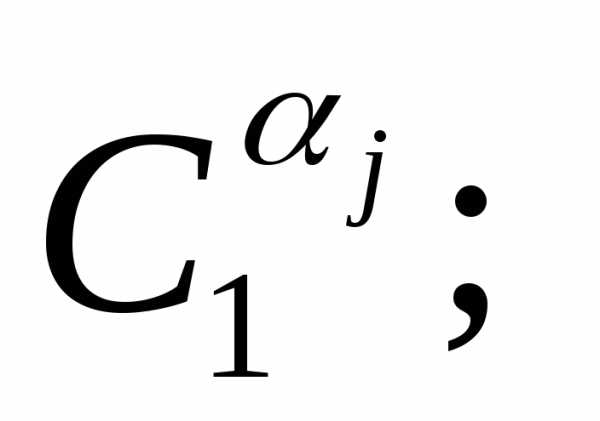 равенством:
равенством:
(**)
Докажите, что
1. Для
любых взаимно простых натуральных 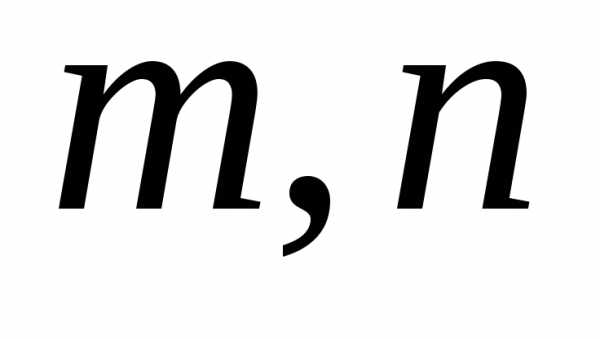
, (свойство мультипликативности)
2.
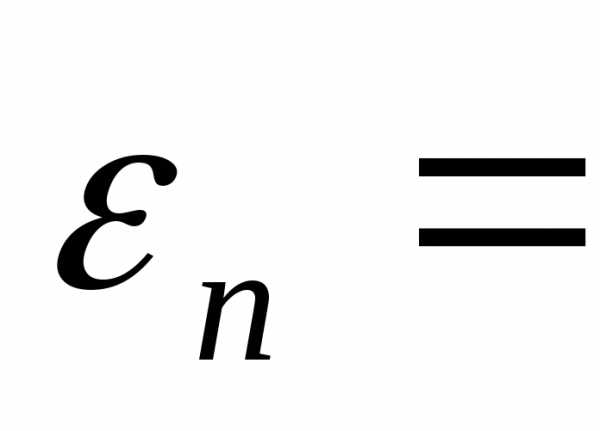
 (свойство ортогональности)
(свойство ортогональности)
где
суммирование ведётся по всем положительным
целым делителям числа 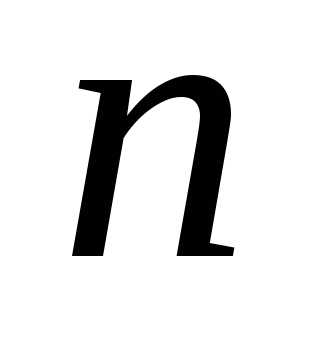 .
.
3. Вычислите функцию
Примечание. Классическая функция Мебиуса определяется несколько иначе. По этому поводу можно обратиться, например, к известным учебникам по теории чисел [3;4]. Определение (**) предложенное здесь выгодно по многим причинам. Во – первых, функция определена одной формулой, во – вторых, легко определяются различные обобщения (речь идёт о функциях
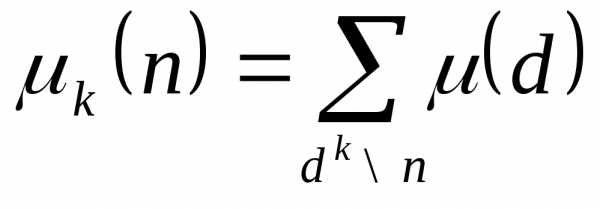 ,
,
которая
равна 0 или 1, смотря по тому, делится
или не делится число 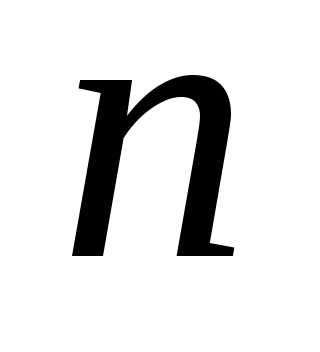 на
на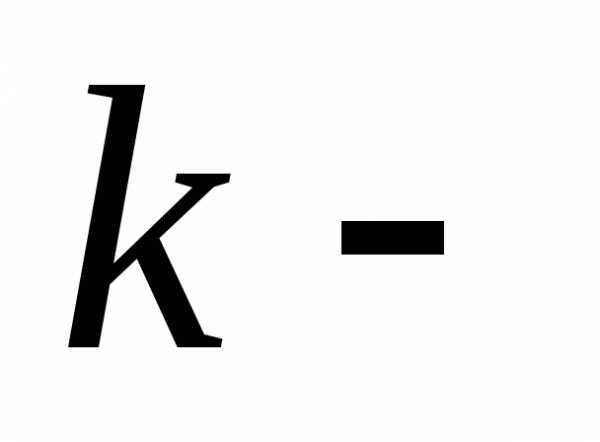 тую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].
тую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].
Читателям интересующихся более обстоятельно этими вопросами, рекомендуем обратиться к фундаментальным источникам по аналитической теории чисел [5-7].
Рассмотрим ещё одну тематику, обобщающую понятие размещения.
8. Размещения данного состава. Полиномиальная формула.
Начнём со следующей простой задачи
 .
Состав строки. Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
— в каждую из них входят три буквы
.
Состав строки. Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
— в каждую из них входят три буквы  и две буквы
и две буквы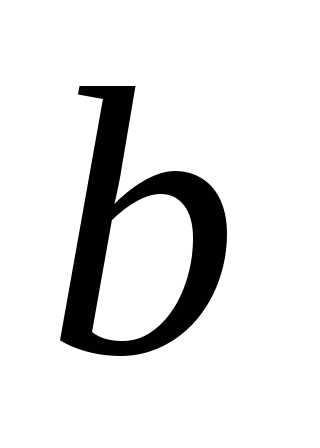 .
Далее, уточним понятиесостава
строки. Пусть
некоторое
.
Далее, уточним понятиесостава
строки. Пусть
некоторое  членное
множество,
членное
множество, 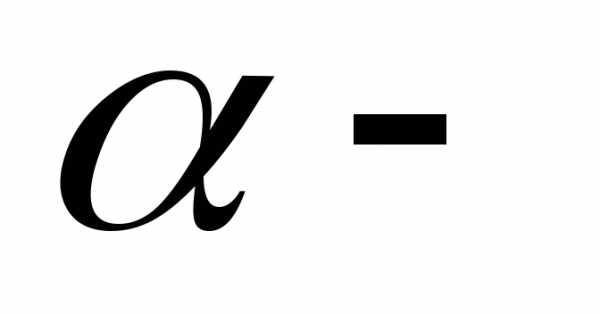 строка длиной
строка длиной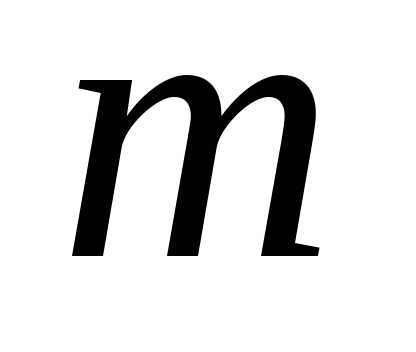 ,
составленная из элементов множества
,
составленная из элементов множества .
Тогда каждому номеру
.
Тогда каждому номеру из совокупности
из совокупности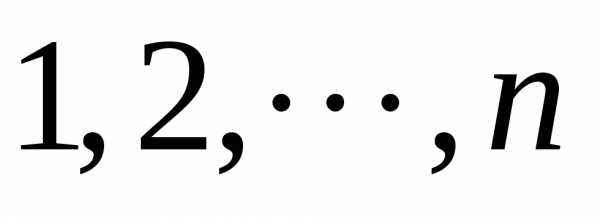 будет
соответствовать число
будет
соответствовать число 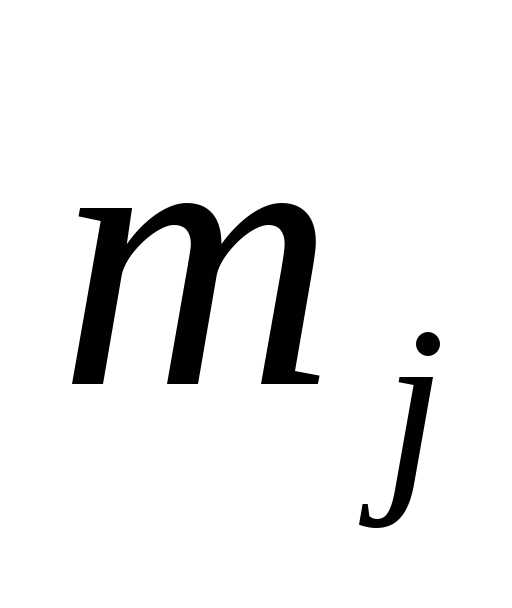 указывающее, на количество участия
элементов
указывающее, на количество участия
элементов в строке
в строке  .
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки
.
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки .
.
Например, если и
,
то строка имеет следующий состав
имеет следующий состав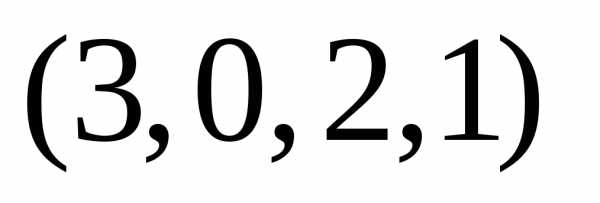 .
Следовательно, в строке
.
Следовательно, в строке элемент
элемент участвует три раза, элемент
участвует три раза, элемент не участвует, элемент
не участвует, элемент участвует два раза, элемент
участвует два раза, элемент участвует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.
участвует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.
Рассмотрим следующую комбинаторную задачу: найти число размещений, имеющий данный состав .
Приведём основное утверждение о числе составов
Теорема
3. Количество 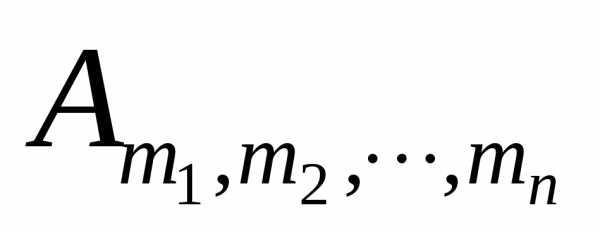 — различных
последовательностей (составов), составленных из элементов , в которых
каждый элемент
— различных
последовательностей (составов), составленных из элементов , в которых
каждый элемент  встречается
встречается 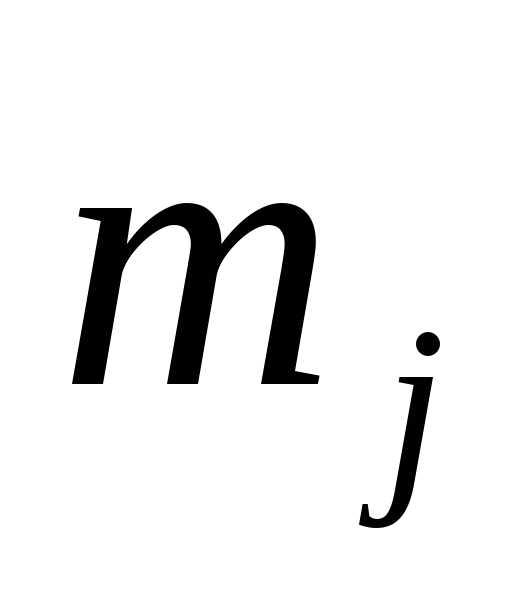 раз (равно
раз (равно
(4) .
Доказательство. Обозначим количество
составов указанных в формулировке
теоремы 1 буквой  .
А так же, положим.
Введём в рассмотрение
.
А так же, положим.
Введём в рассмотрение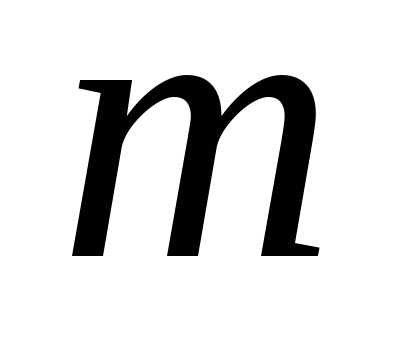 произвольных
различных элементов:
произвольных
различных элементов:
.
Для любой исходной последовательности строим различные перестановки из
указанных 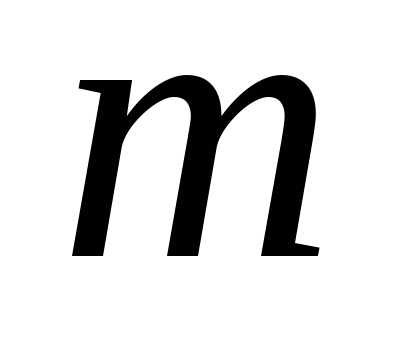 элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же
элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же (этот элемент встречался
(этот элемент встречался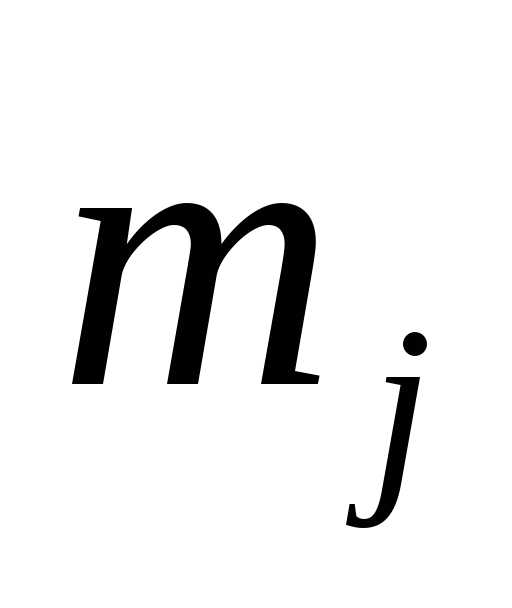 раз), записываем какой-нибудь перестановку
из
раз), записываем какой-нибудь перестановку
из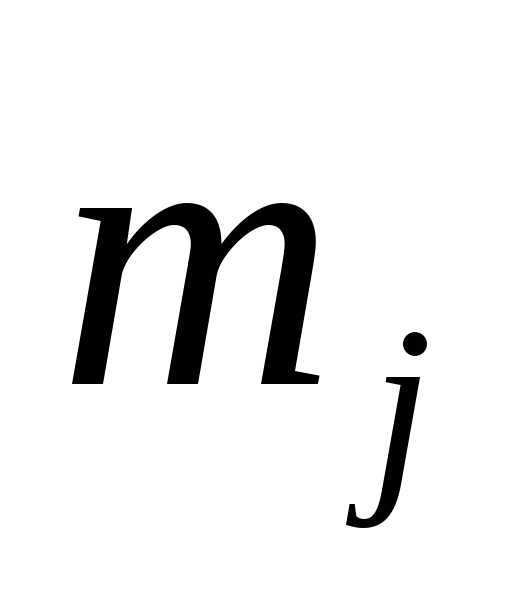 элементов
.
Согласно
равенству (2) такое действие для одного
элементов
.
Согласно
равенству (2) такое действие для одного  можно осуществлять в точности
можно осуществлять в точности различными способами. Проделав такое
действие для каждого
различными способами. Проделав такое
действие для каждого (),
мы получим некоторую перестановку из
(),
мы получим некоторую перестановку из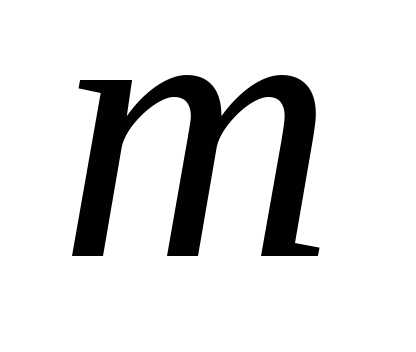 из указанных выше элементов. На основании
формулы умножения (см. пункт
из указанных выше элементов. На основании
формулы умножения (см. пункт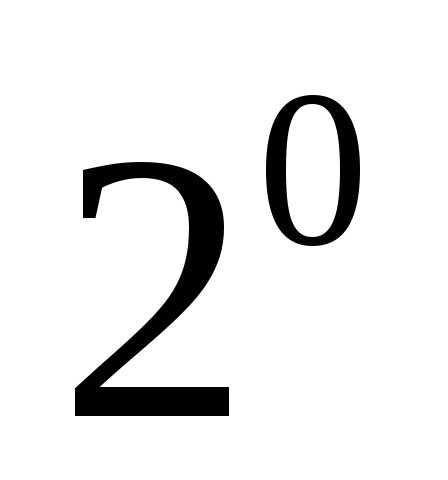 )
для любой последовательности строки
получим всего указанным способом
различных перестановок из
)
для любой последовательности строки
получим всего указанным способом
различных перестановок из  элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятых
элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятых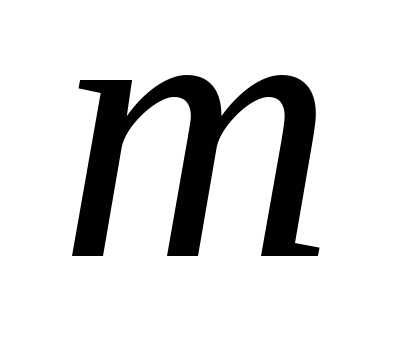 элементов.
При этом любая из выбранных
элементов.
При этом любая из выбранных элементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом
элементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом  для кахдого.
Таким образом, с учётом равенства (2)
получаем:
для кахдого.
Таким образом, с учётом равенства (2)
получаем: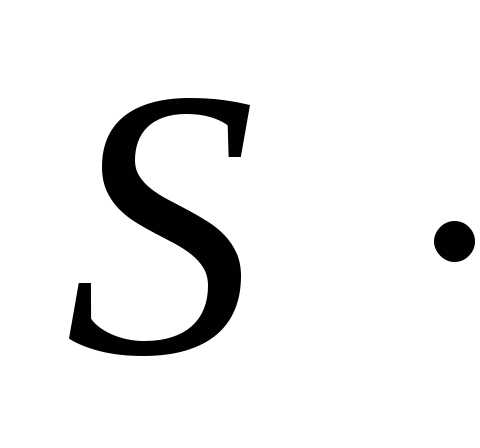 ,
следовательно,
,
следовательно,
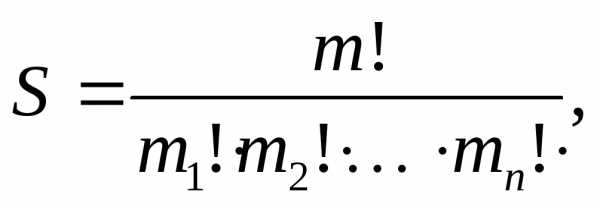
И с учётом нашего обозначения , теорема доказана.
Пример 1. Количество различных 6 — значных натуральных чисел, которые можно записать с помощью цифр 1,2,3 так, чтобы каждая цифра встречалась в записи по два раза, равно:
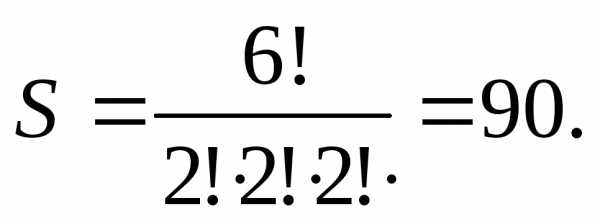
Пример 2. В наличии имеются книги трёх наименований, причём имеется три экземпляра книг одного наименования, пять экземпляров другого и два экземпляра третьего. Количество различных размещений этих книг на одной полке составляет:
Если в наличии
имеются книги 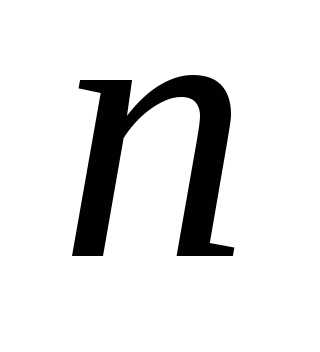 различных наименований, причём по
различных наименований, причём по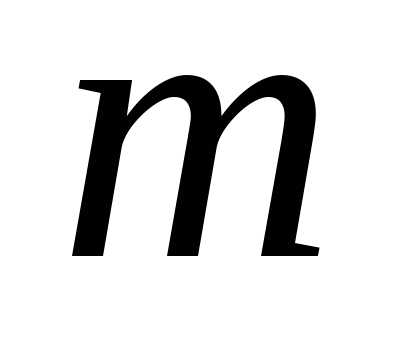 экземпляров книг каждого наименования,
то все
экземпляров книг каждого наименования,
то все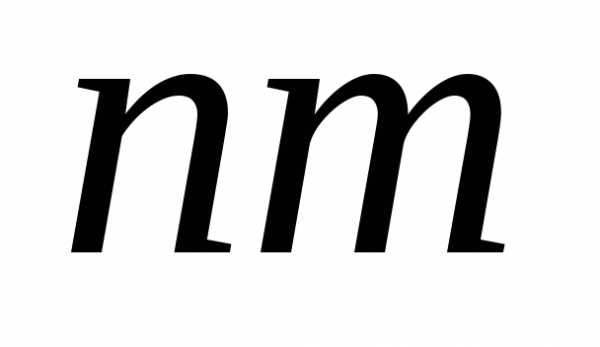 экземпляров
книг могут быть размещены на полке
экземпляров
книг могут быть размещены на полке
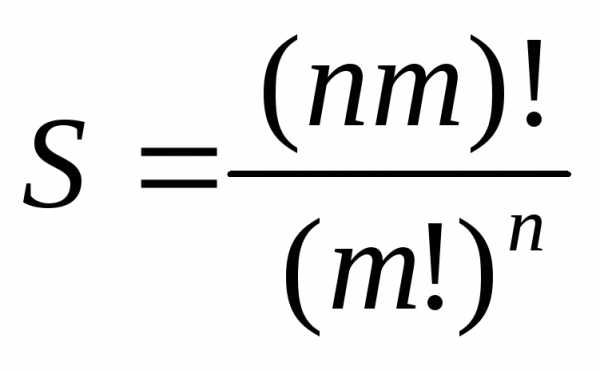
способами.
Пример 3. В одном ряду шахматной доски располагаются: 1 король, 1 ферз, 2 слона, 2 коня, 2 ладьи. Количество всевозможных расположения этих фигур в одном ряду равно:
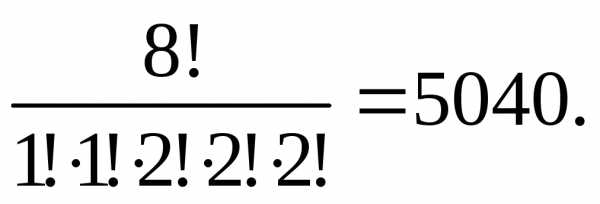
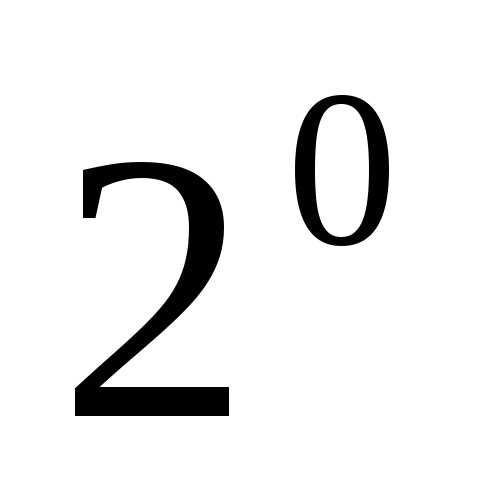 .
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.
.
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.
Пусть любые числа (или произвольные комутативные объекты). Имеет место
следующее утверждение
Теорема 4. Справедлива полиномиальная формула
(4)
где суммирование распространяется на всевозможные целые числа , для которых
.
Следствие.
1) Для случая , получаем формулу
(5)
2) Для случая  имеет
место равенство
имеет
место равенство
Задания: 1. На основании равенство (5) проверьте тождество
.
2. Пусть
,
тогда при целом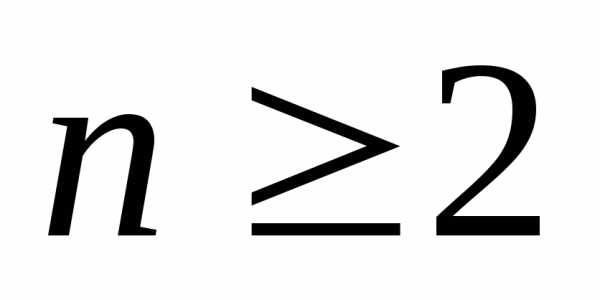 справедливо
неравенство
справедливо
неравенство
Это известное неравенство Бернулли.
Указание. Используйте метод математической индукции.
В завершении этого раздела сформулируем известную формулу Стирлинга без доказательства.
,
где
основание
натурального логарифма. Эта формула
обычно применяется при больших значениях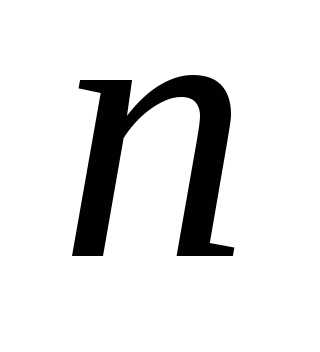 .
В частности, из неё вытекает, что
.
В частности, из неё вытекает, что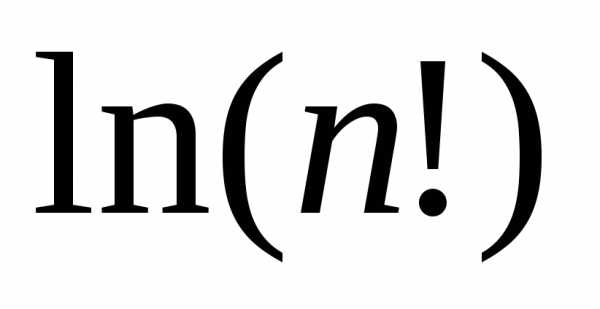 с точностью до
с точностью до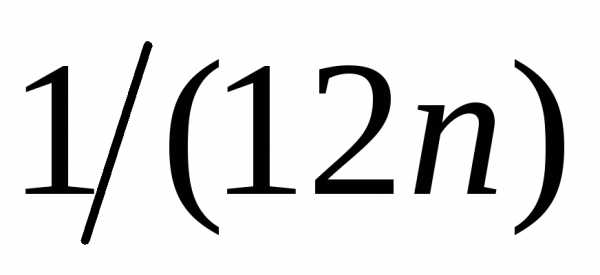 приближается выражением
приближается выражением
.
Другими словами, справедливо (с учётом свойства логарифмической функции) неравенство
studfiles.net
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Формула бинома Ньютона
В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома
(x + y)n
в случаях, когда n = 1, 2, 3, 4, 5, 6.
В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения n .
Материал настоящего раздела близко связан с материалом разделов «Формулы сокращенного умножения: степень суммы и степень разности», «Треугольник Паскаля» и «Комбинаторика: размещения и сочетания».
Утверждение. Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона:
где
| (2) |
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона, а числа сочетаний – коэффициентами разложения или биномиальными коэффициентами.
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:

Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
к доказательству которых мы сейчас и переходим.
Докажем сначала равенство 1.
Это равенство отражает основное свойство треугольника Паскаля, заключающееся в том, что в каждой из строк треугольника Паскаля, начиная со строки с номером 2 , между числами 1 стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.
Для доказательства равенства 1 воспользуемся формулой (2):

что и требовалось.
Для доказательства равенства 2 положим в формуле бинома Ньютона (1) x = 1, y = 1.
Если же в формуле бинома Ньютона (1) взять x = 1, y = –1, то получится равенство 3.
Перейдем к доказательству равенства 4. С этой целью положим в формуле бинома Ньютона (1) y = 1
| (3) |
Воспользовавшись очевидным равенством
перепишем формулу (3) в другом виде
| (4) |
Если теперь перемножить формулы (3) и (4), то мы получим равенство:
 | (5) |
Если к левой части формулы (5) применить формулу бинома Ньютона, а затем, раскрыв в правой части скобки и приведя подобные члены, приравнять коэффициенты при xn в левой и в правой частях, то мы получим следующее равенство:
что и требовалось.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Математика КАК 2х2.: Бином Ньютона.
Навигация по странице.
Бином Ньютона — формула.
Формула бинома Ньютона для натуральных n имеет вид , где — биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а «!» – это знак факториала).К примеру, известная формула сокращенного умножения «квадрат суммы» вида есть частный случай бинома Ньютона при n=2. Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)n, а выражение называют (k+1)-ым членом разложения, k=0,1,2,…,n.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.
Треугольник Паскаля.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Свойства биномиальных коэффициентов.
Для коэффициентов бинома Ньютона справедливы следующие свойства:
- коэффициенты, равноудаленные от начала и конца разложения, равны между собой, p=0,1,2,…,n;
- ;
- сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: ;
- сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Первые два свойства являются свойствами числа сочетаний.
Доказательство формулы бинома Ньютона.
Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .Этим доказана формула бинома Ньютона.
Бином Ньютона — применение при решении примеров и задач.
Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.
Напишите разложение выражения (a+b)5 по формуле бинома Ньютона.
Смотрим на строку треугольника Паскаля, соответствующую пятой степени. Биномиальными коэффициентами будут числа 1, 5, 10, 10, 5, 1. Таким образом, имеем . Найдите коэффициент бинома Ньютона для шестого члена разложения выражения . В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Доказать, что значение выражения , где n – натуральное число, делится на16 без остатка. Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16.
matematika-2014elena-viktorovna.blogspot.com

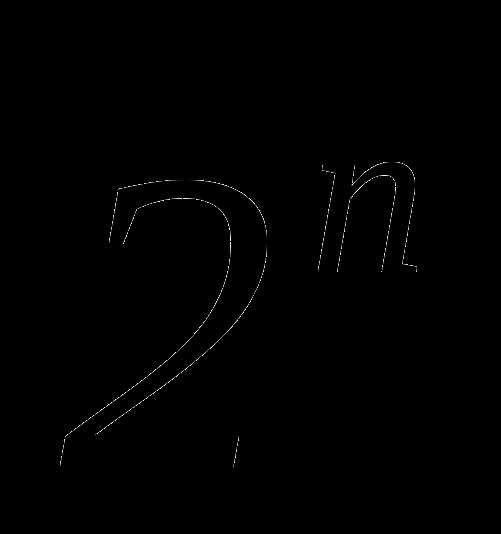
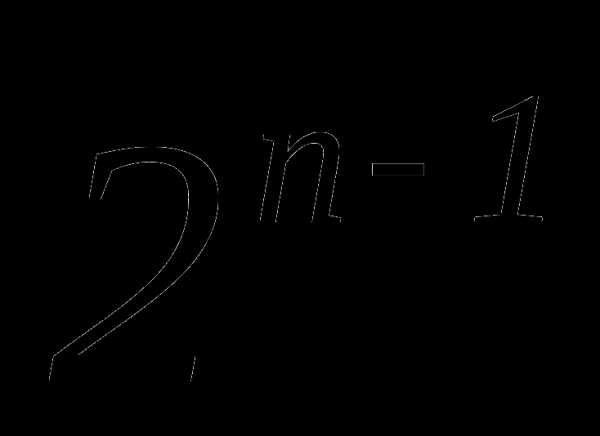
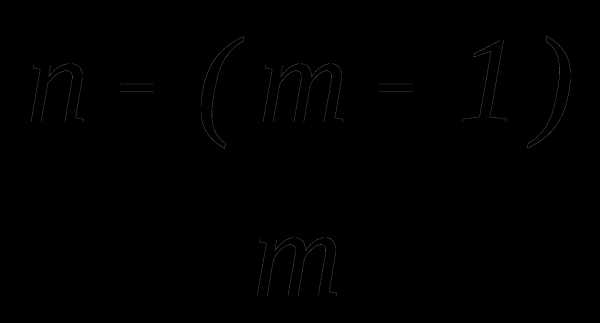
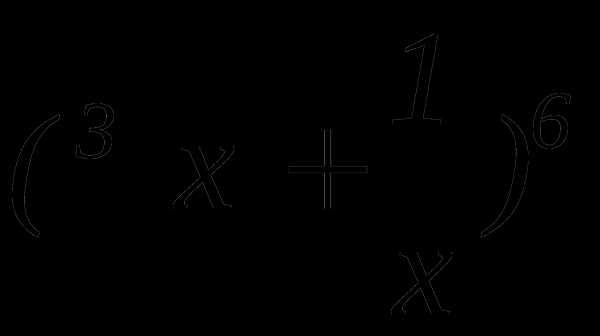 ,
не содержащего х.
,
не содержащего х.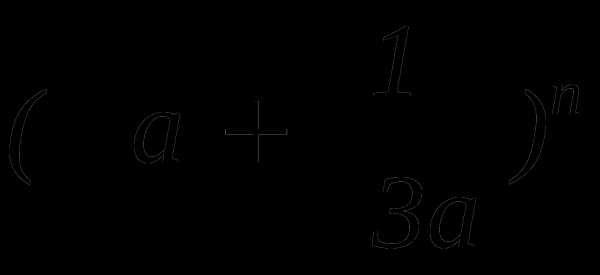 .
.
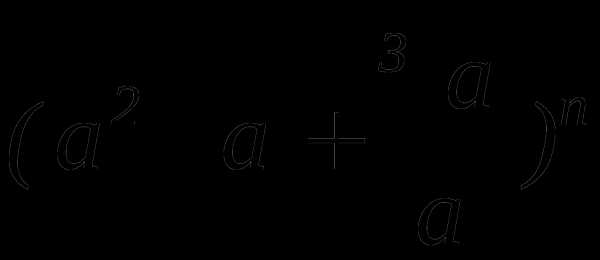 ,
если биномиальный коэффициент третьего
члена равен 36.
,
если биномиальный коэффициент третьего
члена равен 36. .
.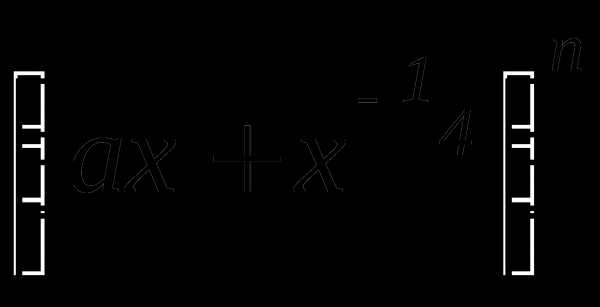 равна 512. Найти слагаемое, не содержащее
равна 512. Найти слагаемое, не содержащее 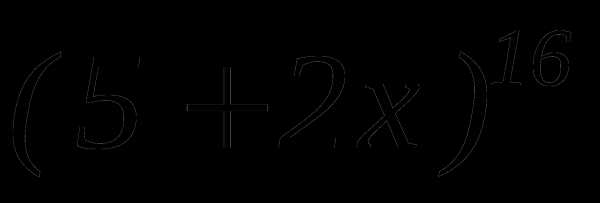 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых? чтобы отношение четвертого слагаемого
разложения к третьему было равно
чтобы отношение четвертого слагаемого
разложения к третьему было равно  ?
?