Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Yandex.RTB R-A-339285-1Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выраженияПусть нужно найти значения выражения 14-2·15÷6-3.
Выполним сначала умножение и деление. Получаем:
14-2·15÷6-3=14-30÷6-3=14-5-3.
Теперь проводим вычитание и получаем окончательный результат:
14-5-3=9-3=6.
Пример 2. Значение числового выраженияВычислим: 0,5-2·-7+23÷234·1112.
Сначала выполняем преобразование дробей, деление и умножение:
0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112
12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
12-(-14)+29=12+14+29=14+
zaochnik.com
Числовые выражения; действия с дробными числами (В.А. Тарасов)
Тема: Математический язык. Математическая модель
Урок: Числовые выражения, действия с дробными числами
Основное свойство дроби заключается в том, что и числитель, и знаменатель можно умножить или разделить на одно и то же число, не равное нулю.
Пример 1: Домножить дробь на k.
Дробь не изменится, если числитель и знаменатель , при условии . Значит:
=
Пример 2: Разделить числитель и знаменатель дроби на число n.
При делении числителя и знаменателя на число nзначение дроби не изменится в случае, если.
=
Пример 3: Домножить дробь на 3.
Ответ:
Пример 4: Сократить дробь .
Для этого разложим и числитель, и знаменатель на простые множители.
Разделим и числитель, и знаменатель на 3 и получим несократимую дробь:
Ответ:
Пример 5: Сократить дробь .
Разложим и числитель, и знаменатель на простые множители.
Разделим числитель и знаменатель на 2 и на 3 и получим несократимую дробь.
Ответ: .
Пример 6: Сократить дробь .
Разложим и числитель, и знаменатель на простые множители и сократим одинаковые.
Ответ: .
Пример 7: Найти значение выражения .
Разложим каждый знаменатель на простые множители и найдем их НОК, который и является общим знаменателем.
;
;
НОК(45;75) =
Дополнительный множитель дроби находится по формуле:
Значит, получаем:
Ответ: .
Правило умножения дроби на дробь.
При умножении дроби на дробь необходимо перемножить числители, и результат поставить в числитель, а также перемножить знаменатели и результат поставить в знаменатель. Получаем:
Правило деления дроби на дробь.
Существует два способа деления дроби на дробь.
1й способ: Для того, чтобы разделить дробь на дробь , надо дробь умножить на обратную дробь , т.е. на .
2й способ: Для того чтобы разделить дробь на дробь , надо числитель первой дроби умножить на знаменатель второй дроби и получить числитель искомой дроби, знаменатель первой дроби умножить на числитель второй дроби и получить знаменатель искомой дроби:
Правило умножения дроби на число.
При умножении дроби на число необходимо числитель умножить на число , а знаменатель оставить неизменным. Данное правило подтверждается еще тем, что любое число можно представить в виде дроби .
Пример 8: Умножить дробь на число 7.
Ответ: 4.
Правило деления дроби на число.
При делении дроби на число необходимо число представить в виде дроби и потом использовать правило деления дроби на дробь.
Пример 9: Разделить дробь на число 7.
.
Ответ:.
Правило деления числа на дробь.
При делении числа n на дробь необходимо помнить, что n – это дробь . И в результате использовать правило деления дроби на дробь.
Пример 10: Решить уравнение .
Для того чтобы найти х, следует и числитель, и знаменатель разделить на одно и то же число – коэффициент перед х.
,
Ответ: 3.
Пример 11: Решить уравнение .
Данное уравнение можно решить двумя способами – в одно и в два действия. В одно действие – надо разделить обе части на коэффициент перед х.
Для решения уравнения в 2 действия, можно сначала умножить на обе части уравнения и получить . Дальше, чтобы получить х, необходимо и левую, и правую часть умножить на 2.
Ответ:.
Пример 12: Решить уравнение .
1-ый способ: Разделим правую и левую часть на коэффициент перед , т.е. на .
2-ой способ: Умножим обе части на 3. Получается тот же результат.
Ответ: 9.
Пример 13: Найти значение алгебраического выражения если .
Первым действием необходимо вычислить данное выражение, подставив значения переменных.
Вторым действием проверим, является ли набор значений допустимым для данного алгебраического выражения.
Напомним, что набор будет допустимым, если при значениях а, b и с выражение можно вычислить.
Подставив значения, видим, что знаменатель выражения не равен нолю, значит, выражение можно вычислить.
Третьим действием необходимо сократить дробь. Исходя из основного свойства дроби, при делении положительного числа на отрицательное получается отрицательное число.
Ответ: .
Итак, в данном уроке мы рассмотрели действия с числовыми и алгебраическими дробями. Также вспомнили основные правила сложения, вычитания, умножения и деления дробей. И мы видим, что вот эти действия и правила полностью переносятся на действия с алгебраическими дробями.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Фестиваль педагогических идей «Открытый урок» (Источник).
2. Интернет-портал podelise.ru (Источник).
3. Интернет-портал Павла Бердова (Источник).
Рекомендованное домашнее задание
1. № 20-23-7 стр. 10-11. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Выполнить умножение или деление:
а) б) в) г)
3. Сократить дробь:
а) б)
4. Найти значение выражения:
а)
б)
interneturok.ru
Показательные выражения
Показательные выражения. Друзья! В состав ЕГЭ по математике входит задание на вычисление или преобразование выражений. Логарифмические выражения мы уже рассмотрели.
В этой статье рассмотрим показательные. Данные задания крайне просты, решение умещается практически в одну строчку. Конечно, необходимо знать свойства показателей степени и иметь хорошую практику решения. В одной из статей эти свойства уже были перечислены, можете также заглянуть в справочник на блоге.
Думал-думал, каким образом подать материал в статье и ничего лучшего не придумал, как разместить подробнейшие решения около тридцати примеров. В ходе решения поэтапно показаны все преобразования, вы без труда поймёте, какое свойство было применено. Некоторым, наверное, даже будет скучненько, но, уверен, что представленные подробные решения для многих будут полезны. Рассмотрим примеры:
26754. Найдите значение выражения:
Ответ: 49
27797. Найдите значение выражения:
Ответ: 5
26801. Найдите значение выражения:
Ответ: 0,25
26813. Найдите значение выражения:
Ответ: 5
26814. Найдите значение выражения:
Ответ: 2
26815. Найдите значение выражения:
Ответ: 7
26816. Найдите значение выражения:
Ответ: 64
26826. Найдите значение выражения:
Ответ: 144
26828. Найдите значение выражения:
Ответ: 121
26831. Найдите значение выражения:
Ответ: 6
26834. Найдите значение выражения:
Ответ: 32
26835. Найдите значение выражения:
Ответ: 27
26836. Найдите значение выражения:
Ответ: 3
26841. Найдите значение выражения:
Ответ: 8
26901. Найдите значение выражения:
Ответ: 16
77393. Найдите значение выражения:
Ответ: 0,0001
77394. Найдите значение выражения:
Ответ: 0,2
77395. Найдите значение выражения:
Ответ: 0,5
77396. Найдите значение выражения:
Ответ: 15
77397. Найдите значение выражения:
Ответ: 150
77398. Найдите значение выражения:
Ответ: 7
77399. Найдите значение выражения:
Ответ: 88
77400. Найдите значение выражения:
Ответ: 121
77401. Найдите значение выражения:
Ответ: 64
77402. Найдите значение выражения:
Ответ: 2
77403. Найдите значение выражения:
Ответ: 2,5
77404. Найдите значение выражения:
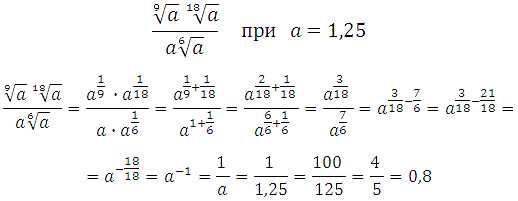
Ответ: 0,8
77406. Найдите значение выражения:
Ответ: 5
77407. Найдите значение выражения:
Ответ: 4
77408. Найдите значение выражения:
Ответ: 2
77409. Найдите значение выражения:
Ответ: 36
77411. Найдите значение выражения:
Ответ: 25
Посмотреть решение
Посмотреть решение
Посмотреть решение
Посмотреть решение
Посмотреть решение
Что можно отметить?
В случае, когда основания показателей степени равны, при решении выражения сразу можно применять свойства показателей степени.
В случае, когда основания показателей степени неравны, требуется выполнить преобразования, целью которых является приведение оснований к равным величинам, а далее уже можно применять оговоренные свойства.
В данной рубрике мы продолжим рассматривать и другие выражения, не пропустите!
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника, что такое переменная — этот вопрос поставит его в ступор, хотя, возможно, он и будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи какие-то решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
Значение переменной a подставляется в исходное выражение.В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле, ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Значение переменной x подставляется в выражение x + 10Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомните второй урок «Основные операции». Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
И вот, имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа мы подставим вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия. В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения при Задание 2. Найдите значение выражения при Задание 3. Найдите значение выражения при Задание 4. Найдите значение выражения при и Задание 5. Найдите значение выражения приПонравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Найдите значение выражения (действия с дробями) – как решать
Формулировка задачи: Найдите значение выражения (действия с дробями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения 5/4 + 7/6 : 2/3.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. И выполним необходимые действия в нужном порядке:
Ответ: 3
Пример задачи 2:
Найдите значение выражения (3,9 – 2,4) ∙ 8,2
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 12,3
Пример задачи 3:
Найдите значение выражения 27 ∙ (1/3 – 4/9 – 5/27).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: –8
Пример задачи 4:
Найдите значение выражения 2,7 / (1,4 + 0,1)
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 1,8
Пример задачи 5:
Найдите значение выражения 1 / (1/9 – 1/12).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 36
Пример задачи 6:
Найдите значение выражения (0,24 ∙ 10^6) / (0,6 ∙ 10^4).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 40
Пример задачи 7:
Найдите значение выражения (1,23 ∙ 45,7) / (12,3 ∙ 0,457).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 10
Пример задачи 8:
Найдите значение выражения (728^2 – 26^2) : 754.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке. Также в данном случае нужно применить формулу разности квадратов:
Ответ: 702
worksbase.ru
Числовые и буквенные показательные выражения
Часть 3.
Здесь смотрим части 1, 2, 4, 5
Часть 1. Числовые показательные выражения
Задание 1.
Найдите значение выражения .
Решение: + показать Мы воспользуемся следующими двумя правилами: и Ответ: 9.
Задание 2.
Найдите значение выражения .
Решение: + показать Воспользуемся следующими правилами: и Ответ: 63.
Задание 3.
Найдите значение выражения .
Решение: + показать Ответ: 16.
Задание 4.
Найдите значение выражения .
Решение: + показать
Задание 5.
Найдите значение выражения: .
Решение: + показать Ответ: 216.
Задание 6.
Найдите значение выражения .
Решение: + показать Ответ: 49.
Часть 2. Буквенные показательные выражения
Задание 1.
Найдите значение выражения .
Решение: + показать Ответ: 3.
Задание 2.
Найдите значение выражения при .
Решение: + показать Ответ: 1.
Задание 3.
Найдите значение выражения при .
Решение: + показать Ответ: 33.
Задание 4.
Найдите значение выражения .
Решение: + показать Ответ: 0,8.
Задание 5.
Найдите значение выражения .
Решение: + показать Ответ: 2.
Задание 6.
Найдите значение выражения .
Решение: + показать Ответ: 3,5.
Задание 7.
Найдите значение выражения при .
Решение: + показать При Ответ: -101.
Задание 8.
Найдите значение выражения , если .
Решение: + показать Ответ: 11.
Задание 9.
Найдите значение выражения при .
Решение: + показать При Ответ: 180.
Самое время передохнуть –> + показать
Не дрефь! Все будет хорошо!
Вы можете пройти тест «Преобразование показательных выражений»
egemaximum.ru
Алгебраические выражения
Алгебраические выражения. В этой статье рассмотрим с вами примеры входящие в состав экзамена по математике, при решении которых у ребят возникают проблемы. Многие таких вообще не видели и в школьном курсе их не касались. Будем преобразовывать алгебраические выражения. Задания есть довольно простые, где достаточно знать формулы сокращённого умножения, свойства степеней, уметь «работать» с дробями. Вот типичные несложные примеры, можете решить и проверить себя:
Далее мы рассмотрим примеры, решения которых просты, но сами условия могут несколько отпугнуть вас, так как подобные задания в курсе школьной программы встречаются редко. Посмотрев процесс решения, уверен, вы всё поймёте без проблем. Есть примеры для самостоятельного решения, практикуйтесь, затем сверьте с решением представленным на блоге.
Найдите p (b)/(p (1/b)), если
Сначала необходимо найти
То есть, вместо b в исходное выражение мы подставили 1/b. Итак:
Ответ: 1
Посмотреть аналогичный пример
Найдите 49a – 41b – 14, если
В подобных примерах не раздумывайте над тем, как данное выражение можно найти, выполните преобразование выражения:
Для того, чтобы найти чему равно данное выражение, необходимо вычесть 34 из обеих частей уравнения:
Ответ: –34
Посмотреть аналогичный пример
Найдите
Так как a/b=3, значит a=3b. Тогда можем преобразовать:
Ответ: 2
Найдите значение выражения 3p (a) – 6a +7, если p (a)=2a–3.
В данном случае просто подставляем p (a) и решаем:
3p (a) – 6a +7 = 3 (2a – 3) – 6a +7 = 6a – 9 – 6a +7 = –2
Ответ: –2
Найдите значение выражения 7x+2y+6z, если 7x+y = 7, 6z + y = 5.
В подобных задачах ищите сумму или разность уравнений под условием «если», результат как правило, будет сведён нахождению значения данного выражения, найдём сумму уравнений:
7x+y+6z+y= 7+5
7x+2y+6z = 12
В других примерах, возможно потребуется разделить или умножить обе части уравнения на какое-либо число.
Ответ: 12
Посмотреть аналогичный пример
Найдите значение выражения q (b–7)–q (b+7), если q (b)=–6b.
Если q (b)=–6b, то q (b–7)=–6 (b–7) и q (b+7)=–6 (b+7).
То есть мы подставляем аргумент в формулу задающую функцию, значит:
q (b–7)–q (b+7)=–6 (b–7)–(–6)(b+7)=–6b+42+6b+42=84
Ответ: 84
Посмотреть аналогичный пример
Найдите значение выражения 5 (p (2x)–2p (x+5)), если p (x)= x–10.
Если p (x)= x–10, то p (2x) =2x–10 и p (x+5) =x+5–10.
Получаем:
5 (p (2x) –2p (x+5)) = 5 (2x–10–2 (x+5–10)) = 5 (2x–2x–10–10+20)=0
Ответ: 0
Найдите p (x–7)+p (13–x), если p (x)=2x+1.
Подставляем аргумент в формулу задающую функцию.
Если p (x)=2x+1, то p (x–7)=2 (x–7)+1 и p (13–x) =2 (13–x)+1.
Находим сумму:
p (x–7)+ p (13–x)=2 (x–7)+1+2 (13–x)+1=2x–14+1+26–2x+1=14
Ответ: 14
Найдите 2p (x+5)–p (2x), если p (x)=2x–6.
Если p (x)=2x–6, то p (x+5)=2 (x+5)–6 и p (2x)=2 (2x)–6.
Находим разность:
2p (x+5)–p (2x)=2 (2 (x+5)–6)–(2 (2x)–6)=2 (2x+4)–4x+6=14
Ответ: 14
Посмотреть аналогичный пример
Найдите p (x) + p (12 –x), если
Если
То
Найдём сумму:
Ответ: 0
В будущем продолжим рассмотрение заданий с выражениями, не пропустите! На этом закончим. Время стремительно бежит, помните об этом. Практикуйтесь, отрабатывайте навыки.
Всего доброго!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
