Натуральные и целые числа действительные числа – натуральные, целые, рациональные, иррациональные, действительные

1.1.1 Целые числа

Видеоурок: Натуральные, целые, рациональные, иррациональные и действительные числа

Лекция: Целые числа

Целые и натуральные числа

К целым числам можно отнести все числа натурального ряда, им противоположные, а также ноль.

 

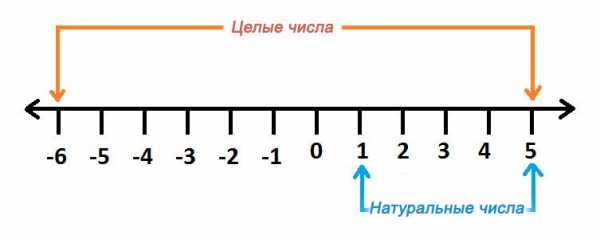То есть это все не дробные положительные, отрицательные числа, а так же ноль — иными словами, все не дробные числа на числовой прямой. Используя термин «натуральные числа» мы понимаем, что это не отрицательные и не дробные числа.

У Вас может возникнуть вопрос, чему же равно максимальное или минимальное целое число — таковых не существует, поскольку числовой ряд бесконечный.

Среди всего множества чисел, целые числа обозначаются буквой Z, а натуральные — 

N.

Все натуральные числа используются для счета. Например, на дереве висит 5 яблок, стол сервирован на 8 персон. Мы же не можем сказать, что на столе 7,5 тарелок, или у цветка -3 листка. Числа, противоположные натуральным, — это не дробные и отрицательные числа.

Арифметические действия

Существует несколько математических операций, которые можно производить с целыми числами. Хотелось пояснить каждую из них.

1. Сложение / Вычитание

При необходимости сложить два числа, имеющие одинаковые знаки, следует сложить их модули и поставить общий знак. Например,

 |+4| + |+6| = |+10|,

 |-8| + |-3| = |-11|.

Если необходимо сложить целые числа, которые имеют противоположные знаки, следует от числа с большим модулем вычесть второе число. Перед суммой поставить знак большего модуля. Например,

 |-10| + |+3| = |-7|,

 |+5| + |-2| = |+3|.

2. Умножение / Деление

Если следует получить произведение (частное) двух чисел, следует перемножить их модули. Перед произведением (частным) ставится знак «+» в том случае, если перемножались (делились) числа с одинаковыми знаками. Если умножение (деление) происходило между числами с разными знаками, то ставят знак «-«. 

Например,

 |-5| *  |-6| = |+30|,

 |+3| * |+7| = |+21|,

 |-4| *  |+3| = |-12|.

Основные правила, используемые при делении, умножении, сложении и вычитании целых чисел.

Рассмотрим арифметические действия, которые производятся над тремя целыми числами а, б, с.

cknow.ru

Методическая разработка лекции на тему:»Целые, рациональные и действительные числа. Приближенное значение величины и погрешности приближений. Комплексные числа.»

Профессионально – педагогический колледж

Государственного образовательного учреждения высшего образования Московской области

«Государственный гуманитарно – технологический университет»

Методическая разработка урока

на тему: «Целые, рациональные и действительные числа. Приближенное значение величины и погрешности приближений. Комплексные числа»

Разработала преподаватель математики

Азовцева Мария Андреевна

Г. Орехово-Зуево, 2017 год

Цели занятия:

Должен уметь:

1. Выполнять арифметические действия над числами. Решать задачи.

2. Находить приближенные значения величин и погрешностей вычислений. Применять практические приемы приближенных вычислений.

3. Выполнять действия над комплексными числами; представлять комплексные числа в тригонометрической и показательной формах; находить модуль и аргумент комплексного числа.

Должен знать:

1. Определение и свойства натуральных и целых чисел. Рациональные числа и его свойства. Иррациональные числа.

2. Приближенные значения. Погрешность приближения. Абсолютная и относительная погрешности приближения и их границы.

3. Определение комплексного числа, понятие равенства и действия сложения и умножения комплексных чисел, модуль и аргумент комплексного числа.

Ход занятия

1. Целые, рациональные и действительные числа.

Определение. Натуральные числа – это числа вида N={1, 2, 3, …,}. Натуральные числа появились в связи с необходимостью подсчета предметов.

Определение. Натуральные числа, числа, противоположные натуральным, и нуль составляют множество Z целых чисел.

Свойства натуральных и целых чисел:

1. — переместительный закон сложения;

2. — сочетательный закон сложения;

3. — переместительный закон умножения;

4. — сочетательный закон умножения;

5. — распределительный закон умножения относительно сложения.

Определение. Рациональные числа – это числа, представимые в виде дроби где — целое число, а — натуральное число. Для обозначения рациональных чисел используется латинская буква . Все натуральные и целые числа – рациональные.

Примеры рациональных чисел:

Свойства рациональных чисел.

1. ;

2. ;

5. ;

6. ;

7. ;

9. где

Определение. Действительные числа (вещественные) – числа, которые применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой . Действительные числа включают в себя рациональные и иррациональные числа.

Иррациональные числа – числа, которые получаются в результате выполнения различных операций с рациональными числами (н-р, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел:

Любое действительное число можно отобразить на числовой прямой.

Вывод: Для перечисленных выше множеств чисел справедливо следующее высказывание:

то есть, множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. А множество рациональных чисел входит во множество действительных чисел.

Модуль действительного числа обозначается и определяется так же, как и модуль рационального числа:

Свойства модулей:

1. ,

2. Приближенные значения. Абсолютная и относительная погрешности.

Приближенное значение величины. Абсолютная погрешность приближения. Граница абсолютной погрешности.

Пусть результат измерения или вычисления величины с некоторой точностью равен . Тогда называется приближенным значением (или приближением) величины . Причем, если то называется приближенным значением с недостатком (или приближением снизу), а если то называется приближенным значением с избытком (или приближением сверху) величины .

Определение. Разность точного и приближенного значений величины называется погрешностью приближения.

Так, если — точное значение, — приближенное значение, то разность — погрешность приближения. Если ее обозначим через то получим

т.е. истинное значение равно сумме приближенного значения и погрешности приближения.

Модуль разности точного и приближенного значений величины называется

абсолютной погрешностью приближения.

Следовательно, если — погрешность приближения, то — абсолютная погрешность приближения.

Во многих практически важных случаях нельзя найти абсолютную погрешность приближения из-за того, что неизвестно точное значение величины. Однако можно указать положительное число, больше которого эта абсолютная погрешность быть не может.

Определение. Любое положительное число, которое больше или равно абсолютной погрешности, называется границей абсолютной погрешности.

Следовательно, если — точное значение, — приближенное значение, то разность — погрешность приближения, то любое число , удовлетворяющее неравенству является границей абсолютной погрешности. В этом случае говорят, что величина приближенно с точностью до равна , и пишут

с точностью до

или Запись означает, что истинное значение величины заключено между границами и т. е.

Если известно, что является приближенным значением величины , и требуется определить границу абсолютной погрешности этого приближенного значения, то эту задачу обычно формулируют так: «Определить (найти) точность приближенного равенства ».

Относительная погрешность. Граница относительной погрешности.

Определение: Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения.

Следовательно, если — точное значение, — приближенное значение, то отношение

является относительной погрешностью приближения.

Относительную погрешность часто выражают в процентах.

В отличие от абсолютной погрешности, которая чаще всего бывает размерной величиной, относительная погрешность является безразмерной величиной.

Определение. Любое положительное число, которое больше или равно относительной погрешности, называется границей относительной погрешности

.

Следовательно, если — погрешность приближения, то любое число , удовлетворяющее неравенству

является границей относительной погрешности. В частности, если — граница абсолютной погрешности, то число

является границей относительной погрешности приближения Отсюда, зная границу относительной погрешности, можно найти границу абсолютной погрешности:

3. Комплексные числа

Как известно из школьного курса, уравнение вида не имеет действительных корней, но существует необходимость решать уравнения такого вида. Для этого придумали так называемые «комплексные числа».

Для определения комплексных чисел сначала введем некоторый символ i, который назовем мнимой единицей. Этому символу приписывается свойство удовлетворять уравнению : , или При этом

.

Комплексным числом z называется выражение , где a и b

– действительные числа. При этом число a называется действительной частью числа z (a = Re z), а b – мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

Числа и называются комплексно-сопряженными.

Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Множество комплексных чисел – неупорядоченное множество, т.е. из двух комплексных чисел нельзя указать последующее и предыдущее. Между двумя комплексными числами нельзя поставить знаки неравенства > или <.

Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части:

Действия над комплексными числами.

1)

2)

3) или

Запись числа в виде z=x+yi называют алгебраической формой комплексного числа.

Запись числа z в виде или называют показательной формой комплексного числа.

Контрольные вопросы

1. Определение и свойства натуральных и целых чисел.

2. Рациональные числа и его свойства.

3. Иррациональные числа.

4. Приближенные значения.

5. Погрешность приближения.

6. Абсолютная и относительная погрешности приближения и их границы.

7. Определение комплексного числа

8. Понятие равенства

9. Действия над комплексными числами

infourok.ru

Целые числа: общее представление

В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как  целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.

Yandex.RTB R-A-339285-1

Целые числа. Определение, примеры

Вначале вспомним про натуральные числа ℕ. Само название говорит о том, что это такие числа, которые естественно использовались для счета с незапамятных времен. Для того, чтобы охватить понятие целых чисел, нам нужно расширить определение натуральных чисел.

Определение 1. Целые числа

Целые числа — это натуральные числа, числа, противоположные им, и число нуль. 

Множество целых чисел обозначается буквой ℤ.

Множество натуральных чисел ℕ — подмножество целых чисел ℤ. Любое натуральное число является целым, но не любое целое число является натуральным.

Из определения следует, что целым является любое из чисел 1, 2, 3.., число 0, а также числа -1, -2, -3,..

В соответствии с этим, приведем примеры. Числа 39, -589, 10000000, -1596, 0 являются целыми числами.

Целые числа и координатная прямая

Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.

Началу отсчета на координатной прямой соответствует число 0, а точкам, лежащим по обе стороны от нуля соответствуют положительные и отрицательные целые числа. Каждой точке соответствует единственное целое число. 

В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.

Положительные и отрицательные целые числа

Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.

Определение 2. Положительные целые числа

Положительные целые числа — это целые числа со знаком «плюс».

Например, число 7 — целое число со знаком плюс, то есть положительное целое число. На координатной прямой это число лежит справа от точки отсчета, за которую принято число 0. Другие примеры положительных целых чисел: 12, 502, 42, 33, 100500.

Определение 3. Отрицательные целые числа

Отрицательные целые числа — это целые числа со знаком «минус».

Примеры целых отрицательных чисел: -528, -2568, -1.

Число 0 разделяет по

zaochnik.com

1-4. Натуральные и целые числа

1. Натуральные и целые числа. Принцип математической индукции. Пример.

Натуральные числа – числа, возникающие естественным путем.

• Перечисление (первый, второй, третий.)

• Количество (Один, два, три)

Свойства натуральных чисел:

X+(Y+Z)=(X+Y)+Z — ассоциативность

X+Y=Y+X – коммутативность

X(YZ)=(XY)Z- ассоциативность

XY=YX– коммутативность

1X=X

X(Y+Z)=XY+XZ – дистрибутивность

Неарифметические свойства связаны с порядком следования.

Для любого натурального Х существует единственное натуральное число Sx=X+1 следующего за числом X.

Sx ≠1 для всех Х

Отношение порядка натуральных чисел а<b, если существует такое натурально n, что b=a+n->x<Sx<S(Sx)

Если x₁,x₂ — различные категории числа, то рассмотрев только те , которые меньше x₁ ивыбрав из них минимальные, получим минимальные из x₁ x₂

Целые числа

Множество целых чисел это Z={-2,-1,0,1,2} определены как замкнутые множества натуральных чисел N относительно арифметических операций сложения и вычитания.

Свойства целых чисел

X+(Y+Z)=(X+Y)+Z — ассоциативность

X+Y=Y+X – коммутативность

Существует единственное число 0, такое что X+0=X

Для любого целого числа X, существует единственное число (-X), называемое противоположным (-X)+(X)=0 (симметритизация)

X(YZ)=(XY)Z- ассоциативность

XY=YX– коммутативность

1X=X

X(Y+Z)=XY+XZ – дистрибутивность

Свойства связанные с порядком следованием, распространяемое с натуральных чисел на целые.

Пусть -X<0<Y тогда по определению -Y<-X<0. Также -X<0<Y, где X и Y – произвольные.

Математическая индукция

Один из методов доказательства. Используется для того, чтобы доказать истинность некого утверждения для всех натуральных чисел.

1. База индукции верно с номером n

2. Индуктивный переход верно для n+1

1³+2³+3³…+n³=((n(n+1))/2)²

1. Проверка для n=1

1³⁼

1=1 – верно

2. Пусть утверждении верно для всех n<k

3. Индуктивный переход

1³+2³+3³…+(n+1)³ = + (n+1)³=()+(n+1)³=–верно

2. Рациональные числа или расширение целых. Соразмерность. Рациональная прямая. Изоморфизм.

Рациональные – числа вида m/n, где m, n – целые, причем n≠0

Равенства и алгебраические операции

1. Равенства дробей a/b=c/d, если ad=cb (a, b, c, d – целые)

Справедливо m/n=(-m)/(-n)

2. Умножение. Пусть r=m/n и s=m’/n’, тогда по определению rs=mm’/(nn’)

3. Сложение. Пусть r=m/n и s=m’/n’, тогда r+s=(mn’+m’n)/(nn’)

4. Определение порядка для рац. чисел:

Пусть R=m/n и S=m’/nэб тогда R<S, если mn’<nm’.

Арифметические свойства:

1. Сложения.

1. x+(y+z)=(x+y)+z

2. x+y=y+x

3. сущ. такое число 0, x+0=x

4. для любого целого x, сущ. одно число (-x), (-x)+x=0.

2. Умножения.

1. x(yz)=(xy)z

2. xy=yx

3. существует одно число = 1, кот. 1x=x

4. Для любого целого числа x≠0, сущ. ед. число x^-1, называемое обратным

x*x^-1=1.

3. Дистрибутивность.

x(y+z)=xy+xz

Если мы представим все рациональные числа в виде k/1, то получится, что рац. вмещают в себя целые.

Если R=m/n и R’=m’/n’ – два произвольных рац. числа, то R=(mn’)s и R’=(m’n)s, где s=1/(nn’)>0.

Соответствующие числа получаются откладыванием отрезка [0,s], соотв. число раз влево и вправо, зависит от знаков R и R’.

Отрезок [0,s] называется общей мерой отрезков [0,|R|] и [0,|R’|].

Рациональная прямая.

R=m/n, где n – натуральное, нужно разделить на отр [0,1], нужно разделить на n частей. Первая справа от нуля точки соответствует дроби 1/n, дробь m/n изображается точкой, получающейся откладыванием 1/n вправо m раз, если m>0, влево (-m) раз m<0.

Для любой рациональной точки R>0 длина отр [0,R] равна R, для R<0 длина отр. То [R,0] равна –R.

Изоморфизм. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.

Сохраняет все алгебраические операции и свойства в задачах алгебры или свойства предельного перехода или непрерывности в началах анализа, то изоморфный образ можно считать копией данного множества.

3. Иррациональные отрезки. Действительные числа и операции над ними. Порядок. Существование корней.

Иррациональный отрезок несоизмерим, мы не можем отложить его или соизмеримый от нуля.

Предположим, что диагональ и сторона соизмеримы, т.е. их длины равны ns и ms., где s – их общая мера, m,n — натуральные числа. Тогда x=m/n, можем предположить, что m/n – несократимая, 2=m²/n², то m²=2n², т.е. m=2k, т.е. n²=2k², n – четно. X – не может быть представимо в виде m/n => 2^1/2 – не рациональное число.

Вещественные или действительные числа.

Действительные числа – мат. абстракция, возникшая из потребности измерения геометрических и физических величин окруж. мира, а также проведение таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений.

Под множеством понимается произвольная совокупность элементов, которая меняется как единое целое.

Действия над действит. числами:

1. a+b=b+a

2. a+(b+c)=(a+b)+с

3. ∃0∈R, a∈R, a+0=a

4. a+(-a)=0

5. ab=ba

6. a(bc)=(ab)c

7. 1∈R, a∈R, a1=a

8. a∈R, a≠0, a^-1∈R, aa^-1=1

9. a, b, c∈R, a(b+c)=ab+ac

10. Нетривиальность поля: 1≠0.

Действия над множествами:

Пересечение: A∩B, A={0,1,2,3}, B={-1,0,1,10}, то A∩B={0,1}

Объединение: A∪B, A={0,1,2}, B={-2,-1,0,1}, то A∪B={-2,-1,0,1,2}

Разность.

Прямое произведение.

4. Числовая ось или прямая – это прямая, на кот. выбраны:

— некоторая точка 0 – начало отсчета

— положительное направление, указанное стрелкой

— масштаб для измерения длин, еденичный отрезок

Полнота:

Лемма о вложенных отрезках. Принцип вложенных отрезков Коши-Кантора.

Для всякой системы вложенных отрезков

[a₁, b₁]->[a₂, b₂]->…->[a_n, b_n]

Существует хотя бы одна точка с, принадлежащая всем отрезкам данной системы.

Длина отрезков системы стремится к нулю.

studfiles.net

Целые числа — Циклопедия

Математика. Урок 6 — Числа: Целые числа

Целые числа — математический объект, представляющий собой множество, получающееся из натуральных чисел добавлением к ним нуля и противоположных натуральным по сложению отрицательных чисел. Целые числа, упорядоченные по возрастанию образуют бесконечный в обе стороны ряд: …, −3, −2, −1, 0, 1, 2, 3, …

Целые числа появляются в арифметике, а с точки зрения алгебры являются кольцом. В современной русскоязычной математической литературе обозначаются символом [math]\mathbb Z[/math].

Отрицательные числа и целые числа как расширение известных с древности натуральных чисел появились в опубликованной в 1544 году книге «Полная арифметика» математика Михаэля Штифеля (1487—1567) и в работах Николя Шюке (1445—1500).

Свойства целых чисел во многом подобны натуральным числам. В отличии от натуральных чисел, по сложению целые числа образуют (бесконечную) коммутативную группу, которая является циклической (порождена единичным элементом). Иначе говоря, сложение целых чисел коммутативно: [math]a + b = b + a[/math], ассоциативно: [math]a + (b + с)= a + (b + c)[/math], 0 — целое число, и для любого целого [math]a[/math]есть противоположное [math]-a[/math] тоже целое: [math]a + (-a)= 0[/math], и, наконец, любое ненулевое целое число [math]n[/math] можно представить как [math]1 + 1 + … + 1[/math] ([math]n[/math] раз) либо [math]-(1 + 1 + … + 1)[/math] ([math]n[/math] раз).

Каждое целое число либо ноль, либо положительное, либо отрицательное. Положительные целые числа — это натуральные числа. Отрицательное число [math]-n[/math] — это такое число, что [math]n[/math] — натуральное число и [math]n + (-n) = 0[/math].

Умножение целых чисел коммутативно и ассоциативно:

[math]a \times b = b \times a[/math]

[math]a \times (b \times с) = a \times (b \times c)[/math]

В кольце целых чисел возможно деление с остатком, то есть в нем присутствует единственность разложения на простые сомножители, которые являются простыми числами (см. Основная теорема арифметики).

Кольцо целых чисел не имеет делителей нуля, то есть произведение любых двух ненулевых целых чисел не равно нулю. Поле частных кольца целых чисел является полем рациональных чисел.

• Бухштаб А. А. Теория чисел — М.: «Просвещение», 1966.
• К. Айерленд, М. Роузен, Классическое введение в современную теорию чисел — М., 1987.

cyclowiki.org

Целые числа Википедия

Целые числа — расширение множества натуральных чисел^[1], получаемое добавлением к нему нуля и отрицательных чисел^[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение^[3].

Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел:

Числа 142857; 0; −273 являются целыми.

Числа 5½; 9,75 не являются целыми.

Множество целых чисел обозначается Z{\displaystyle \mathbb {Z} } (от нем. Zahlen — «числа»^[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.

Положительные и отрицательные числа[ | ]

Согласно своему построению, множество целых чисел состоит из трёх частей:

1. Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)^[5].
2. Ноль — число, обозначаемое 0{\displaystyle 0}. Его определяющее свойство: 0+n=n+0=n{\displaystyle 0+n=n+0=n} для любого числа

ru-wiki.ru

Действительные числа — это… Что такое Действительные числа?

Веще́ственные, или действи́тельные^[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.

Множество вещественных чисел обозначается (Unicode: ℝ) и часто называется вещественной прямой.

Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.

Примеры

Определения

Существует несколько стандартных путей определения вещественных чисел:

Аксиоматическое определение

См. основную статью Аксиоматика вещественных чисел.

Множество вещественных чисел можно определить как топологически полное, упорядоченное поле, то есть поле с отношением , которое удовлетворяет следующим аксиомам:

1. Отношение является отношением линейного порядка:
2. Порядок согласован со структурой поля:
3. Порядок на удовлетворяет условию полноты:

Примечания

Из свойства 3 следует, что у любого непустого ограниченного сверху множества (то есть такого, что для всех x из A все для некоторого ) существует точная верхняя грань (минимальная из всех), то есть число такое, что

1. Для всех x из A все
2. Если свойству (1) удовлетворяет также число , то .

Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля .

Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)

Пополнение рациональных чисел

Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике .

Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {r_i}. На таких последовательностях можно естественным образом ввести арифметические операции: {r_i} + {q_i} = {r_i + q_i} и .

Две такие последовательности и считаются эквивалентными , если при .

Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.

Дедекиндовы сечения

См. основную статью Дедекиндово сечение.

Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества A и B такие, что:

1. для любых и ;
2. B не имеет минимального элемента.

Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.

Например, вещественному числу соответствует дедекиндово сечение, определяемое или и и x² > 2}. Интуитивно, можно представить себе, что для того чтобы определить мы рассекли множество на две части: все числа, что левее и все числа, что правее ; соотвеетственно, равно точной нижней грани множества B.

Бесконечные десятичные дроби

Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.

Бесконечной десятичной дробью (со знаком) называется последовательность вида , где d_i являются десятичными цифрами, то есть .

Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где , либо если это «нулевые» последовательности (все d_i равны 0), отличающиеся только знаком.

Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.

Значение десятичной дроби формально задаётся суммой ряда .

Счетность множества

TODO:

Примечания

1. ↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.

Ссылки

• Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
• Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.

См. также

Wikimedia Foundation. 2010.

dic.academic.ru