Решение линейных и квадратных неравенств. Видеоурок. Алгебра 9 Класс
Тема: Рациональные неравенства и их системы
Урок: Решение линейных и квадратных неравенств
Линейные неравенства – это неравенства вида и они решаются двумя способами: эквивалентными преобразованиями либо с помощью графика функции. Рассмотрим второй способ на примерах:
1. Решить неравенство
Построим график функции. Графиком является прямая, она пересекает ось oy в точке 1, ось ox в т. Корень функции разбивает ось ox на два различных промежутка. На первом промежутке функция отрицательна, на втором – положительна.
Этого достаточно, чтобы решить линейное неравенство.
Ответ:
Линейные неравенства эффективно решаются путем выбора интервалов, на которых функция сохраняет знак, т.е. до корня и после корня. Решением линейного неравенства, как правило, является луч.
Рассмотрим квадратное неравенство
Оно решается с помощью свойств квадратичной функции
Рассмотрим на примере.
2. Решить неравенство
Рассмотрим функцию Построим ее график, для этого вначале найдем корни. По теореме Виета
Схематически изобразим параболу и определим интервалы знакопостоянства и знаки на них. Ветви параболы направлены вверх.
Вне интервала корней функция положительна, внутри интервала корней – отрицательна.
Ответ:
Рассмотрим квадратичную функцию и её свойства в общем виде.
1.
Функция имеет вид
значит, корни квадратного трехчлена различны,
Графиком квадратичной функции является парабола, пересекающая ось ox в точках с абсциссами
ветви параболы направлены вверх.
Вне интервала корней функция имеет положительный знак, внутри интервала корней – отрицательный.
Что можно сказать о функции, если Прежде всего, что она разлагается на линейные множители:
Также для нее справедлива теорема Виета:
Найдем координаты вершины параболы.
Для квадратичной функции есть два возможных варианта неравенств:
Множество значений функции – луч от в положительном направлении. Точка пересечения с осью oy – т..
2.
Как и в предыдущем случае, многочлен раскладывается на множители.
График функции – парабола, ветви направлены вверх.
Парабола касается оси ox в одной точке, которая и является вершиной параболы.
Рассмотрим возможные варианты неравенств:
Множество значений функции:
График функции пересекается с осью oy в т.
3.
Рассмотрим функцию
означает, что уравнение не имеет корней, трехчлен нельзя разложить на множители и не выполняется теорема Виета.
Найдем координаты вершины:
Схематически изобразим график – параболу, ветви направлены вверх.
Множество значений функции
Для более глубокого рассмотрения рекомендуется самостоятельно изучить случаи, когда
1.
2.
3.
Необходимо построить графики и расписать решения стандартных неравенств самостоятельно.
Мы подробно рассмотрели свойства квадратичной функции, которые лежат в основе решения задач.
Рассмотрим примеры.
1. Найти область определения функции.
Область определения функции задается неравенством т.к. трехчлен находится под корнем и в знаменателе.
Умножим обе части неравенства на .
Рассмотрим функцию найдем ее корни.
По теореме Виета
Изобразим график функции. Точки -2 и 1 выколотые, т.к. неравенство строгое.
Поставленному условию удовлетворяет промежуток внутри интервала корней.
Ответ:
Мы увидели на примере, что многие задачи сводятся к решению квадратного уравнения.
2. При каких значениях p данное уравнение имеет
два различных корня?
один корень?
не имеет корней?
Если p принимает конкретное значение, мы имеем конкретный квадратный трехчлен с конкретным значением дискриминанта,
Найдем дискриминант.
Рассмотрим функцию
Найдем корни по теореме Виета.
Рассмотрим ось p и график функции Графиком является парабола, ветви направлены вверх.
Функция сохраняет положительный знак вне интервала корней, отрицательный знак – внутри интервала.
Ответ: Уравнение имеет
1. два различных корня, когда
2. один корень, когда
3. не имеет корней, когда
Мы рассмотрели решение линейных и квадратичных неравенств, некоторые свойства квадратичной функции, которые используются при решении квадратных неравенств.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразова
interneturok.ru
Неравенства и системы неравенств. Алгебра, 9 класс: уроки, тесты, задания.
Вход на портал Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв- Предметы
- 9 класс
-
Линейные и квадратные неравенства
-
Рациональные неравенства
-
Множества и операции над ними
-
Системы рациональных неравенств
| 1. |
Деление неравенства на отрицательное число
Сложность: лёгкое |
2 |
| 2. |
Число, которое является или не является решением неравенства с модулем
Сложность: лёгкое |
1 |
| 3. |
Линейное неравенство
Сложность: лёгкое |
3 |
| 4. |
Дробное неравенство, сводимое к линейному
Сложность: среднее |
4 |
| 5. |
Квадратное неравенство, сводимое к линейному (распределительный закон умножения)
Сложность: среднее |
3 |
| 6. |
Значения переменной, при которых выражение имеет смысл
Сложность: среднее |
4 |
| 7. |
Область определения корня из квадратного трёхчлена
Сложность: среднее |
5 |
| 8. |
Область определения корня из дроби
Сложность: среднее |
6 |
| 9. |
Значения переменной, при которых дробь имеет смысл (корень в знаменателе)
Сложность: среднее |
5 |
| 10. |
Целочисленные значения параметра
Сложность: сложное |
6 |
| 11. |
Натуральное значение параметра (целые числа из множества решений)
Сложность: сложное |
6 |
| 12. |
Натуральное значение параметра (натуральные числа из множества решений)
Сложность: сложное |
6 |
www.yaklass.ru
Обобщающий урок в 9 классе по теме «Линейные неравенства»
Обобщающий урок алгебры в 9 классе по теме:
«Решение линейных неравенств с одной переменной и их систем»
Выполнила: учитель математики Панченко Ирина Сергеевна
ДОШ № 126
г. Донецк.
Класс: 9
УМК: Учебник для 9 класса общеобразовательных учреждений, В.Р. Кравчук.
Тема: Урок систематизации и обобщения изученного материала по теме «Решение линейных неравенств с одной переменной и их систем». Слайд 1.
Девиз урока «Математика учит преодолевать трудности и исправлять собственные ошибки». Слайд 2.
Цели урока:
Образовательная:
Повторить и обобщить знания учащихся по теме «Неравенства с одной переменной и их системы»
Продолжить формирование умений работать по алгоритму.
Развивающая:
Развивать навыки коллективной работы, взаимопомощи, самоконтроля.
Воспитательная:
2. Воспитывать информационные компетенции, математическую зоркость, математическую речь. Слайд 3,4.
Задачи урока – отработать навык решения линейных неравенств с одной переменной, систем неравенств, формирование вычислительных навыков, выявить степень усвоения учащимися изученного материала.
Оборудование:
Медиа-проектор
Экран
Раздаточный материал
Учебник для 9 класса общеобразовательных учреждений, В.Р. Кравчук
Тип урока: Урок систематизации и обобщения изученного материала. Слайд 5.
Структурные элементы урока:
1. Организационный этап.
2. Этап подготовки учащихся к активному сознательному усвоению знаний. Постановкаа целей и задач урока.
3. Этап обобщения и систематизации изученного материала. Повторение
А) тестирование
Б) устный опрос
С) устная работа
4. Повторение. Работа с классом у доски. Решение неравенств с одной переменной.
5. Повторение. Работа с классом у доски, с выбором правильного варианта ответа. Решение систем неравенств с одной переменной.
6. Тренировочные упражнения.
7. Самостоятельная работа учащихся по вариантам. (Взаимопроверка).
8. Подведение итогов урока. Задания на дом.
Ход урока.
1. Организационный этап.
(Проверка готовности учащихся к уроку. Сообщение темы и целей урока.)
Наш урок я хочу начать со слов персидско-таджикского поэта Рудаки:
«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек »
Слайд 6.
2. Этап подготовки учащихся к активному сознательному усвоению знаний.
Выбери промежуток, удовлетворяющий неравенству (взаимопроверка).
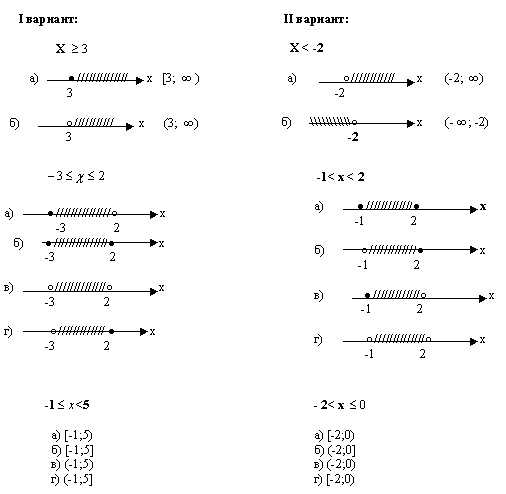
Слайд 7,8.
Найди ошибку в решении неравенств. Объясни почему допущена ошибка. Запиши в тетради правильное решение:
1. 31(2x+1)-12x > 50x
62x+31-12x > 50x
50x-50x > -31
x > 0
ответ: х – любое число.
2. 3(7-4y) > 3y-7
21 -12y > 3y-7
-12y + 3y > -7-21
-9y > — 28
y < 3 1/9
ответ: х ϵ(3 1/9 ;+ ∞)
Слайд 9.
Мы закончили изучение темы «Неравенства с одной переменной и их системы» Этот урок посвящен повторению и обобщению всего материала темы.
3.Этап обобщения и систематизации изученного.
А) Для повторения теории темы, ее понимания и умения применять проведем тестирование с последующей проверкой и беседой по теории темы.
Каждое задание теста предполагает ответ «Да» или «Нет».
«Да» -1 «Нет» — 0.
В результате выполнения теста получится какое-то число.
Вопросы теста:
1) Является ли число 12 решением неравенства 2х>10? (да)
2) Является ли число -6 решением неравенства 4х>12? (нет)
3) Является ли неравенство
5х-15>4х+14 строгим? (да)
4) Существует ли целое число принадлежащее промежутку
[-2,8;-2,6]? (нет)
5) При любом ли значении переменной а верно неравенство
а² +4 >0? (да)
6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется? (нет)
Назовите число, которое у вас получилось.
Давайте проверим ответ. 1010101. Слайд 10,11,12.
Б) Устный опрос.
— Является ли решением неравенства 3х — 11>1 число 5?
— Дайте определение решения неравенства с одной переменной.
— Что значит решить неравенство?
— Сформулируйте свойства равносильности, которые используются при решении неравенств. Слайд 13.
В) Устная работа.
№1 «Найди ошибку!»
1. х ≥7 2. y < -2,5
Ответ: (-∞;7) Ответ: (-∞;2,5)
3. m ≥ 12 4. -3x ≤ 3,9
Ответ: (-∞;12) Ответ: [-∞;-1,3]. Слайд 14.
№2 Наибольшее целое решение для каждого из данных неравенств равно:
1)7 Ответ:6
2)2,5 Ответ:2
3)12 Ответ:11
4)-1,3 Ответ:-1. Слайд 15.
№ 3 Неравенству х ≥ 15 соответствует числовой промежуток:
1) (–∞ ; 15)
2) [15; +∞) – правильный ответ.
3) (–∞ ; 15]
4) (15;+∞) Слайд 16.
4. Повторение. Работа с классом у доски. Решение неравенств с одной переменной.
Используя свойства, решите следующие неравенства:
4 + 12х > 7 + 13х; ответ х ϵ(-∞; -3)
– (2 — 3х) + 4(6 + х)> 1; ответ х ϵ(-3 ;∞)
, ответ х ϵ(-∞; -1]
Слайд 17.
Повторение. Решение неравенств с одной переменной.
1) Решите двойное неравенство:
— 4 < х-9 < 5 ответ х ϵ(5 ; 14)
2) При каких значениях х имеет
смысл выражение: Слайд 18.
3) Решите двойное неравенство — 6 < 3х < 9 и укажите наибольшее и наименьшее целое число, которое является его решением. ответ х ϵ(-2 ; 3), наибольшее равно 2, наименьшее равно -1. Слайд 19.
5. Повторение. Работа с классом у доски, с выбором правильного варианта ответа. Решение систем неравенств с одной переменной.
Работаем дальше, ответьте на вопрос:
— Является ли решением системы неравенств 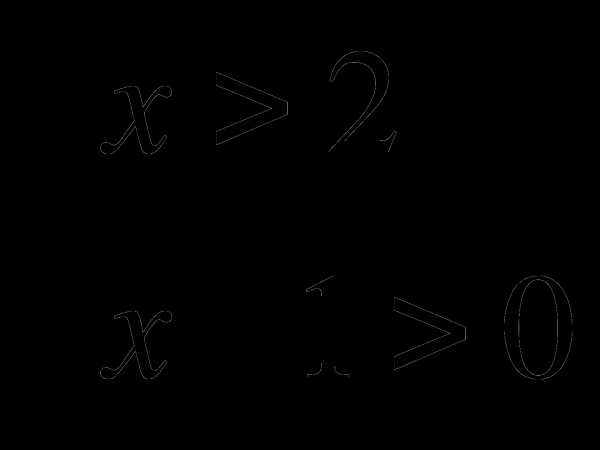 число 3?
число 3?
— Что называется решением системы неравенств?
— Что значит решить систему неравенств? Слайд 20.
Найти множество решений неравенства или системы неравенств, выбрать из полученного множества те решения, которые удовлетворяют дополнительным условиям, поставить в соответствие полученным числам буквы из слова “неравенство”, прочесть слово.
Неравенство:
1) 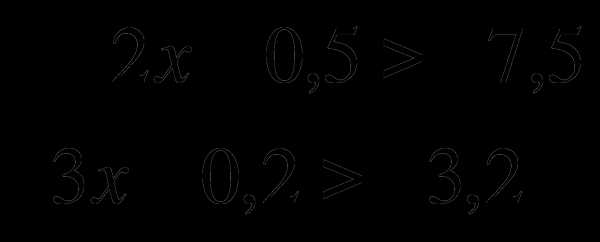 найти наибольшее целое число Ответ: 3, буква “Р”.
найти наибольшее целое число Ответ: 3, буква “Р”.
2) 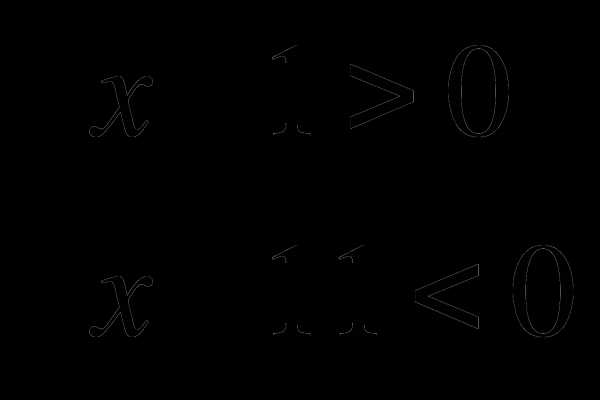 найти наименьшее и наибольшее целые числа. Ответ: 2 и 10, буквы “Е,В”.
найти наименьшее и наибольшее целые числа. Ответ: 2 и 10, буквы “Е,В”.
3) 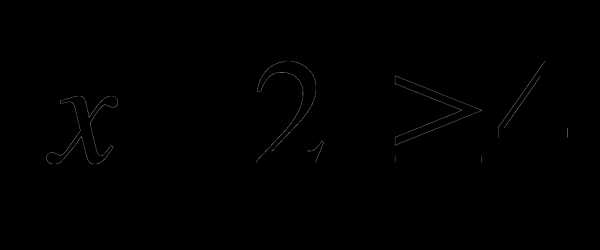 найти наименьшее натуральное число. Ответ: 6, буква “Е”.
найти наименьшее натуральное число. Ответ: 6, буква “Е”.
4) 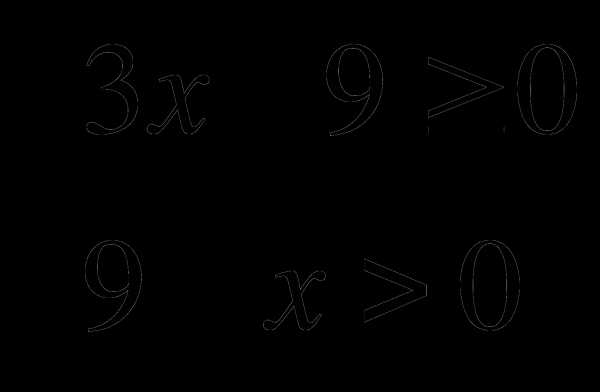 найти наименьшее и наибольшее целые числа. Ответ: 3,8, буквы “Р,С”.
найти наименьшее и наибольшее целые числа. Ответ: 3,8, буквы “Р,С”.
В результате учащиеся должны составить слово “реверс”, а затем учитель должен сообщить значение этого слова. Слайд 21,22,23.
6. Тренировочные упражнения.
Решить данное неравенство различными способами:  ответ х ϵ(-1 ; 4).
ответ х ϵ(-1 ; 4).
а) по определению модуля;
б) через двойное неравенство;
Слайд 24
7. Самостоятельная работа учащихся по вариантам. (Взаимопроверка).
Решите неравенство:
4 +12х > 7+13х; 7-4х < 6х-23;
2) Решите системы неравенств:
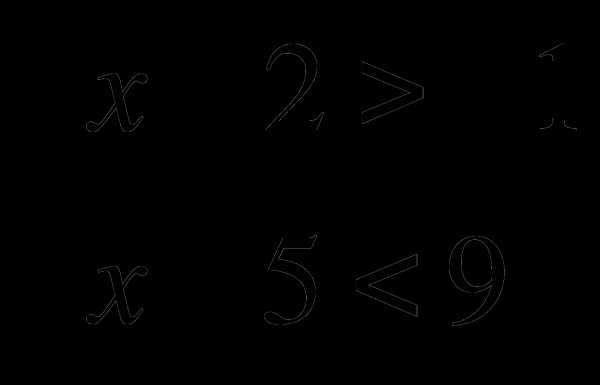
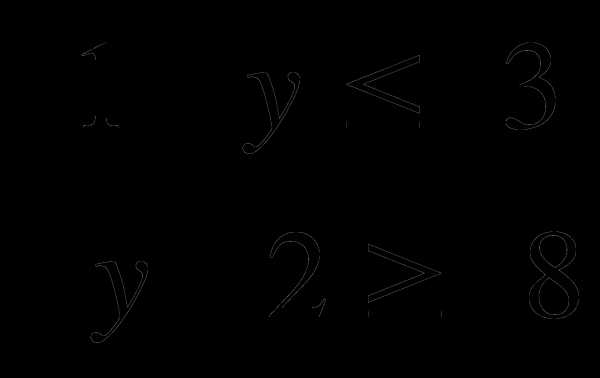
3) Найдите количество целых чисел, являющихся решениями системы
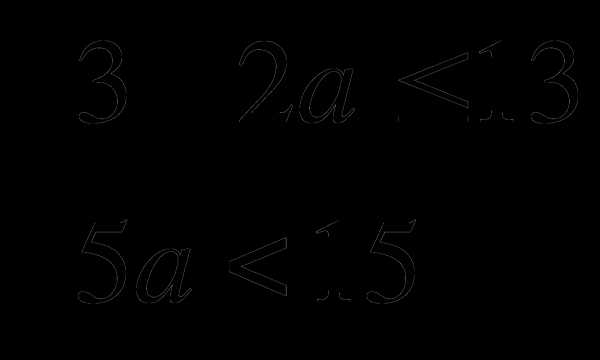
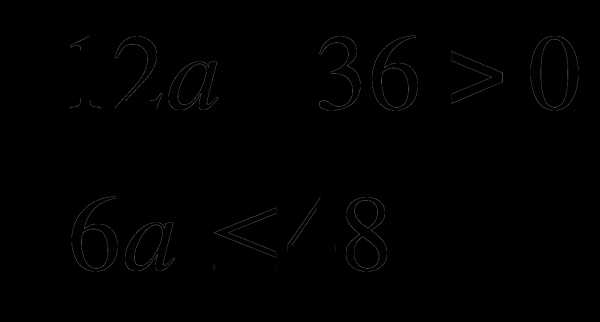
Взаимопроверка. Слайд 25.
Учащиеся сдают работы, предварительно выписав ответы, которые проверяются по окончанию работы.
Ответы самостоятельной работы.
х ϵ(-∞ ; -3) х ϵ(3;∞)
х ϵ(1 ; 4) х ϵ[-6 ; -4]
8: -5,-4,-3,-2, -1,0,1,2 5:4,5,6,7,8. Слайд 26.
8. Подведение итогов урока. Задания на дом. Домашнее задание: Сборник алгебра 9 класс, А. Г. Мерзляк, ТО №1 стр. 112. Слайд 27.
infourok.ru
9 класс. Алгебра. Рациональные неравенства и их системы. — Линейные и квадратные неравенства.
Комментарии преподавателя
На этом уроке мы будем повторять неравенства. Мы вспомним, что такое линейное и квадратное неравенство, частное и общее решение, символическая запись. А также вспомним специфику решения неравенств – три правила равносильных преобразований. И решим несколько примеров на линейные неравенства.
Тема: Рациональные неравенства и их системы. Линейные и квадратные неравенства (повторение)
Урок: Основные понятия, решение линейных неравенств
Рациональные неравенства – основные понятия и решения квадратных и линейных неравенств (9 класс)
Линейное и квадратное неравенство, повторение, урок 1, основные понятия решения линейных неравенств
Неравенство с одной переменной имеет вид: f(x) > 0, вместо (> 0) может быть (≥ 0), (< 0), (≤ 0).
Для определенности будем записывать неравенство в виде f(x) > 0.
x – переменная,
f – функция, выражение, зависящее от х.
В зависимости от f различают разные типы неравенств. Если f – линейная функция, то это линейное неравенство. Если f – квадратичная функция, то это квадратное неравенство.
Итак, линейное неравенство имеет вид ax+b>0, предполагается, что a≠0.
Квадратное неравенство имеет вид .
Значение x, при котором неравенство обращается в верное числовое неравенство, является частным решением неравенства. Решить неравенство – найти все решения неравенства. Множество всех решений неравенства называется общим решением неравенства, или просто решением неравенства.
Рассмотрим пример:
1) Решить неравенство 2x – 5 > 9.
Это линейное неравенство, найдем его решение и обсудим основные понятия.
2x – 5 > 9 <=> 2x > 14 (5 перенесли в левую часть с противоположным знаком), далее разделили все на 2 и получили x > 7. Изобразим множество решений на оси x.
Это положительно направленный луч. Записывается множество решений либо в виде неравенства x > 7, либо в виде интервала (7; ∞). А что является частным решением этого неравенства? Например, x = 10 – это частное решение этого неравенства, x = 12 – это тоже частное решение этого неравенства.
Частных решений много, но наша цель – найти все реше&
www.kursoteka.ru
Урок алгебры по теме «Системы линейных неравенств с одним неизвестным». 9 класс — К уроку — Математика, алгебра, геометрия
Автор:
Степанов Александр Борисович
Место
работы: МКОУ «Покровская СОШ»
Должность:
учитель математики
Дополнительные
сведения: 404615 Волгоградская обл, Ленинский
р-н, с.Покровка, ул.Школьная, 1.
Урок по алгебре в 9 классе (УМК С.М.Никольский и др)
Тема: «Системы линейных неравенств с одним неизвестным».
Тип
урока: повторительно-обобщающий урок.
Оборудование: рабочая
доска, раздаточный материал.
Цели урока:
1)повторить и обобщить знания обучающихся по теме «Неравенства с одной переменной и их системы»; -продолжить формирование умений работать по алгоритму;
2)развивать навыки коллективной работы, взаимопомощи, самоконтроля;
3)воспитывать
информационные компетенции, математическую
зоркость, математическую речь.
Используемая
литература:
Алгебра:
учебник для 9 класса общеобразовательных
учереждений / С.М.Никольского, М.К.Потапов,
Н.Н.Решетников, А.В.Шевкин – М.; Просвещение,
2010.
Алгебра: дидактические материалы
для 9 класса / М.К.Потапов, А.В.Шевкин –
М.; Просвещение, 2008.
Ход урока.
1.Организационный
момент.
Повторение
материала предыдущих уроков. Раздача
материала.
2.Постановка целей урока.
3.Повторение
изученного.
Проверка
домашнего задания.
–В
раздаточном материале отвечаем на
вопросы теста:
а) Проверка усвоение
теории(правил) п 1.3
1.
Число 4 является решением неравенства
2x–
11≥0
а) да б) нет в) нельзя ответить
на поставленный вопрос(да, почему?)
2.Являются
ли равносильными неравенства3,2 + 0,9x<4x
– 4,6 и 0,9x
– 4x<
— 3,2 – 4,6?
а) да б) нет в) нельзя ответить
на поставленный вопрос (да, почему?)
3.Являются
ли равносильными неравенства 11x
– 3x
+ 9x>7
+2 – 21 и 17x>
— 12 ?
а) да б) нет в) нельзя ответить
на поставленный вопрос(да, почему?)
4.Являются
ли равносильными неравенства 2 +9x<11
и 10 + 45x>55?
а)
да б) нет в) нельзя ответить на
поставленный вопрос(нет, почему?)
5.Являются
ли равносильными неравенства – 2x>24
и x<
— 12?
а) да б) нет в) нельзя ответить
на поставленный вопрос(да, почему?)
б)
Проверка умений и навыков решения
линейных неравенств с одной переменной.
(На
доске решается неравенство 5(6x
+ 1) > 2(10x
+ 3) – 7 поэтапно, т.е раскрытие скобок,
группировка и т.д. Каждый шаг выполняется
разными обучающимися).
4.Изучение
нового материала.
–Записываем
тему урока «Системы линейных неравенств
с одним неизвестным».
(Весь класс
разбивается на группы, взяв с собой
карточку и тетрадь:
Группы – A,
B,
C,
D,
в каждой группе в наличии карточки с
заданиями)
– Чтобы успешно решать задания по новой теме, нам надо будет вспомнить знания и умения изученные раннее.
РАБОТА
ПО КАРТОЧКАМ С СООТВЕТСТВУЮЩИМИ
ЗАДАНИЯМИ.
(Ответы
проверяются всеми группами)
1) Является ли число 3 решением системы уравнений и почему:
группа A —(да)группа B — (нет)
группа C — (да) группа D — (нет) ?
2)
На каком из рисунков дано правильное
изображение числового множества,
являющегося решением соответствующего
неравенства:
группа A
– б) группа B
– б) группа C
– а) группа D
– в)
3)
Запишите с помощью числового
промежутка:
группа A
– б) группа B
– а) группа C
– б) группа D
– в)
4) Какому промежутку соответствует данное неравенство:
группа A – б) группа B – в) группа C – в) группа D – б)
–Теперь
мы объединим все эти навыки и умения и
применим их при решении примеров по
новой теме.
ЗАПИСЬ В ТЕТРАДЯХ.
Решите систему неравенств:
Ход решения (проговаривается с учителем):
а) скобки? – нет б) группируем(с неизв. в левую… в правую) в) подобные слагаемые г) решаем каждое нер-во д) изображаем решение каждого неравенства на одной числовой оси е) ищем общие решения(пересечение) ж) записываем ответ(два вида – промежуток, неравенство).Ответ: ( 2; 3 ) или 2 <x< 3
(После
этого всем группам предлагается решить
неравенство(взят пример из данного
пункта)
«сильный» учащийся решает у доски(без
объяснения).
Ответ: ( ; ) или <x<
«сильный» учащийся решает у доски(без объяснения).
Ответ: ( 1,25; + ∞) или x>1,25.
ВСЕ ГРУППЫ РЕШАЮТ СИСТЕМУ НЕРАВЕНСТВ:
Ответ: решений нет.
5.Подведение итогов урока.
–Что делали, что нового узнали на уроке?
6.Домашнее задание.
1)П 1.4(разбор примеров).
2)Решить
№ 49 – 51(а), 55(д – з).
Дополнительно:
№ 50
pedsovet.su
