Действия с матрицами
Матрицы и действия с ними, определителиСложение матриц
Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц \(A=\{A_{ik}\}\) и \(B=\{B_{ik}\}\), матрица \(A+B\), определяется следующим образом: \((A+B)_{ik}=A_{ik}+B_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq n\). Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.
Пример. Пусть
\[
A=\left(
\begin{array}{ccc}
1 &4 & -1 \\
3 & -6 & 7
\end{array}
\right) ,
\]
\[
B=\left(
\begin{array}{ccc}
2 &1 & 0 \\
1 & 3 & 4
\end{array}
\right) ,
\]
тогда
\[
A+B=\left(
\begin{array}{ccc}
3 & 5 & -1 \\
4 & -3 & 11
\end{array}
\right) .
Умножение матрицы на число
Пусть \(A=\{a_{ik}\}\) — матрица типа \((m,n)\), \(\lambda\) — произвольное число. Тогда матрица \(\{\lambda a_{ik}\}\) называется произведением числа \(\lambda \) на матрицу \(A\) и обозначается \(\lambda \cdot A\).
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) . \]
Замечание.
Как и в обычной, в матричной арифметике знак умножения иногда не указывают, так что выражения \(c\cdot A\) и \(cA\) равноправны.
Пусть \[ A=\left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right), B=\left( \begin{array}{cc} 1 & -2 \\ 3 & 4 \end{array} \right). \]
Вычислить \(3A-2B\). T\) (это выражение занимает меньше места).
T\) (это выражение занимает меньше места).
Элементарные свойства операций с матрицами
Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.
1. Для любых матриц \(A,B,C\) одного типа \((A+B)+C=A+(B+C)\)(ассоциативность сложения).
2. Для любых матриц \(A,B\) одного типа \(A+B=B+A\) (коммутативность сложения).
3. Пусть \((m,n)\)-матрица \(O\) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа \((m,n)\), \(A+O=A\), \(0\cdot A=O\) для любой матрицы \(A\) того же типа.
4. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1+c_2)A=c_1A+c_2A\).
5. Для любых матриц \(A,B\) одного типа и любого числа \(c\) верно \(c(A+B)=cA+cB\).
6. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1c_2)A=c_1(c_2A)\).
7. Для любой матрицы \(A\) верно \(1\cdot A=A\).
8. Для любых матриц \(A,B\) одного типа \((A+B)^T=A^T+B^T\). na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]
В данном случае матрица \(A\) имеет тип (2,3), матрица \(B\) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения \(A\) на \(B\) получим матрицу типа \((2,2)\). Получаем:
\[
AB=\left (
\begin{array}{cc}
1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\
3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5
\end{array}
\right )=
\left( \begin{array}{cc} 9 & 8\\ -21 & 20
\end{array} \right). T\).
T\).
6. Для квадратных матриц \(A,B\) одного типа \(det(AB)=detA \cdot detB\).
7. Рассмотрим квадратную матрицу порядка \(n\), \(E=diag\{1,1,1,…,1\}\). Такая матрица играет выделенную роль в умножении матриц: для любых матриц \(A,B\) имеем \(EA=A\), \(BE=B\). Матрица \(E\) называется единичной матрицей порядка \(n\). Согласно описанным выше результатам, \(detE=1\).
1. Умножить матрицы:
а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]
б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]
2. Вычислить
\[
\left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5. {-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.
Найти обратную матрицу для матрицы
1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]
2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]
3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]
Матричные уравнения
Матричными уравнениями называются уравнения вида
\[ AX=G, \quad \quad(12)\]
\[ XB=G, \quad \quad(13)\]
\[ AXB=G, \quad \quad(14)\]
где матрицы \(A,B,G\) заданы и требуется построить матрицу \(X\). {-1}.
\]
{-1}.
\]
1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]
2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]
3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]
4. Найти решение матричного уравнения (13), если
\[
B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) ,
G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]
\]
5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]
6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]
Сложение и вычитание матриц, умножение матриц на число в EXCEL. Примеры и описание
В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.
Операция сложения определена только для матриц одного порядка. Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.
Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.
Сумма двух матриц А и В — это матрица, элементы которой равны сумме соответствующих элементов матриц А и В.
В MS EXCEL операцию сложения матриц реализовать элементарно.
Поместив матрицу А размерности 2х2 в диапазон А8:В9 , а матрицу B той же размерности 2х2 в диапазон D8:E9, в ячейке J8 введем формулу =A8+D8 . Скопировав формулу в нужные ячейки, например, с помощью Маркера заполнения , получим матрицу А+В.
Аналогичного результата можно добиться с использованием
формулы массива
. Выделив диапазон G 8:H9 в
Строке формул
введите формулу
=A8:B9+D8:E9
и нажмите CTRL+SHIFT+ENTER . Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно Невозможно удалить часть массива ).
Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно Невозможно удалить часть массива ).
Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см. файл примера ).
Умножение матриц на число
Операция умножения матрицы на число определена для матриц любого порядка.
Произведение матрицы А и числа k — это матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.
В MS EXCEL это реализовано с помощью формулы
=A21*$D$21
(предполагается, что матрица находится в диапазоне А21:В23 , а число в ячейке D21 ). Обратите внимание, что в формуле использована
абсолютная адресация
на ячейку с числом. Это позволяет при копировании формулы (для отображения всех элементов матрицы k*А) ссылаться на одну и ту же ячейку с числом.
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34. biz
biz
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
Сложение матриц:
Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В cij = aij + bij Аналогично определяется разность матриц.
Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента
 Произведением
матрицы А на число k
называется матрица В, такая что
Произведением
матрицы А на число k
называется матрица В, такая чтоbij = k × aij. В = k × A bij = k × aij. Матрица — А = (-1) × А называется противоположной матрице А.
Свойства сложения матриц и умножения матрицы на число:
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А — А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С — матрицы, α и β — числа.
Умножение матриц (Произведение матриц):
Операция
умножения двух матриц вводится только для случая, когда число
столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p,
называется матрица Сm×p такая, что
сik = ai1 × b1k + ai2 × b2k + . .. + ain × bnk,
т.
е. находиться сумма произведений
элементов i — ой строки матрицы А на соответствующие элементы j — ого
столбца матрицы В. Если матрицы А и В квадратные одного размера, то
произведения АВ и ВА всегда существуют.
Легко показать, что А × Е = Е × А = А, где
А квадратная матрица,
Е — единичная матрица того же размера.
.. + ain × bnk,
т.
е. находиться сумма произведений
элементов i — ой строки матрицы А на соответствующие элементы j — ого
столбца матрицы В. Если матрицы А и В квадратные одного размера, то
произведения АВ и ВА всегда существуют.
Легко показать, что А × Е = Е × А = А, где
А квадратная матрица,
Е — единичная матрица того же размера.
Свойства умножения матриц:
Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких — либо
Умножение
матриц обладает
следующими свойствами:
1. А × (В × С) =
(А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В)
× С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0
= 0; 0 × А = 0;
6. (АВ)Т = ВТАТ;
7.
(АВС)Т = СТВТАТ;
8.
(А + В)Т = АТ + ВТ;
А × (В × С) =
(А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В)
× С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0
= 0; 0 × А = 0;
6. (АВ)Т = ВТАТ;
7.
(АВС)Т = СТВТАТ;
8.
(А + В)Т = АТ + ВТ;
2. Определители 2-го и 3-го порядков. Свойства определителей.
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это
число представляет алгебраическую
сумму, состоящую из шести слагаемых. В
каждое слагаемое входит ровно по одному
элементу из каждой строки и каждого
столбца матрицы.
Каждое слагаемое состоит из произведения
трех сомножителей.
Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Свойства определителей матриц
Свойства определителей матриц:
Свойство № 1:
Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т
Следствие:
Столбцы
и строки определителя
матрицы равноправны,
следовательно, свойства присущие строкам
выполняются и для столбцов.
Свойство № 2:
При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:
Свойство № 3:
Определитель матрицы, имеющий два одинаковых ряда, равен нулю.
Свойство № 4:
Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.
Следствия из свойств № 3 и № 4:
Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5:
Если
все элементы какой–либо строки или
столбца определителя
матрицы равны нулю,
то сам определитель
матрицы равен нулю.
Свойство № 6:
Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:
Свойство № 7:
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.
Пример применения свойств для вычисления определителя матрицы:
Калькулятор онлайн — Операции над матрицами: сложение, вычитание, умножение, деление, возведение в степень. Вычисление определителя матрицы, обратной матрицы, ранга матрицы
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Матрицы и операции над ними
Виды матриц
Определение 1.Матрицей размера \(m \times n \) называют прямоугольную числовую таблицу, состоящую из \(mn\) чисел, которые расположены в \(m\) строках и \(n\) столбцах. Составляющие матрицу числа называют элементами этой матрицы.
Как правило, их обозначают строчной буквой с двумя индексами, например \(a_{ij}\), где \(i\) — номер строки ( \(i=\overline{1,m} \) ), \(j\) — номер столбца ( \(j=\overline{1,n} \) ), в которых расположен этот элемент.
Матрицу записывают так:
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} $$
Если по тексту ясно, в каких пределах изменяются индексы \(i\) и \(j\), то сокращённо матрицу можно записать так: \( \left(a_{ij} \right) \). Матрицу как единый объект обозначают прописной буквой: \(A\), \(B\) и т.д.
Матрицу как единый объект обозначают прописной буквой: \(A\), \(B\) и т.д.
Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, элементами матриц могут быть многочлены или матрицы.
Матрицу называют матрицей-строкой, если матрица имеет размер \(1 \times n \), т.е. если у матрицы всего одна строка. Число элементов
в матрице-строке называют её длиной.
\(A=(a_1, \; …,\; a_n) \)
Матрицу называют матрицей-столбцом, если матрица имеет размер \(m \times 1 \), т.е. если у матрицы один столбец. Число элементов
в матрице-столбце называют её высотой.
\(A = \begin{pmatrix}
a_{1} \\
\vdots \\
a_{m} \\
\end{pmatrix} \)
Матрицу называют квадратной порядка \(n\), если \( m=n\), т.е. когда матрица имеет столько же столбцов, сколько и строк :
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
а если \(m \neq n \) — прямоугольной.
У квадратных матриц выделяют последовательности элементов \( a_{11}, \; a_{22}, \; …, \; a_{nn} \) — главную диагональ, и \( a_{n1}, \; a_{n-1,2}, \; …, \; a_{1n} \) — побочную диагональ. Элементы главной диагонали называют диагональными. Понятия диагонального элемента и главной диагонали распространяют и на прямоугольные матрицы.
Если в квадратной матрице порядка \(n\) все элементы, стоящие вне главной диагонали, равны нулю, т.е. если матрица имеет вид
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
0 & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$,
то её называют диагональной к обозначают \( \text{diag} (a_{11}, \; …, \; a_{nn} ) \).
Если в диагональной матрице порядка \(n\) на
диагонали стоят единицы, то её называют единичной и обозначают обычно \(E\) :
$$ E = \begin{pmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \\
\end{pmatrix} $$,
Матрицу размера \(m \times n \), все элементы которой равны нулю, называют нулевой матрицей соответствующего размера и обозначают
буквой \(\Theta\) или цифрой 0.
Часто используют матрицы и других видов, например верхние треугольные матрицы
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых, наоборот,
элементы над главной диагональю равны нулю:
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
Ступенчатой матрицей (матрицей ступенчатого вида) называют матрицу размера \(m \times n \), если для любой её строки выполнено
следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами строки все элементы матрицы
равны нулю.
Следующие матрицы имеют ступенчатый вид:
\( \begin{pmatrix}
0 & 2 & 3 & 0 \\
0 & 0 & -1 & 1 \\
0 & 0 & 0 & 3 \\
\end{pmatrix} \)
\( \begin{pmatrix}
3 & 1 & 3 & 3 \\
0 & 0 & 2 & 1 \\
0 & 0 & 0 & 0 \\
\end{pmatrix} \)
\( \begin{pmatrix}
1 & 1 & 3 & 3 \\
0 & 3 & 0 & 1 \\
0 & 0 & 1 & -1 \\
\end{pmatrix} \)
Линейные операции над матрицами
Определение 2.
Две матрицы называют равными, если они имеют один и тот же размер и если у них совпадают соответствующие элементы.
Определение 3.
Суммой матриц \( A=(a_{ij}) \) и \( B=(b_{ij}) \) размера \(m \times n \) называют матрицу \( C=(c_{ij}) \) того же размера с элементами
\( c_{ij} = a_{ij} + b_{ij}, \; i=\overline{1,m} , \; j=\overline{1,n} \)
В подробной записи:
\( A+B = \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} + \)
\( \begin{pmatrix}
b_{11} & b_{12} & \cdots & b_{1n} \\
b_{21} & b_{22} & \cdots & b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
b_{m1} & b_{m2} & \cdots & b_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
a_{11}+b_{11} & a_{12}+b_{12} & \cdots & a_{1n}+b_{1n} \\
a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n}+b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1}+b_{m1} & a_{m2}+b_{m2} & \cdots & a_{mn}+b_{mn} \\
\end{pmatrix} = C \)
Сумма определена только для матриц одного размера.
Определение 4.
Произведением матрицы \( A=(a_{ij}) \) размера \(m \times n \) на число \( k \in \mathbb{R}\) называют матрицу
\( C=(c_{ij}) \) размера \(m \times n \) с элементами \( c_{ij} = k \cdot a_{ij} \).
Подробно это произведение выглядит так:
\( k \cdot \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
k \cdot a_{11} & k \cdot a_{12} & \cdots & k \cdot a_{1n} \\
k \cdot a_{21} & k \cdot a_{22} & \cdots & k \cdot a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
k \cdot a_{m1} & k \cdot a_{m2} & \cdots & k \cdot a_{mn} \\
\end{pmatrix} \)
Замечание. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами. {n+m}\).
{n+m}\).
Элементарные преобразования матриц
Следующие три операции называют элементарными преобразованиями строк матрицы :1. Умножение строки матрицы на число не равное нулю.
2. Перестановка двух строк матрицы.
3. Суммирование одной строки с другой строкой, умноженной на число.
Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.
Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную.
Теорема. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду.
Определители
Определители n-го порядка
В теории определителей n-го порядка используются понятия перестановки, подстановки и их четности. Всякое расположение чисел \( 1,\; 2,\; 3,\; …,\; n \) в определенном порядке называют перестановкой из \(n\) чисел.
Всякое расположение чисел \( 1,\; 2,\; 3,\; …,\; n \) в определенном порядке называют перестановкой из \(n\) чисел.
Из \(n\) чисел можно образовать \(n!\) различных перестановок.
В общем случае перестановку записывают в виде матрицы-строки \( \alpha = (\alpha_1,\; \alpha_2,\; …,\; \alpha_n ) \)
Перестановку \( (1,\; 2,\; 3,\; …,\; n) \) называют нормальной.
Два числа \(\alpha_i\) и \(\alpha_j\) в перестановке \( \alpha = (\alpha_1,\; …,\; \alpha_n ) \) образуют инверсию,
если \(\alpha_j > \alpha_i \) но при этом \(\alpha_i\) стоит в перестановке правее \(\alpha_j\) (т.е. \(i>j\) ).
Общее количество инверсий в перестановке \(\alpha \) обозначают \( |\alpha | \), и если это число четное, то перестановку называют
четной, а если оно нечетное — нечетной.
Транспозицией перестановки называют такое её преобразование, при котором в ней меняются местами какие-либо два элемента,
а другие остаются на своих местах.
Теорема. Любая транспозиция меняет четность перестановки.
Из двух перестановок \( ( \alpha_1,\; …,\; \alpha_n ) \) и \( ( \beta_1,\; …,\; \beta_n ) \) одних и тех же чисел можно
составить новый объект
$$ \sigma = \begin{pmatrix}
\beta_1 & \beta_2 & \cdots & \beta_n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} , \tag{1} $$
который называют подстановкой n-й степени.
Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в
противоположном случае.
Четность подстановки \( (1) \) совпадает с четностью числа \( |\beta|+|\alpha| \) — общего количества инверсий
в строках подстановки, которое обозначают \( |\sigma| \).
Транспозицией подстановки называют любую перестановку её столбцов. Поскольку транспозиция подстановки вызывает
транспозиции и в образующих её перестановках, то, согласно предыдущей теореме, очевидно, что транспозиция подстановки не меняет
её четность.
Каждая подстановка вида \( (1) \) задает взаимно однозначное отображение множества чисел \( 1,\; 2,\; 3,\; …,\; n \) на себя,
при котором \( \beta_1 \) отображается в \( \alpha_1 \; , \; \beta_2 \) — в \( \alpha_2\) и т.д.
В соответствии с интерпретацией подстановок как отображений две подстановки считают равными, если они отличаются только
порядком записи своих столбцов.
Например, подстановки
\( \begin{pmatrix}
1 & 3 & 4 & 2 \\
2 & 4 & 1 & 3 \\ \end{pmatrix}
\;\; и \;\;
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 3 & 4 & 1 \\ \end{pmatrix} \)
равны, так как вторая получается из первой перестановкой столбцов.
Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок \(n\)-й степени имеется ровно \(n!\)
Определение. {|\sigma|} a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n} \tag{3} $$
которая берется по всевозможным подстановкам вида
{|\sigma|} a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n} \tag{3} $$
которая берется по всевозможным подстановкам вида
\( \sigma = \begin{pmatrix}
1 & 2 & \cdots & n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} \)
Определитель матрицы \(A\) часто называют просто определителем, или детерминантом, и обозначают
\( \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} \)
или \( \det A\), называя \(A\) матрицей этого определителя.
Свойства определителей
Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология
(порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей,
транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов
и др. T \right| \)
T \right| \)
Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
Свойство 3. Если все элементы \(j\)-го столбца определителя представлены в виде суммы двух слагаемых, то определитель равен
сумме двух определителей, у которых все столбцы, кроме \(j\)-го, такие же, как и в данном определителе, а \(j\)-й столбец
первого определителя состоит из первых слагаемых \(j\)-го столбца данного определителя, а второго — из вторых слагаемых :
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} + \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} + \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} + \beta_{nj} & \cdots & a_{nn} \end{vmatrix} = \)
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} & \cdots & a_{nn} \end{vmatrix} + \)
\( \begin{vmatrix}
a_{11} & \cdots & \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \beta_{nj} & \cdots & a_{nn} \end{vmatrix} \)
Аналогично для строки.
Свойство 4. Общий множитель элементов строки или столбца может быть вынесен за знак определителя.
Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца.
Свойство 5. Определитель равен нулю, если он имеет :
1) нулевую строку (столбец)
2) хотя бы две одинаковые строки (столбца)
3) хотя бы две строки (столбца), элементы которых пропорциональны
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
Свойство 6. Определитель не изменится, если к любой его строке (столбцу) прибавить другую строку (столбцец), умноженную на число.
В матрице \(A\) вычеркнем \(i\)-ю строку и \(j\)-й столбец, в которых стоит элемент \(a_{ij}\). Из оставшихся элементов можно
составить новую квадратную матрицу (n-1)-го порядка, сдвинув строки и столбцы после вычеркивания.
Определитель построенной матрицы обозначают через \( M_{ij} \) и называют минором (матрицы \(A\) и её определителя
\(\Delta\) ), соответствующим элементу \(a_{ij}\). {i+j} a_{ij} M_{ij} \tag{5} $$
( разложение по \(j\)-му столбцу )
{i+j} a_{ij} M_{ij} \tag{5} $$
( разложение по \(j\)-му столбцу )
Разложения по строке (4) и столбцу (5) дают правила, в соответствии с которыми определитель n-го порядка сводится к n
определителям (n-1)-го порядка, раскладывая которые получим n(n-1) определителей (n-2)-го порядка и т.д.
Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей.
Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей.
Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения
по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений.
Свойство 8. Определитель верхней (нижней) треугольной матрицы равен произведению элементов её главной диагонали,
т.е.
$$ \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ \begin{vmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ a_{11}a_{22}. n a_{ii} $$
n a_{ii} $$
С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на —1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения её определителя.
Свойство 9. Определитель произведения двух квадратных матриц A, B равен произведению их определителей, т.е. \( |АВ| = |A||B| \).
Свойство 10. Определитель обратной матрицы: \( \left| А^{-1} \right| = \frac{1}{|A|} \)
Свойство 11. {1+3} a_{13} M_{13} = $$
$$ a_{11} \begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \end{vmatrix}
— a_{12} \begin{vmatrix}
a_{21} & a_{23} \\
a_{31} & a_{33} \end{vmatrix}
+ a_{13} \begin{vmatrix}
a_{21} & a_{22} \\
a_{31} & a_{32} \end{vmatrix} = $$
$$ a_{11}a_{22}a_{33} — a_{11}a_{23}a_{32} — a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} — a_{13}a_{22}a_{31} $$
{1+3} a_{13} M_{13} = $$
$$ a_{11} \begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \end{vmatrix}
— a_{12} \begin{vmatrix}
a_{21} & a_{23} \\
a_{31} & a_{33} \end{vmatrix}
+ a_{13} \begin{vmatrix}
a_{21} & a_{22} \\
a_{31} & a_{32} \end{vmatrix} = $$
$$ a_{11}a_{22}a_{33} — a_{11}a_{23}a_{32} — a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} — a_{13}a_{22}a_{31} $$
Чтобы запомнить, какие произведения элементов берутся со знаком \( «+» \), а какие со знаком \( «-» \) можно
использовать следующее правило треугольников.
Произведения элементов, стоящих на зелёных точках складываются, а на
синих — вычитаются :
Также для вычисления определителя 3-го порядка существует правило Саррюса.
Первый и второй столбцы матрицы записываются справа от основной матрицы.
Произведения элементов, стоящих на зелёных линиях складываются, а на
синих — вычитаются :
Обратная матрица и её свойства
Определение. {-1}\), обратную к \(A\), фактически надо решить матричное уравнение \(AX=E\).
{-1}\), обратную к \(A\), фактически надо решить матричное уравнение \(AX=E\).
Отметим, что если над матрицей \(A\) выполняется какое-либо элементарное преобразование строк, то это же
преобразование осуществляется и над матрицей \(AX\), поскольку любое элементарное преобразование строк матрицы
эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, если в уравнении
\(AX=E\) над матрицами \(A\) и \(E\) одновременно выполнить какое-либо элементарное преобразование строк, т.е.
домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное
уравнение \(A_1X=B_1\). Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное
преобразование строк имеет обратное элементарное преобразование строк.
Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица \(A\)
превратилась в единичную матрицу.
В результате этих s шагов получается уравнение \(A_sX=B_s\), где \(A_s=E\), т. {-1}\).
{-1}\).
Ранг матрицы
Определение.Рангом матрицы называют число, которое равно максимальному порядку среди её ненулевых миноров.
Для ранга матрицы \(A\) используют обозначение \(\text{rang}A\).
Если квадратная матрица порядка n невырождена, то её ранг равен её порядку n : ненулевым является единственный
минор максимального порядка n, совпадающий с определителем матрицы.
В частности, ранг единичной матрицы \(E\) порядка n равен n.
Если квадратная матрица вырождена, то её ранг меньше её порядка : единственный минор максимального
порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок.
Ранг нулевой матрицы полагают равным нулю.
Ранг диагональной матрицы равен количеству её ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его
характеризующее. T = \text{rang} A \)
T = \text{rang} A \)
Теорема. Ранг матрицы не меняется при элементарных преобразованиях её строк и столбцов.
Теорема о базисном миноре
Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.
Определение.
Минор \(M\) матрицы \(M\) называют базисным, если выполнены два условия:
1) он не равен нулю
2) его порядок равен рангу матрицы А
Матрица \(A\) может иметь несколько базисных миноров. Строки и столбцы матрицы \(A\), в которых расположен выбранный базисный минор, называют базисными.
Теорема о базисном миноре. Базисные строки (столбцы) матрицы \(A\), соответствующие любому её базисному минору \(M\), линейно независимы. Любые строки (столбцы) матрицы \(A\), не входящие в \(M\), являются линейными комбинациями базисных строк (столбцов).
Следствие. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы её
строки (столбцы) были линейно независимы.
Теорема. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).
Теорема. Для любой матрицы её ранг равен максимальному количеству её линейно независимых строк (столбцов).
Следствие. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.
Вычисление ранга матрицы
Метод окаймляющих миноров
Минор \(M’\) матрицы \(A\) называют окаймляющим для минора \(M\), если он получается из последнего
добавлением одной новой строки и одного нового столбца матрицы \(A\).
Ясно, что порядок окаймляющего минора \(M’\) на единицу больше, чем порядок минора \(M\).
Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору
последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого
сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот
процесс рано или поздно закончится из-за ограниченных размеров матрицы.
К очередному ненулевому минору
последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого
сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот
процесс рано или поздно закончится из-за ограниченных размеров матрицы.
Теорема. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.
Метод элементарных преобразований
При элементарных преобразованиях строк (столбцов) матрицы её ранг не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.
Например с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг
же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на
пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк. Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его
окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных
преобразований строк позволяет вычислить ранг матрицы.
Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его
окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных
преобразований строк позволяет вычислить ранг матрицы.
Приведенные два метода существенно отличаются друг от друга.
При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество
вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до
минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из её
базисных миноров.
При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений.
Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением её вида. Но этот метод
позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных
преобразований. Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже
известного ранга матрицы.
Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже
известного ранга матрицы.
Линейная алгебра на Python. [Урок 3]. Действия над матрицами
Тема третьего урока: действия над матрицами. В рамках нее будут рассмотрены следующие вопросы: умножение матрицы на число, сложение и умножение матриц.
Действия над матрицамиУмножение матрицы на числоПри умножении матрицы на число, все элементы матрицы умножаются на это число:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> C = 3 * A
>>> print(C)
[[ 3 6 9]
[12 15 18]]
Рассмотрим свойства операции умножения матрицы на число.
Свойство 1. Произведение единицы и любой заданной матрицы равно заданной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4') >>> L = 1 * A >>> R = A >>> print(L) [[1 2] [3 4]] >>> print(R) [[1 2] [3 4]]
Свойство 2. Произведение нуля и любой матрицы равно нулевой матрице, размерность которой равна исходной матрицы:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = 0 * A
>>> R = Z
>>> print(L)
[[0 0]
[0 0]]
>>> print(R)
[[0 0]
[0 0]]
Свойство 3. Произведение матрицы на сумму чисел равно сумме произведений матрицы на каждое из этих чисел:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3
>>> L = (p + q) * A
>>> R = p * A + q * A
>>> print(L)
[[ 5 10]
[15 20]]
>>> print(R)
[[ 5 10]
[15 20]]
Свойство 4. Произведение матрицы на произведение двух чисел равно произведению второго числа и заданной матрицы, умноженному на первое число:
Произведение матрицы на произведение двух чисел равно произведению второго числа и заданной матрицы, умноженному на первое число:
➣ Численный пример
➤Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> p = 2
>>> q = 3
>>> L = (p * q) * A
>>> R = p * (q * A)
>>> print(L)
[[ 6 12]
[18 24]]
>>> print(R)
[[ 6 12]
[18 24]]
Свойство 5. Произведение суммы матриц на число равно сумме произведений этих матриц на заданное число:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> k = 3
>>> L = k * (A + B)
>>> R = k * A + k * B
>>> print(L)
[[18 24]
[30 36]]
>>> print(R)
[[18 24]
[30 36]]Сложение матриц
Складывать можно только матрицы одинаковой размерности — то есть матрицы, у которых совпадает количество столбцов и строк.
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 6 3; 8 2 7')
>>> B = np.matrix('8 1 5; 6 9 12')
>>> C = A + B
>>> print(C)
[[ 9 7 8]
[14 11 19]]
Рассмотрим свойства сложения матриц.
Свойство 1. Коммутативность сложения. От перестановки матриц их сумма не изменяется:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = A + B
>>> R = B + A
>>> print(L)
[[ 6 8]
[10 12]]
>>> print(R)
[[ 6 8]
[10 12]]
Свойство 2. Ассоциативность сложения. Результат сложения трех и более матриц не зависит от порядка, в котором эта операция будет выполняться:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4') >>> B = np.matrix('5 6; 7 8') >>> C = np.matrix('1 7; 9 3') >>> L = A + (B + C) >>> R = (A + B) + C >>> print(L) [[ 7 15] [19 15]] >>> print(R) [[ 7 15] [19 15]]
Свойство 3. Для любой матрицы существует противоположная ей , такая, что их сумма является нулевой матрицей :
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = A + (-1)*A
>>> print(L)
[[0 0]
[0 0]]
>>> print(Z)
[[0 0]
[0 0]]Умножение матриц
Умножение матриц это уже более сложная операция, по сравнению с рассмотренными выше. Умножать можно только матрицы, отвечающие следующему требованию: количество столбцов первой матрицы должно быть равно числу строк второй матрицы.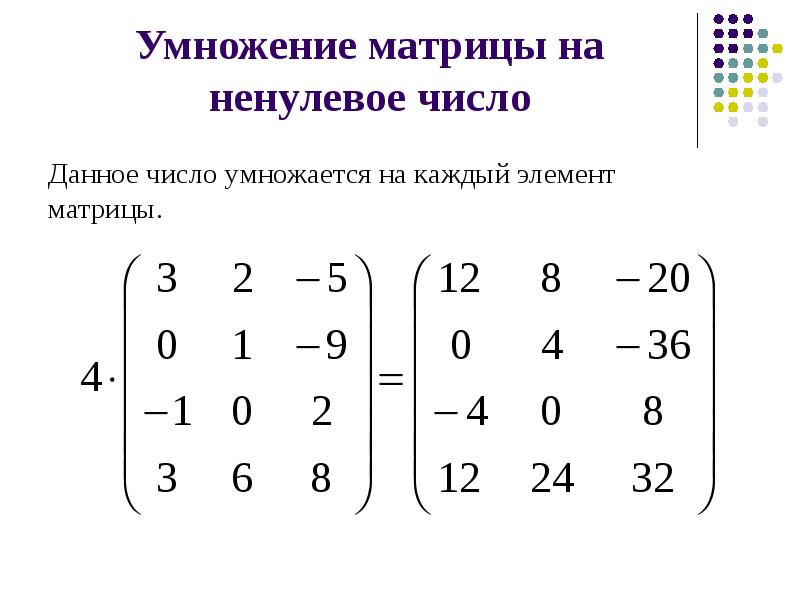
Для простоты запоминания этого правила можно использовать диаграмму умножения, представленную на рисунке 1.
Рисунок 1 — Диаграмма матричного умножения
Рассмотрим умножение матриц на примере.
➣ Численный пример
Каждый элемент cij новой матрицы является суммой произведений элементов i-ой строки первой матрицы и j-го столбца второй матрицы. Математически это записывается так:
➤Пример на Python
Решим задачу умножения матриц на языке Python. Для этого будем использовать функцию dot() из библиотеки Numpy:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8; 9 1; 2 3')
>>> C = A.dot(B)
>>> print(C)
[[31 19]
[85 55]]
Ниже представлены свойства произведения матриц. Примеры свойств будут показаны для квадратной матрицы.
Свойство 1. Ассоциативность умножения. Результат умножения матриц не зависит от порядка, в котором будет выполняться эта операция:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')
>>> L = A.dot(B.dot(C))
>>> R = (A.dot(B)).dot(C)
>>> print(L)
[[192 252]
[436 572]]
>>> print(R)
[[192 252]
[436 572]]
Свойство 2. Дистрибутивность умножения. Произведение матрицы на сумму матриц равно сумме произведений матриц:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('2 4; 7 8')
>>> L = A. dot(B + C)
>>> R = A.dot(B) + A.dot(C)
>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]
dot(B + C)
>>> R = A.dot(B) + A.dot(C)
>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]
Свойство 3. Умножение матриц в общем виде не коммутативно. Это означает, что для матриц не выполняется правило независимости произведения от перестановки множителей:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = A.dot(B)
>>> R = B.dot(A)
>>> print(L)
[[19 22]
[43 50]]
>>> print(R)
[[23 34]
[31 46]]
Свойство 4. Произведение заданной матрицы на единичную равно исходной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4') >>> E = np.matrix('1 0; 0 1') >>> L = E.dot(A) >>> R = A.dot(E) >>> print(L) [[1 2] [3 4]] >>> print(R) [[1 2] [3 4]] >>> print(A) [[1 2] [3 4]]
Свойство 5. Произведение заданной матрицы на нулевую матрицу равно нулевой матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> Z = np.matrix('0 0; 0 0')
>>> L = Z.dot(A)
>>> R = A.dot(Z)
>>> print(L)
[[0 0]
[0 0]]
>>> print(R)
[[0 0]
[0 0]]
>>> print(Z)
[[0 0]
[0 0]]P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Матрица сложение матриц — Энциклопедия по машиностроению XXL
В кинематике механизмов операции сложения матриц и умножения их на скаляр находят применение в действиях над матрицами-столбцами. [c.631]Матрица [/(], называемая глобальной матрицей жесткости или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Л ] по следующему правилу сначала к нулевой матрице размерности NxN добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размера /V х /V, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для 2-го элемента и т. д. на -м шаге добавляется матрица, ненулевые элементы которой расположены на пересечении к и к- строк и к н k- — столбцов и равны соответствующим элементам локальной матрицы жесткости k-ro элемента.
[c.134]
д. на -м шаге добавляется матрица, ненулевые элементы которой расположены на пересечении к и к- строк и к н k- — столбцов и равны соответствующим элементам локальной матрицы жесткости k-ro элемента.
[c.134]
Все остальные неизвестные определяются лишь путем умножения и сложения матриц. Весь процесс вычислений при этом легко программируется с использованием стандартных программ сложения, умножения и обращения матриц. [c.97]
Непосредственным перемножением и сложением матриц (71.29) нетрудно убедиться, что они удовлетворяют соотношениям (71.28), понимая, что в их правой части стоит единичная матрица. Например, для имеем [c.387]
Сложение и вычитание матриц. Две матрицы можно сложить (вычесть). Для этого необходимо, чтобы порядки матриц были одинаковы, и тогда сложить (вычесть) соответствующие элементы матриц. [c.179]
В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
[c.41]
Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
[c.41]
Логическое сложение матриц реализуется путем попарного логического сложения одноименных элементов исходных матриц [c.123]
Рассмотрим, как влияет учет дисперсий на результаты расчета. Формально учет дисперсий выражается в сложении матрицы [а] [а] с диагональной матрицей [ )], имеющей положительные члены. Это способствует улучшению обусловленности матрицы [а] [а], что особенно важно в случаях, когда последняя плохо [c.58]
Сложение матриц. Суммой матриц [c.95]
DN — присвоение значений единицы диагональным элементам двумерного массива А+В — сложение матриц А и В [c.163]
Необходимость применения динамического метода существенно усложняет решение неконсервативных задач устойчивости. Здесь требуется весьма эффективный метод определения частот собственных колебаний. Среди других методов в этом отношении вьщеляется МГЭ. Он позволяет получать точный спектр частот (устраняет недостаток МКЭ), а в трансцендентном частотном уравнении отсутствуют точки разрыва 2-го рода (устраняет недостаток метода перемещений). Дополнительными положительными факторами являются простая логика формирования динамической матрицы устойчивости, отсутствие операций умножения, обращения и сложения матриц, хорошая устойчивость численных операций при вычислении определителя и т.п.
[c.196]
Среди других методов в этом отношении вьщеляется МГЭ. Он позволяет получать точный спектр частот (устраняет недостаток МКЭ), а в трансцендентном частотном уравнении отсутствуют точки разрыва 2-го рода (устраняет недостаток метода перемещений). Дополнительными положительными факторами являются простая логика формирования динамической матрицы устойчивости, отсутствие операций умножения, обращения и сложения матриц, хорошая устойчивость численных операций при вычислении определителя и т.п.
[c.196]
Сложение матриц. Суммой матриц А а В называется матрица С, элементы которой с,у определяются по формуле [c.91]
При сложении матриц жесткости элементов с целью получения глобальной матрицы жесткости необходимо запоминать как матрицы отдельных элементов, так и матрицу [/С]. Это также перегружает оперативную память. [c.251]
Как и в случае матриц, сложению поворотов в случае их активного представления отвечает произведение кватернионов составляющих поворотов в обратном порядке. При этом все кватернионы заданы в исходном базисе к (/ = 1, 2, 3).
[c.46]
При этом все кватернионы заданы в исходном базисе к (/ = 1, 2, 3).
[c.46]
Сложение. Матрицы Л и В могут быть сложены, если они имеют одинаковое число строк и столбцов. [c.634]
В табл. 7.1 приведена скорость выполнения операции умножения матрицы на вектор. В первой колонке представлены выражения для числа тактовых циклов, необходимых для завершения одной операции умножения. Умножение матрицы тХп на вектор /гХ1 требует 2тп операций сложения и умножения. Если предположить, что биты данных проходят в системе с частотой 10 МГц (величина 0,1 мкс/бит является достаточно обоснованной для существующих электронных устройств), то можно вычислить скорость выполнения операций. Представлены два случая. Первый из них соответствует п = т = 32, при /=16 (I эквивалентно точности вычислений), а второй случай относится к п = т=128, / = 32. В табл. 7.2 представлены аналогичные данные для умножителей, выполняющих умножение матрицы на матрицу с точностью I цифр. В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-
[c.207]
В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-
[c.207]
Предположения, которые можно сделать о симметрии, в точности совпадают с предположениями, делавшимися в предыдущих разделах. Сложение матриц S непосредственно дает нижеследующие результаты, представленные здесь наряду с качественной интерпретацией. Объем этой книги не допускает подробного обсуждения этого вопроса. Все эффекты можно вывести из общей формулы распространения, данной в разд. 4.41. [c.73]
Матрица теплопроводности элемента получается сложением матриц (8.15) и (8.17) [c.138]
Матрица [Л] получается сложением матриц [С] и [/С] [c.208]
Пример 3.1. В результате сложения матриц [а]= 3 8 1 И[ВЬ 2 4-1
[c. 155]
155]
Сложение матриц обладает свойством коммутативности (от перестановки матриц их сумма не меняется) и подчиняется сочетательному закону [c.155]
Другой способ нахождения обратной матрицы заключается в последовательном вычислении обратной матрицы путем подбора при помощи единичной матрицы. Записав рядом с заданной матрицей единичную матрицу, производим сложение строк, предварительно подобрав множители так, чтобы на месте заданной матрицы получить единичную. В этом случае на месте единичной матрицы будет искомая обратная матрица. [c.158]
Тем не менее сложение матриц удовлетворяет всем свойствам сложения чисел. Например, из А- -В = А- С следует, что В = С. [c.273]
При сложении двух матриц одинакового размера получается матрица того же размера, каждый элемент которой равеи сумме соответствующих элементов слагаемых матриц. [c.104]
Над матрицами можно выполнять действия транспонирования, сложения, умножения. Матрица А, транспонированная по отношению к матрице А, образуется из матрицы А заменой каждой ее строки на столбец того же номера. Например, при транспонировании матрицы
[c.50]
Матрица А, транспонированная по отношению к матрице А, образуется из матрицы А заменой каждой ее строки на столбец того же номера. Например, при транспонировании матрицы
[c.50]
Множество J n всех л-мерных векторов называют линейным алгебраическим пространством, если в нем определены операции сложения и умножения на скаляр точно так же, как для матриц. Число я называется размерностью пространства Rn- Рассмотрим помимо вектора а другой п-мерный вектор [c.19]
При вычислении матрицы плотности мы будем предполагать, что рассеянные волны имеют беспорядочные фазы и при сложении в среднем дают нуль. Если и г и г лежат слева от слоя, то [c.718]
Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -. [c.63]
[c.63]
Матрица жесткости (13) конструкции образуется сложением матриц жесткости балок и нанелей = Од + Оп- Для панелей [c.483]
Кватернионное сложение поворотов. Как и в случае матриц, сложению поворотов отвечает произведение кватернионов, при этом активная и пассивная точки зрения на преобразования имеют существенные отличия. [c.46]
Линейно-алгебраические операции, рассмотренные в предыдущем параграфе, можно отнести к трем типам, исходя из принципов организации реализующих их вычислительных процессов. К типу коротких отнесем операции, для реализации которых принципиально достаточен однократный обмен файлов, содержащих операнды и результат сложение матриц и векторов, умножение на скаляр и т. п. К типу длинных отнесем операции, для реализации которых принципиально требуется многократный обмен одного файла, содержащего операнд или результат транспонирование, обращение матрицы, умножение двух матриц и т.
 п., в случае когда операнды и результат не размещаются целиком в ОЗУ. К типу условнокоротких отнесем операции, для реализации которых при некоторых дополнительных условиях достаточен однократный обмен файлов. В основном, это весьма распространенная в АСУ операция умножения матрицы на вектор, когда операнды и результат не размещаются в ОЗУ. В общем случае эта операция выполнима по алгоритму умножения двух матриц. Однако, если матрица упорядочена так, что старший индекс ее элементов является индексом, различающим элементы вектора, то эта операция реализуется однократным обменом. Таким образом, при дополнительном условии — при совпадении упорядоченностей элементов матрицы и вектора — эта операция является короткой. Без этого дополнительного условия операция является длинной, так как в этом случае она выполняется либо как умножение двух матриц, либо (что короче) в две стадии сначала выполняется транспонирование матрицы, затем собственно умножение, но при однократном обмене.
[c.
п., в случае когда операнды и результат не размещаются целиком в ОЗУ. К типу условнокоротких отнесем операции, для реализации которых при некоторых дополнительных условиях достаточен однократный обмен файлов. В основном, это весьма распространенная в АСУ операция умножения матрицы на вектор, когда операнды и результат не размещаются в ОЗУ. В общем случае эта операция выполнима по алгоритму умножения двух матриц. Однако, если матрица упорядочена так, что старший индекс ее элементов является индексом, различающим элементы вектора, то эта операция реализуется однократным обменом. Таким образом, при дополнительном условии — при совпадении упорядоченностей элементов матрицы и вектора — эта операция является короткой. Без этого дополнительного условия операция является длинной, так как в этом случае она выполняется либо как умножение двух матриц, либо (что короче) в две стадии сначала выполняется транспонирование матрицы, затем собственно умножение, но при однократном обмене.
[c. 77]
77]Рассмотрение данного примера было вызвано необходимостью обеспечить высокую скорость при выполнении операции внутреннего произведения в линейной алгебре (например, для умножения матрицы на вектор или матрицы на матрицу), в противном случае эти операции становятся бессысленными. Операции внутреннего произведения включают умножение двух чисел и сложение результата с третьим числом. Например, 2-разрядный умножитель-сумматор умножает два 2-раз-рядных числа М ц Ы, прибавляет результат к 5-разрядному входному числу X и выводит результаты в виде 5-разрядного числа У. В синхронизированном режиме работы выходной сигнал У мог бы подаваться по цепи обратной связи на вход X для того, чтобы достичь эффекта многократного накопления результата (если имеется возможность накопления до трех произведений и при этом не возникает переполнение). [c.155]
Быстродействие оптических матричных умножителей было уже описано в табл. 7.1 и 7.2. При вычислении отношения Псалтиса числа в табл. 7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.
[c.210]
7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.
[c.210]
Добавление матрицы
Как и в обычной алгебре, матричная алгебра имеет такие операции, как сложение и вычитание.
Как складывать и вычитать матрицы
Две матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые измерение; то есть в них должно быть одинаковое количество строк и столбцов.
Сложение или вычитание осуществляется путем сложения или вычитания. соответствующие элементы. Например, рассмотрим матрицу A и матрица B .
соответствующие элементы. Например, рассмотрим матрицу A и матрица B .
Обе матрицы имеют одинаковое количество строк и столбцов (2 строки и 3 столбца), поэтому их можно складывать и вычитать. Таким образом,
| A + B = |
|
А,
| A — B = |
|
И, наконец, обратите внимание, что порядок добавления матриц не
важный; таким образом, A + B = В + А .
Проверьте свое понимание
Проблема 1
Рассмотрим представленные ниже матрицы — A , B , C и D
Какие из следующих утверждений верны?
I. A + B = C
II. B + C = D
III. B — C = D
(A) только я
Только
(B) II
Только
(C) III
(D) I и II
(E) I и III
Решение
Правильный ответ — (C), как показано ниже.
|
Обратите внимание, что матрицы A и B нельзя добавить,
потому что B имеет больше столбцов, чем A . Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые
количество строк и такое же количество столбцов.
Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые
количество строк и такое же количество столбцов.
Матрицы сложения и вычитания — ChiliMath
В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.
Если вы знаете, как складывать и вычитать действительные числа, эта тема должна быть действительно легкой. Единственное, что требуется для «легального» выполнения операций сложения или вычитания в «мире» матриц, — это убедиться, что данные матрицы должны иметь одинаковый размер или размерность.
Что означает, что данная матрица имеет одинаковый размер или размерность?
Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размер, потому что у них одинаковое количество строк и столбцов.
Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:
количество строк x количество столбцов
Позвольте мне показать вам несколько примеров…
Последняя матрица размером 5 x 5 также считается «квадратной матрицей», потому что количество строк и количество столбцов равны. Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, — это то, что сначала она должна быть квадратной матрицей.
Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, — это то, что сначала она должна быть квадратной матрицей.
Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.
Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размер. В противном случае мы заключаем, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разные размеры или размеры, не определена!
Теперь давайте посмотрим на общее правило того, как складывать и вычитать матрицы, размеры или размеры которых совпадают.
Правила сложения и вычитания матриц одинакового размера или размерности
Предположим, что матрицы A и B имеют две строки и два столбца (2 × 2) с некоторыми произвольными элементами или записями…
«Формулы» для сложения и вычитания матриц показаны ниже…
- Добавить матрицы , добавив их соответствующие записи
- Вычесть матрицы путем вычитания их соответствующих записей
Давайте поработаем над некоторыми проблемами.
Примеры сложения и вычитания матриц
Пример 1 : Выполните указанную операцию для A + C.
Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «размерность», потому что их количество строк и столбцов одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне о том, что найти их сумму — это нормально.
Добавлю соответствующие записи и упрощу.
Вот как это просто!
Пример 2 : Выполните указанную операцию для B + F.
Обратите внимание, что матрица B имеет размерность 2 × 3 , а матрица F имеет размерность 2 × 2 .
Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена. . Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.
Пример 3 : Выполните указанную операцию для E-B.
Последние два примера показали вам, как складывать матрицы. На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».
На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».
В этом примере нам нужно найти разницу между матрицей E и матрицей B.
Однако кажется, что это невозможно, поскольку они имеют различных размеров или размеров. Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.
Поскольку я не могу выполнить вычитание по входам из-за того, что записи двух матриц не имеют прямого соответствия, я должен заявить, что НЕ возможно, найти их различие.Следовательно, наш ответ — undefined .
Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или размерами. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы знаете, вы будете осторожны в следующий раз, когда столкнетесь с такой проблемой.
Пример 4 : Выполните указанную операцию для F-D.
При быстром просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов.Большой!
Для начала я вычту соответствующие записи F и D. Мое единственное предостережение — будьте очень осторожны при вычитании действительных чисел. Обычно здесь возникают общие ошибки. Помните, что два соседних отрицательных знака оказываются положительными.
Неплохо, правда?
Пример 5 : Выполните указанную операцию для C-A.
Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3 × 3). Это позволяет нам выполнять операцию вычитания.
Вычитая по входу, я получил…
Пример 6 : Выполните указанную операцию для (A + C) + (C-A).
Это отличный пример «многоступенчатой» задачи, которая включает в себя сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.
Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.
Чтобы пропустить некоторые шаги, просмотрите, как мы решили для (A + C) в примере 1 и C-A в примере 5.
Пока у нас есть эти частичные ответы…
Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.
Как видите, сложение и вычитание матриц очень просто. Я надеюсь, что вы приобрели некоторую уверенность и узнали, как с этим справиться.
Пример 7 : Выполните указанную операцию для (A + C) + (C-A).
Это та же проблема, что и в примере 6. Но я хочу решить ее немного иначе, чтобы продемонстрировать тот факт, что есть другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.
Поехали…
Если вы рассматриваете выражение (A + C) + (C-A) как , объединяющее похожие или похожие термины, проблема типа , то имеет смысл быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.
Обратите внимание, что я могу объединить C-термины как 2C.
Теперь, члены A должны сокращаться, потому что они имеют противоположные знаки.
Наша исходная задача сводится к 2C, что составляет вдвое или вдвое больше матрицы C .
Это означает, что я собираюсь умножить каждый элемент матрицы C на 2. На самом деле это тема моего другого урока по алгебре, посвященного скалярному умножению матрицы.
С
, то 2C решается с помощью…
Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?
Практика с рабочими листами
Возможно, вас заинтересует:
Скалярное умножение
Умножение матриц
Матрицы сложения и вычитания
А
матрица
могут быть добавлены (или вычтены из) другой матрицы только в том случае, если две матрицы имеют одинаковые
Габаритные размеры
.
Чтобы добавить две матрицы, просто добавьте соответствующие записи и поместите эту сумму в соответствующую позицию в матрице, которая получится.
Пример 1:
Добавьте матрицы.
[ 1 5 — 4 3 ] + [ 2 — 1 4 — 1 ]
Сначала обратите внимание, что оба слагаемых 2 × 2 матрицы, чтобы мы могли их добавить.
[ 1 5 — 4 3 ] + [ 2 — 1 4 — 1 ] знак равно [ 1 + 2 5 + ( — 1 ) — 4 + 4 3 + ( — 1 ) ]
знак равно [ 3 4 0 2 ]
Вычитание с помощью матриц так же просто.
Пример 2:
Вычесть.
[ 4 5 6 2 3 4 ] — [ 2 4 6 1 2 3 ]
Вычтите соответствующие записи.
[ 4 5 6 2 3 4 ] — [ 2 4 6 1 2 3 ] знак равно [ 4 — 2 5 — 4 6 — 6 2 — 1 3 — 2 4 — 3 ]
знак равно [ 2 1 0 1 1 1 ]
Как складывать и вычитать матрицы
Сложение и вычитание матриц
На этом этапе нашего курса линейной алгебры мы много работали с матрицами, мы выполняли операции со строками для решения систем линейных уравнений, представляя линейную систему в виде матрицы и используя их в наших интересах посредством сокращения строк и эшелонированных форм. Мы также научились понимать не только обозначения матриц, но и их элементы, их размеры, и теперь пора подумать о них в целом и узнать, какие операции могут быть выполнены с ними (обратите внимание: «с ними», НЕ «в их»).
Мы также научились понимать не только обозначения матриц, но и их элементы, их размеры, и теперь пора подумать о них в целом и узнать, какие операции могут быть выполнены с ними (обратите внимание: «с ними», НЕ «в их»).
На этом уроке мы познакомимся с первыми двумя из четырех основных операций, которые можно выполнить с парой (или более) матриц: сложение, вычитание, скалярное умножение и умножение. Мы знаем эти базовые операции из арифметики, поэтому нам просто нужно узнать, как они работают со всей структурой матриц и с результатами, которые они производят.Обратите внимание, что мы не упомянули деление матриц, потому что деления между матрицами не существует (или, по крайней мере, процесс еще не определен), единственное деление, которое мы можем сделать, — это разделить элементы в матрице на скаляр, но разделить матрицу на другую матрицу невозможно.
Сложение и вычитание матриц
Мы начинаем с работы с двумя основными операциями, известными нам с тех пор, как мы впервые познакомились с математикой в начальной школе: сложение и вычитание (или что-то «плюс» и «минус»). Чтобы проработать эти операции в этом уроке, давайте определим набор из двух матриц для сложения и вычитания. Итак, определяем матрицы A и B следующим образом:
Чтобы проработать эти операции в этом уроке, давайте определим набор из двух матриц для сложения и вычитания. Итак, определяем матрицы A и B следующим образом:
Теперь с ними мы настроены для работы через операции сложения и вычитания матриц. К операции будут применяться несколько правил, но мы поговорим о них в следующем разделе, а пока давайте быстро пройдемся по процессу, а затем мы сможем вернуться и проверить, насколько операции были возможны.Начнем с добавления A и B:
Уравнение 2: сложение матриц A и BМы закодировали каждый элемент в матрицах цветом, чтобы вы могли видеть, что было сделано для каждого элемента. Обратите внимание на то, как сложение двух матриц действует в случае отдельных элементов, требуя, чтобы у вас были точно такие же элементы в матрицах, участвующих в операции, и чтобы они распределялись одинаковым образом.
Мы вернемся к этой теме в следующем разделе, но пока вы должны помнить, что при добавлении матриц вы будете добавлять элементы первой матрицы к соответствующей (той, которая находится в «том же месте», той же строке и столбце число) во второй матрице.
Теперь давайте посмотрим на матричное вычитание:
Уравнение 3: вычитание матрицы B из AГлядя на приведенное выше вычитание, мы можем легко заключить, что процесс очень похож на процесс сложения, поскольку вычитание вычисляется по отдельности для каждого из элементов матриц, таким образом давая результат для каждого соответствующего пространства элементов и в результате получается матрица с таким же количеством элементов в той же организации.
Проще говоря, сложение и вычитание матриц работают одинаково, единственная разница между ними — это арифметический знак, который вы используете для работы: знак плюс для сложения и знак минус для вычитания.
Крайне важно, чтобы вы поняли этот вывод, поскольку это может помочь вам не запутаться при работе с различной литературой по данной теме. Дело в том, что некоторые математики, книги или учебные материалы в целом могут относиться к операциям сложения и вычитания как к «сложению» в целом. Эта конкретная ссылка исходит из того факта, что вычитание эквивалентно сложению чисел, в которых хотя бы одно из них отрицательно. Если у вас есть какие-либо вопросы по этому поводу, помните, что вычитание в арифметике также называется «разницей», и все потому, что когда вы складываете числа с разными знаками, результатом становится разница между ними.Мы рассмотрели эту тему в нашем уроке по вычитанию целых чисел, который, хотя и не является частью этого курса линейной алгебры, вы можете проверить в любое время на веб-сайте StudyPug. Вы также можете проверить следующую статью о сложении и вычитании целых чисел, которая содержит дополнительные упражнения и некоторые графические изображения.
Если у вас есть какие-либо вопросы по этому поводу, помните, что вычитание в арифметике также называется «разницей», и все потому, что когда вы складываете числа с разными знаками, результатом становится разница между ними.Мы рассмотрели эту тему в нашем уроке по вычитанию целых чисел, который, хотя и не является частью этого курса линейной алгебры, вы можете проверить в любое время на веб-сайте StudyPug. Вы также можете проверить следующую статью о сложении и вычитании целых чисел, которая содержит дополнительные упражнения и некоторые графические изображения.
Вкратце: Как складывать матрицы? Мы добавляем каждый соответствующий элемент в задействованные матрицы, чтобы создать новую матрицу, в которой такие элементы будут занимать то же место, что и их предшественники.Как вычесть матрицы? Точно так же, как мы вычисляем сложение, за исключением того, что мы используем знак минус для работы вместо знака плюс.
Правила сложения и вычитания матриц
Матричное сложение и вычитание — это две операции, которые, хотя и просты для решения (как показано выше), у вас все же есть несколько правил, которым нужно следовать, чтобы работать.
Например, когда мы добавляли матрицу A к матрице B выше, сначала обратите внимание, что A и B — очень похожие матрицы, они имеют одинаковое количество строк и столбцов каждая и операция сложения применяется к каждому «соответствующему члену» в них.Это приводит к основному правилу сложения и вычитания матриц, которое соответствует размерам матриц, с которыми работают друг с другом.
Также обратите внимание, что вычитание матриц происходит в очень похожем режиме, на самом деле единственное изменение состоит в том, что вместо знака сложения между матрицами и соответствующими элементами в каждом матричном пространстве у вас есть знак вычитания.
С учетом всего этого правила сложения и вычитания матриц следующие:
- Вы можете складывать или вычитать только матрицы с одинаковыми размерами.
- Если задуматься, это происходит из-за того, что добавление матриц с разными размерами создает проблему, потому что не все элементы в каждой матрице будут иметь соответствующий элемент для работы, что делает операцию невозможной.
- Сложение матриц является коммутативным, но вычитание — нет, если сначала вы не примените знак минуса к матрице справа, таким образом сначала преобразуя операцию в сложение.
- Свойство коммутативности означает, что при добавлении двух матриц вы можете изменить порядок их добавления, и это не повлияет на результат.
- Это не так просто при вычитании. В уравнении 3 у нас есть пример вычитания матриц, обратите внимание, что если вы просто измените порядок матриц, не перемещая знак минус, результат не будет таким же, тогда как вычитание матриц может быть коммутативным? Вы должны применить отрицательный знак к матрице, которая вычитается первой! Проверьте процесс шаг за шагом ниже: Уравнение 4: Условие, чтобы сделать вычитание матрицы коммутативным = сначала преобразовать его в сложение! Обратите внимание, как для того, чтобы иметь возможность изменять порядок матриц, не влияя на результат, мы должны преобразовать вычитание в сложение, что просто означает, что вы должны сначала применить отрицательный знак ко второй матрице, тем самым делая все отрицательные числа его элементов (которые произведут операцию вычитания, не беспокоясь о порядке элементов).Это единственный способ изменить порядок матриц при вычитании, поэтому помните об этом процессе при работе с еще более сложными проблемами: например, в случаях, когда у вас может быть более двух матриц и вы связываетесь в группах. Подробнее об ассоциации в следующем пункте.
- Матричное сложение и вычитание ассоциативны.
- Свойство ассоциативности используется в задачах, включающих более двух матриц, которые складываются или вычитаются друг из друга.Это свойство позволяет вам сначала работать с операцией между двумя матрицами, а затем использовать матрицу, полученную в результате такой операции, для выполнения второй текущей операции. Повторяйте такой процесс, пока не выполните все необходимые операции, затрагивающие все матрицы в задаче.
- При сложении или вычитании матриц результирующая матрица будет иметь те же размеры, что и матрица, которая ее произвела.
- Это имеет смысл, поскольку каждый элемент в первой матрице будет работать с соответствующим элементом второй матрицы, таким образом производя результат для каждого пространства элементов.Затем такие результаты станут элементами новой матрицы.
Примеры сложения и вычитания
Далее мы покажем примеры сложения и вычитания матриц. В первом примере упражнения мы сосредоточимся на демонстрации условий, в которых такие операции возможны. Затем мы решаем несколько примеров матричных задач с пошаговым объяснением операций. В конце этого раздела мы решим матричные уравнения, которые включают либо сложение, либо вычитание матриц.
Пример 1
Можем ли мы сложить или вычесть следующие матрицы?
- Случай 1: Уравнение 5: Можете ли вы сложить эти две матрицы вместе? (Дело 1) Обратите внимание, что размеры матриц, участвующих в сложении, не совпадают. Первая матрица имеет три строки и два столбца, таким образом, это матрица 3×2, а вторая содержит две строки и три столбца, что делает ее размер равным 2×3. Наличие таких различий означает, что, хотя они имеют одинаковое количество элементов, их позиции не соответствуют друг другу, и поэтому по правилам сложения матриц сложение невозможно.
- Случай 2: Уравнение 6: Можете ли вы сложить эти две матрицы вместе? (случай 2) Учитывая, что в этом случае мы будем добавлять матрицы 2×2 (явно; обе матрицы имеют одинаковую размерность 2×2), тогда да, добавление этих двух матриц возможно путем добавления каждого из элементов в первой матрице с соответствующим ему элементом из вторая матрица. Результирующая матрица также будет иметь размеры 2×2.
- Случай 3: Уравнение 7: Можете ли вы сложить эти две матрицы вместе? (случай 3) Как вы, возможно, уже подумали, добавить 2 матрицы, подобные приведенным выше, невозможно.Размеры этих матриц не совпадают (одна представляет собой матрицу 3×3, а другая — 2×2), поэтому это добавление невозможно.
Пример 2
Складываем следующие две матрицы:
Уравнение 8: сложение двух матрицПри добавлении двух матриц каждый элемент добавляется к соответствующему элементу в другой матрице. Процесс прост и показан ниже:
Уравнение 9: Решение для сложения двух матрицВыполните те же действия в следующих двух упражнениях.
Пример 3
Складываем следующие две матрицы:
Уравнение 10: сложение двух матрицИтак, мы добавляем каждый элемент в матрицах к соответствующему элементу в другой матрице. Обратите внимание, что, как упоминалось ранее, матрицы должны иметь одинаковые размеры, чтобы возникло поэлементное соответствие:
Уравнение 11: Решение для сложения двух матрицПример 4
Складываем следующие две матрицы:
Уравнение 12: сложение трех матрицПри добавлении более двух матриц вы можете связать две, выполнив сначала их сложение, а затем добавив полученную матрицу к оставшейся матрице.Это то, что мы называем ассоциативным свойством сложения матриц, это и другие свойства сложения матриц будут объяснены в последующих уроках, а пока проверьте процесс решения этой проблемы ниже:
Уравнение 13: Решение для сложения трех матрицИтак, как вы можете видеть, первым шагом было добавление матриц один и два, что привело к новой матрице, которая позже добавляется к третьей. Если добавление матриц содержит больше трех матриц, один и тот же процесс связывания можно повторять столько раз, сколько необходимо, чтобы упростить задачу, пока у вас не получится простая операция с двумя матрицами.
Пример 5
Вычтите следующие матрицы:
Уравнение 14: Вычитание двух матрицЕще раз обратите внимание, что матрицы, участвующие в вычитании, должны иметь одинаковые размеры, чтобы соблюдалось поэлементное соответствие.
Уравнение 15: Решение для вычитания двух матрицПример 6
Вычтите следующие матрицы:
Уравнение 16: Вычитание двух матрицНеважно, насколько велики матрицы, если они имеют одинаковые размеры, вы можете выполнить вычитание.
Уравнение 17: Решение для вычитания двух матрицПример 7
Вычтите следующие матрицы:
Уравнение 18: Вычитание трех матрицОбратите внимание, что для вычитания матриц с более чем двумя матрицами мы можем снова использовать свойство ассоциативности. Помните, что вычитание матриц не коммутативно (вы не можете изменить порядок матриц в операции и получить тот же результат).
Уравнение 19: Решение вычитания трех матрицПример 8
Решите следующее уравнение, содержащее добавление постоянной матрицы к переменной.
Уравнение 20: Найдите A в матричном уравнении (часть 1)Мы начинаем с вычитания матрицы в левой части к обеим частям уравнения, чтобы мы могли легко найти A, выполнив вычитание матрицы:
Уравнение 21: Найдите A в матричном уравнении (часть 2)Пример 9
Решите следующие матричные уравнения
Уравнение 22: Найдите X в матричном уравнении (часть 1)В этом случае самый простой способ найти X — это передать его в правую часть, добавив его к обеим частям уравнения, чтобы оно стало положительным.Мы также вычитаем матрицу, найденную в правой части уравнения, с обеих сторон, и, таким образом, получаем вычитание матрицы, определяющее X.
Уравнение 23: Найдите X в матричном уравнении (часть 2)Решая вычитание матриц, находим X.
Пример 10
Найдите значения элементов a, b, c, d, e и f, решив следующее матричное уравнение наиболее эффективным способом.
Уравнение 24: Нахождение значений элементов в самой левой матрицеВ этой задаче мы можем преобразовать элемент за элементом случай, уравнение, которое позволит нам получить значение каждого из элементов в первой матрице.
Другими словами, вы знаете, что элемент из первой строки и первого столбца (вверху слева) в первой матрице будет добавлен к элементу в первой строке и первом столбце второй матрицы, чтобы получить элемент в этом пространстве. в получившейся матрице справа. Другими словами, мы можем легко записать следующие уравнения для каждого пространства элементов:
Уравнение 25: Набор уравнений для каждой переменной, которую необходимо решитьИ из этого мы можем решить значение каждой переменной:
Уравнение 25: Решение переменных от a до fПосле того, как мы научимся складывать и вычитать матрицы, пришло время изучить другие операции: скалярное умножение матриц и умножение двух или более матриц будут объяснены в следующих двух уроках.
Мы завершаем наш урок на сегодня несколькими полезными ссылками: первая содержит краткий список основных правил сложения матриц и дополнительную лекцию по матричным операциям.
И это все, до встречи на нашем следующем уроке!6.2 — Операции с матрицами
6.2 — Операции с матрицамиРавенство
Две матрицы равны тогда и только тогда, когда
- Порядок матриц одинаковый
- Соответствующие элементы матриц одинаковые
Дополнение
- Порядок матриц должен быть таким же
- Сложите соответствующие элементы вместе
- Матричное сложение коммутативно
- Матрица сложения ассоциативна
Вычитание
- Порядок матриц должен быть одинаковым
- Вычесть соответствующие элементы
- Матричное вычитание не коммутативно (как и вычитание действительных чисел)
- Матричное вычитание не ассоциативно (как и вычитание действительных чисел)
Скалярное умножение
Скаляр — это число, а не матрица.
- Матрица может быть любого порядка
- Умножить все элементы в матрице на скаляр
- Скалярное умножение коммутативно
- Скалярное умножение ассоциативно
Нулевая матрица
- Матрица любого заказа
- Состоит из всех нулей
- Обозначается заглавной буквы O
- Аддитивный идентификатор для матриц
- Любая матрица плюс нулевая матрица является исходной матрицей
Умножение матриц
A m × n × B n × p = C m × p
- Количество столбцов в первой матрице должно быть равно количество строк во второй матрице.То есть внутренние размеры должны быть одинаковыми.
- Порядок произведения — это количество строк в первой матрице на количество столбцов в вторая матрица. То есть габариты изделия — это габариты внешние.
- Поскольку количество столбцов в первой матрице равно количеству строк во второй матрицу, вы можете объединить записи.
- Каждый элемент в строке i из первой матрицы объединяется в пару с элементом в столбце j из вторая матрица.
- Элемент в строке i , столбце j продукта формируется путем умножения этих парных элементов. и суммируя их.
- Каждый элемент в продукте представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
- Будет n продуктов, которые суммируются для каждого элемента в продукте.
См. Полный пример умножения матриц.
Умножение матриц некоммутативное
- Умножение действительных чисел.
- Внутренние размеры могут не совпадать при изменении порядка матриц.
Не просто перемножайте соответствующие элементы вместе
- Поскольку порядок (размеры) матриц не обязательно должны быть одинаковыми, может не быть соответствующие элементы умножаются вместе.
- Умножьте строки первого столбца на столбцы второго и сложите.
Нет матричного деления
- Не существует определенного процесса деления матрицы на другую матрицу.
- Матрица может быть разделена скаляром.
Идентификационная матрица
- Квадратная матрица
- На главной диагонали
- нули везде
- Обозначается I. Если указан нижний индекс, это порядок единичной матрицы.
- I — мультипликативное тождество для матриц
- Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
- Умножение на единичную матрицу коммутативно, хотя порядок единицы может изменение
Идентификационная матрица размера 2
Идентификационная матрица размера 3
| I 3 = | 1 | 0 | 0 | ||
| 0 | 1 | 0 | |||
| 0 | 0 | 1 |
Свойства матриц
| Имущество | Пример |
|---|---|
| Коммутативность сложения | А + В = В + А |
| Ассоциативность добавления | А + (В + С) = (А + В) + С |
| Ассоциативность скалярного умножения | (кд) А = с (дА) |
| Скалярная идентификация | 1А = А (1) = А |
| Распределительный | c (A + B) = cA + cB |
| Распределительный | (с + г) А = сА + дА |
| Идентификатор добавки | А + О = О + А = А |
| Ассоциативность умножения | А (ВС) = (АВ) С |
| Распределительный левый | А (В + С) = АВ + АС |
| Правый распределитель | (А + В) С = АС + ВС |
| Скалярная ассоциативность / коммутативность | c (AB) = (cA) B = A (cB) = (AB) c |
| Мультипликативная идентичность | IA = AI = A |
Свойства вещественных чисел, не являющиеся свойствами матриц
Коммутативность умножения
- Вы не можете изменить порядок задачи умножения и ожидать получить то же самое продукт.AB ≠ BA
- Вы должны быть осторожны при разложении общих множителей, чтобы убедиться, что они одно и тоже боковая сторона. AX + BX = (A + B) X и XA + XB = X (A + B), но AX + XB не учитывается.
Свойство нулевого продукта
- Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.
Мультипликативное свойство равенства
- Если A = B, то AC = BC. Это свойство все еще верно, но обратное не обязательно верно.То, что AC = BC, не означает, что A = B.
- Поскольку умножение матриц не коммутативно, вы должны умножение до или после умножения с обеих сторон уравнения. То есть, если A = B, тогда AC = BC или CA = CB, но AC ≠ CB.
Нет матричного деления
- Надо умножить на обратную матрицу
Оценка функции с помощью матрицы
Рассмотрим функцию f (x) = x 2 — 4x + 3 и матрицу A
Первоначальная попытка оценить f (A) будет заключаться в замене каждого x с A, чтобы получить f (A) = A 2 — 4A + 3.Есть одно небольшое проблема, однако. Константа 3 равна не матрица, и вы не можете добавить матрицы и скаляры вместе. Итак, умножаем константа матрицей идентичности.
f (A) = A 2 — 4A + 3I.
Оцените каждый член функции, а затем сложите их.
| А 2 = | 1 | 2 | * | 1 | 2 | = | 7 | 10 | ||||||
| 3 | 4 | 3 | 4 | 15 | 22 |
| -4 А = -4 | 1 | 2 | = | -4 | -8 | ||||
| 3 | 4 | -12 | -16 |
| 3I = 3 | 1 | 0 | = | 3 | 0 | ||||
| 0 | 1 | 0 | 3 |
| f (А) = | 7 | 10 | + | -4 | -8 | + | 3 | 0 | = | 6 | 2 | ||||||||
| 15 | 22 | -12 | -16 | 0 | 3 | 3 | 9 |
Факторинговые выражения
Показаны некоторые примеры факторинга.Упрощайте и решайте как обычно, но помните эта матрица умножение не коммутативно и нет матричного деления.
2X + 3X = 5X
AX + BX = (A + B) X
ХА + ХВ = Х (А + В)
AX + 5X = (A + 5I) X
AX + XB не учитывает
Решение уравнений
Систему линейных уравнений можно записать как AX = B, где A — коэффициент матрица, X — вектор-столбец, содержащий переменные, а B — правая боковая сторона. В следующем разделе мы узнаем, как решить это уравнение.
Если существует более одной системы линейных уравнений с одним и тем же коэффициентом матрица, то вы можете расширить матрицу B, чтобы она содержала более одного столбца. Ставить каждую правую часть в свой столбец.
Умножение матриц
Умножение матриц включает суммирование произведения. Это уместно там, где вы нужно умножайте вещи вместе, а затем Добавлять. Например, умножение количества единиц на стоимость единицы будет дать общую Стоимость.
Единицы по продукту найдены путем выполнения модульного анализа на матрицы.Этикетки для продукта — это этикетки строк первого матрица и метки столбцов вторая матрица.
Добавление и матрицы вычитания Матрица сложена справедливо простой, и делается по входу.
Мне нужно добавить пары записей, а затем упростите для окончательного ответа: Итак, ответ: До сих пор вы были возможность добавлять любые две вещи, которые вам нравятся: числа, переменные, уравнения, и так далее.Но сложение не всегда работает с матрицами.
Поскольку матрицы складываются по умолчанию, я должен добавить 1 и 4, 2 и 5, 0 и 7, и 3 и 8. Но что мне добавить к 6 а к 9? В первой матрице нет соответствующих записей, которые можно добавить к этим элементам второй матрицы.Итак, ответ: Я не могу добавить эти матрицы, потому что они не одного размера . Это всегда так: Чтобы можно было добавить две матрицы, они должны быть одинакового размера. Если они разного размера (если у них разные «размеры»), тогда сложение «не определено» (не делает математических смысл). Вычитательные работы начальные, тоже.Авторские права Элизабет Стапель 2003-2011 Все права защищены
А и B одинакового размера, по 2 3 матрицы, так что я могу вычесть, рабочий начальный: Однако A и C не одинакового размера, так как A это 2 3 и C равно 2 2.Таким образом, это вычитание не определено. А С не определено, т.к. A и C не одинакового размера. Матричное сложение и вычитание, где определено (то есть, где матрицы имеют одинаковый размер, поэтому добавление и вычитание имеет смысл), можно превратить в домашние задания.
Сначала я упрощу левую часть немного, добавив пошагово: Поскольку матричное равенство работает по входам, Я могу сравнивать записи и составлять простые уравнения, которые я могу решить.В этом случае 1,2-записи скажите мне, что x + 6 = 7, а 2,1-элементы скажи мне, что 2 г 3 = 5. Решая, я получаю: х + 6 = 7 2 y 3 = 5 Верх | Вернуться к индексу
|
Сложение и вычитание матриц и умножение матрицы на константу
При умножении матрицы на скаляр (константа или число), а также при сложении и вычитании матриц операции выполняются построчно.Давайте рассмотрим каждую операцию отдельно, чтобы увидеть, как это работает.
Содержание
- Добавление матриц
- Матрицы вычитания
- Умножение матрицы на константу (скалярное умножение)
- Сочетание сложения, вычитания и скалярного умножения
реклама
Добавление матриц
Чтобы добавить две матрицы, добавьте соответствующие записи, как показано ниже. Обратите внимание, что вам нужно, чтобы матрицы были одинакового размера, чтобы это имело смысл.
Если матрицы разного размера, сложение не определено.
Матрицы вычитания
Вычитание матриц работает точно так же. Вы можете вычесть запись за записью.
Как и в случае сложения, это не было бы определено, если бы матрицы были разных размеров. В этой ситуации ваш ответ будет просто «не определен».
Умножение матрицы на константу (скалярное умножение)
Умножение матрицы на константу или число (иногда называемое скаляром) всегда определяется независимо от размера матрицы.Вам просто нужно убедиться, что каждая запись в матрице умножена на число.
Объединение операций
В некоторых вопросах вас могут попросить объединить сложение, вычитание и умножение на константу. Здесь мы рассмотрим несколько примеров, чтобы убедиться, что вы знаете, как это сделать.
Пример
Найдите \ (- 2A + B \) для:
\ (A = \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] \) и \ (B = \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \)
Не забудьте умножить каждую запись на константу и работать с записью при сложении.
\ (\ begin {align} -2A + B & = 2 \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -2 \ times -4 & -2 \ times 1 \\ -2 \ times 2 & -2 \ times -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 & -2 \\ -4 & 4 \\ \ end {array} \ right] + \ left [\ begin { массив} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 + 9 & -2 + (-4) \\ -4 + 0 & 4 + 8 \\ \ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 17 & -6 \\ -4 & 12 \\ \ end {array} \ right]} \ end {align} \)
Это также работает, когда у вас более двух матриц, как показано в следующем примере.
Пример
Найдите \ (A — 3B + 2C \) для:
\ (A = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] \), \ (B = \ left [\ begin {array} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] \) и \ (C = \ left [\ begin {array} { cc} 5 & 2 \\ 3 & 0 \\ \ end {array} \ right] \)
\ (\ begin {align} A — 3B + 2C & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — 3 \ left [\ begin {массив} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] + 2 \ left [\ begin {array} {cc} 5 & 2 \\ 3 & 0 \\ \ end { массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — \ left [\ begin {array} {cc} 3 \ times2 и 3 \ times1 \\ 3 \ times1 & 3 \ times4 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 2 \ times5 & 2 \ times2 \\ 2 \ times3 & 2 \ times0 \\ \ end {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — \ left [\ begin {array} {cc} 6 & 3 \\ 3 & 12 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 10 & 4 \\ 6 & 0 \\ \ конец {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 — 6 + 10 & 1 — 3 + 4 \\ 0 — 3 + 6 & 0 — 12 + 0 \\ \ end {массив} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 5 & 2 \\ 3 & — 12 \\ \ end {array} \ right]} \ end {align} \ )
Сводка
Запомните следующее для операций с матрицами:
- Для сложения или вычитания переходите ввод за вводом.

 matrix('1 2; 3 4')
>>> L = 1 * A
>>> R = A
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]]
matrix('1 2; 3 4')
>>> L = 1 * A
>>> R = A
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]] matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('1 7; 9 3')
>>> L = A + (B + C)
>>> R = (A + B) + C
>>> print(L)
[[ 7 15]
[19 15]]
>>> print(R)
[[ 7 15]
[19 15]]
matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> C = np.matrix('1 7; 9 3')
>>> L = A + (B + C)
>>> R = (A + B) + C
>>> print(L)
[[ 7 15]
[19 15]]
>>> print(R)
[[ 7 15]
[19 15]] dot(B + C)
>>> R = A.dot(B) + A.dot(C)
>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]]
dot(B + C)
>>> R = A.dot(B) + A.dot(C)
>>> print(L)
[[35 42]
[77 94]]
>>> print(R)
[[35 42]
[77 94]] matrix('1 2; 3 4')
>>> E = np.matrix('1 0; 0 1')
>>> L = E.dot(A)
>>> R = A.dot(E)
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]]
>>> print(A)
[[1 2]
[3 4]]
matrix('1 2; 3 4')
>>> E = np.matrix('1 0; 0 1')
>>> L = E.dot(A)
>>> R = A.dot(E)
>>> print(L)
[[1 2]
[3 4]]
>>> print(R)
[[1 2]
[3 4]]
>>> print(A)
[[1 2]
[3 4]]