Корень кубический из числа: Кубический корень | Онлайн калькулятор

Содержание

Кубический корень. Извлечение кубического корня

Главная
Калькуляторы
Математика
Арифметика
Кубический корень. Извлечение кубического корня

Кубический корень из a, обозначающийся как ³√a или как a^1/3 — решение уравнения x³ = a (обычно подразумеваются вещественные решения).

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.

Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.

Алгоритм извлечения кубического корня

Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.

Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.

Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a²× x+30× a × x²+x³ такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
Запишите под нижним числом результат вычисления по формуле 300 × a² × x+30 × a × x²+x³ и произведите вычитание. Перейдите к пункту 3.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Простые и не очень способы того, как вычислить кубический корень :: SYL.ru

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «аⁿ».

В-третьих, для них справедливы все действия со степенями.

Их можно перемножать. Тогда показатели степеней складываются.
Корни можно разделить. Степени нужно будет вычесть.
И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

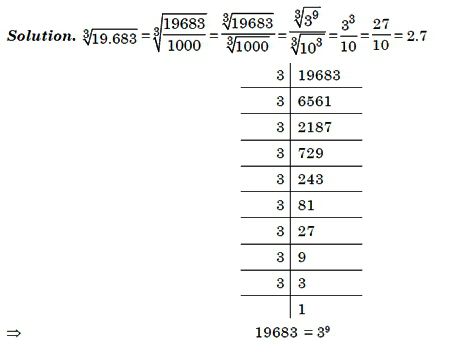
Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

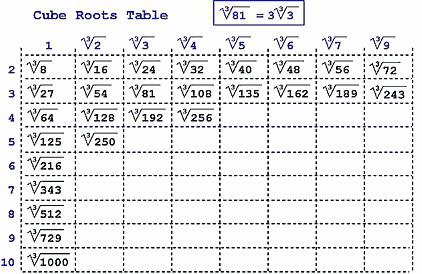
В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
Выполнить вычитание.
К остатку приписать первую группу цифр после запятой.
В черновике записать выражение: а² * 300 * х + а * 30 * х² + х³. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

15> 2³, значит под целой частью записана 8, а над корнем 2.
После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
а = 2. Поэтому: 2² * 300 * х +2 * 30 * х² + х³ < 7000, или 1200 х + 60 х² + х³< 7000.
Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
Вычитание дает 1176, а над корнем появилось число 4.
Приписать к остатку три нуля.
а = 24. Тогда 172800 х + 720 х² + х³< 1176000.
х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
Снова приписать нули.
а = 246. Неравенство получается таким: 18154800х + 7380х² + х³< 113064000.
х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.

Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.

Необычный способ извлечения кубического корня

Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.

К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.

Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.

Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.

Кубический корень — Википедия

Материал из Википедии — свободной энциклопедии

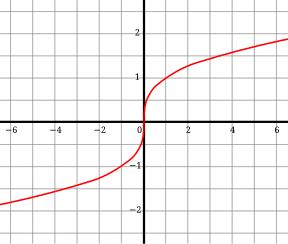График функции y = x 3 {\displaystyle y={\sqrt[{3}]{x}}}

Куби́ческий ко́рень из a, обозначающийся как a 3 {\displaystyle {\sqrt[{3}]{a}}} или как a^1/3 — это число x , {\displaystyle x,} куб которого равен a . {\displaystyle a.} Другими словами, это решение уравнения x 3 = a {\displaystyle x^{3}=a} (обычно подразумеваются вещественные решения).

Вещественный корень

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):

− x 3 = − x 3 {\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}

Комплексный корень

Кубический корень из комплексного числа (из любого числа) c {\displaystyle c} имеет ровно три значения (частный случай свойства корня n-ой степени):

c 3 = | c | 3 ( cos ⁡ ϕ + 2 k π 3 + i sin ⁡ ϕ + 2 k π 3 ) , k = 0 , 1 , 2 , ϕ = arg ⁡ c . {\displaystyle {\sqrt[{3}]{c}}={\sqrt[{3}]{\left|c\right|}}\left(\cos {\frac {\phi +2k\pi }{3}}+i\sin {\frac {\phi +2k\pi }{3}}\right),\quad k=0,1,2,\quad \phi =\arg {c}.}

Здесь под | c | 3 {\displaystyle {\sqrt[{3}]{\left|c\right|}}} понимается арифметический корень из положительного числа | c | . {\displaystyle \left|c\right|.}

В частности

1 3 = { 1 cos ⁡ 2 π 3 + i sin ⁡ 2 π 3 = − 1 2 + i 3 2 cos ⁡ 2 π 3 − i sin ⁡ 2 π 3 = − 1 2 − i 3 2 {\displaystyle {\sqrt[{3}]{1}}={\begin{cases}1\\\cos {\frac {2\pi }{3}}+i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {2\pi }{3}}-i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}

− 1 3 = { − 1 cos ⁡ π 3 + i sin ⁡ π 3 = 1 2 + i 3 2 cos ⁡ π 3 − i sin ⁡ π 3 = 1 2 − i 3 2 {\displaystyle {\sqrt[{3}]{-1}}={\begin{cases}-1\\\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}={\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {\pi }{3}}-i\sin {\frac {\pi }{3}}={\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}

Два комплексных значения кубического корня получаются из вещественных по формуле:

x 3 2 , 3 = x 3 ( − 1 2 ± i 3 2 ) . {\displaystyle {\sqrt[{3}]{x}}_{2,3}={\sqrt[{3}]{x}}\left(-{\frac {1}{2}}\pm i{\frac {\sqrt {3}}{2}}\right).}

Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.

Показательная форма

Корень из комплексных чисел можно определить так:

x 1 / 3 = exp ⁡ ( 1 3 ln ⁡ x ) {\displaystyle x^{1/3}=\exp({\tfrac {1}{3}}\ln {x})}

Где ln — главная ветвь натурального логарифма.

Если представить x {\displaystyle x} как

x = r exp ⁡ ( i θ ) {\displaystyle x=r\exp(i\theta )}

то формула кубического числа такова:

x 3 = r 3 exp ⁡ ( 1 3 i θ ) . {\displaystyle {\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp({\tfrac {1}{3}}i\theta ).}

Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если x {\displaystyle x} комплексное, то − 8 3 {\displaystyle {\sqrt[{3}]{-8}}} будет обозначать не − 2 {\displaystyle -2} , а будет 1 + i 3 . {\displaystyle 1+i{\sqrt {3}}.}

Интересные факты

Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.

При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.

Способы вычисления

Столбиком

Алгоритм таков:

Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
Далее найденный промежуточный ответ заменим буквой a {\displaystyle a} . Вычислите по формуле 300 × a 2 × x + 30 × a × x 2 + x 3 {\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} такое число x {\displaystyle x} , что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x {\displaystyle x} справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
Запишите под нижним числом результат вычисления по формуле 300 × a 2 × x + 30 × a × x 2 + x 3 {\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} и произведите вычитание. Перейдите к пункту 3.

См. также

Литература

Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.