Объем как обозначается – Какой буквой обозначается объём?

Объем, Площадь поверхности, формулы объема

Стандартное обозначение объема есть V. Этим мы измеряем количество (наример, воды), которая может заполнить фигуру.
Только пространственные фигуры имеют объем. Например, треугольники, квадраты не имеют объема, но шар имеет объем (потому что он может быть заполнен чем-то, например водой).

Прямоугольный параллелепипед

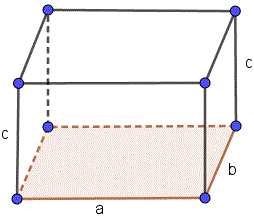
Прямоугольный параллелепипед это фигура, все стороны которой — прямоугольники.
Если длины стороны прямоугольника в основе есть a и b и третье ребро c
тогда формула объема есть:

$V = a \cdot b \cdot c$

Площадь поверхности:

S = $2(a \cdot b + a \cdot c + b \cdot c)$

Куб

Куб есть параллелепипедом, все ребра (стороны) которого равны.

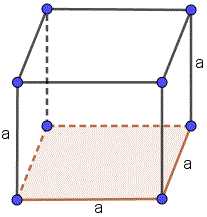
Если длина стороны куба равна a, тогда формула объема:

$V = a.a.a = a^3$

Площадь поверхности:

$S = 6a \cdot a = 6a^2$

Параллелепипед

Параллелепипед это фигура, все стороны которой — параллелограммы. Если площадь основы равна S и высота параллелепипеда равны h,
то формула объема есть:

$V = S \cdot h$

Пирамида

Пирамида это фигура, основа которой есть треугольник, параллелограмм (квадрат, прямоугольник) или другая фигура с n-углами и треугольными сторонами.
Если площадь основы есть S и высота пирамиды есть h,
тогда формула ее объема есть:

$V = \frac{1}{3} \cdot S \cdot h$

Правильный тетраэдр

$V = \frac{\sqrt{2}\cdot a^3}{12}$

Площадь поверхности:

$S = \sqrt{3}\cdot a^2$

Прямой круговой конус

Конус это фигура с основанием в виде окружности и имеющая одну вершину, как у пирамиды.
Если площадь основы есть S и длиныа стороны конуса равна h,
то формула объема есть:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$

Формула площади боковой поверхности конуса:

$S=\pi\cdot r \cdot l$

Формула площади полной поверхности конуса (то есть сумма площадей боковой поверхности и основания):

$S=\pi\cdot r(r + l)$

Сфера

Сфера есть шар.
Она имеет радиус — расстояние от центральной точки сферы к поверхности. Если длина радиуса есть R, то формула объема есть:

$V = \frac{4}{3} \cdot \pi \cdot r^3$

Площадь поверхности:

$S = 4\cdot\pi\cdot r^2$

Цилиндр

Цилиндр это фигура с двумя параллельными окружностями.
Если ралиус основы равен r и высота (расстояние между основами) цилиндра есть h,
то его объем вычисляется по формуле:

$V = \pi \cdot r^2 \cdot h$

Прямой круговой цилиндр

Объём

$V = \pi \cdot r^2 \cdot h$

Площадь боковой поверхности:

$S = 2\cdot\pi\cdot r \cdot h$

Площадь полной поверхности:

$S = 2\cdot\pi\cdot r(h + r)$

---

Тест: объём и площадь поверхности

www.math10.com

Объём — это… Что такое Объём?

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Синонимом вместимости частично является ёмкость, но словом ёмкость обозначают также сосуды и качественную характеристику конденсаторов.

Принятые единицы измерения — в СИ и производных от неё — кубический метр, кубический сантиметр, литр (кубический дециметр) и т. д. Внесистемные — галлон, баррель.

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

Вычисление объёма

Математически

В общем случае математически объём тела вычисляется по следующей интегральной формуле:

,

где — характеристическая функция геометрического образа тела.

Для ряда тел с простой формой более удобным является использование специальных формул. Например, объём куба с длиной стороны, равной a, равен .

Через плотность

Объём находится по формуле:

Единицы объёма жидкости

• 1 л = 1,76 пинты = 0,23 галлона

Английские внесистемные

Американские внесистемные

• 1 американский галлон = 3,785 л (Распространён в США)

Античные внесистемные

Древнееврейские

• Эйфа = 24 883 см³ (Эйфа́)
• Омер = ¹/₁₀ эйфы
• Гин = 4147 см³ ^[1]
• Кав = 1382 см³

Русские внесистемные

Единицы сыпучих веществ

Английские внесистемные

Русские внесистемные

Молярный объём

Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:

Vm = V/n

Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль

• Единица: м³/mol; м³/моль

Прочие единицы измерения

• 1 дюйм кубический = 1,63871·10⁻⁵ м³
• 1 литр = 1·10⁻³ м³
• Лямбда 1 λ = 1·10⁻⁹ м³
• 1 унция = 2,841·10⁻⁵ м³ (анг.)
• 1 унция = 2,957·10⁻⁵ м³ (амер.)
• 1 фут кубический = 2,83168·10⁻² м³
• 1 ярд кубический = 0,76455 м³
• 1 стер = 1 м³
• 1 ае кубическая =3,348071936e+40 км³
• 1 км кубический = 1 000 000 000 м³
• 1 световой год кубический = 8,46590536e+38 км³
• 1 пк кубический = 2,9379989989648103256576e+40 км³
• 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³

Примечания

Литература

dic.academic.ru

Как обозначается объем — Какой буквой обозначается объем???? — 22 ответа



Объем как обозначается

В разделе Домашние задания на вопрос Какой буквой обозначается объем???? заданный автором Особинка лучший ответ это

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Какой буквой обозначается объем????

Ответ от спроситься[новичек]
вроде «V»

Ответ от Dani[гуру]
буквой V

Ответ от Евровидение[гуру]
V объем

Ответ от Аманжолов Тимур[гуру]
V — volume (объем).

Ответ от Spirittrap[гуру]
буквой V

Ответ от Ѝльвина Зайнулина[новичек]
если V объём то какой же буквой скорость, время, расстояние?

Ответ от Jack[новичек]
v-в виде информатики и физики обозначает объём а в математике скорость

Ответ от Yasmina Shukurov[новичек]
v

Ответ от Вареник[новичек]
v

Ответ от Павел Перстнев[активный]
V

Ответ от Лёша коновалов[новичек]
Объём обозначается буквой V

Ответ от Даниил Тихомиров[новичек]
V

Ответ от Максим Максим[новичек]
V обьем

Ответ от Матвей Шмелёв[новичек]
v

Ответ от Андрей 2255446622554466[новичек]
v

Ответ от Александр Коршунов[новичек]
V– чаще всего!

Ответ от Gulziya bizhanova[новичек]
Объем обозначаетсЯ буквой-V

Ответ от Кирилл Грехов[новичек]
v

Ответ от Ёаидселим Абуев[новичек]
буква V

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Объём на Википедии
Посмотрите статью на википедии про Объём

Оливер Стив на Википедии
Посмотрите статью на википедии про Оливер Стив

Оливер и компания на Википедии
Посмотрите статью на википедии про Оливер и компания

Таблица математических символов на Википедии
Посмотрите статью на википедии про Таблица математических символов

 

Ответить на вопрос:

22oa.ru

No related posts.