Умножение и деление десятичных дробей примеры для решения 6 класс: Действия с десятичными дробями – Тренажёр по математике (6 класс) по теме: Тренажер для устного счета «Все действия с десятичными дробями» 6 класс

Тренажёр по математике (6 класс) по теме: Тренажер для устного счета «Все действия с десятичными дробями» 6 класс

1	(3,5 : 7 + 2,5) : 2 – 0,7	0,8	2	(4,2 : 0,6 – 3) : 2+ 1,2 : 3	2,4
3	1,5 + 2 x (0,5 + 0,7) – 2,1	1,8	4	(2,7x 3 – 0,4) x 6 – 1,7	1,3
5	(4,4 – 2,1) x 5 – 3 : 2	10	6	(3,7 + 6,3) : 4 + 7,5 : 5	4
7	(8,1 : 9 + 0,1) – (0,7 x 3 – 2)	0,9	8	(16,4 :2 : 9 + 0,1) : 4	0,25
9	((15,2 – 3,4): 2 + 4,1) : 2,5	4	10	(6,4 : 0,8 – 3,4):2 – 1,7	0,6
11	(10 – 5,5) x 2 – 1,5 x 2 +10	16	12	7,5 x 3 — 2,5 x (40,5- 30,5) : 5	17,5
13	(10 – 5,5) x 2 + 1,5 x 2:1,5	11	14	(0,8 : 0,2+ 1,5) x 2 – 0, 47	10,53
15	(1, 5 + 0,2 x 5) + 7,5	10	16	(16,2 :2 : 9 + 0,1) : 4	0,25
17	(2,7 x 2 + 4,6) : 2,5 – 0,125	3,875	18	(5 – 3,5) x 4 – 1,5 : 3	9,7
19	(12,3 – 2,3): 4 – 1,5 : 3	2	20	(7,8 + 3,2) : 2 – 0,5 x 6	2,5
21	(4,9 : 7+ 0,3)x 5,8 – 1,3	4,5	22	16 – (2,5 + 4,5) : 2	12,5
23	(4,4 : 0,2 – 11)x 0,7 + 2,3	10	24	(5,6 x 2+ 3,8): 2 + 7,3	14,8
25	(2,1 x 3 – 2,3): 0,2 + 1,25	21,25	26	(3,6 + 0,4) : 10 + 0,6	1
27	(10,2 : 2 + 4,9) x 3 – 12,3	17,7	28	5,6 – (4,8 : 6 + 0,2) x 2,5	3,1
29	(4,2 x 2 – 5,4) : 0,2+ 7,3	22,3	30	(2,1 :7 +0,4 x 2) x 3 – 1,2	2,1
31	(7,2 + 0,8): 8 +7,13	8,13	32	(20,8 – 15,8): 2 x 4+ 12,17	22,17
33	(42,6 : 2 + 8,8 : 4) — 3,5	20	34	(16,24 : 4 – 2,06) x 7,2 + 0,8	15,2
35	(5,2 : 2 + 3,4) x 1,3 – 3,9	3,9	36	(7,5 + 13,5) : 2 – 7	3,5
37	24,3 : 3 – 2,7 : 9	7,8	38	1,06 : 2 + 0,47 :0,1	5,23
39	(3,6 : 0,4 – 2,3)x 2 + 6,6	20	40	(1,2 x 3 + 6,4) : 2,5 – 1,7	2,3
41	(1,2 : 0,4 – 1,2) : 3 + 0,4	1	42	(27 : 0,9 – 20) x 3,5 + 4,7	39,7
43	(3,5 : 0,5 – 0,2) : 2 + 5,9	9,3	44	2,8 : 0,4 + 2,6	9,6
45	((5,5 x 2 — 3,5) + 2,5) : 4	2,5	46	(5,4 : 0,6 + 2,7) x 2 – 3,4	20
47	2,4 x 2 + 1,1 x 2	7	48	8,1 : 0,9 + 2,5 : 0,5	14
49	2,2 x 5 – 3,6 : 4	10,1	50	(4,2 : 2 + 0,9) x 3 – 4,27	4,73
51	(3,6 x 2 + 3,2 : 2)x 3 – 6,4	20	52	(6,04 x 2 – 0,08) : 3 + 5,72	9,72
53	(2,7 x 5 + 2,5) – 4,3	11,7	54	(7,8 : 2 + 0,5) x 3 – 3,2	10
55	3,8 : 2 – (0,5 x 2 — 0,3)	1,2	56	5,5 : 1,1 + 3,6 x 2	12,2
57	10 – 0,7 x 6 + 2,6 : 2	6,7	58	(8,6 : 0,2 _ 30) : 4 + 7,7	10,95
59	(2,2 + 0,5) : 3 — 0,3	0,6	60	(44,6 : 2 + 0,2) x 3 – 27,5	40
61	(1,4 : 0,7 — 1,6) + 2,4 x 2	5,2	62	(2,6 x 2 – 0,2) x 3 + 4,7	19,7
63	(12,4 : 2 + 0,8): 2 – 3	0,5	64	32,8 : 4 + 2,8 x 3	16,6
65	(15 : 2 – 3,5) x 3,3 + 7,8	21	66	(5,5 x 3 + 3,5) – 4,6	15,4
67	14,7 : 7 – 3,4 : 2	0,4	68	48,6 : 3 + 2,7 x 3	24,3

Действия с десятичными дробями.

Фарафонова Наталия Игоревна

После прохождения темы «Действия с десятичными дробями» для отработки навыка счета и проверки усвоения материала можно провести индивидуальную работу с учащимися по карточкам. Каждый учащийся должен без ошибок выполнить задания по всем действиям. По каждому действию представлено много вариантов, это дает возможность каждому учащемуся несколько раз решить задание по каждому действию с десятичными дробями и добиться безошибочного результата или выполнить задание с минимальным количеством ошибок. Так как каждый учащийся выполняет индивидуальное задание, учитель имеет возможность, по мере представления ему выполненных заданий, с каждым учеником обсудить их персонально. Если ученик допустил ошибки, то учитель исправляет их, и предлагает сделать задание из другого варианта. Так, до тех пор, пока учащийся не выполнит все задание или его большую часть без ошибок. Карточки лучше делать на цветной бумаге.

На последнем этапе работы, можно предложить решить пример, содержащий несколько действий.

За каждый безошибочно выполненный вариант, независимо от того, с какой попытки было верно выполнено задание, учащимся можно поставить отличную отметку, можно выставить среднюю оценку, после выполнения всей работы, на усмотрение учителя.

 

 

Сложение десятичных дробей.

 

 

1 вариант

7,468 + 2,85

9,6 + 0,837

38,64 + 8,4

3,9 + 26,117

 

2 вариант

19,45 + 34,8

4,9 + 0,716

75,86 + 4,2

5,6 + 44,408

 

3 вариант

24,38 + 7,9

6,5 + 0,952

48,59 + 1,8

35,906 + 2,8

 

4 вариант

7,6 + 319,75

888,99 + 4,5

64,15 + 18,9

4,5 + 0,738

 

5 вариант

7,62 + 8,9

25,38 + 0,09

12,842 + 8,6

412 + 78,83

 

6 вариант

70,7 + 3,8645

3,65 + 0,89

61,22 + 31.719

12,842 + 8,6

 

Ответы: 1 вариант: 10,318; 10,437; 47,04; 30,017;

2 вариант: 54,25; 5,616; 80,06; 50,008;

3 вариант: 32,28; 7,452; 50,19; 38,706;

4 вариант: 327,35; 893,49; 83,05; 5,238;

5 вариант: 16,52; 25,47; 21,442; 490,83;

6 вариант: 74,5645; 4,54; 92,939; 21,442;

 

 

 

Вычитание десятичных дробей.

 

 

1 вариант

26,38 – 9,69

41,12 – 8,6

5,2 – 3,445

7 – 0,346

 

2 вариант

47,62 – 8,78

54,06 – 9,1

7,1 – 6,346

3 — 1,551

 

3 вариант

50,41 – 9,62

72,03 – 6,3

9,2 – 5,453

4 – 2,662

 

4 вариант

60,01 – 8,364

123,61 – 69,8

8,7 – 4,915

10 – 3,817

 

5 вариант

6,52 – 3,8

7,41 – 0,758

67,351 – 9,7

22 – 0,618

 

6 вариант

4,5 – 0,496

61,3 – 20,3268

24,7 – 15,276

50 – 2,38

 

Ответы: 1 вариант: 16,69; 32,52; 1,755; 6,654;

2 вариант: 38,84; 44,96; 0,754; 1,449;

3 вариант: 40,79; 65,73; 3,747; 1,338;

4 вариант: 51,646; 53,81; 3,785; 6,183;

5 вариант: 2,72; 6,652; 57,651; 21,382;

6 вариант: 4,004; 40,9732; 9,424; 47,62;

 

 

 

Умножение десятичных дробей.

 

 

1 вариант

7,4 · 3,5

20,2 · 3,04

0,68 · 0,65

2,5 · 840

 

 

2 вариант

2,8 · 9,7

6,05 · 7,08

0,024 · 0,35

560 · 3,4

 

3 вариант

6,8 · 5,9

6,06 · 8,05

0,65 · 0,014

720 · 4,6

 

4 вариант

34,7 · 8,4

9,06 · 7,08

0,038 · 0,29

3,6 · 540

 

5 вариант

62,4 · 2,5

0,038 · 9

1,8 · 0,009

4,125 · 0,16

 

6 вариант

0,28 · 45

20,6 · 30,5

2,3 · 0,0024

0,0012 · 0,73

 

7 вариант

68 · 0,15

0,08 · 0,012

1,4 · 1,04

0,32 · 2,125

 

8 вариант

4,125 · 0,16

0,0012 · 0,73

1,4 · 1,04

720 · 4,6

 

 

Ответы: 1 вариант: 25,9; 61,408; 0,442; 2100;

2 вариант: 27,16; 42,834; 0,0084; 1904;

3 вариант: 40,12; 48,783; 0,0091; 3312;

4 вариант: 291,48; 64,1448; 0,01102; 1944;

5 вариант: 156; 0,342; 0,0162; 0,66;

6 вариант: 12,6; 628,3; 0,00552; 0,000876;

7 вариант: 10,2; 0,00096; 1,456; 0,68;

8 вариант: 0,66; 0,000876; 1,456; 3312;

 

 

Деление десятичной дроби на натуральное число.

 

 

1 вариант

62,5 : 25

0,5 : 25

9,6 : 12

1,08 : 8

 

2 вариант

0,28 : 7

0,2 : 4

16,9 : 13

22,5 : 15

 

3 вариант

0,75 : 15

0,7 : 35

1,6 : 8

0,72 : 6

 

4 вариант

2,4 : 6

1,5 : 75

0,12 : 4

1,69 : 13

 

5 вариант

3,5 : 175

1,8 : 24

10,125 : 9

0,48 : 16

 

6 вариант

0,35 : 7

1,2 : 3

0,2 : 5

7,2 : 144

 

7 вариант

151,2 : 63

4,8 : 32

0,7 : 25

2,3 : 40

 

8 вариант

397,8 : 78

5,2 : 65

0,9 : 750

3,4 : 80

 

9 вариант

478,8 : 84

7,3 : 4

0,6 : 750

5,7 : 80

 

10 вариант

699,2 : 92

1,8 : 144

0,7 : 875

6,3 : 24

 

Ответы: 1 вариант: 2,5; 0,02; 0,8; 0,135;

2 вариант: 0,04; 0,05; 1,3; 1,5;

3 вариант: 0,05; 0,02; 0,2; 0,12;

4 вариант: 0,4; 0,02; 0,03; 0,13;

5 вариант: 0,02; 0,075; 1,125; 0,03;

6 вариант: 0,05; 0,4; 0,04; 0,05;

7 вариант: 2,4; 0,15; 0,28; 0,0575;

8 вариант: 5,1; 0,08; 0,0012; 0,0425;

9 вариант: 5,7; 1,825; 0,0008; 0,07125;

10 вариант: 7,6; 0,0125; 0,0008; 0,2625;

 

 

 

Деление на десятичную дробь.

 

 

1 вариант

32 : 1,25

54 : 12,5

6 : 125

 

2 вариант

50,02 : 6,1

34,2 : 9,5

67,6 : 6,5

 

3 вариант

2,8036 : 0,4

3,1 : 0,025

0,0008 : 0,16

 

4 вариант

4 : 32

303 : 75

687,4 : 10

1,59 : 100

 

5 вариант

5 : 16

336 : 35

412,5 : 10

24,3 : 100

 

6 вариант

41,82 : 6,8

73,44 : 3,6

7,2 : 0,045

32,89 : 4,6

 

Ответы: 1 вариант: 25,6; 4,32; 0,048;

2 вариант: 8,2; 3,6; 10,4;

3 вариант: 7,009; 124; 0,005;

4 вариант: 0,125; 4,04; 68,74; 0,0159;

5 вариант: 0,3125; 9,6; 41,25; 0,243;

6 вариант: 6,15; 20,4; 160; 7,15;

 

 

Совместные действия с десятичными дробями.

 

 

 

1. 824,72 – 475 : (0,071 + 0,929) + 13,8

2. (7,351 + 12,649) ·105 – 95,48 – 4,52

3. (3,82 – 1,084 + 12,264)·(4,27 + 1,083 – 3,353) + 83

4. 278 – 16,7 – (15,75 + 24,328 + 39,2)

5. 57,18 ·42 – 74,1 : 13 + 21,35 : 7

6. (18,8 : 16 + 9,86 ·3) ·40 – 12,73

7. (2 – 0,25 ·0,8) : (0,16 : 0,5 – 0,02)

8. (3,625 + 0,25 + 2,75) : (28,75 + 92,25 – 15) : 0,0625

 

 

Ответы: 1) 363,52; 2) 2000; 3) 113; 4) 182,022; 5) 2398,91; 6) 1217,47; 7) 6; 8) 1.

Умножение и деление десятичных дробей. Видеоурок. Математика 5 Класс

Что такое запись числа в десятичной системе счисления? Например, запись числа 2536?

Это краткая запись суммы:

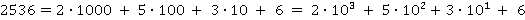
Десятичная дробь – это тоже краткая запись суммы:

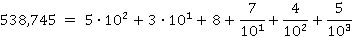
С помощью запятой отделяется целая часть от дробной. Умножение или деление на 10, 100, 0,1, 0,01 и так далее не меняет цифры в записи, а лишь сдвигает запятую.

Напоминание:

 

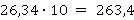
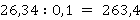
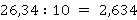
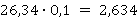
Кроме того, стоит помнить, что любую десятичную дробь можно представить в виде произведения:

 

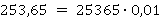
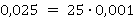
В предыдущем разделе были повторены все необходимые правила для того, чтобы умножать десятичную дробь на целое число или на другую десятичную дробь.

Пример: а) 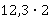; б)

а)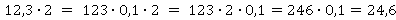

б)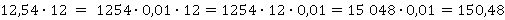

Каждый раз запятая была убрана, но информация о ней сохранялась с помощью множителя 0,1, 0,01 и так далее. Потом было выполнено умножение целых чисел. И снова запятая возвращалась на место, учитывая множитель.

 

Чтобы умножить дробь на целое число, нужно умножать, не обращая внимания на запятую, затем в ответе вернуть запятую на место, то есть отделить ею столько же цифр в дробной части, сколько было в исходном числе.

Пример: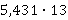

Выполняя умножение, не стоит обращать внимания на запятую.

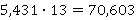
Затем необходимо поставить запятую так, чтобы в дробной части получилось, как и раньше, 3 цифры.

 

Для умножения двух десятичных дробей принцип абсолютно такой же.

Правило

Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая внимания на запятые, затем в ответе отделить запятой столько цифр, сколько их было у обоих чисел вместе.

 

Пример 1

Сначала необходимо переписать каждую дробь в виде целого числа и вспомогательного множителя. Таким образом, каждая дробь будет представлена в виде произведения.

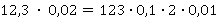
Затем нужно выполнить умножение целых чисел отдельно, вспомогательных множителей отдельно. Полученный результат нужно умножить на 0,001, то есть выполняется отделение запятой дробной части длиной в 3 цифры.

 

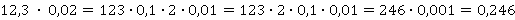
Пример 2

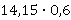
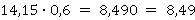
Нужно выполнить умножение, не обращая внимания на запятые. Количество цифр после запятой – 3, поэтому запятая ставится, отделяя 3 цифры. Последний ноль можно убрать из записи.

 

Пример 3

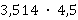
Выполняется умножение в столбик, при этом не обращая внимания на запятые, но помня, что в конце надо будет также отделить запятой 4 цифры.

 

 

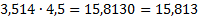
Пример 4

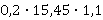
В ходе урока мы уже выяснили, что умножать десятичные дроби технически означает просто умножать целые числа. Далее в ответе нужно отделить запятой знаков столько, сколько их было у всех чисел вместе.

Конечно, это правило распространяется и на случай нескольких множителей:

 

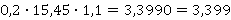
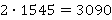
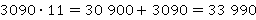
Ситуация с делением десятичных дробей такая же: если уметь делить целые числа одно на другое, то тогда получится и десятичную дробь делить на другую десятичную дробь.

Пример

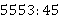
Когда заканчивается целое число, которое надо разделить, то ставится запятая и продолжается выполнение вычислений:

 

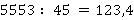
Пример

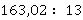
Здесь ситуация ровно такая же: как только кончается целая часть – ставится запятая:

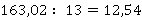
То есть технически не важно, что делить на целое число – дробь или другое целое число. Алгоритм одинаковый.

 

Пусть надо число 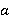 поделить на число 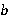. Это можно записать так:

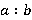 или 

Стоит помнить, что 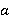 и 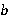 можно умножить на одно и то же число, от этого результат не изменится.

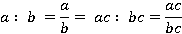
В самом деле, можно делить 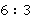, а можно , а можно 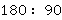. Можно все переписать в виде дробей. Результат все равно один – это равно 2.

 

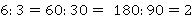
Пример. Одну десятичную дробь разделить на другую десятичную дробь:

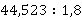
Можно умножить обе части на одно и то же число. В данном случае это 10. Умножение на 10 означает сдвиг запятой вправо на одну позицию. Тогда второе число станет целым. А деление на целое число уже было изучено на этом уроке:

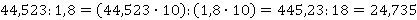
Задание: 1. ; 2.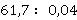

1.     

2.     

 

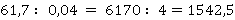
Вывод

На этом уроке были изучены правила деления и умножения десятичных дробей. Кроме того, были также рассмотрены и решены различные примеры на данную тему.

 

Список литературы

1. Виленкин Н.Я.. Математика: учеб. для 5 кл. общеобр. учр. 17-е изд. – М.: Мнемозина, 2005.

2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011.

3. Ершова А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006.

4. Хлевнюк Н.Н., Иванова М.В.. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011.          

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал «Школьный помощник» (Источник)

2. Портал «Школьная математика» (Источник)

3. Портал «МетаШкола» (Источник)

4. Портал Matematika-na.ru (Источник)

 

Домашнее задание

1. Вычислите:

а) 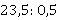; б)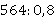

2. Вычислите:

а) 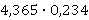; б)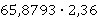

Математика 5-6 классы. 14. Умножение и деление десятичных дробей

Математика 5-6 классы. 14. Умножение и деление десятичных дробей

Подробности

Категория: Математика 5-6 классы

 

Умножение десятичных дробей

 

Десятичная форма записи позволяет выполнять умножение дробей практически по тем же правилам, по которым умножают натуральные числа. Отличие заключается в том, что необходимо определять место запятой в полученном произведении.

Поясним сказанное на примере; вычислим произведение 2,5 • 1,02.

Перенесем запятую в первом множителе на одну цифру вправо, а во втором—на две цифры вправо. Тем самым первый множитель увеличится в 10 раз, второй—в 10² = 100 раз, а произведение—в 10 • 100 = 1000 раз.

Определим произведение натуральных чисел 25 и 102:

25 • 102 = 2550.

Это число в 1000 раз больше, чем требуемое произведение. Поэтому необходимо число 2550 уменьшить в 1000= 10³ раз, т. е. перенести в этом числе запятую влево на 3 цифры. Таким образом,

2,5 • 1,02 = 2,550 = 2,55.

Можно рассуждать по-другому:

Таким образом, чтобы перемножить две десятичные дроби9 достаточно, не обращая внимания на запятые, перемножить их как натуральные числа9 а затем в полученном произведении справа отделить запятой столько цифр, сколько их было после запятых в обоих множителях вместе.

Например,

 

Деление десятичных дробей

Рассмотрим пример деления десятичной дроби на натуральное число.

Пример. Вычислить 46,8 : 2.

Решение. 4 десятка делим на 2—получаем цифру частного 2 (2 десятка).

6 единиц делим на 2 — получаем цифру частного 3 (3 единицы).

Деление целой части закончено—отделяем в частном целую часть запятой.

8 десятых делим на 2 — получаем цифру частного 4 (4 десятых). Остаток равен 0—деление закончено.

Деление десятичной дроби на десятичную дробь сводится к делению на натуральное число переносом запятых в делимом и делителе на столько цифр вправо, чтобы делитель стал натуральным числом.

Пример. Вычислить 4,42:0,2.

Решение. Так как в делителе одна цифра после запятой, то достаточно перенести запятые в делимом и делителе на 1 цифру вправо. Тем самым делимое и делитель увеличиваются в 10 раз, поэтому частное не изменится. При этом делитель будет натуральным числом.

Итак,

4,42:0,2 = 44,2:2.

Дальше деление выполняется так, как показано в предыдущем примере.

Можно рассуждать и таким образом:

Но не всегда получается точный результат при делении десятичных дробей. Чаще приходится довольствоваться приближенным частным.

 

Пример. Найти частное 1,723:0,03.

Решение. Освободимся от запятой в делителе: 1,723:0,03= 172,3:3. Выполним деление.

Начиная с разряда сотых, цифра 3 в частном повторяется без конца, потому что остаток, начиная с третьего этапа процесса деления, все время равен одному и тому же числу 1.

Если оставить у частного первые две цифры после запятой, то получится приближенное равенство: 172,3:3 ≈ 57,43.

 

 

 

5.5.6. Деление на десятичную дробь   математика-повторение

I.  Чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число.

Примеры.

Выполнить деление: 1) 16,38:0,7;   2) 15,6:0,15;    3) 3,114:4,5;   4) 53,84:0,1.

Решение. 

Пример 1)  16,38:0,7.

В делителе 0,7 после запятой стоит одна цифра, поэтому, перенесем запятые в делимом и делителе на одну цифру вправо.

Тогда нам нужно будет разделить 163,8 на 7.

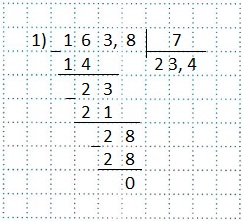Выполним деление по правилу деления десятичной дроби на натуральное  число.

Делим так, как делят натуральные числа. Как снесем цифру 8 — первую цифру после запятой (т.е. цифру в разряде десятых), так сразу поставим в частном запятую и продолжим деление.

Ответ: 23,4.

 

Пример 2) 15,6:0,15.

Переносим запятые в делимом (15,6) и делителе (0,15) на две цифры вправо, так как в делителе 0,15 после запятой стоят две цифры.

Помним, что справа к десятичной дроби можно приписать сколько угодно нулей, и от этого десятичная дробь не изменится.

Тогда:

15,6:0,15=1560:15.

Выполняем деление натуральных чисел.

Ответ: 104.

 

Пример 3) 3,114:4,5.

Перенесем запятые в делимом и делителе на одну цифру вправо и разделим 31,14 на 45 по правилу деления десятичной дроби на натуральное число.

Итак:

3,114:4,5=31,14:45.

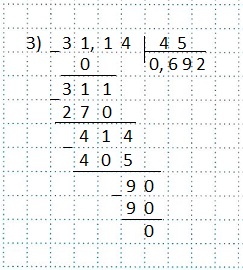
В частном поставим запятую сразу, как сносим цифру 1 в разряде десятых. Затем продолжаем деление.

Чтобы закончить деление нам пришлось приписать нуль к числу 9 — разности чисел 414 и 405. (мы знаем, что справа к десятичной дроби можно приписывать нули)

 

Ответ: 0,692.

Пример 4)  53,84:0,1.

Переносим запятые в делимом и делителе на 1 цифру вправо.

Получаем: 538,4:1=538,4. 

Проанализируем равенство: 53,84:0,1=538,4. Обращаем внимание на запятую в делимом в данном примере и на запятую в полученном частном. Замечаем, что запятая в делимом перенесена на 1 цифру вправо, как если бы мы умножали 53,84 на 10. (Смотрите видео «Умножение десятичной дроби на 10, 100, 1000 и т.д.») Отсюда правило деления десятичной дроби на 0,1; 0,01; 0,001 и т.д.

II. Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т. д., нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр. (Деление десятичной дроби на 0,1; 0,01; 0,001 и т. д. равносильно умножению этой десятичной дроби на 10, 100, 1000 и т.д.)

Примеры.

Выполнить деление: 1) 617,35:0,1;  2) 0,235:0,01;  3) 2,7845:0,001;  4) 26,397:0,0001.

Решение.

Пример 1) 617,35:0,1.

Согласно правилу II деление на 0,1 равносильно умножению на 10, и запятую в делимом перенесем на 1 цифру вправо:

1) 617,35:0,1=6173,5.

Пример 2) 0,235:0,01.

Деление на 0,01 равносильно умножению на 100, значит, запятую в делимом перенесем на 2 цифры вправо:

2) 0,235:0,01=23,5.

Пример 3) 2,7845:0,001.

Так как деление на 0,001 равносильно умножению на 1000, то перенесем запятую на 3 цифры вправо:

3) 2,7845:0,001=2784,5.

Пример 4) 26,397:0,0001.

Разделить  десятичную дробь на 0,0001 — это все равно, что умножить ее на 10000 (переносим запятую на 4 цифры вправо). Получаем:

4) 26,397:0,0001=263970.

Смотрите видео «Деление на десятичную дробь»

 

Самостоятельная работа по математике для 6 класса «Деление десятичных дробей»

Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс	Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс
Вариант I. 1. Выполните умножение: а) 1,62 : 3,6; б) 1,53 : 0,5; в) 2,8623 : 4,06; г) 9 : 16. 2.Найдите значение выражения      70,4 – 67,32 : (30 – 13,5) · 8,4.	Вариант II. 1. Выполните умножение: а) 1,47 : 4,2; б) 9,315 : 2,3; в) 5,6994 : 8,05; г) 5 : 16. 2.Найдите значение выражения      90,3 – 56,12 : (50 – 31,6) · 5,7.
Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс	Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс
Вариант I. 1. Выполните умножение: а) 1,62 : 3,6; б) 1,53 : 0,5; в) 2,8623 : 4,06; г) 9 : 16. 2.Найдите значение выражения      70,4 – 67,32 : (30 – 13,5) · 8,4.	Вариант II. 1. Выполните умножение: а) 1,47 : 4,2; б) 9,315 : 2,3; в) 5,6994 : 8,05; г) 5 : 16. 2.Найдите значение выражения      90,3 – 56,12 : (50 – 31,6) · 5,7.
Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс	Самостоятельная работа по теме: «Деление десятичных дробей» 6 класс
Вариант I. 1. Выполните умножение: а) 1,62 : 3,6; б) 1,53 : 0,5; в) 2,8623 : 4,06; г) 9 : 16. 2.Найдите значение выражения      70,4 – 67,32 : (30 – 13,5) · 8,4.	Вариант II. 1. Выполните умножение: а) 1,47 : 4,2; б) 9,315 : 2,3; в) 5,6994 : 8,05; г) 5 : 16. 2.Найдите значение выражения      90,3 – 56,12 : (50 – 31,6) · 5,7.

«Сложение, вычитание, умножение и деление положительных десятичных дробей».

Урок №117 дата: 06.03.2019 математика 6 класс.

Тема урока «Сложение, вычитание, умножение и деление положительных десятичных дробей».

Тип урока: урок — путешествие

Цель урока: повторение и применение правил сложения, вычитания, умножения и деления десятичных положительных дробей при решении примеров и задач.

Планируемые результаты:

Предметные: применить полученные знания по теме «Десятичные дроби» для решения примеров и задач. Актуализация знаний в чтении, записи, сравнении и выполнении действий с десятичными дробями.

Получит возможность анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию.

Личностные: ответственно относиться к учению; грамотно излагать свои мысли в устной и письменной речи.

Метапредметные: научится осуществлять контроль своей деятельности в процессе достижения результата. Получит возможность формулировать проблемы при решении учебных задач.

Оборудование: мультимедийный проектор, компьютер, карточки.

Ход урока.

«Просто знать – еще не все, знания нужно уметь использовать.» Гете.

1.Органтзационный момент урока (7 мин.)

Интерактивное упражнение «Комплимент»

1)Проверка домашнего задания, игра «Найди ответ»

2)Устный счет (Определение ключевых слов темы урока и его задачи)

Решив примеры найдем ключевые слова темы нашего урока (найдем ответы и соответствующие буквы)

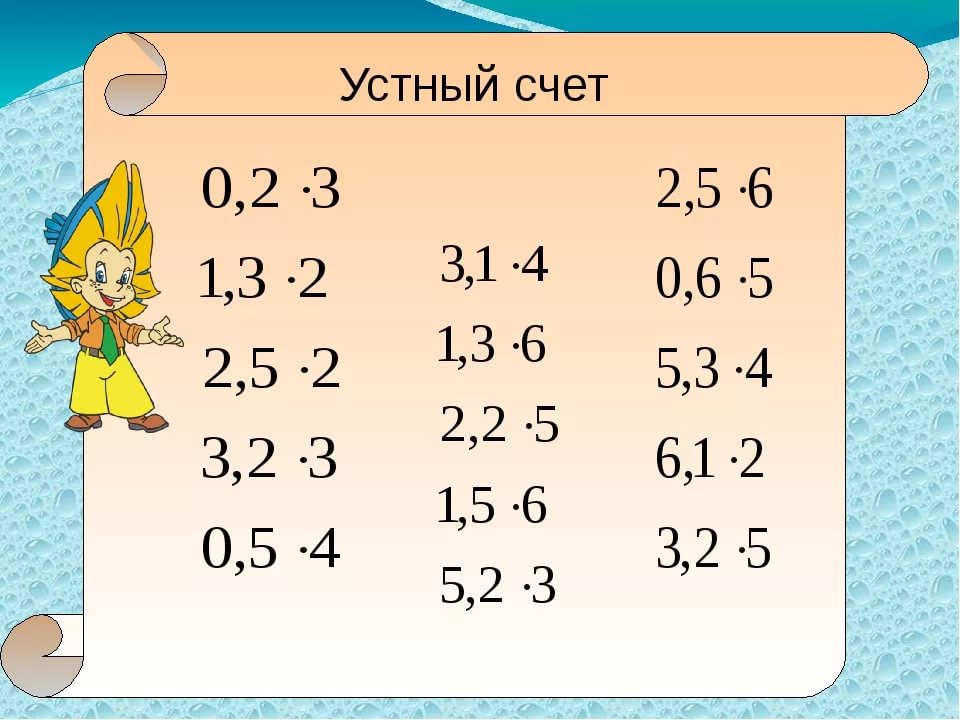
Учитель: Запишем число и тему урока «Сложение, вычитание, умножение и деление положительных десятичных дробей».

Ребята сегодня у нас урок – путешествие по Крыму, а в частности решая задачи, примеры, уравнения мы много узнаем об одном из городов Крыма. Какой же это город? Чтобы ответить на этот вопрос мы напишем математический диктант, но прежде сформулируйте правила сложения, вычитания, умножения и деления десятичных дробей.(3 мин)

Слайды

3)Актуализация опорных знаний

2.Математический диктант (4 мин.) Результаты проверить на экране.

1.Число 6,5 увеличьте на 0,1

2.Число 6,555 уменьшите на 0,001

3.Число 0,42 уменьшите в 7 раз

4.Учеличьте 0,8 в 9 раз

5.Решите уравнения: X + 4,5 =9,6 и 8,6: X = 2

2*Х=2,4

Итак, проверяем математический диктант. Город, о котором пойдет речь на уроке – город Армянск.

Историческая справка 1-2 мин видео

3.Работа у доски и в тетрадях. (6 мин.)

Статус города Армянск получил в …1993….году. Численность населения в 2018 году около …22…тысяч человек.

Чтобы заполнить пробел в предложениях, давайте выполним следующее задания:

Выполните действия:

1777 + (10,79 : 8,3 x 5,6 + 208,72) и

Решите уравнение: (х – 16,6) : 1,8 = 3

4.Самостоятельная работа по карточкам. (10 мин).

Выполнив задания, вы узнаете, что принадлежало городу Перекоп, жители которого в конце XIX века покинули пришедший в упадок город и основали новый — Армянский Базар.

Вариант I

Задания к карточке № 1

1. 2,145+3,02

2. 0,161 : 0,7

3. Реши уравнение : 1- Z = 0,67

4. Найди значение выражения: 1,2 х +4,8 х, если х = 0,6

5. В первый день продали 12,52 м ткани и это на 6, 36 м больше, чем во второй день. Сколько метров ткани продали за два дня?

Вариант II

Задания к карточке № 2

1. 5,145 – 2,105

2. 0,182 : 1,3

3. Реши уравнение : 1- Z = 0,71

4. Найди значение выражения : 2,1 х +6,3 х, если х = 0,5

5. В первый день продали 18,46м ткани и это в 2 раза больше, чем во второй день. Сколько метров ткани продали за два дня?

5.Физминутка (1 мин).

7.Решение задач и примеров (10 мин.)

Решение заданий по учебнику страница 161 № 848 (повторить законы сложения)

дополнительно, если есть время, № 850

8.Подведение итогов . Рефлексия деятельности. (2мин).

Ребята, давайте оценим свою работу на уроке.

Мы вместе отлично поработали, Что вам больше всего понравилось и запомнилось с урока?

Учитель комментирует оценки.

9.Домашнее задание: (1 мин.)

Стр.160 № 841, 851(а,в)

Или Задание на карточке: