Вычисление комплексных чисел онлайн – Калькулятор комлексных чисел | Вычисление выражений, содержащих комплексные числа

Калькулятор комлексных чисел | Вычисление выражений, содержащих комплексные числа

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Калькулятор комплексных чисел

7

8

9

+

—

*

/

^

4

5

6

i

(

)

π

e

1

2

3

sin

cos

tg

ctg

ln

.

0

√

sh

ch

th

cth

abs

Скрыть клавиатуру

Вычислено выражений: 22629

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

• (2+3i)*(5-7i)
• sh(i)
• (4+i) / (3 — 4i)
• sqrt(2i)
• (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)

Комплексные числа

Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi² = (ac — bd) + (bc + ad)i
• деление: = = + i

Примеры

Найти сумму чисел

5+7i и 5.5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i / (3+4i) = 1 - 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a2 + b2)
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: ez = ea·cos(b) + i·ea·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4² + (-3)²) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy, где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

Решение:

• Найдём радиус (модуль) комплексного числа r: r = √(1² + 1²) = √2
• Найдём аргумент числа: φ = arctan() = = 45°
• Запишем результат в тригонометрической форме: √2·(cos(45°) + isin(45°))
• Запишем результат в показательной форме: √2·eπi/4

programforyou.ru

Онлайн калькулятор: Комплексные числа

Начиная с 16 века математики столкнулись с необходимостью введения комплексных чисел, то есть чисел вида a+bi, где a,b — вещественные числа, i — мнимая единица — число, для которого выполняется равенство: i

2=-1.

Интересно проследить, как менялось представление о комплексных числах с течением времени. Вот некоторые цитаты из древних трудов:

• XVI век : Эти сложнейшие величины бесполезны, хотя и весьма хитроумны.
• XVII век : Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.
• XVIII век : Квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Из сего видно, что квадратные корни из отрицательных чисел не могут находиться среди возможных чисел. Поэтому, нам не остается ничего другого, как признать их невозможными числами. Это ведет нас к понятию таких чисел, которые по своей природе невозможны и обычно называются мнимыми или воображаемыми, потому что их только в уме представить можно.
• XIX век Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы и иероглифы нелепых количеств.

Известно три способа записи комплексного числа z:

Алгебраическая запись комплексного числа

,
где a и b — вещественные числа, i — мнимая единица. a — действительная часть, bi — мнимая часть.

Тригонометрическая запись комплексного числа

,
где r — модуль комплексного числа:

, который соответствует расстоянию от точки на комплексной плоскости до начала координат, а φ — угол наклона вектора 0-z к оси действительных значений или аргумент комплексного числа.

Показательная запись комплексного числа

была введена Леонардом Эйлером для сокращения тригонометрической записи.

Точность вычисления

Знаков после запятой: 2

В тригонометрической форме

 

В показательной форме

 

Комплексное число

 

Главный аргумент (радианы)

 

Главный аргумент (градусы)

 

Сопряженное число

 

Комплексная плоскость

Сохранить share extension

Значение аргумент комплексного числа определяется с точностью до , для всех целых k. Главный аргумент — это значение аргумента, лежащее в диапазоне (-π..π].

Главный аргумент вычисляется как арктангенс двух аргументов мнимой и действительной части комплексного числа:
, см Арктангенс с двумя аргументами

Над комплексным числом возможны все алгебраические операции:

ОперацияСложитьВычестьУмножитьПоделитьВозвести в степеньИзвлечь корень

Точность вычисления

Знаков после запятой: 2

Сохранить share extension

Сложение комплексных чисел

Комплексные числа складываются ровно так же, как и многочлены:

Умножение комплексных чисел

Помня о том, что i*i=-1, легко выразить формулу для умножения комплексных чисел:

Деление комплексных чисел

Формулу деления комплексных чисел проще всего вывести, путем умножения числителя и знаменателя на сопряженное комплексное число, для того, чтобы избавиться от мнимой единицы в знаменателе:

Сопряженное комплексное число, это число вида:

Раскрывая скобки получаем:

Возведение в целую степень

Проще всего комплексное число возводить в степень используя показательную форму:

формула вытекает из формулы Муавра:

Вычисление корня степени n

Из формулы Муавра вытекает решение для корней степени n из комплексного числа:
,
всего получается n корней, где k = 0..n-1 — целое число, определяющее индекс корня. Корни располагаются на комплексной плоскости, как вершины правильного многоугольника.

planetcalc.ru

Онлайн Калькулятор комплексного числа

Числа вида x+iy, где x и y — вещественные числа, i — мнимая единица называются комплексными числами. Произвести расчеты с комплексными числами: умножение, деление и извлечение квадратного корня из заданного числа.

Калькулятор комплексного числа

Формулы комплексного числа:

Умножение

(x+iy) × (x+iy)

Деление

(x+iy) / (x+iy)

Квадратный корень:

• r = корень(x² + y²)
• z = sqrt((r-x) / 2)
• x = y / 2z
• r1 = x + iz
• r2 = -x — iz

Пример 1: Умножение дух комплексных чисел.

Умножим (3 + 2i) и (4 + 5i)

Шаг 1:

Производим расчет по формуле (x+iy) × (x+iy)
(3 + 2i)(4 + 5i) = (3 × 4) + (3 × (5i)) + ((2i) × 4) + ((2i) × (5i))
= 12 + 15i + 8i + 10i ²
= 12 + 23i -10 (Представим 10i ² = 10(-1) = -10)
= 2 + 23i

Ответ: (3 + 2i)(4 + 5i) = 2+23i

Пример 2:Поделим одно комплексное число на другое.

Делим (2 + 6i) / (4 + i).

Шаг 1:

Производим расчет по формуле (a+bi) / (a+bi)
Записываем комплексное сопряженное 4+i ie., 4-i

Шаг 2:

Умножаем верхние и нижние выражения

Верхнее = (2 + 6i)(4 — i)
= 8 — 2i + 24i — 6i ²
= 8 + 22i + 6 (Представим как -6i ² = -6(-1) = 6)
= 14 + 22i

Нижнее = (4 + i)(4 — i)

= 16 — 4i + 4i — i ²
= 16 + 0 + 1 (Представим как -i ² = 1)
= 17

Шаг 3:

Произведем деление
Соотношение (14 + 22i) / 17

Ответ: (2 + 6i) / (4 + i) = 14/17 + 22i/17

Пример 3:

Найдем корень комплексного числа 12 + 16i.

Шаг 1:
r = корень(x ² + y ²)
= корень(12 ² + 16 ²)
= корень(144 + 256)
= корень(400)
r = 20

Шаг 2:

Для решения используем формулу.
z = корень((r — x) / 2)
= корень((20 — 12)/2)
= корень(8 / 2)
= корень(4)
z = 2

Шаг 3:

Заменяем значение y b z в x.
x = y / 2z
= 16 / 2 ×2
= 16 / 4
x = 4

Шаг 4:

Найдем корень 12 + 16i подставив значение x и z в r1 and r2.
r1 = x + zi = 4 + 2i
r2 = -x — zi = -4 — 2i

Ответ: корень 12 + 16i является,
r1 = 4 + 2i, r2 = -4 — 2i

wpcalc.com

Комплексные числа: калькулятор онлайн для вычислений

Здравствуйте. Не у каждого пользователя может возникнуть необходимость в вычислении комплексных чисел. При этом те, у кого она все же появляется, обязательно должны знать, что есть возможность вычислять в интернете комплексные числа, калькулятор онлайн для этого и создан. Есть множество таких сервисов, простых в использовании и доступных в любое время. В этой статье мы поговорим о наиболее популярных, и рассмотрим некоторые нюансы, которые следует учитывать в процессе работы.

СОДЕРЖАНИЕ СТАТЬИ:

Для чего используется?

Естественно, тем, кто ищет такой онлайн калькулятор, не нужно объяснять, для чего он нужен, но стоит отметить некоторые функции, с которыми он должен справляться.

Такая программа должна выполнять:

• вычитание;
• сложение;
• умножение;
• деление;
• находить различные формы;
• аргументы и модули;
• геометрическую интерпретацию и прочее.

На некоторых сайтах необходимо просто ввести известные части задачи и выбрать нужную операцию из предлагаемого списка. Ниже будут представлены наиболее функциональные и удобные программы, с которыми легко работать в режиме реального времени.

---

Отличный онлайн калькулятор для комплексных чисел – Kontrolnaya Rabota

Данный сервис можно смело считать одним из самых надежных, он оперативно и правильно вычисляет. Работать с ним нужно так:

• просмотрите инструкцию по вводу значений;

• учитывая правила ввода, впишите выражение в соответствующем поле;

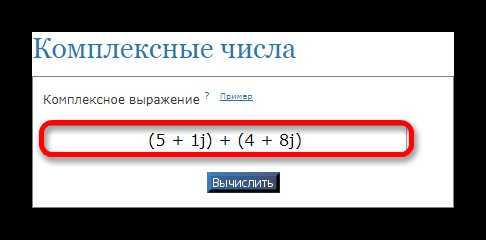
• кликните по клавише «Вычислить» для получения результата;

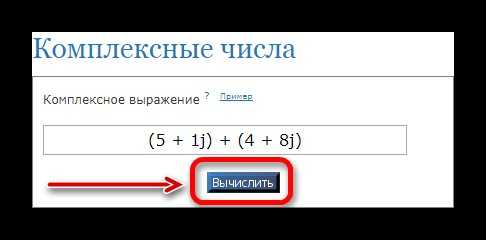
• ответ будет выдан в трех различных формулах.

При необходимости детальный принцип решения найдете под ответами, для этого существует окошко «Описание». Кроме того, сайт можно использовать и для неравенств, уравнений, матриц и прочего.

---

OnlineMSchool

Данный ресурс очень простой и понятный, освоится сразу даже новичок за несколько секунд. Провести действия поможет следующий алгоритм:

• вводите необходимые значения;

• выбираете алгебраическую операцию из перечня, выплывающего при нажатии на стрелку;
• кликом по клавише «=» активируете процесс;

• ниже выходит решение.

С помощью данного ресурса вы получаете детальное описание нужного примера, позволяющее понять принцип вычисления задач с комплексными числами и закрепить пройденное. Доступен для скачивания из сервиса Гугл Плей.

---

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

• вводите условия в соответствующие поля;

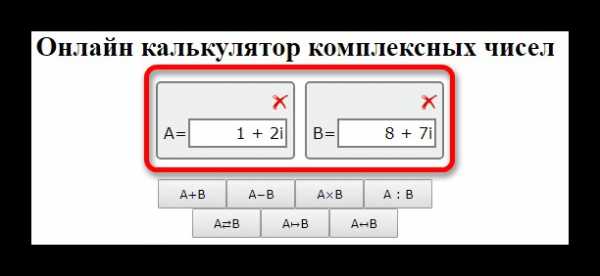
• выбираете нужное действие;
• после нажатия на выбранную операцию будет начато вычисление и выдан результат.

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

---

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре  алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

• просмотрите правила ввода, кликнув на «+»;

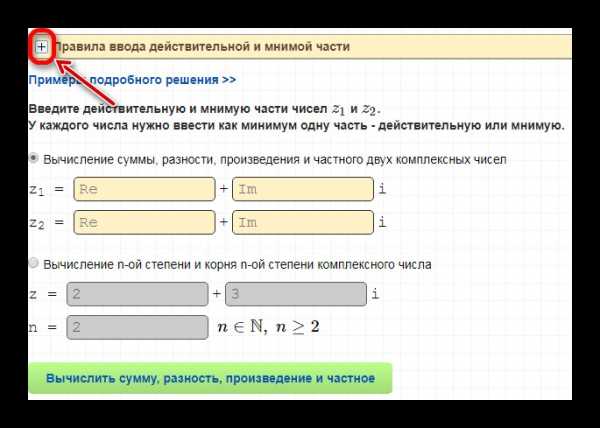
• введите необходимые значения;
• посчитайте, для этого есть специальная кнопка с вычислением;

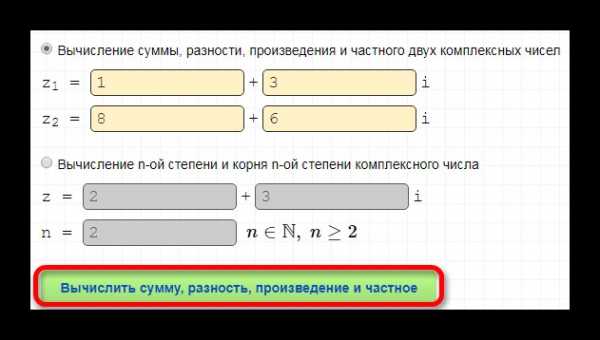
• получите результат и подробное описание.

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Если вам нужно решить задачи, где есть комплексные числа, калькулятор онлайн станет отличным помощником. Ресурсы, отмеченные в этой статье, очень просты в использовании. На каждом из них вам будет выдан не только ответ, но и полное описание принципа решения. Если у вас возникли какие-то вопросы, пишите в комментариях. Подписывайтесь на обновления блога, чтобы не пропустить все самое актуальное и интересное.

Это может быть так же интересным:

life-v.ru

Решить комплексные уравнения онлайн калькулятор

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Сегодня вы можете в режиме онлайн решить уравнение с комплексными числами, однако сложно будет проверить правильность результата, не имея представления о комплексных числах, поэтому мы ознакомим вас с числами данного вида.

Комплексное число — это выражение вида \[x+yi.\] В данном выражении \[x,y\] — действительные числа, \[а i\] — мнимая единица, квадрат которого -1, \[i^2=-1.\] \[b\] называют мнимой частью комплексного числа \[a=x+yi.\] В случае, если \[y=0,\] то вместо \[x+0i\] пишут \[x.\] Над данным типом чисел можно выполнять абсолютно все арифметические действия, что и над действительными.

Так же читайте нашу статью «Решить разностное уравнение онлайн»

Например, вам необходимо решить квадратное уравнение:

\[ c^2-6c+34=0 \]

Изначально необходимо вычислить дискриминант:

\[D= 36-136= -100\]

Поскольку дискриминант отрицательный, то в действительных числах его решить нельзя. Однако можно извлечь корень в комплексных числах:

\[\sqrt D=\pm 10i\]

Получаем 2 корня:

\[z_{1,2}=\frac {r\pm 10i}{2}=3\pm 5i\]

— сопряженные комплексные корни.

Решить комплексное уравнение онлайн решателем вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

No related posts.