ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ — Алгебра 7 класс — Учебно-методическое пособие — Старова Е. А. — 2015 год
Урок № 46. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
Цели:
• обучающая: сформировать понятия области определения и области значений функции; сформировать умение находить область определения и область значений функции, заданных различными способами; • развивающая: формировать умения выделять главное в изучаемом материале; развивать абстрактное мышление;
• воспитательная: воспитывать заинтересованность в познании нового, исполнительность;
Тип урока: усвоение новых знаний, умений и навыков.
Оборудование и наглядность:
Ход урока
И. ОРГАНИЗАЦИОННЫЙ ЭТАП
______________________________________________________
______________________________________________________
______________________________________________________
II. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
1. Проверка задания, заданного по учебнику
______________________________________________________
______________________________________________________
2. Выполнение тестовых заданий
Обведите кружочком букву, которая, по вашему мнению, соответствует правильному ответу
Вариант 1
1) На каком из приведенных рисунков изображена соответствие не является функцией?
2) Функция задана формулой f (x) = |2x — 3|. Какая из приведенных равенств правильное?
А) f(0) = 3; Б) f(1) = 5; В) f(-2) = 1; Г) f(3) = -3.
3) Функция задана формулой f(x) = 0,5x — 15. Найдите значение функции, если аргумент равен 10.
А) 50; Б) 10; В) -10; Г) -20.
4) Найдите значение аргумента, при котором значение функции y = 7х +1 равна -13.
Вариант 2
1) На каком из приведенных рисунков изображена соответствие не является функцией?
2) Функция задана формулой f (x) = |2 — 3x|. Какая из приведенных равенств правильное?
А) f(0) = -3; Б) f(1) = 1; В) f(2) = 2; Г) f(-1) = -5.
3) Функция задана формулой y = -2x + 5. Найдите значение функции, если аргумент равен 11.
А) -3; Б) 17; В) -17; Г) -8.
4) Найдите значение аргумента, при котором значение функции y = 2х — 9 равен 1.
А) -7; Б) 11; В) -4; Г) 5.
Ответы
Вариант 1 | 1 — Г, 2 — А, 3 — В, 4 — Б |
Вариант 2 | 1 — Б, 2 — Б, 3 — В, 4 — Г |
III. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ
Выполнение устных упражнений
1. Функция y = s(а) — это соответствие между стороной квадрата и его площадью. Каких значений может принимать переменная а? переменная?
2. Функция у = k(l) — это соответствие между количеством уток на птицеферме и количеством их лап. Каких значений может принимать переменная l? переменная?
3. При каких значениях переменной х имеет смысл выражение:
4. При каких значениях переменной х не имеет смысла выражение:
IV. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
План изучения темы
1. Определение области определения функции.
2. Определение области значений функции.
3. Нахождение области определения и области значений функций, заданных различными способами:
______________________________________________________
______________________________________________________
V. УСВОЕНИЕ НОВЫХ ЗНАНИЙ И УМЕНИЙ
Работа по учебнику
______________________________________________________
______________________________________________________
VИ. ИТОГИ УРОКА
1.
______________________________________________________
______________________________________________________
2. Фронтальное опрос
1) Функция задана формулой Найдите область определения этой функции.
2) Функция задана таблицей. Запишите область определения и область значений функции
х | -8 | -4 | -2 | 0 | 2 | 4 | 8 |
в | 4 | 2 | 1 | -1 | -2 | -4 | -8 |
3) Функция задана графически. Укажите область определения и область значений функции
VII. ДОМАШНЕЕ ЗАДАНИЕ
1. Задание по учебнику:
______________________________________________________
______________________________________________________
2. Дополнительное задание. Задайте формулой какую-либо функцию, областью определения которой является: 1) все числа, кроме 2 и 3; 2) все числа, кроме -1; 0; 1.
schooled.ru
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ — Урок 2 — Алгебра 7 класс — Учебно-методическое пособие — Старова Е. А. — 2015 год
Урок № 47. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
Цели:
• образовательная: совершенствовать знания определений области определения и области значений функции; усовершенствовать умения находить область определения и область значений функции;
• развивающая: формировать умение рассуждать по аналогии; развивать внимание, логическое мышление, память;
• воспитательная: воспитывать настойчивость в достижении цели, трудолюбие, дисциплинированность;
Тип урока: совершенствование знаний, умений и навыков.
Оборудование и наглядность:
Ход урока
И. ОРГАНИЗАЦИОННЫЙ ЭТАП
______________________________________________________
______________________________________________________
______________________________________________________
II. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
1. Проверка задания, заданного по учебнику
______________________________________________________
______________________________________________________
2. Задания на установление соответствия
Установите соответствие между функцией (1-4) и ее областью определения (А-Д).
Вариант 1 | Вариант 2 | |||||||
1 | f(x) = x2 + 3x | А | Все числа, кроме 0 | 1 | f(x) = x + 5 | А | Все числа кроме -5 и 5 | |
2 | f(x) = 7/x | Бы | Все числа | 2 | Бы | Все числа, кроме 3 и 7 | ||
3 | В | Все числа, кроме -2 и 2 | 3 | В | Все числа, кроме 5 | |||
4 | Г | Все числа, кроме 1 и 2 | 4 | Г | Все числа | |||
Д | Все числа, кроме 2 | Д | Все числа, кроме 0 | |||||
Ответы
Вариант 1 | 1 — Б, 2 — А, 3 — Г, 4 — В |
Вариант 2 | 1 — Г, 2 — Д, 3 — А, 4 — Б |
III. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ
Выполнение устных упражнений
1. Представьте в виде квадрата двучлена:
1) х2 + 4х + 4; 2) x2 — 2х +1; 3) 4x2 + 24x + 36.
2. Решите уравнение:
1) х2 + 2х +1 = 0; 2) х3 — 16х = 0; 3) |х + 4| = 0; 4) |х — 7| = 2.
IV. СОВЕРШЕНСТВОВАНИЕ УМЕНИЙ И НАВЫКОВ
Работа с учебником
_____________________________________________________
______________________________________________________
V. ИТОГИ УРОКА
1.
______________________________________________________
______________________________________________________
2. Выполнение тестовых заданий
Обведите кружочком букву, которая, по вашему мнению, соответствует правильному ответу
Вариант 1
1) Областью определения какой из приведенных функций являются все числа?
2) К области определения какой из нижеперечисленных функций не относится число -2?
3) Областью значений которой из приведенных функций являются все неотрицательные числа?
Вариант 2
1) Областью определения какой из приведенных функций являются все числа?
2) К области определения какой из нижеперечисленных функций не относится число -3?
3) Областью значений которой из приведенных функций есть все недодатні числа?
Ответы
Вариант 1 | 1 — Г, 2 — Б, 3 — Б |
Вариант 2 | 1 — Б, 2 — А, 3 — Г |
VI. ДОМАШНЕЕ ЗАДАНИЕ
1. Задание по учебнику:
______________________________________________________
______________________________________________________
2. Дополнительное задание. При каком значении m областью определения функции:
есть все числа, кроме 3;
есть все числа, кроме 5?
3. Повторить: определение прямоугольной системы координат, координатной плоскости.
schooled.ru
Как найти область определения функции?
Как найти область определения функции? Ученикам средних классов приходится часто сталкиваться с данной задачей.
Родителям следует помочь своим детям разобраться в данном вопросе.
Математические понятия

Задание функции.
Напомним основополагающие термины алгебры. Функцией в математике называют зависимость одной переменной от другой. Можно сказать, что это строгий математический закон, который связывает два числа определенным образом.
В математике при анализе формул числовые переменные подменяют буквенными символами. Наиболее часто используют икс («х») и игрек («у»). Переменную х называют аргументом, а переменную у — зависимой переменной или функцией от х.
Существуют различные способы задания зависимостей переменных.
Перечислим их:
- Аналитический тип.
- Табличный вид.
- Графическое отображение.
Аналитический способ представляют формулой. Рассмотрим примеры: у=2х+3, у=log(х), у=sin(х). Формула у=2х+3 является типичной для линейной функции. Подставляя в заданную формулу числовое значение аргумента, получаем значение y.
 Табличный способ представляет собой таблицу, состоящую из двух столбцов. Первая колонка выделяется для значений икса, а в следующей графе записывают данные игрека.
Табличный способ представляет собой таблицу, состоящую из двух столбцов. Первая колонка выделяется для значений икса, а в следующей графе записывают данные игрека.
Графический способ считается наиболее наглядным. Графиком называют отображение множества всех точек на плоскости.
Для построения графика применяют декартовую систему координат. Система состоит из двух перпендикулярных прямых. На осях откладывают одинаковые единичные отрезки. Отсчет производят от центральной точки пересечения прямых линий.
Независимую переменную указывают на горизонтальной линии. Ее называют осью абсцисс. Вертикальная прямая (ось ординат) отображает числовое значение зависимой переменной. Точки отмечают на пересечении перпендикуляров к данным осям. Соединяя точки между собой, получаем сплошную линию. Она являться основой графика.
Виды зависимостей переменных
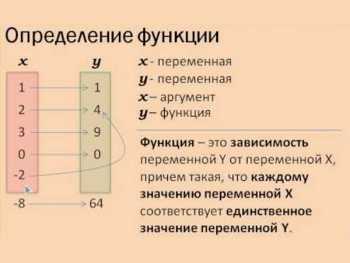
Определение.
В общем виде зависимость представляется как уравнение: y=f(x). Из формулы следует, что для каждого значения числа х существует определенное число у. Величину игрека, которая соответствует числу икс, называют значением функции.
Все возможные значения, которые приобретает независимая переменная, образуют область определения функции. Соответственно, все множество чисел зависимой переменной определяет область значений функции. Областью определения являются все значения аргумента, при котором f(x) имеет смысл.
Начальная задача при исследовании математических законов состоит в нахождении области определения. Следует верно определять этот термин. В противном случае все дальнейшие расчеты будут бесполезны. Ведь объем значений формируется на основе элементов первого множества.
Область определения функции находится в прямой зависимости от ограничений. Ограничения обусловливаются невозможностью выполнения некоторых операций. Также существуют границы применения числовых значений.
При отсутствии ограничений область определения представляет собой все числовое пространство. Знак бесконечности имеет символ горизонтальной восьмерки. Все множество чисел записывается так: (-∞; ∞).
В определенных случаях массив данных состоит из нескольких подмножеств. Рамки числовых промежутков или пробелов зависят от вида закона изменения параметров.
 Укажем список факторов, которые влияют на ограничения:
Укажем список факторов, которые влияют на ограничения:
- обратная пропорциональность;
- арифметический корень;
- возведение в степень;
- логарифмическая зависимость;
- тригонометрические формы.
Если таких элементов несколько, то поиск ограничений разбивают для каждого из них. Наибольшую проблему представляет выявление критических точек и промежутков. Решением задачи станет объединение всех числовых подмножеств.
Множество и подмножество чисел

О множествах.
Область определения выражают как D(f), а знак объединения представлен символом ∪. Все числовые промежутки заключают в скобки. Если граница участка не входит во множество, то ставят полукруглую скобку. В ином случае, когда число включается в подмножество, используют скобки квадратной формы.
Обратная пропорциональность выражена формулой у=к/х. График функции представляет собой кривую линию, состоящую из двух веток. Ее принято называть гиперболой.
Так как функция выражена дробью, нахождение области определения сводится к анализу знаменателя. Общеизвестно, что в математике деление на нуль запрещено. Решение задачи сводится к уравниванию знаменателя к нулю и нахождению корней.
 Приведем пример:
Приведем пример:
Задается: у=1/(х+4). Найти область определения.
Решение:
- Приравниваем знаменатель к нулю.
х+4=0 - Находим корень уравнения.
х=-4 - Определяем множество всех возможных значений аргумента.
D(f)=(-∞ ; -4)∪(-4; +∞)
Ответ: областью определения функции являются все действительные числа, кроме -4.
Значение числа под знаком квадратного корня не может быть отрицательным. В этом случае определения функции с корнем сводится к решению неравенства. Подкоренное выражение должно быть больше нуля.
Область определения корня связана с четностью показателя корня. Если показатель делится на 2, то выражение имеет смысл только при его положительном значении. Нечетное число показателя указывает на допустимость любого значения подкоренного выражения: как положительного, так и отрицательного.
Неравенство решают так же, как уравнение. Существует только одно различие. После перемножения обеих частей неравенства на отрицательное число следует поменять знак на противоположный.
Если квадратный корень находится в знаменателе, то следует наложить дополнительное условие. Значение числа не должно равняться нулю. Неравенство переходит в разряд строгих неравенств.
Логарифмические и тригонометрические функции

Пример.
Логарифмическая форма имеет смысл при положительных числах. Таким образом, область определения логарифмической функции аналогична функции квадратного корня, за исключением нуля.
Рассмотрим пример логарифмической зависимости: y=lоg(2x-6). Найти область определения.
Решение:
Ответ: (3; +∞).
Областью определения y=sin x и y=cos x является множество всех действительных чисел. Для тангенса и котангенса существуют ограничения. Они связаны с делением на косинус либо синус угла.
Тангенс угла определяют отношением синуса к косинусу. Укажем величины углов, при которых значение тангенса не существует. Функция у=tg x имеет смысл при всех значениях аргумента, кроме x=π/2+πn, n∈Z.
Областью определения функции y=ctg x является все множество действительных чисел, исключая x=πn, n∈Z. При равенстве аргумента числу π или кратному π синус угла равен нулю. В этих точках (асимптотах) котангенс не может существовать.
Первые задания на выявление области определения начинаются на уроках в 7 классе. При первом ознакомлении с этим разделом алгебры ученик должен четко усвоить тему.
Следует учесть, что данный термин будет сопровождать школьника, а затем и студента на протяжении всего периода обучения.
lediznaet.ru
Функция. Область определения функции. Область значений функции — АЛГЕБРА — Уроки для 7 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 60
Тема. Функция. Область определения функции. Область значений функции
Цель: закрепить терминологию, отработать навыки работы с понятиями функции; отработать навыки работы с функцией, заданной формулой и таблично; находить функции, аргумента, области определения функции.
Тип урока: усвоение умений и навыков.
Ход урока
I. Организационный момент (традиционно)
II. Проверка домашнего задания
@ Поскольку основная часть домашнего задания — освоение теории (определения понятий), то целесообразно проверку домашнего задания провести в форме математического диктанта.
1. Математический диктант
1) Задайте формулой функцию, которая сопоставляет каждому числу третью степень этого числа [сумму этого числа с числом 5].
2) Функция задана формулой . Найдите ее значение при значении аргумента -2 [-1].
3) Функция задана формулой у = 3х – 7 [у = 5 – 2х]. Найдите значение аргумента, при котором значение функции равно нулю.
4) При каких значениях переменной имеет смысл выражение ?
После выполнения проводится коррекция (работа в парах).
2. Работа с опережающим домашним заданием.
@ Основная цель работы с опережающим домашним заданием на этом уроке — подготовка к восприятию учащимися алгоритма нахождения области определения функции, заданной формулой (вида у = f(х)).
Поэтому далее проводим фронтальную беседу по результатам опережающего домашнего задания.
Вопрос
1. Что называют допустимым значением переменной в выражении? Приведите пример.
2. Что означает термин «область допустимых значений переменной в выражении»? Как коротко обозначается?
3. Как найти ОДЗ в выражении, которое имеет вид: а) многиочлена; б) дроби, где в знаменателе число; в) дроби, знаменателем которого является буквенный выражение; г) целого выражения?
4. Найдите ОДЗ выражений: а) х + 3; б) ; в) ; г) (х + 3)2; д) .
5. Назовите аргумент и зависимую переменную, если функция задана формулой . Каких значений приобретает функция при значении аргумента -1; 2; -3? Можно ли вычислить значение функции при х = 0? Почему? Существует ли еще какое-нибудь значение аргумента, при котором нельзя вычислить значение выражения? Почему? Какой будет область определения функции , исходя из сказанного выше?
6. Сравните вывод п. 4 п. 5. Что вы заметили? Какое предположение можно сделать на основании этого сравнения.
III. Формулировка цели и задач урока
@ Из работы, выполненной на предыдущем этапе урока, учащиеся должны сделать важный вывод: область определения функции может быть найдено через ОДЗ выражения, задающего данную функциональную зависимость. То есть задания функции формулой является наиболее удобным способом задания функции именно потому, что помогает решать задачи с незнакомыми или новыми для учащихся объектами (функция, аргумент, область определения функции) путем выполнения известных учащимся действий (вычислением значений буквенных выражений, решением уравнений и нахождением ОДЗ выражения).
Следовательно, учителю остается обобщить эти мысли, и главной целью урока можно определить: отработка навыков работы с функцией, заданной формулой (нахождения аргумента функции и области определения).
IV. Дополнение знаний
@ Единственным относительно новым моментом урока является обобщающий логический шаг от алгоритма нахождение ОДЗ выражения (см. начало учебного года) до нахождения области определения функции, заданной формулой как ОДЗ выражения в левой части этой формулы.
Обратившись к выводам и предположения, сделанных после выполнения опережающего домашнего задания, формулируем вопрос:
— Существует общее правило (алгоритм) для нахождения области определения функции, которая задана формулой?
Выполнив несколько упражнений и сравнив результаты (например, найти ОДЗ выражения х+3 и найти область определения функции у = х + 3 и т. д.), приходим к выводу, который можно записать в конспекты учеников.
Конспект 16 | |||
Как найти область определения функции | |||
№ | Вид функции | Формулировка | Пример |
1 | Многочлен | Область определения: х — любое число | у = х2 + 3х – 2 — многочлен; область определения: х — любое число |
2 | Целый выражение | Область определения: х — любое число | у = (х + 3)2 – (х – 1)2 — целое выражение; область определения: х — любое число |
3 | Дробный выражение (знаменатель — буквенный выражение) | Область определения: те значения х, при которых знаменатель не равен нулю | — дробный выражение, х + 3 ≠ 0, х ≠ -3. Область определения: х ≠ -3 (х — любое число, кроме -3) |
V. Первичное закрепление материала
Выполнение устных упражнений
1. Дано функцию: 1) у = х + 3; 2) у = х2 + (х – 1)2; 3) .
а) Какова область определения функции? Почему?
б) какое значение приобретает функция при значении аргумента х = 1; х = -1?
в) существует Ли такое значение аргумента, при котором функция равна 0?
VI. Применение умений и навыков
Выполнение письменных упражнений
1. Функцию задано формулой . Заполните таблицу.
х | -12 | -6 |
|
|
|
| 3 | -4 |
| 1,5 |
в |
|
| 1 | 2 | -3 | 4 |
|
| 0,5 |
|
2. Найдите область определения функции, заданной формулой:
1) у = х2 + 1; 2) ; 3) ; 4) .
3. Функцию задано формулой у = х2 – 4х + 1. Составьте таблицу значений функции с шагом 1, где -3 ≤ х ≤ 4.
4. У мальчика было 1 грн. 50 к. Он купил х календариков по 25 к за штуку. Обозначив число копеек, оставшихся у мальчика, буквой у, задайте формулой зависимость у от х. Какова область определения этой функции? А область значений функции?
5*. Дополнительно (логическое упражнение). Найдите пропущенное число, букву, выражение или рисунок.
VII. Итоги урока
Какие основные понятия темы «Функция» были рассмотрены на уроке?
Установите логическую связь между названными понятиями.
VIII. Домашнее задание
Повторив содержание основных теоретических положений урока (см. схему), выполните упражнения.
№ 1. Функцию задано формулой: .
Заполните таблицу:
х | -12 | -6 |
|
|
|
| 24 | -24 |
в |
|
| 2 | 3 | -4 | -6 |
|
|
№ 2. (Придумайте) задайте формулой функцию, в которой область определения:
1) любое число; 2) все числа, кроме 2; 3) все числа, кроме чисел -2 и 2?
№ 3. Опережающее домашнее задание.
а) Решите уравнение:
1) х2 – 2х + 1 = 0; 2) х2 – 2х = 0; 3) х2 +1 = 0; 4) |х – 3| = 0; 5) |х– 3| + 1 = 0.
б) При которых х является правильной неравенство:
1) х2 – 2х + 1 ≠ 0; 2) х2 – 2х ≠ 0; 3) х2 + 1 ≠ 0; 4) |х – 3| ≠ 0; 5) |х– 3| + 1 ≠ 0?
schooled.ru
Область определения функции
Сегодня потренируемся в отыскании области определения выражения и функции.
Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции – время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю
Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.
Например, функции и имеют разные области определения: для первой это – вся числовая ось, а вторая не определена в точке 0. То же относится к функциям и – у первой область определения – также вся числовая ось, а у второй – [)
1. Найдите область определения выражения:
Перепишем выражение:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:
Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:
Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
Наносим полученные точки на координатную прямую и расставляем знаки. Так как (старший член) – со знаком «плюс», то ветви параболы направлены вверх, на самом правом отрезке ставим знак «плюс», а далее знаки меняются. Точки выкалываем, поскольку неравенство строгое:

Ответ: – круглые скобки показывают, что концы интервалов не входят в ответ.
2. Найдите область определения выражения:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:
Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
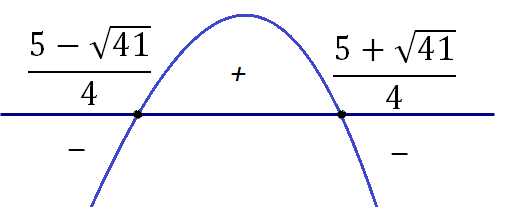
Наносим полученные точки на координатную прямую и расставляем знаки. Так как (старший член) в исходном неравенстве – со знаком «минус», то ветви параболы направлены вниз, на самом правом отрезке ставим знак «минус», а далее знаки меняются. Точки закрашиваем, поскольку неравенство нестрогое.
Ответ: – квадратные скобки показывают, что концы отрезка входят в ответ.
3. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения – ищем естественную область определения функции. Данное выражение имеет смысл только при – задача сводится к решению этого неравенства. Определяем точки перемены знака:
Изображаем полученные точки на числовой оси, ставим знаки:
Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: (] [)
4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения – ищем естественную область определения функции. Данное выражение имеет смысл только при ; – задача сводится к решению системы неравенств. Определяем точки перемены знака:
Изображаем полученные точки на числовой оси:
Решение системы неравенств:
Область определения функции: [ )
5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную область определения функции. Данное выражение имеет смысл только при – задача сводится к решению неравенства.
Рассмотрим два случая:
Решение:
Или
Решение:
Область определения функции: [)
6. Найти область определения функции:
Решение:
Ответ:
7. Найти область определения функции:
Решение:
Ответ:
8. Найти область определения функции:
Решение:
Ответ:
easy-physic.ru
Функция. Область определения функции. Область значений функции — АЛГЕБРА — Уроки для 7 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 60
Тема. Функция. Область определения функции. Область значений функции
Цель: закрепить терминологию, отработать навыки работы с понятиями функции; отработать навыки работы с функцией, заданной формуле и таблично; находить функции, аргумента, области определения функции.
Тип урока: усвоение умений и навыков.
Ход урока
I. Организационный момент (традиционно)
II. Проверка домашнего задания
@ Поскольку основная часть домашнего задания — освоение теории (определения понятий), то целесообразно проверку домашнего задания провести в форме математического диктанта.
1. Математический диктант
1) Задайте формулой функцию, которая сопоставляет каждому числу третий степень этого числа [сумма этого числа с числом 5].
2) Функция задана формулой . Найдите ее значение при значении аргумента -2 [-1].
3) Функция задана формулой у = 3х — 7 [у = 5 — 2х]. Найдите значение аргумента, при котором значение функции равно нулю.
4) При каких значениях переменной имеет смысл выражение ?
После выполнения проводится коррекция (работа в парах).
2. Работа с опережающим домашним заданием.
@ Основная цель работы с опережающим домашним заданием на этом уроке — подготовка к восприятию учащимися алгоритма нахождения области определения функции, заданной формулой (вида у = f(х)).
Поэтому далее проводим фронтальную беседу по результатам опережающего домашнего задания.
Вопрос
1. Что называют допустимым значением переменной в выражении? Приведите пример.
2. Что означает термин «область допустимых значений переменной в выражении»? Как кратко обозначается?
3. Как найти ОДЗ в выражении, которое имеет вид: а) многиочлена; б) дроби, где в знаменателе число; в) дроби, знаменателем которого является буквенный выражение; г) целого выражения?
4. Найдите ОДЗ выражений: а) х + 3; б) ; в) ; г) (х + 3)2; д) .
5. Назовите аргумент и зависимую переменную, если функция задана формулой . Каких значений приобретает функция при значении аргумента -1; 2; -3? Можно ли вычислить значение функции при х = 0? Почему? Существует ли еще какое-либо значение аргумента, при котором нельзя вычислить значение выражения? Почему? Какой будет область определения функции , исходя из сказанного выше?
6. Сравните вывод п. 4 п. 5. Что вы заметили? Какое предположение можно сделать на основании этого сравнения.
III. Формулировка цели и задач урока
@ Из работы, выполненной на предыдущем этапе урока, учащиеся должны сделать важный вывод: область определения функции может быть найдено через ОДЗ выражения, задающего данную функциональную зависимость. То есть задания функции формулой является наиболее удобным способом задания функции именно потому, что помогает решать задачи с незнакомыми или новыми для учеников объектами (функция, аргумент, область определения функции) путем выполнения знакомых ученикам действий (вычислением значений буквенных выражений, решением уравнений и нахождением ОДЗ выражения).
Следовательно, учителю остается обобщить эти мнения, и главной целью урока можно определить: отработка навыков работы с функцией, заданной формулой (нахождения аргумента функции и области определения).
IV. Дополнение знаний
@ Единственным относительно новым моментом урока является обобщающий логический шаг от алгоритма нахождения ОДЗ выражения (см. начало учебного года) до нахождения области определения функции, заданной формулой как ОДЗ выражения в левой части этой формулы.
Обратившись к выводам и предположения, сделанных после выполнения опережающего домашнего задания, формулируем вопрос:
— Существует общее правило (алгоритм) для нахождения области определения функции, которая задана формулой?
Выполнив несколько упражнений и сравнив результаты (например, найти ОДЗ выражения х+3 и найти область определения функции у = х + 3 и т. д.), приходим к выводу, который можно записать в конспекты учащихся.
Конспект 16 |
|||
Как найти область определения функции |
|||
№ |
Вид функции |
Формулировка |
Пример |
1 |
Многочлен |
Область определения: х — любое число |
у = х2 + 3х — 2 — многочлен; область определения: х — любое число |
2 |
Целый выражение |
Область определения: х — любое число |
у = (х + 3)2 — (х — 1)2 — целое выражение; область определения: х — любое число |
3 |
Дробный выражение (знаменатель — буквенный выражение) |
Область определения: те значения х, при которых знаменатель не равен нулю |
— дробное выражение, х + 3 ≠ 0, х ≠ -3. Область определения: х ≠ -3 (х — любое число, кроме -3) |
V. Первичное закрепление материала
Выполнение устных упражнений
1. Дано функцию: 1) у = х + 3; 2) у = х2 + (х — 1)2; 3) .
а) Какова область определения функции? Почему?
б) какое значение приобретает функция при значении аргумента х = 1; х = -1?
в) существует Ли такое значение аргумента, при котором функция равна 0?
VI. Применение умений и навыков
Выполнение письменных упражнений
1. Функция задана формулой . Заполните таблицу.
х |
-12 |
-6 |
|
|
|
|
3 |
-4 |
|
1,5 |
в |
|
|
1 |
2 |
-3 |
4 |
|
|
0,5 |
|
2. Найдите область определения функции, заданной формулой:
1) у = х2 + 1; 2) ; 3) ; 4) .
3. Функция задана формулой у = х2 — 4х + 1. Составьте таблицу значений этой функции с шагом 1, где -3 ≤ х ≤ 4.
4. У мальчика было 1 грн. 50 к. Он купил х календариков по 25 к за штуку. Обозначив число копеек, оставшихся у мальчика, буквой у, задайте формулой зависимость у от х. Какова область определения этой функции? А область значений функции?
5*. Дополнительно (логическая упражнение). Найдите пропущенное число, букву, выражение или рисунок.
VII. Итоги урока
Какие основные понятия темы «Функция» были рассмотрены на уроке?
Установите логическую связь между названными понятиями.
VIII. Домашнее задание
Повторив содержание основных теоретических положений урока (см. схему) выполните упражнения.
№ 1. Функция задана формулой: .
Заполните таблицу:
х |
-12 |
-6 |
|
|
|
|
24 |
-24 |
в |
|
|
2 |
3 |
-4 |
-6 |
|
|
№ 2. (Придумайте) задайте формулой функцию, в которой область определения:
1) любое число; 2) все числа, кроме 2; 3) все числа, кроме чисел -2 и 2?
№ 3. Опережающее домашнее задание.
а) Решите уравнение:
1) х2 — 2х + 1 = 0; 2) х2 — 2х = 0; 3) х2 +1 = 0; 4) |х — 3| = 0; 5) |х — 3| + 1 = 0.
б) При которых х является правильной неравенство:
1) х2 — 2х + 1 ≠ 0; 2) х2 — 2х ≠ 0; 3) х2 + 1 ≠ 0; 4) |х — 3| ≠ 0; 5) |х — 3| + 1 ≠ 0?
na-uroke.in.ua
Как найти область определения функции???
При решении многих задач приходится искать область определения функции. Особенно это нужно знать при построении графика и исследовании функции. Именно поэтому я решил рассмотреть основные варианты, которые могут быть при нахождении области определения функции. Их не так много, наверняка, многие это знают и сами, но думаю, напомнить не будет лишним.
И так, область определения функции – это множество всех тех значений переменной х, при каких функция f(x) имеет смысл. То есть значения переменной х, при которых функция от этой переменной существует, а могут быть и такие, при каких она не существует, нам нужны, только те, при которых – существует.
Рассмотрим конкретные варианты, в каких случаях функция может существовать не при всех значениях переменной:
- Во-первых, когда есть дробь, в этом случае знаменатель дроби, недолжен быть равным нулю, потому, что такая дробь не может существовать. То есть, если ваша функция — дробь и в знаменателе есть переменная (потому, что если там только число, то оно никогда не станет нулём) то вам надо всё то выражение, что в знаменателе прировнять к нулю. И решив полученное уравнение, вы найдёте те значения переменной x, которые необходимо исключить с области определения.
- Во-вторых, когда есть корень чётной степени, думаю, вы знаете, что в поле вещественных чисел, корень чётной степени может быть только с положительного числа. То есть если в вас есть функция с корнем чётной степени, то что бы найти те числа, которые не будут попадать в область определения, вам надо решить неравенство, где выражение, что под корнем будет меньше нуля.
- В-третьих, когда есть логарифм. Здесь понятно, что область определения логарифма все числа, которые больше ноля. То есть что бы найти те значения переменной, которые надо исключить с области определения, вам надо составить и решить неравенство, где выражение, которое будет под логарифмом должно быть меньше нуля.
- В-четвёртых, не надо забыть о таких обратных тригонометрических функциях, как арксинус и арккосинус, которые определены, только на промежутке [-1;1]. Соответственно вам надо следить, что бы выражение, которое будет под этими функциями, также попадало в этот промежуток и исключить все значения переменной, которые туда не попадают.
- И в-пятых, в одном примере может быть несколько этих случаев. Надо разбирать всё, до мельчайших подробностей. Например, в знаменателе дроби, может быть корень из арксинуса :), поэтому вам надо отобрать, только те значения переменной, при которых существует арксинус, при чём значение этого арксинуса должно не должно быть равное нулю (так как оно в знаменателе) и также не должно быть отрицательным (так как есть корень).
Я постарался собрать самые основные случаи, когда область определения функции – это не все вещественные числа. Конечно, примеры могут быть на много сложнее, потому что даже эти четыре варианты можно так скомбинировать, что на то что бы разобраться, что там и от чего зависит, пойдёт не мало времени. И ещё, я даже не все перечислил.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
