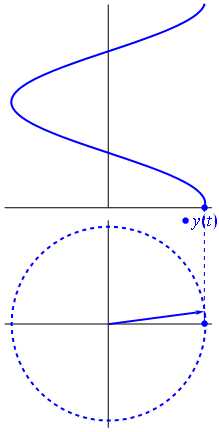
Wiki-учебникПоиск по сайтуРеклама от партнёров: | Свойства синуса
Свойства косинуса
Свойства тангенса
Свойства котангенса
На рисунке ниже представлены несколько единичных окружностей, в которых указаны знаки синуса, косинуса, тангенса и котангенса в различных координатных четвертях. Нужна помощь в учебе?Предыдущая тема: Определение синуса, косинуса, тангенса и котангенса и примеры Следующая тема:   Радианная мера угла: что означает, таблица соответствий с градусами Все неприличные комментарии будут удаляться. |
www.nado5.ru
Область значений cosx
Чтобы найти область значений cosx, нужно вспомнить определение косинуса.
Косинус альфа на единичной окружности — это абсцисса точки, полученной при повороте из точки P0 на угол альфа.
Таким образом, наименьшее значение косинуса равно-1, так как на единичной окружности наименьшее значение х равно -1 (точка с наименьшей абсциссой находится слева, в α=П).
Наибольшее значение косинуса равно 1, поскольку наибольшее значение x на единичной окружности равно 1 (оно достигается справа, в α=0).
Следовательно, область значений косинуса — промежуток [-1;1]. С помощью двойного неравенства область значений косинуса можно записать так:
Область значений косинуса не зависит от аргумента (за исключением случаев, когда аргумент представляет собой сложное выражение с дополнительными ограничениями на область определения и область значений):
Таким образом, наименьшее значение cos x, cos(15α), cos(5-11x) и т.д. равно -1;
наибольшее значение cos x, cos(4φ), cos(5х+3) и т.д. равно 1.
Область значений функции y=cos x — также промежуток [-1;1].
Так как число в четной степени неотрицательно, область значений квадрата косинуса — промежуток[0;1] или
Аналогично находим область значений модуля косинуса — промежуток [0;1] или
Далее рассмотрим, как, опираясь на ограничения значений косинуса и синуса, можно оценить значения тригонометрического выражения и найти область значения функции.
www.uznateshe.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения
| ||||||||||||||||||||||
dpva.ru
Свойства тригонометрических функций
Свойства синуса
- Область определения – множество всех действительных чисел.
- Область изменения (множество значений) – отрезок .
- Функция – нечетная, то есть .
- Функция периодическая, с периодом .
- Нули функции: при .
- Промежутки знакопостоянства
- Функция непрерывная и имеет производную при любом значении аргумента:
- Функция возрастает при , и убывает при .
- Функция имеет минимальные значения, равные , при , и максимальные значение равные 1, при .
Подробнее про синус угла читайте по ссылке.
Свойства косинуса
- Область определения – множество всех действительных чисел.
- Область изменения (множество значений) – отрезок .
- Функция – четная, то есть .
- Функция периодическая, с периодом .
- Нули функции: при .
- Промежутки знакопостоянства
- Функция непрерывная и имеет производную в любом значении аргумента
- Функция возрастает при , и убывает при .
- Минимальные значения функции равные принимает при , а максимальные значение равные 1, при .
Подробнее про косинус угла читайте по ссылке.
Свойства тангенса
- Область определения – множество всех действительных чисел, кроме чисел
- Область изменения (множество значений) – множество всех действительных чисел.
- Функция – нечетная, то есть .
- Функция периодическая, её период равен .
- Нули функции: при .
- Промежутки знакопостоянства
- Функция непрерывная и дифференцируема при любом значении аргумента из области определения функции:
- Функция возрастает в каждом из промежутков .
Свойства котангенса
- Область определения – множество всех действительных чисел, кроме чисел
- Область изменения (множество значений) – множество всех действительных чисел.
- Функция – нечетная, то есть .
- Функция периодическая, её период равен .
- Нули функции: при .
- Промежутки знакопостоянства
- Функция непрерывная и дифференцируема при любом значении аргумента из области определения функции:
- Функция убывает в каждом из промежутков .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т — период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
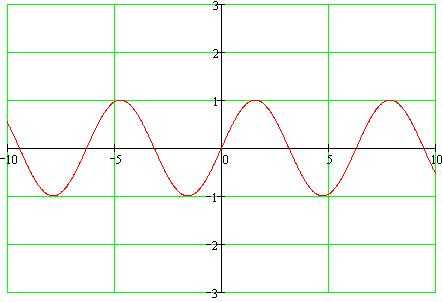
Функция синус y = sin(x).
Изобразим график функции синус, его называют «синусоида».
Свойства функции синус y = sinx.
Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
Наименьший положительный период функции синуса равен двум пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
Функция синус — нечетная, так как .
Функция убывает при , возрастает при .
Функция синус имеет локальные максимумы в точках , локальные минимумы в точках .
Функция y = sinx вогнутая при , выпуклая при .
Координаты точек перегиба .
Асимптот нет.
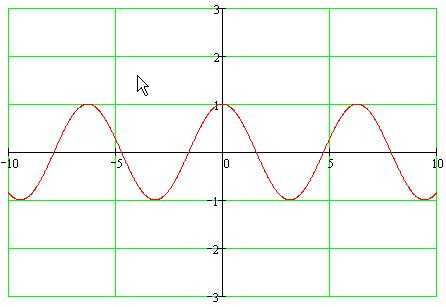
Функция косинус y = cos(x).
График функции косинус (его называют «косинусоида») имеет вид:
Свойства функции косинус y = cosx.
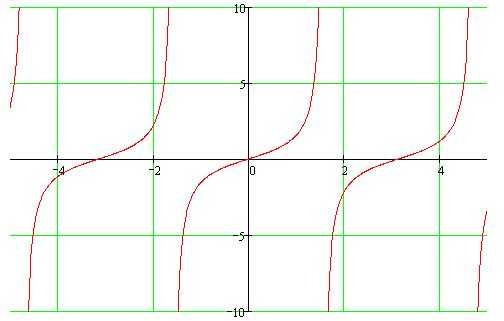
Функция тангенс y = tg(x).
График функции тангенс (его называют «тангенсоида») имеет вид:
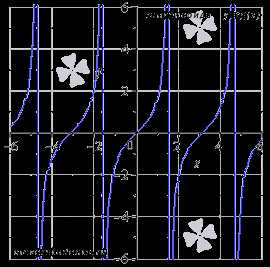
Свойства функции тангенс y = tgx.
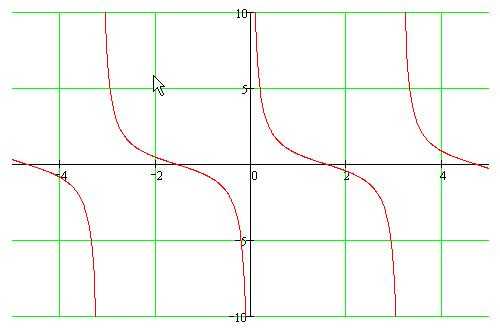
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют «котангенсоида»):
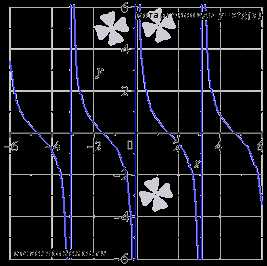
Свойства функции котангенс y = ctgx.
studfiles.net
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
Свойства функции синуса
Понятие синуса
Перед изучением функции синуса и её свойств, вспомним понятие самого синуса. Определение синуса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью тригонометрической окружности.
Определение 1
Синусом острого угла называется отношение длины противолежащего катета к гипотенузе прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{a}{c}\]Рисунок 1. Прямоугольный треугольник.
Определение 2
Синусом острого угла называется ордината единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан (рис. 2).

Рисунок 2. Значение синуса с помощью единичной окружности.
Введем таблицу некоторых значений синуса (таблица 1).
Рисунок 3. Значения синуса.
Свойства функции $f(x)=sinx$
Рассмотрим теперь свойства функции $f\left(x\right)=sinx$.
- Область определения — все числа.
- Так как по определению 2 значение синуса определяется с помощью единичной окружности, то область значения данной функции отрезок $[-1,\ 1]$.
- $f\left(-x\right)={sin \left(-x\right)\ }=-sinx=-f(x)$, следовательно, функция$f\left(x\right)=sinx$ нечетна.
- $f\left(x+2\pi \right)={sin \left(x+2\pi \right)\ }=sinx=f(x)$, следовательно, функция $f\left(x\right)=sinx$ периодическая с минимальным периодом $2\pi $.
- Пересечение с осями координат: При $x=0$, $f\left(0\right)=sin0=0$. При $y=0$, $x=\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in (2\pi n,\pi +2\pi n),n\in Z$.
- Функция ниже оси $Ox$ при $x\in (-\pi +2\pi n,2\pi n),n\in Z$.
- $f’ (x)=(sinx)’=cosx$.\[cosx=0\] \[x=\frac{\pi }{2}+\pi n,\ n\in Z\]
Функция $f\left(x\right)=sinx$ возрастает, при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right)$.
Функция $f\left(x\right)=sinx$ убывает при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right)$.
Точки максимума $(\frac{\pi }{2}+2\pi n,1)$.
Точки минимума $(\frac{3\pi }{2}+2\pi n,-1)$.
- Функция непрерывна на всей области определения.
График функции $y=sinx$
Графиком функции $y=sinx$ является синусоида (рис. 3).
Рисунок 4. Синусоида.
Задачи на построение синусоид
Пример 1
Построить график функции $y=sinx-1$.
График данной функции получается из функции $y=sinx$ путем смещения вдоль оси $Oy$ на 1 единицу вниз:
Рисунок 5.
Пример 2
Построить график функции $y=sin\left(x+\frac{\pi }{2}\right)$.
График данной функции получается из функции $y=sinx$ путем смещения вдоль оси $Ox$ на $\frac{\pi }{2}$ единиц влево.
Рисунок 6.
spravochnick.ru