Второй признак равенства треугольников / Треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Второй признак равенства треугольников
Теорема
| Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
Пример:
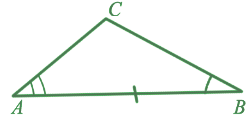
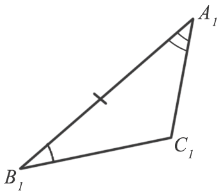
 ABC =
ABC = 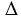 A1B1C1
A1B1C1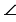 A =
A = 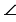 A1,
A1, 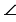 B =
B = 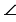 B1.
B1.
Доказательство:
Дано: 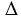 ABC,
ABC, 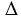 A1B1C1, AB = A1B1,
A1B1C1, AB = A1B1, 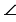 A =
A = 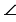 A1,
A1, 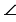 B =
B = 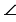 B1.
B1.
Доказать: 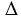 ABC =
ABC = 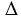 A1B1C1
A1B1C1
Доказательство:


Рассмотрим 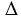 ABC и
ABC и 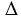
Поскольку 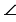 A =
A = 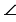 A1 и
A1 и 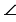 B =
B = 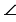
Таким образом
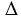 ABC и
ABC и 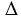 A1B1C1 полностью совместятся, поэтому они равны, что и требовалось доказать.
A1B1C1 полностью совместятся, поэтому они равны, что и требовалось доказать.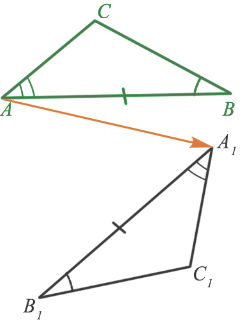
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольникСвойства равнобедренного треугольника
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 126, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 129, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 131, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 139, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 170, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 204, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 337, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 342, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 371, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
math-public:priznaki-ravenstva-treugolnikov [Президентский ФМЛ №239]
Определение
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.Определение
Треугольники называются равными, если их можно совместить наложением.
Теорема
Пусть на прямой $AB$ точка $O$ лежит между точками $A$ и $B$. Если от лучей $OA$ и $OB$ в разные полуплоскости отложить лучи $OC$ и $OD$ соответственно так, чтобы $\angle COA=\angle DOB$, то точки $C, O$ и $D$ лежат на одной прямой.
Доказательство
Предположим противное.
Тогда продолжим луч $CO$ за точку $O$: получим луч $OC_1$
Тогда $\angle COA=\angle BOC_1$, как вертикальные, и от луча $OB$ отложены два равных угла $\angle DOB$ и $\angle COC_1$, что противоречит аксиоме.
Первый признак равенства треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, AC=A_1C_1, \angle A=\angle A_1$.
Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.
Так как $\angle A=\angle A_1$, то согласно аксиоме треугольник $ABC$ можно наложить на треугольник $A_1B_1C_1$ так, что вершина $A$ совместиться с вершиной $A_1$, а стороны $AB$ и $AC$ наложатся соответственно на лучи $A_1B_1$ и $A_1C_1$.
В силу аксиомы, так как $AB=A_1B_1$ и $AC=A_1C_1$, то стороны $AB$ и $A_1B_1$, $AC$ и $A_1C_1$ совместиться.
В частности совместятся точки $B$ и $B_1$, $C$ и $C_1$.
Следовательно, по аксиоме совместятся и стороны $BC$ и $B_1C_1$.
Итак, треугольники $ABC$ и $A_1B_1C_1$ полностью совместились.
Следовательно, согласно определению, они равны.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, \angle A=\angle A_1, \angle B=\angle B_1$.
Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.
Наложим треугольник $ABC$ на треугольник $A_1B_1C_1$ так, чтобы вершина $A$ совместилась с вершиной $A$, сторона $AB$ – с равной ей стороной $A_1B_1$, а вершины $C$ и $C_1$ оказались по одну сторону от прямой $A_1B_1$.
Так как $\angle A=\angle A_1$ и $\angle B=\angle B_1$, то по сторона $AC$ наложится на луч $A_1C_1$, а сторона $BC$ – на луч $B_1C_1$.
Поэтому вершина $C$ – общая точка сторон $AC$ и $BC$ – окажется как лежащей на луче $A_1C_1$, так и на луче $B_1C_1$ и, следовательно, совместиться с общей точкой этих лучей – вершиной $C_1$.
Значит, совместятся стороны $AC$ и $A_1C_1$, $BC$ и $B_1C_1$.
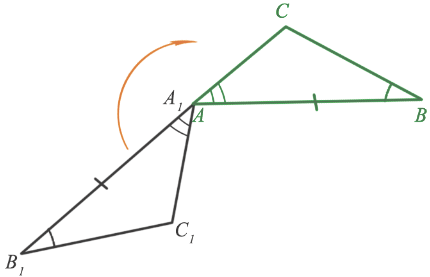
Итак треугольники $ABC$ и $A_1B_1C_1$ полностью совместятся.
Следовательно, они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство
Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $AB=A_1B_1, AC=A_1C_1, BC=B_1C_1$.
Докажем, что $\triangle ABC=\triangle A_1B_1C_1$.
Приложим треугольник $ABC$ к треугольнику $A_1B_1C_1$ так, чтобы вершина $A$ совместилась с вершиной $A_1$, вершина $B$ – C вершиной $B_1$, а вершины $C$ и $C_1$ оказались по разные стороны от прямой $A_1B_1$.
Возможны три случая:
луч $C_1C$ проходит внутри угла $A_1C_1B_1$
луч $C_1C$ совпадает с одной из сторон этого угла
луч $C_1C$ проходит вне угла $A_1C_1B_1$.
Рассмотрим первый случай.
По условию теоремы $AB=A_1B_1, AC=A_1C_1, BC=B_1C_1$, следовательно, треугольники $A_1C_1C$ и $B_1C_1C$ – равнобедренные.
По теореме $\angle 1=\angle 2, \angle 3=\angle 4$, поэтому $\angle A_1CB_1=\angle A_1C_1B_1$.
Итак, $AC=A_1C_1, BC=B_1C_1, \angle C=\angle C_1$.
Следовательно, треугольники $ABC$ и $A_1B_1C_1$ равны по первому признаку равенства треугольников.
Рассмотрим второй случай.
Пусть луч $C_1C$ совпадает со стороной $C_1B$ угла $A_1C_1B_1$.
Тогда, так как $AC=A_1C_1$, то треугольник $СA_1C_1$ равнобедренный, и ,следовательно, $\angle C=\angle C_1$.
Тогда треугольники $A_1BC_1$ и $ABC$ равны по первому признаку равенства треугольников.
Рассмотрим третий случай.
Третий случай доказывается аналогично первому.
math-public/priznaki-ravenstva-treugolnikov.txt · Последние изменения: 2016/05/06 11:15 — labreslav
Второй признак подобия треугольников. Видеоурок. Геометрия 8 Класс
Подобными называются такие треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника (см. рис. 1).
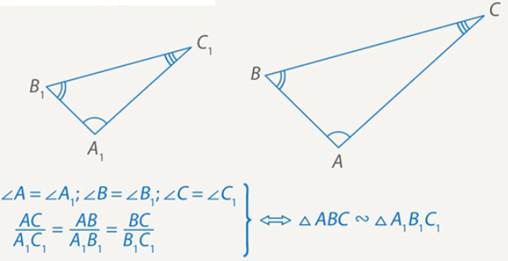
Рис. 1. Подобные треугольники
Отношение длин сторон одного треугольника к сходственным сторонам другого называется коэффициентом подобия (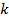 ):
): 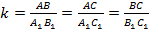 .
.
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны (см. рис. 2).

Рис. 2. Первый признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум другим сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Дано: 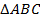 ;
; 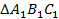 ;
; 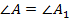 ;
; 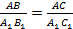 (см. рис. 3).
(см. рис. 3).
Доказать: подобие данных треугольников 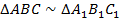 .
.
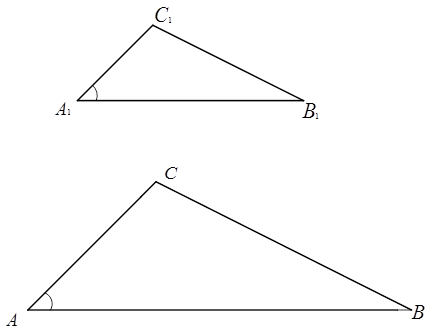
Рис. 3. Иллюстрация к доказательству
Доказательство
Согласно первому признаку подобия треугольников, треугольники подобны, если два угла одного соответственно равны двум углам другого. Поэтому для доказательства того, что 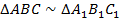 , необходимо доказать, что угол
, необходимо доказать, что угол 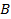 равен углу
равен углу 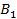 (угол
(угол 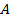 равен углу
равен углу 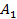 по условию).
по условию).
Построим треугольник 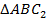 (см. рис. 4), у которого
(см. рис. 4), у которого 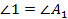 , а
, а 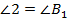 . Согласно первому признаку подобия треугольников
. Согласно первому признаку подобия треугольников 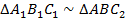 (признак подобия по двум углам).
(признак подобия по двум углам).
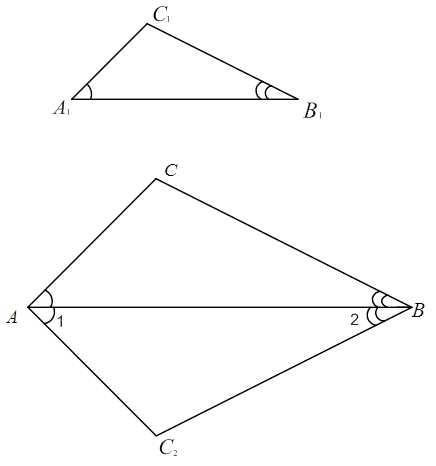
Рис. 4. Иллюстрация к доказательству
Из подобия этих треугольников следует, что сторона 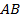 относится к стороне
относится к стороне 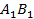 как сторона
как сторона 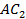 относится к стороне
относится к стороне 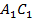 :
:
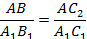
Из условия известно, что 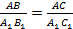 . Следовательно,
. Следовательно, 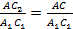 . Таким образом,
. Таким образом, 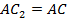 .
.
Получаем, что треугольники 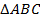 и
и 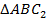 равны, так как у них равны две стороны и угол между ними (
равны, так как у них равны две стороны и угол между ними (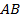 – общая сторона,
– общая сторона, 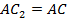 и
и 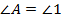 , поскольку
, поскольку 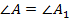 и
и 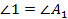 ).
).
Отсюда следует, что 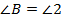 , а так как
, а так как 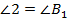 , то
, то 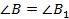 .
.
У треугольников 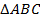 и
и 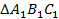 :
: 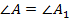 , а
, а 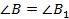 . Согласно первому признаку подобия треугольников эти треугольники подобны:
. Согласно первому признаку подобия треугольников эти треугольники подобны: 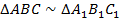 . Что и требовалось доказать.
. Что и требовалось доказать.
По данным рисунка 5 найти длину x, доказать, что 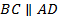 .
.
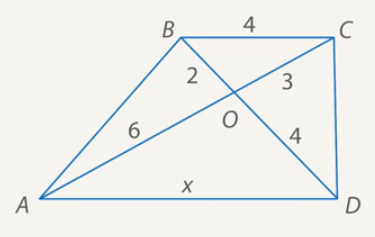
Рис. 5. Иллюстрация к задаче
Решение
1) Рассмотрим два треугольника с общей вершиной 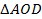 и
и  :
: 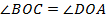 , так как они вертикальные.
, так как они вертикальные.
Прилегающие стороны у этих треугольников пропорциональны: 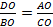 .
.
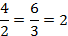
Следовательно, эти треугольники подобны (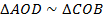 ), согласно второму признаку подобия. Коэффициент подобия равен 2. С помощью него определим длину
), согласно второму признаку подобия. Коэффициент подобия равен 2. С помощью него определим длину 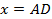 .
.
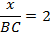
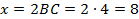
2) Так как 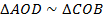 , то все углы у них равны.
, то все углы у них равны.  – эти углы являются накрест лежащими при пересечении прямых
– эти углы являются накрест лежащими при пересечении прямых  и
и 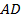 секущей
секущей 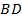 . Таким образом,
. Таким образом, 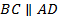 , что и требовалось доказать.
, что и требовалось доказать.
Ответ: параллельность прямых  и
и 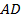 доказана;
доказана; 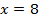 .
.
По данным рисунка найти длину 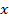 , отметить равные углы и доказать, что
, отметить равные углы и доказать, что 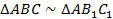 (см. рис. 6).
(см. рис. 6).
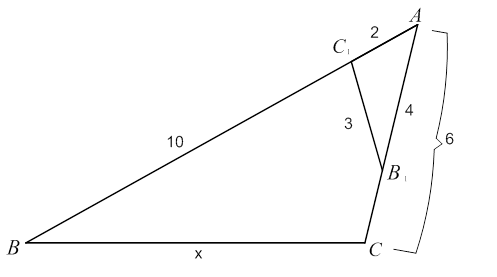
Рис. 6. Иллюстрация к задаче
Решение
1) 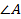 является общим для треугольников
является общим для треугольников 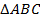 и
и 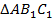 . К данному углу прилегают сторона
. К данному углу прилегают сторона 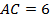 и сторона
и сторона 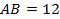 треугольника
треугольника 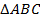 , а также сторона
, а также сторона 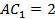 и сторона
и сторона 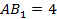 треугольника
треугольника 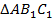 .
.
Видно, что 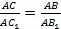 .
.
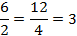
Следовательно, 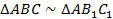 , согласно второму признаку подобия треугольников (общий угол и пропорциональность прилежащих сторон).
, согласно второму признаку подобия треугольников (общий угол и пропорциональность прилежащих сторон).
2) Коэффициент подобия у этих треугольников равен 3, поэтому можно определить сторону 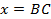 :
: 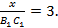
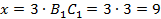
3) Стороны 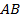 и
и 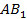 являются сходственными, следовательно, они лежат напротив равных углов:
являются сходственными, следовательно, они лежат напротив равных углов: 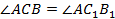 .
.
Стороны 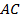 и
и 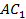 также являются сходственными, следовательно,
также являются сходственными, следовательно, 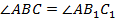 .
.
Отметим равные углы на рисунке (см. рис. 7).
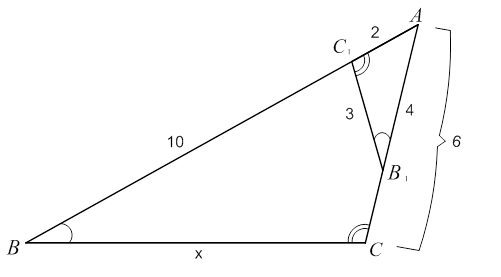
Рис. 7. Иллюстрация к задаче
Ответ: 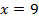 ;
; 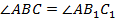 ;
; 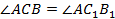 ;
; 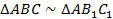 .
.
Найти длину 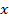 , отметить равные углы и доказать, что
, отметить равные углы и доказать, что 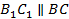 (см. рис. 8).
(см. рис. 8).
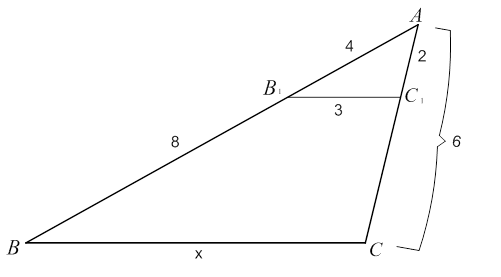
Рис. 8. Иллюстрация к задаче
Решение
1) 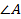 является общим для треугольников
является общим для треугольников 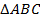 и
и 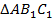 . К данному углу прилегают сторона
. К данному углу прилегают сторона 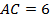 и сторона
и сторона 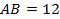 треугольника
треугольника 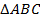 , а также сторона
, а также сторона 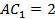 и сторона
и сторона 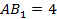 треугольника
треугольника 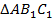 .
.
Видно, что 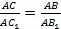 .
.
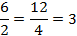
Стороны треугольников, прилежащие к 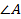 , пропорциональные, следовательно,
, пропорциональные, следовательно, 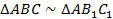 , согласно второму признаку подобия треугольников.
, согласно второму признаку подобия треугольников.
2) Стороны 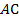 и
и 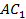 являются сходственными, следовательно, они лежат напротив равных углов:
являются сходственными, следовательно, они лежат напротив равных углов: 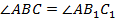 .
.
Стороны 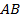 и
и 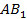 также являются сходственными, следовательно,
также являются сходственными, следовательно, 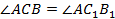 .
.
Отметим равные углы на рисунке (см. рис. 9).
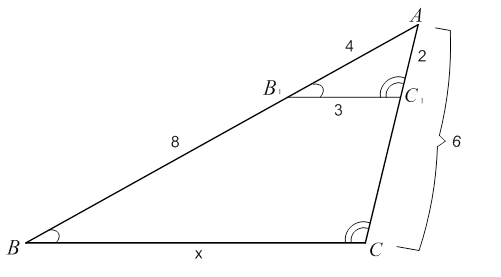
Рис. 9. Иллюстрация к задаче
3) 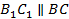 , так как эти прямые пересекаются секущей
, так как эти прямые пересекаются секущей 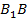 и при этом соответственные углы равны (
и при этом соответственные углы равны (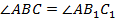 ).
).
4) Коэффициент подобия у треугольников 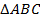 и
и 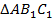 равен 3, поэтому можно определить сторону
равен 3, поэтому можно определить сторону 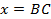 :
: 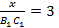 .
.
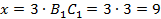
Ответ: 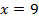 ;
; 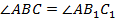 ;
; 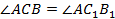 ; параллельность прямых
; параллельность прямых 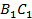 и
и  доказана.
доказана.
Домашнее задание
- Задачи 557, 559- Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. Геометрия, 7-9 классы (Источник).
 ;
;  ;
;  ;
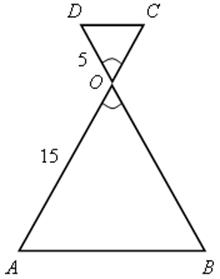
;  (см. рис. 10). Найти
(см. рис. 10). Найти  и
и  .
. 
Рис. 10. Иллюстрация к задаче- В треугольнике
 точка
точка  лежит на стороне
лежит на стороне  ,
,  ,
,  ,
,  . Докажите, что
. Докажите, что  (см. рис. 11).
(см. рис. 11). 
Рис. 11. Иллюстрация к задаче
Список рекомендованной литературы
- Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. Геометрия, 7-9 классы – М.: Просвещение, 2010.
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Рекомендованные ссылки на ресурсы сети Интернет
- Tutoronline.ru (Источник).
- Youtube.com
Второй и третий признаки равенства треугольников — урок. Геометрия, 7 класс.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

MN=PR;∡N=∡R;∡M=∡P.
Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как MN=PR, то эти отрезки совмещаются, если совместить их конечные точки.
2. Так как ∡N=∡R и ∡M=∡P, то лучи \(MK\) и \(NK\) наложатся соответственно на лучи \(PT\) и \(RT\).
3. Если совпадают лучи, то совпадают точки их пересечения \(K\) и \(T\).
4. Совмещены все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит, они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

MN=PR;KN=TR;MK=PT.
Опять попробуем совместить треугольники ΔMNK и ΔPRT наложением и убедиться, что соответственно равные стороны гарантируют и равенство соответственных углов этих треугольников, и они полностью совпадут.

Совместим, например, одинаковые отрезки \(MK\) и \(PT\). Допустим, что точки \(N\) и \(R\) при этом не совмещаются.
Пусть \(O\) — середина отрезка \(NR\). Соответственно данной информации MN=PR, KN=TR. Треугольники \(MNR\) и \(KNR\) равнобедренные с общим основанием \(NR\).
Поэтому их медианы \(MO\) и \(KO\) являются высотами, значит, перпендикулярны \(NR\). Прямые \(MO\) и \(KO\) не совпадают, так как точки \(M\), \(K\), \(O\) не лежат на одной прямой. Но через точку \(O\) прямой \(NR\) можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
Доказано, что должны совместиться и вершины \(N\) и \(R\).
Третий признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда говорят, что треугольник — жёсткая фигура. Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.
Но своеобразную устойчивость, стабильность и совершенство числа \(3\) люди оценивали и выделяли давно.
Об этом говорят сказки.
Там мы встречаем «Три медведя», «Три ветра», «Три поросёнка», «Три товарища», «Три брата», «Три счастливца», «Трое умельцев», «Три царевича», «Три друга», «Три богатыря» и др.
Там даются «три попытки», «три совета», «три указания», «три встречи», исполняются «три желания», нужно потерпеть «три дня», «три ночи», «три года», пройти через «три государства», «три подземных царства», выдержать «три испытания», проплыть через «три моря».

И в заключение ещё раз вспомним все признаки равенства треугольников.
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Второй признак подобия треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Второй признак подобия треугольников
Теорема
Доказательство
Дано: 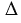 АВС и
АВС и 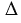 А1В1С1,
А1В1С1,  А =
А =  А1,
А1, 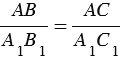
Доказать: 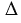 АВС
АВС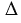 А1В1С1
А1В1С1
Доказательство:
Рассмотрим 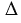 АВС и
АВС и 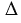 А1В1С1, у которых
А1В1С1, у которых 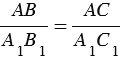 и
и  А =
А =  А1:
А1:

Для доказательства теоремы, учитывая первый признак подобия треугольников, достаточно доказать, что  В =
В =  В1.
В1.
Рассмотрим 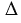 АВС2, у которого
АВС2, у которого  1 =
1 =  А1,
А1,  2 =
2 =  В1.
В1.
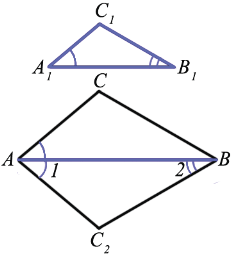
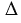 АВС2
АВС2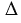 А1В1С1 по первому признаку подобия треугольников, поэтому
А1В1С1 по первому признаку подобия треугольников, поэтому 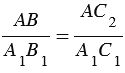 . С другой стороны, по условию
. С другой стороны, по условию 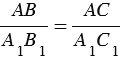 . Из этих двух равенств получаем АС = АС2.
. Из этих двух равенств получаем АС = АС2.
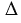 АВС =
АВС =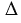 АВС2 по первому признаку равенства треугольников (АВ — общая сторона, АС = АС2 и
АВС2 по первому признаку равенства треугольников (АВ — общая сторона, АС = АС2 и  А =
А =  1, поскольку
1, поскольку  А =
А =  А1 и
А1 и  1 =
1 =  А1). Отсюда следует, что
А1). Отсюда следует, что  В =
В =  2, а так как
2, а так как  2 =
2 =  В1, то
В1, то  В =
В =  В1. Теорема доказана.
В1. Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 553, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 613, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 626*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 630, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 849, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 854, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Признаки равенства треугольников [wiki.eduVdom.com]
Рис.1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Рис.2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Рис.3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого
треугольника, то такие треугольники равны (подробнее).
Пример 1. В треугольниках ABC и DEF (рис. 4)
Рис.4
∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Сравнить треугольники ABC и DEF. Какой угол в треугольнике DEF равен углу В?
Решение. Данные треугольники равны по первому признаку. Угол F треугольника DEF равен углу В треугольника ABC, так как эти углы лежат против соответственно равных сторон DE и АС.
Пример 2. Отрезки АВ и CD (рис. 5) пересекаются в точке О, которая является серединой каждого из них. Чему равен отрезок BD, если отрезок АС равен 6 м?
Рис.5
Решение. Треугольники АОС и BOD равны (по первому признаку): ∠ АОС = ∠ BOD (вертикальные), АО = ОВ, СО = OD (по условию).
Из равенства этих треугольников следует равенство их сторон, т. е. АС = BD. Но так как по условию АС = 6 м, то и BD = 6 м.
Пример 3. В треугольниках ABC и DEF (см. рис. 4) АВ = EF, ∠A = ∠E, ∠B = ∠F.
Рис.4
Сравнить эти треугольники. Какие стороны в треугольнике DEF равны соответственно сторонам ВС и СА?
Решение. Треугольники ABC и DEF равны по второму признаку. Стороны DF и DE треугольника DEF равны соответственно сторонам ВС и СА треугольника ABC, так как стороны DF и ВС (DE и СА) лежат против равных углов Е и A (F и В).
Пример 4. На рисунке 6 углы DAB и СВА, CAB и DBA равны, СА = 13 м. Найти DB.
Решение. Треугольники АСВ и ADB имеют одну общую сторону АВ и по два равных угла, которые прилежат к этой стороне. Следовательно, треугольники АСВ и ADB равны (по второму признаку). Из равенства этих треугольников следует равенство сторон BD и АС, т. е. BD = 13 м.
Второй признак равенства треугольников
Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство:
Пусть АВС и А1В1С1 — треугольники, у которых АВ=А1В1, ∠А=∠А1, ∠В=∠В1. Доказать, что ∆ АВС= ∆ А1В1С1.

Наложим треугольник АВС на треугольник А1В1С1 таким образом, чтобы вершина А совместилась с вершиной А1, сторона АВ — с равной ей стороной А1В1, а вершины С и С1 оказались по одну сторону от прямой А1В1.

Так как ∠А=∠А1 и ∠В=∠В1, то сторона АС наложится на луч А1С1, а сторона ВС — на луч В1С1. Поэтому вершина С (общая точка сторон АС и ВС) окажется лежащей на лучах А1С1 и В1С1, а следовательно, совместится с общей точкой этих лучей — вершиной С1. Значит, совместятся стороны АС и А1С1, ВС и В1С1. Получаем, что ∆ АВС и ∆ А1В1С1 полностью совместятся, то есть они равны.
Пример.
Доказать, что в равнобедренном треугольнике биссектрисы, поведённые к боковым сторонам, равны между собой.

Пусть треугольник АВС равнобедренный, у которого АВ=ВС. АМ и CN — биссектрисы. Рассмотрим треугольники АМВ и CNB. У них угол В — общий, АВ=ВС по условию, углы NСВ и МАВ равны как половинки двух равных углов при основании равнобедренного треугольника.
Тогда получаем, что ∆ АМВ=∆ CNB по второму признаку. Откуда следует, что АМ=СN.
Пример.
Точки Е и F лежат соответственно на сторонах АВ и CD квадрата ABCD так, что ∠FВС=∠ЕDА. Доказать, что ∆ СBF= ∆ ADE.

Рассмотрим ∆ СBF и ∆ ADE. У них сторона ВС=AD, так как все стороны квадрата равны, ∠ВСF=∠DAE, так как все углы квадрата прямые, ∠FВС=∠ЕDА по условию задачи. А следовательно, ∆ СBF и ∆ ADE равны по второму признаку равенства треугольников.
Пример.
Отрезки АВ и CD пересекаются в точке Е, которая является серединой отрезка АВ, а ∠EAD и ∠EBC — равны. Доказать, что ∆ СВЕ и ∆ ADE равны. Чему равна длина отрезка AD, если отрезок СВ=7 см?

Рассмотрим ∆ СВЕ и ∆ ADE. У них сторона АЕ=ВЕ, так как Е — середина отрезка АВ. ∠EAD и ∠EBC равны по условию задачи. А ∠СЕВ и ∠AED равны как вертикальные. Получаем, что ∆ СВЕ и ∆ ADE равны по второму признаку. Следовательно, у них соответственные стороны равны. Значит, сторона AD=СВ. То есть AD=7 см.

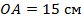 ;
; 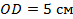 ;
; 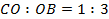 ;
; 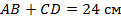 (см. рис. 10). Найти
(см. рис. 10). Найти 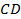 .
. 
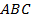 точка
точка 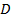 лежит на стороне
лежит на стороне 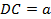 ,
, 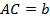 ,
, 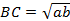 . Докажите, что
. Докажите, что 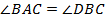 (см. рис. 11).
(см. рис. 11).