Транспонированная матрица
Если
в матрице 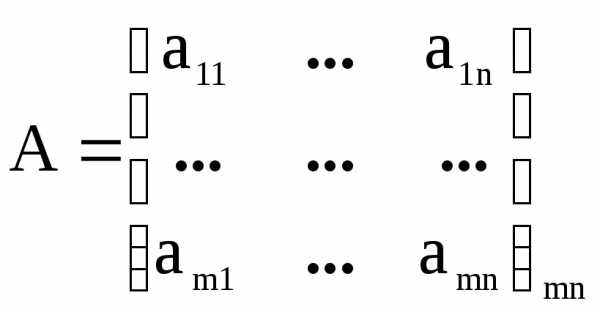 строки
и столбцы поменять местами, то получим
транспонированную матрицу.
строки
и столбцы поменять местами, то получим
транспонированную матрицу.
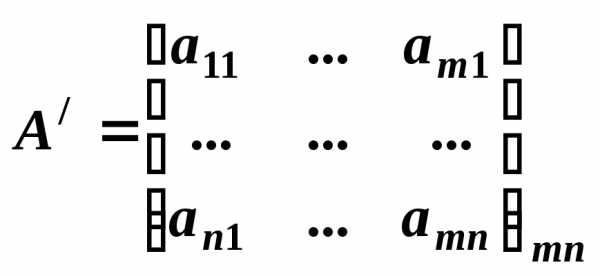
Свойства:
дважды транспонированная матрица равна исходной
А = (А )= А;
(А+В) =А+ В;
(АВ) =ВА, т.е. (АВ) ≠ АВ;
Если А=А, то матрица А— симметричная
(аij=aji
Обратная матрица
Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А-1.
АА-1=А-1А=Е.
Нахождение обратной матрицы для данной называется обращением данной матрицы.
Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы.
Пусть имеем матричное равенство
АС=В.
Умножим правую и левую часть равенства на обратную матрицу А-1
А-1АС= А-1В.
Поскольку известно, что А-1А=Е, то
ЕС= А -1В.
И поскольку известно, что ЕС=С, то
С= А-1В.
То есть, мы равенство АС=В преобразовали в равенство С= А-1В, выразив матрицу С.
Если
бы у нас были простые алгебраические
числа а, bи с, то аналогичные
преобразования были бы следующие: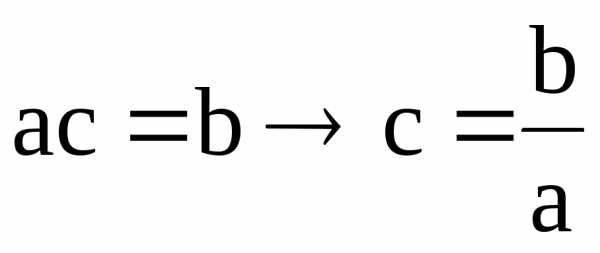 .
.
Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.
Алгоритм получения обратной матрицы
Вычисление det A;
Транспонирование матрицы ;
Определение алгебраических дополнений Аji,j=1,N;i
Составление союзной матрицы
 ;
;Вычисление обратной матрицы
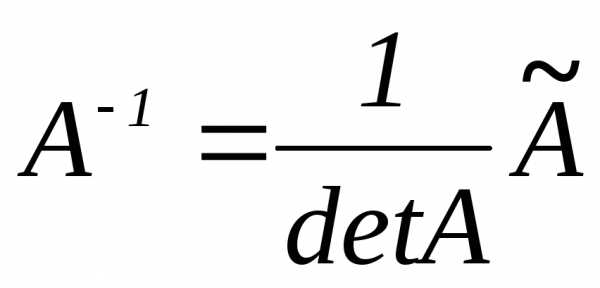
 ;
;
Проверка А-1А=Е.
Существуют другие, более удобные способы вычисления обратной матрицы, например, методом Жордана – Гаусса, с которым познакомимся позднее.
Классический метод получения обратной матрицы
Пусть данная матрица:
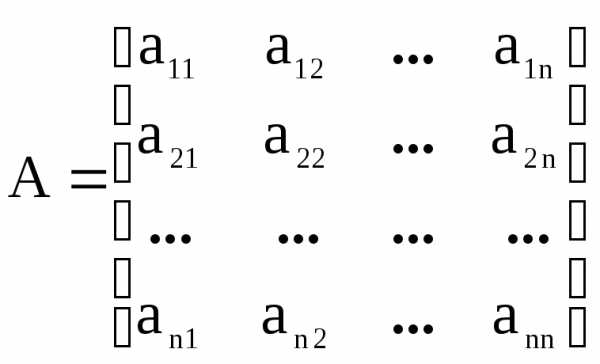 .
.
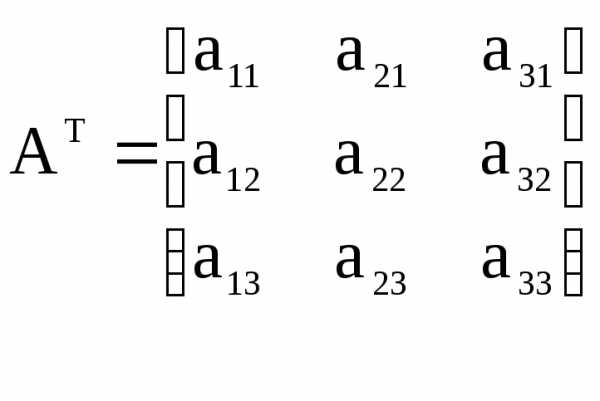
Транспортируем
ее 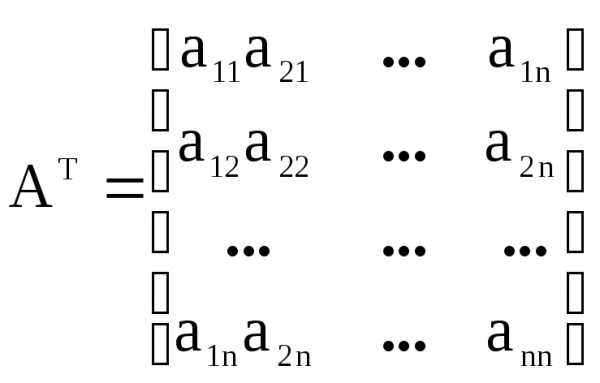 .
.
Найдем для каждого элемента аjiтранспортированной матрицыАТалгебраические дополненияАji.
Теперь составим для матрицы А так называемую присоединенную (или союзную) матрицу
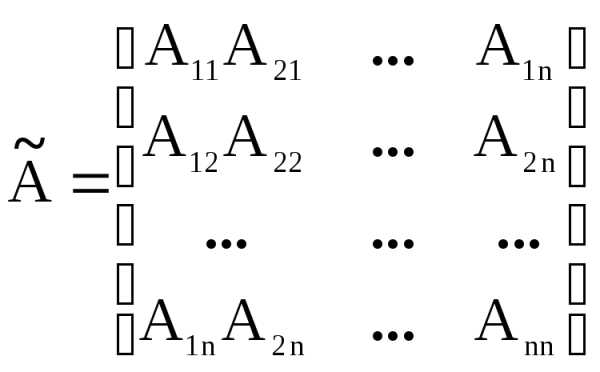 .
.
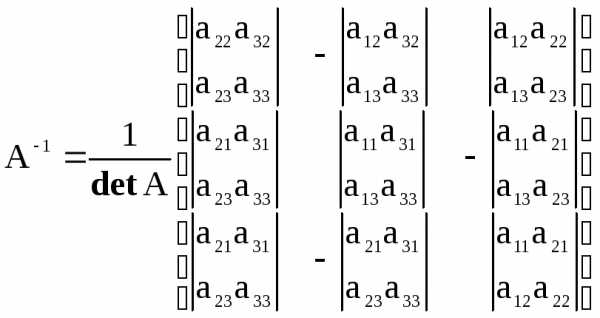
Обратная матрица будет равна
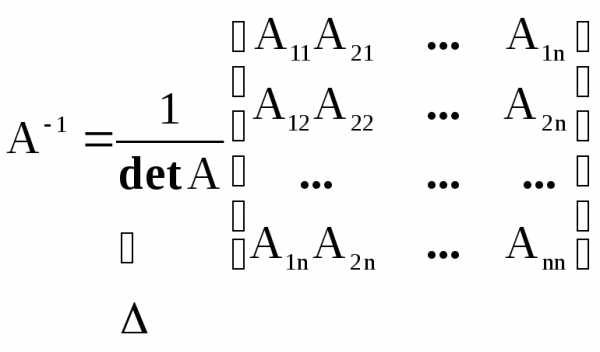 .
.
Например: найти обратную матрицу для матрицы третьего порядка.
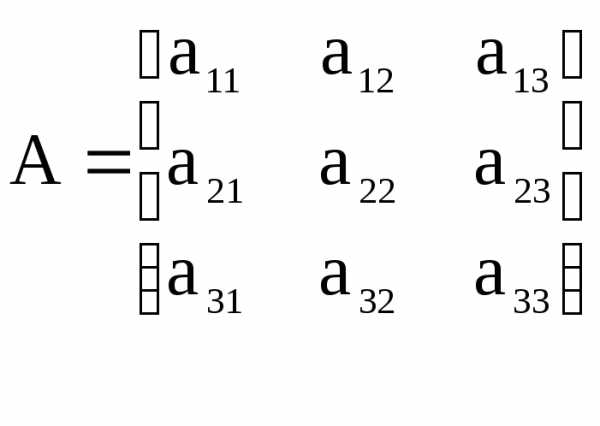
 .
.
Основные свойства обратной матрицы
Учитывая, что det(AB)=detA∙ detB,можем записатьdetA-1 detA=detE=1.
Отсюда
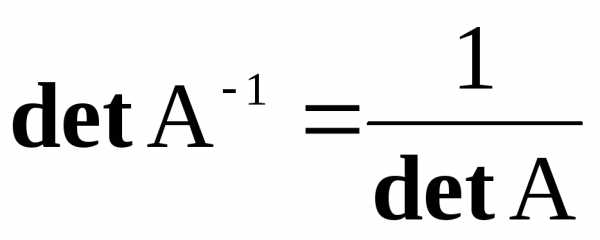 .
.
Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
2. (АВ)-1=В-1А-1
3. (А-1)=(A1)-1.
Тема 2.1. Теория графов в электроэнергетике
Некоторые сведения об электрических системах
Следует иметь в виду, что предлагаемая дисциплина читается до изучения основных курсов по специальности 140204 (100100). Поэтому для того, чтобы приблизить излагаемый материал не только по содержанию, но и по форме к будущим специальным курсам, вспомним некоторые понятия, уже знакомые по курсу “Введение в специальность”.
Рис.1. Принципиальная схема энергосистемы
Энергетическая системаначинается с топлива и воды и кончается потребителем (рис.1).
Электрическая системаначинается с генератора и кончается потребителем, т.е. электрическая система – это электрическая часть энергетической системы, состоящая из совокупности элементов, вырабатывающих, преобразующих, передающих, распределяющих и потребляющих электроэнергию.
Электрическая сетьначинается с повышающего трансформатора и кончается потребителем.
Работа электрической системы прежде всего характеризуется значениями мощностей в МВт (и энергии в МВт.час), вырабатываемых, преобразуемых, передаваемых и потребляемых всеми ее элементами.
Режим системы– это ее состояние в любой момент времени, которое характеризуется совокупностью параметров.
Параметры режима– это напряжение в различных точках системы, токи в ее элементах, углы расхождения векторов ЭДС и напряжений, активные и реактивные мощности генераторов, потоки активной и реактивной мощности в линиях и трансформаторах, потери мощности, энергии и напряжения в элементах системы и т.д.
При анализе различают два основных вида режимов электросистем:
установившийся режим (нормальный или послеаварийный) ;
переходный режим (нормальный или аварийный ).
Установившиеся режимы в электрической системе описываются законами Ома и Кирхгофа или вытекающими из них уравнениями узловых напряжений и контурных токов. Математический анализ установившихся режимов работы электрических систем сводится к составлению и решению систем линейных и нелинейных уравнений. Переходные процессы электрических систем описываются системами дифференциальных уравнений. Наиболее широко применяемые при анализе режимов электрических систем методы решения линейных, нелинейных и дифференциальных уравнений будут изложены во втором разделе данного курса.
Электрической схемой системыназывается графическое изображение последовательности соединения ее элементов между собой. Элементы электрической системы обладают активными и реактивными (индуктивными или емкостными) сопротивлениями, активной и реактивной (индуктивной или емкостной) проводимостями. Если заменить в электрической схеме элементы системы их сопротивлениями и проводимостями, то получим схему замещения электрической системы. Расчеты и анализ режимов электрической системы производятся на основе ее схемы замещения. Каждый элемент системы имеет свою схему замещения. ЛЭП 110 — 220 кВ обычно представляются П -образной схемой замещения, а двухобмоточный трансформатор – Г-образной. на рис.1 и 2 приведены соответственно электрическая схема сети и ее схема замещения.
Рис.2. Электрическая схема сети
Рис.3. Схема замещения
Перед тем, как начать рассчитывать режим работы электрической системы (т.е. определять параметры режима) составляют схему замещения электрической системы (или сети) и вычисляют все параметры схемы замещения – сопротивления и проводимости. Электрическая схема сети и ее схема замещения, представленные на рис.1 и 2, очень малы, и рассчитать режимы для такой схемы можно “вручную”. Однако реальные электрические системы достигают больших размеров, их схемы замещения очень сложны и без использования современных ЭВМ выполнить анализ режимов электрических систем невозможно. Использование же ЭВМ для указанной цели основано на применении матричной алгебры и теории графов.
studfiles.net
Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)
Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)
Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.
Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.
Вырожденной матрицей называется такая матрица, определитель которой равен нулю.
Теорема:
Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством).
1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A.
2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами.
Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли.
Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы.
Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества.
Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая.
Теорема Кронекера-Капелли:
Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы. При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
Решение систем линейных уравнений: матричный метод, формулы Крамера (с выводом).
Матричный метод.
Вывод: Матрица-столбец X неизвестных равна произведению обратной матрицы системы на столбец свободных членов.
Формулы Крамера.
Последовательно заменяются столбцы системы столбцом свободных членов. Определители = значения неизвестных, соответственно заменённым столбцам.
Решение систем линейных уравнений методом Гаусса.
Метод – последовательное исключение неизвестных путём элементарных преобразований матрицы.
Однородные системы линейных уравнений, фундаментальная система решений.
Однородная система – если свободные члены в системе равны нулю. ( => всегда совместна )
Чтобы система имела ненулевые решения, необходимо и достаточно, чтобы а) ранг её основной матрицы был меньше количества неизвестных, б) определитель = 0.
Множество решений, полученных при решении методом Гаусса – фундаментальная система решений.
9) Векторы: Основные определения, линейные операции над векторами, проекция вектора на ось.
Вектор – направленный отрезок.
Модуль вектора – его длина (| расстояние между его началом и концом |).
Нулевой вектор – начало и конец совпадают.
Единичный вектор – длина равна единице.
Векторы коллинеарные, если они лежат на одной или на параллельных прямых. Три вектора, если на одной или на параллельных плоскостях.
Операции:
Сумма векторов – вектор, начало которого совпадает с началом первого, а конец с концом второго, при условии, что второй вектор отложен из конца первого.
Разность двух векторов – такой вектор, который при сложении с меньшим равен большему.
Произведение вектора на число
Проекция вектора на ось – число, равное произведению длины вектора и угла между осью и этим вектором.
Декартовы прямоугольные координаты вектора в пространстве. Действия над векторами, заданными своими координатами. Деление отрезка в данном отношении.
Декартовы прямоугольные координаты вектора – его проекции на координатные оси.
Действия над векторами:
Сумма векторов – сумма соответствующих координат.
Разность – разность соответствующих координат.
Произведение вектора на число – произведение координат на число.
Деление отрезка в данном отношении:
Прямая на плоскости: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору; общее уравнение прямой; исследование общего уравнения прямой; взаимное расположение прямых, заданных общими уравнениями.
Уравнение:
Даны точка и вектор ,
Т.к вектор и прямая перпендикулярны, их скалярное произведение равно нулю, т.е, в координатной форме: Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Общее уравнение прямой —
Исследование прямой:
При A=0, прямая будет параллельна оси Ox;
При B=0, прямая будет параллельна оси Oy;
При C=0, прямая будет проходить через начало координат;
При A=C=0, при B не= 0, прямая совпадает с осью Ox; при B=C=0, А не= 0, с осью Oy.
Взаимное расположение двух прямых:
Параллельны и совпадают, если A/A1 = B/B1 = C/C1,
Параллельны и не совпадают, если A/A1 = B/B1 не= C/C1,
Пересекаются, если A/A1 не= B/B1.
Прямая на плоскости: векторное уравнение прямой; параметрические уравнения прямой; каноническое уравнение прямой; уравнение прямой, проходящей через две точки; взаимное расположение двух прямых, заданных каноническими уравнениями.
r = r0 + st — векторное уравнение прямой.
S (m, n) – направляющий вектор, M0(r0)точка на прямой М0(x0, y0).
Параметрическое уравнение:
{х = х0 + mt
{y= y0 + nt
Выразим t:
x – x0 / m = t и y – y0 / n = t, т.е,
x – x0 / m = y – y0 / n = t – каноническое ур-е прямой.
Уравнение прямой, через две точки.
Условие параллельности — равное соотношение соответствующих величин.
Перпендикулярности – скалярное произведение направляющих векторов = 0.
Прямая на плоскости: уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой с угловым коэффициентом; взаимное расположение двух прямых, заданных уравнениями с угловым коэффициентом; расстояние от точки до прямой.
По направлению:

С угловым коэффициентом:
Число называется угловым коэффициентом прямой.
y = kx + b – уравнение прямой с угловым коэффициентом.
b – отрезок, отсекаемы на оси Oy.
Прямые:
Расстояние от точки до прямой:
25) Кривые второго порядка. Эллипс: основные определения; вывод канонического уравнения.
Эллипс – множество точек плоскости, сумма расстояний до которых до двух данных точек плоскости, называемых фокусами – постоянная величина.
отношение фокального расстояния к длине большой оси (эксцентриситет).
Директрисы: (две прямые, перпендикулярные оси Ox, на расстоянии от центра)

26) Кривые второго порядка. Гипербола: основные определения; вывод канонического уравнения.
Гипербола – множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек этой плоскости, называемых фокусами – постоянная величина.
отношение фокального расстояния к длине действительной(фокальной) оси (эксцентриситет).
Директрисы:
Ось, сопряженная с гиперболой:

27) Кривые второго порядка. Парабола: основные определения; вывод канонического уравнения.
Парабола – множество всех точек плоскости, равноудалённых от точки-фокуса и данной прямой, называемой директрисой.
Директриса:

Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)
Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.
Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.
Вырожденной матрицей называется такая матрица, определитель которой равен нулю.
Теорема:
Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством).
1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A.
2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами.
Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли.
Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы.
Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества.
Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая.
Теорема Кронекера-Капелли:
Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы. При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
infopedia.su
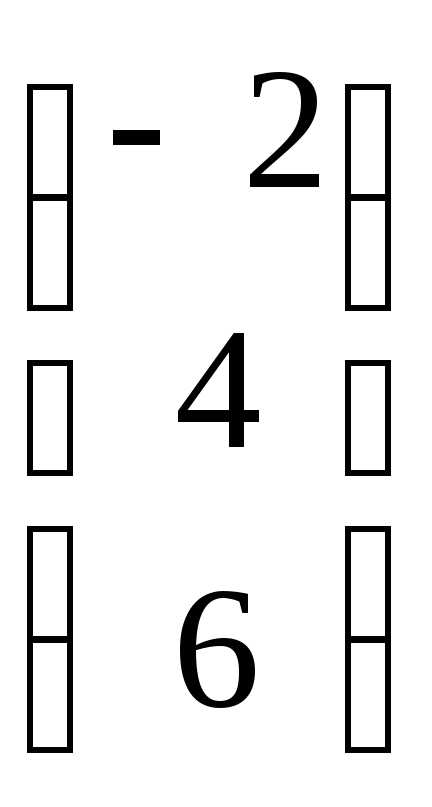
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
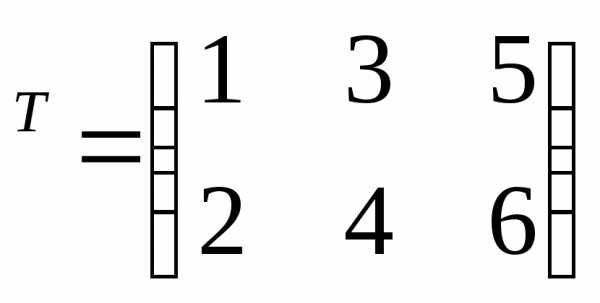
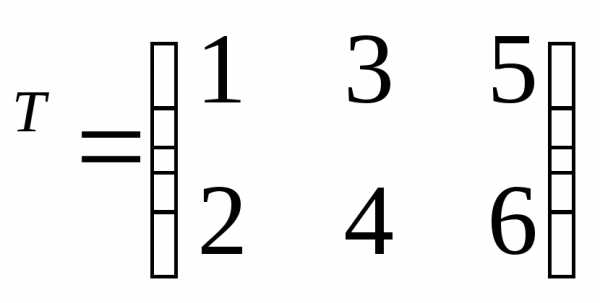
ОПРЕДЕЛЕНИЕ. Транспонированной матрицей 
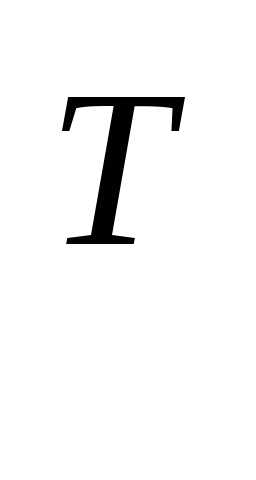 для матрицы
для матрицы размера
размера называется матрица размера
называется матрица размера ,
полученная из
,
полученная из заменой всех ее строк столбцами с теми
же порядковыми номерами.
заменой всех ее строк столбцами с теми
же порядковыми номерами.
То есть, если  =
=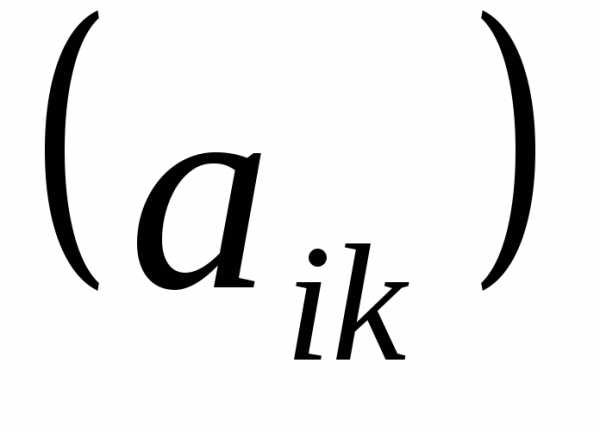 ,
то
,
то
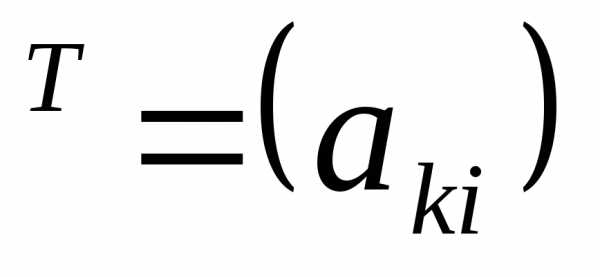 ,
,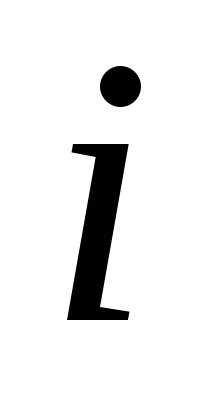 =1,2,…,
=1,2,…,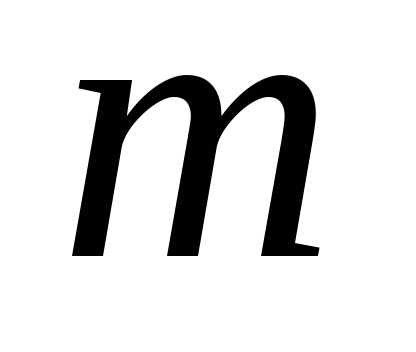 ,
, =1,2,…,
=1,2,…, .
.
ПРИМЕР.
 =
=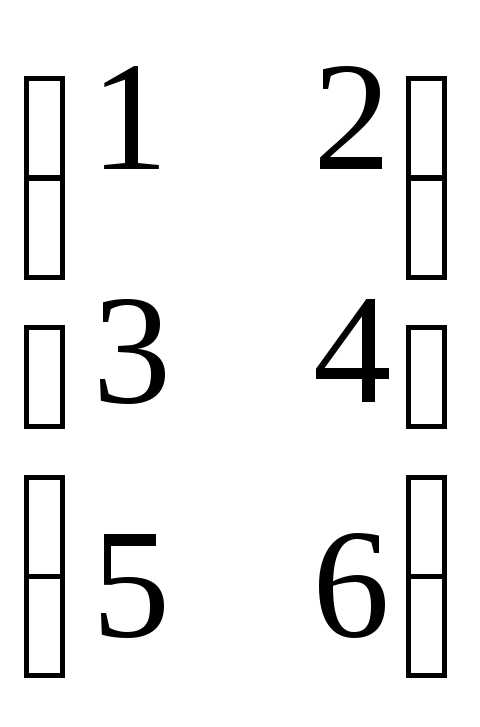
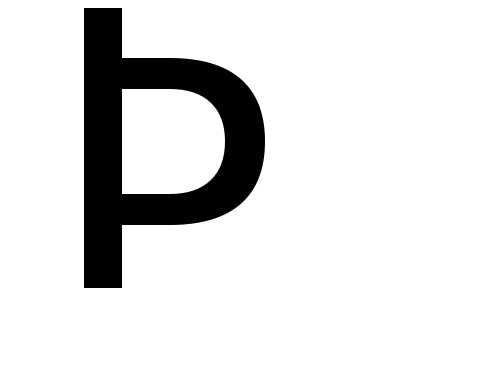

 ;
; 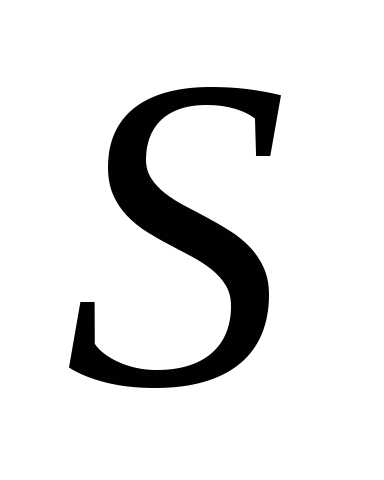 =
= =
= 
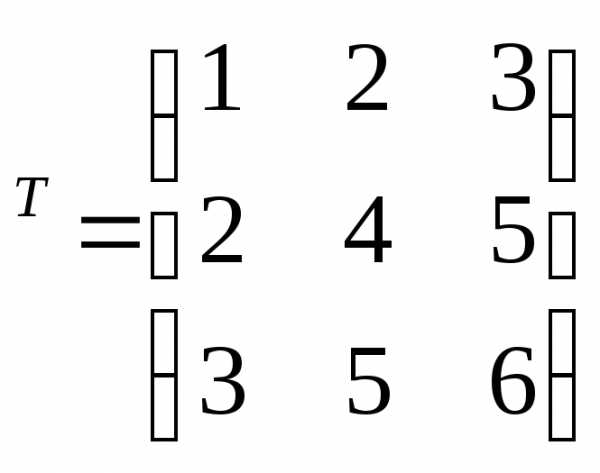
3х2 2х3 3х3 3х3
ОПРЕДЕЛЕНИЕ.
Если  =
=
 ,
то матрицаА называется симметрической.
,
то матрицаА называется симметрической.
Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
ОПРЕДЕЛЕНИЕ.
Пусть  =
=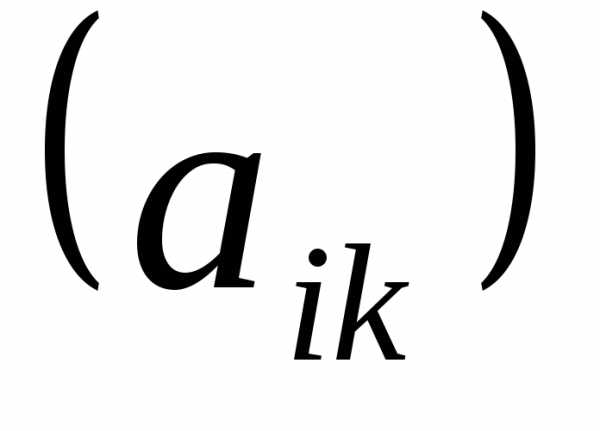 – матрица размера
– матрица размера ,
, =
=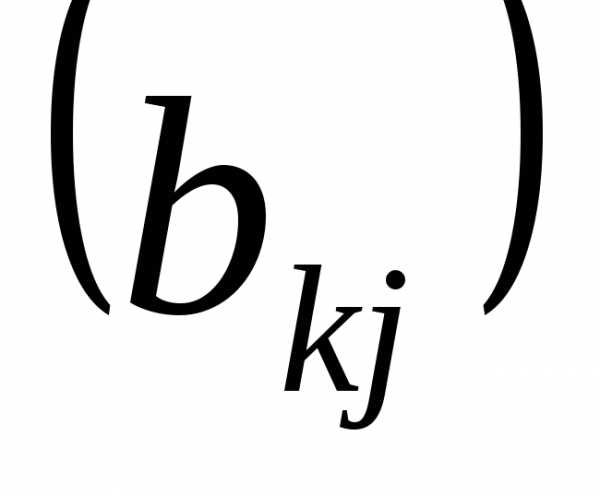 – матрица размера
– матрица размера .
Произведение этих матриц
.
Произведение этих матриц
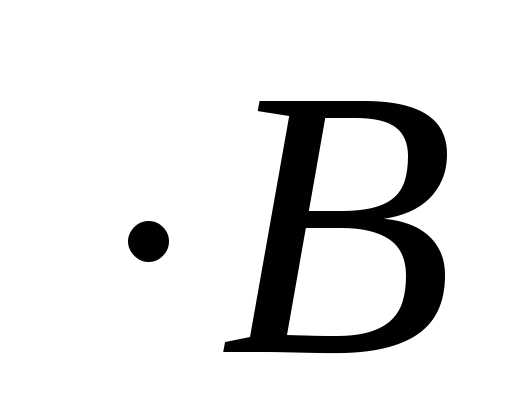 – матрица
– матрица =
=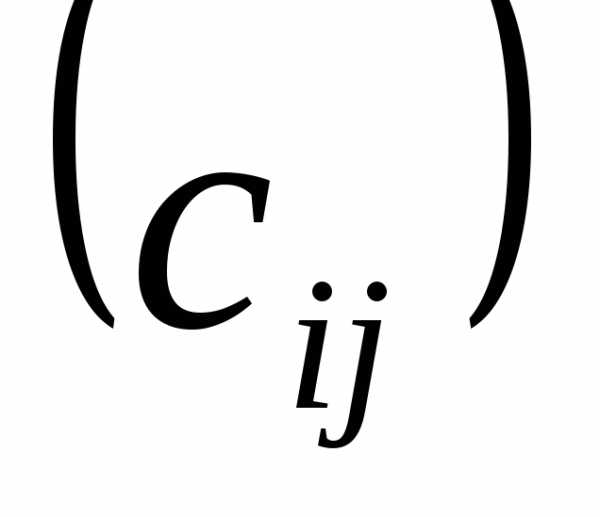 размера
размера ,
элементы которой вычисляются по формуле:
,
элементы которой вычисляются по формуле:
, 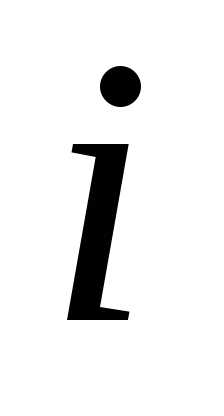 =1,2,…,,
=1,2,…,,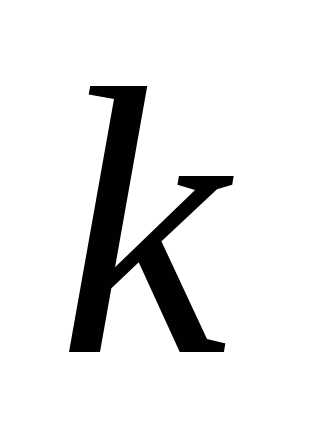 =1,2,…,
=1,2,…,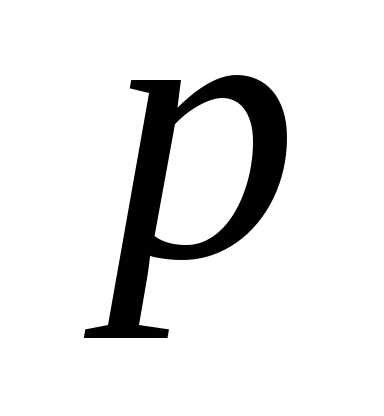 ,
,
то есть элемент 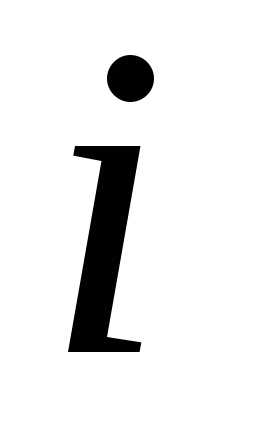 -й
строки и
-й
строки и -го
столбца матрицы
-го
столбца матрицы равен сумме произведений соответствующих
элементов
равен сумме произведений соответствующих
элементов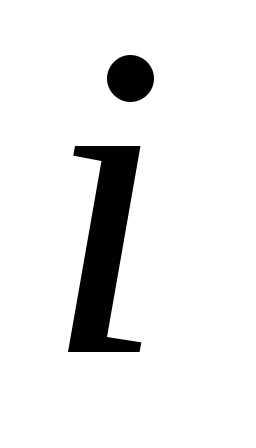 -й
строки матрицы
-й
строки матрицы и
и -го
столбца матрицы
-го
столбца матрицы .
.
ПРИМЕР.
 =
=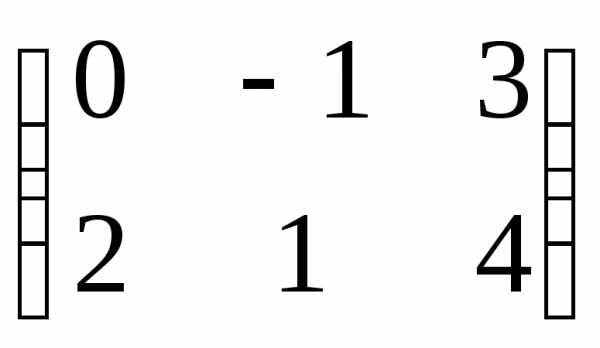 ,
,  =
=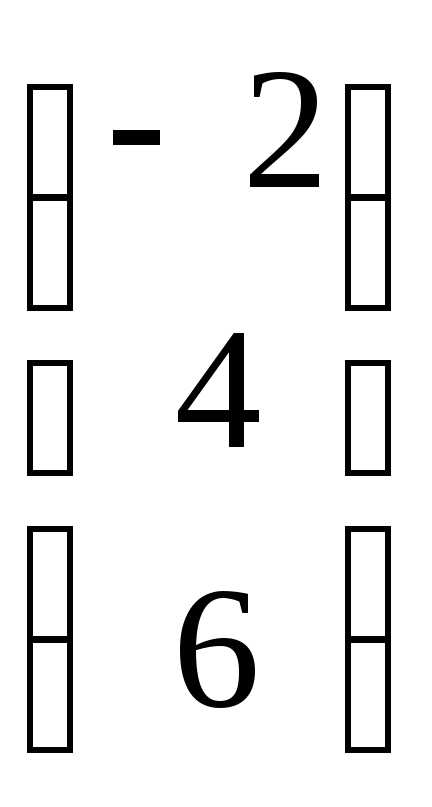


2х3 3х1 2х3 3х1 2х1
Произведение 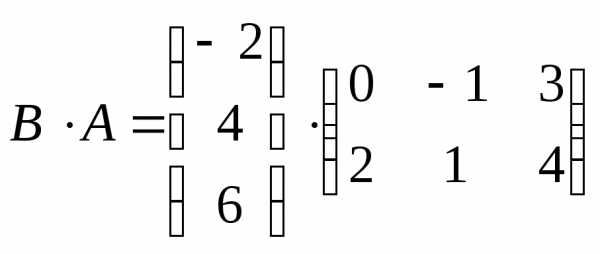 – не существует.
– не существует.
3х1 2х3
CВОЙСТВА ОПЕРАЦИИ УМНОЖЕНИЯ МАТРИЦ
1. , даже если оба произведения определены.
ПРИМЕР. 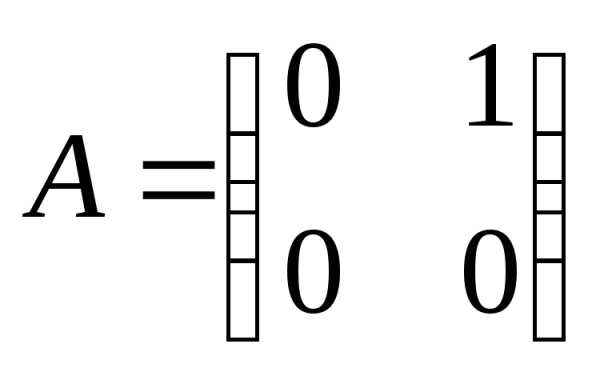 ,
,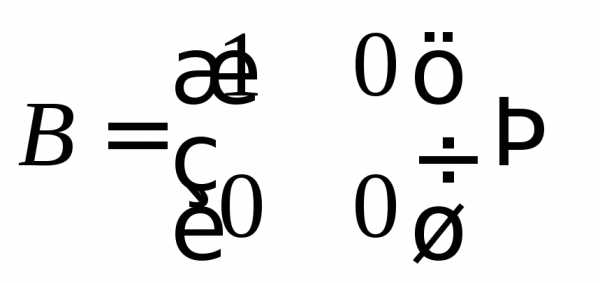
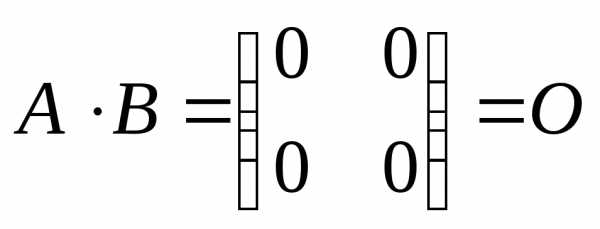 ,
хотя
,
хотя
ОПРЕДЕЛЕНИЕ.
Матрицы  и
и называютсяперестановочными,
если
,
в противном случае
называютсяперестановочными,
если
,
в противном случае и
и называютсянеперестановочными.
называютсянеперестановочными.
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
ПРИМЕР.
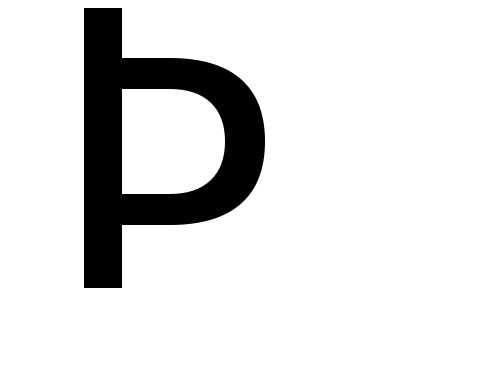 матрицы
матрицы  и
и перестановочные.
перестановочные.
, то есть ,
значит,  и
и – перестановочные матрицы.
– перестановочные матрицы.
Вообще единичная
матрица перестановочна с любой квадратной
матрицей того же порядка, и для любой
матрицы
.
Это свойство матрицы объясняет, почему именно она называется
единичной: при умножении чисел таким
свойством обладает число 1.
объясняет, почему именно она называется
единичной: при умножении чисел таким
свойством обладает число 1.
Если соответствующие произведения определены, то:
2.
3. ,
4.
5.
ПРИМЕР.
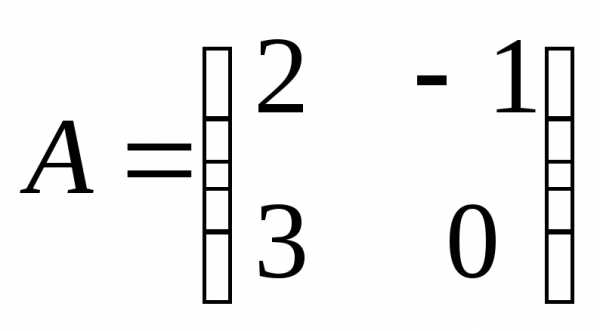 ,
, 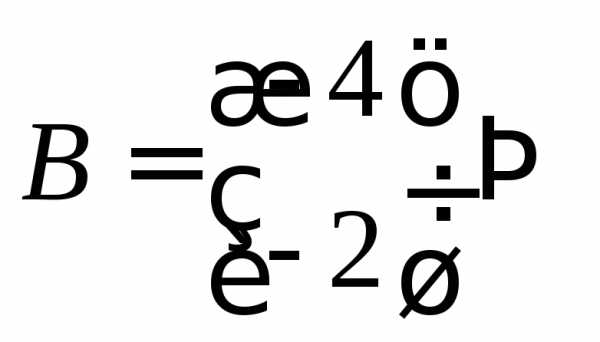
2х2 2х1 2х1 1х2
1х2 2х2 1х2
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
ПРИМЕР. 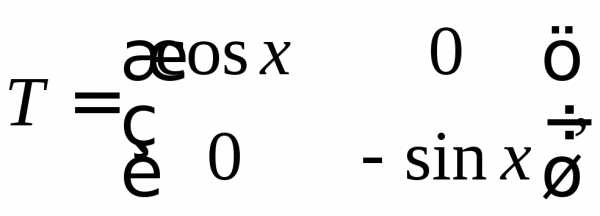
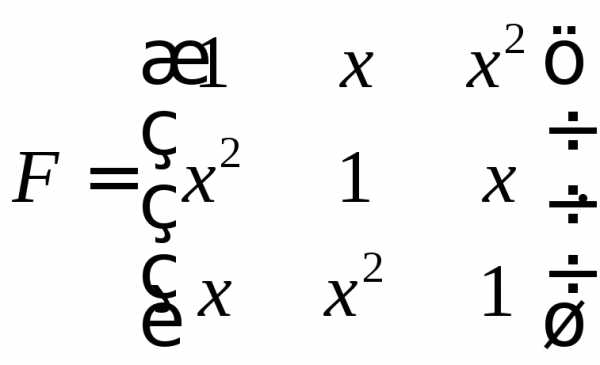
Определители и их свойства
Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим
квадратную матрицу второго порядка: 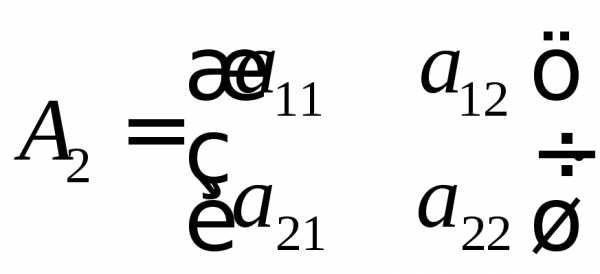
Её определителем называется число, которое записывается и вычисляется так:
(1.1)
Такой определитель называется определителем второго порядка и может
обозначаться
по-другому: 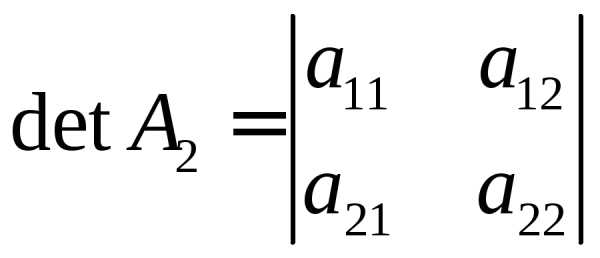 или
или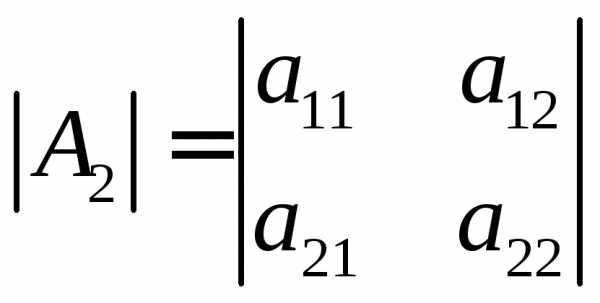 .
.
Определителем
третьего порядка называется число, соответствующее
квадратной матрице  ,
которое вычисляется по правилу:
,
которое вычисляется по правилу:
(1.2)
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:
ПРИМЕР.
;
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
(1.3)
То есть при
вычислении определителя третьего
порядка используются определители
второго порядка, причем 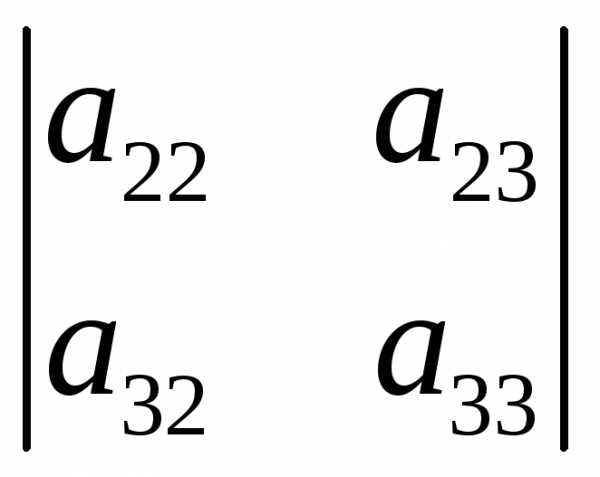 – определитель матрицы, полученный из
– определитель матрицы, полученный из вычеркиванием элемента
вычеркиванием элемента (точнее, первой строки и первого столбца,
на пересечении которых стоит
(точнее, первой строки и первого столбца,
на пересечении которых стоит ),
), – вычеркиванием элемента
– вычеркиванием элемента ,
,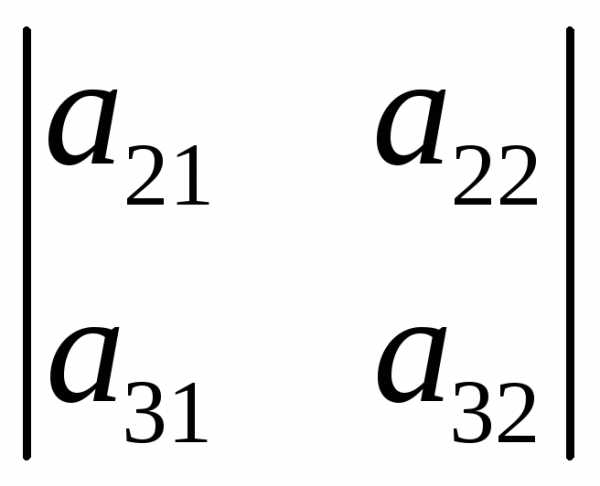 – элемента
– элемента .
.
ОПРЕДЕЛЕНИЕ. Дополнительным
минором 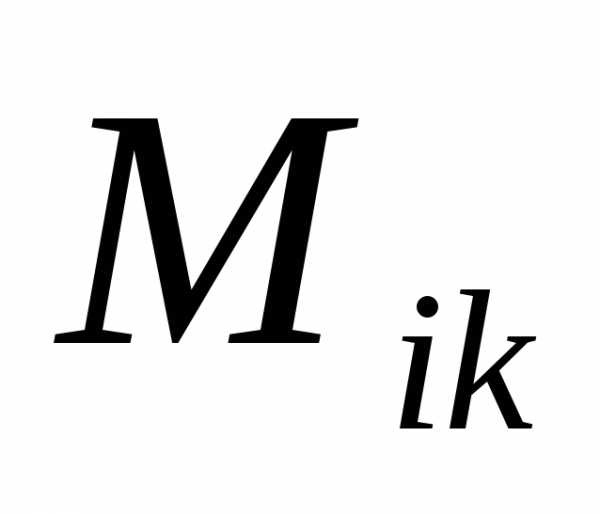 элементаквадратной матрицы
элементаквадратной матрицы называется определитель матрицы,
получаемой из
называется определитель матрицы,
получаемой из вычеркиванием
вычеркиванием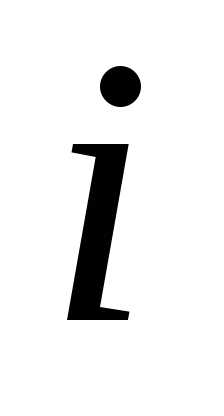 -ой
строки и
-ой
строки и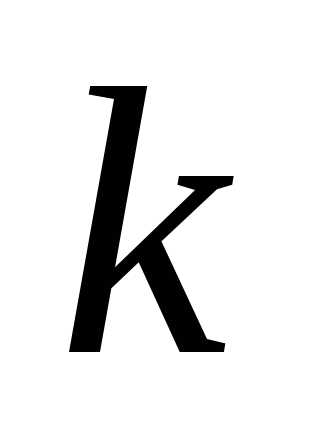 -го
столбца.
-го
столбца.
ПРИМЕР.

и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
ОПРЕДЕЛЕНИЕ. Алгебраическим
дополнением элемента 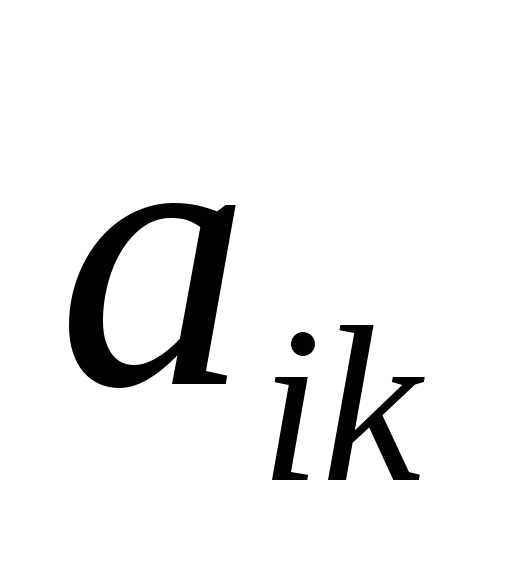 квадратной матрицы
квадратной матрицы называется число.
называется число.
ПРИМЕР.
Для матрицы  :
:
Для матрицы  :и так далее.
:и так далее.
Итак, с учетом сформулированных определений (1.3) можно переписать в виде: .
Перейдем теперь к общему случаю.
ОПРЕДЕЛЕНИЕ. Определителем квадратной матрицы 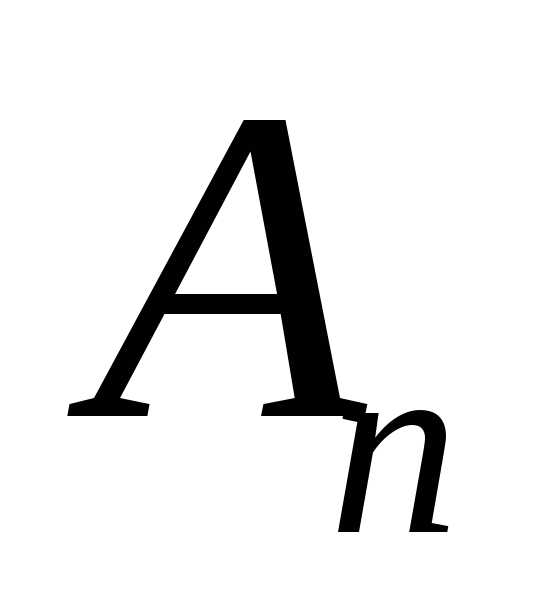 порядка
порядка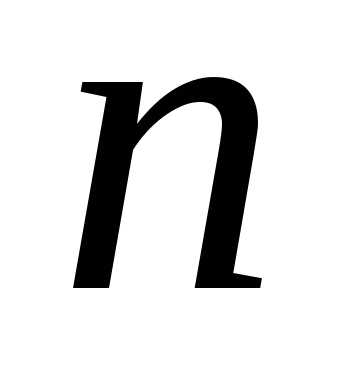 называется число, которое записывается
и вычисляется следующим образом:
называется число, которое записывается
и вычисляется следующим образом:
(1.4)
Равенство (1.4)
называется разложением
определителя по элементам первой строки.
В этой формуле алгебраические дополнения
вычисляются как определители 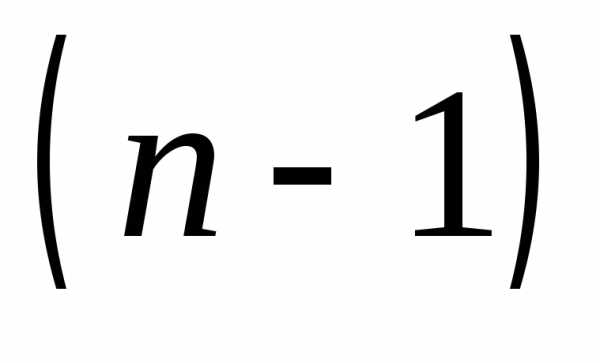 -го
порядка. Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
-го
порядка. Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
ПРИМЕР.
Рассмотрим (без доказательства) свойства определителей:
Определитель можно разложить по элементам первого столбца:
(1.5)
ПРИМЕР.
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
При транспонировании матрицы величина ее определителя не меняется: .
Отсюда следует, что строки и столбцы определителя равноправны.
Если в определителе поменять местами две строки (два столбца), то определитель изменит свой знак, не изменившись по абсолютной величине.
Определитель, имеющий две равные строки (столбца), равен нулю.
Если все элементы некоторой строки (столбца) определителя умножить на число
 ,
то величина определителя умножится
на это число.
,
то величина определителя умножится
на это число.
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
Определитель можно разложить по элементам любой строки (любого столбца): (1.6)
или
(1.7)
Равенство
(1.6) называется разложением
определителя по элементам 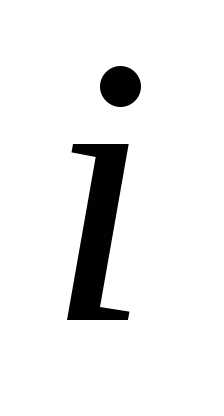 -й
строки.
-й
строки.
Равенство
(1.7) называется разложением
определителя по элементам 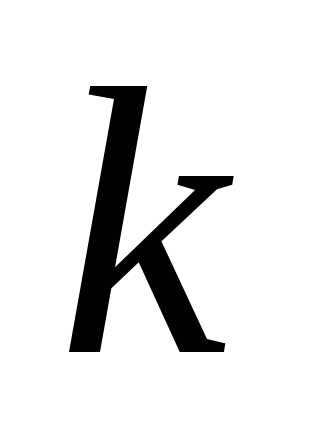 -го
столбца.
-го
столбца.
Сумма произведений всех элементов некоторой строки (столбца) на
алгебраические дополнения соответствующих элементов другой строки
(столбца) равна
нулю, то есть при 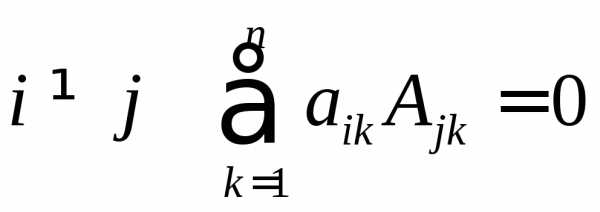 и
и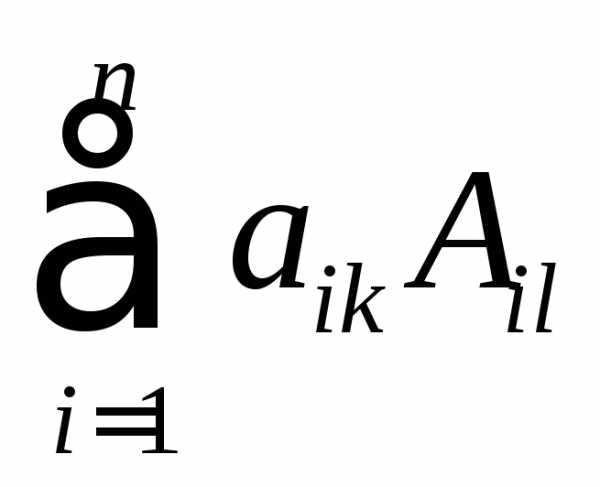 при
при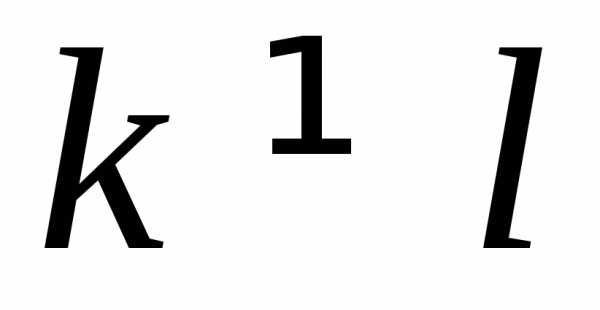 .
.
Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: (
 – квадратные матрицы одного порядка).
– квадратные матрицы одного порядка).
ПРИМЕР. 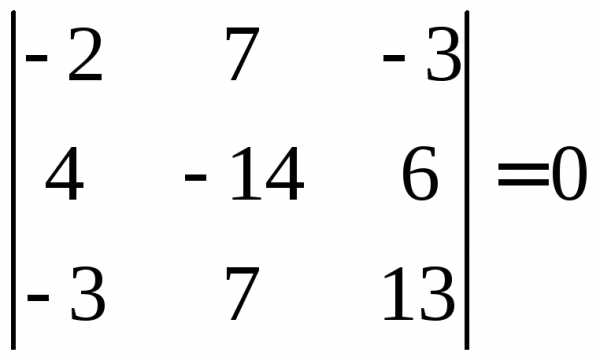 ,
так как элементы первой и второй строк
этого определителя соответственно
пропорциональны (свойство 6).
,
так как элементы первой и второй строк
этого определителя соответственно
пропорциональны (свойство 6).
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
ПРИМЕР.
studfiles.net
9.Операция транспонирования матрицы и её свойства.
Определение: Матрица А’ получающаяся из матрицы А путем замены строк столбцами называется транспонированной по отношению к матрице А.


Справедливы следующие правила транспонирования матриц:
(αА+αВ)’=αA’ + αB’
(AB)’=B’A’
Идея доказательства показать что матрицы (AB)’ и B’A’ имеют одинаковую размерность и у них равны соответствующие элементы.
Определение: Если А –
произвольная квадратная матрица и A=A’
(-A=A’),
то матрица А называется симметрической или кососимметрической
или кососимметрической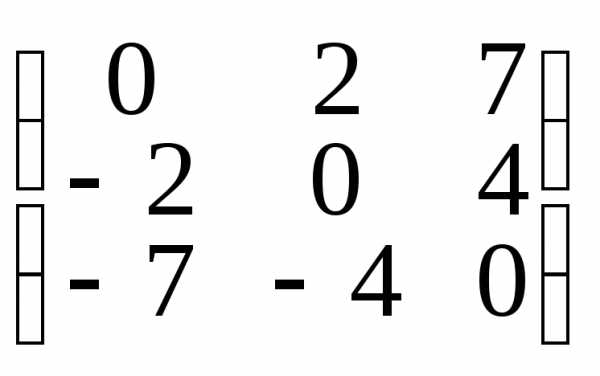
10. Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.
Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)
Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А-1
А А-1= А-1А=Е Отсюда следует что для матрицы А-1 обратной будет (А-1)-1=А
Теорема: У каждой обратимой матрицы существует единственное обращение.
Доказательство: Предположим что у матрицы А существует наряду с Х еще одна обратная матрица У, т.е. АУ=Е. Тогда
(ХА)У=ЕУ=У ┐
Х(АУ)=ХЕ=Х ┘Следовательно Х=У. Т.е. у матрицы А существует единственное обращение.(ч.т.д.)
11. Определение обратной матрицы. Доказать что (АВС)-1=С-1В-1А-1.
Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)
Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А-1
А А-1= А-1А=Е Отсюда следует что для матрицы А-1 обратной будет (А-1)-1=А (3)
Теорема: Если квадратные матрицы А, В, С одного и того же порядка обратимы, то их произведение тоже обратимо и (АВС)-1=С-1В-1А-1.
Доказательство: А(В(СС-1)В-1)А-1=Е и С-1(В-1(А-1А)В)С=Е (ч.т.д.)
Для любого натурального m по определению Аm=А*А*…*А – m-раз.
По определению А0=Е.
Определение: Для каждой обратимой матрицы А, А-2=А-1*А-1; А-3= А-1*А-1*А-1 (4)
Из (3) и (4) следует что для каждой обратимой матрицы А и любых целых чисел р и q имеют место обычные правила действия со степенями:
АрАq =Ар+q
(АВ)р=АрВр если АВ=ВА
(Ар)q=Ар*q
12.Доказать что в результате транспонирования обратимой матрицы получается снова обратимая матрица и (A’)-1=(A-1)’.
Теорема: В результате транспонирования обратимой матрицы А получается снова обратимая матрица и (A’)-1=(A-1)’.
Доказательство: Применим правила транспонирования к соотношению АХ=ХА=Е:
(АХ)’=(ХА)’=Е’
А’Х’=Х’А’=Е
Из определения обратной матрицы следует что (A’)-1= Х’=(A-1)’(ч.т.д.)
13. Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.
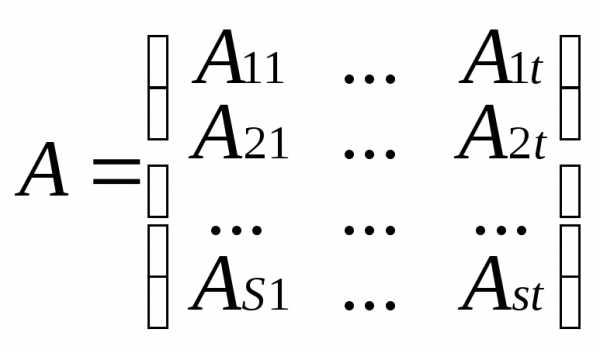
Прямоугольную матрицу А можно вертикальными и горизонтальными линиями разбить на прямоугольные клетки(блоки). В частности матрица может быть разбита только горизонтальными или только вертикальными линиями. (Аα,β)s,t– блочная матрица. Рассмотрим две матрицы А и В одинаковой размерности и с одинаковым разбиением на блоки. Соответствующие блоки Аα,β и Вα,β имеют одинаковую размерность mα x n β , α=1..s, β=1..t. Тогда в соответствии с правилом сложения матриц операция сложения блочных матриц одинаковых размеров с одинаковым разбиением на блоки, производится точно также как если бы вместо блоков стояли числовые элементы.
Чтобы распространить правило умножения матриц на блочные матрицы необходимо чтобы все горизонтальные размеры блоков первой матрицы совпали с соответствующими размерами второго сомножителя. Число столбцов блока Аα,β равно числу строк блока Вβ,с .
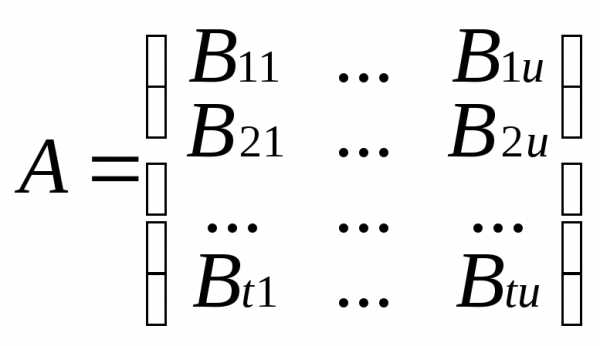
Β
изменяется от 1 доt,
с изменяется от 1 до u.
Таким образом возможно умножение матриц
А и В формально также как если бы вместо
блоков стояли числовые элементы. 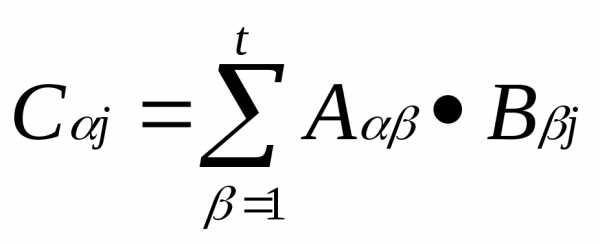
Определение: Квадратная матрица у которой все элементы расположенные под(над) главной диагональю равны 0 называется верхней(нижней) треугольной матрицей. Аналогичные понятия вводятся и для блочных матриц.
Определение: Блочная матрица А называется верхней(нижней) квазитреугольной матрицей если все диагональные блоки и сама матрица А квадратные матрицы, и все не диагональные блоки расположенные под(над) диагональными блоками нулевые матрицы.
Определение: Блочная матрица А называется квазидиагональной если все диагональные блоки и сама матрица А квадратные матрицы, а все недиагональные блоки – нулевые матрицы.
Теорема: Определитель квазитреугольной матрицы связан с определителем диагональных матриц следующим соотношением:
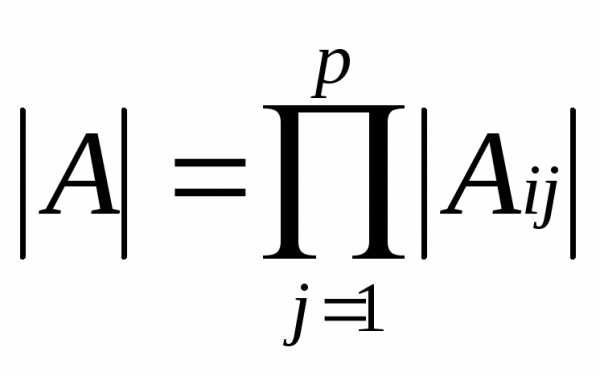 (♀)
где П – произведение.
(♀)
где П – произведение.
Доказательство: Рассмотрим
сначала квазитреугольную матрицу 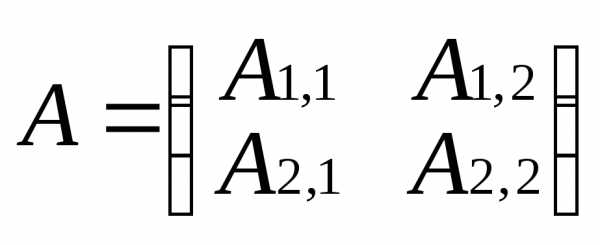 где А12=0,
где А12=0, 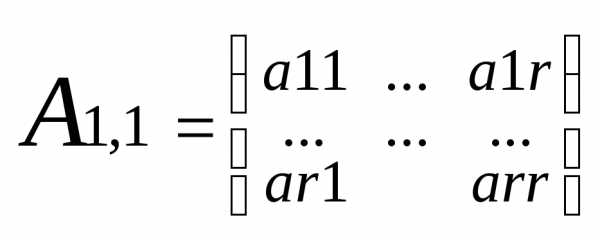 ,,
,,
По определению
Т.к.
А12=0
то из всех произведений
могут быть ≠0 только те в которых индексы.
Вследствие этого остальные индексы
могут принимать значения только из
множества.
В этих условиях число инверсий в
перестановке равно:
равно:
т.е.
Учитывая это находим что
Отсюда следует что
Рассматривая
в общем случае квазитреугольную матрицу 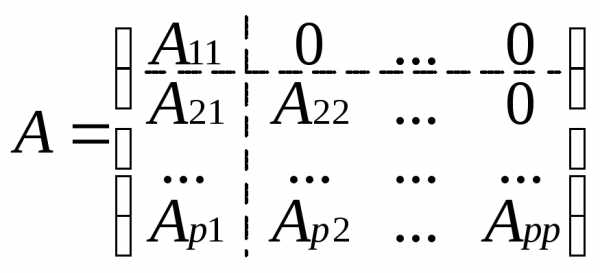
Как
матрицу 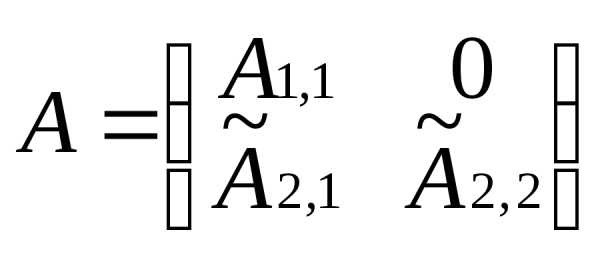 где
где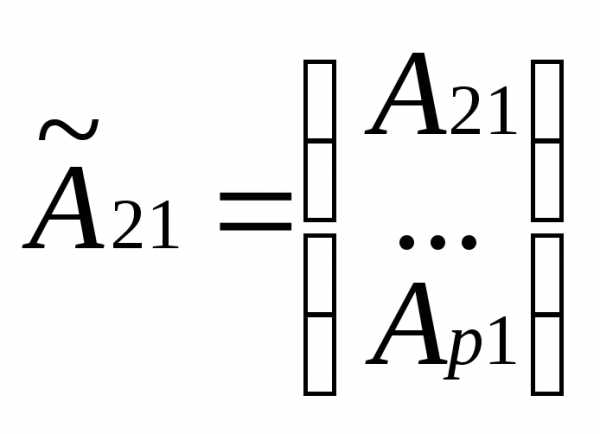
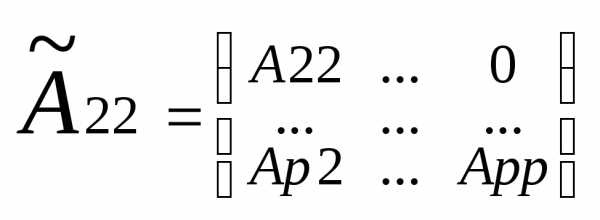 согласно (*) будем иметь.
Матрица
согласно (*) будем иметь.
Матрица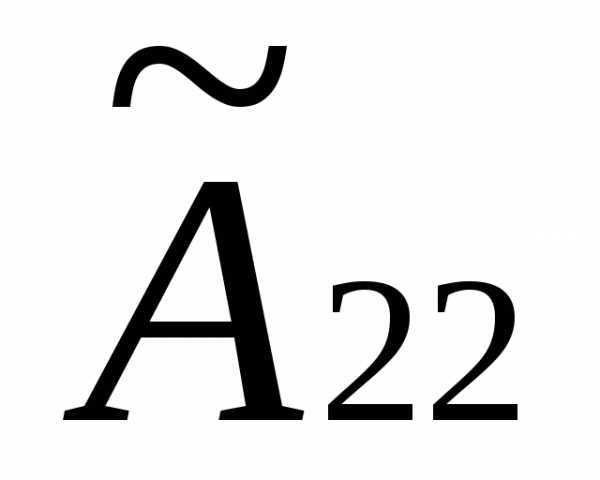 снова квазитреугольная. Проделав над
ней туже операцию, получим. После (р-1) таких шагов придем к (♀).
снова квазитреугольная. Проделав над
ней туже операцию, получим. После (р-1) таких шагов придем к (♀).
Аналогично доказывается равенство (♀) применительно к верхней квазитреугольной матрице.(ч.т.д.)
studfiles.net
Свойства транспонированных матриц
Логическим завершением арифметических операций над матрицами должна быть операция деления — обратная для операции умножения. Для введения этой операции необходима числовая характеристика матриц, называемая определителем или детерминантом.
1.3 Определители матриц
Квадратную матрицу, размера  будем называтьквадратной матрицей
будем называтьквадратной матрицей 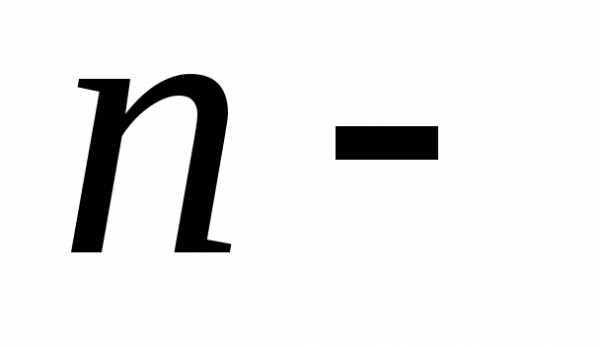 го
порядка.
го
порядка.
Всякой квадратной матрице А 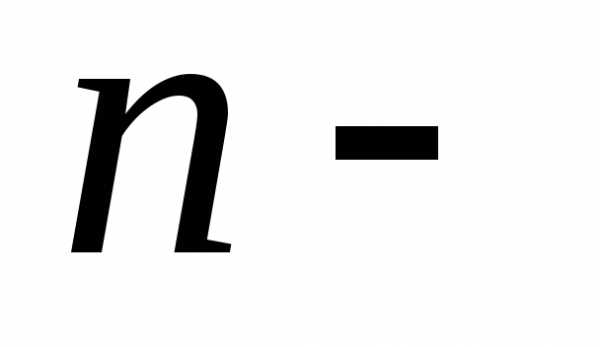 го
порядка ставится в соответствиечисло,
вычисляемое по элементам данной матрицы
по определенному правилу и называемоеопределителем матрицы
го
порядка ставится в соответствиечисло,
вычисляемое по элементам данной матрицы
по определенному правилу и называемоеопределителем матрицы 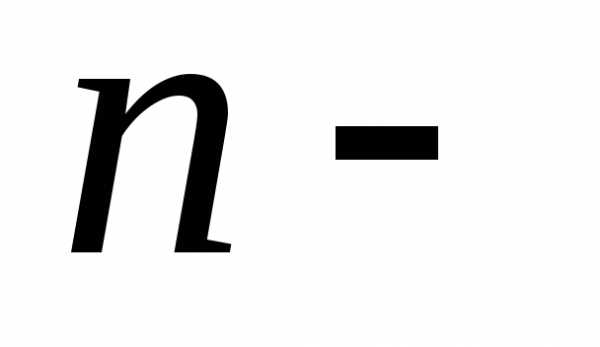 го
порядка.
го
порядка.
Определитель есть числовая характеристика квадратной матрицы.
Определитель квадратной матрицы А обозначается: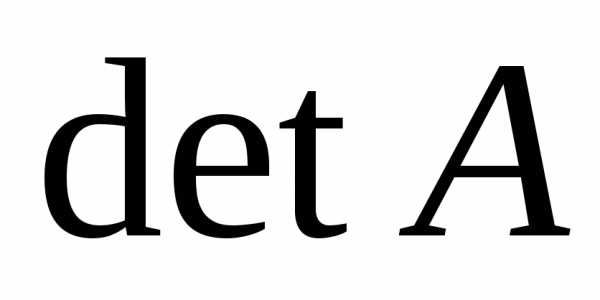 (детерминант),
(детерминант), или
или .
.
Введем правила вычисления определителей первого, второго и третьего порядков.
Определитель первого порядка.
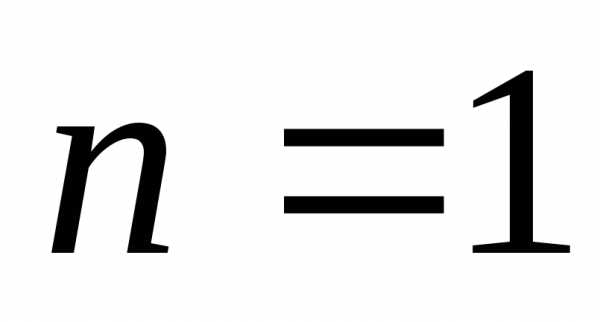 ,.
,.
Определитель второго порядка.
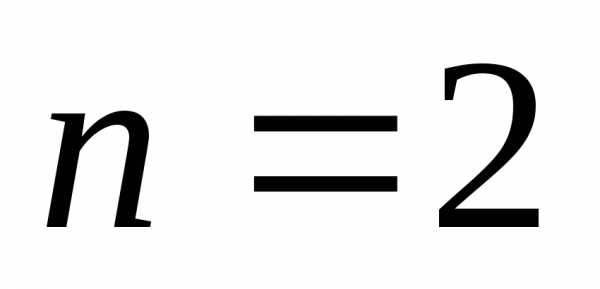 ,.
,.
Правиловычисления определителя
2-го порядка: чтобы вычислить определитель
второго порядка необходимо найти
произведение элементов главной диагонали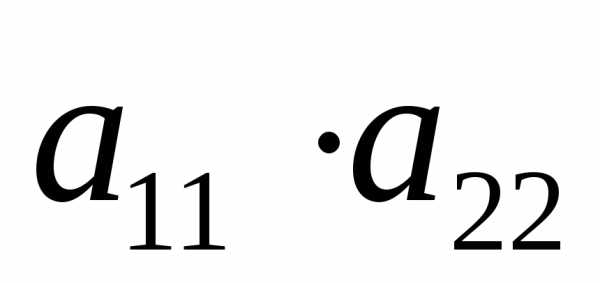 и вычесть из него произведение элементов
побочной диагонали
и вычесть из него произведение элементов
побочной диагонали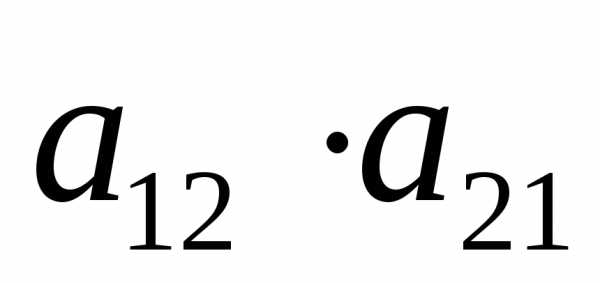 .
.
Пример.
.
Определитель третьего порядка.
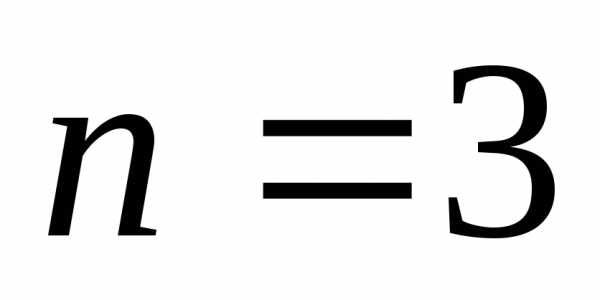 ,
,
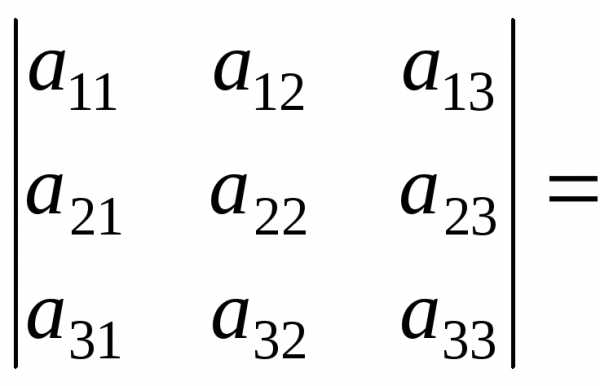 .
.
Данную формулу можно не запоминать, а применять по схематическому правилу треугольников.
.
Пример.
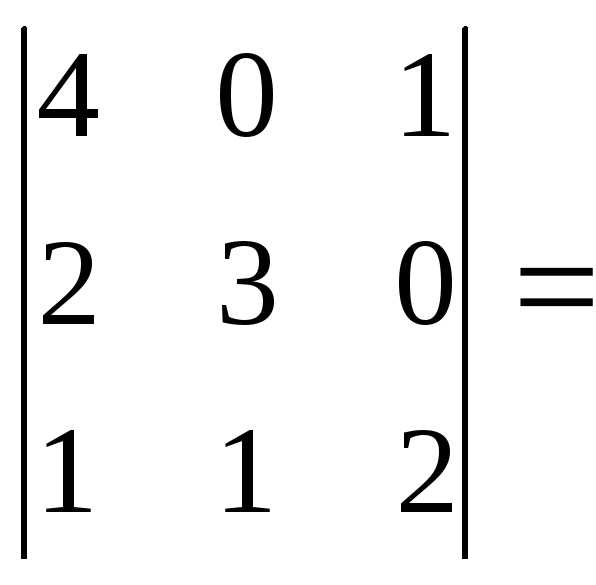 .
.
Для того чтобы обобщить методику вычисления определителей квадратных матриц, введем понятие минора и алгебраического дополнения.
Определение 1.8 Минором 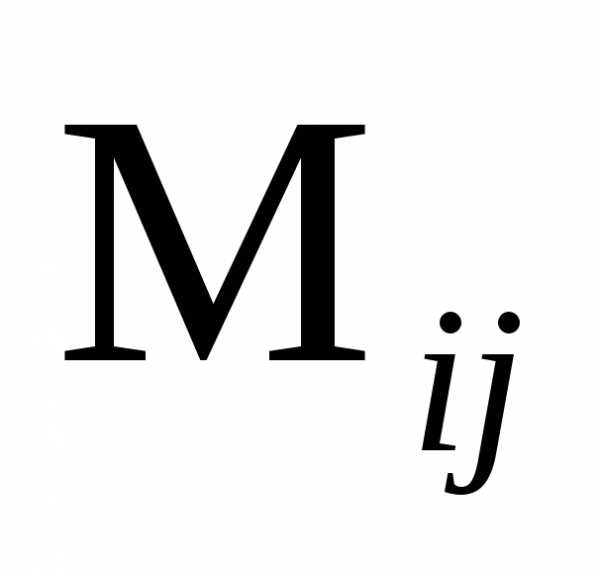 выбранного
элемента
выбранного
элемента  матрицыn-го
порядка называется
определитель (п–1)-го
порядка, полученный из исходной матрицы
путем вычеркивания
в ней строки и столбца, на пересечении
которых находится этот
элемент.
матрицыn-го
порядка называется
определитель (п–1)-го
порядка, полученный из исходной матрицы
путем вычеркивания
в ней строки и столбца, на пересечении
которых находится этот
элемент.
Например, если исходной матрицей является матрица 3-го порядка
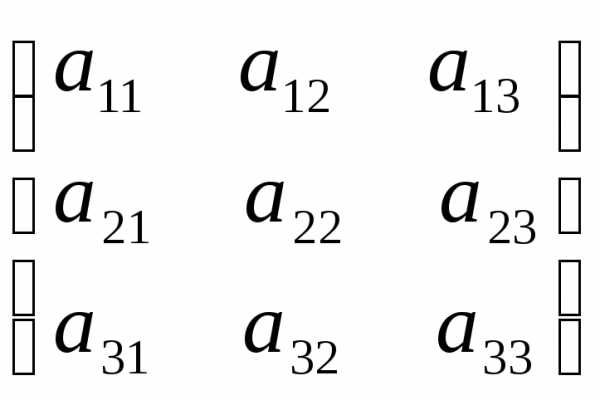 ,
то
,
то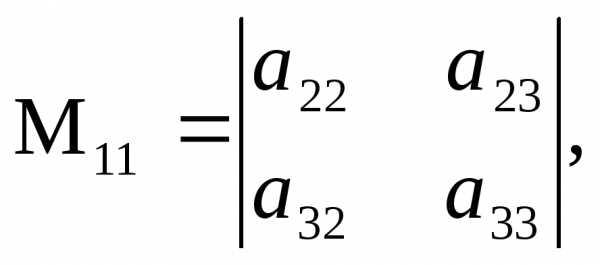 а
а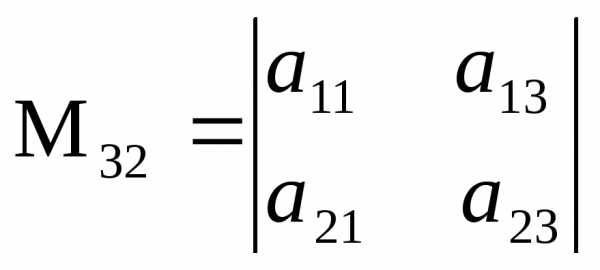 .
.
Определение 1.9 Алгебраическим
дополнением элемента
элемента квадратной матрицы называется ее минор,
взятый со знаком плюс, если сумма индексов
выбранного элемента
квадратной матрицы называется ее минор,
взятый со знаком плюс, если сумма индексов
выбранного элемента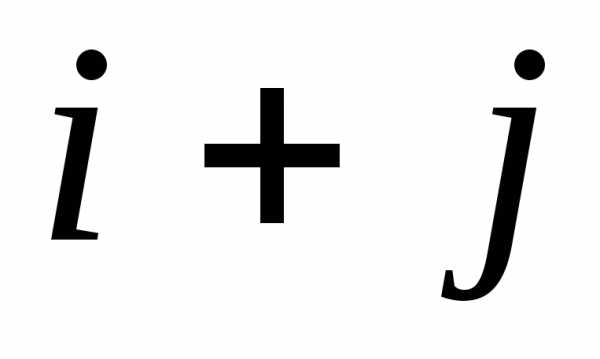 –
четное число, и со знаком минус, если
эта сумма нечетная, т. е.
–
четное число, и со знаком минус, если
эта сумма нечетная, т. е.
Рассмотрим матрицу n-го
порядка 
Пример. Дана
матрица 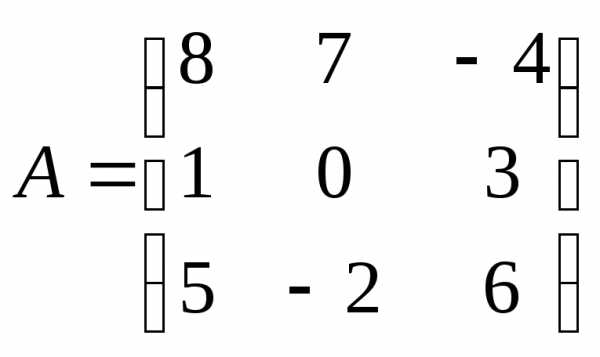 .
.
1) Найдем минор и алгебраическое
дополнение к элементу 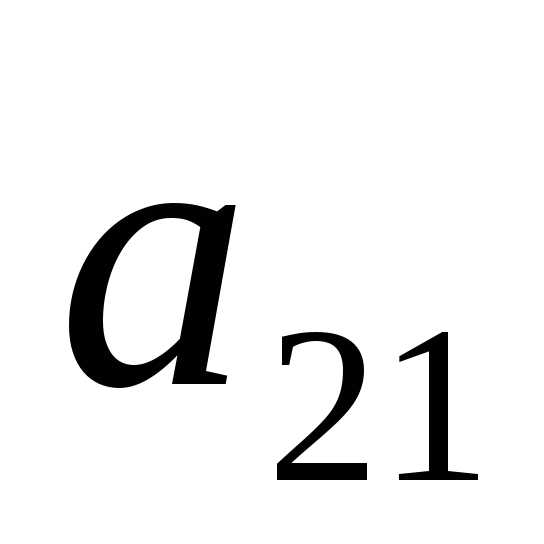 .
.
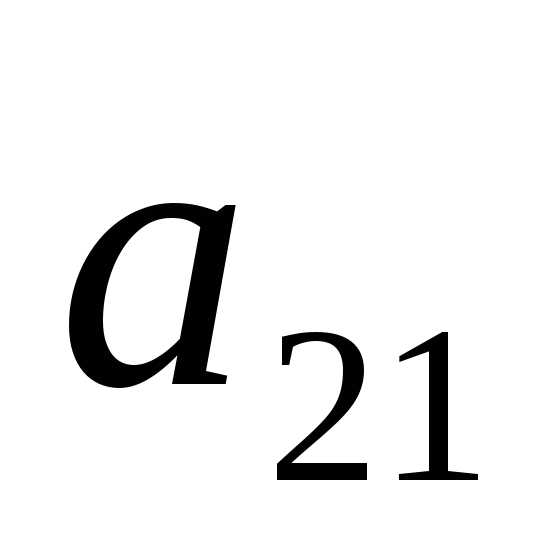 =
1;
=
1; 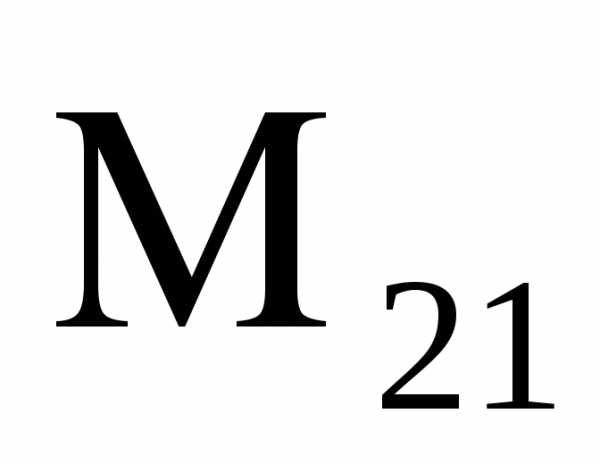 =
= =
= 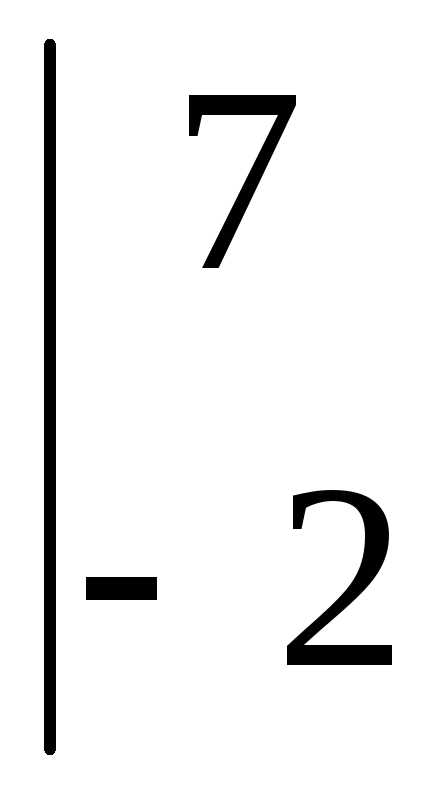
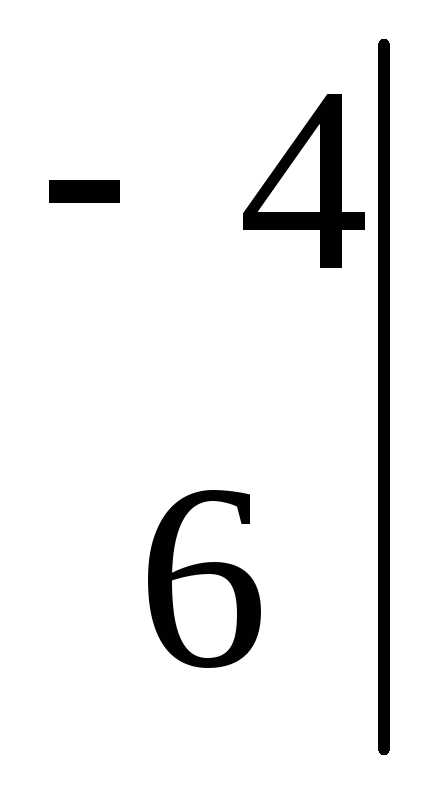 =
42 – (-4)(-2) = 34
;
=
42 – (-4)(-2) = 34
;
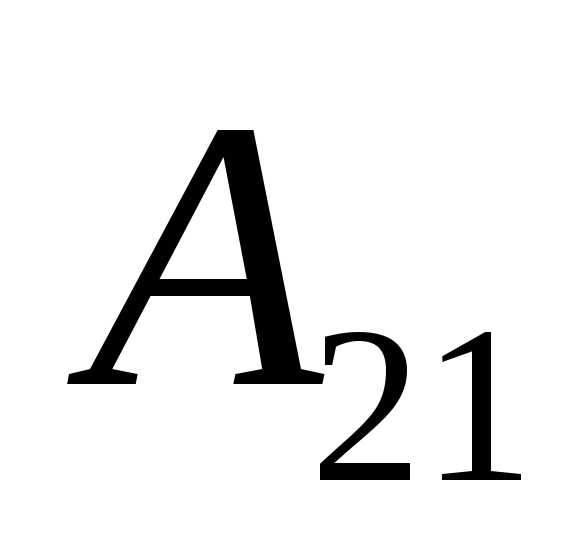 =
(-1) 2+1
=
(-1) 2+1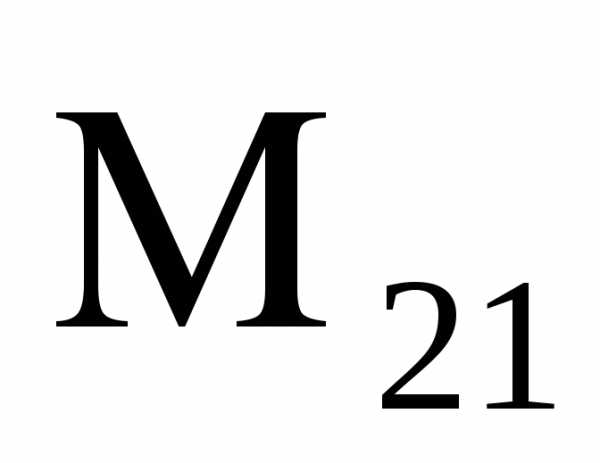 =-
=- 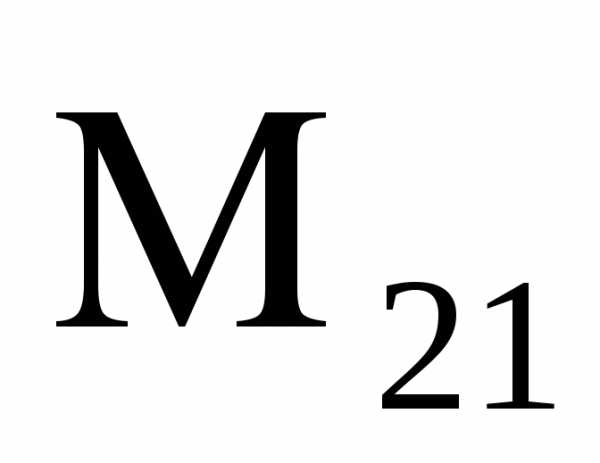 =
—
34.
=
—
34.
Найдем минор и алгебраическое дополнение к элементу
 .
.
 =6;
=6;  =
= 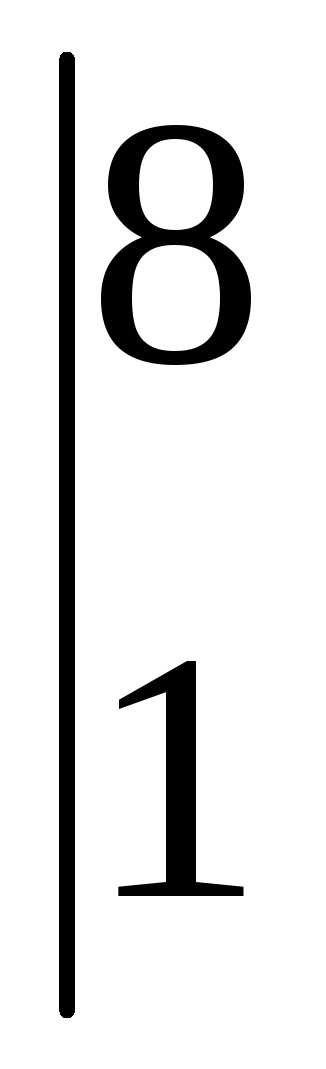
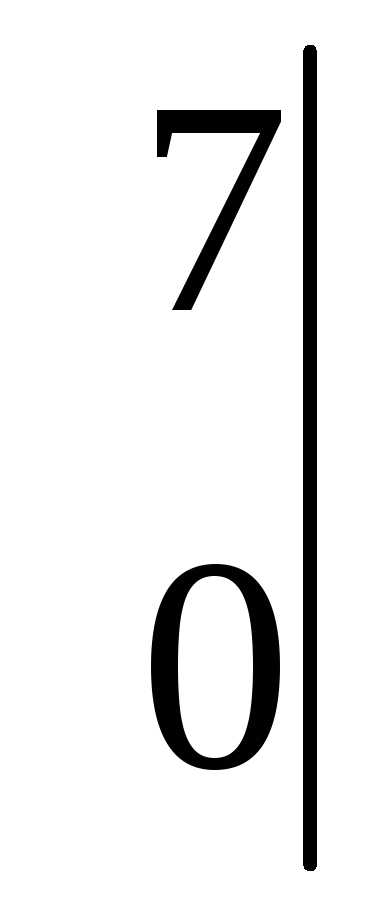 =
0 –7 = -7;
=
0 –7 = -7;  =(-1) 3+3 (-7)= — 7.
=(-1) 3+3 (-7)= — 7.
Рассмотрим матрицу n-го
порядка  и введем общее правило подсчета
определителяn-го
порядка.
и введем общее правило подсчета
определителяn-го
порядка.
Теорема Лапласа.
Определитель матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) матрицы на соответствующие им алгебраические дополнения.
Этот способ вычисления определителя называется разложением определителя по элементам некоторой строки (столбца) или разложением Лапласа.
При этом схемы разложений определителя по выбранной строке или выбранному столбцу будут выглядеть соответственно:
;
—
Пример.
Вычислим определитель третьего порядка, разложив его по элементам первой строки:
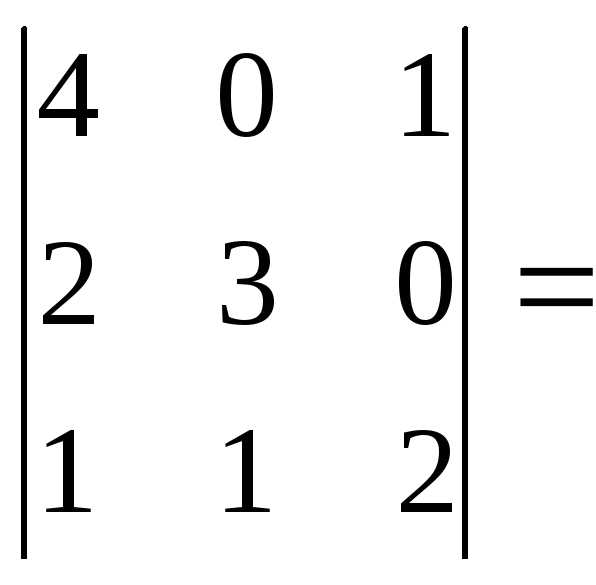 =
=
.
Свойства определителя
Определитель матрицы не меняется при её транспонировании.
Определитель не меняется, если ко всем элементам некоторой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тот же число.
Коротко: к строке определителя можно прибавить другую строку, умноженную на любое число.
Определитель меняет знак при перестановке любых двух строк (столбцов).
Общий множитель строки (столбца) можно вынести за знак определителя.
Определитель, содержащий нулевую строку (столбец), равен нулю.
Определитель, имеющий равные строки (столбцы), равен нулю.
Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
Определитель произведения двух квадратных матриц равен произведению определителей этих матриц.
Если элементы какой-либо строки определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Из этих свойств следует, что удобно считать определитель по той строке или тому столбцу, который содержит максимальное число элементов, равных нулю. Если нулевые элементы отсутствуют, то их можно получить, используя свойство 2.
studfiles.net
транспонирование матриц — ПриМат
1. Выполнить сложение матриц:
.
Для сложения матриц нам необходимо каждый элемент первой матрицы сложить с соответствующим элементом из второй:
.
Следует также отметить, что операция сложения матриц коммутативна и ассоциативна. Например, пусть даны матрицы , и . Тогда:
.
Покажем выполнение ассоциативности сложения матриц:
;
.
;
.
Как видим, .
2. Выполнить умножение матрицы на число:
.
Для умножения матрицы на число мы умножаем каждый элемент матрицы на данное число:
.
Операция умножения матрицы на число ассоциативна, то есть , . Покажем это на конкретном примере:
Пусть дана матрица и .
Тогда ;
.
;
.
Как видим, .
3. Вычислить произведение матриц:
.
Для удобства будем называть первую матрицу а вторую матрицу . Для начала убедимся, что произведение данных матриц возможно. Даны матрицы размерностей и , следовательно умножение возможно, так как количество столбцов первой матрицы равно количеству строк второй. Для вычисления первого элемента результирующей матрицы умножим каждый элемент первой строки матрицы на соответствующие элементы первого столбца матрицы . Полученные значения сложим. Данную последовательность действий можно проиллюстрировать следующим образом:
Получим следующее:
.
Далее вычисляем первый элемент второго столбца результирующей матрицы. Умножаем все элементы первой строки матрицы на соответствующие им элементы из второго столбца матрицы и складываем полученные значения:
.
Для вычисления первого элемента второй строки результирующей матрицы мы будем аналогично умножать элементы второй строки матрицы на элементы первого столбца матрицы , складывая результаты:
.
Оставшиеся элементы вычисляются аналогично:
.
Отметим, что произведение матриц в общем случае некоммутативно и покажем это на примере.
Пусть даны матрицы .
Тогда .
.
Как видим, .
4. Возвести матрицу в степень:
.
Для возведения в степень необходимо данную матрицу умножить саму на себя. Заметим, что возводить в степень можно только квадратные матрицы.
.
5. Транспонировать матрицу:
.
Для транспонирования матрицы достаточно записать строки столбцами, а столбцы строками:
.
Таблица лучших: Действия над матрицами. Групповые свойства некоторых матриц
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Действия над матрицами. Групповые свойства некоторых матриц
Лимит времени: 0
Информация
Тест на тему «Действия над матрицами. Групповые свойства некоторых матриц».
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 4
Ваше время:
Время вышло
| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
Источники:
- Г. С. Белозеров. Конспект лекций.
- В. В. Воеводин «Линейная алгебра» (Издание второе, переработанное и дополненное, 1980г.), стр. 194-197.
- А. Г. Курош «Курс высшей алгебры» (Издание девятое, 1968 г.), стр. 99-102.
- И. В. Проскуряков. «Сборник задач по линейной алгебре» (1984 г.), стр. 112-115.
Поделиться ссылкой:
ib.mazurok.com
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
ОПРЕДЕЛЕНИЕ. Транспонированной матрицей 
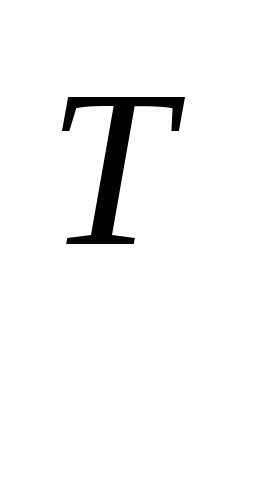 для матрицы
для матрицы размера
размера называется матрица размера
называется матрица размера ,
полученная из
,
полученная из заменой всех ее строк столбцами с теми
же порядковыми номерами.
заменой всех ее строк столбцами с теми
же порядковыми номерами.
То есть, если  =
=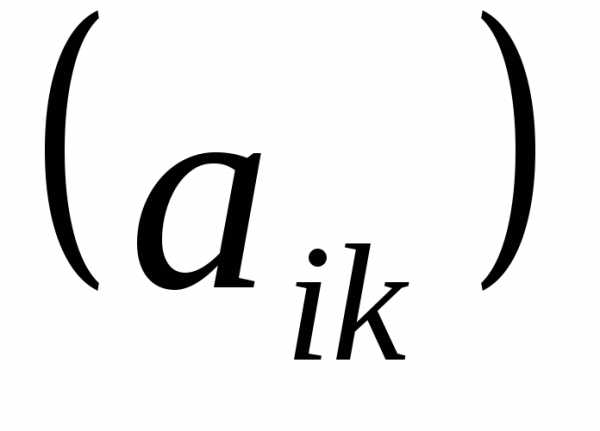 ,
то
,
то
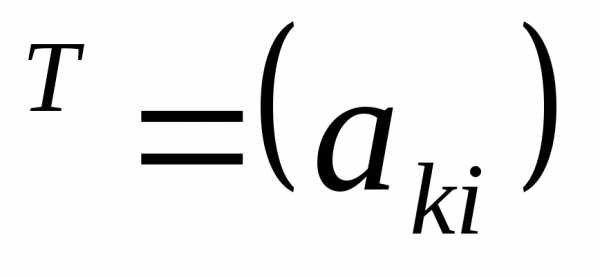 ,
,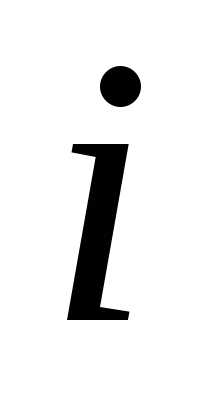 =1,2,…,
=1,2,…,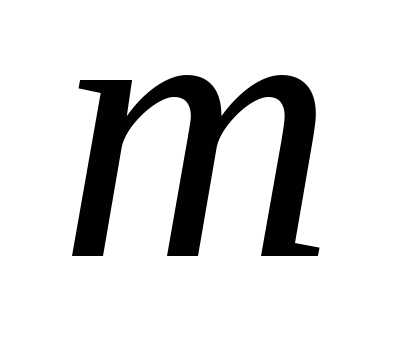 ,
, =1,2,…,
=1,2,…, .
.
ПРИМЕР.
 =
=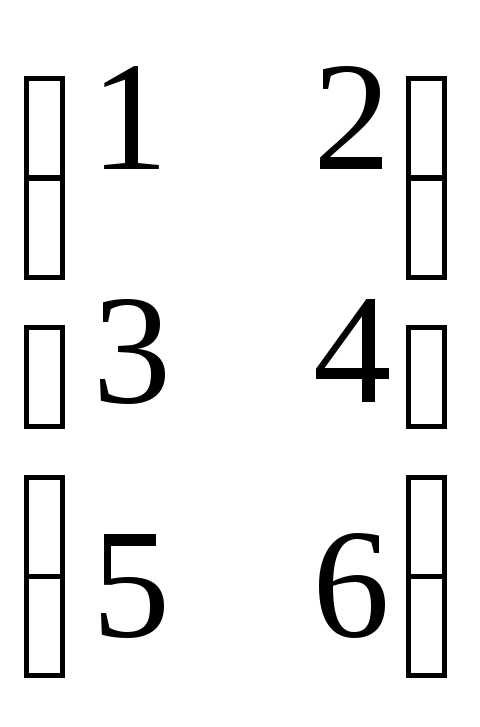
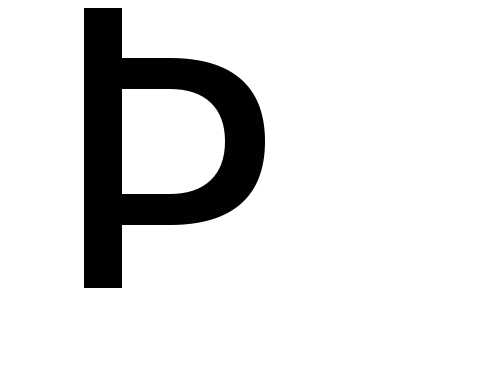

 ;
;  =
=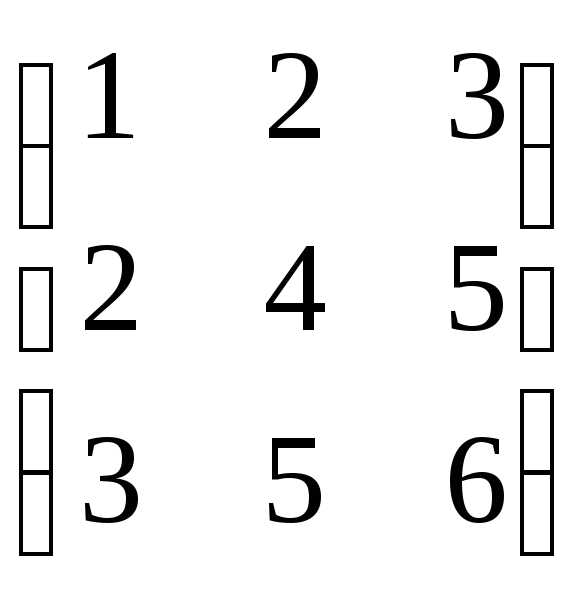 =
= 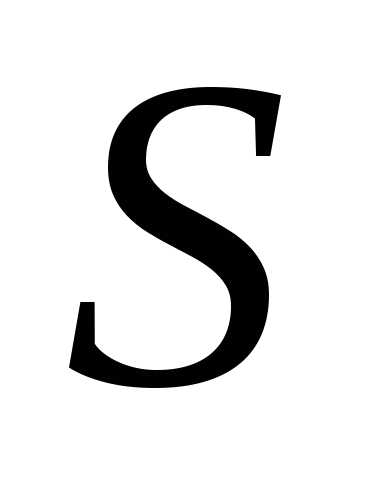

3х2 2х3 3х3 3х3
ОПРЕДЕЛЕНИЕ.
Если  =
=
 ,
то матрицаА называется симметрической.
,
то матрицаА называется симметрической.
Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
ОПРЕДЕЛЕНИЕ.
Пусть  =
=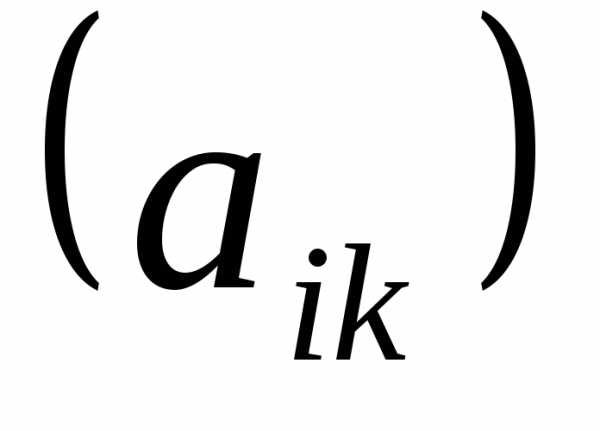 – матрица размера
– матрица размера ,
, =
=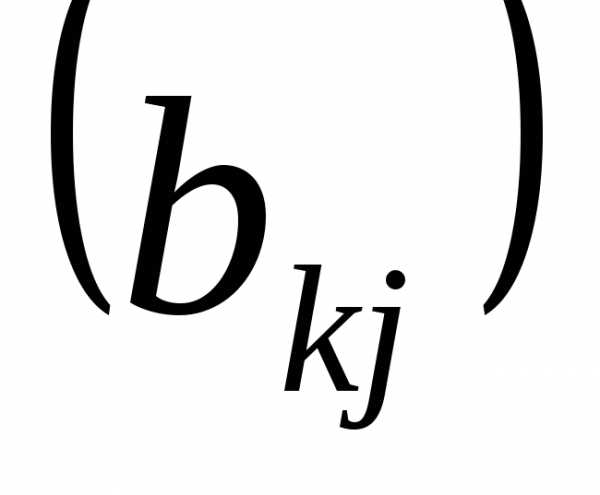 – матрица размера
– матрица размера .
Произведение этих матриц
.
Произведение этих матриц
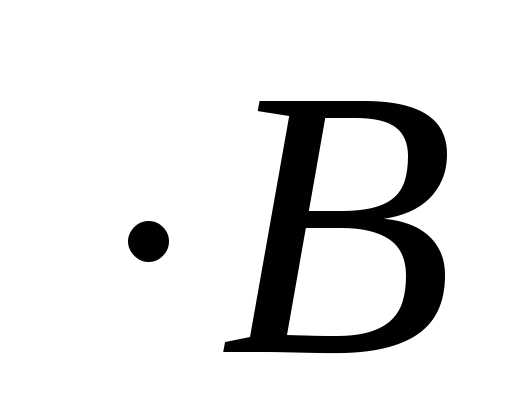 – матрица
– матрица =
=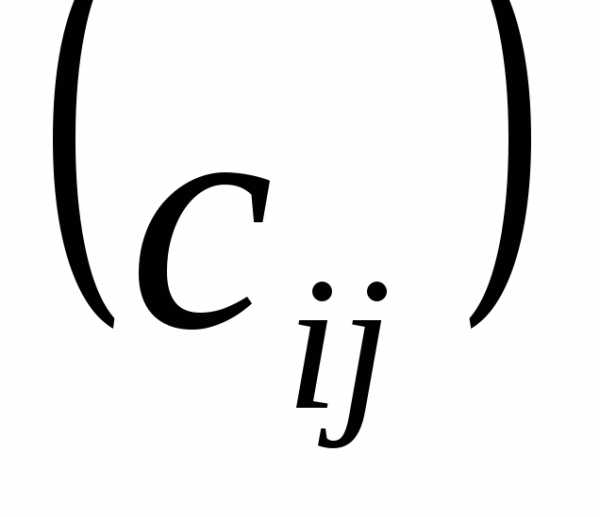 размера
размера ,
элементы которой вычисляются по формуле:
,
элементы которой вычисляются по формуле:
, 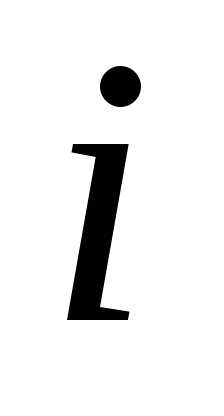 =1,2,…,
=1,2,…,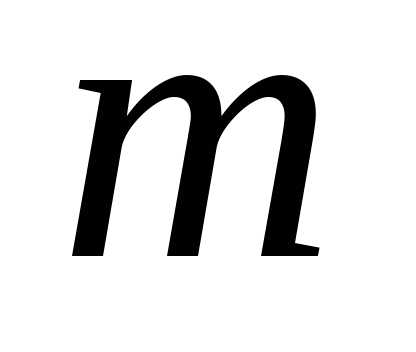 ,
,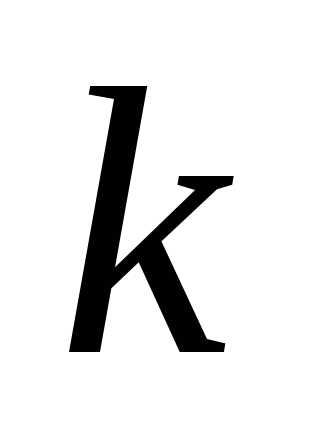 =1,2,…,
=1,2,…,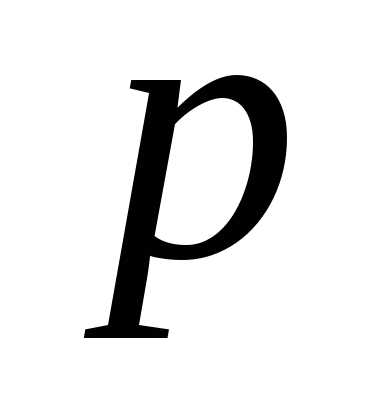 ,
,
то есть элемент 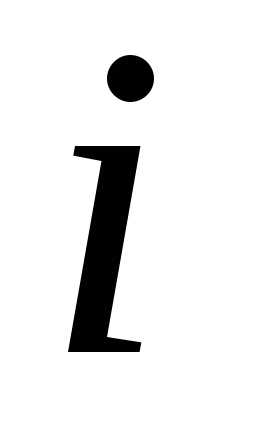 -й
строки и
-й
строки и -го
столбца матрицы
-го
столбца матрицы равен сумме произведений соответствующих
элементов
равен сумме произведений соответствующих
элементов -й
строки матрицы
-й
строки матрицы и
и -го
столбца матрицы
-го
столбца матрицы .
.
ПРИМЕР.
 =
=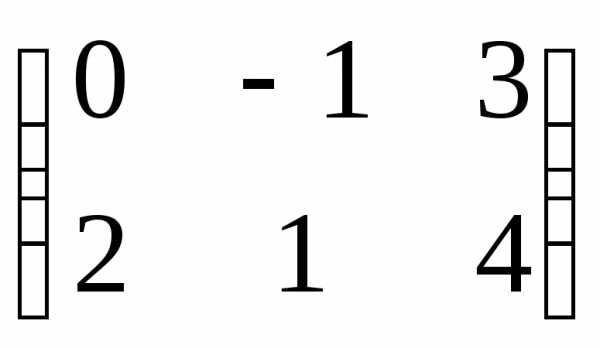 ,
,  =
=


2х3 3х1 2х3 3х1 2х1
Произведение 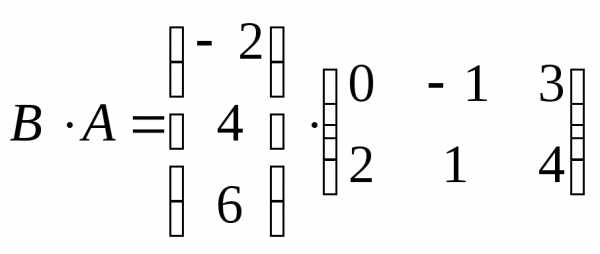 – не существует.
– не существует.
3х1 2х3
CВОЙСТВА ОПЕРАЦИИ УМНОЖЕНИЯ МАТРИЦ
1. , даже если оба произведения определены.
ПРИМЕР. 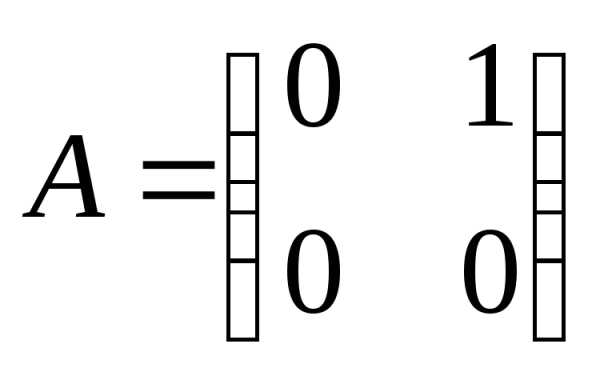 ,
,
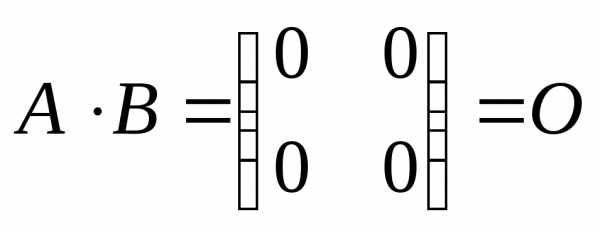 ,
хотя
,
хотя
ОПРЕДЕЛЕНИЕ.
Матрицы  и
и называютсяперестановочными,
если
,
в противном случае
называютсяперестановочными,
если
,
в противном случае и
и называютсянеперестановочными.
называютсянеперестановочными.
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
ПРИМЕР.
 матрицы
матрицы  и
и перестановочные.
перестановочные.
, то есть ,
значит,  и
и – перестановочные матрицы.
– перестановочные матрицы.
Вообще единичная
матрица перестановочна с любой квадратной
матрицей того же порядка, и для любой
матрицы
.
Это свойство матрицы объясняет, почему именно она называется
единичной: при умножении чисел таким
свойством обладает число 1.
объясняет, почему именно она называется
единичной: при умножении чисел таким
свойством обладает число 1.
Если соответствующие произведения определены, то:
2.
3. ,
4.
5.
ПРИМЕР.
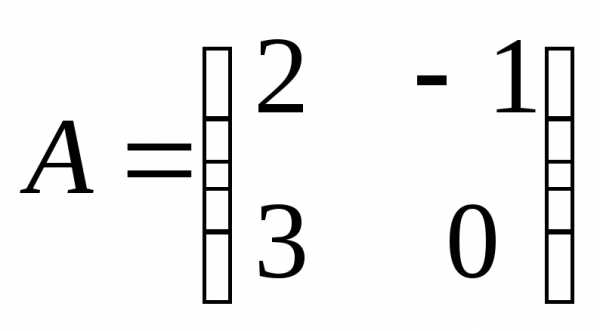 ,
, 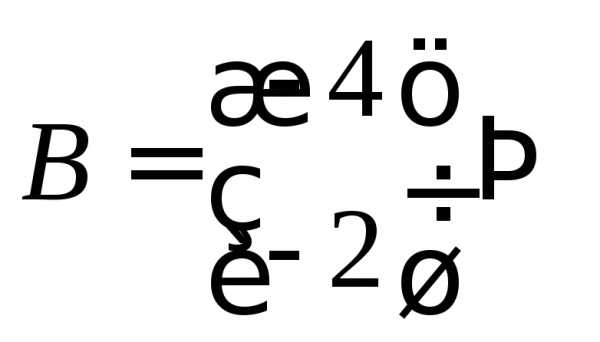
2х2 2х1 2х1 1х2
1х2 2х2 1х2
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
ПРИМЕР. 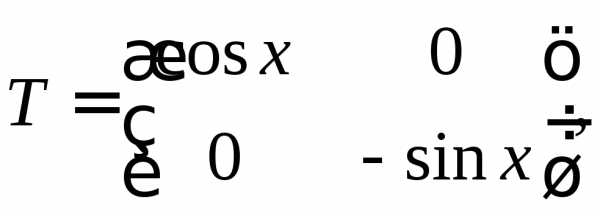
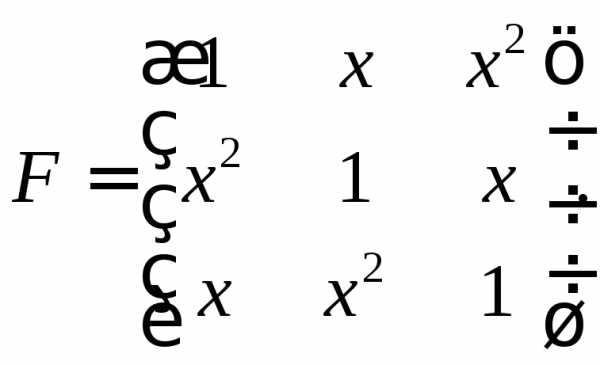
Определители и их свойства
Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим
квадратную матрицу второго порядка: 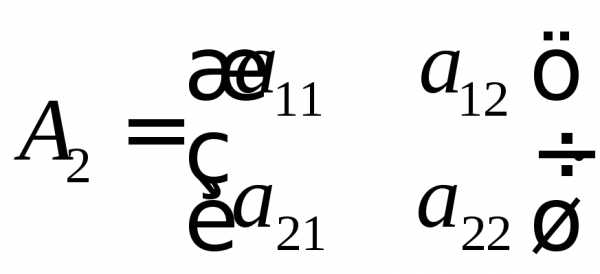
Её определителем называется число, которое записывается и вычисляется так:
(1.1)
Такой определитель называется определителем второго порядка и может
обозначаться
по-другому: 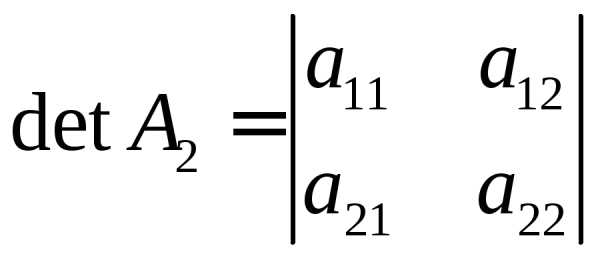 или
или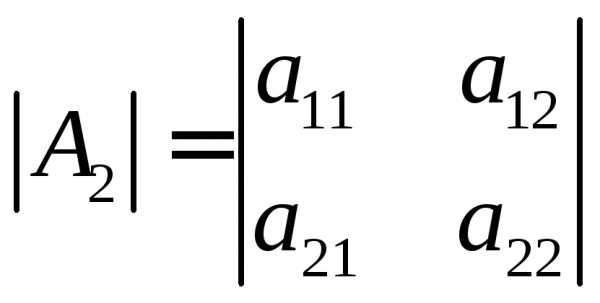 .
.
Определителем
третьего порядка называется число, соответствующее
квадратной матрице  ,
которое вычисляется по правилу:
,
которое вычисляется по правилу:
(1.2)
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:
ПРИМЕР.
;
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
(1.3)
То есть при
вычислении определителя третьего
порядка используются определители
второго порядка, причем 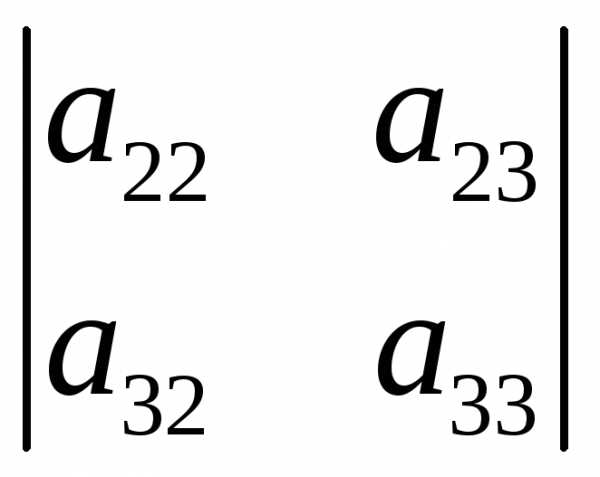 – определитель матрицы, полученный из
– определитель матрицы, полученный из вычеркиванием элемента
вычеркиванием элемента (точнее, первой строки и первого столбца,
на пересечении которых стоит
(точнее, первой строки и первого столбца,
на пересечении которых стоит ),
), – вычеркиванием элемента
– вычеркиванием элемента ,
,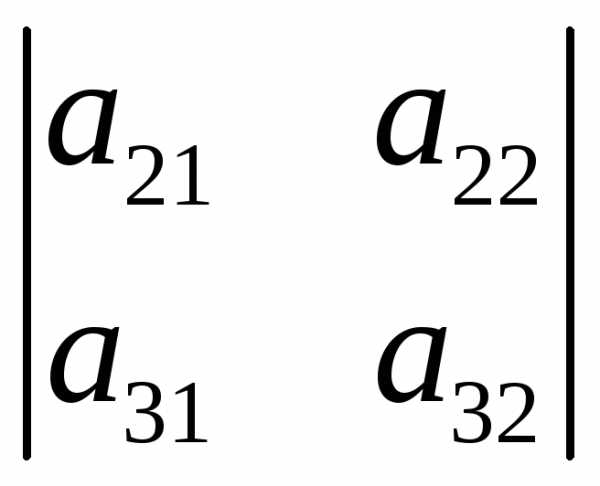 – элемента
– элемента .
.
ОПРЕДЕЛЕНИЕ. Дополнительным
минором элемента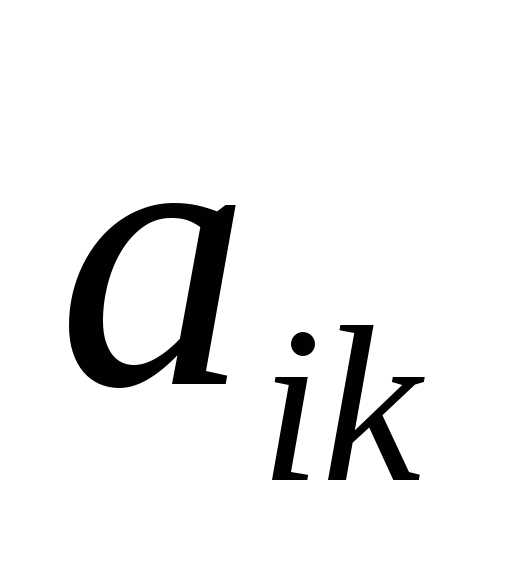 квадратной матрицы
квадратной матрицы называется определитель матрицы,
получаемой из
называется определитель матрицы,
получаемой из вычеркиванием
вычеркиванием -ой
строки и
-ой
строки и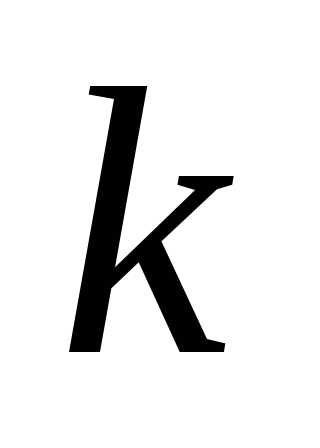 -го
столбца.
-го
столбца.
ПРИМЕР.

и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
ОПРЕДЕЛЕНИЕ. Алгебраическим
дополнением элемента 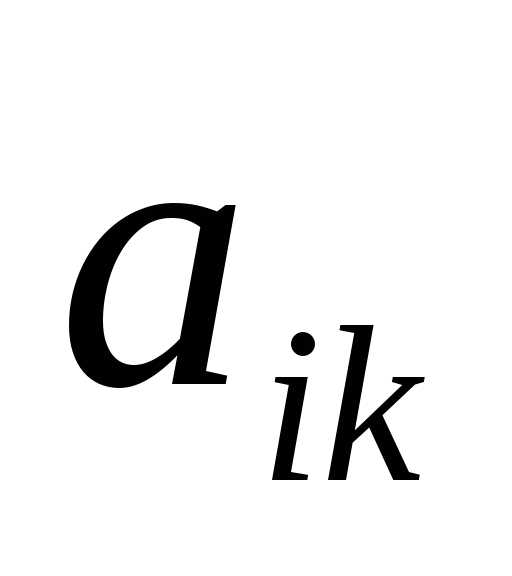 квадратной матрицы
квадратной матрицы называется число.
называется число.
ПРИМЕР.
Для матрицы  :
:
Для матрицы  :и так далее.
:и так далее.
Итак, с учетом сформулированных определений (1.3) можно переписать в виде: .
Перейдем теперь к общему случаю.
ОПРЕДЕЛЕНИЕ. Определителем квадратной матрицы 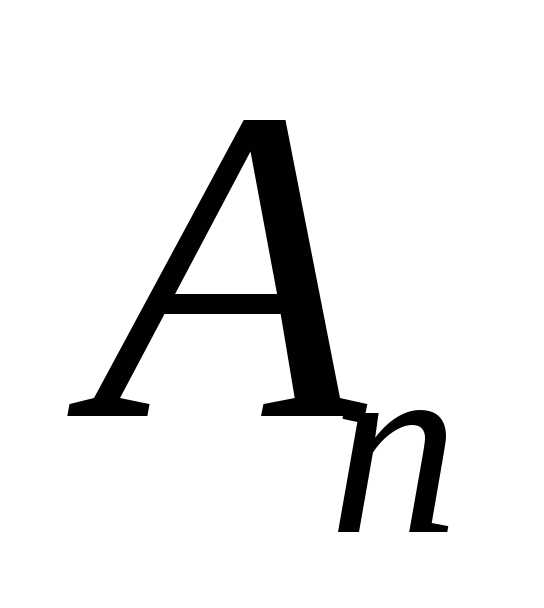 порядка
порядка называется число, которое записывается
и вычисляется следующим образом:
называется число, которое записывается
и вычисляется следующим образом:
(1.4)
Равенство (1.4)
называется разложением
определителя по элементам первой строки.
В этой формуле алгебраические дополнения
вычисляются как определители 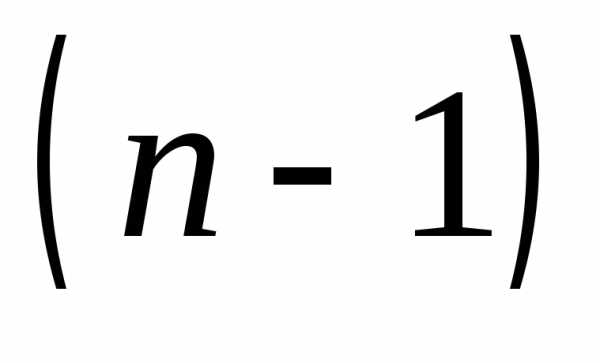 -го
порядка. Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
-го
порядка. Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
ПРИМЕР.
Рассмотрим (без доказательства) свойства определителей:
Определитель можно разложить по элементам первого столбца:
(1.5)
ПРИМЕР.
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
При транспонировании матрицы величина ее определителя не меняется: .
Отсюда следует, что строки и столбцы определителя равноправны.
Если в определителе поменять местами две строки (два столбца), то определитель изменит свой знак, не изменившись по абсолютной величине.
Определитель, имеющий две равные строки (столбца), равен нулю.
Если все элементы некоторой строки (столбца) определителя умножить на число
 ,
то величина определителя умножится
на это число.
,
то величина определителя умножится
на это число.
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
Определитель можно разложить по элементам любой строки (любого столбца): (1.6)
или
(1.7)
Равенство
(1.6) называется разложением
определителя по элементам 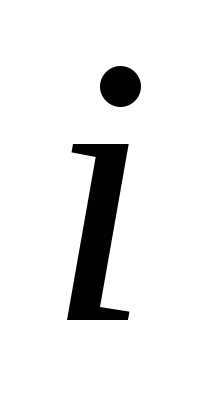 -й
строки.
-й
строки.
Равенство
(1.7) называется разложением
определителя по элементам 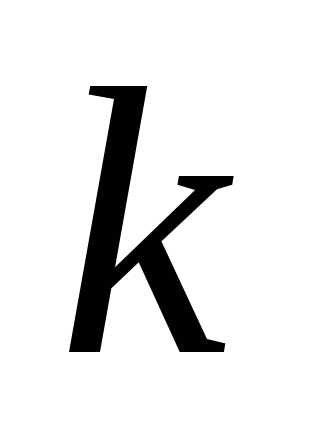 -го
столбца.
-го
столбца.
Сумма произведений всех элементов некоторой строки (столбца) на
алгебраические дополнения соответствующих элементов другой строки
(столбца) равна
нулю, то есть при 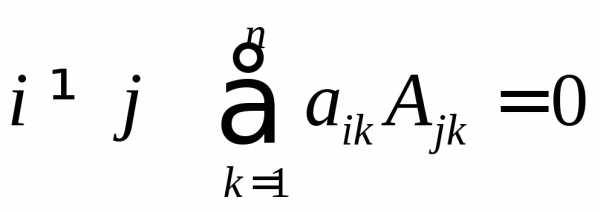 и
и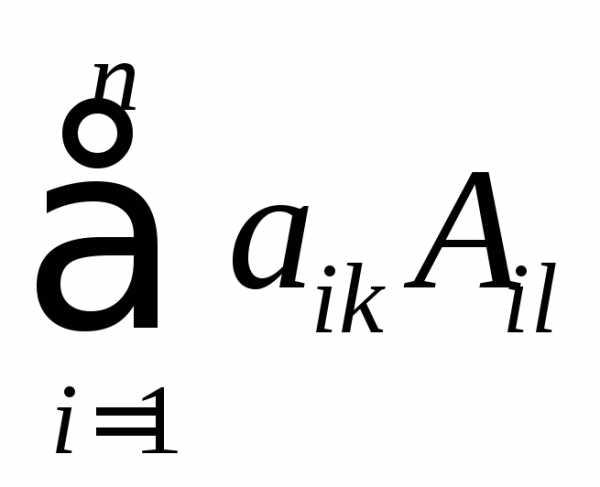 при
при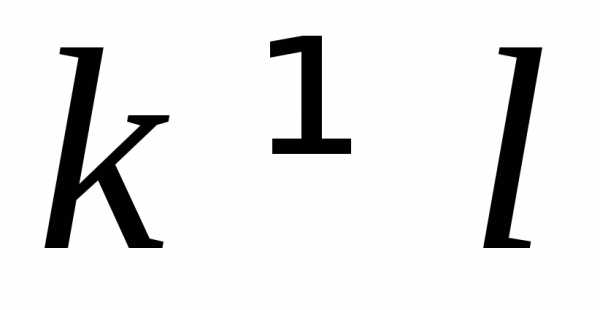 .
.
Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: (
 – квадратные матрицы одного порядка).
– квадратные матрицы одного порядка).
ПРИМЕР. 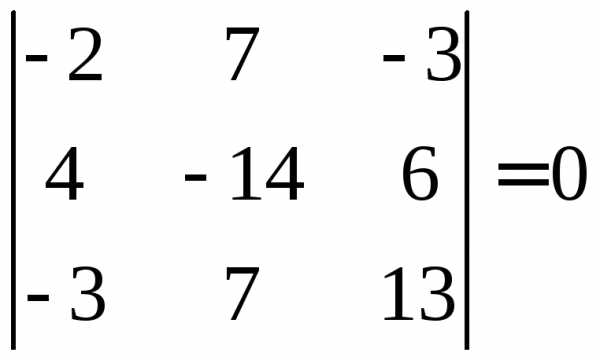 ,
так как элементы первой и второй строк
этого определителя соответственно
пропорциональны (свойство 6).
,
так как элементы первой и второй строк
этого определителя соответственно
пропорциональны (свойство 6).
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
ПРИМЕР.
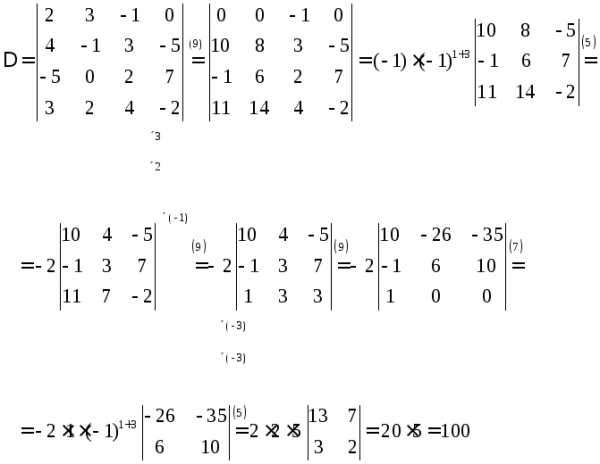
studfiles.net

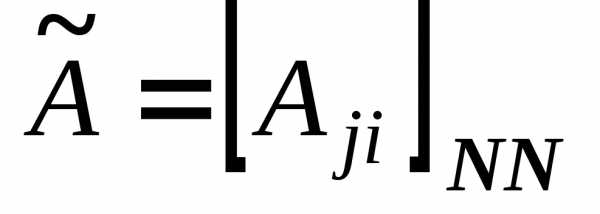 ;
; ,
то величина определителя умножится
на это число.
,
то величина определителя умножится
на это число. – квадратные матрицы одного порядка).
– квадратные матрицы одного порядка).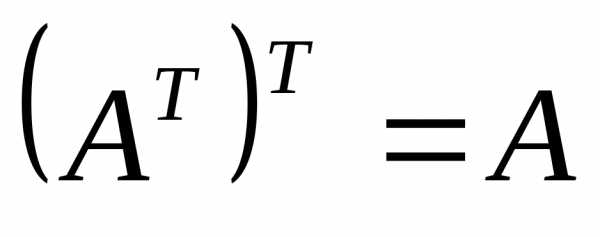
 .
. ,
то величина определителя умножится
на это число.
,
то величина определителя умножится
на это число. – квадратные матрицы одного порядка).
– квадратные матрицы одного порядка).