Множества равны когда: Понятие о множествах — ПриМат

Понятие о множествах — ПриМат

Понятие множества

Множество — это совокупность определенных объектов, которые могут иметь конкретные свойства.
Георг Кантор, который создал данную теорию давал следующее определение — «Под «множеством» мы понимаем соединение в некое целое $M$ определённых хорошо различимых предметов $m$ нашего созерцания или нашего мышления (которые будут называться «элементами» множества $M$).».

Множество состоит из отдельных объектов — элементов множества.

Множество обозначается большими буквами латинского алфавита, а его элементы — маленькими буквами латинского алфавита. Множества записываются в фигурных скобках $(X=\left\{a,b\right\})$.

Принято использовать следующие обозначения:

• $a\in\ X$ — символ принадлежности, читается как «элемент $a$ принадлежит множеству $X$»;
• $a\notin\ X$ — символ отрицания принадлежности, читается как«элемент $a$ не принадлежит множеству $X$»;
• $\forall$ — квантор произвольности, общности, читается как «любой» или «какой бы не был», или «для всех»;
• $\exists$ — квантор существования, например, $\exists\ y\in\ B$ — «существует (найдется) элемент $y$ из множества $B$»;
• $\exists!$ — квантор существования и единственности, например, $\exists!\ b\in\ C$ — «существует единственный элемент $b$ из множества $C$»;
• $:$ — символ пояснения, читается как «такой, что« или «обладающий свойством»;
• $\Rightarrow$ — символ следствия, читается как «отсюда следует« или «отсюда вытекает«;
• $\Leftrightarrow$ — квантор эквивалентности, равносильности, читается как «тогда и только тогда».

Существует два типа множеств — конечные и бесконечные.
Конечное множество — это множество, которое состоит из конечного числа элементов. Например, множество букв английского алфавита — представляет собой конечное множество.
Бесконечное множество — множество, которое состоит из бесконечного числа элементов. Например, множество рациональных чисел — представляет собой бесконечное множество.

Мощность множества — это число элементов, которое содержится в конечном множества $A$. Мощность обозначается как $\left|A\right|$.
Пустое множество — это множество, которое не содержит ни одного элемента — $\varnothing$.
Равные множества — это множества, которые включают в себя одни и те же элементы, то есть являются эквивалентными по отношению друг к другу.
Множества $X$ и $Y$ называются не равными ($X\ne\ Y$), если множество $X$ содержит в себе элементы, которые не содержит в себе множество $Y$. Другими словами — множество $X$ имеет элементы, которые не принадлежат множеству $Y$.

Символ равенства множеств имеет следующие свойства:

• $X=X$; — рефлексивность;
• если $X=Y$, $Y=X$ — симметричность;
• если $X=Y$, $Y=Z$, то $X=Z$ — транзитивность.

Согласно такому определению равенства множеств следует, что все пустые множества равны между собой или что существует только одно пустое множество.

Литература:

• Конспект лекций Г.С. Белозерова
• Линейная алгебра. Воеводин В.В. М.: Наука. Главная редакция физико-математической литературы, 1980, с.9-13
• Лекции по общей алгебре (издание второе). Курош А.Г. М.: Наука. Главная редакция физико-математической литературы, 1973, с.14-17

Поделиться ссылкой:

Похожее

что это такое, виды математических множеств

Что такое множество в математике? Математическое множество — это несколько отдельных элементов, рассматриваемых, как единое целое. Если обозначить такой элемент буквой a, а само множество — буквой А, то запись будет выглядеть следующим образом:

a ∈ A.

проговаривается эта запись так: a принадлежит А, или А содержит а, или а — элемент А.

Для перечисления элементов множества используются фигурные скобки — {}. То есть, например, множество, в котором а ∈ А, b ∈ A и c ∈ A, будет записываться в таком виде:

{a, b, c}.

Виды множеств.

Пустые множества.

Пустое множество – это то множество, которое вообще не содержит никаких элементов. Обозначается оно цифрой 0 или специальным значком ∅.

Примером пустого множества может служить любое нелогичное понятие, противоречащее самому себе — «множество птиц, живущих на дне океана», или «множество деревьев на Луне». Поскольку оба множества лишены смысла и не отвечают реальности, то, следовательно, они являются пустыми. Скажем, количество деревьев на Луне – 0, поэтому «множество деревьев на Луне» будет пустым (не будет содержать ни одного элемента).

Равные множества.

Равные множества – это два или более множеств, состоящих из равных наборов элементов. Приведём пример. Скажем, все члены Вашей семьи находятся на кухне. Таким образом, Множество «Члены семьи на кухне» будет равно множеству «Члены семьи в квартире».

Если два множества — А и B — состоят из одинакового набора элементов, то они будут равны, то есть А = B. Элементы множеств могут перечисляться в любой последовательности, на результат это никак не влияет. Множество {a, b, c} можно с тем же успехом записать, как {a, c, b}, или {с, b, a}, или {b, c, a}.

Подмножества и надмножества.

Если множества А и B состоят из одинаковых элементов {a, b, c}, то А будет считаться подмножеством B, а B — надмножеством А. Записывается это следующим образом:

A ⊆ B, B ⊇ A.

Бывает так, что множество В содержит в себе каждый из элементов множества А, но в то же время в нем присутствуют и другие элементы, множеству А не принадлежащие. В этом случае множество В становится собственным надмножеством А, в то время как множество А становится собственным подмножеством В.

Иначе говоря, если А ⊆ В, но при этом А ≠ В, то А ⊂ В, В ⊃ А.

Похожие статьи

Множества: понятие, определение, примеры

• Главная
• Справочник
• Алгебра
• Теория множеств
• Множества: понятие, определение, примеры

Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий и не поддается точному определению. Нижеследующие замечания имеют своей целью пояснить, что такое множество, но не претендуют на то, чтобы служить его определением.

Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.

Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.

Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.

Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.

Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество \(M\) состоит из предметов \(a,\,b,\,c,\,\ldots\) и только из этих предметов, то пишут

\(M=\{a,\,b,\,c,\,\ldots\}\)

Предметы, составляющие какое-либо множество, принято называть его элементами. Тот факт, что предмет т является элементом множества \(M\) , записывается в виде

\(\Large{m\in M}\)

и читается: » \(m\) принадлежит \(M\) «, или » \(m\) есть элемент \(M\) «. Если же предмет \(m\) не принадлежит множеству \(M\) , то пишут: \(m\notin M\) . Каждый предмет может служить лишь одним элементом заданного множества; иными словами, все элементы (одного и того же множества отличны
друг от друга.

Элементы множества \(M\) могут сами быть множествами, однако, во избежание противоречий, приходится требовать, чтобы само множество \(M\) не было одним из своих собственных элементов: \(M\notin M\) .

Множество, не содержащее ни одного элемента, называется пустым множеством. Например, множество всех действительных корней уравнения

\(x^2+1=0\)

есть пустое множество. Пустое множество в дальнейшем будем обозначать через \(\varnothing\) .

Если для двух множеств \(M\) и \(N\) каждый элемент \(x\) множества \(M\) является также элементом множества \(N\) , то говорят, что \(M\) входит в \(\) , что \(M\) есть часть \(N\) , что \(M\) есть подмножество \(M\) или что \(M\) содержится в \(N\) ; это записывается в виде

\(M\subseteq N\) или \(N\supseteq M\)

Например, множество \(M=\{1,2\}\) есть часть множества \(N=\{1,2,3\}\) .

Ясно, что всегда \(M\subseteq M\) . Удобно считать, что пустое множество есть часть любого множества.

Два множества равны, если они состоят из одних и тех же элементов. Например, множество корней уравнения \(x^2-3x+2=0\) и множество \(M=\{1,2\}\) между собою равны.

Определим правила действий над множествами.

---

Объединение или сумма множеств

Пусть имеются множества \(M,N,P,\ldots\) . Объединением или суммой этих множеств называется множество \(X\) , состоящее из всех элементов, принадлежащих хотя бы одному из «слагаемых»

\(X=M+N+P+\ldots\) или \(X=M\cup N\cup P\cup\ldots\)

При этом, даже если элемент \(x\) принадлежит нескольким слагаемым, то он входит в сумму \(M\) лишь один раз. Ясно, что

\(M+M=M\cup M=M\)

и если \(M\subseteq N\) , то

\(M+N=M\cup N=N\)

---

Пересечение множеств

Пересечением или общей частью множеств \(M,N,P,\ldots\) . называется множество \(Y\) , состоящее из всех тех элементов, которые принадлежат одновременно всем множествам \(M,N,P,\ldots\) .

Ясно, что \(M\cdot M=M\) , и если \(M\subseteq N\) , то \(M\cdot N=M\) .

Если пересечение множеств \(M\) и \(N\) пусто: \(M\cdot N=\varnothing\) , то говорят, что эти множества не пересекаются.

Для обозначения операции суммы и пересечения множеств употребляют также знаки \(\textstyle{\sum}\) и \(\textstyle{\prod}\) . Таким образом,

\(E=\sum E_i\) есть сумма множеств \(E_i\) , a \(F=\prod E_i\) — их пересечение.

Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом

\(M(N+P)=MN+MP,\)

а также законом

\(M+NP=(M+N)(M+P).\)

---

Разность множеств

Разностью двух множеств \(M\) и \(N\) называется множество \(Z\) всех тех элементов из \(Z\) , которые не принадлежат \(N\) :

\(Z=M-N\) или \(Z=M\setminus N\) .

Если \(N\subseteq M\) , то разность \(Z=M\setminus N=M-N\) называют также дополнением к множеству \(N\) относительно \(M\) .

Нетрудно показать, что всегда

\(M(N-P)=MN-MP\) и \((M-N)+MN=M.\)

Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.

---

Конечные и бесконечные множества

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.

Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.

Если множество \(M\) конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств \(M\) и \(N\) достаточно сосчитать число элементов в \(M\) , число элементов в \(N\) и сравнить полученные числа. Естественно также считать, что если одно из множеств \(M\) и \(N\) конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.

Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.

---

Взаимно однозначное соответствие множеств

Пусть снова \(M\) и \(N\) — два конечных множества. Как узнать, какое из этих множеств содержит больше элементов, не считая числа элементов в каждом множестве? Для этого будем составлять пары, объединяя в пару один элемент из \(M\) и один элемент из \(N\) . Тогда, если какому-нибудь элементу из \(M\) не найдется парного к нему элемента из \(N\) , то в \(M\) больше элементов, чем в \(N\) . Поясним это рассуждение примером.

Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.

Рассмотрим множество всех натуральных чисел

\(M=\{1,\,2,\,3,\,4,\,\ldots\}\)

и множество всех четных чисел

\(N=\{2,\,4,\,6,\,8,\,\ldots\}\)

Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.

Таблица 1

\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}M} &{\color{black}1} &{\color{black}2} &{\color{black}3} &{\color{black}4} &{\color{black}\cdots}\\\hline {\color{black}N} &{\color{black}2} &{\color{black}4} &{\color{black}6} &{\color{black}8} &{\color{black}\cdots} \end{array}}\)

Ни один элемент \(M\) и ни один элемент \(N\) не остается без пары. Правда, мы могли бы также образовать пары и так:

Таблица 2

\({\color{blue}\begin{array}{c|c|c|c|c|c|c} {\color{black}M}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}5}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}4}&{\color{black}-}&{\color{black}\cdots} \end{array}}\)

Тогда многие элементы из \(M\) остаются без пар. С другой стороны, мы могли бы составить пары и так:

Таблица 3

\({\color{blue}\begin{array}{c|c|c|c|c|c|c|c|c} {\color{black}M}&{\color{black}-}&{\color{black}1}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}3}&{\color{black}-}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}10}&{\color{black}12}&{\color{black}14}&{\color{black}\cdots} \end{array}}\)

Теперь многие элементы из \(M\) остаются без пар.

Таким образом, если множества \(A\) и \(B\) бесконечны, то различным способам образования пар соответствуют разные результаты. Если существует такой способ образования пар, при котором у каждого элемента \(A\) и каждого элемента \(B\) имеется парный к нему элемент, то говорят, что между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие. Например, между рассмотренными выше множествами \(M\) и \(N\) можно установить взаимно однозначное соответствие, как
это видно из табл. 1.

Если между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из \(A\) всегда остаются без пар, то говорят, что множество \(A\) содержит больше элементов, чем \(B\) , или что множество \(A\) имеет большую мощность, чем \(B\) .

Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.

Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества \(A\) и элементами множества всех натуральных чисел

\(Z=\{1,\,2,\,3,\,\ldots\},\)

то говорят, что множество \(A\) счетно. Иными словами, множество \(A\) счетно, если все его элементы можно занумеровать посредством натуральных чисел, т. е. записать в виде последовательности

\(a_1,~a_2,~\ldots,~a_n,~\ldots\)

Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).

Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.

Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть \(G\) есть множество всех четных чисел, \(H\) — множество всех нечетных чисел и \(Z\) — множество всех натуральных чисел. Как показывает таблица 4, множества \(G\) и \(H\) счетны. Однако множество \(Z=G+H\) вновь счетно.

Таблица 4

\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}G}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}\cdots}\\\hline {\color{black}H}&{\color{black}1}&{\color{black}3}&{\color{black}5}&{\color{black}7}&{\color{black}\cdots}\\\hline {\color{black}Z}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}\cdots} \end{array}}\)

Нарушение правила «целое больше части» для бесконечных множеств показывает, что свойства бесконечных множеств качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.

Докажем, что множество всех рациональных чисел счетно. Для этого расположим все рациональные числа в такую таблицу:

Таблица 5

\(\)

Здесь в первой строке помещены все натуральные числа в порядке их возрастания, во второй строке 0 и целые отрицательные числа в порядке их убывания, в третьей строке — положительные несократимые дроби со знаменателем 2 в порядке их возрастания, в четвертой строке — отрицательные несократимые дроби со знаменателем 2 в порядке их убывания и т. д. Ясно, что каждое рациональное число один и только один раз находится в этой таблице. Перенумеруем теперь

все числа этой таблицы в том порядке, как это указано стрелками. Тогда все рациональные числа разместятся в порядке одной последовательности:

Номер места, занимаемого
рациональным числом 1 2 3 4 5 6 7 8 9 . . .
Рациональное число 1. 2, О, 3, — 1, 4 —2 _

Этим установлено взаимно однозначное соответствие между всеми рациональными числами и всеми натуральными числами. Поэтому множество всех рациональных чисел счетно.

---

Множества мощности континуума

Если можно установить взаимно однозначное соответствие между элементами множества \(M\) и точками отрезка \(0\leqslant x\leqslant1\) , то говорят, что множество \(M\) имеет мощность континуума. В частности, согласно этому определению, само множество точек отрезка \(0\leqslant x\leqslant1\) имеет мощность континуума.

Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.

Нетрудно показать, что множества точек любого интервала \(x\in[a,b]\) и всей числовой прямой \(x\in[-\infty,+\infty]\) — имеют мощность континуума.

Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Множество всех множеств Википедия

U       =       ∅ ∁ {\displaystyle \mathbb {U} ~~~=~~~\varnothing ^{\complement }} 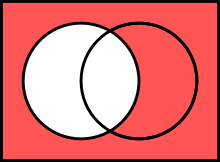A ∁       =       U ∖ A {\displaystyle A^{\complement }~~~=~~~\mathbb {U} \setminus A}

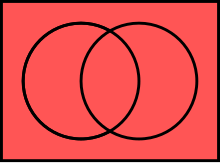
Универса́льное мно́жество — в математике множество, содержащее все объекты и все множества. В тех аксиоматиках, в которых универсальное множество существует, оно единственно.

Универсальное множество обычно обозначается U {\displaystyle \mathbb {U} } (от англ. universe, universal set), реже E {\displaystyle \mathbb {E} } .

В аксиоматике Цермело — Френкеля парадокс Рассела со схемой выделения и парадокс Кантора показывают, что предположение о существовании такого множества ведёт к противоречию.

В аксиоматике фон Неймана — Бернайса — Гёделя существует универсальный класс — класс всех множеств, но множеством он не является. Класс всех множеств является классом объектов категории Set.

В некоторых аксиоматиках существует универсальное множество, но при этом схема выделения не выполняется. Примером является теория New Foundations^[en] У. В. О. Куайна.

Также универсальным множеством называют множество объектов, рассматриваемых в каком-либо разделе математики. Для элементарной арифметики универсальным множеством является множество целых чисел, для аналитической геометрии плоскости универсальным множеством является множество всех упорядоченных пар действительных чисел^[1].

На диаграммах Венна универсальное множество (в обоих значениях) изображается множеством точек некоторого прямоугольника; подмножества его точек изображают подмножества универсального множества^[1].

В дальнейшем речь идёт о первом значении термина. Нижеприведённые формулы (за исключением U ∈ U {\displaystyle \mathbb {U} \in \mathbb {U} } ) верны и для второго значения, если через a {\displaystyle a} и A {\displaystyle A} обозначены соответственно любой элемент и любое подмножество множества U {\displaystyle \mathbb {U} }

Равные и эквивалентные наборы (определение и примеры)

• • Классы
    • Класс 1-3
    • Класс 4-5
    • Класс 6-10
    • Класс 11-12
  • КОНКУРСНЫЙ ЭКЗАМЕН
    • BNAT 000 NC
      • 000 NC Книги
        • Книги NCERT для класса 5
        • Книги NCERT для класса 6
        • Книги NCERT для класса 7
        • Книги NCERT для класса 8
        • Книги NCERT для класса 9
        • Книги NCERT для класса 10
        • Книги NCERT для класса 11
        • Книги NCERT для класса 12
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT 9000 9000
        • NCERT Exemplar Class
          • Решения RS Aggarwal, класс 12
          • Решения RS Aggarwal, класс 11
          • Решения RS Aggarwal, класс 10
          90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • RD Sharma Class 6 Решения
          • Решения RD Sharma
          Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • PHYSICS
          • Механика
          • Оптика
          • Термодинамика Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • MATHS
          • Теорема Пифагора
          0004
          • 000300030004
          • Простые числа
          • Взаимосвязи и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Деление фракций
        • 000
        • 000
        • 000
        • 000
        • 000
        • 000 Microology
        • 000
        • 000 Microology
        • 000 BIOG3000
          FORMULAS
          • Математические формулы
          • Алгебраические формулы
          • Тригонометрические формулы
          • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы
            • 0003000 PBS4000
            • 000300030002 Примеры калькуляторов химии
            Класс 6
            • Образцы документов CBSE для класса 7
            • Образцы документов CBSE для класса 8
            • Образцы документов CBSE для класса 9
            • Образцы документов CBSE для класса 10
            • Образцы документов CBSE для класса 11
            • Образцы документов CBSE чел для класса 12
          • CBSE Контрольный документ за предыдущий год
            • CBSE Контрольный документ за предыдущий год Класс 10
            • Контрольный документ за предыдущий год CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Class 11 Physics
            • Решения HC Verma, класс 12, физика
          • Решения Лакмира Сингха
            • Решения Лакмира Сингха, класс 9
            • Решения Лакмира Сингха, класс 10
            • Решения Лакмира Сингха, класс 8
          • Заметки CBSE
          • , класс
            CBSE Notes
            Примечания CBSE класса 7
            • Примечания CBSE класса 8
            • Примечания CBSE класса 9
            • Примечания CBSE класса 10
            • Примечания CBSE класса 11
            • Примечания CBSE класса 12
            • Примечания к редакции CBSE
              • Примечания к редакции
              • CBSE
              • Примечания к редакции класса 10 CBSE
              • Примечания к редакции класса 11 CBSE 9000 4
              • Примечания к редакции класса 12 CBSE
            • Дополнительные вопросы CBSE
              • Дополнительные вопросы по математике класса 8 CBSE
              • Дополнительные вопросы по науке 8 класса CBSE
              • Дополнительные вопросы по математике класса 9 CBSE
              • Дополнительные вопросы по науке класса 9 CBSE
              Дополнительные вопросы по математике для класса 10
              • Дополнительные вопросы по науке, класс 10 по CBSE
            • CBSE, класс
              • , класс 3
              • , класс 4
              • , класс 5
              • , класс 6
              • , класс 7
              • , класс 8
              • , класс 9 Класс 10
              • Класс 11
              • Класс 12
            • Учебные решения
          • Решения NCERT
            • Решения NCERT для класса 11
              • Решения NCERT для класса 11 по физике
              • Решения NCERT для класса 11 Химия
              Решения для биологии класса 11
              • Решения NCERT для математики класса 11
              9 0003 NCERT Solutions Class 11 Accountancy
              • NCERT Solutions Class 11 Business Studies
              • NCERT Solutions Class 11 Economics
              • NCERT Solutions Class 11 Statistics
              • NCERT Solutions Class 11 Commerce
            • NCERT Solutions For Class 12
              • NCERT Solutions For Класс 12 по физике
              • Решения NCERT для химии класса 12
              • Решения NCERT для класса 12 по биологии
              • Решения NCERT для класса 12 по математике
              • Решения NCERT Класс 12 Бухгалтерия
              • Решения NCERT, класс 12, бизнес-исследования
              • Решения NCERT, класс 12 Экономика
              • NCERT Solutions Class 12 Accountancy Part 1
              • NCERT Solutions Class 12 Accountancy Part 2
              • NCERT Solutions Class 12 Micro-Economics
              • NCERT Solutions Class 12 Commerce
              • NCERT Solutions Class 12 Macro-Economics
            • NCERT Solutions For Класс 4
              • Решения NCERT для математики класса 4
              • Решения NCERT для класса 4 EVS
            • Решения NCERT для класса 5
              • Решения NCERT для математики класса 5
              • Решения NCERT для класса 5 EVS
            • Решения NCERT для класса 6
              • Решения NCERT для математики класса 6
              • Решения NCERT для науки класса 6
              • Решения NCERT для социальных наук класса 6
              • Решения NCERT для класса 6 Английский
            • Решения NCERT для класса 7
              • Решения NCERT для класса 7 Математика
              • Решения NCERT для класса 7 Наука
              • Решения NCERT для класса 7 по социальным наукам
              • Решения NCERT для класса 7 Английский
            • Решения NCERT для класса 8
              • Решения NCERT для класса 8 Математика
              • Решения NCERT для класса 8 Science
              • Решения NCERT для социальных наук 8 класса
              • Решение NCERT ns для класса 8 Английский
            • Решения NCERT для класса 9
              • Решения NCERT для социальных наук класса 9
            • Решения NCERT для математики класса 9
              • Решения NCERT для математики класса 9 Глава 1
              • Решения NCERT для Математика класса 9 Глава 2
              • Решения NCERT для математики класса 9 Глава 3
              • Решения NCERT для математики класса 9 Глава 4
              Решения NCERT
              • для математики класса 9 Глава 5
              • Решения NCERT для математики класса 9 Глава 6
              • Решения NCERT для Математика класса 9 Глава 7
              • Решения NCERT для математики класса 9 Глава 8
              Решения NCERT
              • для математики класса 9 Глава 9
              Решения NCERT
              • для математики класса 9 Глава 10
              • Решения NCERT для математики класса 9 Глава 11
              • Решения NCERT для Математика класса 9 Глава 12
              • Решения NCERT для математики класса 9 Глава 13
              Решения
              • NCERT для математики класса 9 Глава 14
              • Решения NCERT для математики класса 9 Глава 15
            • Решения NCERT для науки класса 9
              • Решения NCERT для науки класса 9 Глава 1
              • Решения NCERT для науки класса 9 Глава 2
              • Решения NCERT для класса 9 Наука Глава 3
              • Решения NCERT для Науки Класса 9 Глава 4
              • Решения NCERT для Науки Класса 9 Глава 5
              • Решения NCERT для Науки Класса 9 Глава 6
              • Решения NCERT для Науки Класса 9 Глава 7
              • Решения NCERT для Класса 9 Наука Глава 8
              • Решения NCERT для Науки Класса 9 Глава 9
              • Решения NCERT для Науки Класса 9 Глава 10
              • Решения NCERT для Науки Класса 9 Глава 12
              • Решения NCERT для Науки Класса 9 Глава 11
              • Решения NCERT для Класса 9 Наука Глава 13
              • Решения NCERT для класса 9 Наука Глава 14
              • Решения NCERT для класса 9 по науке Глава 15
            • Решения NCERT для класса 10
              • Решения NCERT для класса 10 по социальным наукам
            • Решения NCERT для математики класса 10
              • Решения NCERT для математики класса 10 Глава 1
              • Решения NCERT для математики класса 10 Глава 2
              • Решения NCERT для математики класса 10 Глава 3
              • Решения NCERT для математики класса 10 Глава 4
              • Решения NCERT для математики класса 10 Глава 5
              • Решения NCERT для математики класса 10 Глава 6
              • Решения NCERT для математики класса 10 Глава 7
              • Решения NCERT для математики класса 10 Глава 8
              • Решения NCERT для математики класса 10 Глава 9
              Решения NCERT
              • для математики класса 10 Глава 10
              Решения
              • NCERT для математики класса 10 Глава 11
              • Решения NCERT для математики класса 10 Глава 12
              • Решения NCERT для математики класса 10 Глава 13
              • NCERT Sol Решения NCERT для математики класса 10 Глава 14
              • Решения NCERT для математики класса 10 Глава 15
            • Решения NCERT для науки класса 10
              • Решения NCERT для науки класса 10 Глава 1
              • Решения NCERT для науки класса 10 Глава 2
              • Решения NCERT для науки класса 10, глава 3
              • Решения NCERT для науки класса 10, глава 4
              • Решения NCERT для науки класса 10, глава 5
              • Решения NCERT для науки класса 10, глава 6
              • Решения NCERT для науки класса 10, глава 7
              • Решения NCERT для науки 10 класса, глава 8
              • Решения NCERT для науки класса 10 Глава 9
              • Решения NCERT для науки класса 10 Глава 10
              • Решения NCERT для науки класса 10 Глава 11
              • Решения NCERT для науки класса 10 Глава 12
              • Решения NCERT для науки 10 класса Глава 13
              • Решения NCERT для науки 10 класса Глава 14
              • Решения NCERT для науки класса 10 Глава 15
              Решения NCERT
              • для науки класса 10 Глава 16
            • Учебный план NCERT
            • NCERT
          • Commerce
            • Class 11 Commerce Syllabus
              ancy Account
              • Учебная программа по бизнесу 11 класса
              • Учебная программа по экономике 11 класса
            • Учебная программа по коммерции 12 класса
              • Учебная программа по бухгалтерии 12 класса
              • Учебная программа по бизнесу 12 класса
              • Учебная программа по экономике
              • 9000
                • Образцы документов по коммерции класса 11
                • Образцы документов по коммерции класса 12
                • TS Grewal Solutions
                  • TS Grewal Solutions Class 12 Accountancy
                  • TS Grewal Solutions Class 11 Accountancy
                • Отчет о движении денежных средств
                • Что такое Entry eurship
                • Защита прав потребителей
                • Что такое основной актив
                • Что такое баланс
                • Формат баланса
                • Что такое акции
                • Разница между продажей и маркетингом
              • ICSE
                • Документы ICSE
                • Вопросы ICSE
                • ML Aggarwal Solutions
                  • ML Aggarwal Solutions Class 10 Maths
                  • ML Aggarwal Solutions Class 9 Maths
                  • ML Aggarwal Solutions Class 8 Maths
                  • ML Aggarwal Solutions Class 7 Maths
                  • ML 6 Maths
                  • ML Aggarwal Solutions Class 6 Maths
                  • ML Aggarwal Solutions Class
                • Selina Solutions
                  • Selina Solutions для класса 8
                  • Selina Solutions для Class 10
                  • Selina Solutions для Class 9
                • Frank Solutions
                  • Frank Solutions для математики класса 10
                  • Frank Solutions для математики класса 9
                • Класс ICSE 9000 2
                • ICSE Class 6
                • ICSE Class 7
                • ICSE Class 8
                • ICSE Class 9
                • ICSE Class 10
                • ISC Class 11
                • ISC Class 12
            • IAS
              Exam
              • IAS
              • Civil
              • Сервисный экзамен
              • Программа UPSC
              • Бесплатная подготовка к IAS
              • Текущие события
              • Список статей IAS
              • Пробный тест IAS 2019
                • Пробный тест IAS 2019 1
                • Пробный тест IAS 2019 2
            • Экзамен KPSC KAS
            • Экзамен UPPSC PCS
            • Экзамен MPSC
            • Экзамен RPSC RAS ​​
            • TNPSC Group 1
            • APPSC Group 1
            • Экзамен BPSC
            • WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
            • Вопросник UPSC 2019
              • Ключ ответов UPSC 2019
            • Коучинг IAS
              • IA S Coaching Бангалор
              • IAS Coaching Дели
              • IAS Coaching Ченнаи
              • IAS Coaching Хайдарабад
              • IAS Coaching Мумбаи
          • JEE
            • BYJU’SEE
            • 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
            • Вопросник JEE
            • Биномиальная теорема
            • Статьи JEE
            • Квадратичное уравнение
          • NEET
            • Программа BYJU NEET
            • NEET 2020
            • NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
            • Поддержка
              • Разрешение жалоб
              • Служба поддержки
              • Центр поддержки
          • Государственные советы
            • GSEB
              • GSEB Syllabus
              • GSEB4
              • GSEB3 Образец статьи
              GSEB3 004
              • MSBSHSE
                • MSBSHSE Syllabus
                • MSBSHSE Учебники
                • Образцы статей MSBSHSE
                • Вопросники MSBSHSE
              • AP Board
                • APSCERT
                • APS4
                • Syll
                • AP
                • Syll 9000SC4
                • Syll
                • AP 9000S4 9000 Syll
                • Syll
              • MP Board
                • MP Board Syllabus
                • MP Board Образцы документов
                • Учебники MP Board
              • Assam Board
                • Assam Board Syllabus
                • Assam Board Учебники 9000 9000 Board4 BSEB
                  • Bihar Board Syllabus
                  • Bihar Board Учебники
                  • Bihar Board Question Papers
                  • Bihar Board Model Papers
                • BSE Odisha
                  • Odisha Board Syllabus
                  • Odisha Board Syllabus
                  • Программа PSEB
                  • Учебники PSEB
                  • Вопросы PSEB
                • RBSE
                  • Rajasthan Board Syllabus
                  • RBSE Учебники
                  • RBSE Question Papers
                • HPBOSE
                • HPBOSE
                • HPBOSE
                • JKBOSE
                  • Программа JKBOSE
                  • Образцы документов JKBOSE
                  • Шаблон экзамена JKBOSE
                • TN Board
                  • TN Board Syllabus
                  • TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 Paper 9000 Paper
                  JAC
                  • Учебник JAC
                  • Учебники JAC
                  • Вопросники JAC
                  • Telangana Board
                    • Telangana Board Syllabus
                    • Telangana Board Учебники
                    • Papers
                    • Telangana Board Учебники
                    • Учебный план KSEEB
                    • Типовой вопросник KSEEB
                  • KBPE
                    • Учебный план KBPE
                    • Учебники KBPE
                    • Документы по KBPE
                  • 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
                • Совет по Западной Бенгалии
                  • Учебный план Совета по Западной Бенгалии
                  • Учебники для Совета по Западной Бенгалии
                  • Вопросы для Совета по Западной Бенгалии
                • UBSE
                • TBSE
                • Гоа Совет
                • 000
                • NBSE0003 Доска
                • Доска Manipur
                • Доска Haryana
              • Государственные экзамены
          .Производительность

          — эффективное сравнение двух наборов в python

          Переполнение стека
          1. Около
          2. Товары
          3. Для команд
          1. Переполнение стека Общественные вопросы и ответы
          2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
          3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
          4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
          5. Реклама Обратитесь к разработчикам и технологам со всего мира
          6. О компании

          Загрузка…

          .Схема

          — Сравнение двух списков (наборов)

          Переполнение стека
          1. Около
          2. Товары
          3. Для команд
          1. Переполнение стека Общественные вопросы и ответы
          2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
          3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
          4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
          5. Реклама Обратитесь к разработчикам и технологам со всего мира
          6. О компании
          .

          java — почему метод equals (), когда у нас есть оператор ==?

          Переполнение стека
          1. Около
          2. Товары
          3. Для команд
          1. Переполнение стека Общественные вопросы и ответы
          2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
          3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
          4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
          5. Реклама Обратитесь к разработчикам и технологам со всего мира
          6. О компании
          .

          No related posts.