РАЗЛОЖЕНИЕ ЧИСЛА на простые множители, таблица простых чисел
Разложение числа на простые множители – это часто встречающаяся задача, которую нужно уметь решать. Разложение на простые множители может потребоваться при нахождении НОД (наибольший общий делитель) и НОК (наименьшее общее кратное), а также при проверке, являются ли числа взаимно простыми.
Все числа можно разделить на два основных типа:
- Простое число – это число, которое делится только на само себя и на 1.
- Составное число – это число, которое имеет другие делители, кроме самого себя и 1.
Чтобы проверить, является ли число простым или составным, можно воспользоваться специальной таблицей простых чисел.
Таблица простых чисел
Для удобства вычислений все простые числа были собраны в таблицу. Ниже приведена таблица простых чисел из диапазона от 1 до 1000.
| 2 | 3 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | |
| 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 409 | 419 | 421 | 431 | 433 | |
| 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Разложение на простые множители
Для разложения числа на простые множители можно использовать таблицу простых чисел и признаки делимости чисел. До тех пор, пока число не станет равно 1, нужно подбирать простое число, на которое делится текущее, и выполнять деление. Если не удалось подобрать ни одного множителя, не равного 1 и самому числу, то число простое. Рассмотрим, как это делается на примере.
Пример:
Разложить на простые множители число 63140.
Решение:

Чтобы не потерять множители, будем записывать их в столбик, как показано на картинке. Такое решение является достаточно компактным и удобным. Рассмотрим его подробнее.
Число 63140 четное, поэтому оно делится на 2:
Число 31570 четное, поэтому оно делится на 2:
Число 15785 нечетное, поэтому на 2 не делится. Сумма цифр числа
не делится на 3, поэтому число 15785 на 3 не делится. Зато оно заканчивается на 5, поэтому оно делится на 5:
Число 3157 заканчивается на 7, поэтому оно не делится на 5. Зато число 3157 делится на 7:
Число 451 больше на 7 не делится. Поэтому проверяем следующее простое число – 11: чтобы число 451 делилось на 11, нужно чтобы сумма цифр на нечетных местах была равна сумме цифр на четных местах:
Поэтому 451 делится на 11:
Число 41 является простым, поэтому следующий множитель равен 41.
Таким образом, число 63140 было разложено на множители:
63140 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 41
worksbase.ru
Разложение на простые множители
Любое число, которое является составным, можно показать в виде произведения отдельных множителей.
150 = 2 × 3 × 5 × 5
225 = 3 × 3 × 5 × 5
1470 = 2 × 3 × 5 × 7 × 7
Небольшие числа можно легко разложить, используя таблицу умножения. Для больших же чисел, следует воспользоваться таблицей простых чисел.
В качестве примера разложим число 1463 на простые множители с помощью таблицы простых чисел:
| 2 | 23 | 61 | 103 | 151 |
| 3 | 29 | 67 | 107 | 157 |
| 4 | 31 | 71 | 109 | 163 |
| 5 | 37 | 73 | 113 | 167 |
| 7 | 41 | 79 | 127 | 173 |
| 11 | 43 | 83 | 131 | 179 |
| 13 | 47 | 89 | 137 | 181 |
| 17 | 53 | 97 | 139 | 191 |
| 19 | 59 | 101 | 149 | 193 |
Просматриваем простые числа данной таблицы и выбираем то число, которым можно разделить исходное число, например 7.
Число 1463 делим на 7, в результате получаем 209.
Далее повторяем процесс поиска простых чисел для 209 по признакам делимости, и выбираем число 11, которое представляет собой его делитель.
Делим число 209 на 11 и в результате получаем число 19, в свою очередь, являющееся простым числом, в соответствии таблицей простых чисел.
Таким образом, делителями для числа 1463 будут числа 7, 11 и 19.
1463 = 7 × 11 × 19
Описанную последовательность можно записать следующим образом:
| Делимое | Делитель |
| 1463 | 7 |
| 209 | 11 |
| 19 | 19 |
simple-math.ru
Разложение на множители, разбор основных заданий
По сути, здесь приведены основные формулы сокращенного умножения. Но формулы представлены так, что именно из суммы получено произведение. Чаще всего именно так приходится работать с формулами, будь то сокращение дробей, решение неравенств методом интервалов и т.п.
Основные способы разложения многочлена на множители
1. Вынесение общего множителя за скобку
2. (формула разности квадратов)
3. (формула квадрата суммы/разности)
4. (формула суммы/разности кубов)
5. (формула куба суммы/разности)
6. Способ группировки
Например,
7. ,
где – корни уравнения
Пример 1.
Разложить на множители: .
Решение: + показать
Пример 2.
Разложить на множители: .
Решение: + показать
Пример 3.
Разложить на множители: .
Решение: + показать
Пример 4.
Разложить на множители: .
Решение: + показать
Пример 5.
Разложить на множители: .
Решение: + показать
Пример 6.
Сократить дробь:.
Решение: + показать
Чтобы сократить дробь, следует разбить на множители числитель и\или знаменатель. Применяем способ группировки (п.6) (а также формулу “разность квадратов”, п.2) к числителю:
Пример 7.
Разложить на множители: .
Решение: + показать
Пример 8.
Сократить дробь:
Решение: + показать
Для полного квадрата (п.3) первым трем слагаемым числителя не хватает коэффициента 2 перед вторым слагаемым. Представим как , что, кстати, еще и поможет нам в дальнейшем выйти на разность квадратов (п.2):
Пример 9.
Разложить на множители: .
Решение: + показать
egemaximum.ru
Конспект «Разложение на множители» — УчительPRO
Разложение на множители
Очень часто числитель и знаменатель дроби представляют собой алгебраические выражения, которые сначала нужно разложить на множители, а потом, обнаружив среди них одинаковые, разделить на них и числитель, и знаменатель, то есть сократить дробь. Заданиям разложить многочлен на множители посвящена целая глава учебника по алгебре в 7-м классе. Разложение на множители можно осуществить 3 способами, а также комбинацией этих способов.
1. Применение формул сокращенного умножения
Как известно, чтобы умножить многочлен на многочлен, нужно каждое слагаемое одного многочлена умножить на каждое слагаемое другого многочлена и полученные произведения сложить. Есть, как минимум, 7 (семь) часто встречающихся случаев умножения многочленов, которые вошли в понятие «Формулы сокращенного умножения». Например,
Таблица 1. Разложение на множители 1-м способом

2. Вынесение общего множителя за скобку
Этот способ основан на применении распределительного закона умножения. Например,
Каждое слагаемое исходного выражения мы делим на множитель, который выносим, и получаем при этом выражение в скобках (то есть в скобках остаётся результат деления того, что было, на то, что выносим). Прежде всего нужно правильно определить множитель, который надо вынести за скобку.
Общим множителем может быть и многочлен в скобках:
При выполнении задания «разложите на множители» надо быть особенно внимательным со знаками при вынесении общего множителя за скобки. Чтобы поменять знак у каждого слагаемого в скобке (b — a), вынесем за скобку общий множитель -1, при этом каждое слагаемое в скобке разделится на -1: (b — a) = — (a — b).
В том случае если выражение в скобках возводится в квадрат (или в любую чётную степень), то числа внутри скобок можно менять местами совершенно свободно, так как вынесенные за скобки минусы при умножении всё равно превратятся в плюс: (b — a)2 = (a — b)2, (b — a)4 = (a — b)4 и так далее…
3. Способ группировки
Иногда общий множитель имеется не у всех слагаемых в выражении, а только у некоторых. Тогда можно попробовать сгруппировать слагаемые в скобки так, чтобы из каждой можно было какой-то множитель вынести. Способ группировки — это двойное вынесение общих множителей за скобки.
4. Использование сразу нескольких способов
Иногда нужно применить не один, а несколько способов разложения многочлена на множители сразу.
Это конспект по теме «Разложение на множители». Выберите дальнейшие действия:
Разложение на множители
5 (100%) 8 vote[s]uchitel.pro
Разложение многочлена на множители. Теорема Безу и схема Горнера
Разложение многочлена на множители. Теорема Безу и схема Горнера
При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.
Как обычно, обратимся за помощью к теории.
Теорема Безу утверждает, что остаток от деления многочлена на двучлен равен .
Но для нас важна не сама теорема, а следствие из нее:
Если число является корнем многочлена , то многочлен делится без остатка на двучлен .
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где — корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.
Остановимся подробнее на этих моментах.
1. Как найти корень многочлена.
Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.
Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.
Например, в многочлене сумма коэффициентов равна нулю: . Легко проверить, что является корнем многочлена.
Если сумма коэффициентов многочлена при четных степенях равна сумме коэффициентов при нечетных степенях, то число является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку , а — четное число.
Например, в многочлене сумма коэффициентов при четных степенях : , и сумма коэффициентов при нечетных степенях : . Легко проверить, что является корнем многочлена.
Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.
Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент — коэффициент при — равен единице) справедлива формула Виета:
, где — корни многочлена .
Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
Из этой формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.
Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.
Рассмотрим, например, многочлен
Делители свободного члена: ; ; ;
Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.
Сумма коэффициентов при четных степенях :
Сумма коэффициентов при нечетных степенях :
, следовательно, число -1 также не является корнем многочлена.
Проверим, является ли число 2 корнем многочлена: , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен делится без остатка на двучлен .
2. Как разделить многочлен на двучлен.
Многочлен можно разделить на двучлен столбиком.
Разделим многочлен на двучлен столбиком:
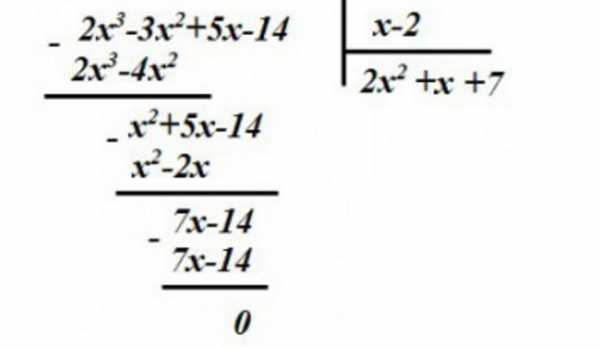
Есть и другой способ деления многочлена на двучлен — схема Горнера.
Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.
Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 — так же, как при составлении таблицы для схемы Горнера.
Итак, если нам нужно разделить многочлен на двучлен и в результате деления мы получаем многочлен , то коэффициенты многочлена мы можем найти по схеме Горнера:
Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена , то остаток от деления многочлена на равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число корнем многочлена и делим этот многочлен на двучлен .
Пример. Решить уравнение:
1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.
Делители числа 24:
2. Проверим, является ли число 1 корнем многочлена.
Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.
3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.
А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.
Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при пишем 0. Слева пишем найденный корень: число 1.
Б) Заполняем первую строку таблицы.
В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
Будем делить дальше. Нам нужно найти корни многочлена . Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
Легко проверить, что числа 1 и -1 не являются корнями многочлена
В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :
Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.
В последнем столбце мы получили -40 — число, не равное нулю, следовательно, многочлен делится на двучлен с остатком, и число 2 не является корнем многочлена.
Идем дальше.
В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:
Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена на двучлен в таблице изображены зеленым цветом.
В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:
Итак, корни исходного уравнения :
{}
Ответ: {}
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Что значит разложить на множители? Разложите на простые множители число 24. Как разложить число на простые множители
Что значит разложить на множители?
Что значит разложить на множители? Это значит найти числа, произведение которых равно исходному числу.
Чтобы понять, что значит разложить на множители, рассмотрим пример.
Пример разложения числа на множители
Разложить на множители число 8.
Решение.
Число 8 можно представить в виде произведения 2 на 4:
8 = 2 * 4
Представление 8 в виде произведения 2 * 4 и значит разложение на множители.
Обратите внимание, что это не единственное разложение 8 на множители.
Ведь 4 разлагается на множители так:
4 = 2 * 2
Отсюда 8 можно представить:
8 = 2 * 2 * 2 = 23
Проверяем наш ответ. Найдем, чему равно разложение на множители:
2 * 2 * 2 = 8
То есть получили исходное число, ответ верный.
Разложите на простые множители число 24
Как разложить на простые множители число 24?
Простым называют число, если оно нацело делится только на единицу и на себя.
Число 8 можно представить в виде произведения 3 на 8:
24 = 3 * 8
Здесь число 24 разложено на множители. Но в задании сказано «разложить на простые множители число 24», т.е. нужны именно простые множители. А в нашем разложении 3 является простым множителем, а 8 не является простым множителем.
В предыдущем примере мы получили разложение числа 8 на простые множители:
8 = 2 * 2 * 2 = 23
Отсюда получаем для 24:
24 = 3 * 8 = 3 * 2 * 2 * 2 = 3 * 23
Итак, разложение числа 24 на простые множители:
24 = 3 * 23
www.sbp-program.ru
Примеры разложения многочленов на множители
1. Примеры с решением квадратного уравнения
Пример 1.1
Разложить многочлен на множители:
x4 + x3 – 6x2.
Решение
Выносим x2 за скобки:
.
Решаем квадратное уравнение x2 + x – 6 = 0:
.
Корни уравнения:
, .
Отсюда получаем разложение многочлена на множители:
.
Ответ
.
Пример 1.2
Разложить на множители многочлен третьей степени:
x3 + 6x2 + 9x.
Решение
Выносим x за скобки:
.
Решаем квадратное уравнение x2 + 6x + 9 = 0:
Его дискриминант: .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.
Отсюда получаем разложение многочлена на множители:
.
Ответ
.
Пример 1.3
Разложить на множители многочлен пятой степени:
x5 – 2x4 + 10x3.
Решение
Выносим x3 за скобки:
.
Решаем квадратное уравнение x2 – 2x + 10 = 0.
Его дискриминант: .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
, .
Разложение многочлена на множители имеет вид:
.
Если нас интересует разложение на множители с действительными коэффициентами, то:
.
Ответ
.
Примеры разложения многочленов на множители с помощью формул
Примеры с биквадратными многочленами
Пример 2.1
Разложить биквадратный многочлен на множители:
x4 +x2 – 20.
Решение
Применим формулы:
a2 + 2ab + b2 = (a + b)2;
a2 – b2 = (a – b)(a + b).
;
.
Ответ
.
Пример 2.2
Разложить на множители многочлен, сводящийся к биквадратному:
x8 +x4 + 1.
Решение
Применим формулы:
a2 + 2ab + b2 = (a + b)2;
a2 – b2 = (a – b)(a + b):
;
;
.
Ответ
.
Пример 2.3 с возвратным многочленом
Разложить на множители возвратный многочлен:
.
Решение
Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = –1. Делим многочлен на x – (–1) = x + 1. В результате получаем:
.
Делаем подстановку:
, ;
;
;
.
Ответ
.
Примеры разложения многочленов на множители с целыми корнями
Пример 3.1
Разложить многочлен на множители:
.
Решение
Предположим, что уравнение
имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6.
Подставляем поочередно эти значения:
(–6)3 – 6·(–6)2 + 11·(–6) – 6 = –504;
(–3)3 – 6·(–3)2 + 11·(–3) – 6 = –120;
(–2)3 – 6·(–2)2 + 11·(–2) – 6 = –60;
(–1)3 – 6·(–1)2 + 11·(–1) – 6 = –24;
13 – 6·12 + 11·1 – 6 = 0;
23 – 6·22 + 11·2 – 6 = 0;
33 – 6·32 + 11·3 – 6 = 0;
63 – 6·62 + 11·6 – 6 = 60.
Итак, мы нашли три корня:
x1 = 1, x2 = 2, x3 = 3.
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.
Ответ
.
Пример 3.2
Разложить многочлен на множители:
.
Решение
Предположим, что уравнение
имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2.
Подставляем поочередно эти значения:
(–2)4 + 2·(–2)3 + 3·(–2)3 + 4·(–2) + 2 = 6;
(–1)4 + 2·(–1)3 + 3·(–1)3 + 4·(–1) + 2 = 0;
14 + 2·13 + 3·13 + 4·1 + 2 = 12;
24 + 2·23 + 3·23 + 4·2 + 2 = 54.
Итак, мы нашли один корень:
x1 = –1.
Делим многочлен на x – x1 = x – (–1) = x + 1:
Тогда,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x2 = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
