Одна шестая в десятичной дроби
Мой опыт работы во Франции
Итак, я работаю в школе, а точнее в школах. А еще точнее в двух школах и одном колледже. Во французском колледже учатся дети с 11 до 15 лет, что соответствует российским 6, 7, 8 и 9 классам. Мое рабочее время поделено между тремя учениками так: по шесть …..
Читать полностью…1 Мальчик жил в семье уже полтора года.Но привыкнуть к нему так,чтобы чувствовать себя совершенно свободно-не получалось. Мальчик казался противным,очень раздражали всякие неприятные привычки.В какой-то момент мне стало казаться,что ничего не получится,что мы так и промучаемся рядом,пока не получится друг от друга избавиться.От того,чтобы отдать обратно, удерживало только то,что на курсах предупреждали об ответственности.Сама ответственность как-то не вырастала.Я решила все-таки сходить к психологу.К тому,вернее,той-с курсов.О чем говорили-я сейчас уже и не помню.Но вышла с твердым решением-постараться увидеть,как ему тревожно и…
Читать полностью… Yata 26 августа 2012, 09:41Есть один форум, который я ещё год назад начала читать время от времени. И есть там ветка, где пишут рассказы о том, как люди становятся родными. И такая жизненная концентрация в них, что просто диву даюсь. Перечитывала уже не раз. И решила поделиться этими историями.В большинстве своём о приёмных детях…
Читать полностью…www.babyblog.ru
Дроби. Десятичные дроби. Проценты.
Переводы
Рассмотрим преобразования дробей, процентов и десятичных дробей.
Перевод процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь нужно: разделить число на 100 и убрать знак процента «%».
Деление на 100 можно интерпретировать как перенос позиционный запятой на 2 позиции влево.
| Проценты→Десятичные дроби | |
|---|---|
45% 0.45 |
Переносим позиционную запятую(точку) на 2 позиции влево и убираем знак процента % |
Перевод десятичной дроби в проценты
Чтобы перевести десятичную дробь в проценты нужно: умножить дробь на 100 и добавить знак процента «%».
Умножение на 100 можно интерпретировать как перенос позиционный запятой на 2 позиции вправо.
| Десятичные дроби→Проценты | |
|---|---|
0.45 45% |
Переносим позиционную запятую(точку) на 2 позиции вправо и добавляем знак процента % |
Перевод дроби в десятичную дробь
Чтобы перевести дробь в десятичную дробь нужно: разделить числитель на знаменатель.
Пример Преобразовать в десятичную дробь
Разделим 3 на 4: 3 ÷ 4 = 0.75
Ответ: = 0.75
Перевод десятичной дроби в дробь
Рассмотрим перевод десятичной дроби в дробь на примере.
Пример Преобразовать десятичную дробь 0.45 в дробь
Первое, запишем число в виде дроби, с знаменателем 1 |
|
Посчитаем количество знаков после запятой(точки) и умножим столько раз на 10 числитель и знаменатель. |
|
После выполнения умножения получается дробь в корректной форме |
|
Сократим дробь и получим завершенное преобразование. |
Перевести дроби в проценты
Чтобы перевести дробь в проценты нужно разделить числитель на знаменатель, затем умножить результат на 100 и добавить знак процентов «%».
Пример Преобразовать дробь в проценты
Сначала разделим числитель 3 на знаменатель 4: 3 ÷ 4 = 0.75
Затем умножим полученный результат на 100: 0.75*100=75
Добавим знак процента «%»: 75%
Ответ: = 75%.
Преобразование процентов в дробь
Чтобы преобразовать проценты в дробь нужно разделить проценты на 100, получим десятичную дробь и следом преобразуем десятичную дробь в обычную дробь.
Пример Преобразовать 60% в дробь.
Преобразуем 60% в десятичную дробь, разделим 60 на 100 |
0,6 |
запишем 0.6 в виде дроби с знаменателем 1 |
|
Посчитаем количество знаков после запятой(точки) и умножим столько раз на 10 числитель и знаменатель. |
|
После выполнения умножения получается дробь в корректной форме |
|
Сократим дробь и получим завершенное преобразование. |
calcs.su
| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | 8^2 | |
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
www.mathway.com
Десятичные дроби
Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обеими видов дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Выражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:
Рассмотрим следующий пример. Показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, требуется показать 6 см и 3 мм в сантиметрах, но в дробном виде. 6 целых сантиметров у нас уже есть:
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
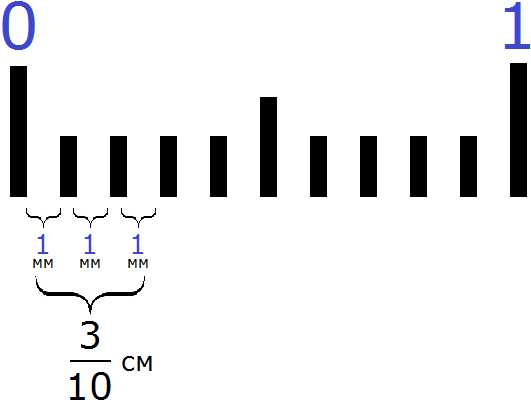
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.
В результате имеем шесть целых сантиметров и три десятых сантиметра:
При этом 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6
6
Целая часть записана. Сразу же после написания целой части ставим запятую:
6,
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
6,3
Любое число, которое представляется в таком виде, называется десятичной дробью.
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
Выглядеть это будет следующим образом:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части стоят числа 10, 100, 1000 или 10000.
Как и смешанное число, десятичная дробь имеет целую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:
0,5
Читается как «ноль целых, пять десятых».
Перевод смешанных чисел в десятичные дроби
Когда мы записываем смешанные числа без знаменателя, мы тем самым переводим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того, как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.
Сначала записываем целую часть и ставим запятую:
3,
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать количество нулей в знаменателе дробной части.
Итак, считаем количество нулей в дробной части смешанного числа . В знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
3,2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2.
Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа находится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем целую часть и ставим запятую:
5,
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно перевести это смешанное число в десятичную дробь. Записываем целую часть и ставим запятую:
5,
И записываем числитель дробной части:
5,03
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа находится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смотрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
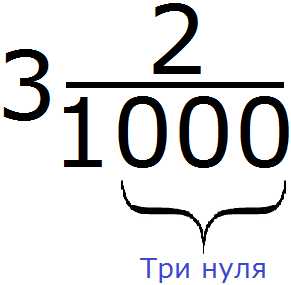
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это число 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед число 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
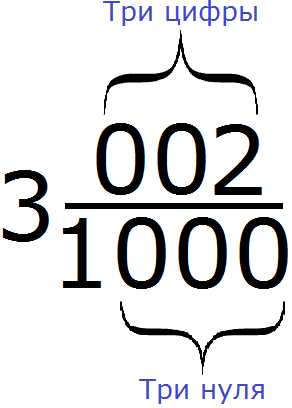
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала целую часть и ставим запятую:
3,
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа находится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
0,
Теперь смотрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой число 5
0,5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и ставим запятую:
0,
Теперь смотрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед числом 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
0,02
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и ставим запятую:
0,
Теперь считаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед числом 5 дописать четыре нуля:
Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь. Записываем после запятой числитель дроби
0,00005
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя. Встречаются неправильные дроби, у которых в знаменателе находятся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные дроби. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять целую часть.
Пример 1. Перевести неправильную дробь в десятичную дробь.
Дробь является неправильной дробью. Чтобы перевести такую дробь в десятичную дробь, нужно в первую очередь выделить у нее целую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этому уроку и изучить его.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10
Посмотрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Число 11 будет целой частью, число 2 — числителем дробной части, число 10 — знаменателем дробной части.
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
11,
Теперь считаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
11,2
В полученной десятичной дроби 11,2 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе находится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим 450 на 100 уголком:
Соберём новое смешанное число — получим . А как переводить смешанные числа в десятичные дроби мы уже знаем.
Записываем целую часть и ставим запятую:
4,
Теперь считаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
4,50
В полученной десятичной дроби 4,50 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена верно.
Значит неправильная дробь при переводе в десятичную дробь обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны. Поставим между ними знак равенства:
4,50 = 4,5
Возникает вопрос: а почему так происходит? Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное число
Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби. Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
6
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
3
и рядом записываем две тысячных:
3
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
4
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Попробуем доказать, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и . Настало время вспомнить основное свойство дроби, которое говорит, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не изменяется.
Давайте разделим первую дробь на 10
Получили , а это вторая дробь. Значит и равны между собой и равны одному и тому же значению:
=
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
0
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль по не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
0,66666666666666…
0,33333333333333…
0,68181818181818…
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби, и как с ними работать.
Получаем периодическую дробь
Давайте попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в пункте деление меньшего числа на большее. Продвинутый уровень.
Итак, делим 1 на 3
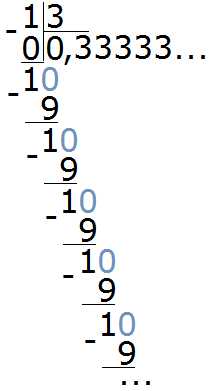
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется снова и снова. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разумнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять и из одной, как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают целую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере цифра, которая повторяется это цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
0, (3)
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
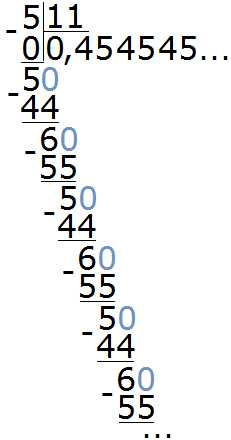
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
0, (45)
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
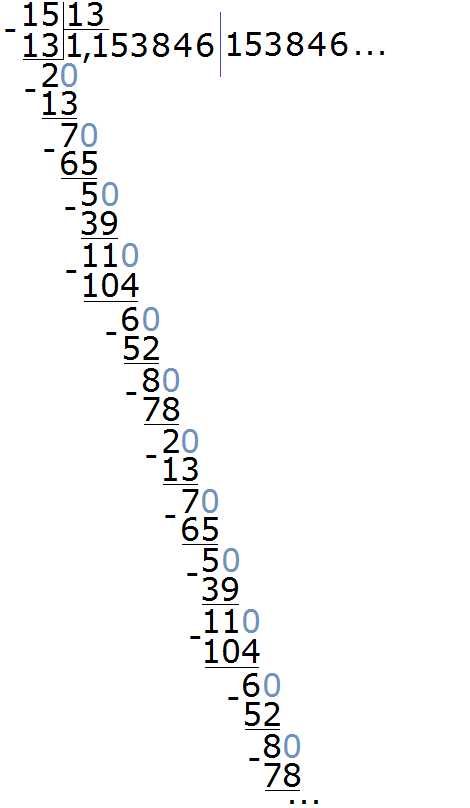
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
1, (153846)
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
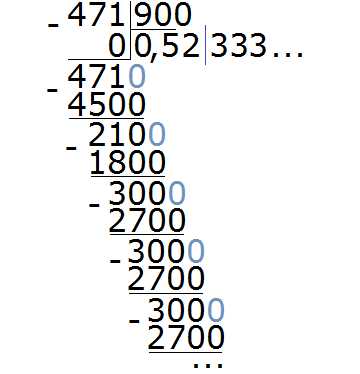
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
0, 52 (3)
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смешанные.
Если в периодической дроби период начинается сразу же после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
0, (3)
0, (6)
0, (5)
Видно, что в этих дробях период начинается сразу же после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смешанной. Например, следующие периодические дроби являются смешанными:
0,52 (3)
0,16 (5)
0,31 (6)
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нужного разряда.
Например округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
0, (3) ≈ 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
6,31 (6) ≈ 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для нашего же развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби. Итак, записываем в числителе период дроби 0,(3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь можно сократить на 3, тогда получим следующее:
Получили обыкновенную дробь .
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь можно сократить эту дробь на 9, тогда получим следующее:
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
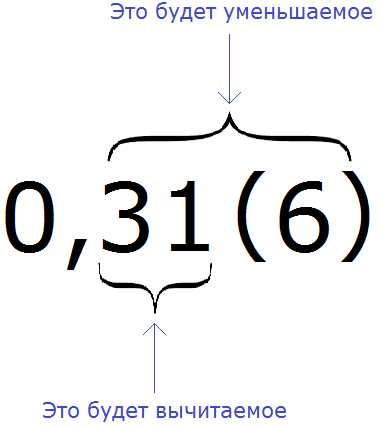
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
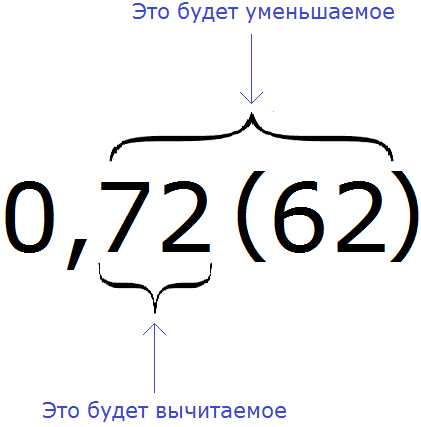
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
