Олимпиадные задачи физика 8 класс – Олимпиадные задания по физике (8 класс) по теме: Олимпиадные задачи по физике для 8 класса с ответами | скачать бесплатно

Физика 8 класс, муниципальный (второй) этап, г. Москва, 2016 год

Задача 1

Машина проехала расстояние L = 160 км от города до деревни за время T = 2 часа. Её скорость на первом, хорошем, участке пути была на ∆V = 10 км/час больше средней  скорости  на  всём  пути,  а  на  втором,  плохом,  участке –  на ∆V = 10 км/час  меньше  средней  скорости  на  всём  пути.  Чему  равна  длина  s плохого участка пути?

Возможное решение

Средняя  скорость  машины  на  всём  пути  V_ср = L / T = 80 км/ч.  Тогда  на  первом участке пути машина имела скорость V₁ = 90 км/ч, а на втором – V₂ = 70 км/ч.

Среднюю скорость на всём пути можно выразить через длины участков пути и скорости на них:

откуда

Ответ: S = 70 км

Критерии оценивания

Найдена средняя скорость на всём пути	1 балл
Найдены скорости на первом и втором участках	2 балла
Средняя скорость на всём пути выражена через длины участков	4 балла
Получено выражение для длины плохого участка	2 балла
Получено численное значение для длины плохого участка	1 балл

Задача 2

На  середину  плоской  льдины  толщиной  H = 60 см,  плавающей  в  воде,  ставят маленький  медный  кубик,  в  результате  чего  глубина  погружения  льдины увеличивается  на  Δh = 0,5 см.  Чему  станет  равна  глубина H_п  погружения  этой льдины, если на её середину вместо медного кубика поставить железный кубик с вдвое  большей  стороной?  Плотность  льда  ρ_л = 900  кг/м³,  плотность  воды ρ_в = 1000  кг/м³,  плотность  меди  ρ_м = 8900 кг/м³,  плотность  железа ρ_ж = 7800 кг/м³.

Возможное решение

В отсутствие кубиков сила тяжести, действующая на льдину, уравновешивается силой  Архимеда.  Над  водой  выступает  часть  льдины  высотой  h = H/10 = 6 см.

Это следует из условия плавания:

S∙H∙ρ_л = S∙ρ_в∙g∙(H-h),

где S – площадь льдины.

Сила  тяжести,  действующая  на  кубик,  уравновешивается  добавочной  силой Архимеда.  Запишем  условия  равновесия  только  для  добавочных  сил.  Для медного кубика:  S∙Δh∙ρ_{в =} ρ_м ∙a³∙g. Для железного кубика:  S∙ΔH∙ρ_в∙g ₌ ρ_ж ∙8a³∙g, где ΔH – добавочная  глубина  погружения  льдины  с  железным  кубиком.  Разделив  одно уравнение на другое, получим:

Отсюда H_п = (H – h) + ΔH = 57,5 см.

Это значение меньше толщины льдины, следовательно, она не утонет.

Критерии оценивания

Записано условие плавания льдины без кубиков	1 балл
Найдена высота выступающей части h (или глубина погружения)	2 балла
Записаны условия равновесия для плавания с кубиками (по 1 баллу)	2 балла
Правильно определено отношение масс кубиков	2 балла
Получено  выражение  для  добавочной  глубины  погружения  ΔH  льдины с железным кубиком	2 балла
Получено численное значение для новой глубины погружения льдины	1 балл

Задача 3

Рисунок 3.1

Сосуды,  частично  заполненные  ртутью,  над  которой находится  воздух,  сообщаются  трубками.  Левый верхний сосуд и верхняя трубка открыты в атмосферу. Ртуть  по  трубкам  не  перетекает.  Найдите  давление воздуха  в  точке  А,  ответ  выразите  в  мм рт. ст.

Определите  высоту  L  столба  ртути  в  верхней  трубке. Высота  h = 5  см.  Атмосферное  давление p₀ = 760 мм рт. ст.

Возможное решение

Так  как  жидкость  в  системе  находится  в  равновесии, можно  связать  друг  с  другом  гидростатические  давления  на  разных  глубинах.

Давление воздуха в нижнем сосуде равно давлению на поверхности граничащей с ним ртути: p

1 = p₀ + 8 ρ∙g∙h = 1160 мм рт. ст. (здесь ρ – плотность ртути). Такое же давление воздуха и в правом верхнем сосуде (то есть в точке А).

На  поверхности  жидкости  в  среднем  сосуде  давление  равно p₂ = p₀ + 11 ρ∙g∙h,  но иначе его можно выразить через высоту L следующим образом:  p₂ = p₀ +  ρ∙g∙(L + 4h)

Отсюда L = 7h = 35 см.

Ответ: L = 35 см

Задача 4

В калориметре смешали десять порций воды. Первая порция имела массу m = 1 г и температуру  t = 1 °С, вторая – массу 2m и температуру 2t, третья – 3m и 3t, и так далее, а десятая – массу 10m и температуру 10t. Определите установившуюся температуру смеси. Потерями теплоты пренебречь.

Возможное решение

Так  как  по  условию  система  теплоизолирована,  воспользуемся  законом сохранения  энергии.  Определим  количество  теплоты,  которое  выделится  при остывании всех порций воды до 0 °С.

Q = cmt + 2m∙c∙2t + … + 10m∙c∙10t = 385 cmt

Это  количество  теплоты  пустим  на  нагревание  всей  воды,  имеющей  массу m + 2m + … + 10m = 55m от 0 °С до искомой температуры t_x: Q = 55cmt_x = 385 cmt, откуда  t_x = 7 °С.

Ответ: t_x = 7 °С

Критерии оценивания

Составлено верное уравнение теплового баланса (в любом виде)	5 баллов
Получено выражение для установившейся температуры	3 балла
Найдено численное значение установившейся температуры	2 балла

Общие рекомендации по оцениванию работы

• За каждое верно выполненное действие баллы складываются.
• При  арифметической  ошибке (в  том  числе  ошибке  при  переводе  единиц измерения) оценка снижается на 1 балл.
• Максимум за 1 задание – 10 баллов.
• Всего за работу – 40 баллов.

olimpiadnye-zadanija.ru

Олимпиада по физике 8 класс, задания с ответами

В этом разделе собраны примеры олимпиадных заданий по физике. Мы советуем обратить внимание на предложенный комплект заданий всем учителям и учащимся 8 класса. Используйте данный материал для того, чтобы подготовиться к олимпиаде. На уроках физики предложенные тесты и задачи могут использоваться для контроля и систематизации знаний, а во время домашней самоподготовки они помогут ученикам оценить свои силы.

К тестовым вопросам и задачам указаны правильные ответы и решения. Это очень удобно, ведь олимпиадные задания по физике с ответами можно решать без помощи учителя. Ответы расположены в самом низу страницы, чтобы ученик не увидел ответ до того, как попробует решить задание самостоятельно.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Тестовые задания

1. В каком состоянии вещество принимает форму сосуда?
А) в твердом
Б) в жидком
В) в газообразном
Г) в твердом и газообразном

2. В какой жидкости утонет кусок парафина?
А) в воде
Б) в ртути
В) в морской воде
Г) в бензине

3. Внутренняя энергия свинцового тела изменится, если:
А) сильно ударить по нему молотком
Б) поднять его над землей
В) бросить его горизонтально
Г) изменить нельзя

4. Какой вид теплопередачи наблюдается при обогревании комнаты батареей водяного отопления?
А) теплопроводность
Б) конвекция
В) излучение
Г) всеми тремя способами одинаково

5. Какая физическая величина обозначается буквой L и имеет размерность Дж/кг?
А) удельная теплоемкость
Б) удельная теплота сгорания топлива
В) удельная теплота плавления
Г) удельная теплота парообразования

6. В процессе кипения температура жидкости…
А) увеличивается
Б) не изменяется

В) уменьшается
Г) нет правильного ответа

7. Если тела взаимно отталкиваются, то это значит, что они заряжены …
А) отрицательно
Б) разноименно
В) одноименно
Г) положительно

8. В каком случае атом некоторого вещества превращается в отрицательный ион?
А) если атом приобретает «лишний» электрон
Б) если атом теряет свой собственный электрон

9. Сопротивление вычисляется по формуле:
А) R=I /U
Б) R = U/I
В) R = U*I
Г) правильной формулы нет

10. В каком состоянии вещества действуют наименьшие силы притяжения между молекулами?
А) силы притяжения одинаковы во всех состояниях
Б) в твердом
В) в жидком
Г) в газообразном

Открытые вопросы

Вопрос 1
Девочки сделали снеговика, а мальчики соорудили точную его копию, но в два раза большей высоты. Какова масса копии, если масса оригинала равна 50 кг? (Плотность снега в обоих снеговиках одинаковая)

Вопрос 2
Группа туристов, двигаясь цепочкой по обочине дороги со скоростью 3,6 км/ч, растянулась на 200 м. Замыкающий посылает велосипедиста к вожатому, который находится впереди группы. Велосипедист едет со скоростью 7 м/с; выполнив поручение, он тут же возвращается к замыкающему группы с той же скоростью. Через сколько времени после получения поручения велосипедист вернулся обратно?

Вопрос 3
В каком случае подъемная сила у самодельного бумажного воздушного шара, заполненного горячим воздухом, больше: когда ребята запускали его в помещении школы или на дворе школы, где было довольно прохладно?

Вопрос 4
В доску толщиной 5 см забили гвоздь длиной а=10 см так, что половина гвоздя прошла навылет. Чтобы вытащить его из доски, необходимо приложить силу 1,8 кН. Гвоздь вытащили из доски. Какую при этом совершили механическую работу?

Вопрос 5
Закрытый бидон из железа частично заполнен керосином. Предложите один из способов, позволяющих, не пользуясь никакими измерительными приборами (и не открывая бидон), определить примерный уровень керосина в бидоне.

Ответы на тесты

Тестовое задание	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	А	А	В	В	Б

Тестовое задание	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	В	А	Б	Б	А

Ответы на открытые вопросы

Ответ на вопрос 1:
При изготовлении точной копии все размеры (длина, ширина и высота) должны быть увеличены в 2 раза. Следовательно, объем снеговика, сделанного мальчиками, будет в 8 раз больше объема оригинала, а масса копии m =50 кг · 8=400 кг.

Ответ на вопрос 2:
Скорость велосипедиста в системе отсчета, связанной с группой, при движении к вожатому равна υ₂-υ₁ при возвращении обратно равна υ₂+υ₁. Поэтому время движения велосипедиста к вожатому t₁= L/ υ₂-υ₁ , а время возвращения велосипедиста к замыкающему t₂= L / υ₂+υ₁ , где L — длина цепочки. Общее время движения велосипедиста t= t₁+ t₂. Таким образом можно записать:

t= L / υ₂-υ₁+ L / υ₂+υ₁= 2 L · υ₂/ υ₂²-υ₁²
Подставив числовые значения величин, получим: t ≈58,3 с.

Ответ на вопрос 3:
Подъемная сила воздушного шара равна разности между весом воздуха в объеме шара и весом газа, заполняющего шар. Чем больше разница в плотностях воздуха и газа, заполняющего шар, тем больше подъемная сила. Поэтому подъемная сила шара больше на улице, где воздух менее прогрет.

Ответ на вопрос 4:
Чтобы переместить гвоздь на пути а, надо совершить работу А₁=F·а. При дальнейшем перемещении гвоздя сила будет убывать от F до 0. Поэтому работу надо находить для средней силы: А₂=1/2·F·а. Следовательно, полная работа
А= А₁+А₂=F·а +1/2·F·а= 3/2· F·а=1,5 · F·а
135 Дж

Ответ на вопрос 5:
Можно, например, вначале хорошо охладить бидон с керосином. Затем поместить его в теплое помещение. В помещении в результате конденсации пара бидон покроется капельками воды. По мере нагревания бидона в теплом помещении вода на нем будет испаряться. Так как масса воздуха и паров бензина в верхней части его значительно меньше массы керосина, находящегося в нижней части бидона, то при нагревании бидона в тёплом помещении испарение будет происходить быстрее с верхней части его. В результате в какой-то момент времени можно будет наблюдать резкую границу между сухой поверхностью бидона и частью его, еще покрытой капельками воды. Эта граница и укажет на уровень керосина в бидоне.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Другие классы

Обновлено: 16/06/2015 , автор: Валерия Токарева

ruolimpiada.ru

силы и блоки, 8 класс.

Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «статика». Поговорим про блоки, посчитаем силы, установим равновесие.

Задача 1. Черный ящик, привязанный через систему блоков и нитей к стенке, покоится на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть его с места, непосредственно к нему необходимо приложить горизонтальную силу чуть больше   Н. Какую минимальную силу надо прикладывать к черному ящику, чтобы он оставался неподвижным, если к веревке приложена сила   Н? Ответ дать в Ньютонах, округлив до целых. Считать, что   м/c.

Рисунок 1

Расставим силы:

Рисунок 2

Теперь видно, что на блок действуют три силы , поэтому общая сила равна 45 Н. 16 из них «съест» сила трения, поэтому, чтобы удержать такой ящик, не хватает Н.

Ответ: 29 Н.

Задача 2. Все блоки в системе, представленной на рисунке − невесомые. Масса левого тела   кг. При какой массе  правого тела система останется в равновесии? Ответ дать в килограммах, округлив до целых. Считать, что   м/c.

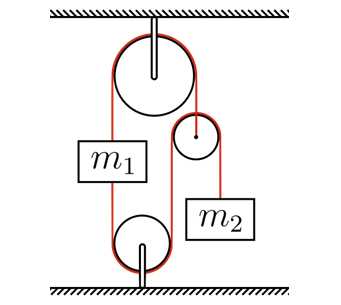
Рисунок 3

Расставим силы:

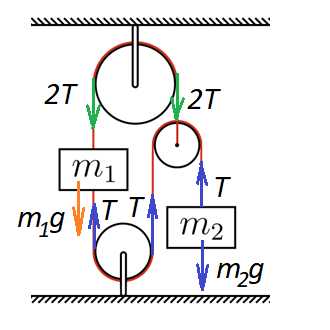
Рисунок 4

Теперь запишем условия равновесия:

   

   

Откуда

   

И

   

Ответ: 2 кг.

Задача 3. Спасатели с помощью веревок, перекинутых через систему блоков, перемещают равномерно и прямолинейно массивную плиту так, как показано на рисунке. С какой результирующей силой верёвки действуют на плиту? Спасатели тянут свой конец веревки с силой   Н. Массами веревок и блоков пренебречь. Ответ дать в Н, округлив до целых. Считать, что   м/c.

Замечание: требуется найти только силу, с которой нити действуют непосредственно на плиту. Силу, действующую на плиту со стороны верхнего крепления в ответ включать не надо.

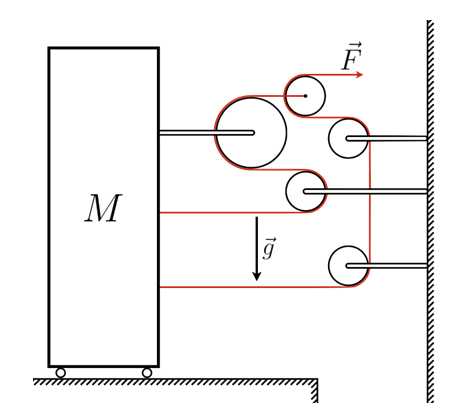
Рисунок 5

Расставим силы:

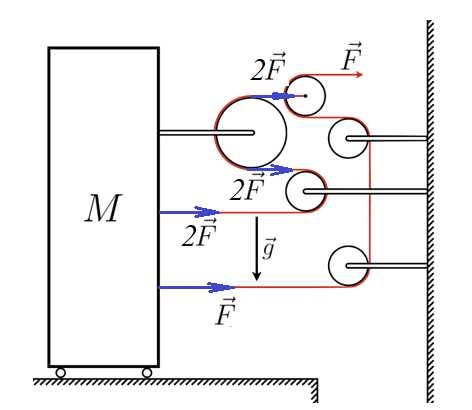
Рисунок 6

Теперь видно, что «за нитки» плиту тянут Н, а полная сила (с учетом верхнего крепления – Н.

Ответ: 600 Н.

Задача 4. Какую горизонтальную силу надо прикладывать к шкафу, чтобы удержать его на месте? Массы грузов равны   кг,   кг. Ответ дать в Ньютонах, округлив до целых. Считать, что   м/c.

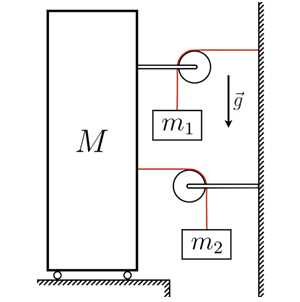
Рисунок 7

На шкаф действуют две силы тяжести: первого груза (20 Н) и второго (50 Н). Итого 70 Н.

Ответ: 70 Н.

Задача 5. Два ящика покоятся на горизонтальной поверхности. Чтобы преодолеть трение и сдвинуть с места левый ящик, к нему необходимо приложить горизонтальную силу чуть больше  26 Н. Чтобы сдвинуть правый − чуть больше  14 Н. Ящики соединили нитью, переброшенной через блоки, прикреплённые к ящикам так, как показано на рисунке. Какую минимальную силу надо приложить к концу нити, чтобы расстояние между ящиками начало уменьшаться? Ответ дать в Ньютонах, округлив до целых.

Рисунок 8

Расстояние будет уменьшаться при сдвиге любого из ящиков, поэтому нужно выяснить, какой легче сдвинуть. Для этого расставляем силы:

Рисунок 9

Теперь видно, что на левый ящик действует сила , а на правый – . Если

   

То Н, а если

   

То Н. Поэтому ответ – 7 Н. Этого будет достаточно, чтобы сдвинуть правый ящик и тем самым сократить расстояние.

easy-physic.ru

Олимпиада по физике 8 класс

           Вариант 1                      Вариант 2

Задание 1 :

Сплав золота и серебра массой 400 г имеет плотность 14·10³ кг/м³.
Полагая объем сплава равным сумме объемов его составных частей,
определите массу золота и процентное содержание его в сплаве.
Плотность золота – 19 300 кг/м³, плотность серебра – 10 500 кг/м³.

Задание 2 :

Как определить плотность неизвестной жидкости, используя только стакан, воду и весы с разновесом?

Задание 3 :

Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 мин. Какова скорость поезда, если длина моста 360 м?

Задание 4 :

Коробок в форме куба заполнен водой. Определите давление воды на дно коробка, если масса воды в нем равна 64 г.
Плотность воды 1000 кг/м³.

Задание 5 :

Почему мокрая бумага рвется легче, чем сухая?

Задание 6 :

Выяснить экспериментально, какая из сил больше и во сколько раз: вес бруска или сила тяги при равномерном его движении по поверхности стола?

Задание 7 :

Необходимо как можно точнее узнать диаметр сравнительно тонкой проволоки располагая для этой цели только школьной тетрадью в клетку и карандашом. Как следует поступить?

Задание 8 :

Используя динамометр и латунную гирю массой 200 г, определить плотность данной жидкости.

Задание 9 :

Пуля, летящая со скоростью 650 м/c, имеет температуру 75 °C.
Она попадает в сугроб и застревает в нем.
Температура снега в сугробе 0 °C.
При этом 6,5 г снега тает и обращается в воду с температурой 0 °C.
Найдите массу пули.
Удельную теплоту плавления снега считать равной 3,4·105 Дж/кг.
А удельная теплоемкость свинца равна 130 Дж/(кг·°C).

Задание 10 :

В сосуде со ртутью плавает стальной брусок. Как изменится глубина погружения бруска в ртуть, если в сосуд налить воды так, что брусок окажется под водой? Построить график изменения давления на дно сосуда.

Задание 11 :

Предположим, что найдена жидкость, которая не меняет свой объем при нагревании. Как будет вести себя такая жидкость, если ее налить в кастрюлю и поставить на плиту?

Задание 12 :

Что труднее: тянуть нагруженные санки за веревку по горизонтальной поверхности или толкать их перед собой палкой такой же длины, как веревка? Ответ обоснуйте и подтвердите рисунками действующих сил.

Задание 13 :

Какие приборы Вам понадобятся, чтобы определить: является ли данный Вам алюминиевый шар сплошным или пустотелым и как это сделать? Как можно рассчитать объем возможной полости? Какой из предложенных Вами способов является наиболее точным, экономичным?

Задание 14 :

Почему жареная пища вкуснее вареной? Ответ обосновать.

Задание 15 :

Пригородный поезд, состоящий из 8 вагонов, проезжает 240 км за 5 часов. Коэффициент сопротивления движению в среднем к=0,01. Какое количество дизельного топлива с удельной теплотой сгорания 42МДж/кг расходует тепловоз за 1 рейс, если масса каждого вагона равна 60 тонн, а КПД его дизельных двигателей 40%? Какую среднюю механическую мощность развивает тепловоз?

Задание 16 :

Как определить плотность неизвестной жидкости, используя только стакан, воду и весы с разновесом?

Задание 17 :

Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 мин.
Какова скорость поезда, если длина моста 360 м?

Задание 18 :

Коробок в форме куба заполнен водой.
Определите давление воды на дно коробка, если масса воды в нем равна 64 г.
Плотность воды 1000 кг/м³.

Задание 19 :

Почему мокрая бумага рвется легче, чем сухая?

Задание 20 :

Сплав золота и серебра массой 400 г имеет плотность 14·10³ кг/м³.
Полагая объем сплава равным сумме объемов его составных частей,
определите массу золота и процентное содержание его в сплаве.
Плотность золота – 19 300 кг/м³, плотность серебра – 10 500 кг/м³.

Задания олимпиады по физике 8 класс

           Вариант 1                      Вариант 2

eruditu.ru

Олимпиада по физике для 8 класса – ФГОС online

Физика 8 класс

Лимит времени: 0

Информация

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 10

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

• Вы ответили правильно на все вопросы олимпиады и заняли 1 место! Вы можете заказать изготовление персонального диплома 1 степени по этой ссылке!

• Вы ответили правильно на большую часть вопросов олимпиады и заняли 2 место! Вы можете заказать изготовление персонального диплома 2 степени по этой ссылке!

• Вы ответили правильно на большую часть вопросов олимпиады и заняли 3 место! Вы можете заказать изготовление персонального диплома 3 степени по этой ссылке!

• Вы ответили правильно на большую часть вопросов олимпиады! Вы можете заказать изготовление персонального диплома участника олимпиады по этой ссылке!

1. С ответом
2. С отметкой о просмотре

fgosonline.ru

Олимпиадные задания по физике для 8 класса

1.Сплав золота и серебра массой 400 г имеет плотность 1, 4 · 104 кг/м³. Полагая объем сплава равным сумме объемов его составных частей, определите массу золота в сплаве.

Решение: Масса сплава всегда равна сумме масс его составных частей: m_сп = m_c + m_з. По условию задачи, объем сплава равен сумме объемов его составных частей: V_сп = V_c + V_з. Из формулы для плотности p=m/V следует, что V=m/p.

Подставляя выражение для объемов в последнюю формулу и выражая массу серебра через массу сплава и массу золота, получаем: m_с = m_cп — m_з и 

Решаем совместно эти уравнения относительно неизвестной массы m_з: . Откуда  Выполняя соответствующие алгебраические преобразования, находим искомую величину: 

. Вычисления дают следующие результаты: 

 

 

2.В сосуды, соединённые трубкой с краном, налита вода (см. рисунок). Гидростатическое давление в точках А и В  равно p_A = 4кПа и р_В = 1 кПа  соответственно, площади поперечного сечения левого и правого сосудов составляют SA = 3 дм² и SB = 6 дм² соответственно. Какое гидростатическое давление установится в точках А и В если открыть кран?

Решение: До открытия крана масса воды в левом сосуде равна p_AS_A/g,  в правом сосуде p_BS_B/g. После открытия крана в точках А и В  устанавливается одинаковое гидростатическое давление p, поэтому суммарная масса воды в сосудах равна p(S_A+S_B)/g. Поскольку масса воды сохраняется, то p_AS_A + p_BS_B = p(S_A+S_B).  Таким образом, 

 

3. Парафиновая свечка горит так, что её длина уменьшается со скоростью v = 5 · 10⁻⁵ м/с, а испаряющийся парафин полностью сгорает, не стекая вниз. Свечка плавает в широком сосуде с водой. Её слегка поддерживают в вертикальном положении, чтобы она не опрокидывалась. С какой скоростью V свечка движется относительно сосуда во время сгорания? Плотность воды p_В = 1000 кг/м³, плотность парафина p_П = 900 кг/м³.

Решение:  Пусть L — длина свечки в некоторый момент времени, H — длина её подводной части, S — площадь её поперечного сечения. Согласно условию плавания тел, p_ВgHB = p_ПgLS, откуда H/L = p_П/p_В. За время Δt длина свечки уменьшилась на величину ΔL = vΔt, а глубина погружения её нижнего конца уменьшилась на . Следовательно, нижний конец свечки (как и вся свечка) движется со скоростью  относительно сосуда.

 

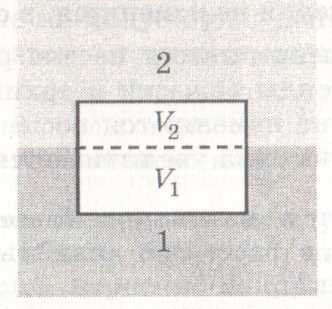4. Брусок находится на границе двух жидкостей, имеющих плотности p₁ и p₂, вытесняя объемы V₁ и V₂ соответствующих жидкостей (см. рисунок). Какая архимедова сила F_A действует на брусок?

Решение: Архимедова сила представляет собой сил давления жидкости на каждый из участков поверхности тела. В данном случае эта равнодействующая равна разности сил давления на нижнюю и верхнюю грани бруска: F_A = F_H — F_B = S(p_H и p_B). Здесь S — площадь нижней и верхней граней, p_H и p_B — давления жидкости на соответствующие грани. Обозначим через h₁ и h₂ высоты частей бруска, находящихся в соответствующих жидкостях. Тогда p_H — p_B = p₁gh₁ + p₂gh₂, откуда F_A = p₁gSh₁ + p₂gSh₂ = p₁V₁+p₂V₂. Итак, архимедова сила равна полному весу вытесненной бруском жидкости.

 

5. Определите, какое количество теплоты выбрасывает в атмосферу автомобиль за день, если он движется со скоростью 60 км/ч примерно по 5 часов ежедневно, расходуя в среднем 8 литров бензина на 100 км пути, имея среднюю мощность 60 кВт.

Решение: Работа полезная: An = N * t. Количество теплоты выделяющееся при сгорании топлива Q = q * m. Путь, пройденный автомобилем S = v * t, тогда за день имеем . Количество теплоты, выбрасываемое в атмосферу, тогда равно: 

Вконтакте

Facebook

Twitter

Google+

Одноклассники

olimpotvet.ru

Олимпиада по физике 8 класс

Школьный тур олимпиады

Физика

8 класс

1. Танкер «река — море» из реки переходит в море. Как изменится сила Архимеда, действующая на танкер в пресной воде реки, по сравнению с ее действием в соленой воде моря? (10 баллов)

2. Теплоход проходит расстояние между двумя городами вверх по течению за 80 часов, а вниз по течению за 60 часов. Определите время, за которое расстояние между городами проплывет плот. (20 баллов)

3. В воду массой 1 кг при 20 ⁰С брошен кусок мокрого снега массой 250 г. Когда весь снег растаял, общая температура стала равной 5 ⁰С. Определите количество воды в комке снега. Удельная теплота плавления снега 334 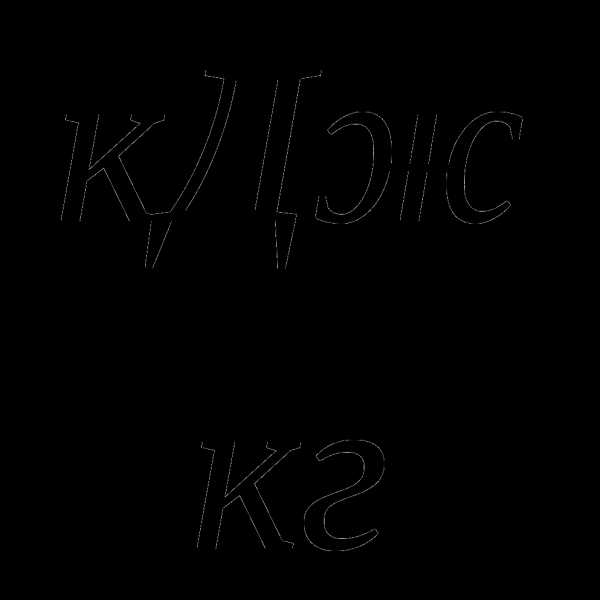, удельная теплоемкость воды 4200 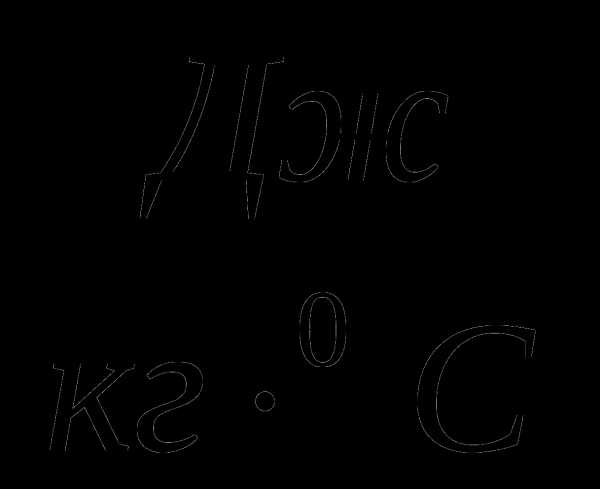. (35 баллов)

4. Поверх жидкости плотности налита жидкость плотности (>), причем жидкости не смешиваются. Очевидно, что тело плотности (>>) будет плавать у границы раздела этих жидкостей. Определите, какая часть объема тела будет погружена в более плотную жидкость. (35 баллов)

Решения заданий

1. Танкер «река — море» из реки переходит в море. Как изменится сила Архимеда, действующая на танкер в пресной воде реки, по сравнению с ее действием в соленой воде моря? (10 баллов)

Решение

Не изменится, так как при плавании тела на поверхности жидкости сила Архимеда равна силе тяжести.

2. Теплоход проходит расстояние между двумя городами вверх по течению за 80 часов, а вниз по течению за 60 часов. Определите время, за которое расстояние между городами проплывет плот. (20 баллов)

Решение

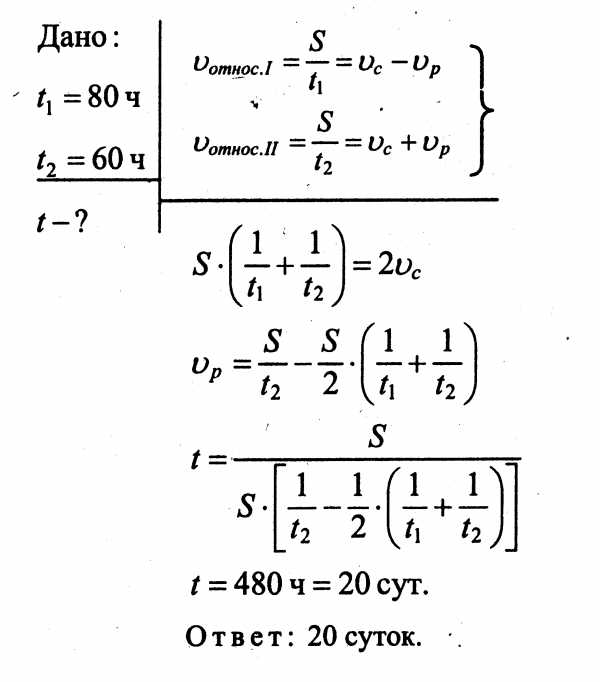
3. В воду массой 1 кг при 20 ⁰С брошен кусок мокрого снега массой 250 г. Когда весь снег растаял, общая температура стала равной 5 ⁰С. Определите количество воды в комке снега. Удельная теплота плавления снега 334 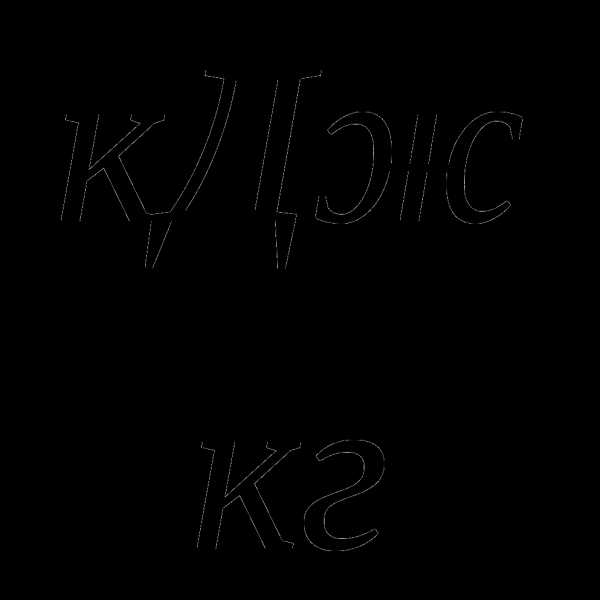, удельная теплоемкость воды 4200 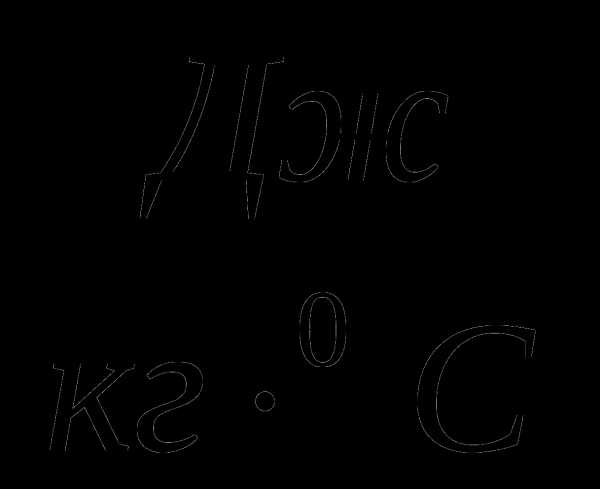. (35 баллов)

Решение

4. Поверх жидкости плотности налита жидкость плотности (>), причем жидкости не смешиваются. Очевидно, что тело плотности (>>) будет плавать у границы раздела этих жидкостей. Определите, какая часть объема тела будет погружена в более плотную жидкость. (35 баллов)

Решение

infourok.ru