Онлайн калькулятор полином жегалкина – Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн

alexxlab / / Школьная жизнь

Полином Жегалкина. Пример решения задачи на Викиматик

Полином (многочлен) Жегалкина представляет собой полином, коэффициентами которого являются числа $0$ или $1$, причем в качестве операций умножения и сложения выступают соответственно конъюнкция и сумма по модулю $2$. Например, для булевой функции $f\left(x_1,\ x_2,\ x_3\right)$ от трех переменных $x_1,\ x_2,\ x_3$ полином Жегалкина будет иметь следующий вид:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_{12}x_1x_2\bigoplus a_{13}x_1x_3\bigoplus a_{23}x_2x_3\bigoplus a_{123}x_1x_2x_3.$$ 

Коэффициенты $a_0,\ a_1,\ \dots ,\ a_{123}\in \left\{0,\ 1\right\}$, то есть могут принимать значения либо $0$, либо $1$ в зависимости от того, какое значение принимает булева функция $f\left(x_1,\ x_2,\ x_3\right)$ на том или ином наборе значений переменных.

С помощью полинома Жегалкина можно представить любую булеву функцию, причем единственных образом. Поэтому можно сказать, что полином Жегалкина является еще одним способом представления булевых функций в алгебре операций $\bigoplus $ — суммы по модулю $2$, $\cdot $ — конъюнкции и константы $1$.

Операция $\bigoplus $ имеет и другие названия: сумма Жегалкина, неравнозначность, исключающее ИЛИ-НЕ. Иногда, для удобства ее обозначения используют привычную запись сложения $+$, но не стоит путать с дизъюнкцией и, тем более, с обычной арифметической операцией сложения. Таблица истинности данной операции имеет вид:

$$\begin{array}{|c|c|}
\hline
x & y & x\bigoplus y \\
\hline
0 & 0 & 0 \\
\hline
0 & 1 & 1 \\
\hline
1 & 0 & 1 \\
\hline
1 & 1 & 0 \\
\hline
\end{array}$$

Сумма $x\bigoplus y$ принимает истинное значение тогда и только тогда, когда истинно одно и только одно составляющее высказывание. Если сравнить таблицы истинности основных логических операций, то можно заметить, что $x\bigoplus y=\overline{x\leftrightarrow y}$. То есть операция сумма Жегалкина $\bigoplus $ есть отрицание эквиваленции.

Для двух введенных операций $\bigoplus ,\ \cdot $ (суммы по модулю 2 и конъюнкции) выполняются все логические законы:

  1. Коммутативность: $x\bigoplus y=y\bigoplus x$;
  2. Ассоциативность: $\left(x\bigoplus y\right)\bigoplus z=x\bigoplus \left(y\bigoplus z\right)$, то есть результат $x\bigoplus y\bigoplus z$ не зависит от расстановки скобок;
  3. Дистрибутивность: $x\left(y\bigoplus z\right)=xy\bigoplus xz$;
  4. $x\bigoplus x=0$;
  5. $0\bigoplus x=x$;
  6. $\overline{x}=x\bigoplus 1$.

Для построения полинома Жегалкина можно использовать различные методы:

  • Метод неопределенных коэффициентов;
  • Метод треугольника Паскаля;
  • Преобразование ДНФ;
  • Преобразование СДНФ.

Метод неопределенных коэффициентов

Найдем полином Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2$, используя метод неопределенных коэффициентов. Для этого сначала необходимо построить таблицу истинности данной булевой функции $f\left(x_1,\ x_2,\ x_3\right)$.

$\begin{array}{|c|c|}
\hline
x_1 & x_2 & x_3 & x_1x_2 & x_1x_2\vee x_3 & f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2 \\ 
0 & 0 & 0 & 0 & 0 & 1 \\ 
\hline
0 & 0 & 1 & 0 & 1 & 1 \\ 
\hline
0 & 1 & 0 & 0 & 0 & 1 \\ 
\hline
0 & 1 & 1 & 0 & 1 & 0 \\ 
\hline
1 & 0 & 0 & 0 & 0 & 1 \\ 
\hline
1 & 0 & 1 & 0 & 1 & 1 \\ 
\hline
1 & 1 & 0 & 1 & 1 & 0 \\ 
\hline
1 & 1 & 1 & 1 & 1 & 0 \\ 
\hline
\end{array}$

Общий вид полинома Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)$ трех переменных $x_1,\ x_2,\ x_3$:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_{12}x_1x_2\bigoplus a_{13}x_1x_3\bigoplus a_{23}x_2x_3\bigoplus a_{123}x_1x_2x_3.$$ 

Последовательно подставляем наборы значений переменных и находим коэффициенты $a_0,\ a_1,\ \dots ,\ a_{123}$.

$f\left(0,\ 0,\ 0\right)=a_0=1;$ 

$f\left(0,\ 0,\ 1\right)=a_0\bigoplus a_3=1\Rightarrow 1\bigoplus a_3=1\Rightarrow a_3=0;$ 

$f\left(0,\ 1,\ 0\right)=a_0\bigoplus a_2=1\Rightarrow 1\bigoplus a_2=1\Rightarrow a_2=0;$

$f\left(0,\ 1,\ 1\right)=a_0\bigoplus a_2\bigoplus a_3\bigoplus a_{23}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{23}=0\Rightarrow 1\bigoplus a_{23}=0\Rightarrow a_{23}=1;$

$f\left(1,\ 0,\ 0\right)=a_0\bigoplus a_1=1\Rightarrow 1\bigoplus a_1=1\Rightarrow a_1=0.$

$f\left(1,\ 0,\ 1\right)=a_0\bigoplus a_1\bigoplus a_3\bigoplus a_{13}=1\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{13}=1\Rightarrow 1\bigoplus a_{13}=1\Rightarrow a_{13}=0;$

$f\left(1,\ 1,\ 0\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_{12}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_{12}=0\Rightarrow 1\bigoplus a_{12}=0\Rightarrow a_{12}=1;$

$f\left(1,\ 1,\ 1\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_3\bigoplus a_{12}\bigoplus a_{13}\bigoplus a_{23}\bigoplus a_{123}=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus 0\bigoplus 1\bigoplus 0\bigoplus 1\bigoplus a_{123}=0\Rightarrow 1\bigoplus a_{123}=0\Rightarrow a_{123}=1;$ 

Подставляя найденные коэффициенты, получаем полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_1x_2\bigoplus x_2x_3\bigoplus x_1x_2x_3.$$ 

Метод треугольника Паскаля

Построим полином Жегалкина для функции из предыдущего метода, используя треугольник Паскаля.

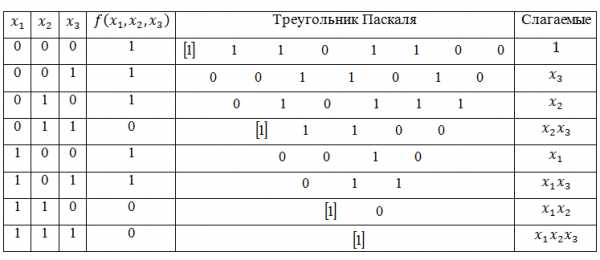
Поясним, как заполняется треугольник Паскаля. Верхняя строка треугольника задает вектор значений булевой функции $f=\left(11101100\right)$. В каждой строке, начиная со второй, любой элемент такого треугольника вычисляется как сумма по модулю $2$ двух соседних элементов предыдущей строки. Так, элементы второй строки: $1\bigoplus 1=0,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 1=1,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 0=0$. Аналогично вычисляются элементы других строк.

Левой стороне треугольника Паскаля соответствуют наборы значений переменных исходной функции $f\left(x_1,\ x_2,\ x_3\right)$. Соединяя знаком конъюнкции переменные, значения которых в наборе равны $1$, мы получим слагаемое в полиноме Жегалкина. Набору $\left(000\right)$ соответствует $1$, набору $\left(001\right)$ соответствует $x_3$, и т.д.

Поскольку единицам левой стороны треугольника соответствуют слагаемые $1,\ x_2x_3,\ x_1x_2,\ x_1x_2x_3$, то полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3.$$ 

Преобразование ДНФ

Используя основные законы алгебры логики, приведем сначала данную функцию к ДНФ.

$f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to {\overline{x}}_2=$ $\{$используем равносильность $x\to y=\overline{x}\vee y$$\}$ $=\overline{x_1x_2\vee x_3}\vee {\overline{x}}_2=$ $\{$используем закон де Моргана $\overline{x\vee y}=\overline{x}\ \overline{y}$$\}$ $=\overline{x_1x_2}\cdot {\overline{x}}_3\vee {\overline{x}}_2=$ $\{$используем закон де Моргана $\overline{xy}=\overline{x}\vee \overline{y}$$\}$ $=\left({\overline{x}}_1\vee {\overline{x}}_2\right){\overline{x}}_3\vee {\overline{x}}_2=$ $\{$используем закон дистрибутивности $\left(x\vee y\right)z=xz\vee yz$$\}$ $={\overline{x}}_1{\overline{x}}_3\vee \underbrace{{\overline{x}}_2{\overline{x}}_3}_{поглощается\ {\overline{x}}_2}\vee {\overline{x}}_2={\overline{x}}_1{\overline{x}}_3\vee {\overline{x}}_2$ —ДНФ.

Далее в полученной ДНФ необходимо «избавиться» от дизъюнкции, используя законы де Моргана:

$${\overline{x}}_1{\overline{x}}_3\vee {\overline{x}}_2=\overline{{\overline{{\overline{x}}_1{\overline{x}}_3}x}_2}.$$ 

Заменяем каждое отрицание $\overline{x}=1\bigoplus x$ и применяем написанные выше логические законы, получаем:

$\overline{{\overline{{\overline{x}}_1{\overline{x}}_3}x}_2}=1\bigoplus {\overline{{\overline{x}}_1{\overline{x}}_3}x}_2=1\bigoplus \left(1\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_3\right)\right)x_2=1\bigoplus \left(1\bigoplus 1\bigoplus x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus \left(x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

Преобразование СДНФ

$\begin{array}{|c|c|}
\hline
x_1 & x_2 & x_3 & f\left(x_1,\ x_2,\ x_3\right) \\
\hline
0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 1 \\
\hline
0 & 1 & 0 & 1 \\
\hline
0 & 1 & 1 & 0 \\
\hline
1 & 0 & 0 & 1 \\
\hline
1 & 0 & 1 & 1 \\

\hline
1 & 1 & 0 & 0 \\
\hline
1 & 1 & 1 & 0 \\
\hline
\end{array}$

Для построения СДНФ по таблице истинности выбираем наборы, на которых функция $f$ принимает значение, равное 1. Если значение переменной в этом наборе равно 0, то она берется с отрицанием, если значение переменной равно 1, то переменная берется без отрицание. Соединив знаком конъюнкции переменные соответствующего набора, получим элементарную конъюнкцию. Тогда дизъюнкция всех таких элементарных конъюнкций есть СДНФ.

$$f\left(x_1,\ x_2,\ x_3\right)={\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\vee {\overline{x}}_1{\overline{x}}_2x_3\vee {\overline{x}}_1x_2{\overline{x}}_3\vee x_1{\overline{x}}_2{\overline{x}}_3\vee x_1{\overline{x}}_2x_3.$$ 

Чтобы построить полином Жегалкина через СДНФ, необходимо исключить операции дизъюнкции и отрицания, затем раскрыть скобки.

$f\left(x_1,\ x_2,\ x_3\right)={\overline{x}}_1{\overline{x}}_2{\overline{x}}_3\bigoplus {\overline{x}}_1{\overline{x}}_2x_3\bigoplus {\overline{x}}_1x_2{\overline{x}}_3\bigoplus x_1{\overline{x}}_2{\overline{x}}_3\bigoplus x_1{\overline{x}}_2x_3=\left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)x_3\bigoplus \left(1\bigoplus x_1\right)x_2\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)x_3=1\bigoplus x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_3\bigoplus x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

wikimatik.ru

Полином Жегалкина. Пример. / Алгебра логики [Ф.Г. Кораблёв] / 3dstroyproekt.ru

Имеем следующую логическую функцию.

$f = xy\vee \bar { y } \bar { z } $. Преобразовать функцию так, чтобы она содержала две операции.

Вспомним таблицу истинности $\oplus$ и $\wedge$:

$x$$y$$x\oplus y$$xy$
$0$$0$$0$$0$
$0$$1$$1$$0$
$1$$0$$1$$0$
$1$$1$$0$$1$

Составим таблицу истинности:

$x$$y$$z$$\bar { y } $$\bar { z } $$xy$$\bar { y } \bar { z } $$f$
$0$$0$$0$$1$$1$$0$$1$$1$
$0$$0$$1$$1$$0$$0$$0$$0$
$0$$1$$0$$0$$1$$0$$0$$0$
$0$$1$$1$$0$$0$$0$$0$$0$
$1$$0$$0$$1$$1$$0$$1$$1$
$1$$0$$1$$1$$0$$0$$0$$0$
$1$$1$$0$$0$$1$$1$$0$$1$
$1$$1$$1$$0$$0$$1$$0$$1$

Запишем общий вид полинома Жегалкина $f = xy\vee \bar { y } \bar { z } = \overset { 0 } { a_ { 123 } } xyz\oplus \overset { 1 } { a_ { 12 } } xy\oplus \overset { 0 } { a_ { 13 } } xz\oplus \overset { 1 } { a_ { 23 } } yz\oplus \overset { 0 } { a_ { 1 } } x\oplus \overset { 1 } { a_ { 2 } } y\oplus \overset { 1 } { a_ { 3 } } z\oplus \overset { 1 } { a_ { 0 } } = xy\oplus yz\oplus y\oplus z\oplus 1 $

$f(0,0,0) = \overset { 1 } { a_ { 0 } } = 1$

$f(0,0,1) = \overset { 1 } { a_ { 3 } } \oplus \overset { 1 } { a_ { 0 } } = 0$

$f(0,1,0) = \overset { 1 } { a_ { 2 } } \oplus \overset { 1 } { a_ { 0 } } = 0$

$f(0,1,1) = \overset { 1 } { a_ { 23 } } \oplus \overset { 1 } { a_ { 2 } } \oplus \overset { 1 } { a_ { 3 } } \oplus \overset { 1 } { a_ { 0 } } = 0$

$f(1,0,0) = \overset { 0 } { a_ { 1 } } \oplus \overset { 1 } { a_ { 0 } } = 1$

$f(1,0,1) = \overset { 0 } { a_ { 13 } } \oplus \overset { 0 } { a_ { 1 } } \oplus \overset { 1 } { a_ { 3 } } \oplus \overset { 1 } { a_ { 0 } } = 0$

$f(1,1,0) = \overset { 1 } { a_ { 12 } } \oplus \overset { 0 } { a_ { 1 } } \oplus \overset { 1 } { a_ { 2 } } \oplus \overset { 1 } { a_ { 0 } } = 1$

$f(1,1,1) = \overset { 0 } { a_ { 123 } } \oplus \overset { 1 } { a_ { 12 } } \oplus \overset { 0 } { a_ { 13 } } \oplus \overset { 1 } { a_ { 23 } } \oplus \overset { 0 } { a_ { 1 } } \oplus \overset { 1 } { a_ { 2 } } \oplus \overset { 1 } { a_ { 3 } } \oplus \overset { 1 } { a_ { 0 } } = 1$

3dstroyproekt.ru

Вариант 7

I. Дискретные множества

Докажите тождества двумя способами:

А) используя определения равенства множеств и операций над множествами;

Б) с помощью алгебры логики.

Решение:

А)

Б) . Преобразуем левую часть по формулам алгебры логики:

, что и требовалось доказать.

II. Функции алгебры логики. Многочлены Жегалкина

Для заданной булевой функции трех переменных:

А) Постройте таблицу истинности, найти двоичную форму булевой функции и привести функцию к СДНФ и СКНФ,

Б) Найдите двумя способами многочлен Жегалкина и ответить на вопрос, является ли данная булева функция линейной,

В) С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ.

Решение:

А) Составим таблицу истинности:

Двоичная форма функции: 01010011.

СДНФ: .

СКНФ: .

Б) Преобразуем данную функцию к многочлену Жегалкина:

Функция линейной не является.

Построим полином Жегалкина методом неопределенных коэффициентов. Общий вид полинома Жегалкина:

Найдем коэффициенты:

Функция примет вид:

.

Итак, .

Оба метода дали один и тот же результат.

В) С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ.

Вариант 8

I. Дискретные множества

Докажите тождества двумя способами:

А) используя определения равенства множеств и операций над множествами;

Б) с помощью алгебры логики.

Решение:

А)

Б) . Преобразуем левую часть по формулам алгебры логики:

, что и требовалось доказать.

II. Функции алгебры логики. Многочлены Жегалкина

Для заданной булевой функции трех переменных:

А) Постройте таблицу истинности, найти двоичную форму булевой функции и привести функцию к СДНФ и СКНФ,

Б) Найдите двумя способами многочлен Жегалкина и ответить на вопрос, является ли данная булева функция линейной,

В) С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ.

Решение:

А) Составим таблицу истинности:

Двоичная форма функции: 10101100.

СДНФ: .

СКНФ: .

Б) Преобразуем данную функцию к многочлену Жегалкина:

Функция линейной не является.

Построим полином Жегалкина методом неопределенных коэффициентов. Общий вид полинома Жегалкина:

Найдем коэффициенты:

Функция примет вид:

.

Итак, .

Оба метода дали один и тот же результат.

В) С помощью эквивалентных преобразований приведите функцию к ДНФ, КНФ, СДНФ, СКНФ.

< Предыдущая   Следующая >

matica.org.ua

Построение полинома Жегалкина

Построение полинома Жегалкина.

Пример.

Рассмотрим пример построения полином Жегалкина по таблице истинности, содержащей 3 переменные Методом неопределенных коэффициентов.

x

y

z

f

a0

0

0

0

1

a1

0

0

1

1

a2

0

1

0

0

a3

0

1

1

1

a4

1

0

0

0

a5

1

0

1

0

a6

1

1

0

1

a7

1

1

1

0

Запишем общий вид полинома Жегалкина:

1) 1=a0;

2) 1=a0a1*z, 1=1a1.Каким должно быть a1, чтобы выполнялось равенство? Воспользуемся таблицей функции:

X1

X2

f

0

0

0

0

1

1

1

0

1

1

1

0

Из таблицы видно, что равенство равно 1, когда значения переменных разные. Следовательно, a1=0;

3) 0=а0a1*za2*y, 0=10*0a2*1, 0=10a2. Упростим равенство: принимая во внимание, что 10=1, получаем: 0=1a2, из чего по таблице определяем, чтоa2=1;

4) 1=a0a1*za2*ya3*y*z, 1=101a3. Упростим:10=1 11=0, получим: 1=0a3.По таблицеa3=1;

5) 0=a0a1*za2*ya3*y*za4*x, 0=1000a4. Упростим:10=1, 10=1, 1=1. Получим: 0=1a4, по таблице: a4=1;

6) 0=a0a1*za2*ya3*y*za4*xa5*x*z,0=10001a5, упрощаем как делали выше, получаем:a5=0;

7) 1=a0a1*za2*ya3*y*za4*xa5*x*za6*x*y,1=10100a6. a6=0;

8) 0=a0a1*za2*ya3*y*za4*xa5*x*za6*x*ya7*x*y*z, 0=1011100a7. a7=0;

Подставляем коэффициенты в общую форму полинома:

F(x,y,z)=11*x1*y0*z0*x*y1*y*z0*x*z1*x*y*z=1xyyz

Проверка:

x

y

z

f

0

0

0

1

0

0

1

1

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

0

1

1

0

1

1

1

1

0

Проверка выполняется путем подстановки значенийx,y,z в полученную формулу. Разберем пример подстановки для 4й строчки:f(0,1,1)=1011*1, 11=0, 01=1. f(0,1,1)=1, поэтому все верно.

Результат проверки считается положительным, если все результаты постановки в полученный полином совпадают с соответствующими значениями функции. Или, что проще, если полученная таблиц совпадает с исходной.

studfiles.net

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *