Числовые неравенства и их свойства
С неравенствами мы познакомились в школе, где применяем числовые неравенства. В данной статье рассмотрим свойства числовых неравенств, не которых строятся принципы работы с ними.
Свойства неравенств аналогичны свойствам числовых неравенств. Будут рассмотрены свойства, его обоснования, приведем примеры.
Числовые неравенства: определение, примеры
При введении понятия неравенства имеем, что их определение производится по виду записи. Имеются алгебраические выражения, которые имеют знаки ≠, <, >, ≤ , ≥. Дадим определение.
Определение 1Числовым неравенством называют неравенство, в записи которого обе стороны имеют числа и числовые выражения.
Числовые неравенства рассматриваем еще в школе после изучения натуральных чисел. Такие операции сравнения изучаются поэтапно. Первоначальные имею вид 1<5, 5+7>3. После чего правила дополняются, а неравенства усложняются, тогда получаем неравенства вида 523>5,1(2), ln 0.
73-172<0.
Свойства числовых неравенств
Чтобы правильно работать с неравенствами, необходимо использовать свойства числовых неравенств. Они идут из понятия неравенства. Такое понятие задается при помощи утверждения, которое обозначается как «больше» или «меньше».
Определение 2- число a больше b, когда разность a-b – положительное число;
- число a меньше b, когда разность a-b – отрицательное число;
- число a равно b, когда разность a-bравняется нулю.
Определение используется при решении неравенств с отношениями «меньше или равно», «больше или равно». Получаем, что
Определение 3- a больше или равно b, когда a-b является неотрицательным числом;
- a меньше или равно b, когда a-b является неположительным числом.
Определения будут использованы при доказательствах свойств числовых неравенств.
Основные свойства
Рассмотрим 3 основные неравенства. Использование знаков < и > характерно при свойствах:
Определение 4- антирефлексивности, которое говорит о том, что любое число a из неравенств a<a и a>a считается неверным.
Известно, что для любого a имеет место быть равенство a−a=0, отсюда получаем, что а=а. Значит, a<a и a>a неверно. Например, 3<3 и -41415>-41415 являются неверными. - ассиметричности. Когда числа a и b являются такими, что a<b, то b>a, и если a>b, то b<a. Используя определение отношений «больше», «меньше» обоснуем его. Так как в первой части имеем, что a<b, тогда a−b является отрицательным числом. А b−a=−(a−b) положительное число, потому как число противоположно отрицательному числу a−b. Отсюда следует, что b>a. Аналогичным образом доказывается и вторая его часть.
Известно, что для любого a имеет место быть равенство a−a=0, отсюда получаем, что а=а. Значит, a<a и a>a неверно. Например, 3<3 и -41415>-41415 являются неверными.Например, при заданном неравенстве 5<11 имеем, что 11>5, значит его числовое неравенство −0,27>−1,3 перепишется в виде −1,3<−0,27.
Перед тем, как перейти к следующему свойству, заметим, что при помощи ассиметричности можно читать неравенство справа налево и наоборот. Таким образом, числовое неравенство можно изменять и менять местами.
Определение 5- транзитивности.
Первое утверждение можно доказать. Условие a<b и b<c означает, что a−b и b−c являются отрицательными, а разность а-с представляется в виде (a−b)+(b−c), что является отрицательным числом, потому как имеем сумму двух отрицательных a−b и b−c. Отсюда получаем, что а-с является отрицательным числом, а значит, что a<c. Что и требовалось доказать.
Аналогичным образом доказывается вторая часть со свойством транизитивности.
Пример 2Разобранное свойство рассматриваем на примере неравенств −1<5 и 5<8. Отсюда имеем, что −1<8. Аналогичным образом из неравенств 12>18 и 18>132 следует, что 12>132.
Числовые неравенства, которые записываются с помощью нестрогих знаков неравенства, обладают свойством рефлексивности, потому как a≤a и a≥a могут иметь случай равенства а=а. им присуща ассиметричность и транзитивность.
Неравенства, имеющие в записи знаки ≤ и≥, имеют свойства:
- рефлексивности a≥a и a≤a считаются верными неравенствами;
- антисимметричности, когда a≤b, тогда b≥a, и если a≥b, тогда b≤a.
- транзитивности, когда a≤b и b≤c, тогда a≤c, а также, если a≥b и b≥c, то тогда a≥c.
Доказательство производится аналогичным образом.
Другие важные свойства числовых неравенств
Для дополнения основных свойств неравенств используются результаты, которые имеют практическое значение. Применяется принцип метода оценка значений выражений, на которых и базируются принципы решения неравенств.
Данный пункт раскрывает свойства неравенств для одного знака строгого неарвенства. Аналогично производится для нестрогих. Рассмотрим на примере, сформулировав неравенство если a<b и c являются любыми числами, то a+c<b+c. Справедливыми окажутся свойства:
- если a>b, то a+c>b+c;
- если a≤b, то a+c≤b+c;
- если a≥b, то a+c≥b+c.
Для удобного представления дадим соответствующее утверждение, которое записывается и приводятся доказательства, показываются примеры использования.
Определение 7Прибавление или вычисления числа к обеим сторонам. Иначе говоря, когда a и b соответствуют неравенству a<b, тогда для любого такого числа имеет смысл неравенство вида a+c<b+c.
Доказательство 2Чтобы доказать это, необходимо, чтобы уравнение соответствовало условию a<b. Тогда (a+c)−(b+c)=a+c−b−c=a−b. Из условия a<b получим, что a−b<0. Значит, (a+c)−(b+c)<0, откуда a+c<b+c. Множество действительных числе могут быть изменены с помощью прибавления противоположного числа –с.
Пример 3К примеру, если обе части неравенства 7>3 увеличиваем на 15, тогда получаем, что 7+15>3+15. Это равно 22>18.
Определение 8Когда обе части неравенства умножить или разделить на одно и то же число c, получим верное неравенство. Если взять число c отрицательным, то знак поменяется на противоположный.
Иначе это выглядит так: для a и b неравенство выполняется, когда a<b и c являются положительными числами, то a·c<b·c, а если v является отрицательным числом, тогда a·c>b·c.
Когда имеется случай c>0, необходимо составить разность левой и правой частей неравенства. Тогда получаем, что a·c−b·c=(a−b)·c. Из условия a<b, то a−b<0, а c>0, тогда произведение (a−b)·c будет отрицательным. Отсюда следует, что a·c−b·c<0, где a·c<b·c. Другая часть доказывается аналогичным образом.
При доказательстве деление на целое число можно заменить умножением на обратное заданному, то есть 1c. Рассмотрим пример свойства на определенных числах.
Разрешено обе части неравенства 4<6 умножаем на положительное 0,5, тогда получим неравенство вида −4·0,5<6·0,5, где −2<3. Когда обе части делим на -4, то необходимо изменить знак неравенства на противоположный . отсюда имеем, что неравенство примет вид −8:(−4)≥12:(−4), где 2≥−3.
Теперь сформулируем вытекающие два результата, которые используются при решении неравенств:
- Следствие 1. При смене знаков частей числового неравенства меняется сам знак неравенства на противоположный, как a<b, как −a>−b. Это соответствует правилу умножения обеих частей на -1. Оно применимо для перехода. Например, −6<−2, то 6>2.
- Следствие 2. При замене обратными числами частей числового неравенства на противоположный, меняется и его знак, причем неравенство останется верным. Отсюда имеем, что a и b являются положительными числами, a<b, 1a>1b.
При смене знаков частей числового неравенства меняется сам знак неравенства на противоположный, как a<b, как −a>−b. Это соответствует правилу умножения обеих частей на -1. Оно применимо для перехода. Например, −6<−2, то 6>2.При делении обеих частей неравенства a<b разрешается на число a·b. Данное свойство используется при верном неравенстве 5>32 имеем, что 15<23. При отрицательных a и b c условием, что a<b , неравенство 1a>1b может получиться неверным.
Пример 5Например, −2<3, однако, -12>13 являются неверным равенством.
Все пункты объединяет то, что действия над частями неравенства дают верное неравенство на выходе. Рассмотрим свойства, где изначально имеется несколько числовых неравенств, а его результат получим при сложении или умножении его частей.
Когда числа a, b, c, d справедливы для неравенств a<b и c<d, тогда верным считается a+c<b+d. Свойство можно формировать таким образом: почленно складывать числа частей неравенства.
Доказательство 4Свойство применяется для почленного сложения трех, четырех и более числовых неравенств. Числам a1, a2, …, an и b1, b2, …, bn справедливы неравенства a1<b1, a2<b2, …, an<bn , можно доказать метод математической индукции , получив a1+a2+…+an<b1+b2+…+bn.
Пример 6Например, при данных трех числовых неравенствах одного знака −5<−2, −1<12 и 3<4.
Почленное умножение обеих частей дает в результате положительное число. При a<b и c<d, где a, b, c и d являются положительными числами, тогда неравенство вида a·c<b·d считается справедливым.
Доказательство 5Чтобы доказать это, необходимо обе части неравенства a<b умножить на число с, а обе части c<d на b. В итоге получим, что неравенства a·c<b·c и b·c<b·d верные, откуда получим свойство транизитивности a·c<b·d.
Это свойство считается справедливым для количества чисел, на которые необходимо умножить обе части неравенства. Тогда a1, a2, …, an и b1, b2, …, bnявляются положительные числами, где a1<b1, a2<b2, …, an<bn, то a1·a2·…·an<b1·b2·…·bn.
Заметим, что при записи неравенств имеются неположительные числа, тогда их почленное умножение приводит к неверным неравенствам.
Пример 7К примеру, неравенство 1<3 и −5<−4 являются верными, а почленное их умножение даст результат в виде 1·(−5)<3·(−4), считается, что −5<−12 это является неверным неравенством.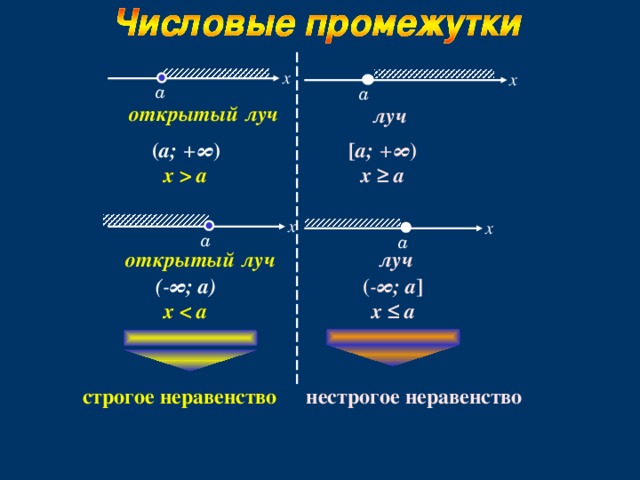
Следствие: Почленное умножение неравенств a<b с положительными с a и b, причем получается an<bn.
Свойства числовых неравенств
Рассмотрим ниже свойства числовых неравенств.
- a<a, a>a — неверные неравенства,
a≤a, a≥a- верные неравенства. - Если a<b, то b>a — антисимметричность.
- Если a<b и b<c то a<c — транзитивность.
- Если a<b и c — любоое число, то a+с<b+c.
- Если a<b и c — положительное число, то a·c<b·c,
Если a<b и c — отрицательное число, то a·c>b·c.
Следствие 1: если a<b, то -a>-b.
Следствие 2: если a и b — положительные числа и a<b, то 1a>1b.
- Если a1<b1, a2<b2,…, an<bn, то a1+a2+…+an<b1+b2+…+bn.
- Если a1, a2,…, an, b1, b2,…,bn- положительные числа и a1<b1, a2<b2,…, an<bn, то a1·a2·…·an<b1·b2·. ..bn.
..bn.Cледствие 1: если a<b, a и b — положительные числа, то an<bn.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
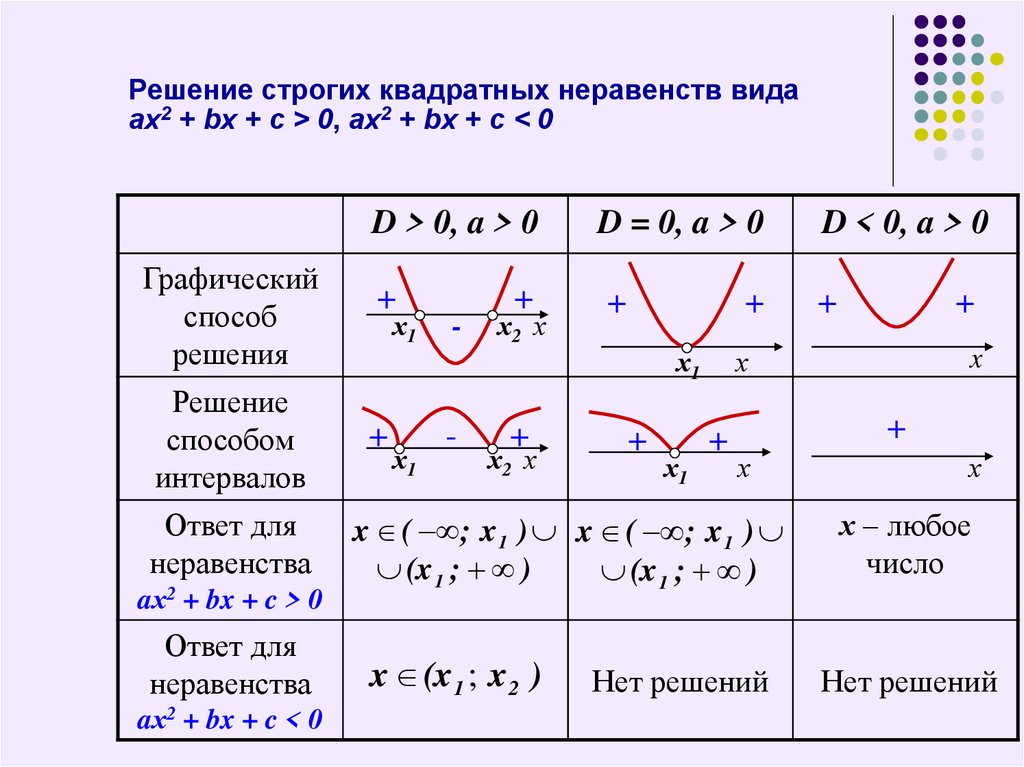
Метод интервалов
Метод интервалов — универсальный метод решения неравенств. С его помощью можно решить неравенства самого разного вида. Рассмотрим алгоритм метода интервалов, а затем перейдем к примерам решения неравенств этим методом.
Алгоритм решения неравенств методом интервалов.
Прежде чем применить метод интервалов для решении неравенства, необходимо все дроби привести к наименьшему общему знаменателю и все слагаемые перенести в левую часть, чтобы справа остался нуль. Для начала рассмотрим алгоритм решения неравенств вида
1. Приравниваем к нулю левую часть:
(Таким образом мы находим нули функции
а также ее область определения).
2.Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
3.
Полученные точки отмечаем на числовой прямой с учетом области определения функции. Точки разбивают числовую прямую на промежутки, в каждом из которых рассматриваемая функция имеет определенный знак. Выбираем любое число из любого промежутка (удобнее всего брать нуль, если он не входит в отмеченные точки), и подставляем это число в последнее неравенство (то есть в упрощенное неравенство, в котором все слагаемые стоят в левой части и дроби приведены к наименьшему общему знаменателю). В результате определяем знак на выбранном промежутке. Остальные знаки расставляем в шахматном порядке.
4. «Петля»
1)Если есть кратный корень четной степени, то в нем — «петля»:
2) Если один и тот же корень встречается четное число раз, то в нем — «петля»:
так как корень x2 встречается четное количество раз (два раза).
3) Если дискриминант равен нулю, то в соответствующем корне x=-b/2a — «петля».
(В этом случае x1=x2, то есть один и тот же корень встретился два раза).
4) Если корень стоит под знаком модуля, а выражение с модулем является множителем (а не слагаемым!), то в таком корне — «петля»:
5. Выбираем промежутки с нужным знаком: если в неравенстве знак > или ≥, берем промежутки с «+»; если < или ≤ — с «-«.
Точки, в которых знаменатель обращается в нуль, всегда выколотые!!!
В остальных случаях запомнить, выколотая точка или закрашенная, можно с помощью ассоциации.
Замечание
Отдельно стоящие закрашенные точки включаем в решение:
(Знаки в «петлях» — «виртуальные». В этих точках функция обращается нуль либо не определена. «Петля» служит только для сохранения порядка чередования знаков).
Кому принадлежит идея «петли», я не знаю. Этот способ очень удобный для расстановки знаков. Почему его нет в литературе? Именно потому, что знак в «петле»- «виртуальный».
Точки, которые мы отмечаем на числовой прямой, являются либо нулями функции, либо не входят в её область определения.
Нуль не является ни положительным, ни отрицательным числом (он отделяет положительные числа от отрицательных). Ставя знак в «петлю», мы совершаем грубую ошибку.
Поэтому использовать «петлю» можно, но ставить в неё знак — нельзя. Предлагаю бороться с этим противоречием, либо поставить знак карандашом, а потом его стереть, либо ставить знак в черновик, но не переносить его в чистовик.
Далее рассмотрим различные примеры решения неравенств с помощью этого метода.
неравенство — Неравенства, когда здесь меняется знак?
Задавать вопрос
спросил
Изменено 8 лет, 3 месяца назад
Просмотрено 4к раз
$\begingroup$
Я столкнулся с проблемой неравенства.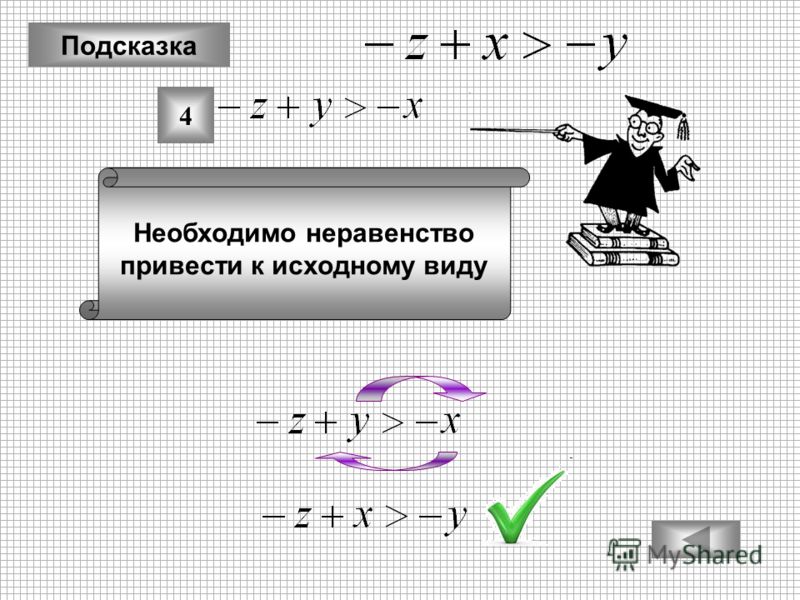
Я просматривал примеры, предоставленные двумя веб-сайтами, которые «решают» неравенства, однако, когда я пытаюсь использовать свой собственный метод, чрезвычайно простой «сложение, вычитание, умножение, деление», я получаю неправильный знак неравенства.
Я сделал следующее:
$$\frac{x-3}{x+3} < 4$$ $$x-3 < 4(x+3)$$ $$x-3 < 4x+12$$ $$x < 4x+15$$ $$-3x < 15$$ $$3x > -15$$ $$x > -5$$
Я догадался, что проблема где-то в первых двух строках, смущающе, однако я не уверен, что я делаю неправильно; «калькуляторы» говорят мне, что ответ $x <-5$ или $x>-3$.
Что я делаю не так со своим решением, чтобы получить $x > -5$ неправильно? Каким другим путем я могу найти $x > -3$?
Было бы лучше, если бы мне не приходилось начинать использовать «таблицу» для проверки всех решений, но если это единственный способ, то все в порядке.
- неравенство
- делимость
- решение задач
$\endgroup$
1
$\begingroup$
Ваша проблема возникает, когда вы умножаете обе части на $(x+3)$, что может быть отрицательным числом, и в этом случае неравенства будут обратными.
Вам нужно иметь дело с двумя случаями: x+3>0 и x+3<0.
Вы используете $x+3>0$ (или $x>-3$), чтобы получить $x>-5$, комбинация обоих дает $x>-3$, что является частью правильного ответа.
Теперь используйте $x+3<0$ (или $x<-3$), измените направление неравенства при умножении в обе стороны и получите другое направление, $x<-5$. Сочетание $x<-3$ и $x<-5$ дает только $x<-5$.
Удачи.
$\endgroup$
8
$\begingroup$
Ваша ошибка во второй строке. Если $(x+3)$ отрицательно, то вам нужно переключить неравенство туда. Таким образом, вы должны рассмотреть два случая: первый, когда $(x+3)$ положителен (т.е. $x \geq -3$) и когда $(x+3)$ отрицателен (т.е. $x \leq -3$) . Остальные ваши расчеты были правильными
$\endgroup$
$\begingroup$
Если вы хотите решить такие неравенства, стандартный способ — проверить, как они соотносятся с нулем.
Например, у вас будет $$ \frac{x-3}{x+3}-4<0$$ и, следовательно, $$\frac{-3x-15}{x+3}<0$$. У вас будет использовать эту таблицу, как вы сказали, но это самый безопасный способ избежать ошибок.
$\endgroup$
$\begingroup$
Если обе части умножить на $(x+3)$, если $x < -3$, это значение будет отрицательным, и неравенство изменится на противоположное. 92$$ как квадратное неравенство.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Графики линейных неравенств: примеры — ChiliMath
Теперь мы готовы применить предложенные шаги по построению графика линейного неравенства из предыдущего урока. Давайте рассмотрим четыре (4) примера, охватывающих различные типы символов неравенства.
Пример 1: Нарисуйте график линейного неравенства y>2x-1.
Прежде всего необходимо убедиться, что переменная y сама по себе находится слева от символа неравенства, что и имеет место в этой задаче. Далее нужно нарисовать граничную линию, мгновенно изменив символ неравенства на символ равенства.
Начертите линию y>2x-1 по оси xy удобным для вас способом. Поскольку символ неравенства просто больше «>», а 90 103, а не 90 104 больше или равен «≥», граница обозначена пунктирной или пунктирной линией. Итак, вот как это должно выглядеть на данный момент.
Последним шагом является затенение выше или ниже линии границы.
Из предложенных шагов нам сказали заштриховать верхнюю сторону граничной линии, если у нас есть символы неравенства > (больше) или ≥ (больше или равно). Всегда помните, что «больше чем» подразумевает «верхнее».
Чтобы проверить правильность итогового графика неравенства, мы можем выбрать любые точки в заштрихованной области. Для этого возьмем точку (−1, 1).
Оцените значения x и y точки в неравенстве и проверьте, верно ли утверждение. В точке (−1,1) значения x=-1 и y=1.
Поскольку контрольная точка из заштрихованной области дает истинное утверждение после сверки с исходным неравенством, это показывает, что наш окончательный график верен!
Пример 2: Нарисуйте график линейного неравенства y \ge -x+2.
Переменная y находится слева. Это хорошо! Обратите внимание, у нас есть символ «больше или равно». «Равный» аспект символа говорит нам о том, что граница будет сплошной. Итак, давайте изобразим линию y=-x+2 на декартовой плоскости.
Как и в примере 1, мы заштрихуем верхнюю часть граничной линии, потому что у нас есть случай «больше чем».
Проверьте правильность нашего графика, выбрав точку (4,2) в заштрихованном разделе и оценив значения x и y точки в заданном линейном неравенстве.
Из выбранной контрольной точки, x=4 и y=2
У нас есть истинное утверждение, которое дает нам уверенность в том, что наш окончательный график неравенства также верен.
Пример 3: Постройте график решения линейного неравенства \large{y < {1 \over 2}x - 1} .
Глядя на задачу, символ неравенства «меньше чем», а не «меньше или равно». Из-за этого график граничной линии будет ломаным или пунктирным. Кроме того, «меньше чем» означает, что мы заштрихуем регион ниже строки. Вот и все!
Вот график граничной линии \large{y = {1 \over 2}x — 1} .
Поскольку символ неравенства на 90 103 меньше, чем на 90 104 ( < ), мы затеняем область 90 103 ниже 90 104 пунктирной линии.
Я оставлю вам возможность убедиться, что это правильный график, выбрав любые контрольные точки из заштрихованной области и сравнив их с исходным линейным равенством.
Пример 4: Постройте график решения линейного неравенства y \le — {2 \over 3}x + 2 .
Так как мы уже рассмотрели несколько примеров, я думаю, что вы можете решить это в уме. Вы можете произвести впечатление на своего учителя, предложив такое же короткое решение.
Я вижу, что символ неравенства «меньше или равен» ( ≤ ), что делает границу сплошной. Более того, решение находится ниже граничной линии из-за его аспекта «меньше чем». Вот правильный график неравенства.
В приведенных выше примерах вы видели линейные неравенства, в которых переменные y всегда находятся слева. Вы даже можете думать о них как о линейных неравенствах в форме линии с пересечением наклона.
На этот раз нас интересуют примеры, когда переменные x и y расположены по одну сторону от символа неравенства.
Мы можем назвать их линейными неравенствами в Стандартной форме . Ниже приведены четыре общих случая, когда A, B и C являются просто числами или константами.
Что нам нужно сделать, так это переписать данное неравенство или манипулировать им так, чтобы переменная y оставалась в левой части. Другими словами, мы собираемся найти у через х. После этого мы можем применить предложенные шаги для построения графика линейного неравенства, как обычно.
Давайте рассмотрим несколько примеров.
Пример 5: Нарисуйте график линейного неравенства в стандартной форме 4x + 2y < 8. правая сторона. Сделайте это, вычитая обе части на 4x и разделив все неравенство на коэффициент y, который равен 4. Поскольку мы делим на положительное число, направление символа неравенства остается прежним.
Поскольку у нас есть символ «меньше чем» (<) и , а не символ «меньше или равно» (≤), граничная линия будет иметь вид с точками или со штрихами .
На случай, если вы забыли, где взять границу, замените пока неравенство на символ равенства, то есть с y<-2x+4 на y=-2x+4. Затем нарисуйте уравнение линии, используя любой из этих методов.
Итак, следующий очевидный шаг — решить, какую область заштриховать. Будет ли он выше или ниже пограничной линии? Мы заштрихуем нижнюю часть граничной линии, потому что у нас есть « меньше, чем ” после того, как мы преобразовали исходную задачу о неравенстве в форму, в которой y находится в левой части.
Мы можем проверить правильность построения графика, выбрав любые контрольные точки, найденные в заштрихованной области. Лучшей контрольной точкой является начало координат, т. е. точка (0,0), потому что ее легко вычислить.
Контрольная точка (0,0) означает x=0 и y=0. Оцените эти значения в преобразованном неравенстве или в исходном неравенстве, чтобы убедиться, что вы получили верное утверждение.
Работает! Таким образом, мы заштриховали правильную область, которая находится ниже пунктирной линии.