Онлайн построение интегральных кривых – Построение графиков онлайн

построение графиков функций с помощью онлайн калькулятора.

Как построить график функции онлайн на этом сайте?

Чтобы построить график функции онлайн, нужно просто ввести свою функцию в специальное поле и кликнуть куда-нибудь вне его. После этого график введенной функции нарисуется автоматически. Допустим, вам требуется построить классический график функции «икс в квадрате». Соответственно, нужно ввести в поле «x^2».

Если вам нужно построить график нескольких функций одновременно, то нажмите на синюю кнопку «Добавить еще». После этого откроется еще одно поле, в которое надо будет вписать вторую функцию. Ее график также будет построен автоматически.

Цвет линий графика вы можете настроить с помощью нажатия на квадратик, расположенный справа от поля ввода функции. Остальные настройки находятся прямо над областью графика. С их помощью вы можете установить цвет фона, наличие и цвет сетки, наличие и цвет осей, наличие рисок, а также наличие и цвет нумерации отрезков графика. Если необходимо, вы можете масштабировать график функции с помощью колесика мыши или специальных иконок в правом нижнем углу области рисунка.

После построения графика и внесения необходимых изменений в настройки, вы можете скачать график с помощью большой зеленой кнопки «Скачать» в самом низу. Вам будет предложено сохранить график функции в виде картинки формата PNG.

Зачем нужно строить график функции?

На этой странице вы можете построить интерактивный график функции онлайн. Построение графика функции позволяет увидеть геометрический образ той или иной математической функции. Для того чтобы вам было удобнее строить такой график, мы создали специальное онлайн приложение. Оно абсолютно бесплатно, не требует регистрации и доступно для использования прямо в браузере без каких-либо дополнительных настроек и манипуляций. Строить графики для разнообразных функций чаще всего требуется школьникам средних и старших классов, изучающим алгебру и геометрию, а также студентам первых и вторых курсов в рамках прохождения курсов высшей математики. Как правило, данный процесс занимает много времени и требует кучу канцелярских принадлежностей, чтобы начертить оси графика на бумаге, проставить точки координат, объединить их ровной линией и т.д. С помощью данного онлайн сервиса вы сможете рассчитать и создать графическое изображение функции моментально.

Как работает графический калькулятор для графиков функций?

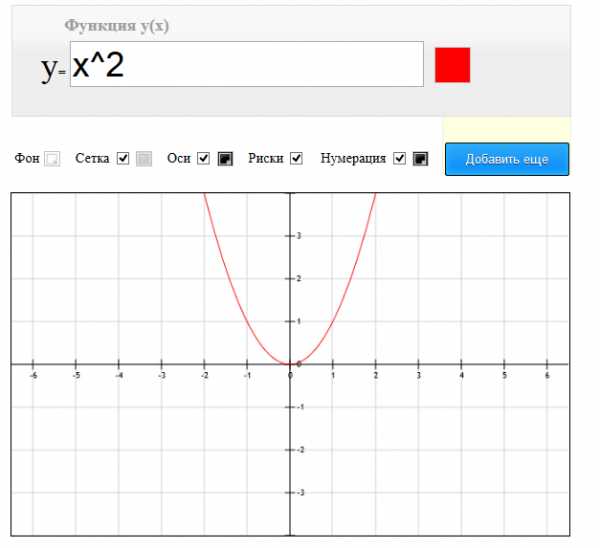
Онлайн сервис работает очень просто. В поле на самом верху вписывается функция (т.е. само уравнение, график которого необходимо построить). Сразу после ввода приложение моментально рисует график в области под этим полем. Все происходит без обновления страницы. Далее, можно внести различные цветовые настройки, а также скрыть/показать некоторые элементы графика функции. После этого, готовый график можно скачать, нажав на соответствующую кнопку в самом низу приложения. На ваш компьютер будет загружен рисунок в формате .png, который вы сможете распечатать или перенести в бумажную тетрадь.

Какие функции поддерживает построитель графиков?

Поддерживаются абсолютно все математические функции, которые могут пригодиться при построении графиков. Тут важно подчеркнуть, что в отличии от классического языка математики принятого в школах и ВУЗах, знак степени в рамках приложения обозначается международным знаком «^». Это обусловлено отсутствием на клавиатуре компьютера возможности прописать степень в привычном формате. Далее приведена таблица с полным списком поддерживаемых функций.

Приложением поддерживаются следующие функции:

Тригонометрические функции
Синус	Косинус	Тангенс	Секанс	Косеканс	Котангенс	Арксинус	Арккосинус	Арктангенс	Арксеканс	Арккосеканс	Арккотангенс
sin(x)	cos(x)	tan(x)	sec(x)	csc(x)	cot(x)	asin(x)	acos(x)	atan(x)	asec(x)	acsc(x)	acot(x)
Гиперболические функции
sinh(x)	cosh(x)	tanh(x)	sech(x)	csch(x)	coth(x)	asinh(x)	acosh(x)	atanh(x)	asech(x)	acsch(x)	acoth(x)
Прочее
Натуральный логарифм		Логарифм		Квадратный корень		Модуль		Округление в меньшую сторону		Округление в большую сторону
ln(x)		log(x)		sqrt(x)		abs(x)		floor(x)		ceil(x)
Минимум						Максимум
min(выражение1,выражение2,…)						max(выражение1,выражение2,…)

function-graph.ru

Построение поверхности 3D, заданной уравнением — Контрольная Работа РУ

Введите уравнение

Построим поверхность, заданную уравнением f(x, y, z) = 0, где a < x < b, c < y < d, m < z < n.

Другие примеры:

• y = x^2
• z = x^2 + y^2
• 0.3 * z^2 + x^2 + y^2 = 1
• z = sin((x^2 + y^2)^(1/2))
• x^4+y^4+z^4-5.0*(x^2+y^2+z^2)+11.8=0

Канонический вид кривой и поверхности

Вы можете определить вид кривой и поверхности 2-го порядка онлайн с подробным решением:

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

e

e число, которое примерно равно 2.7

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

pi

Число — «Пи», которое примерно равно 3.14

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7.5, не 7,5

2*x

— умножение

3/x

— деление

x^3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

www.kontrolnaya-rabota.ru

Изоклины — Составление дифференциального уравнения семейства кривых

Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.

1. С помощью изоклин начертить (приближенно) решение уравнения: y’ = y — x².

6. С помощью изоклин начертить (приближенно) решение уравнения: xy’ = 2y.

7. С помощью изоклин начертить (приближенно) решение уравнения: xy’ + y = 0.

16. Написать уравнение геометрического места точек перегиба графиков решений уравнений: а) y’ = y — x²; б) y’ = x — e^y; в) x² + y²y’ = 1; г)…

17. Составить дифференциальные уравнения данных семейств линий: y = e^Cx.

18. Составить дифференциальные уравнения данных семейств линий: y = (x — C)³.

19. Составить дифференциальные уравнения данных семейств линий: y = Cx³.

20. Составить дифференциальные уравнения данных семейств линий: y = sin(x + C).

21. Составить дифференциальные уравнения данных семейств линий: x² + Cy² = 2y.

22. Составить дифференциальные уравнения данных семейств линий: y² + Cx = x³.

23. Составить дифференциальные уравнения данных семейств линий: y = C(x — C)².

24. Составить дифференциальные уравнения данных семейств линий: Cy = sin Cx.

25. Составить дифференциальные уравнения данных семейств линий: y = ax² + be^x.

26. Составить дифференциальные уравнения данных семейств линий: (x — a)² + by² = 1.

27. Составить дифференциальные уравнения данных семейств линий: ln y = ax + by.

28. Составить дифференциальные уравнения данных семейств линий: y = ax³ + bx² + cx.

29. Составить дифференциальные уравнения данных семейств линий: x = ay² + by + c.

30. Составить дифференциальное уравнение окружностей радиуса 1, центры которых лежат на прямой у = 2х.

31. Составить дифференциальное уравнение парабол с осью, параллельной Оу, и касающихся одновременно прямых у = 0 и у = х.

32. Составить дифференциальное уравнение окружностей, касающихся одновременно прямых y = 0 и x = 0 и расположенных в первой и третьей четвертях.

33. Составить дифференциальное уравнение всех парабол с осью, параллельной Оу, и проходящих через начало координат.

34. Составить дифференциальное уравнение всех окружностей, касающихся оси абсцисс.

35. Найти системы дифференциальных уравнений, которым удовлетворяют линии данных семейств: ax + z = b, y² + z² = b².

36. Найти системы дифференциальных уравнений, которым удовлетворяют линии данных семейств: x² + y² = z² — 2bz, y = ax + b.

37. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y = Cx⁴, φ = 90°.

38. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y² = x + C, φ = 90°.

39. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: x² = y + Cx, φ = 90°.

40. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: x² + y² = a², φ = 45°.

41. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y = kx, φ = 60°.

42. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: 3x² + y² = C, φ = 30°.

43. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y² = 2px, φ = 60°.

44. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: r = a + cos θ, φ = 90°.

45. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: r = a cos² θ, φ = 90°.

47. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y = x ln x + Cx, φ = arctg 2.

48. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: x² + y² = 2ax, φ = 45°.

49. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: x² + C² = 2Cy, φ = 90°.

50. Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом φ: y = Cx + C³, φ = 90°.

xn--e1avkt.xn--p1ai

∫ Решение определённых интегралов — Калькулятор Онлайн

Введите функцию, для которой необходимо вычислить интеграл

Калькулятор предоставляет ПОДРОБНОЕ решение определённых интегралов.

Этот калькулятор находит решение определенного интеграла от функции f(x) с данными верхними и нижними пределами.

Примеры

С применением степени
(квадрат и куб) и дроби

(x^2 - 1)/(x^3 + 1)

Квадратный корень

sqrt(x)/(x + 1)

Кубический корень

cbrt(x)/(3*x + 2)

С применением синуса и косинуса

2*sin(x)*cos(x)

Арксинус

x*arcsin(x)

Арккосинус

x*arccos(x)

Применение логарифма

x*log(x, 10)

Натуральный логарифм

ln(x)/x

Экспонента

exp(x)*x

Тангенс

tg(x)*sin(x)

Котангенс

ctg(x)*cos(x)

Иррациональне дроби

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Арктангенс

x*arctg(x)

Арккотангенс

x*arсctg(x)

Гиберболические синус и косинус

2*sh(x)*ch(x)

Гиберболические тангенс и котангенс

ctgh(x)/tgh(x)

Гиберболические арксинус и арккосинус

x^2*arcsinh(x)*arccosh(x)

Гиберболические арктангенс и арккотангенс

x^2*arctgh(x)*arcctgh(x)

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

e

e число, которое примерно равно 2.7

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

pi

Число — «Пи», которое примерно равно 3.14

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7.5, не 7,5

2*x

— умножение

3/x

— деление

x^3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

www.kontrolnaya-rabota.ru

∫ Решение интегралов онлайн с подробным решением

Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!

Это онлайн сервис в один шаг:

• Ввести подинтегральное выражение (подинтегральную функцию)

Перейти: Онлайн сервис «Неопределенный интеграл» →

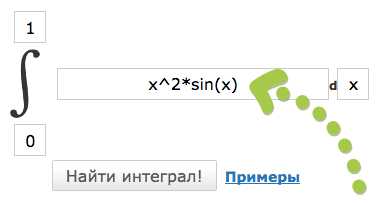
Это онлайн сервис в один шаг:

• Ввести подинтегральное выражение (подинтегральную функцию)
• Ввести нижний предел для интеграла
• Ввести верхний предел для интеграла

Перейти: Онлайн сервис «Определенный интеграл» →

• Ввести подинтегральное выражение (подинтегральную функцию)
• Ввести нижний и верхний пределы для первой области интегрирования
• Ввести нижний и верхний предел для второй области интегрирования

Перейти: Онлайн сервис «Двойной интеграл» →

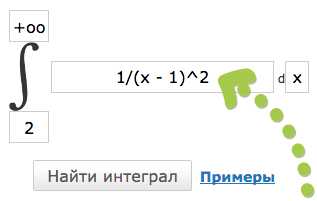
• Ввести подинтегральное выражение (подинтегральную функцию)
• Введите верхнюю область интегрирования (или + бесконечность)
• Ввести нижнюю область интегрирования (или — бесконечность)

Перейти: Онлайн сервис «Несобственный интеграл» →

• Ввести подинтегральное выражение (подинтегральную функцию)
• Ввести нижний и верхний пределы для первой области интегрирования
• Ввести нижний и верхний предел для второй области интегрирования
• Ввести нижний и верхний предел для третьей области интегрирования

Перейти: Онлайн сервис «Тройной интеграл» →

Данный сервис позволяет проверить свои вычисления на правильность

Возможности

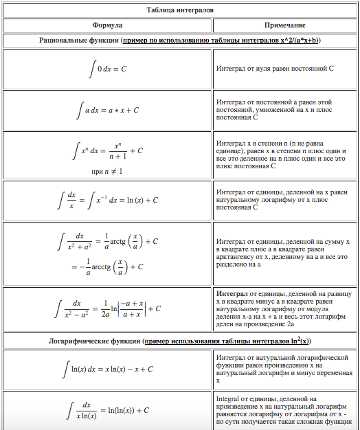
Таблица интегралов

Вы также можете воспользоваться таблицей интегралов, чтобы самостоятельно посчитать любой интеграл, перейти:

www.kontrolnaya-rabota.ru

Построение графика функции онлайн!

Оператор	Описание
+ — * : / () [] {}	Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * писать не обязательно, например: 2*сos(5*x) можно писать как 2cos(5x). Используйте различные скобки для группирования выражений.
x^n или p(x,n)	Возведение в степень: xn, например p(x,3) или x^3 значит x в кубе, также можно написать xxx или x*x*x.
root(x,n)	Корень n-ой степени из x. Например: root(x,3) есть корень 3й степени из x.
sqrt()	Квадратный корень. Эквивалентно root(аргумент,2)
cbrt()	Кубический корень. Эквивалентно root(аргумент,3)
logn(x,a)	Логарифм x пооснованию a
ln()	Натуральный логарифм (с основанием е)
lg()	Логарифм по основанию 10 (Десятичный логарифм), то же, что и logn(аргумент,10).
lb()	Логарифм по основанию 2
exp()	Экспоненциальная функция (e в заданной степени), эквивалентно e^аргумент
sin()	Синус
cos()	Косинус
tan()	Тангенс
cot()	Котангенс
sec()	Секанс, определяется как 1/cos()
csc()	Косеканс, определяется как 1/sin()
asin()	Арксинус
acos()	Арккосинус
atan()	Арктангенс
acot()	Арккотангенс
asec()	Арксеканс, обратный секанс
acsc()	Арккосеканс, обратный косеканс
sinh()	Гиперболический синус, шинус
cosh()	Гиперболический косинус, чосинус
tanh()	Гиперболический тангенс
coth()	Гиперболический котангенс
sech()	Гиперболический секанс
csch()	Гиперболический косеканс
asinh()	Гиперболический арксинус, функция обратная sinh()
acosh()	Гиперболический арккосинус, функция обратная cosh()
atanh()	Гиперболический арктангенс, функция обратная tanh()
acoth()	Гиперболический арккотангенс, функция обратная cotanh()
asech()	Гиперболический арксеканс, функция обратная sech()
acsch()	Гиперболический арккосеканс, функция обратная csch()
gaussd(x,среднее,сигма)	Нормальное распределение (Распределение Гаусса). Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1.
min(число1,число2)	Вычисляет наименьшее из 2х значений
max(число1,число2)	Вычисляет наибольшее из 2х значений
round()	Округляет аргумент до целого значения
floor()	Округление вниз
ceil()	Округление вверх
abs() или | |	Модуль (абсолютное значение)
sgn()	Функция сигнум, определяет знак аргумента sgn(x)  =    1 for x > 0  0 for x = 0 -1 for x < 0
rand	Случайное число от 0 до 1

matemonline.com

9.1.3. Задача Коши. Особые и частные решения

В дальнейшем эту функцию будем называть искомой функцией. Процесс нахождения решения ОДУ называется интегрированием дифференциального уравнения.

Определение 1. Задача, в которой требуется найти решение дифференциального уравненияF(x, y, y′)= 0 илиy′ = f (x, y), удовлетворяющее начальному условиюy(x0 )= y0 , называется

задачей Коши.

Теорема существования и единственности решения

задачи Коши.	Пусть дано дифференциальное		уравнение
y′ = f(x, y), где	функция f (x, y)	определена в	некоторой

области D плоскостиOxy , содержащей точку(x0 , y0 ). Если функцияf (x, y) удовлетворяет условиям:

1)f (x, y) есть непрерывная функция двух переменныхx

иy в областиD;

2)f (x, y) имеет частную производную∂∂fy , ограниченную

в области D,

тогда найдется интервал (x0 − h,x0 + h), на котором существует

единственное

решение

y = ϕ(x)

данного

уравнения,

удовлетворяющее условию ϕ(x0 )= y0 .

Доказательство теоремы в данном курсе опускается ввиду сложности. С ним можно ознакомиться в монографии [8].

Определение 2. Функцияy = ϕ(x,C), гдеC — произвольная

постоянная, называется общим решением	уравнения
F(x, y, y′)= 0 , если
1) она является решением этого уравнения	при любых
допустимых значениях произвольной постоянной C ;

2) каково бы ни было начальное условие y(x0 )= y0 , где точка(x0 , y0 ) принадлежит области, в которой выполняются

10

условия существования и единственности решения задачи Коши, можно подобрать такое единственное значение C0 постоянной

C , чтоϕ(x0 ,C0 )= y0 .

Определение 3. ФункцияΦ(x, y,C)= 0 называетсяобщим

интегралом уравнения, если она задает общее решение уравнения в неявном виде.

Определение 4. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называетсяособым решением.

Определение 5. Решение, полученное из общего при некотором допустимом значении произвольной постоянной, называетсячастным решением.

Замечание. Частное решение может быть получено из общего решения при некотором значении константыC . Особое решение не может быть получено из общего ни при каком значении произвольной постояннойC .

Пример 1. Найти интегральную кривую дифференциального
уравнения y′ = 2x , проходящую через точкуM (1;1).
Решение. Общим решением уравнения является функция
вида y = x2 +C ,	где C	— произвольная константа.
Действительно, y′ = 2x , отсюдаy = ∫2xdx = x2 +C .
Функции y = x2 ,	y = x2 +1 ,	y = x2 + 2 , полученные из

общего решения при конкретных значениях C , являются частными решениями данного уравнения.

Построив графики решения при различных значениях C , получим бесконечное множество непересекающихся интегральных кривых, которое будем называтьсемейством интегральных кривых (рис. 2).

11

y

1 M

1 x

Рис. 2. Интегральные кривые уравнения

Построим	интегральную кривую, проходящую через точку
M (1;1). Для этого требуется решить задачу Коши с начальным
условием y(1)=1.
Подставим	значения	x0=1, y0	=1в	общее	решение.
Полученное	равенство	1 =1+C	решим	относительно
произвольной	постоянной	C , получим	C = 0 .	Таким	образом,

решением поставленной задачи Коши является функция						y = x2 .
На	рис. 2. это интегральная кривая,			проходящая	через точку
M	(1;1), ее график выделен жирной линией.
	Данное	уравнение не	имеет особых решений,			так как
f (x, y)= 2x		непрерывная	функция	и частная	производная
∂f	= 0 ограничена.
∂y

Пример 2. Построить интегральные кривые уравнениеy′=2 y .Решение. Данное уравнение можно записать в виде

	1		y илиx	′	1
	x′= 2				= 2 y .
	Найдем для f (x, y)= 2	y	производную
	∂f	=	∂(2 y )	=	1 .
	∂y		∂y		y
	12

y(x0 )= 0 , то

При y = 0 нарушается условие теоремы о существовании и единственности решения задачи Коши. Уравнение может иметь особое решение видаy = 0 .

Общим решение данного дифференциального уравнения является x = y +C . Заметим, что при этом преобразовании мы

могли потерять решение y = 0 .
Частным решением уравнения являются функции	x = yпри
C = 0 ,x = y +1 приC =1 и т.д. Семейство	интегральных

кривых показано на рис. 3.

Рассмотрим функцию y = 0 . Она является решением исходного

уравнения, которое не может быть получено из общего ни при каких значениях произвольной постоянной. Следовательно, это особое решение, в каждой точке такого решения нарушается единственность задачи Коши.

Действительно, если задать начальное условие

поставленная задача Коши будет иметь два решения. Одно получится из общего решения. Если в формуле общего решения

положить x = x0 , y = 0 , тоC = x0 и решением задачи Коши

является функция x = y + x0 .		Это решение проходит через точку
(x0 ,0).	Вторым решением, проходящим через эту точку, является
функция	y = 0 . Таким образом,	в каждой точке решения y = 0

нарушается единственность задачи Коши. Такое решение является особым.

y = 0

Рис. 3.

13

studfiles.net