Графики тригонометрических функций
Графики синуса и косинуса
График функции изображен на рисунке 1.
Рис. 1
График функции изображен на рисунке 2.
Рис. 2
Кривая, описывающая функцию синуса, называется синусоидой, а косинуса – косинусоидой.
График функции можно получить из графика функции сдвигом последнего влево на . Аналогично, график функции можно получить из графика функции сдвигом последнего вправо на .
Графики тангенса и котангенса
График функции изображен на рисунке 3. Кривая, задающая функцию тангенса, называется тангенсоидой.
Рис. 3
График функции изображен на рисунке 4.
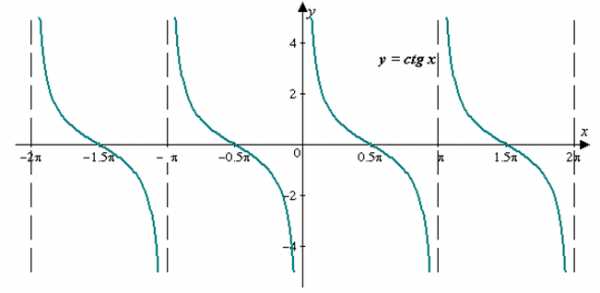
Рис. 4
Примеры решения задач
ПРИМЕР 1| Задание | |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси абсцисс вправо на (рис. 5).
 Рис. 5 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси ординат вверх на 1 (рис. 6) .
 Рис. 6 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции растяжением последнего вдоль оси ординат в три раза (увеличением расстояния от каждой точки графика до оси абсцисс в три раза) (рис. 7).
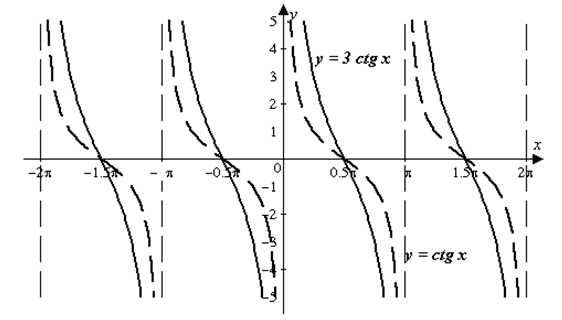 Рис. 7 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции . Осуществив параллельный перенос графика функции вдоль оси абсцисс влево на , получим (рис. 8)
Рис. 8 Затем, отразив график функции симметрично относительно оси абсцисс, получим искомый график (рис. 9). Рис. 9 |
Простейшие тригонометрические уравнения
Тригонометрические функции числового аргумента
Свойства тригонометрических функций
Упрощение тригонометрических выражений
Косинус суммы
Построение графиков тригонометрических функций — АЛГЕБРА — Уроки для 10 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК 9
Тема. Построение графиков тригонометрических функций
Цель урока: построение графиков функций у = sin х, у = cos x, у = tg х, у = ctg x.
Формирование умений строить графики функций: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx + b).
И. Проверка домашнего задания
1. Один ученик воспроизводит решение упражнения № 24 (1-3).
2. Фронтальная беседа:
1) Назовите явления в природе, которые периодически повторяются.
2) Дайте определение периодической функции.
3) Если функция у = f(x) имеет периодом число Т, то будет периодом этой функции число 2Т, 3T…? Ответ обоснуйте.
4) Найдите наименьший положительный период функций:
a) y = cos; б) y = sin ; в) у = tg ; г) у = .
5) периодическая функция у = С? Если да, то укажите период этой функции.
II. Построение графика функции у = sin х
Для построения графика функции у = sin x воспользуемся единичным кругом. Построим единичный круг радиусом 1 см (2 клетки). Справа построим систему координат, как на рис. 57.
На ось ОХ нанесем точки ; π; ; 2π (соответственно 3 ячейки, 6 ячеек 9 ячеек, 12 ячеек). Разделим первую четверть единичного круга на три равные части и на столько же частей отрезок оси абсцисс. Перенесем значение синуса до соответствующих точек оси ОХ. Получим точки, которые надо соединить плавной линией. Затем разделим вторую, третью и четвертую четверть единичного круга также на три равные части и перенесем значение синуса до соответствующей точки оси ОХ. Последовательно соединив все полученные точки, получим график функции у = sin х на промежутке [0;π].
За то что функция у = sin x периодическая с периодом 2π, то для построения графика функции у = sin x на всей прямой ОХ достаточно параллельно перенести построен график вдоль оси ОХ на 2π, 4π, 6π… единиц влево и вправо (рис. 58).
Кривая, которая является графиком функции у = sin x, называют синусоидой.
Выполнение упражнений______________________________
1. Постройте графики функций.
а) у = sin ; б) у = sin 2х; в) у = 2sin х; г) у = sin (-x).
Ответы: а) рис. 59; б) рис. 60; в) рис. 61; г) рис. 62.
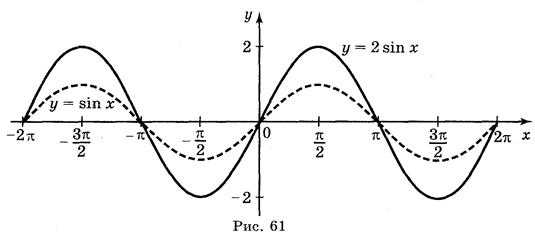
III. Построение графика функции у = cos x
Как известно, cos х = sin , поэтому у = cos x и у = sin — одинаковые функции. Для построения графика функции у = sin воспользуемся геометрич-ими преобразованиями графиков: сначала построим (рис. 63) график функции у = sin х, затем у = sin (-х) и в конце у = sin .
Выполнение упражнений________________________________
1. Постройте графики функций:
a) y = cos ; б) y = cos ; в) y =cos х; г) у = |cos x|.
Ответ: а) рис. 64; б) рис. 65; в) рис. 66; г) рис. 67.
IV. Построение графика функции у = tg x
График функции у = tg x построим с помощью линии тангенсов на промежутке , длина которого равна периоду π этой функции. Построим единичный круг радиусом 2 см (4 ячейки) и проведем линию тангенсов. Справа построим систему координат, как на рис. 68.
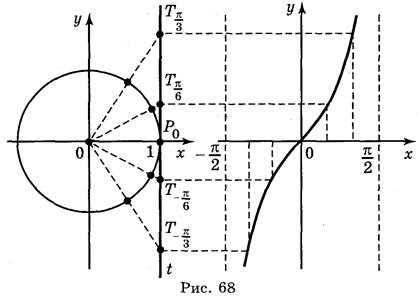
На ось ОХ нанесем точки ; (6 ячеек). Разделим первую и четвертую четверть окружности на 3 равные части и на столько же частей каждый из отрезков и . Найдем значения тангенсов чисел ; ; 0; ; с помощью линии тангенсов (ординаты точек ; ; ; ; линии тангенсов). Перенесем значения тангенсов до соответствующих точек оси ОХ. Последовательно соединив все полученные точки, получим график функции у = tg x на промежутке .
За то что функция у = tg x периодическая с периодом π, для построения графика функции у = tg x на всей прямой ОХ достаточно параллельно перенести построен график вдоль оси ОХ на π, 2π, 3π, 4π… единиц влево и вправо (рис. 69).
График функции у = tg x называется тангенсоїдою.
Выполнение упражнений
1. Постройте график функций
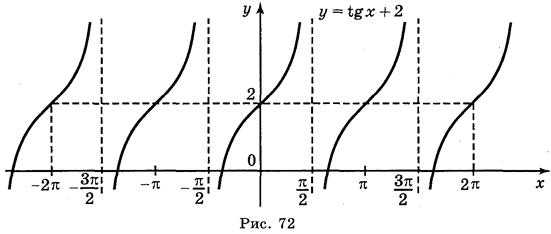
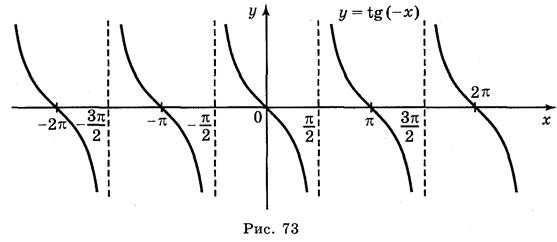
а) у = tg 2х; б) у = tgx; в) у = tg x + 2; г) у = tg (-x).
Ответы: а) рис. 70; б) рис. 71; в) рис. 72; г) рис. 73.
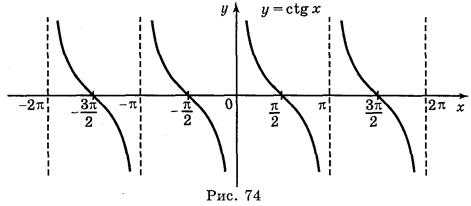
V. Построение графика функции у = ctg x
График функции у = ctg x легко получить, воспользовавшись формулой ctg x = tg и двумя геометрическими преобразованиями (рис. 74) симметрия относительно оси ΟΥ параллельный перенос вдоль оси ОХ на .
IV. Домашнее задание
Раздел И § 6. Вопросы и задания для повторения раздела И № 50-51. Упражнения № 28 (а-г).
V. Итог урока
na-uroke.in.ua
Графики тригонометрических функций. Синусоида | Подготовка к ЕГЭ по математике
Категория: Справочные материалыФункции и графикиГрафик функции y=sinx
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на
Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.
Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
График функции называется
График функции y=cosx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и .
Поступим несколько иначе.
Согласно формулам приведения .
Из чего мы делаем вывод, что график функции будет получен смещением графика функции на единиц влево.
То есть график функции – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.
Преобразования синусоиды
Приглашаю посмотреть небольшой видеоролик о том, как меняется поведение синусоиды в зависимости от умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.
egemaximum.ru
Онлайн калькулятор: Тригонометрические функции
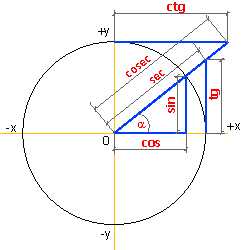Простейшие тригонометрические функцииТригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
Знаков после запятой: 10
Сохранить share extension
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Котангенс: (отношение длины прилежащего к углу катета к противоположному катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Косеканс: (отношение длины гипотенузы к противоположному катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
planetcalc.ru
Синусоида — онлайн построение графика
Следующий калькулятор служит для построения параметрической синусоиды в диапазоне от 0 до 2П.
при чем коэффициент k может задать сам пользователь.
Есть 3-и возможности введения коэффициентов: в радианах, градусах, пи радианах. По дефолту k = 1, а = 0, при этом функция графика выглядит так:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
hostciti.net
График синуса, с примерами построения
График синуса имеет вид как показано на рисунке 1. Кривая, задающая график синуса, называется синусоидой.
Рис. 1
График функции пересекает ось в точках Максимальные значения равные функция принимает в точках а минимальные значения, равные (), в точках График функции возрастает при и убывает при
Примеры решения задач
ПРИМЕР 1| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции Сначала произведем сжатие графика вдоль оси в три раза (уменьшение расстояния от каждой точки графика до оси ординат в три раза), получим график функции (рис. 2).
Рис. 2 Затем, сместив график на 2 единицы вниз, получим искомый график (рис. 3).  Рис. 3 |
| Задание | Построить график функции
|
| Решение | Построим заданный график с помощью элементарных преобразований графика функции Сначала сместим график на влево, получим график (рис. 4).
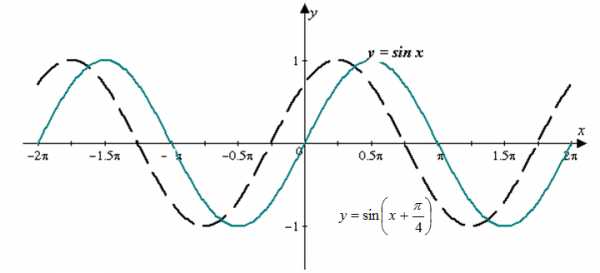 Рис. 4 Затем, сжатием графика в два раза (уменьшением расстояния от каждой точки графика до оси абсцисс в два раза), получим искомый график (рис. 5). 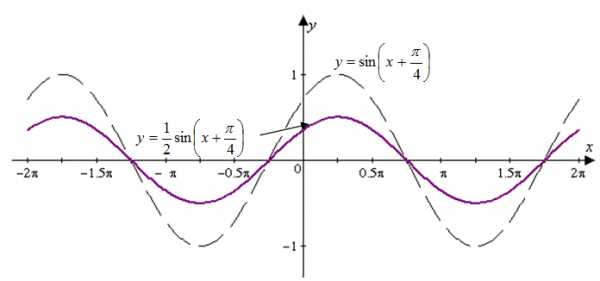 Рис. 5 |
Гиперболический синус
Разность синусов
Произведение синусов
Косинус угла
Косинус 0 градусов
Косинус 30 градусов
Графики тригонометрических функций
ru.solverbook.com
График косинуса, с примерами построения
График косинуса имеет вид как показано на рисунке 1. Кривая, задающая график косинуса, называется косинусоидой.
Рис. 1
График функции пересекает ось в точках Максимальные значения, равные функция принимает в точках а минимальные, равные – при График функции возрастает при и убывает при
Примеры решения задач
ПРИМЕР 1| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси ординат вверх на 1 единицу (рис. 2)
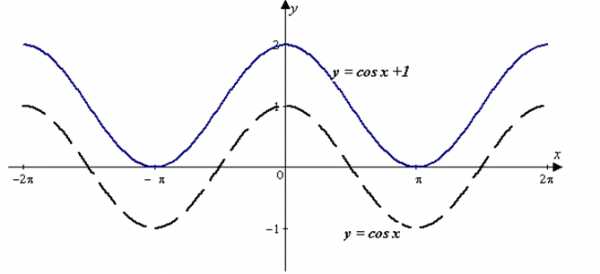 Рис. 2 |
| Задание | Построить график функции |
| Решение | Искомый график получается из графика функции в результате параллельного переноса вдоль оси абсцисс вправо на (рис. 3).
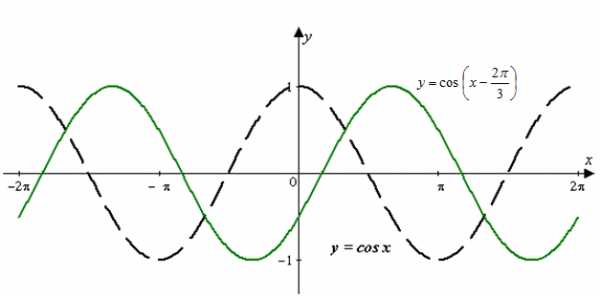 Рис. 3 |
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции Сначала графика функции растянем вдоль оси ординат в три раза (увеличим расстояния от каждой точки графика до оси абсцисс в три раза), получим график функции (рис. 4).
 Рис. 4 Затем, отразим график функции симметрично относительно оси абсцисс, получим искомый график (рис. 5).  Рис. 5 |
Разность косинусов
Косинус суммы
Сумма синусов
Таблица брадиса косинусы
Косинус умножить на косинус (Произведение косинусов)
Тригонометрический круг (окружность)
ru.solverbook.com