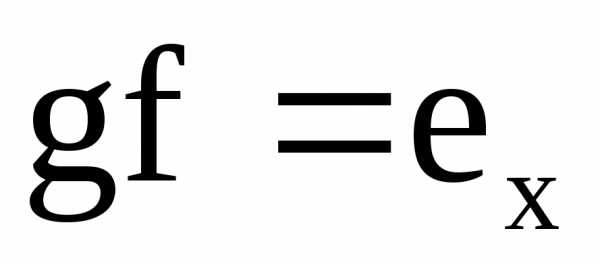§7.Функция (отображение) как бинарное отношение. Область определения и область значения функций. Образ и прообраз подмножества при отображении.
Фундаментальную роль в математике играет понятие функции (отображения), которое является частным случаем функционального отношения.
Определение 1. Бинарное
отношение f
между элементами множеств А и В (то есть
)
называетсяфункциональным
отношением, если 
изи
Из определения 1 следует, что бинарное отношение является функциональным, когда каждому значению первой координаты пары из f соответствует единственная вторая координата, которая обозначается через y=f(x). И говорят в этом случае, что y является функцией от x.
Определение 2. называется областью определения функционального отношения.
Определение 3. Функциональное
отношение f
между элементами множеств А и В называется
Множество А называется областью определения функции, множество В -областью значения функции.
Если y=f(x), то y называется образом при отображении f точки x, а x называется прообразом при отображении f точки y.
Пусть 
,
тогданазываетсяобразом
множества (подмножества) М при
отображении f.
В частности,
образ множества А при отображенииf.
Пусть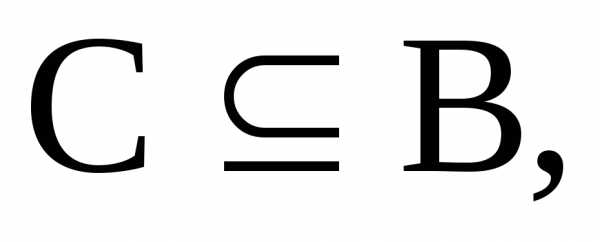 
тогдапрообраз множества С при отображенииf.
В частности,
Примеры: следующие отношения являются отображениями:
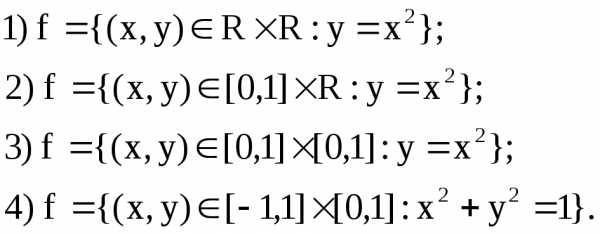
Следующие отображения не являются отображениями:
§8.Композиция функций. Теорема об ассоциативности произведения функций.
Определение 1. Пусть f
и g
– функции, причем g:
A→B,
f:
B→C. Композицией (суперпозицией, произведением) функций
f
и g
называется отображение A
в C,
значением которого для произвольного 
служитf(g(x)).
Обозначение: или , то есть (fg)(x)=f(g(x)).
Определение 2. Отображение иназывается равными тогда и только тогда, когдаf(x)=g(x)
Пример: Пусть и– функции, определяемые следующим образом:
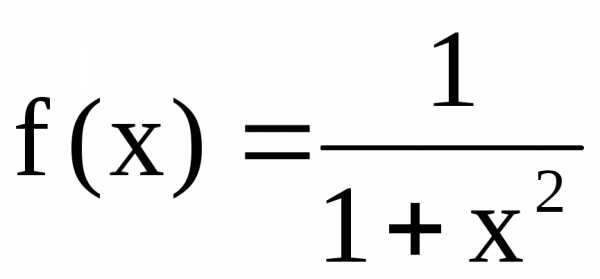; g(x)=1–x.
Тогда
; 
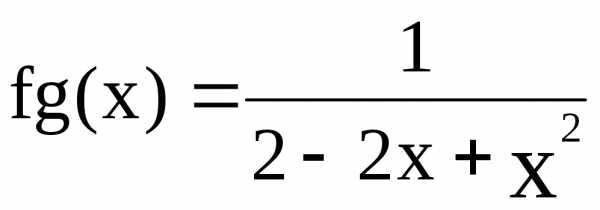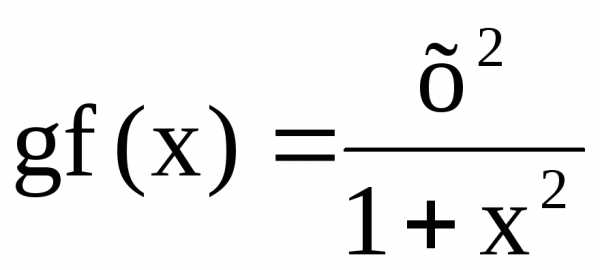
Из примера видно, что .
Теорема 1: Пусть
,и– отображения. Тогда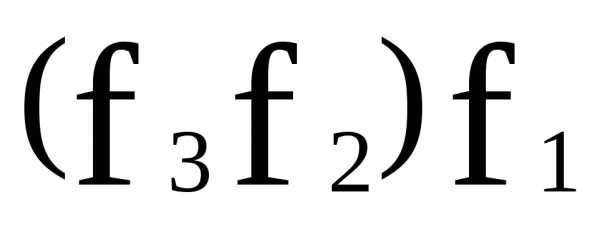 
—
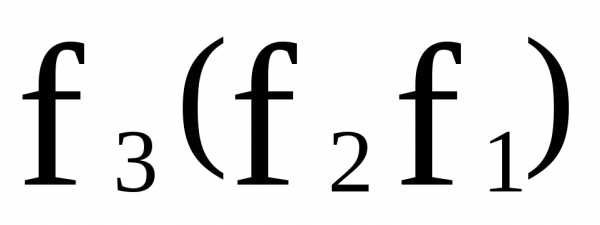отображенияA
в D
, причем (1),
то есть произведения отображений
ассоциативно Доказательство.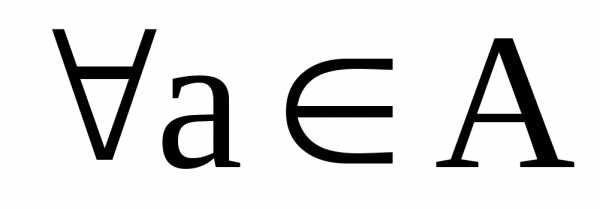 
имеем:
Следовательно, равенство (1) справедливо. Что и требовалось доказать.
§9. Тождественное
отображение множества на себя. Обратимое
отображение. Сюръекция, инъекция,
биекция. Доказательство инъективности f и сюрьективности g,
удовлетворяющих условию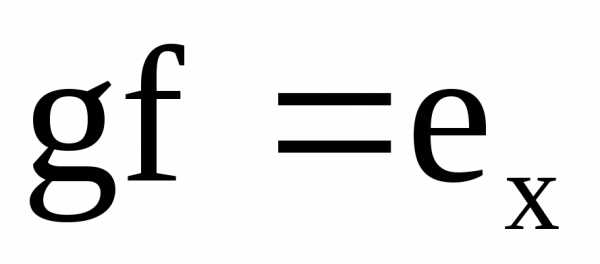 
.
Теорема об обратимом отображении.
Определение 1: Отображение называетсяпреобразованием множества A.
Определение 2: Преобразование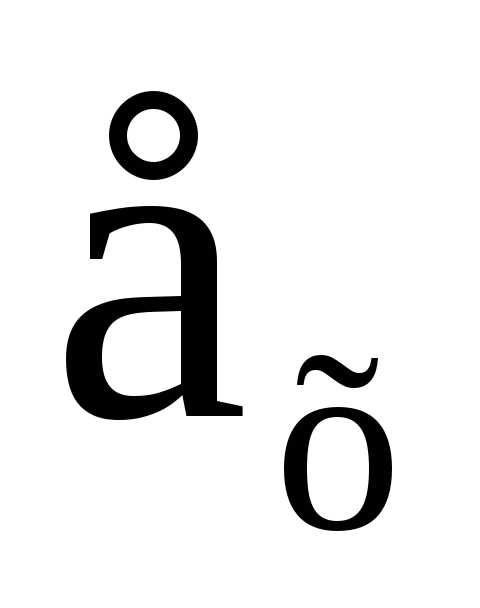 
множестваX
называется тождественным или единичным преобразованием, если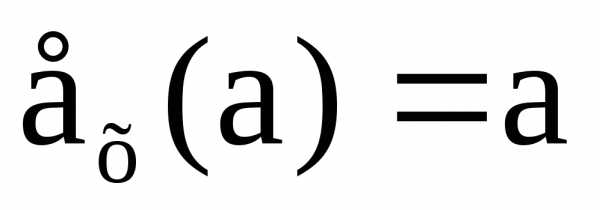 
,
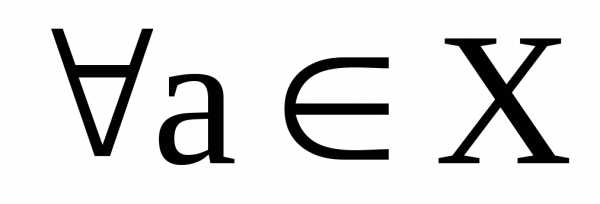то есть преобразование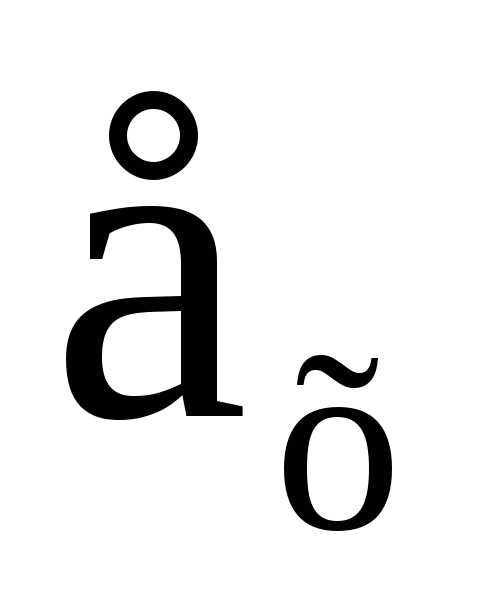
каждую точку изX
переводит в себя.
Определение 3: Пустьи.
Если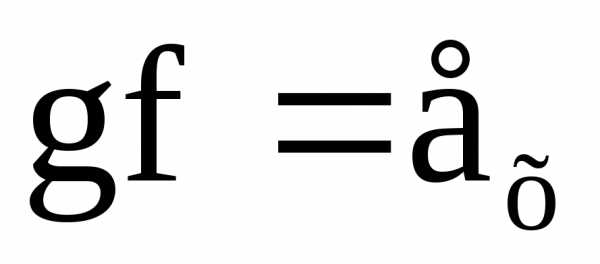
(1) , тоg
называется левым
обратным отображением для f.
Если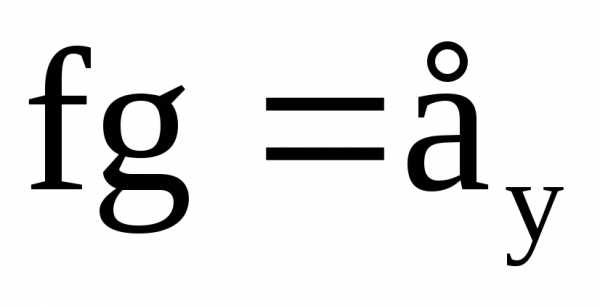 
(2), тоg
называется правым
обратным отображением для f.
Если выполняются равенства (1) и (2)
одновременно, то g
называется обратным
отображением для f.
Если для f
существует обратное отображение g,
то f
называется обратимым отображением
.Обозначение: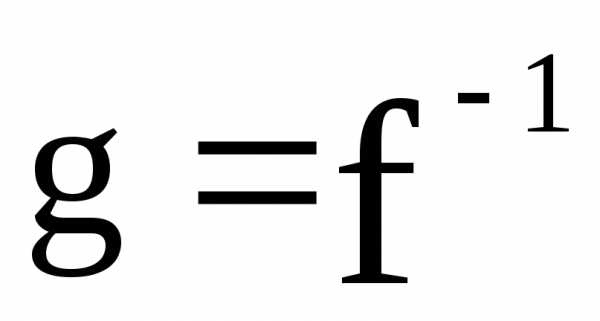 
.
Лемма1. Пусть f
– отображение X
в Y.
Тогда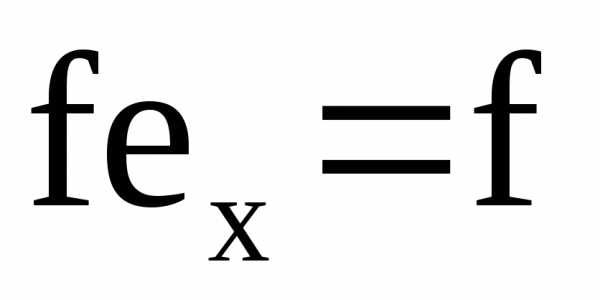 
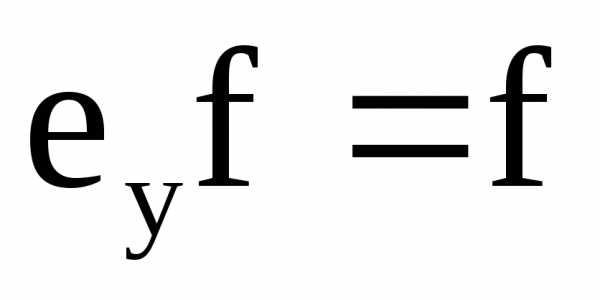.Доказательство. имеем:
.
Аналогично доказывается второе равенство.
Лемма 2. Если обратное отображение для f существует, то оно единственное.
Доказательство: Пусть
и
пусть
и
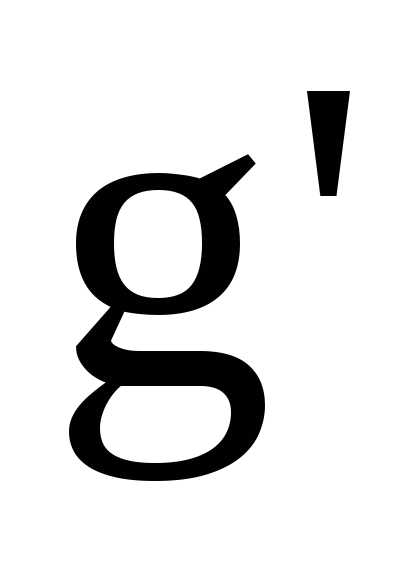– обратные отображения дляf
(здесь
и).
Тогда дляg
и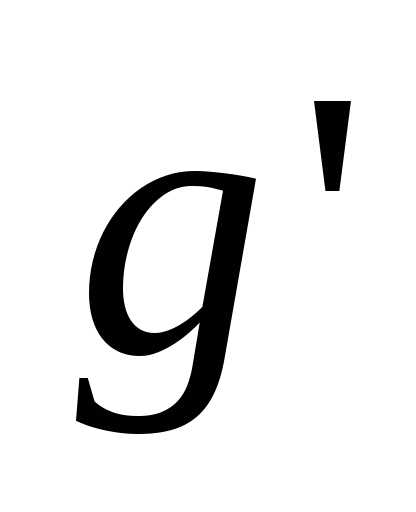 
выполняются равенства:
и (5)
Тогда, по лемме 1,
имеем: то есть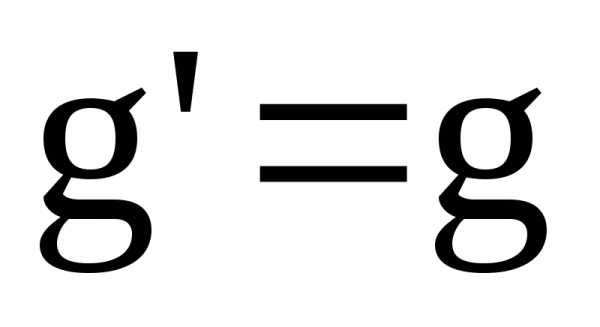 
.
Определение 4. Отображение называетсясюръективным отображением или сюръекцией, если Imf = B. То есть сюръекция – это отображение “на” B,
Определение 5. Отображение , называетсяинъективным отображением (инъекцией) или взаимно однозначным отображением A в B, если из, то есть различные точки изA отображаются при f в различные точки из B.
Определение 6. Отображение называетсябиективным отображением (биекцией) или взаимно однозначным соответствием, если f сюръективно и инъективно.
Лемма 3: Если
ии
(1) , тоf
– инъекция и g
– сюръекция .
Доказательство: Покажем, что f – инъекция.
Пусть
Предположим, что(*). Тогда,,
то есть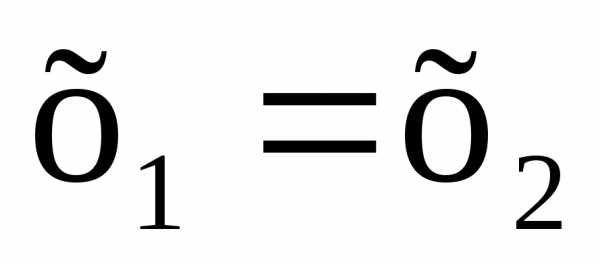
и, значит,f–
инъективно.
Покажем, что g – сюръекция. имеем:
, то есть существуети значит,g — сюръекция.
Теорема 1. Отображение обратимо тогда и только тогда, когдаf – биекция.
Доказательство. 1)Необходимость.
Пусть f
– обратимо, тогда для f
существует обратная функция g: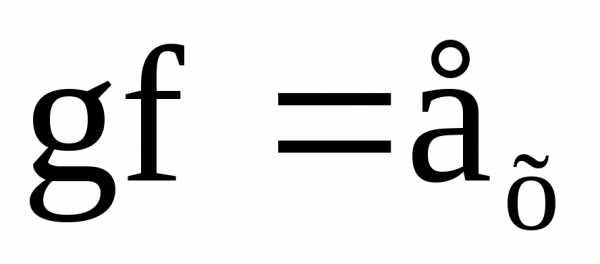 
(1)
и
(2). Из (1) по лемме 3 следует, чтоf
– инъекция. Из (2) по лемме 3 следует, что
f
– сюръекция.
2)Достаточность.
Пусть f
– биекция. Покажем, что f
является обратимым отображением. Так
как f
– биекция, то – f
инъекция (то есть различным точкам х1,
х2
Х
соответствуют различные точки изY)
и f
– сюръекция ( то есть f(Х)=Y
).
Определим новое
биективное отображение g
по правилу 
Покажем, что g
– функциональное отношение, то есть 
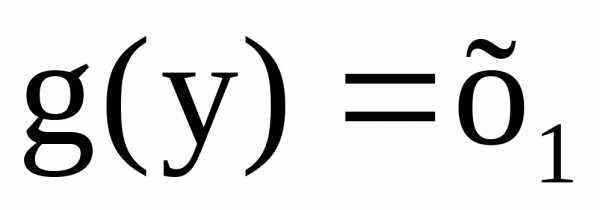и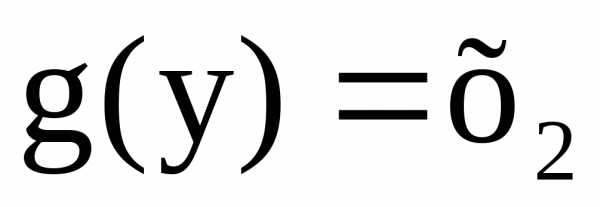
,
где.
Допустим, что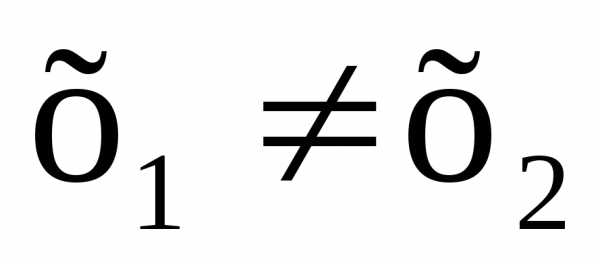
,
тогда из инъективностиf
,
но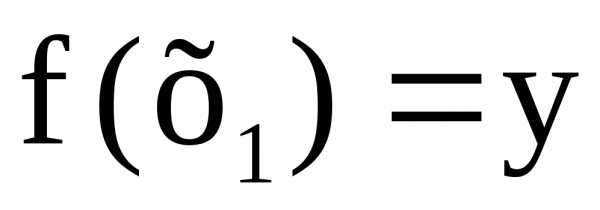
и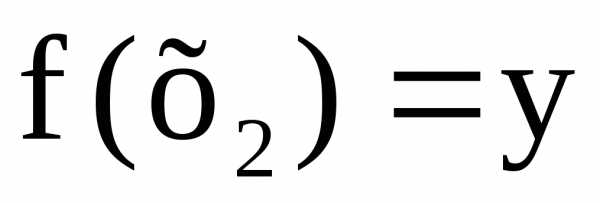
.
Получили противоречие следовательно,х1=х2.Итак, g – функциональное отношение.
Покажем, что
функциональное отношение g
является отображением. Действительно,
так как f
– сюръекция, то 
а, значит, 
Итак, g — отображение.
Теперь необходимо показать, что Действительно,
и
Следовательно, g — обратная функция для f , то есть f – обратима.
СОДЕРЖАНИЕ
Введение.…………………………………………………………………………. | 3 |
§ 1. Понятие множества, подмножества. Равенство множеств………………. | 3 |
§2. Операции над множествами, их свойства………………………………….. | 4 |
§3. Прямое (декартово) произведение множеств. Бинарные (n-арные) отношения, их свойства…………………………………………………………. | 7 |
§4. Область бинарного отношения. Операции над бинарными отношениями. …………………………………………………………………… | 9 |
§ 5. Отношение эквивалентности. Теорема о разбиении множества отношением эквивалентности на классы………………………………………. | 11 |
§6. Отношение порядка и предпорядка. Линейный порядок. Упорядоченные множества. Наибольший (наименьший), максимальный (минимальный) элементы упорядоченного множества…………………….. | 13 |
§7.Функция (отображение) как бинарное отношение. Область определения и область значения функций. Образ и прообраз подмножества при отображении………………………………………………………………… | 15 |
§8. Композиция функций. Теорема об ассоциативности произведения функций………………………………………………………………………….. | 16 |
§9. Тождественное
отображение множества на себя. Обратимое
отображение. Сюръекция, инъекция,
биекция. Доказательство инъективности
f
и сюрьективности g,
удовлетворяющих условию | 17 |
Надежда Владимировна Силенок
МНОЖЕСТВА И ОТНОШЕНИЯ
Методические рекомендации по курсу «Алгебра»
Подписано в печать ___________ 2008 г. Формат 6084 1/16
Печать офсетная. Бумага офсетная.
Усл. п. л. 1,2. Тираж 100 экз. Заказ №______
РИО Брянского государственного университета
Имени академика И. Г. Петровского
studfiles.net
1. Определение функции нескольких переменных. Основные понятия.
Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,)
Область определения функции z — совокупность пар (х,у), при которых функция z существует.
Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения.
График функции двух переменных — множество точек P, координаты которых удовлетворяют уравнению z=f(x,y)
Окрестность точки M0 (х0;y0) радиуса r – совокупность всех точек (x,y), которые удовлетворяют условию<r
2. Область определения и область значений функции нескольких переменных. График функции нескольких переменных. (см1)
3. Предел и непрерывность функции нескольких переменных.
Число А называется пределом функции f(x,y) при стремлении точки М(х,у) к точке М0(х0,уо), если для любого числа Е>0 найдётся такое число r>0, что для любой точки М(х,у), для которых верно условие ММ0<r также верно условие
Записывают:
Пусть точка М0(х0,у0) принадлежит области определения функции f(x,y). Тогда функция z=f(x,y) называется непрерывной в точке М0(х0,у0), если , причём точка М(х,у) стремится к точке М0(х0,у0) произвольным образом.
Если в какой-либо точке условие не выполняется, то эта точка разрыва функции f(x,y). Это может быть в случаях:
Функция z=f(x,y) не определена в точке М0(х0,уо)
Не существует предел в точке М0(х0,уо),
Этот предел существует, но не равно f(х0,уо)
4. Дифференцируемость функции нескольких переменных, частные производные, полный дифференциал.
Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде:, где А1, А2, …, Аm– некоторые не зависящие от ∆х1, ∆х2, …, ∆хm числа, а α1, α2, …, αm – бесконечно малые при функции, равные 0 при ∆х1=∆х2=…∆хm=0.
Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен: =
Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:: =
Полный дифференциал функции z=f(x,y) — главная линейная относительно и ∆у часть приращения функции ∆z в точке (х,у).
dz=(x,y)dx+(x,y)dy
Если функция f(x,y) определена в некоторой области D, то её частные производные f’x(x,y), f’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
5. Экстремум функции двух переменных: необходимое и достаточное условия.
Точка max М0 – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М0(х0,у0), верно неравенство f(x0,y0)≥f(x,y)
Точка min М0 – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М0(х0,у0), верно неравенство f(x0,y0)≤f(x,y)
Необходимое условие: если функция f(x,y) в точке (х0,у0) имеет экстремум, то в этой точке либо обе её частные производные первого порядка равны 0
f´y(x0,y0)=0, f´x(x0,y0)=0,
либо хотя бы одна из них не существует. Эту точку (х0, у0) будут называть критической точкой.
Достаточное условие: пусть в окрестности критической точки (х0,у0) функция f(x,y) имеет непрерывные частные производные до второго порядка включительно.
Рассмотрим выражение:
Если ∆(х0,у0)>0, то в точке (х0, у0) функция f(x,y) имеет экстремум,
Если (x0, y0)<0 – max, если (x0, y0)>0 – min.
Если ∆(х0,у0)<0, то в точке (х0,у0) функция f(x,y) не имеет экстремума.
Если ∆=0, вывод о наличии экстремума сделать нельзя.
studfiles.net
Функция ооф и озф 9 класс
Урок 1. Функция. Область определения и область значений функции.
(длительность урока 90 минут)
Тезисы к уроку изучения нового материала по теме «Функция. Область определения и область значения функции».
Быстро меняется время, меняется время, меняются задачи, стоящие перед школой. Одной из задач является формирование у школьников исследовательских умений. Сейчас почти в каждой российской семье есть компьютер, особенно там, где есть дети, которые учатся.
Решение правительства нашей страны повысить уровень компьютерной грамотности населения выполняется в полной мере.
Предлагаю разработку урока где используются мультимедийные средства.
В процессе изучения нового ученики знакомятся с методами исследования, учатся устанавливать связи вопросов, рассмотренных в течение урока, устанавливают закономерности событий, делают выводы и обобщения.
Использование на уроке презентаций позволяет рационально использовать время урока, способствует активизации внимания и развития памяти.
Цель урока:
Узнать, что означает в математике запись y=f(x), дать определение понятия что такое область определения функции и область значений функции, развивать умение строить графики различных функций и читать их свойства.
1. Организационный момент.
Актуализация знаний.
1) Устная работа.
Дана функция: F(x)=x2-2x;
x -5 -1 0 3 100
F(x) Вычислите: f(-5), f(-1), f(0), f(3), f(100).
Заполните таблицу.
2) На доске построим график какой-либо функции и с помощью графика повторим основные этапы чтения графика.
Построим график функции, заданной формулой: f=x-2a)область определения функции: x≥0; x≥2.
б) Построим таблицу
x 2 6 11 18 27
y 0 2 3 4 5
0
2
xyв) Построим график.
3. Изложение нового материала.
ФУ́НКЦИЯ, в математике — 1) зависимая переменная величина. 2) Соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента, или независимого переменного) соответствует определенное значение другой величины y (зависимой переменной, или функции). Такое соответствие может быть задано различным образом, напр. формулой, графически или таблицей (типа таблицы логарифмов). С помощью функции математически выражаются многообразные количественные закономерности в природе.
Примеры функций:
1.Круг деятельности человека, подлежащая исполнению работа:
Быть учителем, быть штукатуром, быть артистом.
2.Предметы или сложные приборы выполняют свои функции: детские игрушки развивают, сотовый телефон служит средством связи, холст на котором рисует художник.
3.Явления природы, например изменение температуры.
Понятие Ф. введено в научн
educontest.net
§8. Числовая функция. Область определения и область значений функции
Рассмотрим числовые функции, т.е. функции, область определения и область значения которых – числовые множества.
Определение. Пусть X и Y – некоторые числовые множества (X R, Y R). Числовой функцией называется такое соответствие между элементами множеств X и Y , при котором каждому числу х из множества X соответствует не более одного числа у из множества Y.
Функции принято обозначать буквами: f,q,h, и др. В общем случае, элемент y Y, соответствующий элементу x A, называется значением функции f и записывается так: y = f(x).
Сложилась традиция переменную x называть аргументом функции.
Например, X = {1, 2, 3, 4, 5, 6}, Y = {5, 6, 8, 9, 10, 11, 12}. Соответствие f: « х меньше y на 4». Каждому x Î X соответствует не более одного yÎ Y (y =4 + x): 1 ® 5; 2 ® 6; 4 ® 8, 5 ® 9; 6 ® 10, поэтому это соответствие функция.
Из множества X выделим подмножество тех элементов х, для которых есть соответствующий элемент во множестве У . Это множество называют областью (или множеством) определения функции. Его обозначают D(f). В нашем примере D(f) = {1, 2, 4, 5, 6}. Множество всех элементов y Y, которые являются значениями функции f, называются множеством (областью) значений функции (E(f)).
В нашем примере E(f) = {5, 6, 8, 9, 10}.
С учетом этого можно дать другое определение функции.
Определение. Пусть X и Y – некоторые числовые множества (X Í R, Y Í R). Числовой функцией, определенной на X и принимающей значения из Y, называется такое соответствие f, при котором каждому числу x Î X соответствует единственное число y Î Y.
Например, A = {a a N 1 a 8}, B = {3, 5}, соответствие : «а делится на b ».
В
Так как каждому a A соответствует не более одного b B , то это соответствие – функция.
Так как числовая функция – частный случай соответствия, то все способы задания соответствия являются и способами задания функции.
Вспомним их:
1) задание числовой функции путём перечисления всех пар элементов, которые находятся в данном соответствии. Если область определения функции – конечное множество, число элементов которого не очень велико, то такую функцию можно задать путем перечисления всех пар соответственных элементов.
Отношение q, заданное перечислением пар, является функцией, если оно не содержит двух разных пар с одинаковыми первыми элементами.
б) задание числовой функции графом.
Соответствие j в примере 2 задано графом.
Соответствие, заданное графом, является функцией, если граф не содержит двух разных стрелок с общим началом.
в) графический способ задания числовой функции.
Если функция задана перечислением пар, то в декартовой системе координат каждую пару можно изобразить точкой. Множество построенных точек и называют графиком функции. Построим график функции q.
График соответствия, которое является функцией, не содержит двух разных точек с одинаковой абсциссой.
г) задание числовой функции указанием характеристического свойства.
Примерами являются примеры 1, 2.
Частный случай: задание числовой функции формулой.
Если область определения функции, заданной формулой, явно не указана и нет каких-либо дополнительных ограничений, то считают, что функция определена на множестве всех тех значений аргумента, при которых все указанные в формуле операции выполнимы.
Например, характеристическое свойство в примере 1 можно записать в виде уравнения с двумя переменными:
у = 4 + х, т.е. в виде формулы.
От одного способа задания функции можно переходить к другому.
studfiles.net
График показательной функции, область определения и область значений функции — Алгебра 11 класс — Osvita.name
1. Функция y=3x−1 образована от показательной функции y=3x (показательной функцией называется функция, которая записана в виде y=ax, где (a>0, a≠1). Чтобы построить график этой функции, необходимо составить следующую таблицу с произвольно выбранными значениями аргумента x:
| x | −2 | −1 | 0 | 1 | 2 |
| y |
2. Чтобы вычислить соответствующие значения функции, необходимо подставить соответствующие значения аргумента x в формулу функции y=3x:
a) y=3−2=132=19
б) y=3−1=131=13
в) y=30=1
г) y=31=3
д) y=32=9
3. Вычисленные значения функции записываем в таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 19 | 13 | 1 | 3 | 9 |
4. Используя таблицу, строим график функции y=3x:
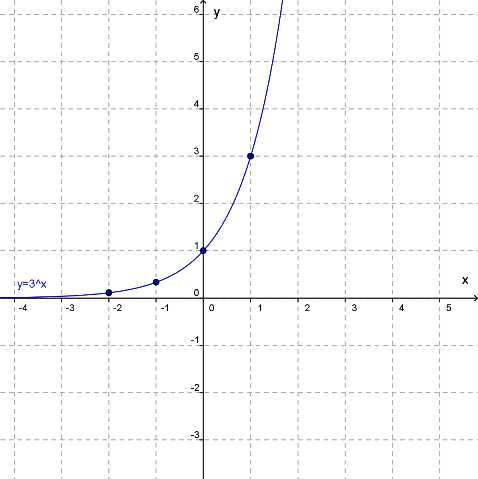
5. Функцию y=3x−1 можно записать в виде y=f(x)+a, где a≠0.
* Если a>0, то график функции y=f(x) переместится вдоль оси Oy на a единиц вверх.
* Если a<0, то график функции y=f(x) переместится вдоль оси Oy
osvita.name