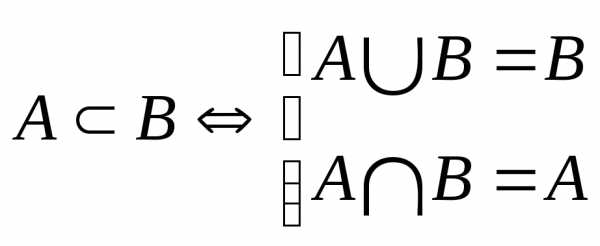
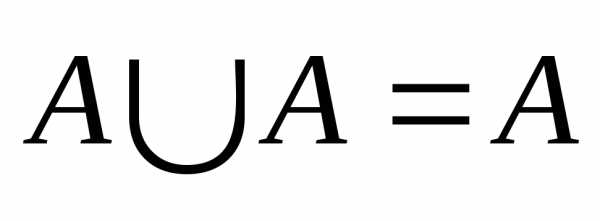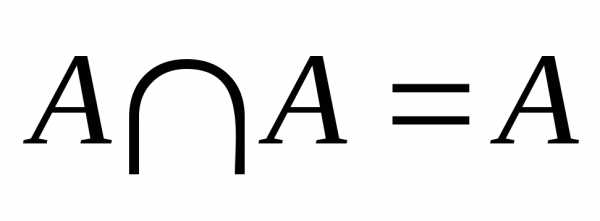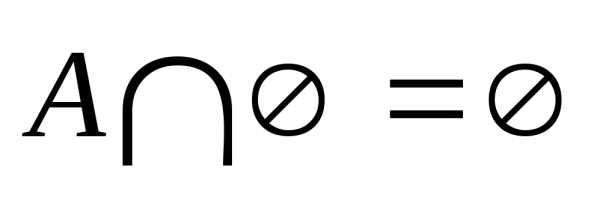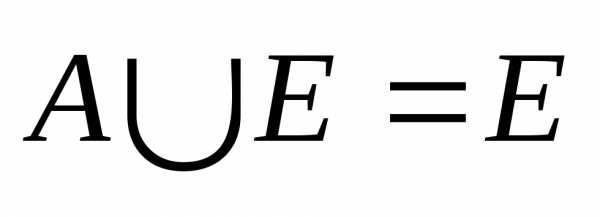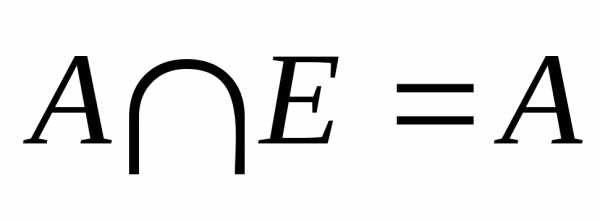1.2. Основные операции над множествами
Объединением множеств А и В называется множество АВ, все элементы которого являются элементами множества А или множества В:
АВ={x:xA или хВ},
где – знак объединения.
На диаграмме Эйлера это может быть показано штриховкой (рис. 2).
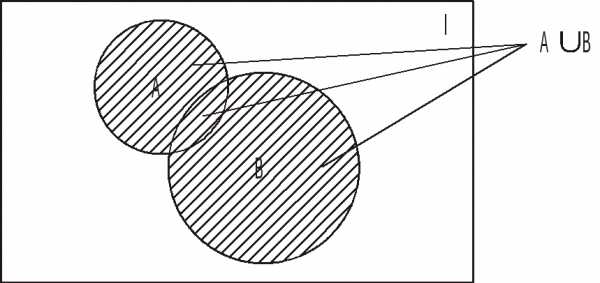
Рис. 2. Объединение множеств АВ
Пересечением множеств А и В называется множество АВ, элементы которого являются элементами обоих множеств:
АВ={x:xA и хВ},
где – знак пересечения.
Соответствующая диаграмма Эйлера изображена на рис. 3.
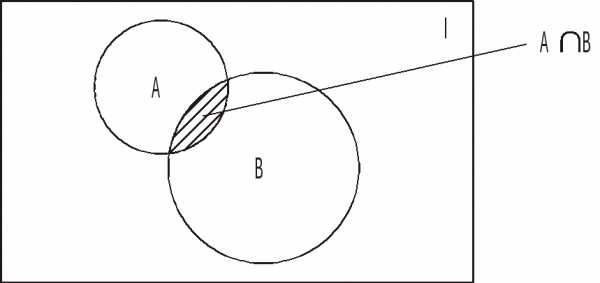
Рис. 3. Пересечение множеств АВ
Разностью множеств А и В называется множество А\В, состоящее из элементов, принадлежащих множеству А и не принадлежащих множеству В:
А\В={x:xA и хВ},
где – знак непринадлежности (отрицание принадлежности), \ – знак разности.
Соответствующая диаграмма Эйлера изображена на рис. 4.
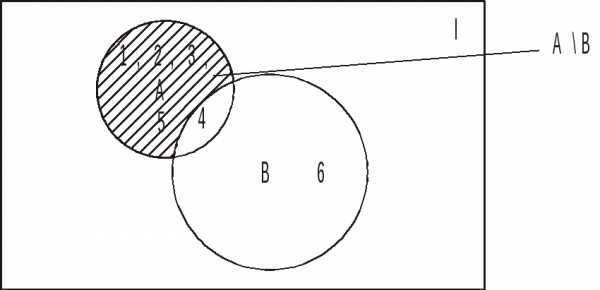
Рис. 4. Разность множеств А\В
Так, если А={1,2,3,4,5}, В={4,6}, то А\В={1,2,3,5}, В\А={6}.
Симметрической разностью множеств А и В называется множество АВ=(А\В)(В\А), изображенное на рис. 5, – знак симметрической разности.
Так, если А={1,2,3}, В={3,4,5}, то АВ={1,2,4,5}.
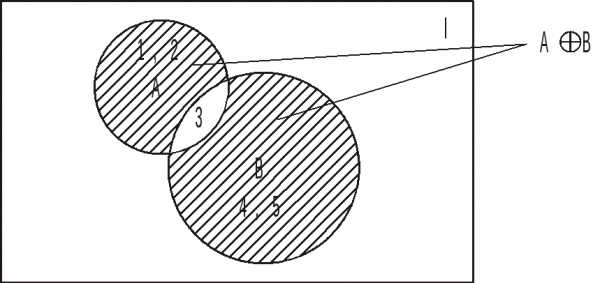
Рис. 5. Симметрическая разность множеств АВ
Рассмотренные операции являются двухместными (бинарными). Имеется одноместная (унарная) операция дополнения.
Дополнением множества А является множество  ,
содержащее элементы универсума I, не
включенные во множество А:
,
содержащее элементы универсума I, не
включенные во множество А:
где – знак дополнения, «инверсия», читается «не А».
Соответствующая диаграмма Эйлера изображена на рис. 6.
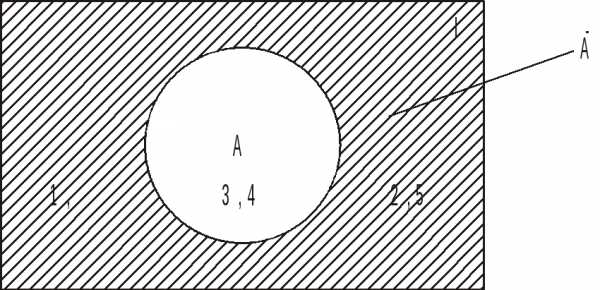
Рис. 6. Дополнение множества А до универсума I
Так, если А={3,4}, а I={1,2,3,4,5}, тоA={1,2,5}.
Используя рассмотренные операции, можно выражать одни множества через другие, при этом сначала выполняется одноместная операция дополнения, затем пересечения и только потом – операция объединения (разности). Для изменения порядка выполнения операций в выражении используют скобки.
1.3. Декартово произведение множеств
Одним из важных понятий теории множеств является понятие декартова произведения множеств.
Декартовым произведением АВ множеств А и В называется множество М вида
М={(ai,bj):aiA, bjB}.
Здесь круглыми скобками () обозначается последовательность, т.е. множество, в котором зафиксирован порядок элементов (упорядоченное множество). Другое название такой последовательности – вектор (кортеж). Элементы, образующие вектор, называются координатами или компонентами, нумеруемыми слева направо. Векторы длины 2 часто называют упорядоченными парами, длины 3 – тройками и т.д. Вектор U длины n иногда называют n-кой («энкой»). Проекцией прiU вектора U называется его i-я компонента. Таким образом, М=АВ это множество пар.
В частности, если А=В, то обе координаты принадлежат одному множеству А2 (В2).
Аналогично понятию декартова произведения двух множеств определяется декартово произведение n множеств:
1.4. Соответствия и функции
Соответствием между множествами А и В называется подмножество их декартова произведения GА·В.
Если (а,b)G, то b соответствует а при соответствии G. Множество проекций пр1G называется областью определения соответствия, множество пр2G – областью значений соответствия. Если пр2G=А, то соответствие полностью определенное (в противном случае – частичное). Если пр2G=В, то соответствие сюрьективно.
Множество всех bВ, соответствующих элементу а, в А называется образом а в В при соответствии G. Множество всех а, которым соответствует b, называется прообразом b в А при соответствии G.
Подмножество FX·Y называется функцией, если для каждого элемента х, хХ найдется не более одного элемента yY в парах вида (х,y)F. При этом, если для каждого элемента х имеется один элемент y, то функция полностью определена, в противном случае – частично определена (недоопределена). Множество Х – область определения функции F, множество Y – область значений функции. Часто вместо записи (х,y)F используют запись y=F(х), при этом элемент х называют аргументом или переменной, а y – значением функции F. Количество аргументов определяет местность функции.
Сопоставим с декартовым произведением двух множеств прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения [9-10].
На рис. 7а изображено подмножество декартова произведения множеств Х={х1
,х2,х3,х4} и Y={y1,y2,y3}, не являющееся функцией, на рис. 7б – являющееся полностью определенной функцией; на рис. 7в – являющееся частично определенной функцией.а) F1XY, не являющееся функцией, т.к. одному значению х может соответствовать два значения y. | б) F2XY, являющееся полностью определенной функцией. | в) F3XY, являющееся недоопределенной функцией, не определенной на значении аргумента х3. |
Рис.7. Подмножества декартова произведения XY
Соответствие G между множествами Х и Y называется взаимно однозначным, если каждому элементу хХ соответствует определенный элемент yY, и, наоборот, каждый элемент yY оказывается поставленным в соответствие одному элементу хХ.
Соответствие между множеством функций и множеством чисел называется функционалом [19]. Часто говорят «функционал качества».
Например, функционалом может быть определенный интеграл, ставящий в соответствие некоторой функции число.
Соответствие между двумя множествами функций называется оператором. Например, имеется оператор дифференцирования.
Множество А называется эквивалентным множеству В, если существует взаимнооднозначное соответствие множеств А и В, это обозначается как
А=В или АВ.
Этот факт позволяет определять неизвестную мощность одних множеств по известной мощности других, им эквивалентным. Множества, эквивалентные (равномощные) множеству натуральных чисел, называются счетными. В счетных множествах возможна нумерация элементов. Пример множества, не являющегося счетным – множество всех действительных чисел отрезка [0,1]. Это доказывается теоремой Кантора [19]. Попробуем пронумеровать это множество. Расположим все числа, изображенные бесконечными десятичными дробями в порядке нумерации:
0, а11 а12 а13 …
0, а21 а22 а23 …
0, а31 а32 а33 …
. . . . . .,
где первая цифра индекса – номер бесконечной десятичной дроби. Рассмотрим теперь любую бесконечную десятичную дробь 0, b1 b2 b3… такую, что b1а11, b2а22, b3а33 и т.д. Такая дробь не входит в указанную последовательность, так как отличается от первого числа первой цифрой, от второго числа – второй цифрой и т.д. Следовательно, все числа из отрезка [0,1] не могут быть пронумерованы, т.е. это множество несчетно. Его мощность называется континуум и все эквивалентные ему множества называются континуальными. Так, множество всех подмножеств счетного множества континуально.
studfiles.net
Тема 1. Множества и операции над ними
Содержание
Понятие множества и элемента множества.
Способы задания множества.
Отношения между множествами. Подмножества.
Изображение отношений между множествами при помощи кругов Эйлера.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 2, 31, 82, 87, 92
Введение
Успешное обучение математике младших школьников требует от учителя не только мастерства, но и глубокого понимания сути математических понятий и факторов. Дело не только в том, что в начальных классах закладываются основы таких важнейших понятий, как «число» и «величина», происходит ознакомление с элементами буквенной символики и геометрии, развиваются логические умения, но и в том, что многие математические понятия младшие школьники используют без строгих определений, а во многих случаях и неявно. Все это предъявляет особые требования к математической подготовке учителя начальных классов. Он должен владеть понятиями натурального числа и величины, знать различные определения арифметических действий над числами, их свойства, уметь выполнять и объяснять устные и письменные вычисления, обосновывать выбор действия и устанавливать вид зависимости между величинами при решении текстовых задач. Учителю необходимо и умение использовать уроки математики для воспитания учащихся, в частности для формирования у них основ научного мировоззрения.
Математика, как и другие науки изучает окружающий нас мир, природные и общественные явления, но изучает лишь их особые стороны. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие их свойства: цвет, массу, твердость. От всего этого отвлекаются, абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят: «Геометрическая фигура».
Результатом абстрагирования являются и такие важнейшие математические понятия, как «число» и «величина».
Вообще, любые математические объекты – это результат выделения из предметов и явлений окружающего мира количественных и пространственных свойств и отношений и абстрагирования их от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических фигур, чисел и т.д. Все они созданы человеческим умом в процессе исторического развития общества и существуют лишь в мышлении человека.
Более того, при образовании математических объектов происходит не только абстрагирование от многих свойств предметов, но и приписывание им таких свойств, которыми никакие реальные предметы не обладают. Например, свойство неограниченной протяженности в обоих направлениях – прямой не обладает ни какой реальный предмет.
Эта лекция будет посвящена одному из таких математических объектов — понятию множества.
1. Понятие множества и элемента множества
Множество – одно из основных понятий современной математики, используемое почти во всех ее разделах.
Во многих вопросах приходится рассматривать некоторую совокупность элементов как единое целое. Так, биолог, изучая животный мир и растительный мир данной области, классифицирует все особи по видам, виды по родам. Каждый вид является некоторой совокупность живых существ, рассматриваемой как единое целое.
Для математического описания таких совокупностей и было введено понятие множества. По словам одного из создателей теории множеств – немецкого математика Георга Кантора (1845–1918), «множество есть многое, мыслимое нами как целое». Разумеется, эти слова не могут рассматриваться как математически строгое определение множества, такового определения не существует, поскольку понятие множества является исходным, на основе которого строятся остальные понятия математики. Но из этих слов ясно, что можно говорить о множестве чисел от 1 до 10, натуральных числах, множестве треугольников и квадратов на плоскости.
Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве учащихся некоторого класса, о множестве гласных букв русского алфавита, о множестве натуральных чисел.
Математический смысл слова «множество» отличается от того, как оно используется в обычной речи, где его связывают с большим количеством предметов. В математике этого не требуется. Здесь рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
В основном множества обозначают буквами латинского алфавита: A, B, C, …, Z, L.
Определение. Множество, не содержащее ни одного объекта, называют пустым и обозначают знаком .
Определение. Объекты, из которых образовано множество, называют его элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, …, z.
В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что число 5 натуральное. Другими словами, число 5 принадлежит множеству натуральных чисел. Или, например, число 0,45 не является натуральным числом. Это означает, что число 0,45 не принадлежит множеству натуральных чисел.
Предложение вида “ Объект а принадлежит множеству А” можно записать, используя символы: аА. Прочитать его можно по-разному:
Объект а принадлежит множеству А.
Объект а – элемент множества А.
Множество А содержит элемент а.
Предложение “ Объект а не принадлежит множеству А” можно записать так: а А. Его читают:
Объект а не принадлежит множеству А.
Объект а не является элементом множества А.
Множество А не содержит элемента а.
Пример
Пусть А – множество однозначных чисел. Тогда предложение “7А” можно прочитать: “Число 7 однозначное”, а запись “ 14 А” означает: “Число 14 не является однозначным”.
Множества бывают конечными и бесконечными. Так, множество дней недели конечно, а множество точек прямой бесконечно. Бесконечными множествами являются и такие множества, как множество натуральных чисел (N), множество целых чисел (Z), множество рациональных чисел (Q), множество действительных чисел (R).
studfiles.net
Лекция 1.Множества. Операции над множествами
Дискретная математика — область математики, в которой изучаются свойства структур конечного характера, а также бесконечных структур, предполагающих скачкообразность происходящих в них процессов или отделимость составляющих их элементов.
Список литературы:
Яблонский С.В. — Введение в дискретную математику
Белоусов А.И. — Дискретная математика
Капитонова Ю.В. и др. – Лекции по дискретной математике
Судоплатов С.В., Овчинникова Е.В. — Элементы дискретной математики
Хаггарти Р. Дискретная математика для программистов
Зайцева С.С. Дискретная математика
К разделам дискретной математики обычно относятся: теория множеств, комбинаторика, общая алгебра, теория графов, математическая логика, теория алгоритмов, теория автоматов, теория кодирования и т.д.
1. Множества. Операции над множествами.
1.1. Множество. Способы задания множеств.
Дискретная математика изучает в основном конечные множества и операции на них.
В 1872 г. Георг Кантор, создатель теории множеств, дал следующие определения для множества:
Множество – это объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью.
Множество – это определенная совокупность объектов. Эти объекты называются элементами множества.
Множества обозначаются прописными буквами латинского алфавита: A, B, X, Y, A1, A2, …, элементы множеств – строчными буквами: a, b, x, y, a1, a2, … .
Числовые множества:
N — множество всех натуральных чисел;
N0 — множество неотрицательных целых чисел
Z -множество целых чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел;
R — множество действительных чисел;
C — множество комплексных чисел;
Символ обозначает принадлежность.
Запись 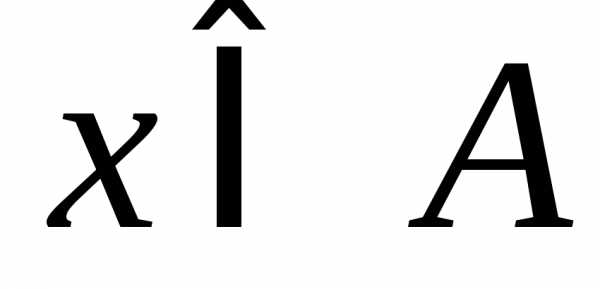 означает, что элементx принадлежит множеству A.
означает, что элементx принадлежит множеству A.
Если
элемент x не принадлежит множеству A,
то пишут 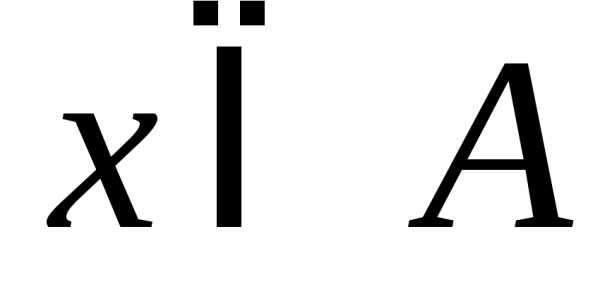 .
.
Множества бывают:
конечные; частный случай – единичное (одноэлементное) множество, например, множество преподавателей в этой аудитории, или множество десятичных цифр;
бесконечные; пример – множество натуральных чисел;
пустое (Ø).
Пустым множеством называют множество, не содержащее ни одного элемента.
Способы задания (описания) множеств:
1) Множество A определяется непосредственным перечислением всех своих элементов a1, a2, …, an, т.е. записывается в виде: A=a1, a2, …, an. При задании множества перечислением обозначения элементов обычно заключают в фигурных скобках и разделяют запятыми.
Перечислением можно задавать только конечные множества.
2) Множество A определяется как совокупность тех и только тех элементов из некоторого основного множества T, которые обладают общим свойством P(x). В этом случае используется обозначение , т.е. элементы множества задаетсяхарактеристическим предикатом (условием).
Характеристическим предикатом можно задать как конечные, так и бесконечные множества.
3) Множество A можно задать порождающей процедурой (рекурсивное задание, задание алгоритмом). Используется обозначение .
Порождающая процедура – это процедура, которая в процессе работы порождает некоторые объекты, являющиеся элементами определенного множества.
Пример .. – множество натуральных чисел от 1 до 4. Множество заданоперечислением всех своих элементов. Причем, элемент 3A, а 5A.
Пример .. M=C, C++, Java, C# – множество языков программирования, имеющих С-подобный синтексис. Задано перечислением.
Пример .. Множество A из примера 1.1. можно задать характеристическим предикатом .
Пример .. Зададим рекурсивно множество X алгоритмом:
1) 3X;
2)
если xX,
то элемент 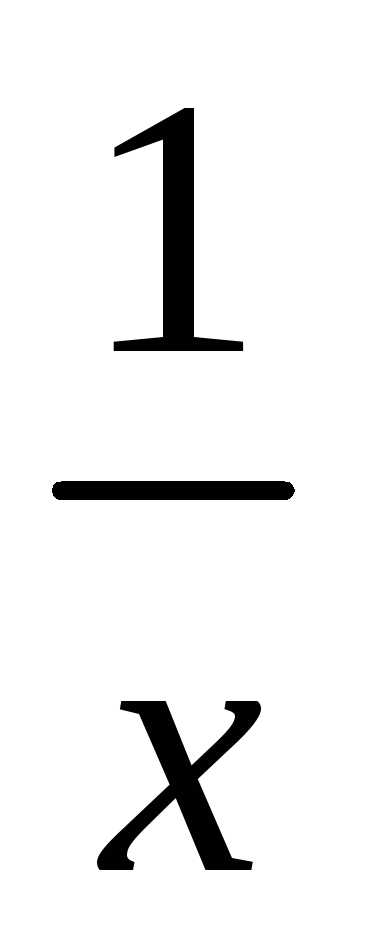 и (1x)
принадлежат X;
и (1x)
принадлежат X;
3) других элементов в X нет.
Заметим, что это множество – конечное, и его можно было задать выписыванием его элементов
.
Частным случаем рекурсивного задания множества является способ задания, основанный на процедуре, называемой математической индукцией. Рассмотрим его на примере задания множества натуральных чисел.
Пример .. Множество N задается следующими правилами:
1) задается базис индукции (исходный элемент):
1N;
2) указывается индуктивный переход:
если nN, то (n+1)N;
3) устанавливается правило замыкания:
других элементов, кроме построенных правилами 1 и 2, в N нет.
Задача: Определить различными способами множество М2n-1 всех нечетных чисел, не превышающих 10.
1.2. Подмножество. Равенство множеств.
Универсум. Булеан.
Определение 1.1. Множество A называется подмножеством множества B (обозначается AB), если каждый элемент A есть элемент B, т.е. если xA, то xB.
Символ обозначает отношение включение между множествами.
Пример .. Пусть 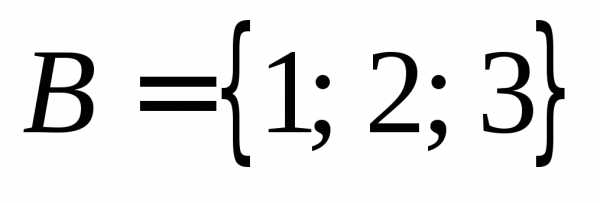 и.
ТогдаBA.
и.
ТогдаBA.
Но .
В частности, каждое множество есть подмножество самого себя, т.е. AA.
Определение 1.2. Пусть A и B – некоторые множества. Говорят, что A равно B, и пишут A=B, если для любого x имеем: xA тогда и только тогда, когда xB.
Иначе говоря, A=B тогда и только тогда, когда AB и BA.
Если AB и AB, то это записывается AB, и говорят, что A есть собственное подмножество B. Пустое множество есть подмножество любого данного множества A, т.е. A.
Таким образом, доказательство равенства двух множеств A и B состоит из двух этапов:
1) Доказать, что A есть подмножество B.
2) Доказать, что B есть подмножество A.
Определение 1.3. Универсальное множество U (или универсум) есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.
В теории чисел универсальное множество обычно совпадает с множеством всех целых или натуральных чисел. В математическом анализе универсальное множество может быть множество всех действительных чисел или множество всех точек n-мерного пространства.
Следует отметить, что универсальное множество U, хотя, и названо универсальным, однозначно не определено, если точно не указана область рассмотрения (предметная область). Конечно, любое множество, содержащее U, может быть использовано как универсальное множество.
По определению, каждое множество есть подмножество универсального множества.
Пример .. Так, для множества за универсум можно взять множество натуральных чисел, т.е.U=N.
Определение 1.4. Булеаном множества A (обозначается (A)) называется множество, состоящее из всех подмножеств множества A.
Пример .. Пусть 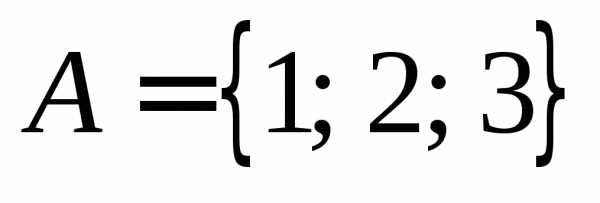 .
.
Следовательно, булеан множества A есть множество (A)=.
Множество A из примера 1.8. содержит три элемента, а булеан (A) состоит из 23=8 элементов. В общем случае, если множество A содержит n элементов, множество (A) включает 2n элементов, т.к. A имеет 2n подмножеств.
По этой причине (A) часто обозначают через 2A.
1.3. Операции над множествами.
Множество часто задают графически с помощью диаграмм Эйлера Л. Эйлер (1707-1783) – швейцарский математик, механик и физик.
Например, задание множеств M1=a, b, c, d и M2=a, c, e, f приведено на рисунке, где замкнутые линия, называемые кругами Эйлера, ограничивают элементы одного множества.
В дальнейшем графическое изображение множеств было плодотворно исследовано Дж. Венном (1834-1923), создавшим диаграммную теорию изучения множеств различной природы.
Диаграммы, задающие множества, принято называть диаграммы Эйлера-Венна.
Если имеются некоторые множества, то из них можно получать новые с помощью определенных операций. Для наглядного изображения операций над множествами воспользуемся диаграммами Эйлера-Венна.
Определение 1.5. Объединением множеств A и B называется множество, (которое обозначается AВ) состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В.
Пример .9. Пусть , .
Тогда .
Определение 1.6. Пересечением множеств А и В называется множество, (которое обозначается АВ) которое состоит из общих элементов этих множеств.
Пример .10. Пусть ,. Тогда.
Определение 1.7. Разностью множеств А и В называется множество, (которое обозначается А\В) всех тех и только тех элементов множества А, которые не принадлежат В.
Определение 1.8. Симметрическая разность множеств А и В (обозначается А∆В) есть множество (А\В)(В\А).
Пример .11. Пусть ,.
Тогда ,,
.
Определение
1.9. Дополнением
множества А (обозначается  )
–это
множество элементов универсума, которые
не принадлежат А, т.е.
)
–это
множество элементов универсума, которые
не принадлежат А, т.е. 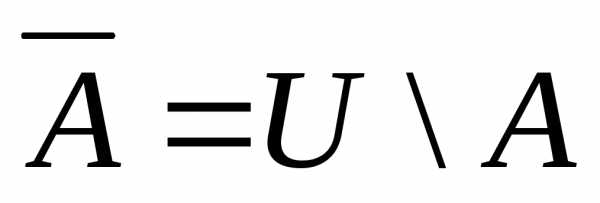 .
.
Пример .12. Пусть.
Тогда,
если
,
то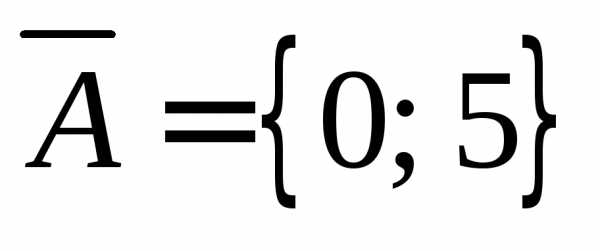 .
.
Операции пересечения и объединения допускают следующее обобщение.
Пусть
задано семейство множеств 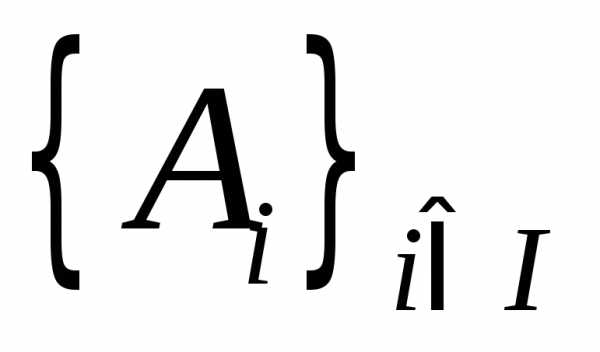 ,
где.
Тогда
,
где.
Тогда
Операции над множествами обладают рядом важных свойств.
Теорема 1.1. Пусть задан универсум U. Тогда A, B, C U выполняются следующие свойства:
1. Свойства коммутативности: АВ=ВА
АВ=ВА
2. Свойства ассоциативности: А(ВС)=(АВ)С
А(ВС)=(АВ)С
3. Свойства дистрибутивности: А(ВС)=(АВ)(АС)
А(ВС)=(АВ)(АС)
4. Свойства тождества: А=А А=
АU=U АU=А
5. Законы идемпотентности: АA=A
АA=A
6. Свойства поглощения: А(АВ)=А
А(АВ)=А
7. Двойное дополнение: 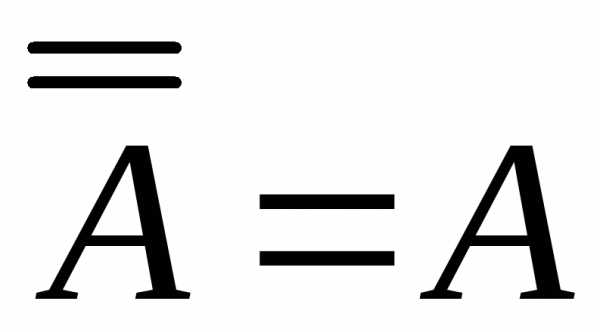
8.
Свойства дополнения: А =U
=U
А =
=
9. Законы
де Моргана: 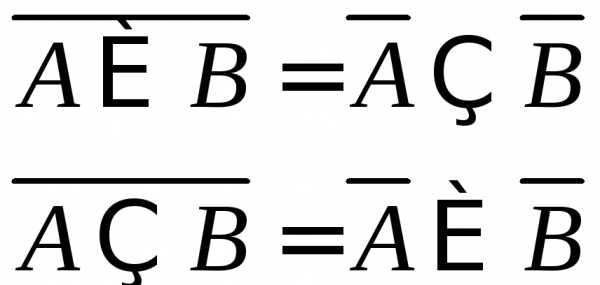
Кроме того, .
Докажем свойство дистрибутивности относительно :
А(ВС)=(АВ)(АС).
Доказательство.
Пусть M= А(ВС) и K=(АВ)(АС).
1) Докажем, что MK.
Пусть элемент xM, тогда либо xA, либо x(ВС).
Если xA, то x(АВ) и x(АС). Значит x(АВ)(АС), т.е. xK.
Если x(ВС)., то xВ и xС. Значит x(АВ) и x(АС). Т.о. x(АВ)(АС), т.е. xK.
Значит, MK.
2) Докажем, что KM.
Пусть элемент xK, тогда x(АВ)(АС).
Это возможно только тогда, когда и x(АВ) и x(АС).
Здесь возможны 2 варианта.
xA. Но тогда получаем, что xА(ВС), т.е. xM.
xA. Но тогда получаем, что и xВ и xС. Т.е. x(ВС). Но это значит, что xА(ВС), т.е. xM.
Значит, KM.
3) Так как MK и KM, то M=K, то есть А(ВС)=(АВ)(АС).
Остальные тождества доказываются аналогично.
Определение
1.10. Покрытием множества A называется набор подмножеств 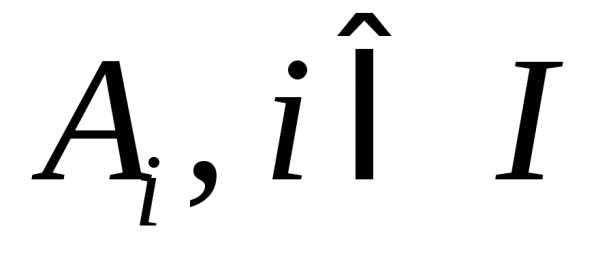 ,
гдеI – некоторое множество индексов, если
каждый элемент A принадлежит хотя бы одному из Ai.
,
гдеI – некоторое множество индексов, если
каждый элемент A принадлежит хотя бы одному из Ai.
Пример .3. Пусть A=, , , .
Тогда , , , , , является покрытием множества A.
Определение
1.11. Разбиением множества A называется набор его попарно
непересекающихся подмножеств 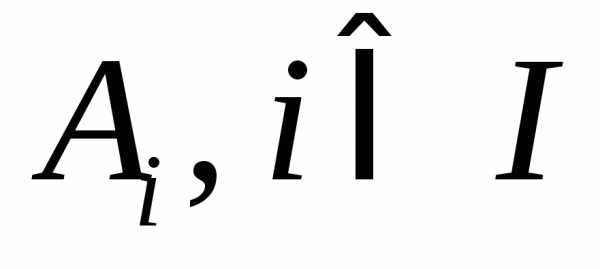 ,
гдеI – некоторое множество индексов.
,
гдеI – некоторое множество индексов.
— разбиение множества A, если выполняются два условия:
1) ;
2) 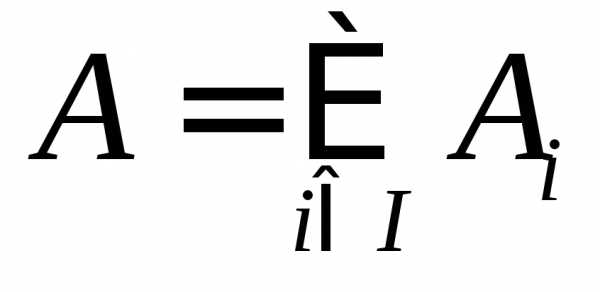 ,
т.е.aA тогда и только тогда, когда aAi для некоторого iI.
,
т.е.aA тогда и только тогда, когда aAi для некоторого iI.
Пример .. Пусть A=, , , .
Тогда множество A=, , , является разбиением множества A.
Всего возможны 17 вариантов разбиения множества A.
studfiles.net
Тема 2. Операции над множествами
Содержание
Пересечение множеств.
Объединение множеств.
Законы пересечения и объединения множеств.
Вычитание множеств. Дополнение одного множества до другого.
Понятие разбиения множества на классы.
Декартово произведение множеств.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 82, 87, 92
1. Пересечение множеств
Из элементов двух и более множеств можно образовать новые множества. Считают, что эти новые множества являются результатомопераций над множествами.
Пример
Пусть даны два множества: А = 2, 4, 6, 8 и В = 5, 6, 7, 8, 9.
Образуем множество С, в которое включим общие элементы множеств А и В: С = 6, 8 . Так, полученное множество С называют пересечением множеств А и В.
Определение. Пересечением множеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А В. Тогда определение можно представить в символической записи:
х х и х .
Если изображать множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной частью.
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А В = .
Замечание. Операция, при помощи которой находят пересечение множеств, называется также пересечением
Если элементы множеств А и В перечислены, то, чтобы найти АВ, достаточно перечислить элементы, которые принадлежат А и В, т.е. их общие элементы.
Если множества заданы при помощи характеристических свойств элементов, то характеристическое свойство множества А В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».
Пример
Найдем пересечение множества А – четных натуральных чисел и множества В – двузначных натуральных чисел.
Характеристическое свойство элементов множества А – «быть четным натуральным числом», характеристическое свойство элементов множества В – «быть двузначным натуральным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четным и двузначным натуральным числом». Таким образом, множество А В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 АВ, поскольку число 24 четное и двузначное.
Пример
Найти пересечение множества А – четных натуральных чисел и множества В – натуральных чисел, кратных 4. Данные множества А и В бесконечные, и множество В – подмножество множества А. Поэтому элементами, принадлежащими множеству А и множеству В, будут элементы множества В. Следовательно, А В = В.
2. Объединение множеств
Для того, чтобы объяснить школьнику, что 2 + 3 = 5, учитель берет 2 красных кружка и 3 синих. Просит перечислить эти кружки, затем предлагает к красным кружкам придвинуть синие (т.е. объединить эти две совокупности, два множества) и пересчитать все кружки совокупности. Устанавливается, что их 5, т.е. 2 +3 = 5. Таким образом, сложение чисел опирается на операцию объединения двух множеств.
В рассмотренном примере объединялись множества, не имеющие общих элементов. В математике приходится выполнять объединение и пересекающихся множеств.
Определение. Объединением множеств А и В называется множество, содержащее такие элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают . В символической записи: х х или х .
Если изобразить пересекающиеся множества при помощи кругов Эйлера, то их объединение изобразится заштрихованной областью (рис. 1). Если множества А и В не пересекаются, то их объединение изображают так (рис. 2).
Рис 1. Рис. 2.
Операция, при помощи которой находят объединение множеств, называют также объединением.
Если все элементы множеств А и В перечислены, то, чтобы найти , достаточно перечислить элементы, принадлежащие А или В, т.е. хотя одному из множеств.
Пример
Так, если А = 2, 4, 6, 8, В = 5, 6, 7, 8, 9, то А В = 2, 4, 5, 6, 7, 8, 9.
Если множества заданы при помощи характеристических свойств элементов, то характеристическое свойство множества А В составляется из характеристических свойств множеств А и В с помощью союза «или».
Пример
Найти объединение множества А четных чисел и множества В двузначных чисел. Так как свойство элементов множества А – «быть четным числом», а свойство элементов В – «быть двузначным числом», то в объединение данных множеств войдут числа, характеристическое свойство которых — «быть четным или двузначным числом».
Например, в А В есть числа: 8, поскольку оно четное; 17, поскольку оно двузначное; 36, поскольку оно четное и двузначное.
Пример
Найти объединение множеств А – четных натуральных чисел и множества В – натуральных чисел, кратных 4.
Ранее было установлено, что В А. Поэтому элементами, принадлежащими множеству А , будут элементы множества А.
Следовательно, в данном случае = А.
studfiles.net
Операции над множествами
Пусть некоторое множество, содержащее все элементы, которые могут быть использованы в некоторый момент их рассмотрения. Такое множество назовем Универсальным. Тогда для любого множества справедливо АÎP(E).
Рис.1.5. Соотношение и дополнения
Назовем Дополнением в множество или такое, что
. (1.30)
Например, для ={1,2,3,4,5} и ={2,4} Þ ={1,3,5}. Иллюстрация дополнения на диаграмме Эйлера представлена на рис. 1.5. Если множество задано по форме от , то определяется следующей эквиваленцией:
, (1.31)
Откуда следует ÛÛÎ, а отсюда:
. (1.32)
Из свойств дополнений можно отметить:
1. = Æ и =,
2. =Û,
3. ÛÍ.
Последнюю эквиваленцию для примера докажем. Если AÍB, то Þ и Þ и Þ и, как следствие,
.
Если же Í, то
А, следовательно,
Эквиваленция доказана.
Если А и В заданы «формулами от » и соответственно, то утверждение ÛÍ эквивалентно следующему
. (1.33)
Иногда для множеств и , таких, что вводят понятие дополнения до и обозначается
. (1.34)
Положим и и определим Объединение множеств , элементы которого принадлежат или (рис.1.6) или иначе:
Рис.1.6. Иллюстрация объединения множеств
. (1.35)
Если и определены через формы от и соответственно, то
.
Из свойств объединения отметим:
1. ,
2.
3. , то есть [P(X) или P(X)] Û P(X),
4. Коммутативность: AÈB = BÈA, то есть [P(X) или Q(X)] Û [Q(X) или P(X)],
5. Ассоциативность: AÈ(BÈC) = (AÈB)ÈC.
Следует отметить, что
А, следовательно, можно записать
. (1.36)
Пример 1.1.
A) Если A = {1,2,3,4}, B = {3,4,5,6} Þ AÈB = {1,2,3,4,5,6}.
Б) Если A = {X | X Кратное 5}, B = {X | X кратное 2} Þ AÈB = {X | X кратное 5 или Х кратное 2}. Если xÏAÈB Þ (X не кратное 5 и не кратное 2).
Теперь для множеств и введем множество, называемое Пересечением А и В: ,такое, что его элементы принадлежат и А и В (рис.1.7), т. е.:
Рис.1.7. Иллюстрация пересечения множеств
,
Или
. (1.37)
Пример 1.2.
A) A = {1,2,3,4}, B = {3,4,5,6} Þ AÇB = {3,4}.
B) Если A = {X | X кратное 5} и B = {X | X кратное 2} Þ AÇB = {X | X кратное 5 и кратное 2} = {X | X кратное 10}.
Если и заданы как формы от и соответственно:
Заметим, что
,
Так что справедливо
. (1.38)
Если АÇВ=Æ, то множества и называются Непересекающимися.
К свойствам операции пересечения можно отнести:
1.
2.
3. , то есть
4. Коммутативность: , то есть
5. Ассоциативность: AÇ(BÇC) = (AÇB)ÇC = AÇBÇC.
Взаимодействие операций объединения и пересечения множеств рассмотрим на множествах , заданных на свойствах соответственно:
1. Дистрибутивность пересечения относительно объединения:
, (1.39)
То есть (опуская аргумент Х):
.
Действительно:
2. Дистрибутивность объединения относительно пересечения:
(1.40)
То есть
.
Доказательство этого свойства такое же, как в предыдущем случае.
3. Исходя из принципа исключения третьего справедливо:
,
.
4. Теорема де Моргана
(1.41)
Действительно, используя (1.38), получим:
Û ( и ) Û [( или ) и ] Û [ и ] или [ и ] Û Или .
Точно так же, используя (1.30), можно доказать, что
. (1.42)
Для множеств и можно ввести операцию «Вычитания» множеств A\BÎP(E), которая определяет множество элементов, принадлежащих и не принадлежащих (рис.1.8).
Рис.1.8. Иллюстрация разности множеств
,
Или
. (1.43)
Пример 1.3.
1) A={1,2,3,4}, B={3,4,5,6}, A\B={1,2}.
2) A={X | X кратно 5}, B={X | X кратно 2} Þ A\B={X | X кратно 5 и Х не кратно 2}Þ A\B={X | X оканчивается на 5}.
Если и заданы формами от , и соответственно, то
. (1.44)
Запись (1.43) можно видоизменить, учитывая, что
,
Тогда
(1.45)
Или иначе
,
Что и отражается в (1.44). Очевидно, что, если A¹B, то:
.
Используя понятие разности множеств, выражение (1.34) для дополнения B при AÍB можно записать
.
Учитывая свойства операций объединения и пересечения можем установить так называемые «законы поглощения»:
(1.46)
(1.47)
Для доказательства (1.46) предварительно покажем, что
.
Действительно, например, для первого соотношения
Û и Þ .
Кроме того, если , так как (Или ) Þ ( или ) Þ . Теперь в (1.46) можем записать , а отсюда .
Для доказательства (1.47) следует учесть, что
,
Так, например,
Þ ( или ) Þ .
Но тогда, если обозначить , то получим:
( и ) Þ ( и ) Þ .
Рассмотрим теперь вопрос о мощности множеств, получаемых при операциях с ними. Пусть заданы A1,A2,…,AnÎP(E), причём | Ai | = ni. Рассмотрим объединение . Тогда число можно получить, перечислив все элементы , а затем все элементы . Но в этом случае общие элементы будут перечислены дважды (рис.1.6), т. е.:
| A1 | + | A2 | = | A1ÈA2 | + |A1ÇA2| Û |A1ÈA2| = |A1| + |A2| — |A1ÇA2|. (1.48)
Для трёх множеств, используя (1.48), получим:
Тогда по индукции можем для объединения n множеств записать
(1.49)
po-teme.com.ua
Свойства операций над множествами
№ | свойство | название |
6. | коммутативность объединения | |
7. | коммутативность пересечения | |
8. | ассоциативность объединения | |
9. | ассоциативность пересечения | |
10. |
| идемпотентность объединения |
11. |
| идемпотентность пересечения |
12. | дистрибутивность пересечения | |
13. | дистрибутивность объединения | |
14. |
| |
15. |
| |
16. |
| |
17. |
| |
18. |
|
Свойства 1 —
18 обладают двойственностью в том смысле,
что если заменять символы « » на «», « »
на «
»
на « »
и «» на «», то получится снова одно из свойств 1
— 18. Таким образом, каждой теореме,
доказанной на основании формул 1-18,
соответствует двойственная теорема.
Свойства 6 — 18 доказывается методом
встречных включений. В качестве примера
докажем свойство 12.
»
и «» на «», то получится снова одно из свойств 1
— 18. Таким образом, каждой теореме,
доказанной на основании формул 1-18,
соответствует двойственная теорема.
Свойства 6 — 18 доказывается методом
встречных включений. В качестве примера
докажем свойство 12.
Доказательство свойства 12:
.
Обозначим 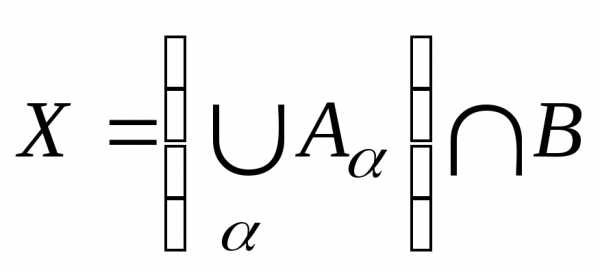 ,
,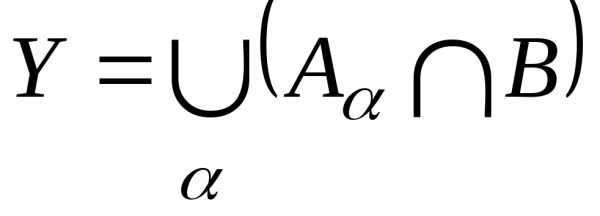 .
.
1. Пусть 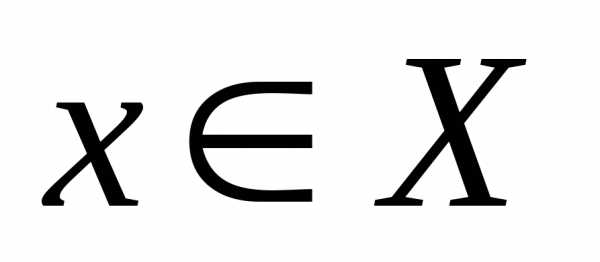 .
Покажем, что
.
Покажем, что .
.
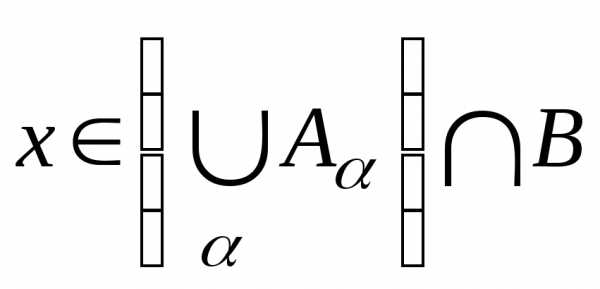 (хотя
бы одному из множеств
(хотя
бы одному из множеств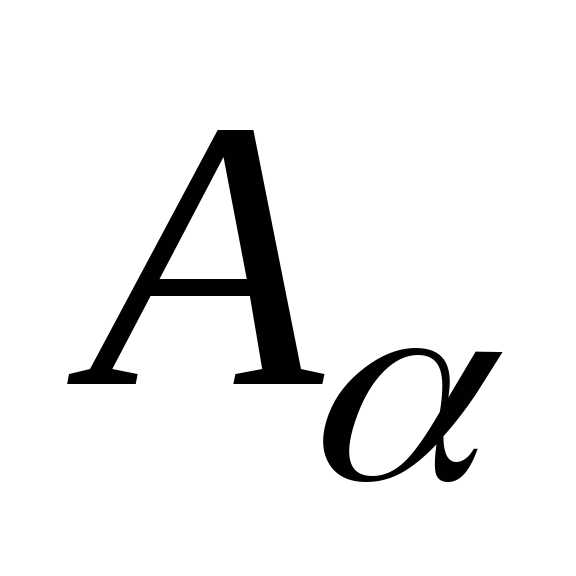 )
)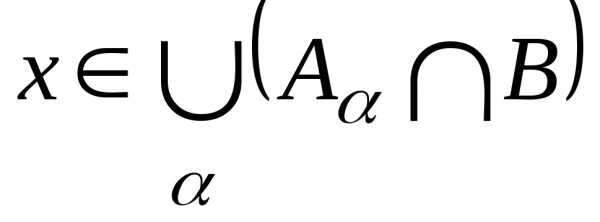
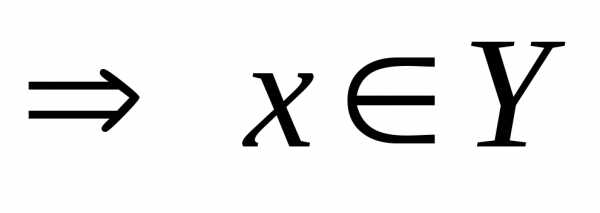 .
.
2. Пусть 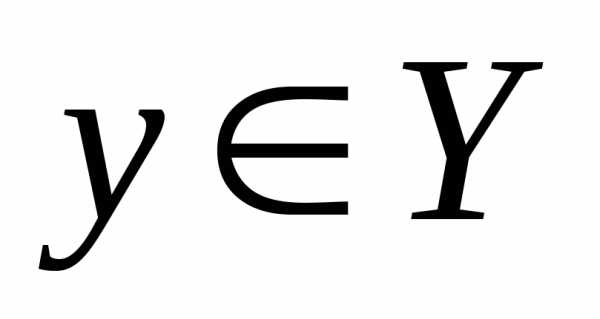 .
Покажем, что
.
Покажем, что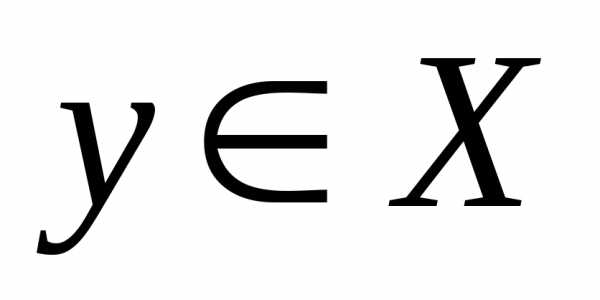 .
.
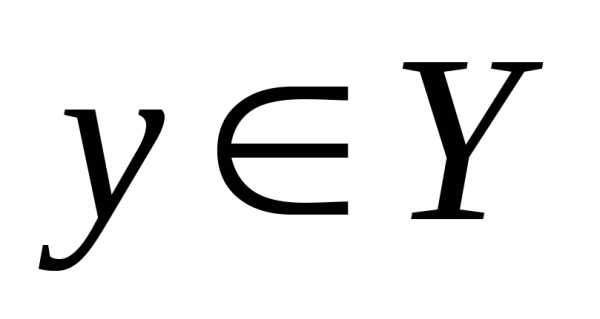
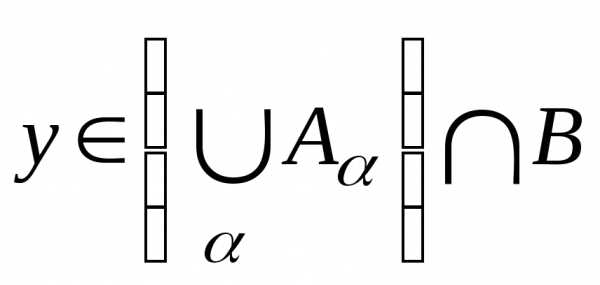 .
.
Из 1) и 2)
следует, что 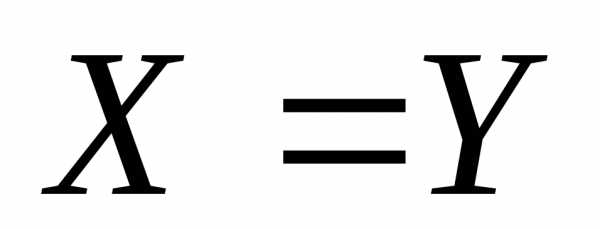 .
.
Упражнение. Доказать самостоятельно свойства 6-18.
Разность множеств. Дополнение
Определение 7.Разностью множеств и называется множество, состоящее из тех элементов множества А, которые не принадлежатВ.
Обозначается . Таким образом,
.
Заметим, что между свойствами операций над множествами и свойствами арифметических операций над числами прослеживается некоторая аналогия (свойства 6-9,12).Однако эта аналогия неполная (свойства 10-11). Приведём ещё два примера по поводу этого замечания.
Пример
1.Пусть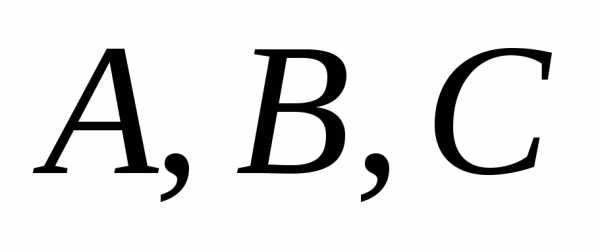 — произвольные множества. Тогда
— произвольные множества. Тогда
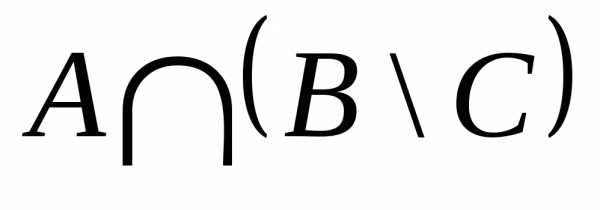 =.
=.
Упражнение. Доказать самостоятельно утверждение примера 1.
Пример 2..
Доказательство примера 2:
1. Пусть верно равенство
.
Так как
слагаемое есть часть суммы, то  .
.
2. Пусть  .
Множество
.
Множество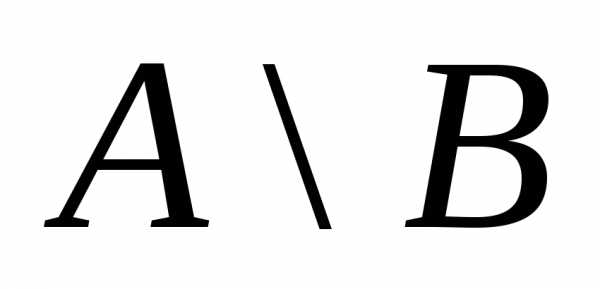 состоит из элементов множестваА,
не принадлежащих множествуВ.
Объединяя это множество со множествомВ, получим множествоА.
состоит из элементов множестваА,
не принадлежащих множествуВ.
Объединяя это множество со множествомВ, получим множествоА.
Если множество В имеет элементы, не входящие во
множествоА, то при объединенииВс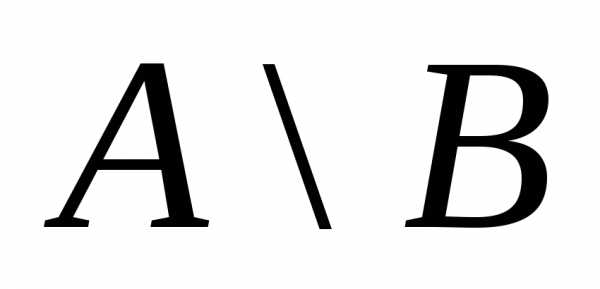 получим множество, отличное отА.
получим множество, отличное отА.
Определение 8.Дополнением СА множества А называется множество элементов из множестваЕ, которые не принадлежатА, то есть
.
Справедливы следующие свойства:
19. ;
20.  ;
;
21. ;
22. ;
23. ;
24. Дополнение объединения равно пересечению дополнений:
а) ;
б) 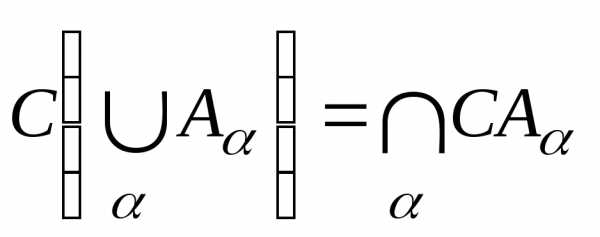 ;
;
25. Дополнение пересечения равно объединению дополнений:
а) ;
б) ;
26. .
Свойства 19-26 также как и свойства 1-18 обладают двойственностью. Свойства 24 и 25 выражают так называемый принцип двойственности.
Определение 9.Симметрической разностью множеств А и Вназывается множество
.
Обозначается 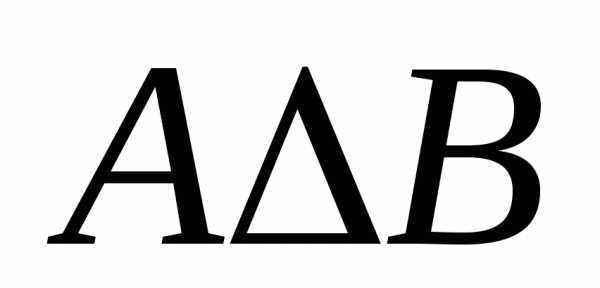 .
Легко видеть, что
.
Легко видеть, что
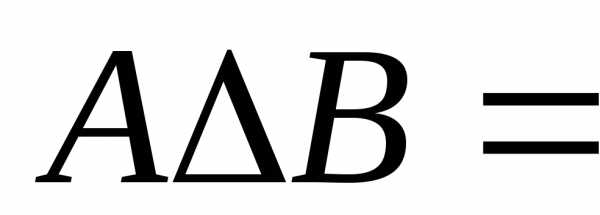 .
.
Упражнение. Доказать самостоятельно последнее утверждение и свойства 19-26.
§2. Отображение
Пусть А, В — произвольные множества изЕ,.
Определение 1.Отображением множества
А во множество Вназывается
соответствиеf, которое
каждому элементу относит один и только один элемент
относит один и только один элемент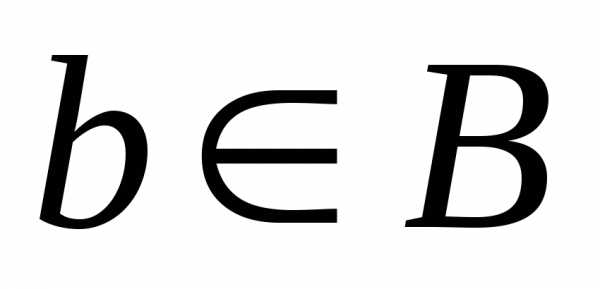 ,
который обозначается
,
который обозначается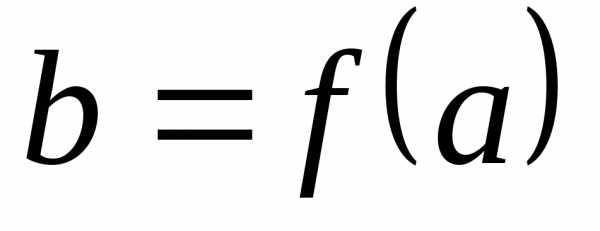 и называетсязначением
отображения f или образом элемента а
при отображении f.МножествоАназываетсяобластью
определения отображения.
и называетсязначением
отображения f или образом элемента а
при отображении f.МножествоАназываетсяобластью
определения отображения.
Обозначается или.
Определение 2.Образом подмножества
D из А при отображении fназывается совокупность элементов вида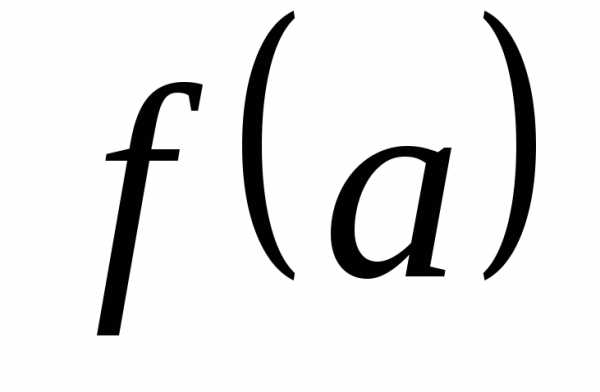 ,
гдеапробегает всё множествоD.
,
гдеапробегает всё множествоD.
Обозначается 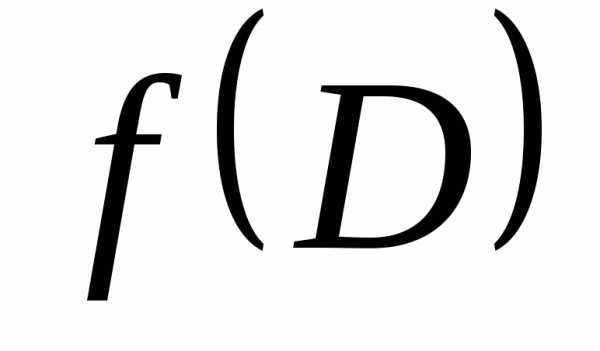 .
Таким образом,
.
Таким образом,
.
Определение 3.Множество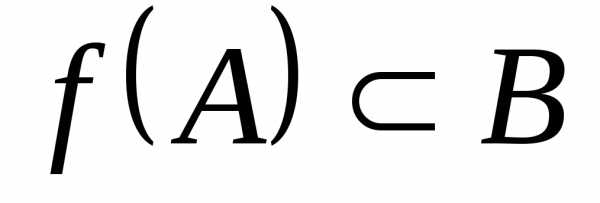 называетсямножеством
значений отображения f.
называетсямножеством
значений отображения f.
Отображение также называютфункцией с областью определения А и множеством значений, лежащим в В.В некоторых разделах математики в зависимости от природы множествАиВи свойствf отображениеfназываютфункционалом, оператороми так далее.
Определение 4.Прообразом элемента bВназывается совокупность всех элементов ,
что
,
что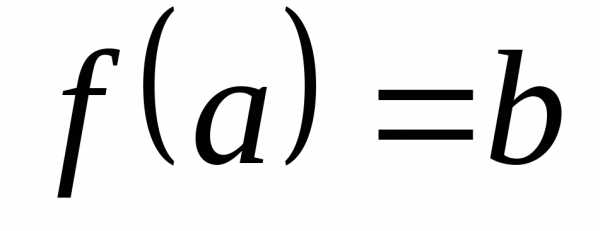 .
.
Обозначается 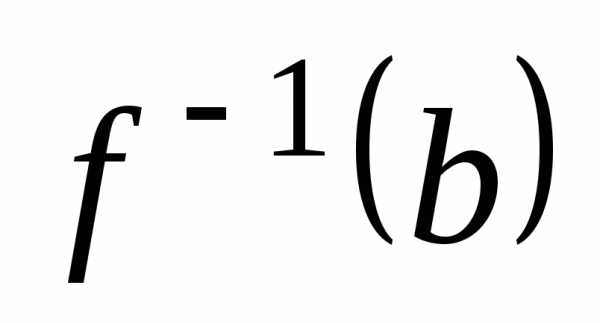 .
Таким образом,
.
Таким образом,
.
Если
,
то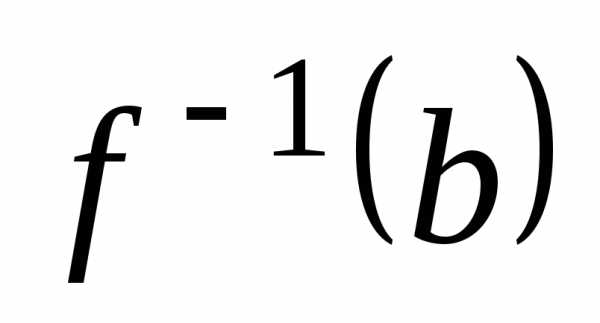 =.
=.
Определение 5. Прообразом множества Кназывается множество
.
Для прообразов
множеств  и
и справедливы следующие соотношения:
справедливы следующие соотношения:
1. ;
2. ;
3. ;
4. Если 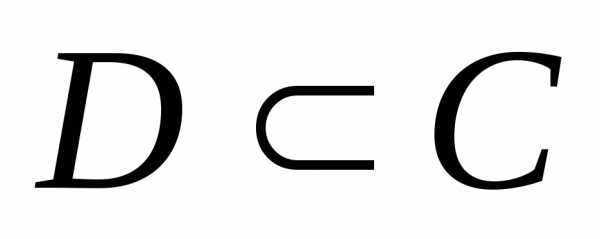 ,
то.
,
то.
Упражнение.
а) доказать самостоятельно соотношения 1-4;
б) выяснить,
верны ли аналогичные соотношения для
образов множеств  и
и :
:
1.;
2.;
3.;
4.
Если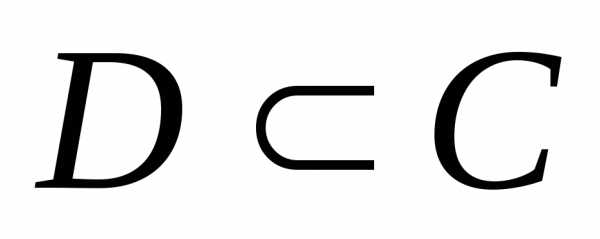 ,
то.
,
то.
Определение 6.Отображениеназываетсяотображением
А на В или сюрьективным отображением,если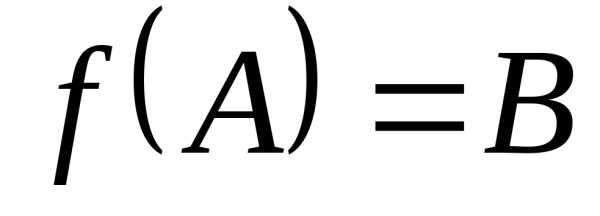 ,
то есть если
,
то есть если
.
Определение 7.Отображениеназываетсяинъективным
отображением,если для любого
элемента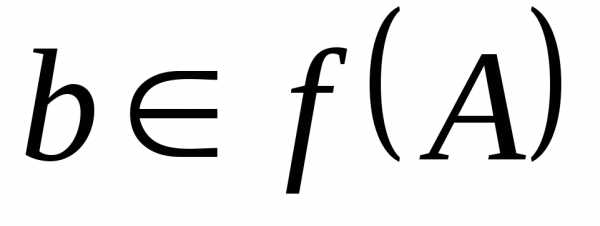 его полный прообраз
его полный прообраз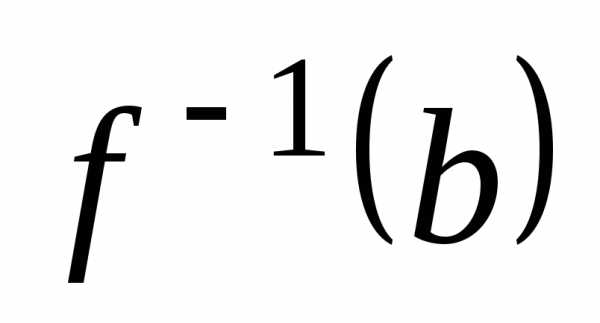 состоит ровно из одного элемента, или
если для любого элемента
состоит ровно из одного элемента, или
если для любого элемента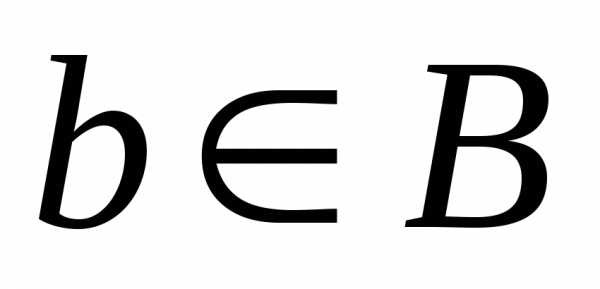 его полный прообраз состоит не более
чем из одного элемента.
его полный прообраз состоит не более
чем из одного элемента.
Определение 7.Отображениеназываетсяинъективным
отображением,если различным
элементам соответствуют различные элементы
соответствуют различные элементы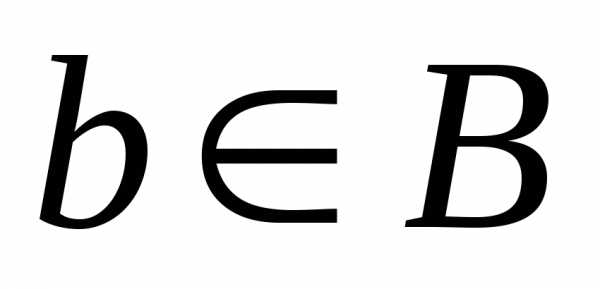 ,
то есть
,
то есть
.
Определение 8.Отображениеназываетсявзаимно-однозначным
или биективным отображением,если для любого элемента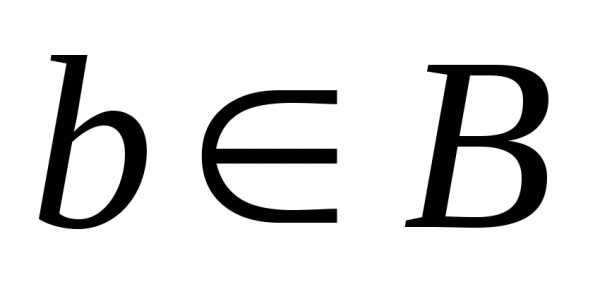 его прообраз
его прообраз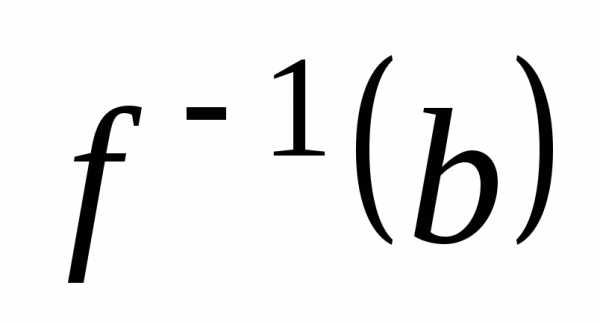 состоит ровно из одного элемента
состоит ровно из одного элемента ,
или если оно одновременно является
инъективным и сюрьективным.
,
или если оно одновременно является
инъективным и сюрьективным.
studfiles.net
|
Два множества называются Непересекающимися (или расчлененными) если . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются Классификацией). Разбиением множества называется такая расчлененная система непустых подмножеств множества , что каждый элемент множества является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение. Для подмножеств данного множества выполняются следующие законы: · Закон коммутативности (переместительный закон): ; ; · Закон ассоциативности (сочетательный закон) для любой тройки множеств , и : ; ; · Закон дистрибутивности (распределительный закон) для любой тройки множеств , и : ; ; · ; ; · ;; · ; ; · ; · ; · ; ; · ; ; · ; ; · ; . Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения. Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой на , на и наоборот. Такие выражения называются Двойственными друг другу. Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством. Очевидно, что операция Разность не обладает свойствами коммутативности и ассоциативности, в то же время операция Симметрическая разность и коммутативна, и ассоциативна. Большое значение в современной математике имеет множественная операция Декартово произведение. Если заданы два множества и , то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств и называется множество , составленное из упорядоченных пар (). Декартово произведение множеств и обозначается . Очевидно, что и ‑ различные множества, т. е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
|
matica.org.ua