МП-1 / Практ. по алгебре / Практикум по алгебре в среде MATLAB_Жаркова / ржавинская лекции / ржавинская лекции / Лекция_6
Лекция 6
Матрицы
Определение и некоторые свойства определителей порядка n. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства этих операций |
6.1. Основные понятия
Определение 1.Матрицей называется прямоугольная таблица чисел.
Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:
.
Числа, составляющие матрицу, называются
ее элементами, элемент
 расположен в ее
расположен в ее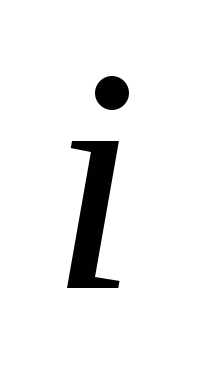 -й
строке и
-й
строке и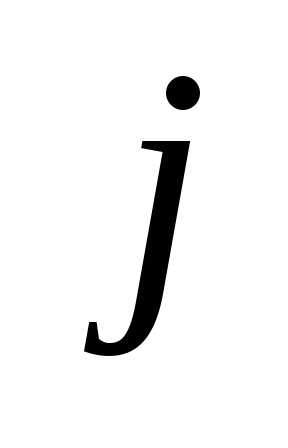 -м
столбце.
-м
столбце. Числа  и
и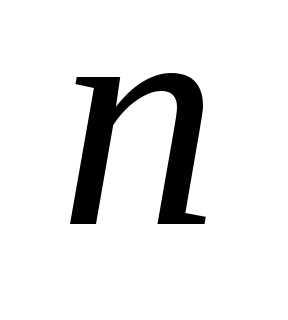 (число строк и столбцов матрицы) называются
ее порядками.
(число строк и столбцов матрицы) называются
ее порядками.
Говорят также, что  — матрица размером
— матрица размером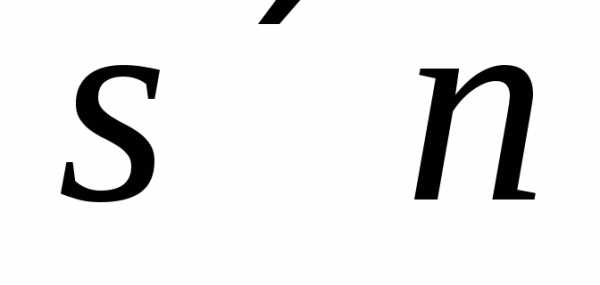 .
.
Если 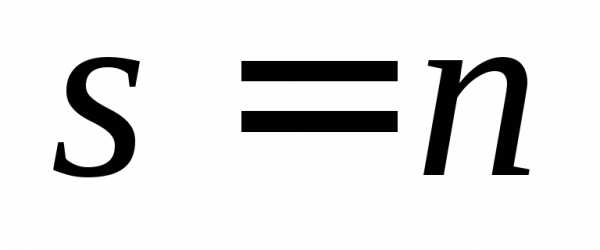 ,
матрица
,
матрица называетсяквадратной.
называетсяквадратной.
Для краткой записи используется также
обозначение 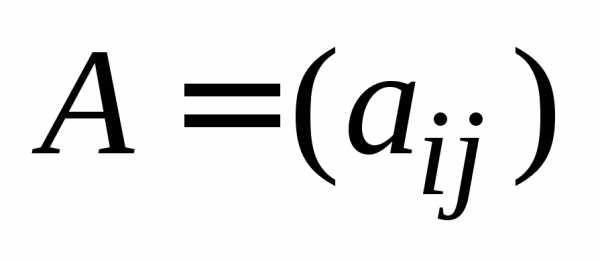
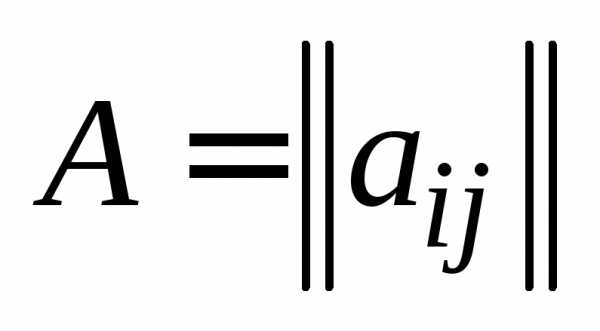 )
и далее указывается, в каких пределах
изменяются
)
и далее указывается, в каких пределах
изменяются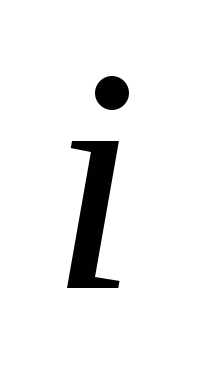 и
и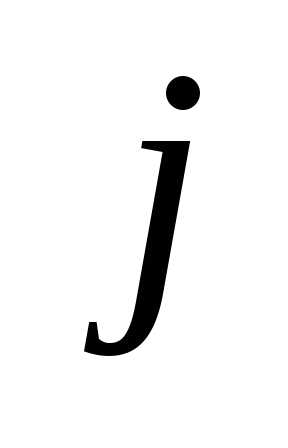 ,
например,
,
например,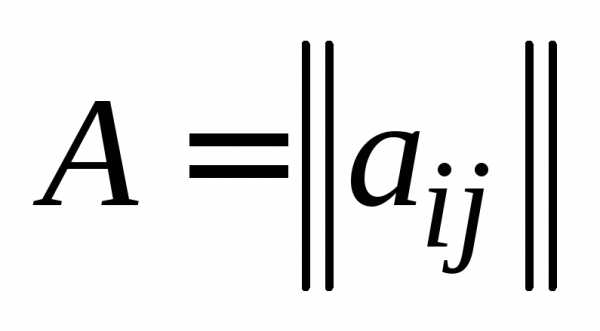 ,,.
(Запись читается так: матрица
,,.
(Запись читается так: матрица с элементами
с элементами ,
,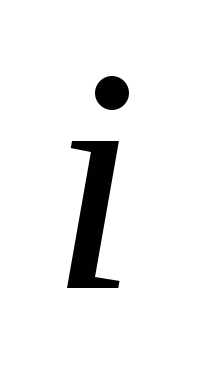 изменяется от
изменяется от до
до ,
,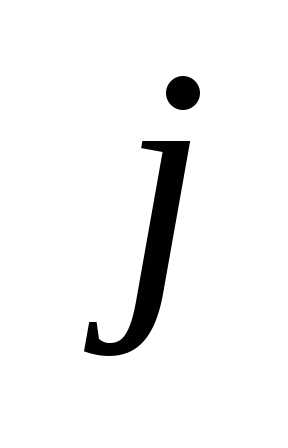 — от
— от
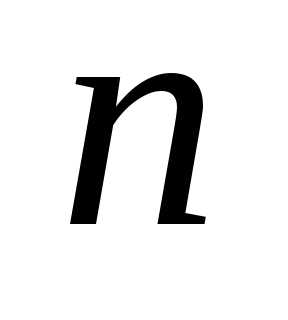 .)
.) Среди квадратных матриц отметим диагональные матрицы, у которых все
элементы с неравными индексами (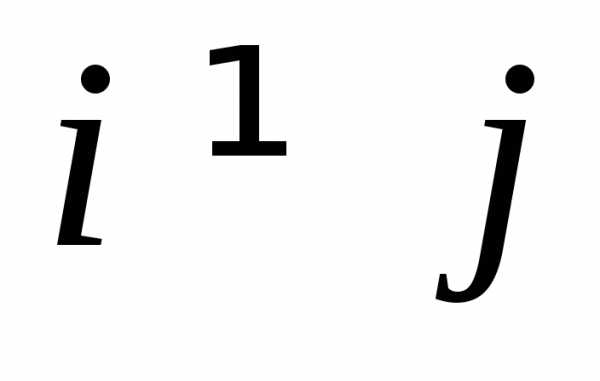 )
равны нулю:
)
равны нулю:
 .
.
Будем говорить, что элементы расположены на главной диагонали.
Диагональная матрица вида

называется единичнойматрицей.
В дальнейшем будут встречаться матрицы вида
 и
и ,
,
которые называются треугольнымиматрицами, а также матрицы, состоящие из одного столбца:
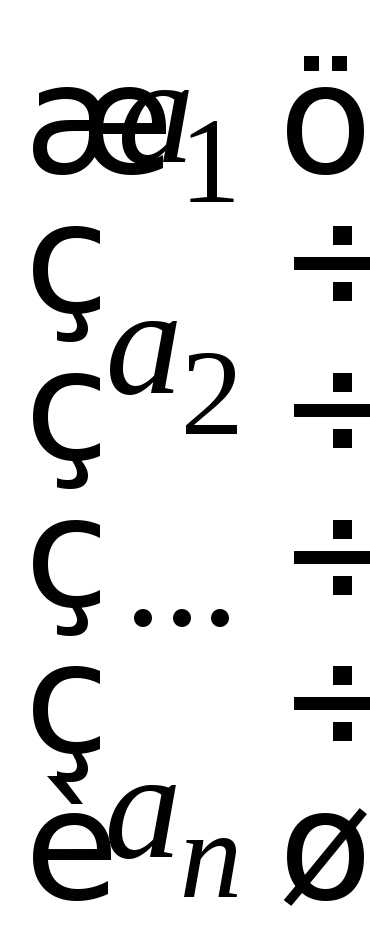
и одной строки:
(матрица-столбец и матрица-строка).
Матрица, все элементы которой равны нулю, называется нулевой.
6.2. Определители порядка n
Пусть дана квадратная матрица порядка 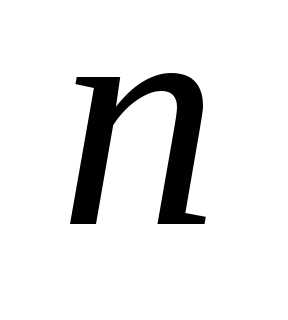 :
:
 .
(6.1)
.
(6.1)
Составим всевозможные произведения 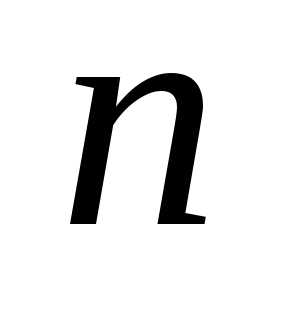 элементов матрицы, расположенных в
разных строках и разных столбцах, т.е.
произведения вида
элементов матрицы, расположенных в
разных строках и разных столбцах, т.е.
произведения вида
. (6.2)
Число произведений вида (6.2) равно 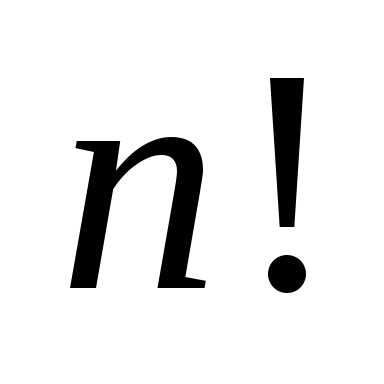 (примем этот факт без доказательства).
(примем этот факт без доказательства).
Будем считать все эти произведения
членами определителя порядка 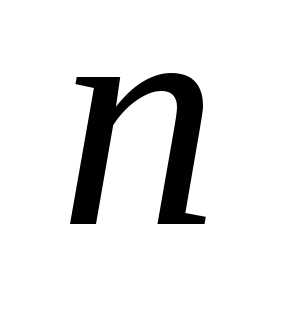 ,
соответствующего матрице (6.1).
,
соответствующего матрице (6.1).
Вторые индексы множителей в (6.2) составляют
перестановку первых 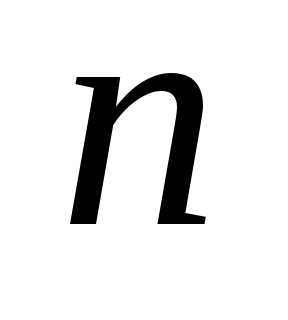 натуральных чисел
натуральных чисел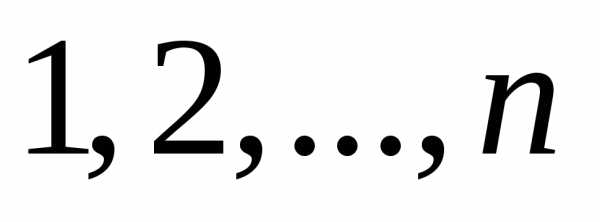 .
.
Говорят, что числа 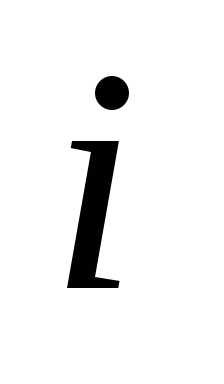 и
и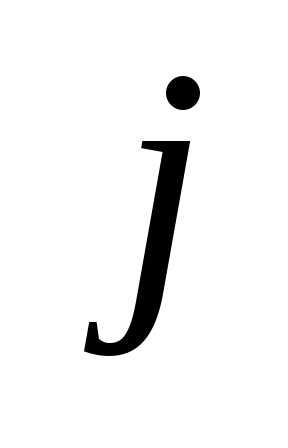 в перестановке составляютинверсию,
если
в перестановке составляютинверсию,
если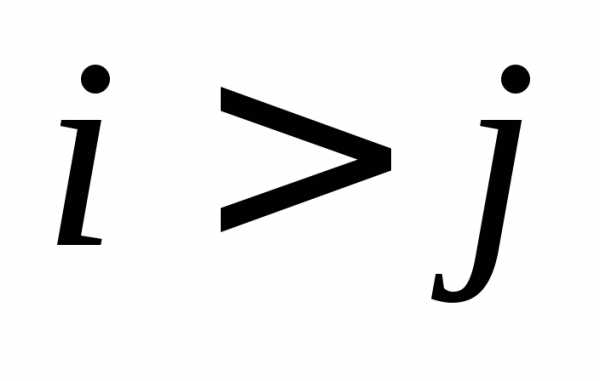 ,
а в перестановке
,
а в перестановке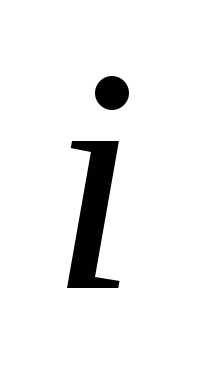
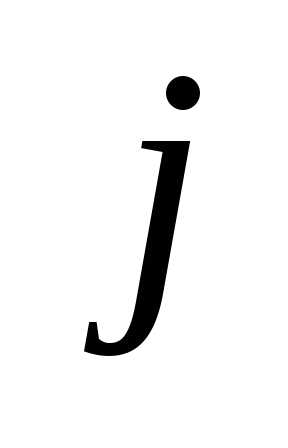 .
. Пример 1.В
перестановке шести чисел,,
числа и,
и, и
и ,
, и
и ,
, и
и ,
, и
и составляют инверсии.
составляют инверсии.
Перестановка называется четной,
если число инверсий в ней четно, и
Пример 2.Перестановка- нечетная, а перестановка- четная ( инверсий).
инверсий).
Определение 2.Определителем
порядка 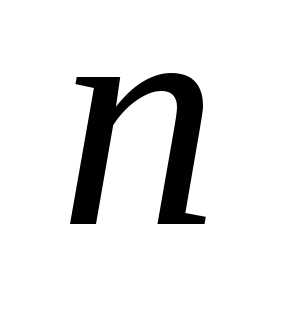 , соответствующим матрице (6.1),
называется алгебраическая сумма
, соответствующим матрице (6.1),
называется алгебраическая сумма 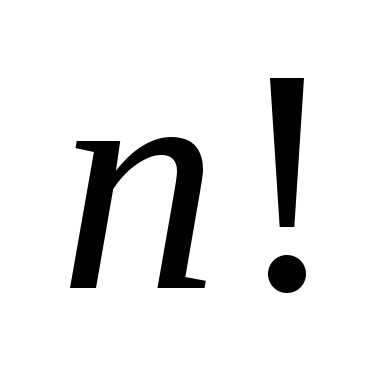 членов, составленная следующим
образом: членами определителя служат
всевозможные произведения
членов, составленная следующим
образом: членами определителя служат
всевозможные произведения 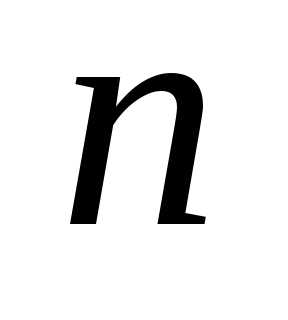 элементов матрицы, взятых по одному
из каждой строки и каждого столбца, причем слагаемое берется со знаком «+», если множество вторых индексов является
четной перестановкой чисел
элементов матрицы, взятых по одному
из каждой строки и каждого столбца, причем слагаемое берется со знаком «+», если множество вторых индексов является
четной перестановкой чисел 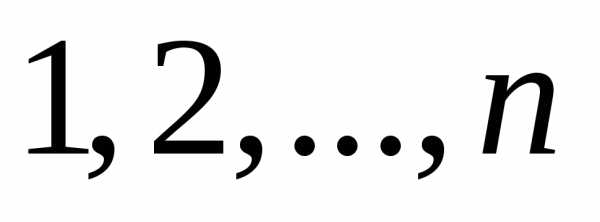 , и со знаком «–», если нечетной.
, и со знаком «–», если нечетной.
Обозначать определитель матрицы (6.1) принято так:
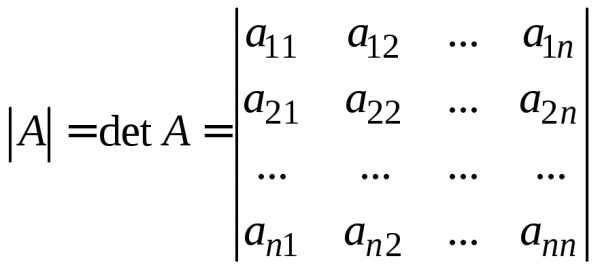 .
.
Замечание.Определение 2 для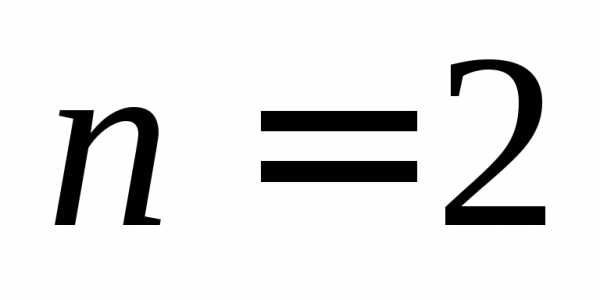 и
и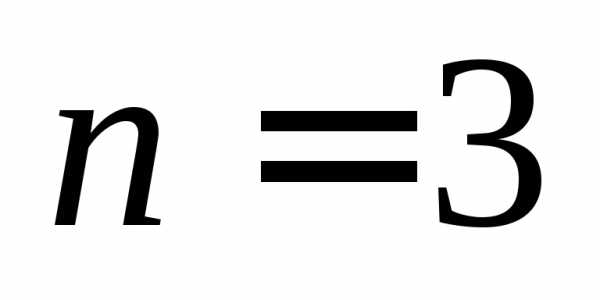 приводит к уже знакомым нам определителям
2-го и 3-го порядка:
приводит к уже знакомым нам определителям
2-го и 3-го порядка:
,
.
Транспонированием вокруг главной
диагонали матрицы называется переход к матрице
называется переход к матрице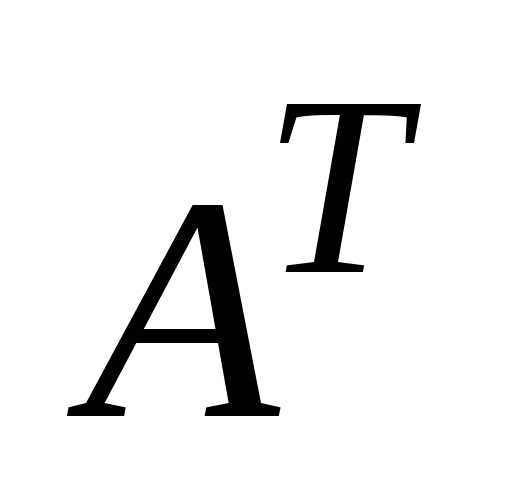 ,
для которой строки матрицы
,
для которой строки матрицы являются столбцами, а столбцы — строками:
являются столбцами, а столбцы — строками:
 .
. Будем говорить, что определитель 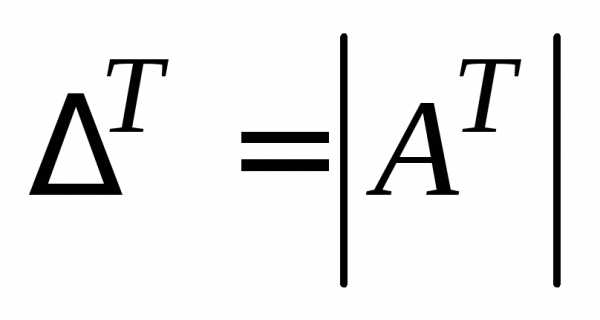 получен транспонированием определителя
получен транспонированием определителя .
.
Свойства определителя порядка п:
1. 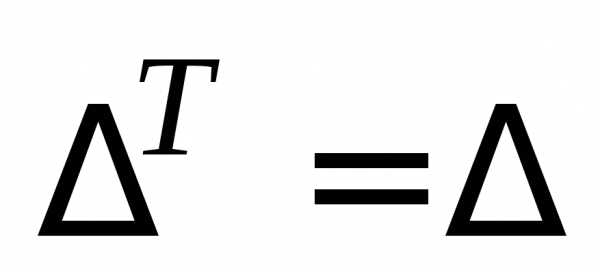 (определитель не меняется при
транспонировании вокруг главной
диагонали).
(определитель не меняется при
транспонировании вокруг главной
диагонали).
2. Если одна из строк определителя состоит из нулей, определитель равен нулю.
3. От перестановки двух строк определитель меняет лишь знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки
определителя умножить на число 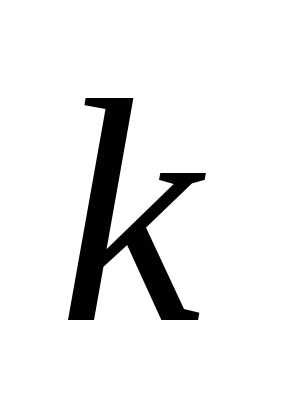
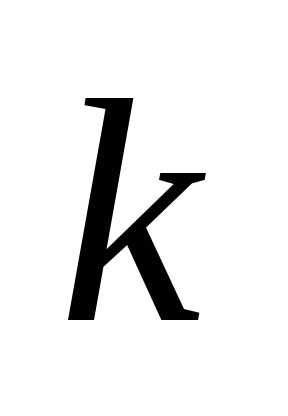 .
.6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы 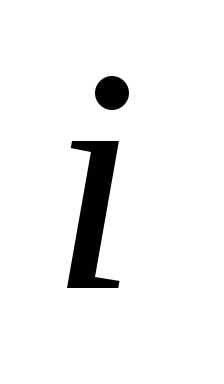 -й
строки определителя представлены в
виде суммы,
то определитель равен сумме двух
определителей, у которых все строки,
кроме
-й
строки определителя представлены в
виде суммы,
то определитель равен сумме двух
определителей, у которых все строки,
кроме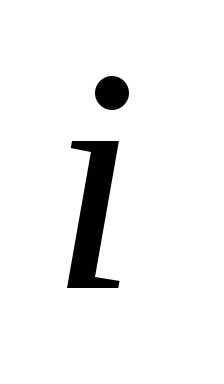 -й,
такие же, как в исходном определителе,
а
-й,
такие же, как в исходном определителе,
а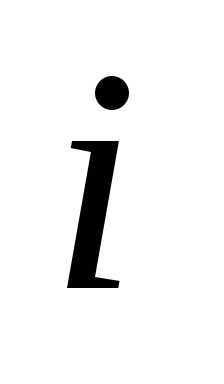 -я
строка в одном определителе состоит
из
-я
строка в одном определителе состоит
из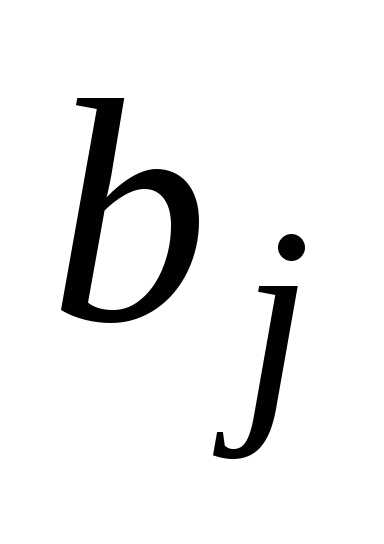 ,
а в другом — из
,
а в другом — из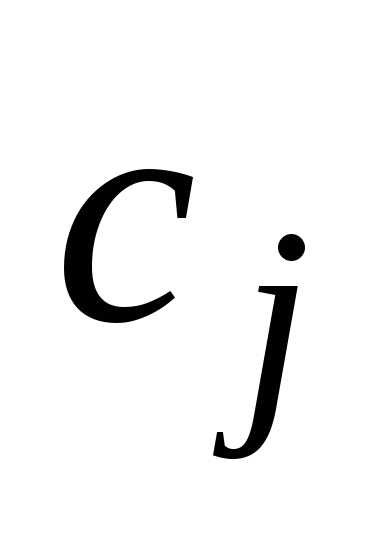 .
.
Определение 3.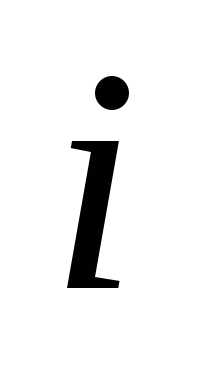 -я
строка определителя называется линейной
комбинацией остальных его строк
-я
строка определителя называется линейной
комбинацией остальных его строк
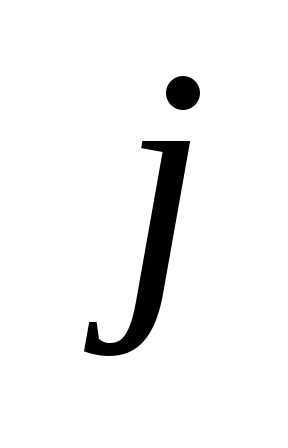 -ю
строку на
-ю
строку на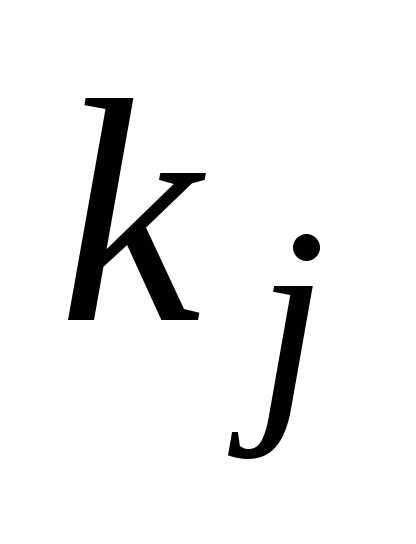 , а затем складывая все строки, кроме
, а затем складывая все строки, кроме 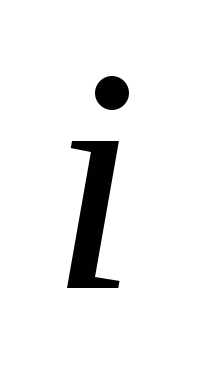 -й, получаем
-й, получаем 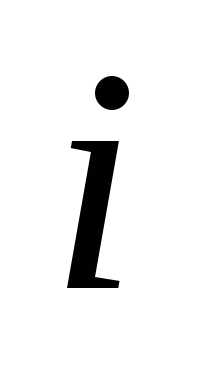 -ю
строку.
-ю
строку.8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.
9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.
Замечание.Мы сформулировали свойства определителя
для строк. В силу свойства 1 (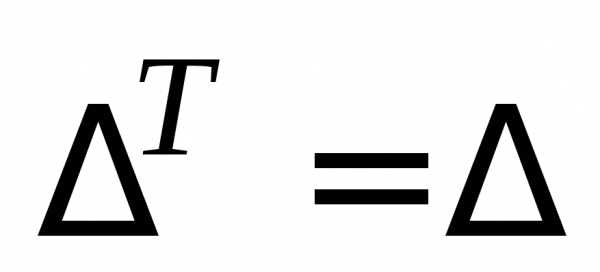 )
они справедливы и для столбцов.
)
они справедливы и для столбцов.
Все приведенные свойства были доказаны
на практических занятиях для 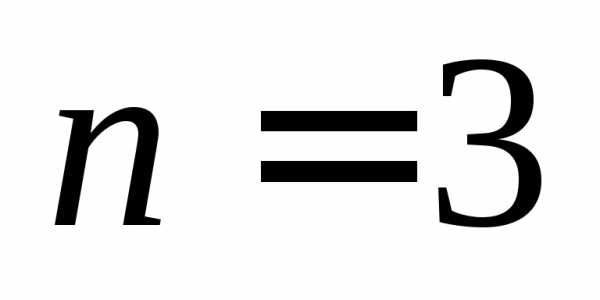 ;
для произвольного
;
для произвольного примем их без доказательства.
примем их без доказательства.
Если в определителе  порядка
порядка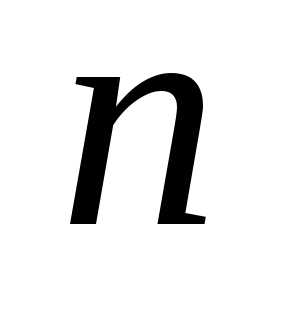 выбрать элемент
выбрать элемент и вычеркнуть столбец и строку, на
пересечении которых расположен
и вычеркнуть столбец и строку, на
пересечении которых расположен ,
оставшиеся строки и столбцы образуют
определитель порядка
,
оставшиеся строки и столбцы образуют
определитель порядка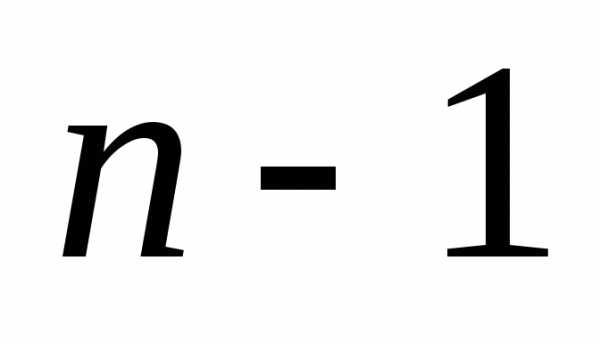 ,
который называетсяминором определителя
,
который называетсяминором определителя ,
соответствующим элементу
,
соответствующим элементу .
.
Пример 3.В определителе
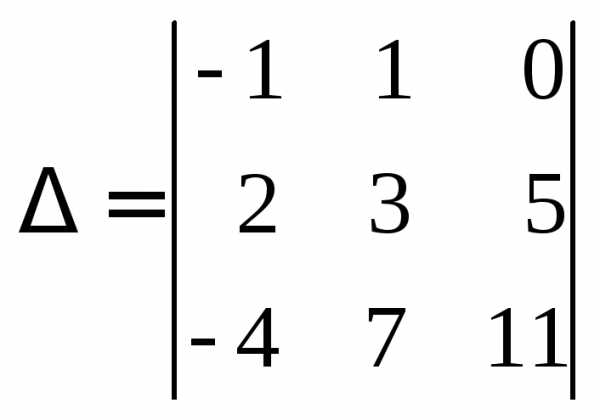
минором элемента 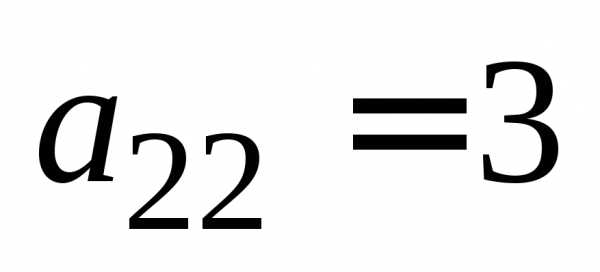 является определитель
является определитель .
.
Определение 4.Алгебраическим
дополнением  элемента
элемента определителя
определителя называется его минор, умноженный
на
называется его минор, умноженный
на  , где
, где 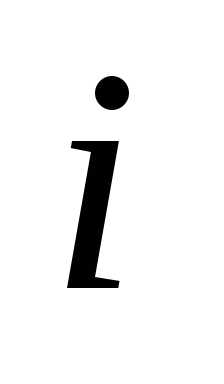 — номер строки,
— номер строки, 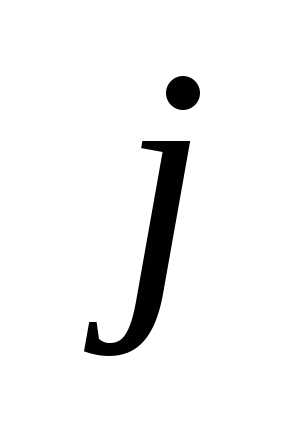 — номер столбца, в которых расположен
выбранный элемент
— номер столбца, в которых расположен
выбранный элемент  .
.
Пример 4. В определителе

алгебраическое дополнение .
Теорема 1 (о разложении по строке).Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.
Теорема 1 позволяет свести вычисление
определителя порядка  к вычислению
к вычислению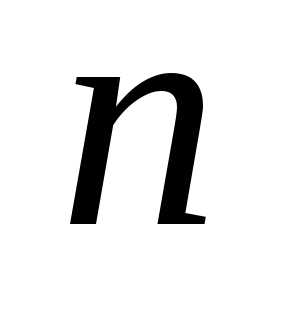 определителей порядка
определителей порядка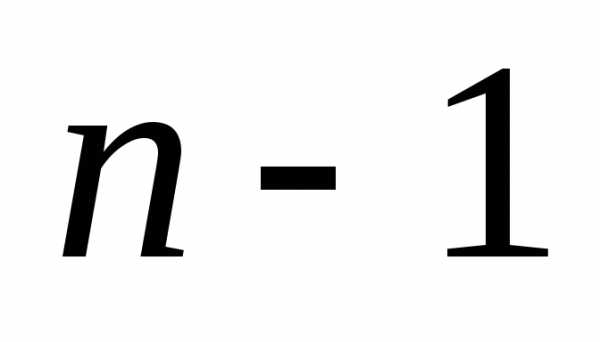 .
.
Пример 5.Вычислить определитель четвертого порядка:
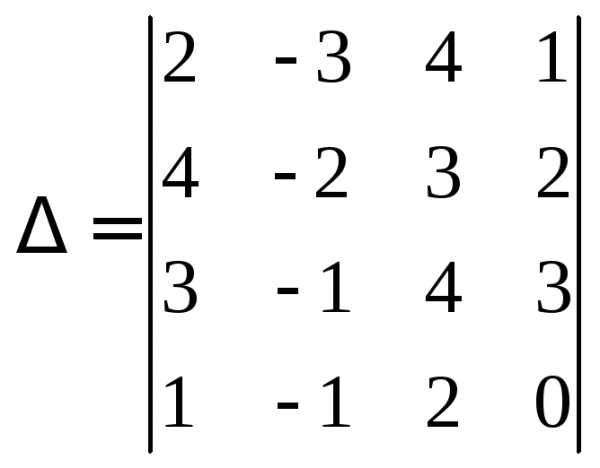 .
.
Воспользуемся теоремой 1 и разложим
определитель  по 4-й строке:
по 4-й строке:
.
Замечание.Можно вначале упростить определитель,
воспользовавшись свойством 9, а затем
использовать теорему 1. Тогда вычисление
определителя порядка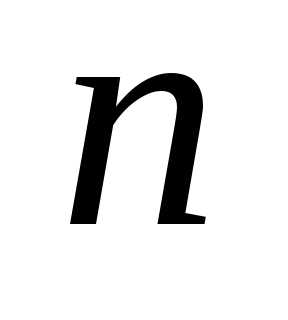 сведется к вычислениювсего одногоопределителя порядка
сведется к вычислениювсего одногоопределителя порядка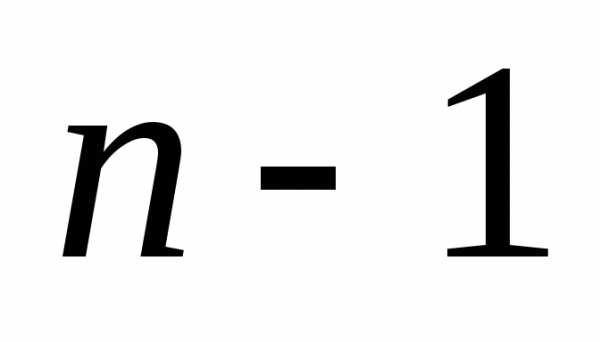 .
.
Пример 6.Вычислить
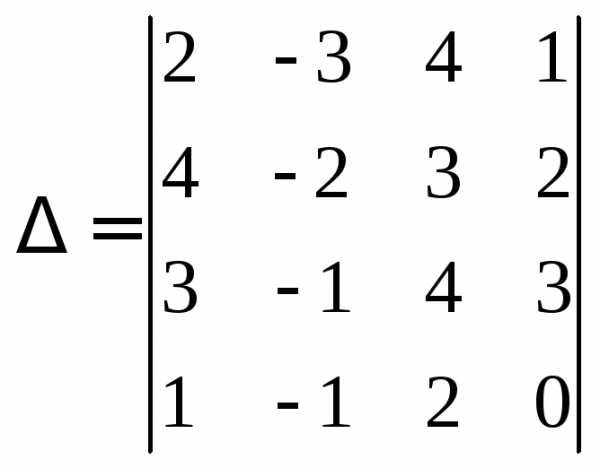 .
.
Прибавим первый столбец ко второму и
первый столбец, умноженный на (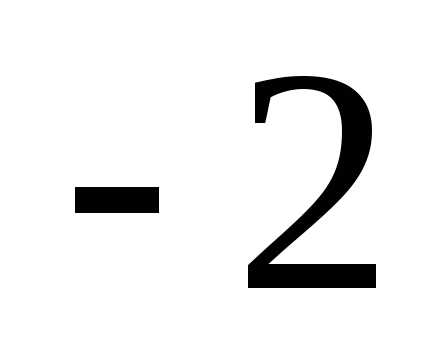 ),
к третьему, в результате получим
),
к третьему, в результате получим
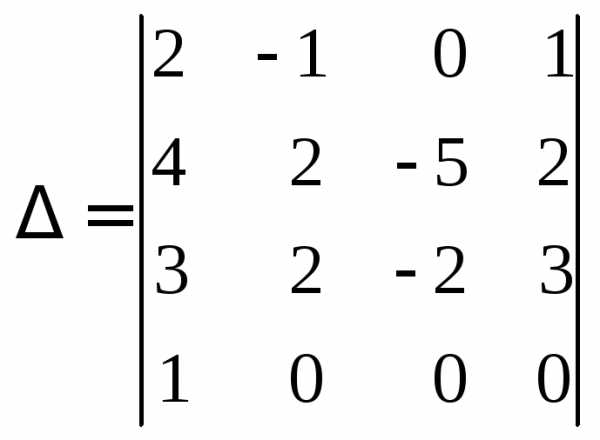 .
.
Теперь применим теорему 1 и разложим по последней строке:
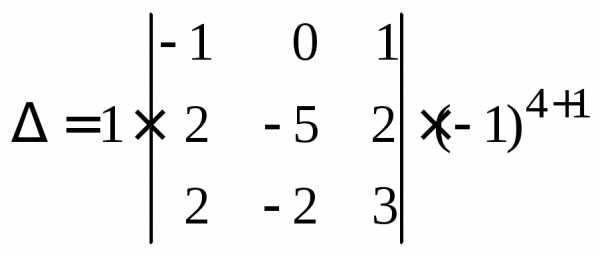 ,
,
вычисление определителя 4-го порядка свелось к вычислению всего одного определителя 3-го порядка.
Далее аналогично к первому столбцу прибавим третий и полученный определитель разложим по первой строке:
,
вычисление определителя третьего порядка свелось к вычислению всего одного определителя второго порядка.
Пример 7.Вычислить определитель порядка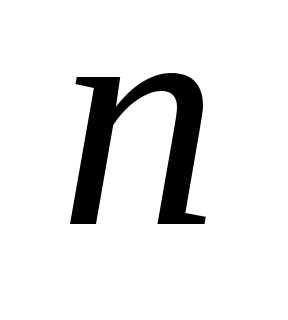 :
:
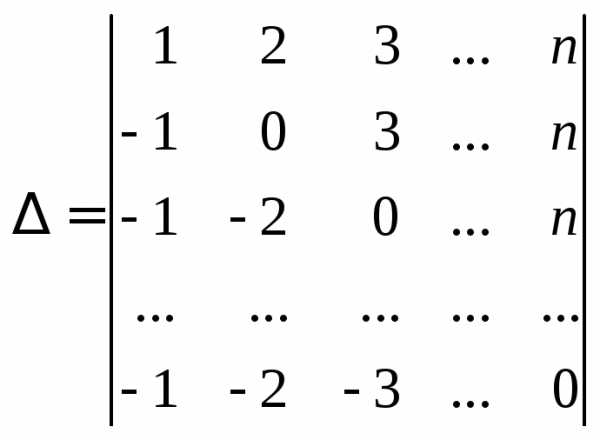 .
.
Первую строку прибавим ко второй, третьей
и т.д.  -й
строке. Придем к определителю
-й
строке. Придем к определителю
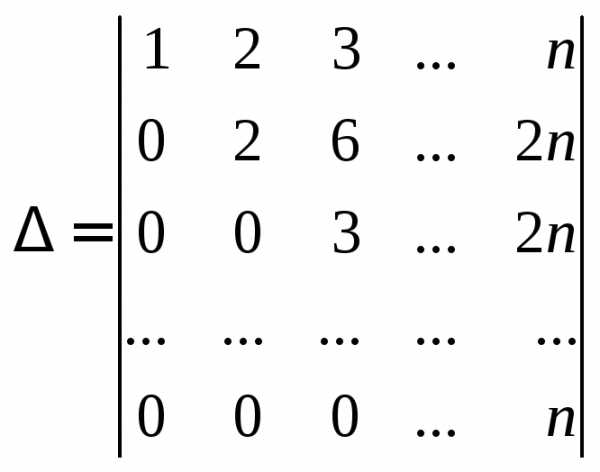 .
.
Получен определитель треугольного вида.
Применим 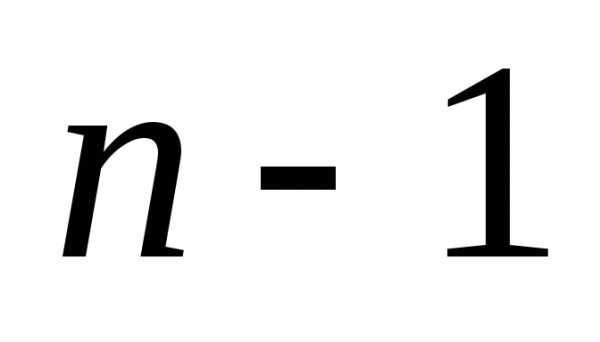 раз теорему 1 (разложим по первому
столбцу) и получим
раз теорему 1 (разложим по первому
столбцу) и получим
.
Замечание.Определитель треугольного вида равен произведению элементов главной диагонали.
6.3. Основные операции над матрицами
Определение 5.Две матрицы 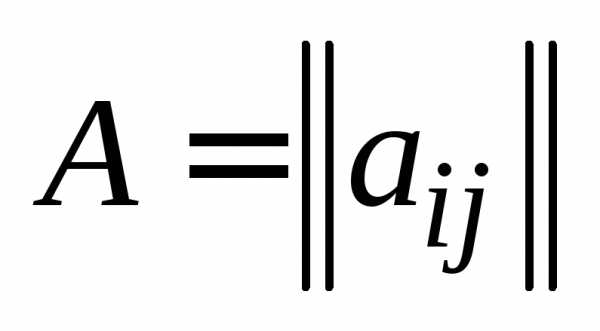 , , , и
, , , и 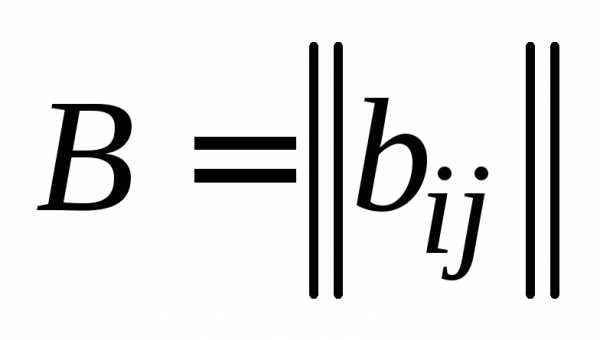 , , , будем называть равными, если
.
, , , будем называть равными, если
.
Краткая запись:  .
.
Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.
Определение 6.Суммой двух матриц 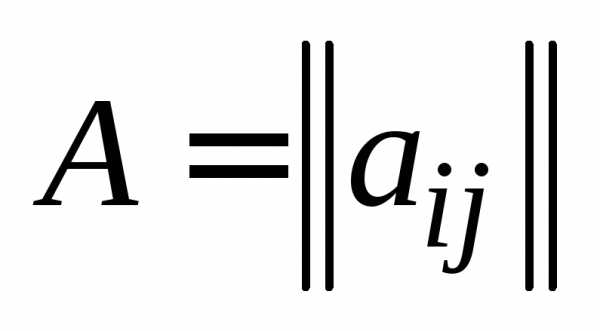 , , , и
, , , и 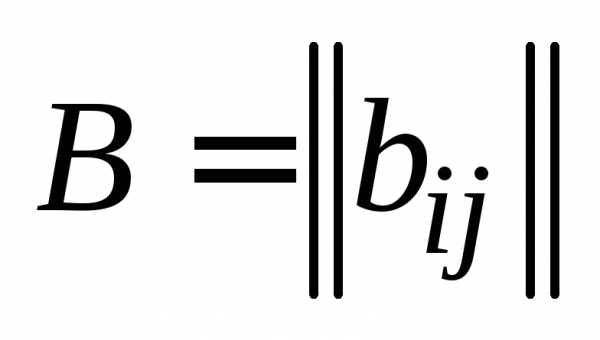 , , , называется такая матрица
, , , называется такая матрица 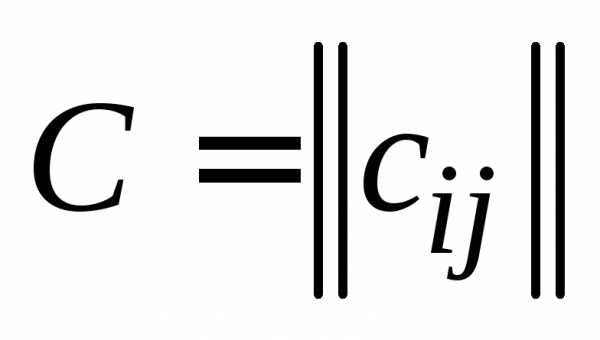 , , , что
.
, , , что
.
Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.
Пример 8.Найти сумму матриц
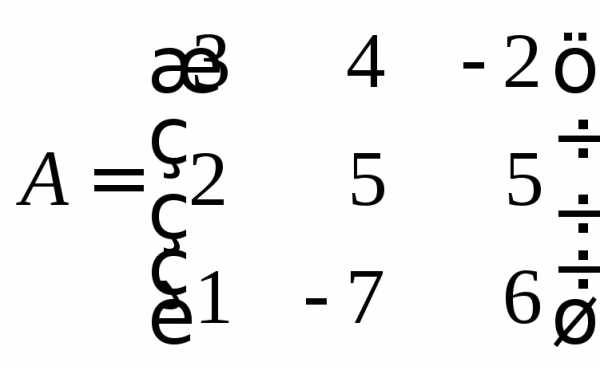 и
и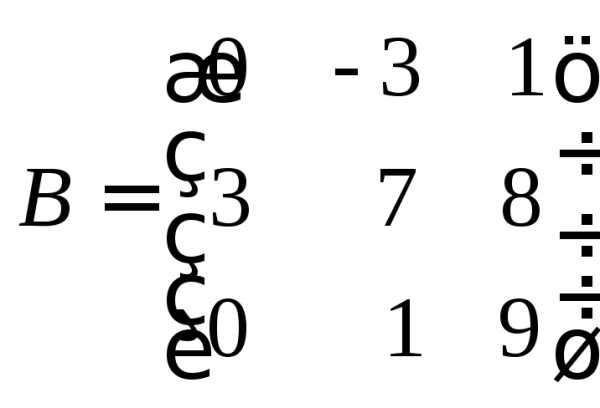 .
.
В соответствии с определением 6 найдем
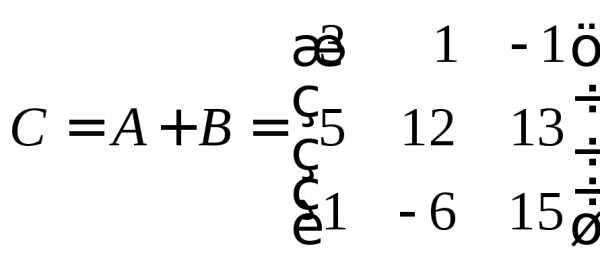 .
.
Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.
Определение 7.Произведением
матрицы 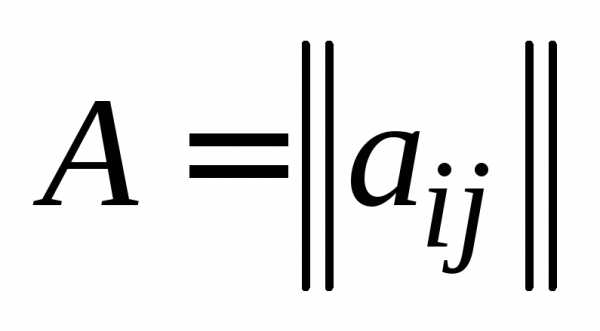 , , , на вещественное число
, , , на вещественное число 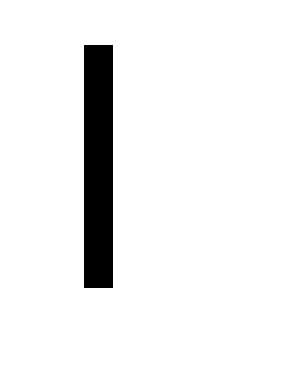 называется такая матрица
называется такая матрица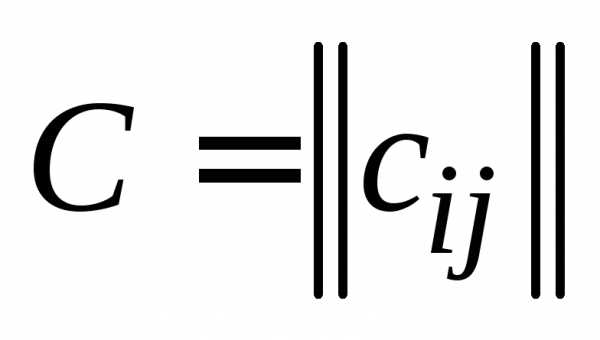 , , , для которой
.
, , , для которой
.
Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.
Пример 9.Найти линейную комбинациюматриц
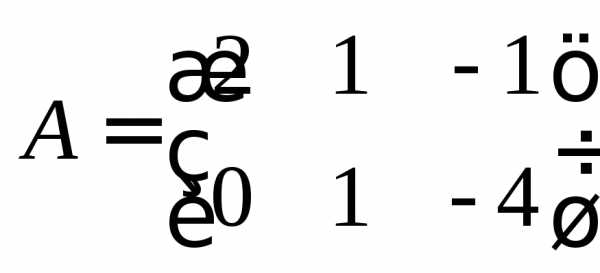 и
и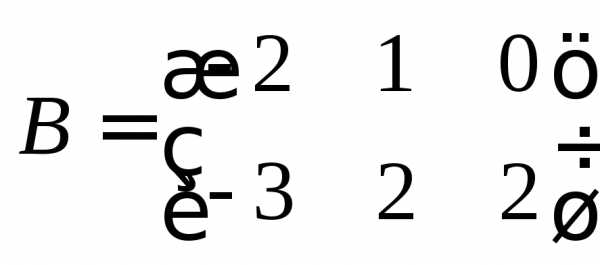 .
.
Пользуясь определением 7, получаем
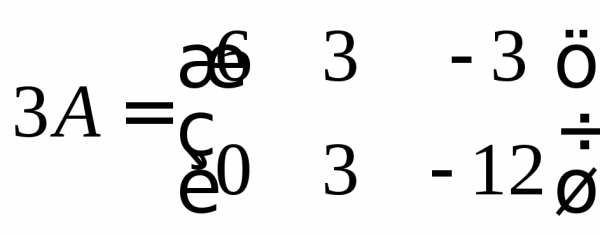 ,
,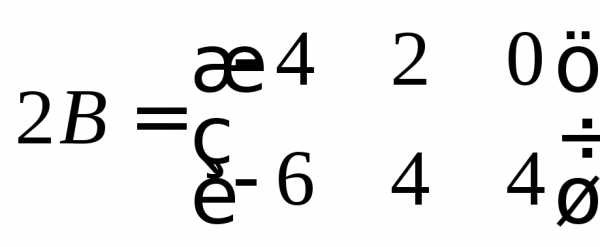 ,
,
далее привлекаем определение суммы матриц (определение 6):
.
Свойства операций сложения матриц
и умножения на число:
1. Сложение коммутативно: .
2. Сложение ассоциативно:.
3. Существует нулевая матрица  ,
удовлетворяющая условиюдля всехА.
,
удовлетворяющая условиюдля всехА.
4. Для любой матрицы Асуществует противоположная матрицаВ, удовлетворяющая условию.
Для любых матриц А иВи любых
действительных чисел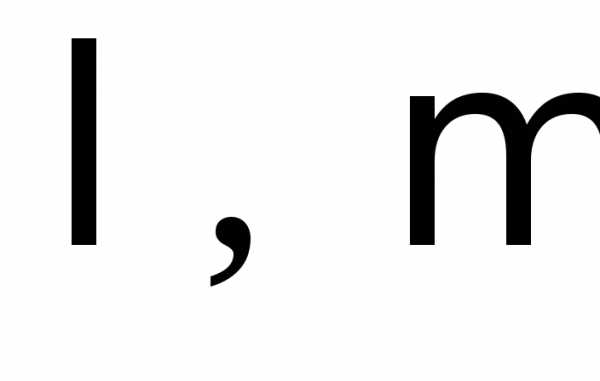 имеют место равенства:
имеют место равенства:
5. .
6. .
7. .
8. .
Проверим свойство 1. Обозначим
,.
Пусть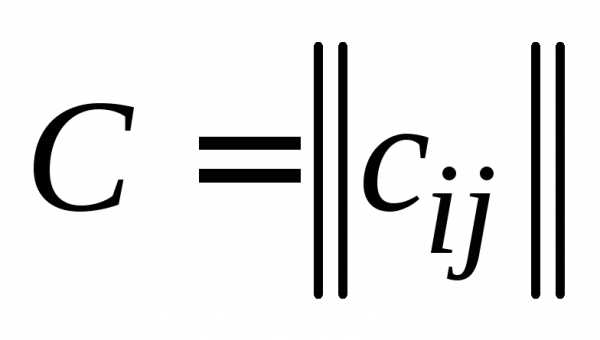 ,
,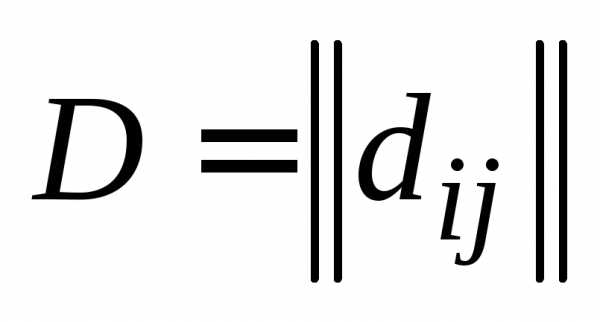 ,.
Имеем
,.
Имеем
,
и так как равенство доказано для
произвольного элемента, в соответствии
с определением 5 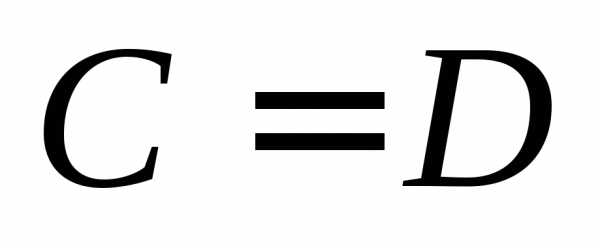 .
Свойство 1 доказано.
.
Свойство 1 доказано.
Аналогично доказывается свойство 2.
В качестве матрицы  возьмем матрицу порядка
возьмем матрицу порядка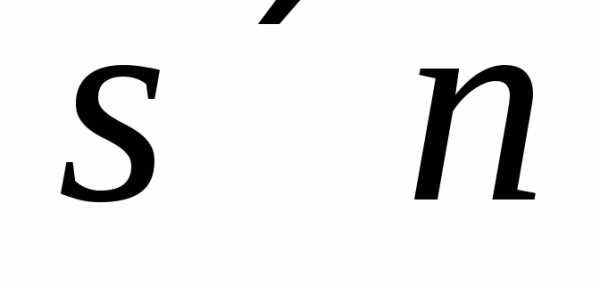 ,
все элементы которой равны нулю.
,
все элементы которой равны нулю.
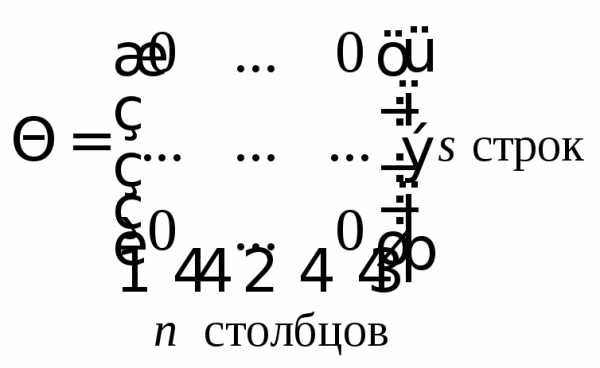
Сложив  с любой матрицей
с любой матрицей по правилу, данному в определении 6, мы
матрицу
по правилу, данному в определении 6, мы
матрицу не изменим, и свойство 3 справедливо.
не изменим, и свойство 3 справедливо.
Проверим свойство 4. Пусть  .
Положим
.
Положим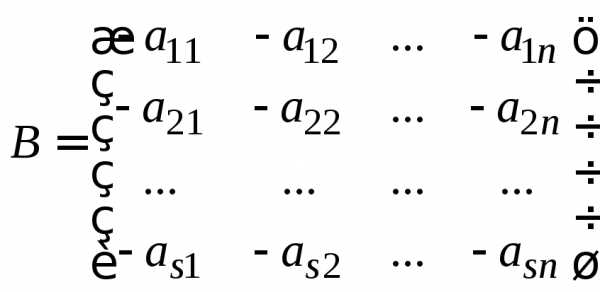 .
Тогда,
следовательно, свойство 4 справедливо.
.
Тогда,
следовательно, свойство 4 справедливо.
Проверку свойств 5 — 8 опустим.
Определение 8. Произведением
матрицы 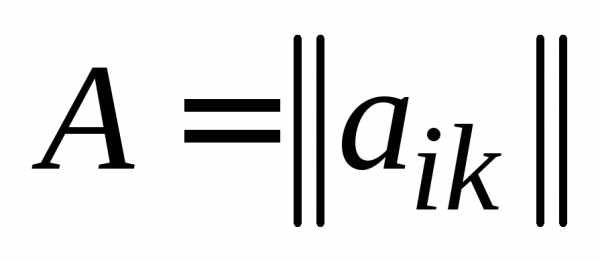 , , , на матрицу
, , , на матрицу 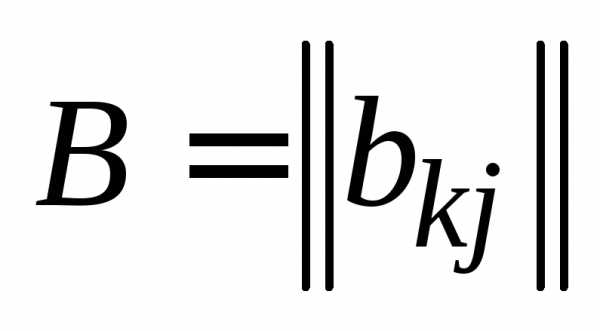 , , , называется матрица
, , , называется матрица 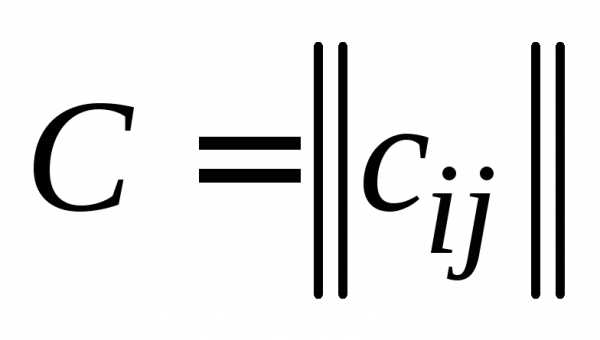 , , , с элементами
.
, , , с элементами
.
Краткая запись: 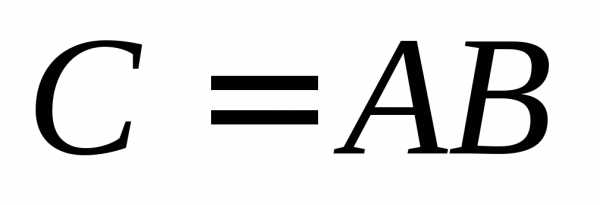 .
.
Пример 10. Найти произведение матриц
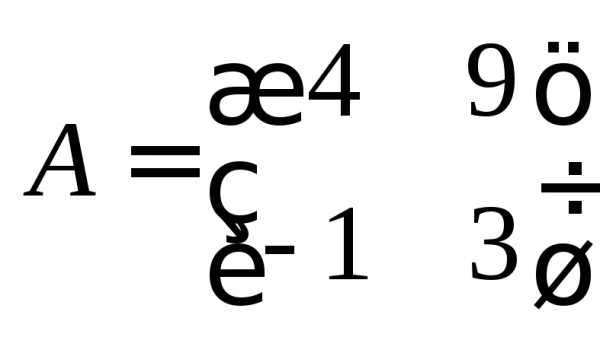 и
и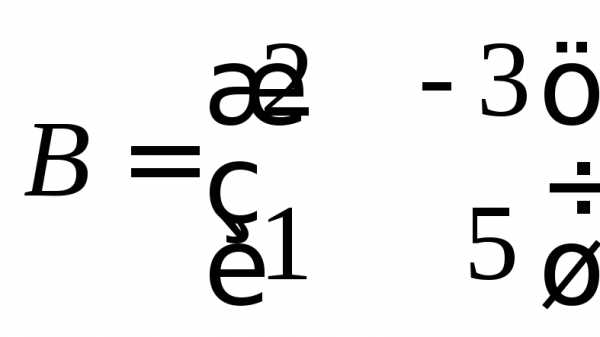 .
.
В соответствии с определением 8 найдем
.
Пример 11.Перемножить матрицы
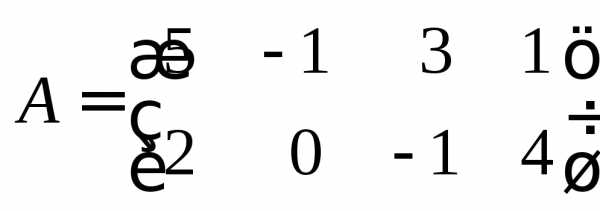 и
и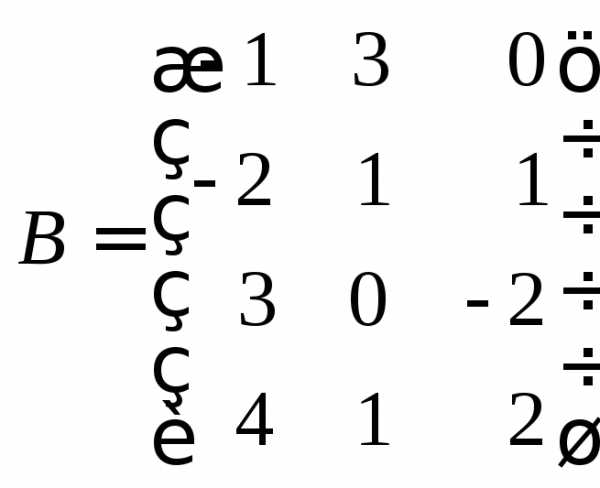 .
.
Имеем
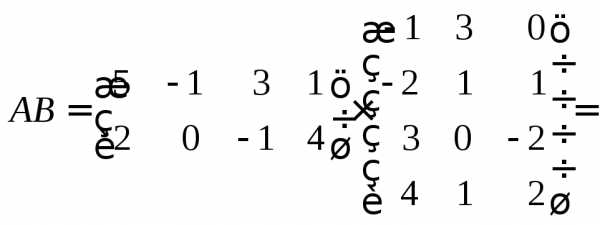
.
Замечание 1.Число элементов в строке матрицы равно числу элементов в столбце матрицы
равно числу элементов в столбце матрицы (число столбцов матрицы
(число столбцов матрицы равно числу строк матрицы
равно числу строк матрицы ).
).
Замечание 2.В матрице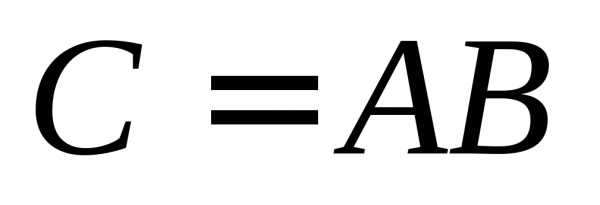 строк столько же, сколько в матрице
строк столько же, сколько в матрице ,
а столбцов столько же, сколько в
,
а столбцов столько же, сколько в .
.
Замечание 3. Вообще говоря,(умножение матриц некоммутативно).
Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.
Пример 12.Перемножим в обратном порядке матрицы и
и из примера 10.
из примера 10.
,
таким образом, в общем случае .
Отметим, что в частном случае равенство возможно.
Матрицы  и
и ,
для которых выполняется равенство,
называютсяперестановочными,иликоммутирующими.
,
для которых выполняется равенство,
называютсяперестановочными,иликоммутирующими.
Упражнения.
1. Найти все матрицы, перестановочные с данной:
а) 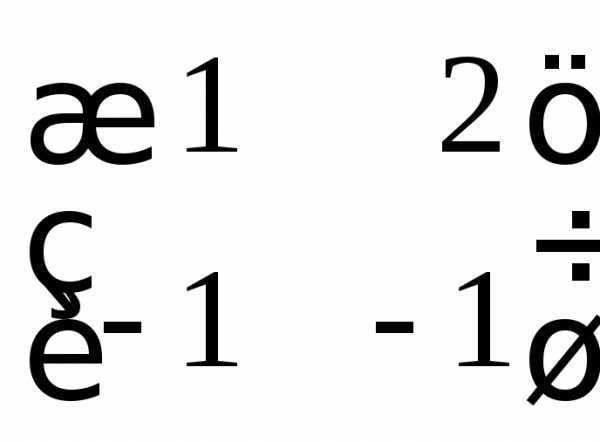 ;
б)
;
б) .
.
2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.
3. Доказать, что .
Свойства умножения матриц:
Умножение дистрибутивно:
studfiles.net
1 Курс, 1 семестр.
Лекции по высшей математике
Линейная алгебра
Лекция 1. Определители. (рассм. На прк)
Определителем второго порядка называется выражение:
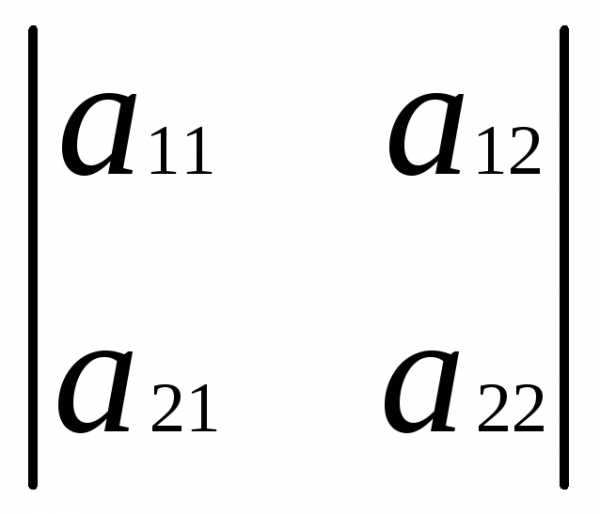 ,
равное a11a22—a12a21
,
равное a11a22—a12a21
Определителем третьего порядка называется выражение:
 , равное a11a22a33+a12a23a31+a12a21a32-a13a22a31-a12a21a33-a11a23a32
, равное a11a22a33+a12a23a31+a12a21a32-a13a22a31-a12a21a33-a11a23a32
Мнемоническое правило вычисления определителей (только третьего порядка)
+ —
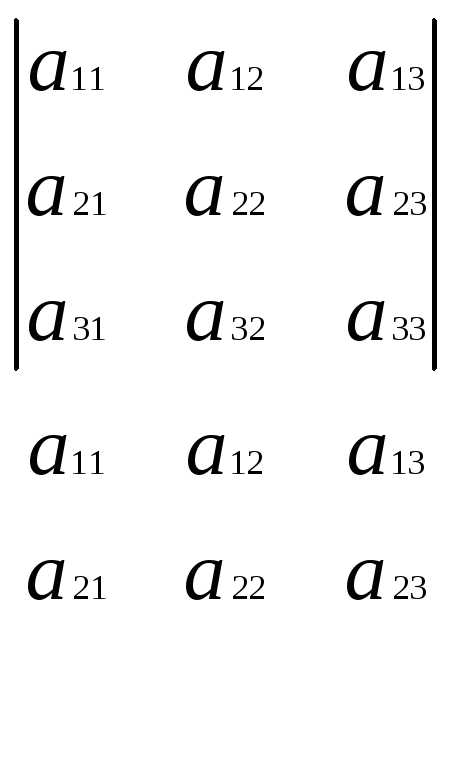
Свойства определителей (справедливы для определителей любого порядка)
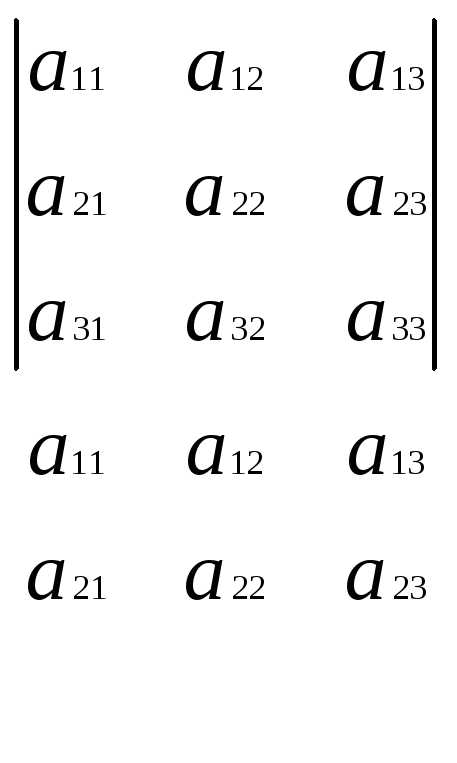
Определитель не меняется от замены строк столбцами (и наоборот)
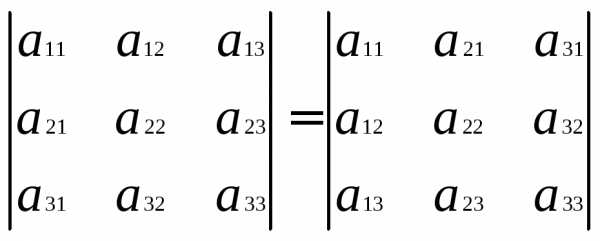
Если переставить две соседние строчки определителя, то он поменяет знак
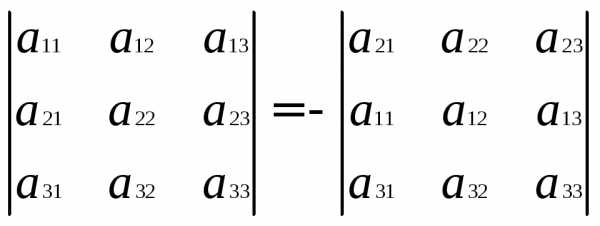
Если у определителя две одинаковые строчки или столбца, то он равен 0
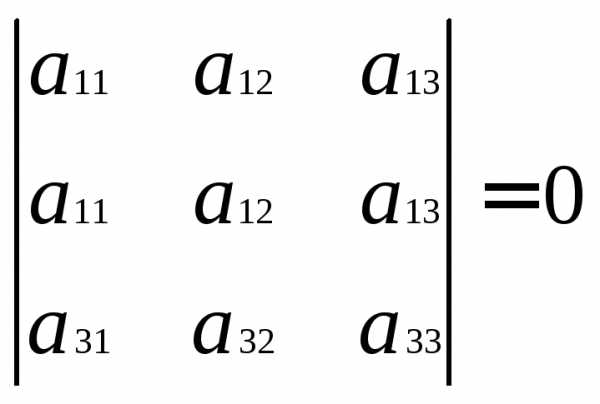
Если элементы строки или столбца умножить на k, то соответствующий определитель умножится на k
Если все элементы некоторой строчки или столбца равны 0, то определитель равен 0
Если элементы строчек или столбцов пропорциональны, то определитель равен 0
Если элементы строчки или столбца представлены в виде суммы aij+bij, то определитель можно представить в виде суммы двух, в соответствующей строчке (столбце) одного из них будет стоять aij, а другого – bij
Если к какой-либо строчке или столбцу определителя прибавить другую строчку или столбец определителя, умноженную на k, то определитель от этого не изменится
Определитель можно разложить по строчке или столбцу:
Минором Mij определителя n-го порядка называется определитель порядка n-1, получающийся вычеркиванием i-той строчки и j-того столбца.
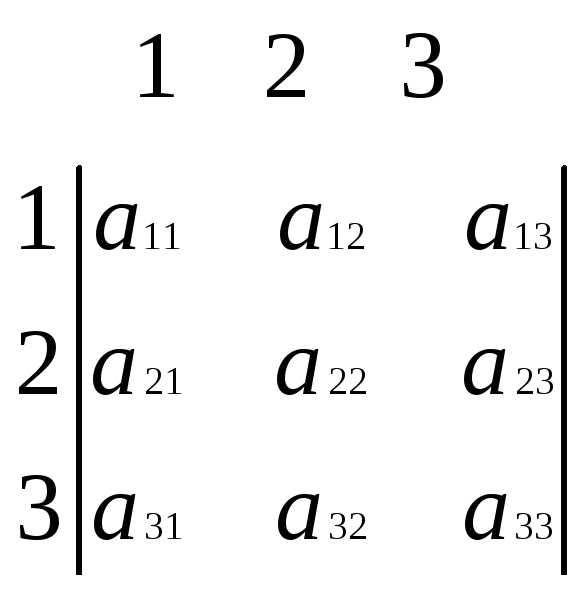 ,
, 
Алгебраическим дополнением Aij называют выражение Aij=(-1)i+jMij. Знаки алгебраических дополнений:
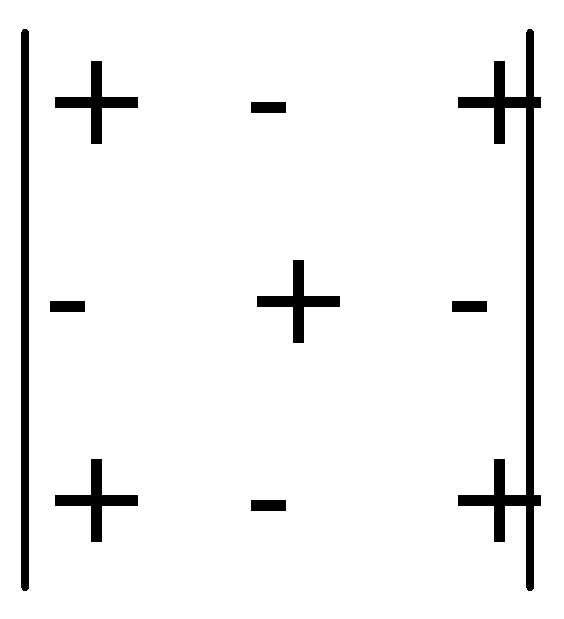
Разложение определителя по строке или столбцу:
Более подробно эта формула запишется в таком виде (это разложение по первой строке):
Вычисление определителей 4-го и более высоких порядков.
Для вычисления определителей порядка выше третьего используется метод разложения определителя по строке или столбцу, который позволяет понизить порядок вычисляемых определителей. Понизив порядок определителей до 3-го (или 2-го) используют описанные выше способы их вычисления.
Задача. Вычислить определитель 4-го порядка  .
.
Решение. Сначала найдем в заданном определителе такую строку (или столбец), в которой содержится наибольшее число нулевых элементов. В данной задаче это четвертая строка (или четвертый столбец). Для определенности будем проводить разложение по четвертой строке, образуем сумму, состоящую из произведений элементов этой строки на соответствующее алгебраическое дополнение.
Вычислим миноры нужных элементов.
Соответствующие алгебраические дополнения: ,
Вычислим данный определитель:
Замечание. Вычисление определителя, например, 6-го порядка, сначала сводится к вычислению определителей 5-го порядка, которые затем сводятся к определителям 4го порядка, каждый из которых вычисляется как показано выше. Таким образом, можно вычислять определители любого (конечного) порядка.
Векторная алгебра.
Лекция 2. Понятие геометрического вектора. Проекции координат вектора. Направляющие косинусы вектора. Операции над геометрическими векторами. Разложение вектора по базису.
Коллинеарность и компланарность векторов.
1.Понятие геометрического вектора.
Под геометрическим
вектором 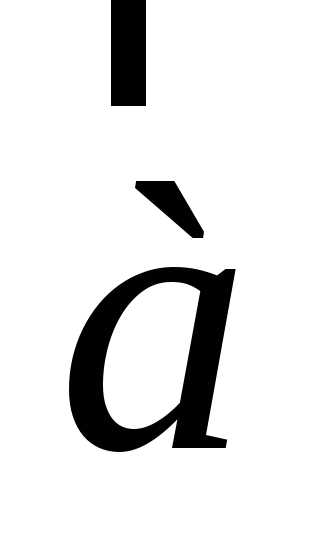 мы
будем понимать совокупность равных и
одинаково направленных отрезков.
Геометрический вектор однозначно
определяется заданием его длины и
направления на плоскости –R2 – или в пространстве – R3.
мы
будем понимать совокупность равных и
одинаково направленных отрезков.
Геометрический вектор однозначно
определяется заданием его длины и
направления на плоскости –R2 – или в пространстве – R3.
2.Проекция вектора на ось
Проекцией
вектора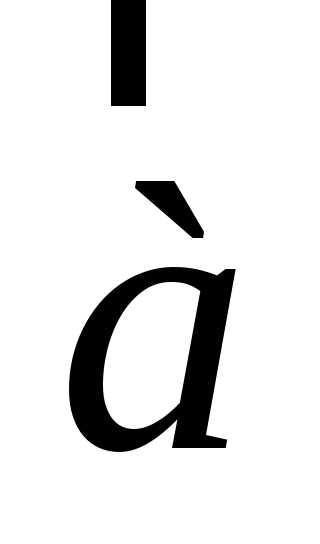 на
осьOx называется вектор
на
осьOx называется вектор 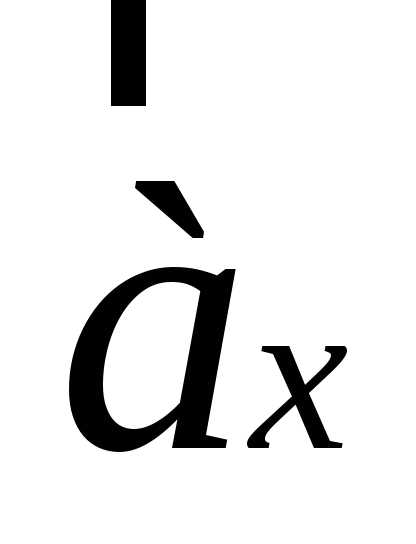 ,
который сонаправлен с осьюOx или
противоположно направлен ей и имеет
длину
,
где
,
который сонаправлен с осьюOx или
противоположно направлен ей и имеет
длину
,
где — угол между направлением вектора
— угол между направлением вектора и
осьюOx.
и
осьюOx.
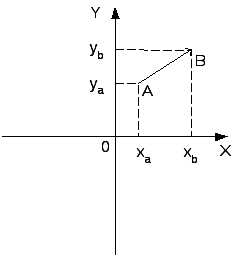

3.Длина и направляющие косинусы вектора
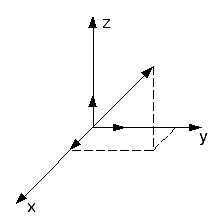 Проекции вектора
Проекции вектора 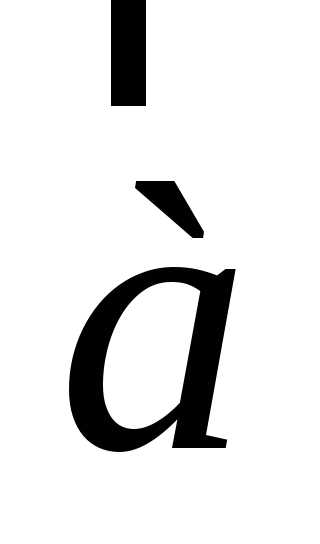 на
оси системы координат можно задать
двумя способами.
на
оси системы координат можно задать
двумя способами.
 — координатами.
— координатами.— в виде разложения вектора по ортам системы координат.
В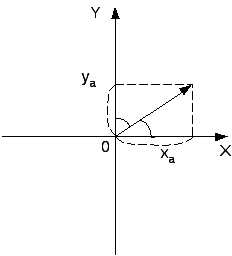 ектор
ектор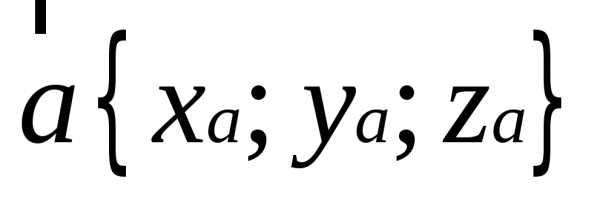 имеет длину
имеет длину
Под направляющими
косинусами
мы будем понимать косинусы углов между
осями системы координат и направлением
данного вектора.  —
угол между осьюOx
и направлением вектора,
—
угол между осьюOx
и направлением вектора, 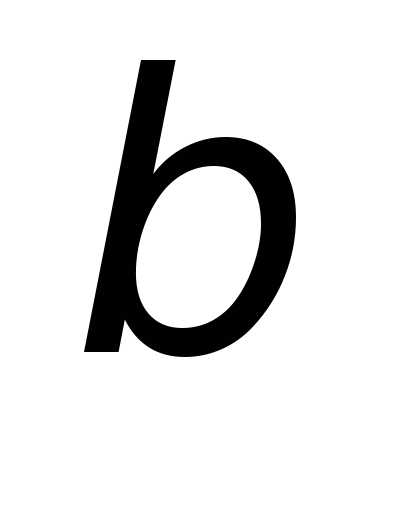 —
угол между осьюOy
и направлением вектора,
—
угол между осьюOy
и направлением вектора,  —
угол между осьюOz
и направлением
вектора.
—
угол между осьюOz
и направлением
вектора.
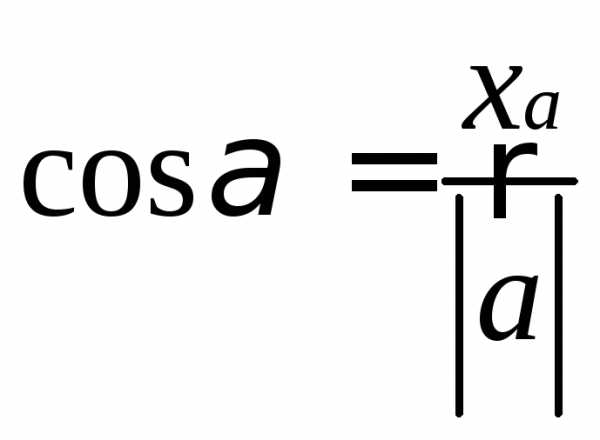
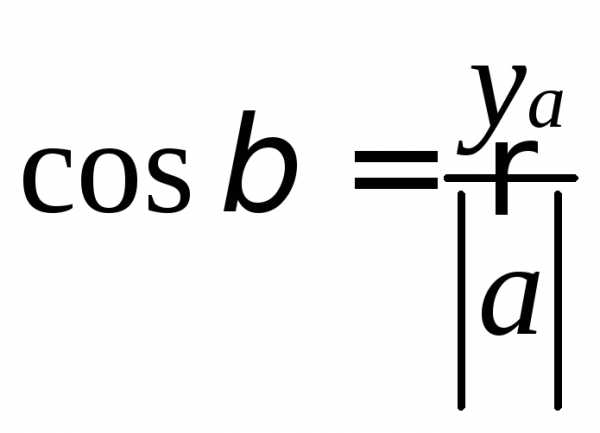

Для направляющих
косинусов выполняется тождество
.
Действительно, подставив вместо ,
,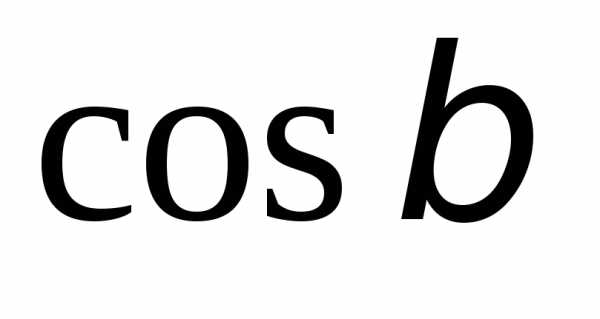 и
и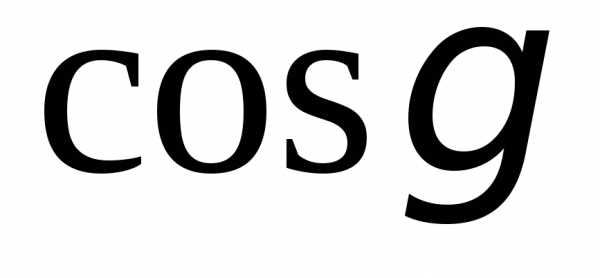 их определения через отношение
соответствующей проекции вектора к его
длине, получим:
их определения через отношение
соответствующей проекции вектора к его
длине, получим:
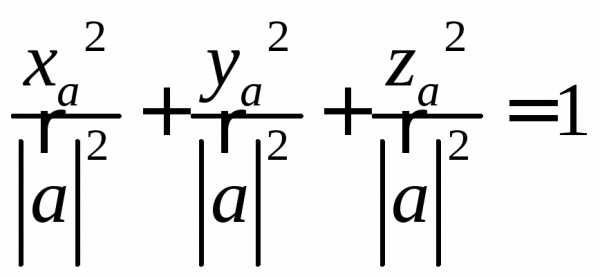
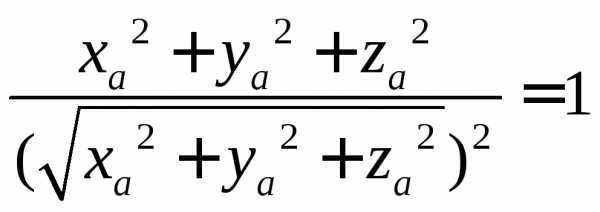
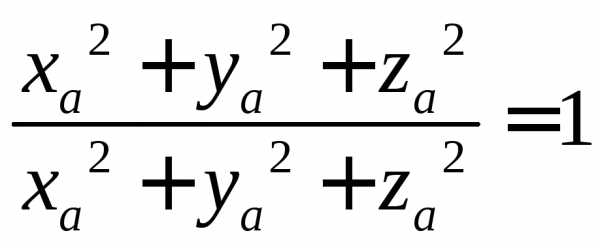
Понятие направляющих
косинусов тесно связано с понятием орта
вектора. Вектор 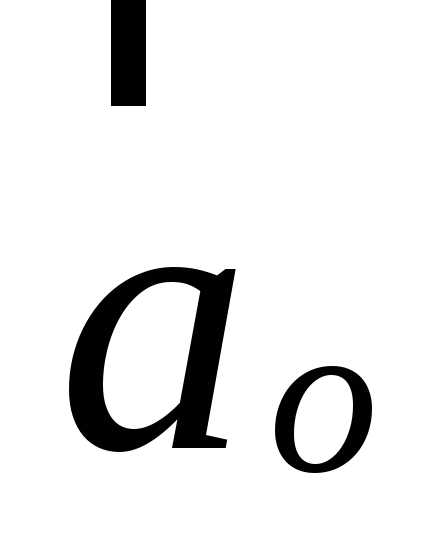 будем называть ортом вектора
будем называть ортом вектора ,
если он имеет единичную длину и такое
же направление, что и вектор
,
если он имеет единичную длину и такое
же направление, что и вектор .
.
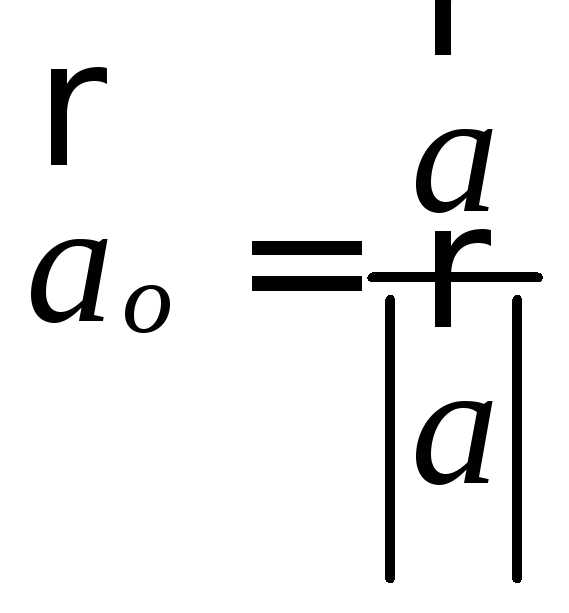
4.Операции над геометрическими векторами
Вектор 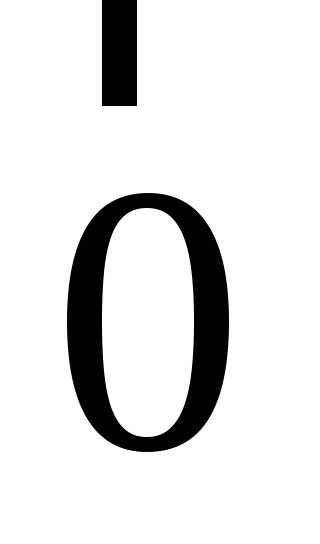 ,
начало которого совпадает с концом,
будем называть нулевым.
,
начало которого совпадает с концом,
будем называть нулевым.
Вектор 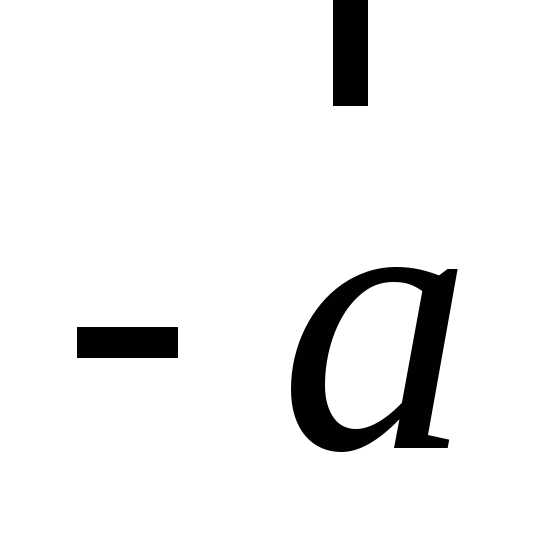 ,
имеющий ту же длину, что и
,
имеющий ту же длину, что и и противоположно ему направленный,
будем называть противоположным вектором.
и противоположно ему направленный,
будем называть противоположным вектором.
Умножение вектора на число.
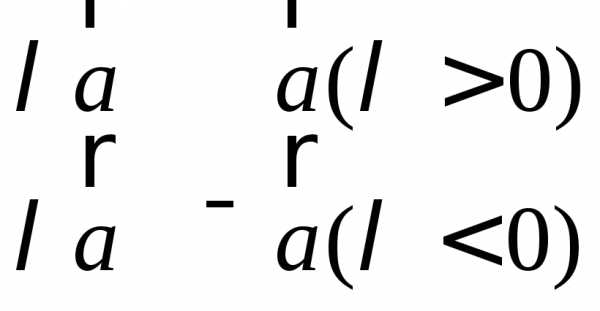
При умножении вектора на число нужно все его координаты умножить на это число:
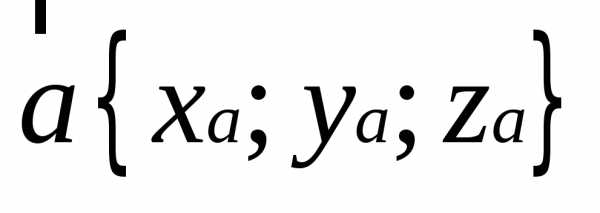
Сложение векторов.
Два вектора складываются по правилу треугольника или по правилу параллелограмма.
В координатах
сумма вектора  и вектора
и вектора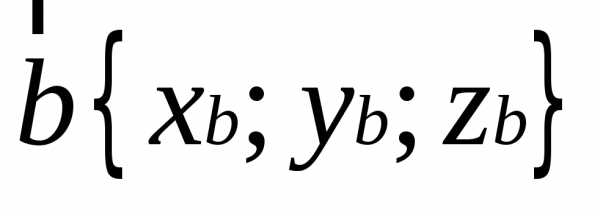 имеет координаты
имеет координаты
5. Свойства операций над векторами
5.1 Свойства умножения вектора на число:
5.2 Свойства сложения векторов:
(коммутативность, или перестановочность сложения)
(дистрибутивность относительно числа)
(дистрибутивность относительно векторов)
Множество всех векторов с вышеперечисленными свойствами называется векторным пространством.
6. Коллинеарность и компланарность векторов
6.1 Коллинеарность векторов
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных. Нулевой вектор коллинеарен любому вектору.
Условие коллинеарности векторов в координатах:

Два вектора в пространстве коллинеарны друг другу, если отношение их соответствующих координат постоянно.
6.2 Компланарность векторов
Три ненулевых вектора называются компланарными если они, будучи приведенными к одному началу, лежат в одной плоскости. Если хотя бы один из векторов нулевой, то вся тройка компланарна.
Необходимое и достаточное условие компланарности векторов с координатами

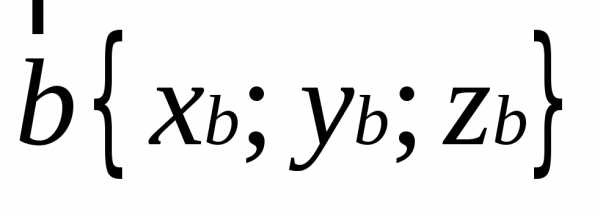
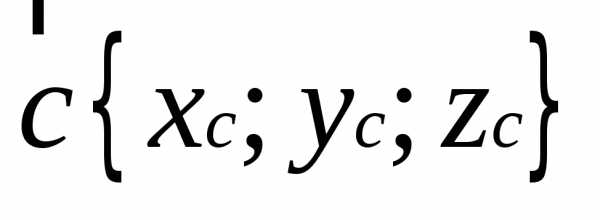 записывается в
виде:
записывается в
виде:
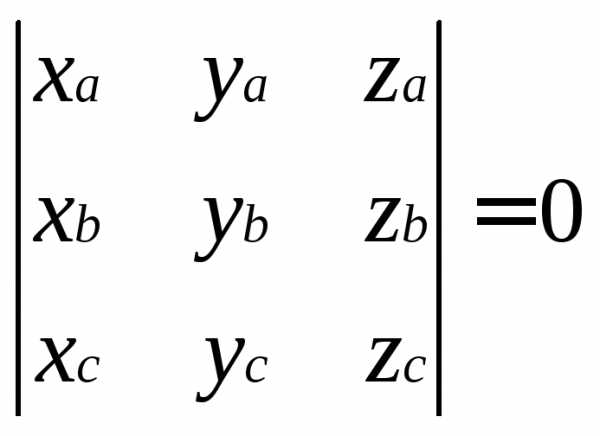
Оно вытекает из свойств смешанного произведения векторов, которое будет рассмотрено далее.
7. Базисы R2 и R3. Разложение вектора по базису.
Два (три ) вектора называют базисными R2 (R3), если произвольный вектор из R2 (R3) можно разложить через базисные, а сами векторы друг через друга не выражаются.
Два неколлинеарных
вектора на плоскости образуют базис
R2.
В этом случае разложение вектора 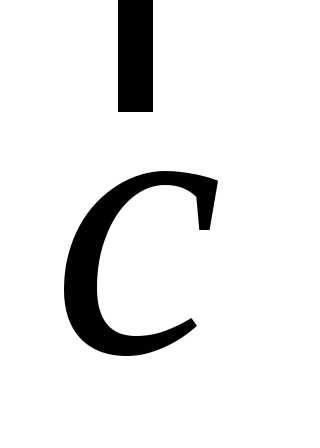 по
базису
по
базису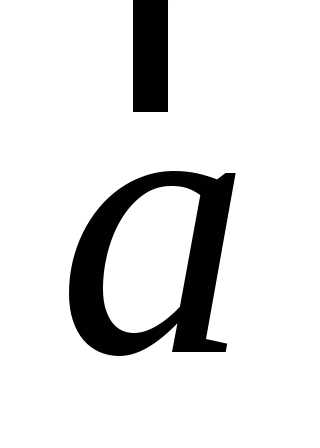 ,
,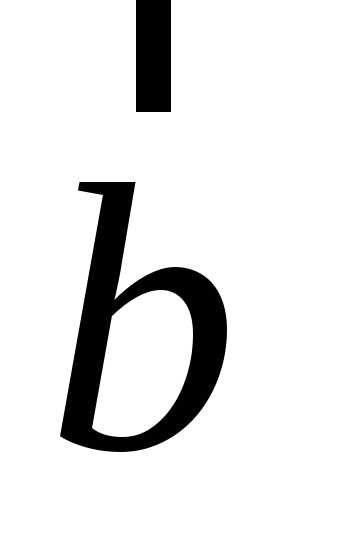 можно представить в виде,
где
и
– коэффициенты разложения.
можно представить в виде,
где
и
– коэффициенты разложения.
Тройка некомпланарных векторов образует базис R3.
Пример разложения
вектора 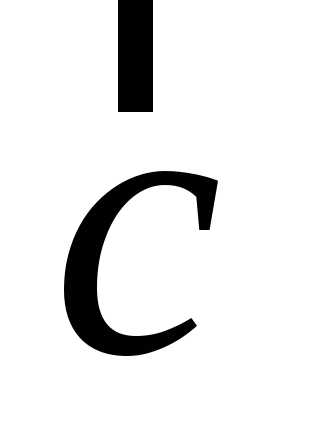 по базису
по базису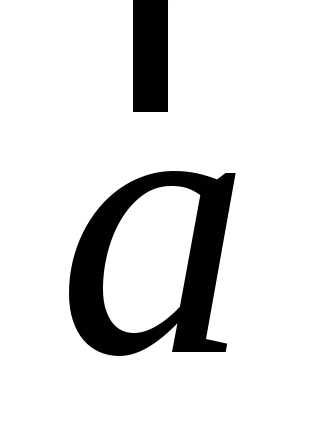 ,
,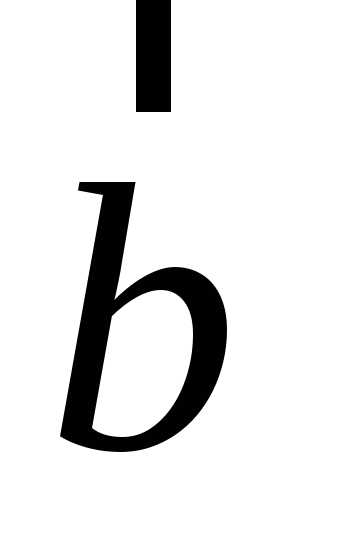 на
плоскости:
на
плоскости:
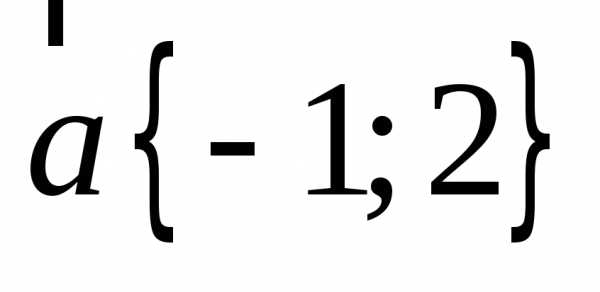
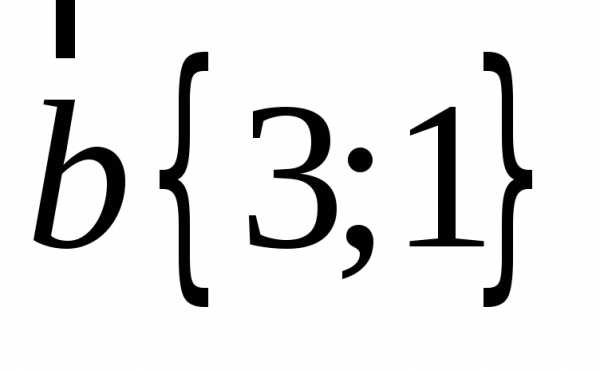
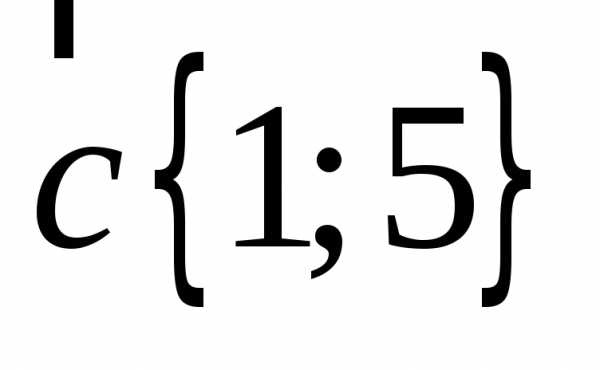
Проверяем неколлинеарность базисных векторов:
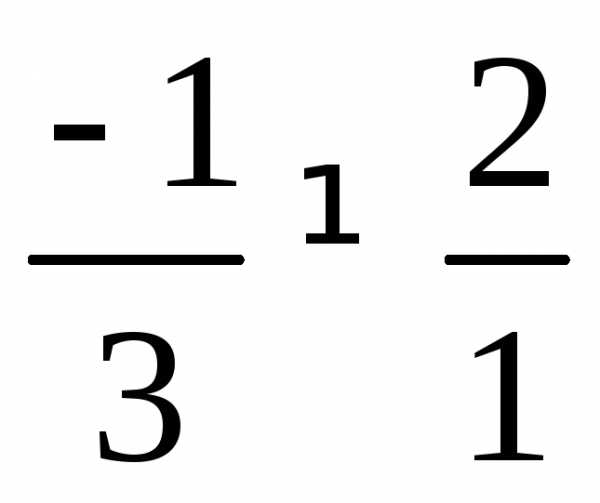 ,
значит базисные вектора неколлинеарны
и возможно разложение единственным
образом.
,
значит базисные вектора неколлинеарны
и возможно разложение единственным
образом.
Представим вектор
 в виде,
тогда можно написать:,
или в виде системы двух уравнений:
в виде,
тогда можно написать:,
или в виде системы двух уравнений:
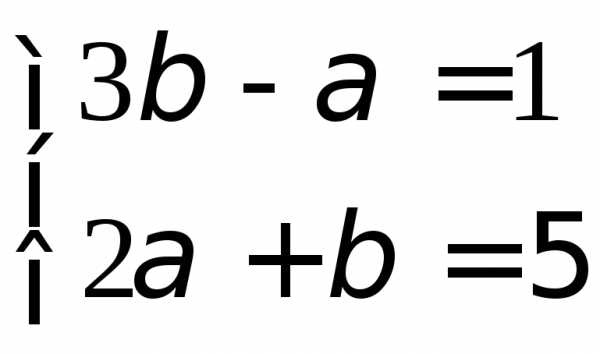 ,
решая которую найдем =2,
.
Таким образом,
,
решая которую найдем =2,
.
Таким образом, 
studfiles.net
МП-1 / Практ. по алгебре / Практикум по алгебре в среде MATLAB_Жаркова / ржавинская лекции / Лекция_6
Лекция 6
Матрицы
Определение и некоторые свойства определителей порядка n. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства этих операций |
6.1. Основные понятия
Определение 1.Матрицей называется прямоугольная таблица чисел.
Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:
.
Числа, составляющие матрицу, называются
ее элементами, элемент матрицы
матрицы расположен в ее
расположен в ее -й
строке и
-й
строке и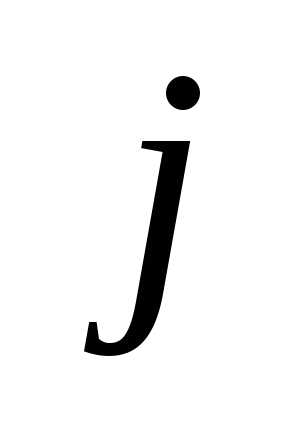 -м
столбце.
-м
столбце.
Числа  и
и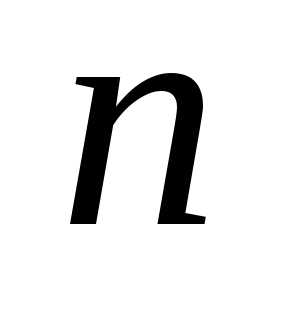 (число строк и столбцов матрицы) называются
ее порядками.
(число строк и столбцов матрицы) называются
ее порядками.
Говорят также, что  — матрица размером
— матрица размером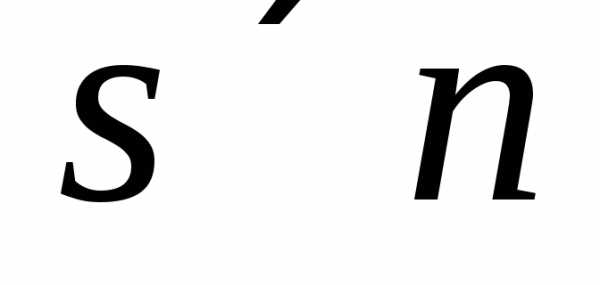 .
.
Если 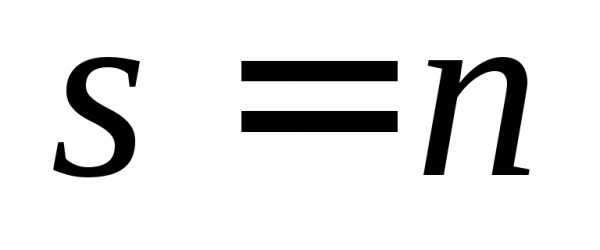 ,
матрица
,
матрица называетсяквадратной.
называетсяквадратной.
Для краткой записи используется также
обозначение
(или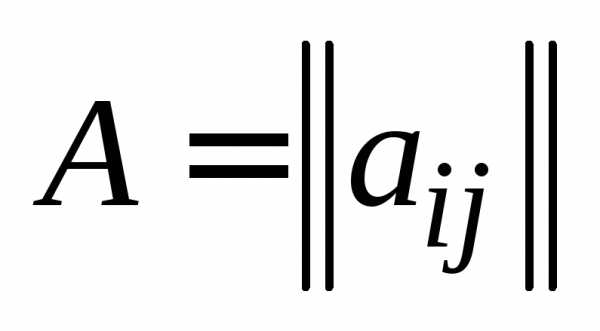 )
и далее указывается, в каких пределах
изменяются
)
и далее указывается, в каких пределах
изменяются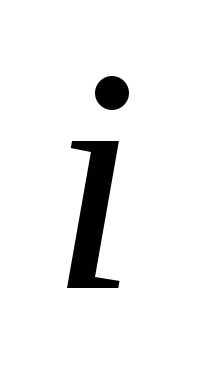 и
и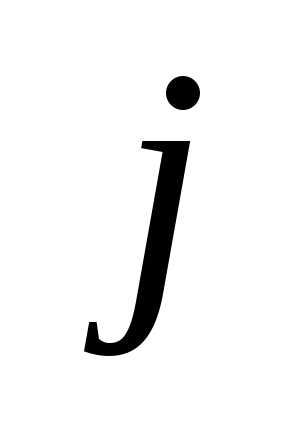 ,
например,
,
например,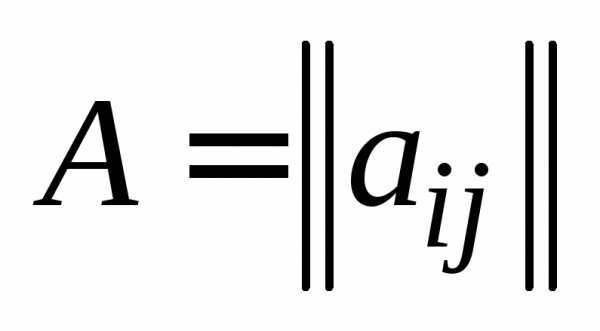 ,,.
(Запись читается так: матрица
,,.
(Запись читается так: матрица с элементами
с элементами ,
,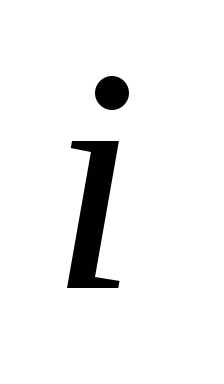 изменяется от
изменяется от до
до ,
, — отдо
— отдо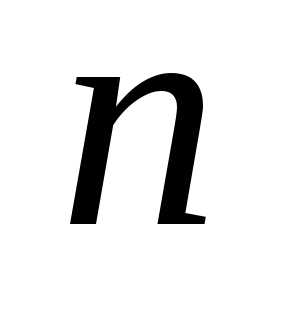 .)
.)
Среди квадратных матриц отметим диагональные матрицы, у которых все
элементы с неравными индексами (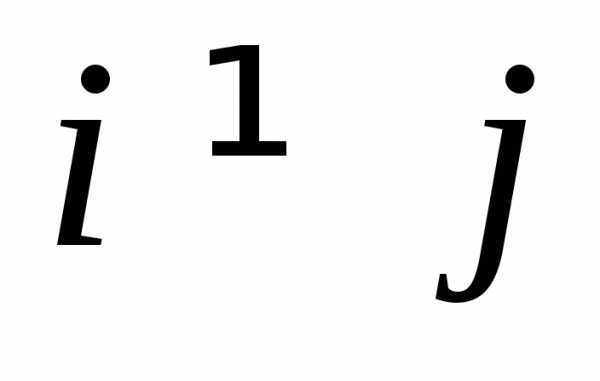 )
равны нулю:
)
равны нулю:
 .
.
Будем говорить, что элементы расположены на главной диагонали.
Диагональная матрица вида

называется единичнойматрицей.
В дальнейшем будут встречаться матрицы вида
 и
и ,
,
которые называются треугольнымиматрицами, а также матрицы, состоящие из одного столбца:
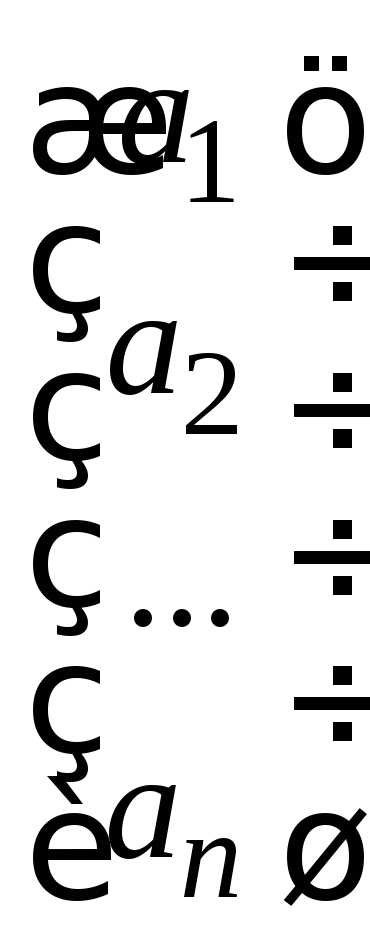
и одной строки:
(матрица-столбец и матрица-строка).
Матрица, все элементы которой равны нулю, называется нулевой.
6.2. Определители порядка n
Пусть дана квадратная матрица порядка 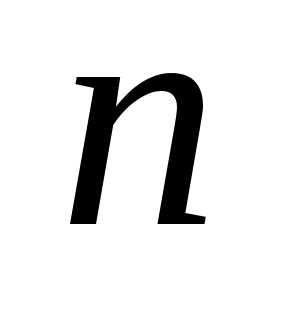 :
:
 .
(6.1)
.
(6.1)
Составим всевозможные произведения 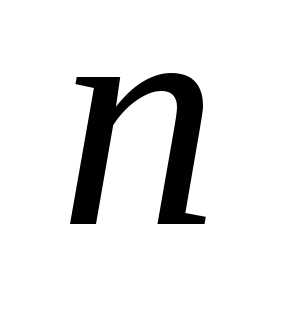 элементов матрицы, расположенных в
разных строках и разных столбцах, т.е.
произведения вида
элементов матрицы, расположенных в
разных строках и разных столбцах, т.е.
произведения вида
. (6.2)
Число произведений вида (6.2) равно 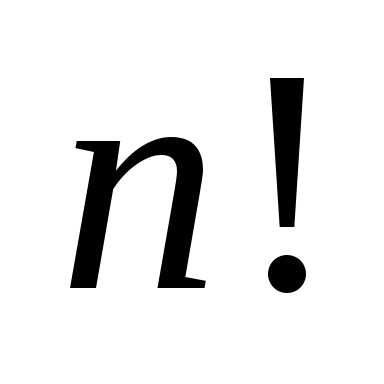 (примем этот факт без доказательства).
(примем этот факт без доказательства).
Будем считать все эти произведения
членами определителя порядка 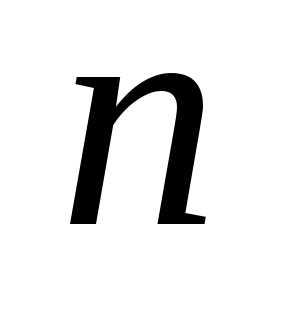 ,
соответствующего матрице (6.1).
,
соответствующего матрице (6.1).
Вторые индексы множителей в (6.2) составляют
перестановку первых 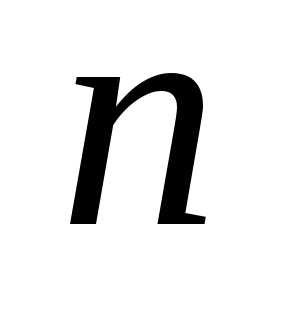 натуральных чисел
натуральных чисел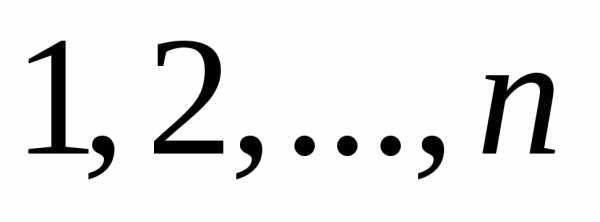 .
.
Говорят, что числа 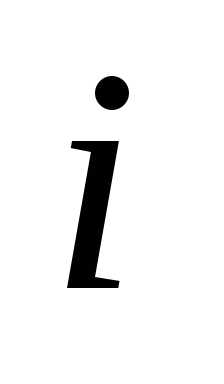 и
и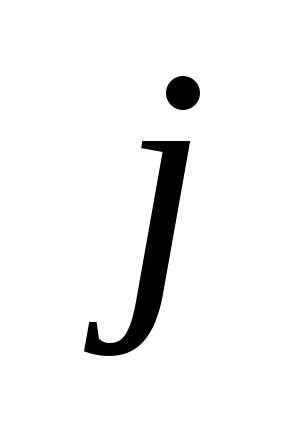 в перестановке составляютинверсию,
если
в перестановке составляютинверсию,
если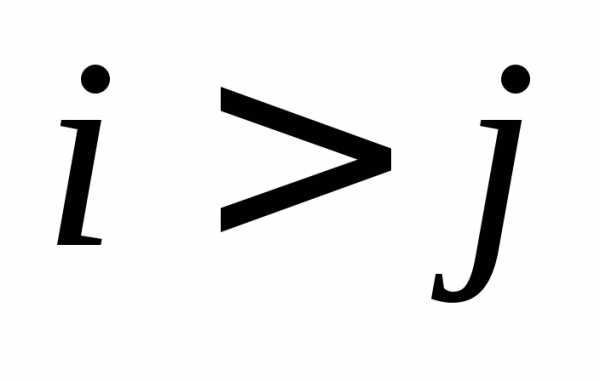 ,
а в перестановке
,
а в перестановке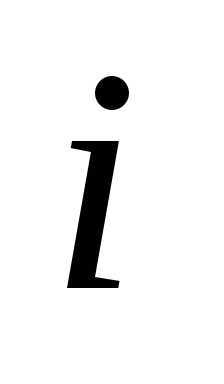 расположено раньше
расположено раньше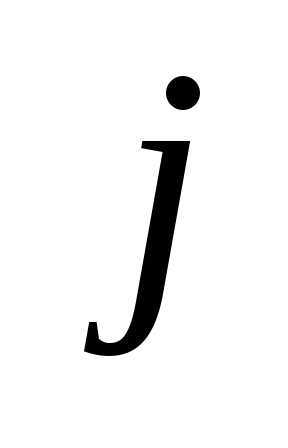 .
.
Пример 1.В
перестановке шести чисел,,
числа и
и ,
, и
и ,
, и
и ,
, и
и ,
, и
и составляют инверсии.
составляют инверсии.
Перестановка называется четной, если число инверсий в ней четно, инечетной, если число инверсий в ней нечетно.
Пример 2.Перестановка- нечетная, а перестановка- четная (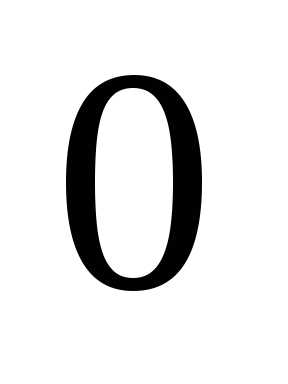 инверсий).
инверсий).
Определение 2.Определителем
порядка 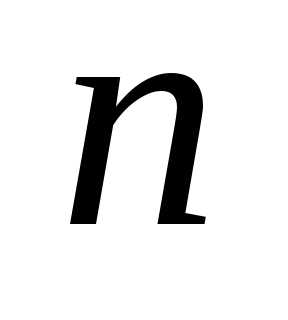 , соответствующим матрице (6.1),
называется алгебраическая сумма
, соответствующим матрице (6.1),
называется алгебраическая сумма 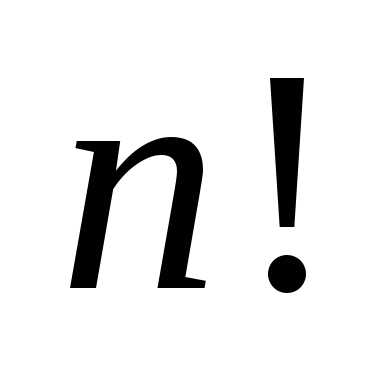 членов, составленная следующим
образом: членами определителя служат
всевозможные произведения
членов, составленная следующим
образом: членами определителя служат
всевозможные произведения 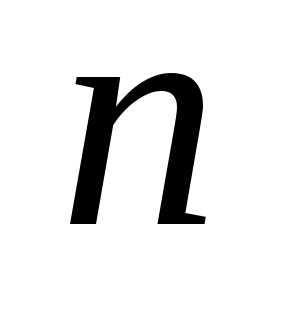 элементов матрицы, взятых по одному
из каждой строки и каждого столбца, причем слагаемое берется со знаком «+», если множество вторых индексов является
четной перестановкой чисел
элементов матрицы, взятых по одному
из каждой строки и каждого столбца, причем слагаемое берется со знаком «+», если множество вторых индексов является
четной перестановкой чисел 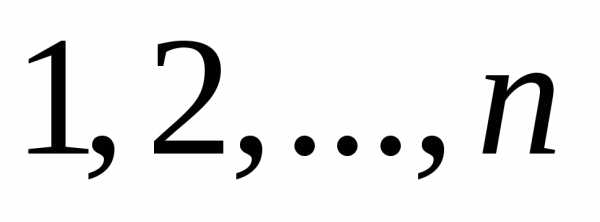 , и со знаком «–», если нечетной.
, и со знаком «–», если нечетной.
Обозначать определитель матрицы (6.1) принято так:
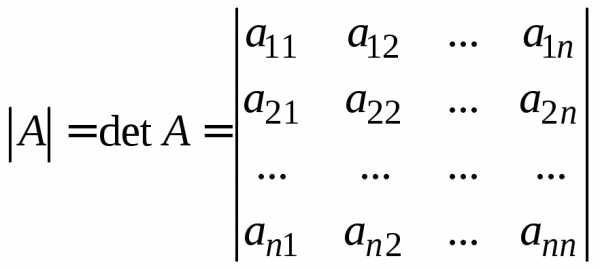 .
.
Замечание.Определение 2 для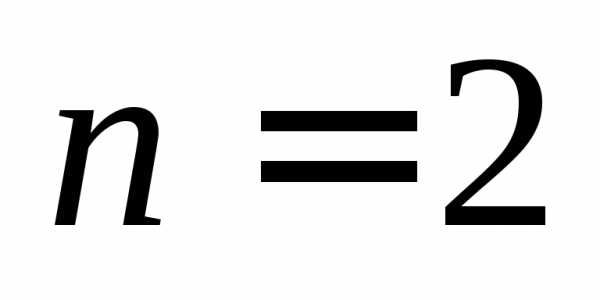 и
и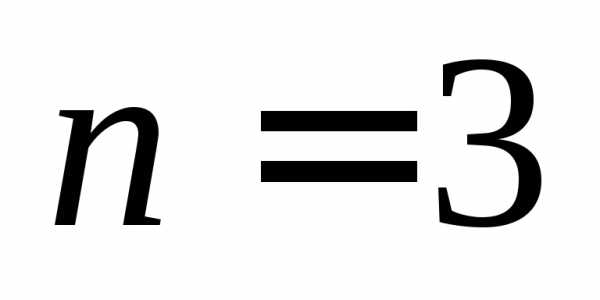 приводит к уже знакомым нам определителям
2-го и 3-го порядка:
приводит к уже знакомым нам определителям
2-го и 3-го порядка:
,
.
Транспонированием вокруг главной
диагонали матрицы называется переход к матрице
называется переход к матрице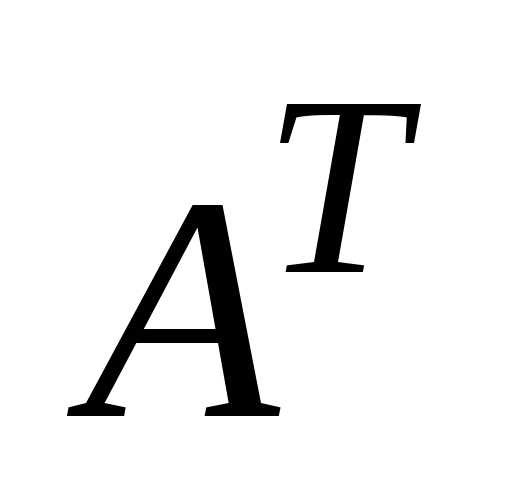 ,
для которой строки матрицы
,
для которой строки матрицы являются столбцами, а столбцы — строками:
являются столбцами, а столбцы — строками:
 .
.
Будем говорить, что определитель 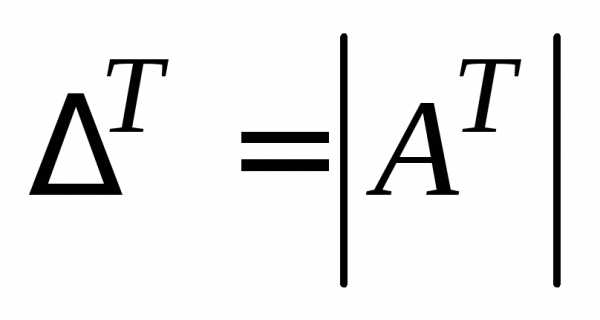 получен транспонированием определителя
получен транспонированием определителя .
.
Свойства определителя порядка п:
1. 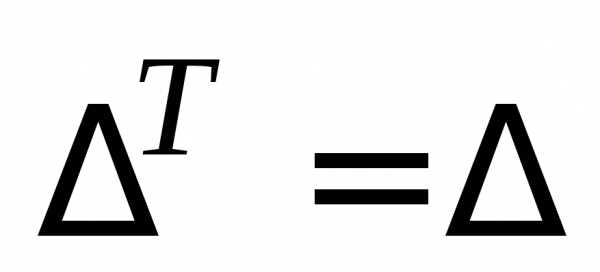 (определитель не меняется при
транспонировании вокруг главной
диагонали).
(определитель не меняется при
транспонировании вокруг главной
диагонали).
2. Если одна из строк определителя состоит из нулей, определитель равен нулю.
3. От перестановки двух строк определитель меняет лишь знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки
определителя умножить на число 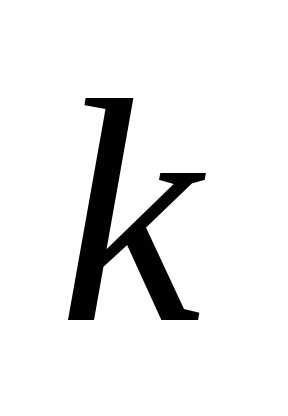 ,
определитель умножится на
,
определитель умножится на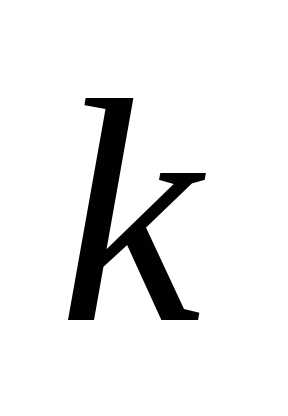 .
.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы  -й
строки определителя представлены в
виде суммы,
то определитель равен сумме двух
определителей, у которых все строки,
кроме
-й
строки определителя представлены в
виде суммы,
то определитель равен сумме двух
определителей, у которых все строки,
кроме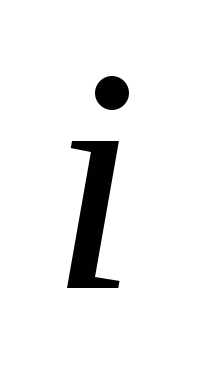 -й,
такие же, как в исходном определителе,
а
-й,
такие же, как в исходном определителе,
а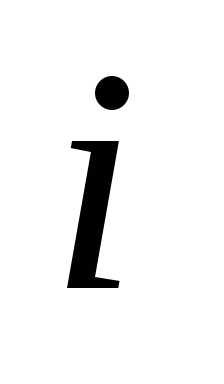 -я
строка в одном определителе состоит
из
-я
строка в одном определителе состоит
из ,
а в другом — из
,
а в другом — из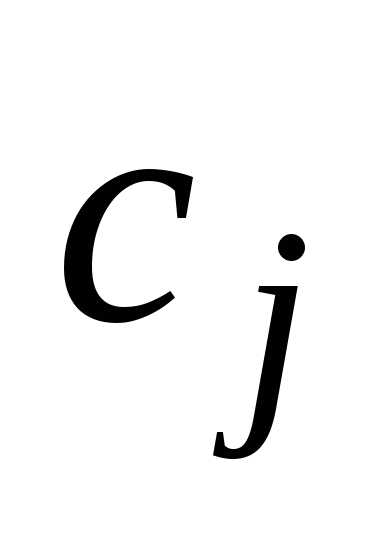 .
.
Определение 3.-я
строка определителя называется линейной
комбинацией остальных его строк, если
такие, что, умножая 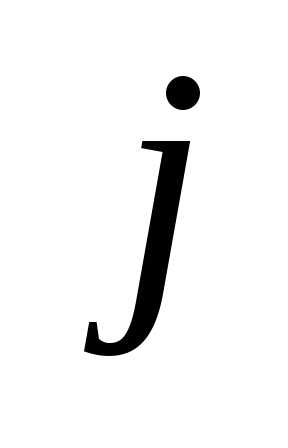 -ю
строку на
-ю
строку на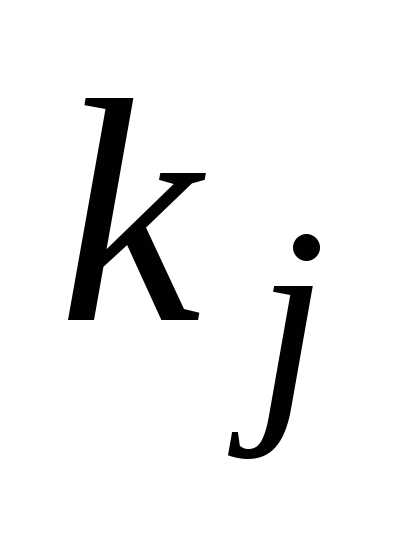 , а затем складывая все строки, кроме
, а затем складывая все строки, кроме 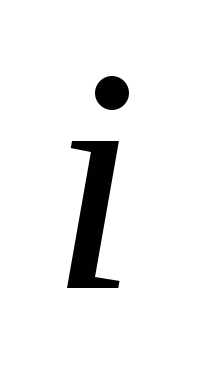 -й, получаем
-й, получаем 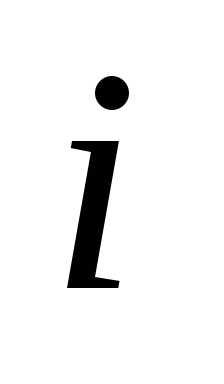 -ю
строку.
-ю
строку.
8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.
9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.
Замечание.Мы сформулировали свойства определителя
для строк. В силу свойства 1 (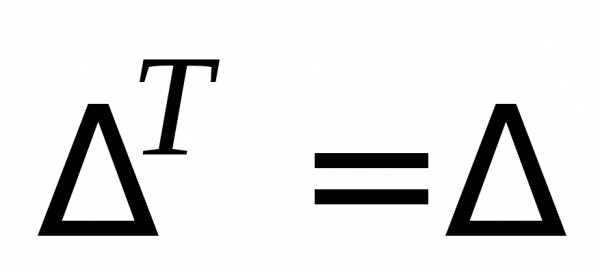 )
они справедливы и для столбцов.
)
они справедливы и для столбцов.
Все приведенные свойства были доказаны
на практических занятиях для 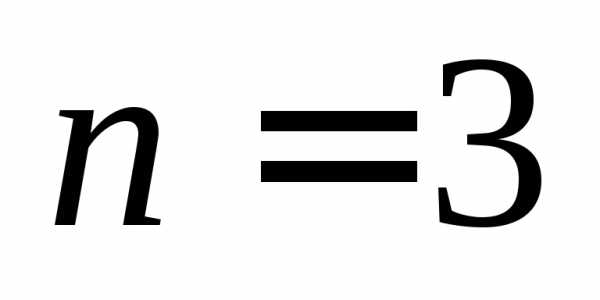 ;
для произвольного
;
для произвольного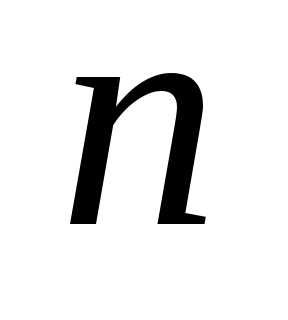 примем их без доказательства.
примем их без доказательства.
Если в определителе  порядка
порядка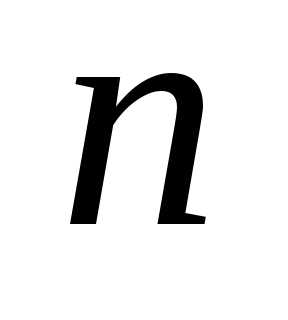 выбрать элемент
выбрать элемент и вычеркнуть столбец и строку, на
пересечении которых расположен
и вычеркнуть столбец и строку, на
пересечении которых расположен ,
оставшиеся строки и столбцы образуют
определитель порядка
,
оставшиеся строки и столбцы образуют
определитель порядка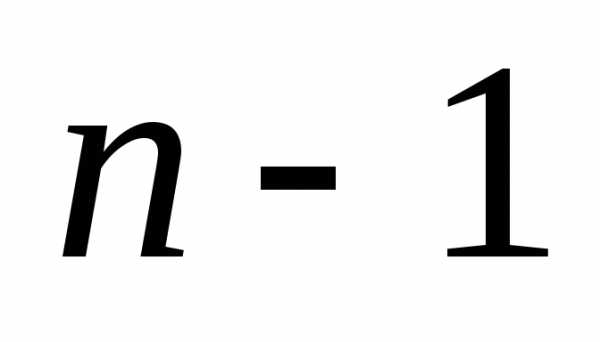 ,
который называетсяминором определителя
,
который называетсяминором определителя ,
соответствующим элементу
,
соответствующим элементу .
.
Пример 3.В определителе
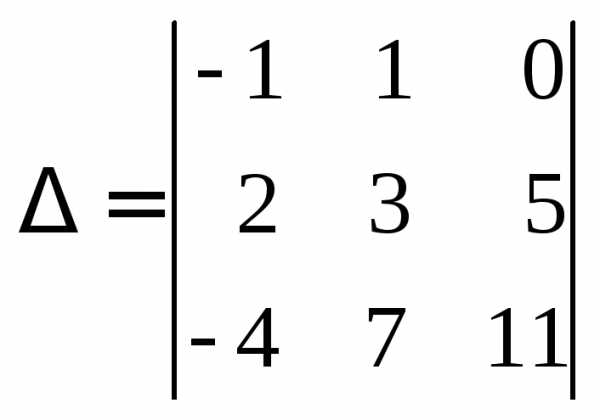
минором элемента 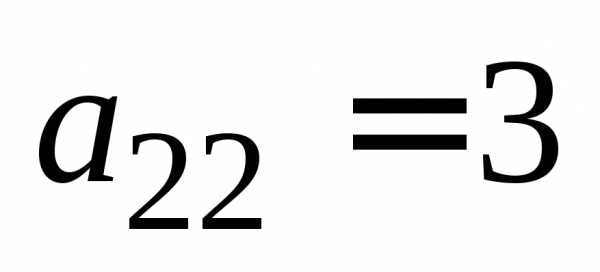 является определитель
является определитель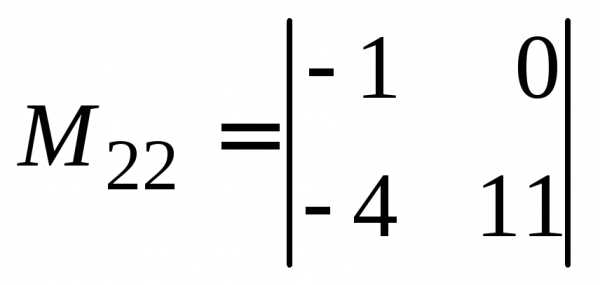 .
.
Определение 4.Алгебраическим
дополнением  элемента
элемента определителя
определителя называется его минор, умноженный
на
называется его минор, умноженный
на 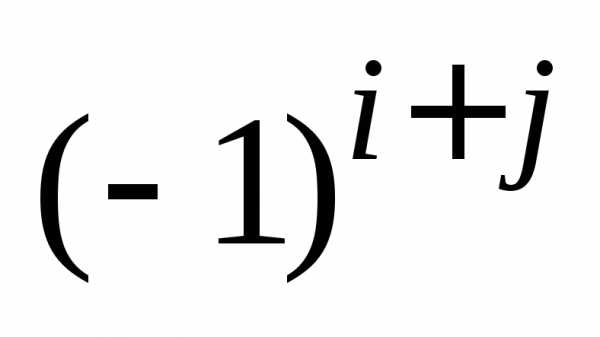 , где
, где  — номер строки,
— номер строки, 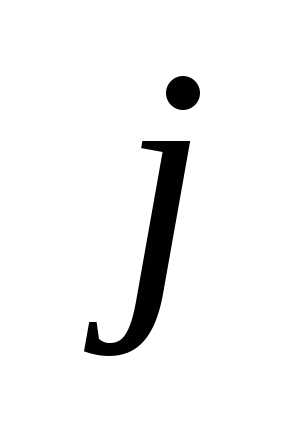 — номер столбца, в которых расположен
выбранный элемент
— номер столбца, в которых расположен
выбранный элемент  .
.
Пример 4. В определителе
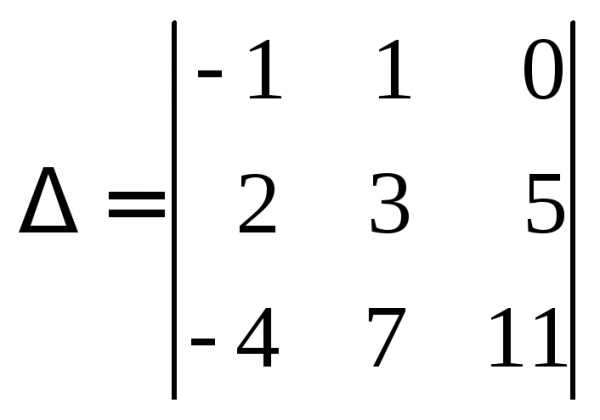
алгебраическое дополнение .
Теорема 1 (о разложении по строке).Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.
Теорема 1 позволяет свести вычисление
определителя порядка 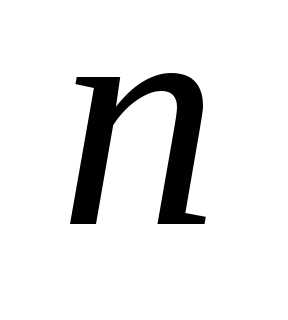 к вычислению
к вычислению определителей порядка
определителей порядка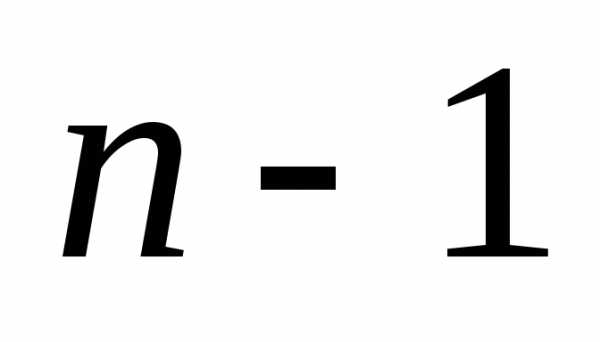 .
.
Пример 5.Вычислить определитель четвертого порядка:
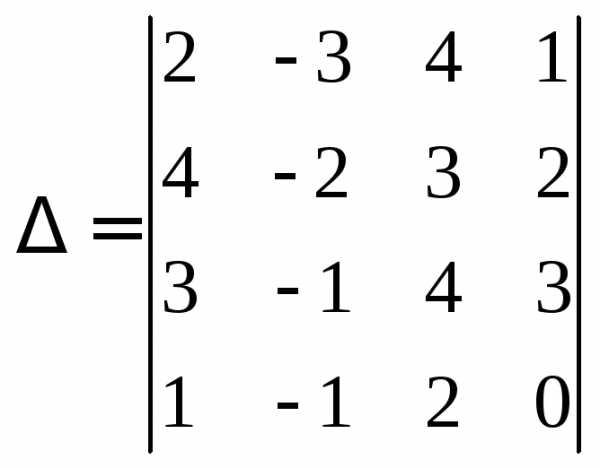 .
.
Воспользуемся теоремой 1 и разложим
определитель  по 4-й строке:
по 4-й строке:
.
Замечание.Можно вначале упростить определитель,
воспользовавшись свойством 9, а затем
использовать теорему 1. Тогда вычисление
определителя порядка сведется к вычислениювсего одногоопределителя порядка
сведется к вычислениювсего одногоопределителя порядка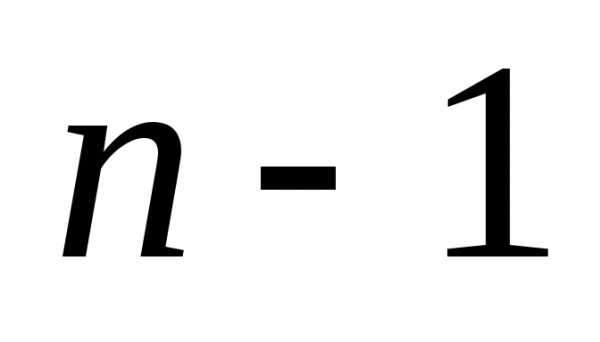 .
.
Пример 6.Вычислить
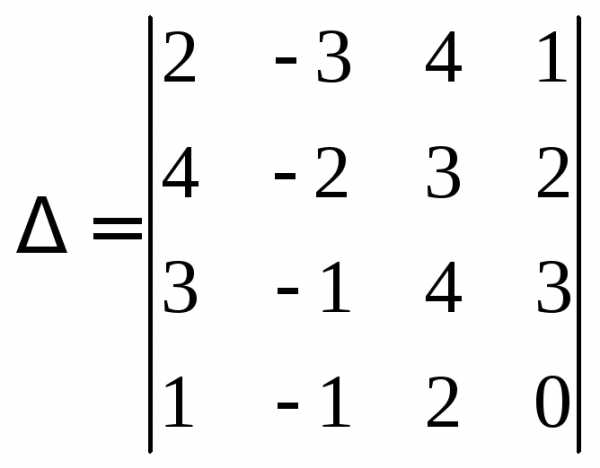 .
.
Прибавим первый столбец ко второму и
первый столбец, умноженный на (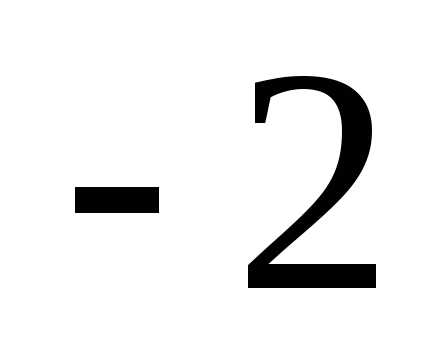 ),
к третьему, в результате получим
),
к третьему, в результате получим
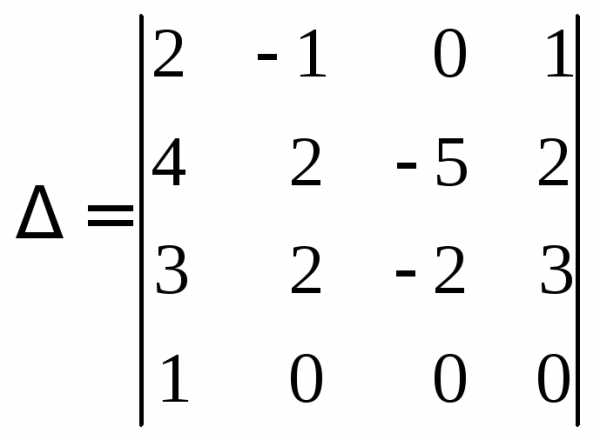 .
.
Теперь применим теорему 1 и разложим по последней строке:
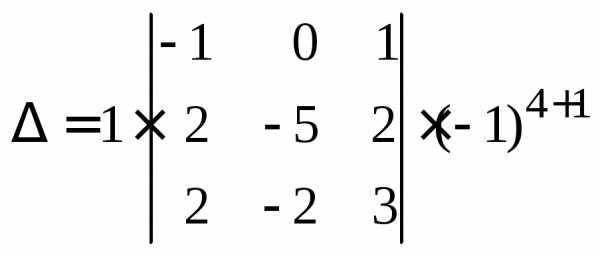 ,
,
вычисление определителя 4-го порядка свелось к вычислению всего одного определителя 3-го порядка.
Далее аналогично к первому столбцу прибавим третий и полученный определитель разложим по первой строке:
,
вычисление определителя третьего порядка свелось к вычислению всего одного определителя второго порядка.
Пример 7.Вычислить определитель порядка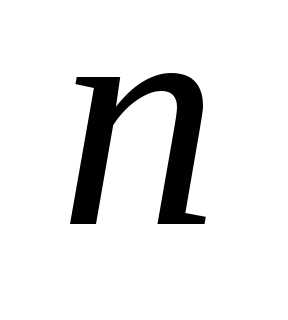 :
:
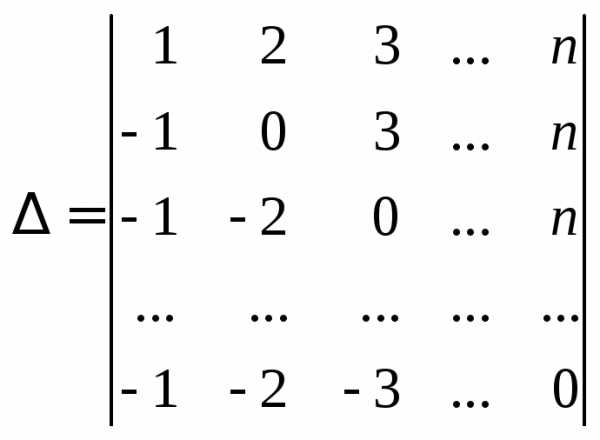 .
.
Первую строку прибавим ко второй, третьей
и т.д. 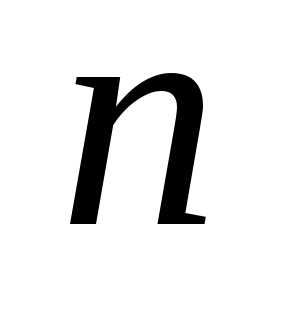 -й
строке. Придем к определителю
-й
строке. Придем к определителю
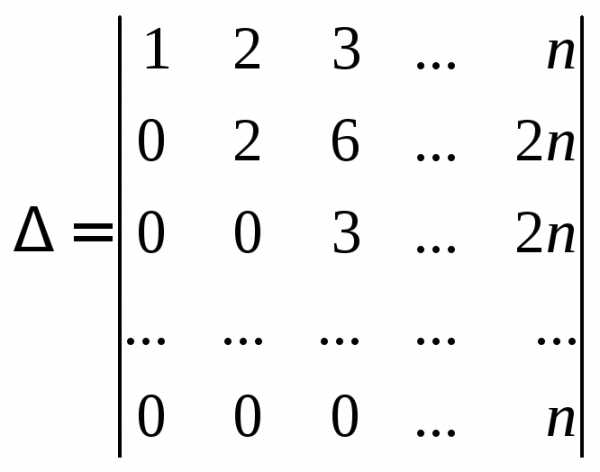 .
.
Получен определитель треугольного вида.
Применим 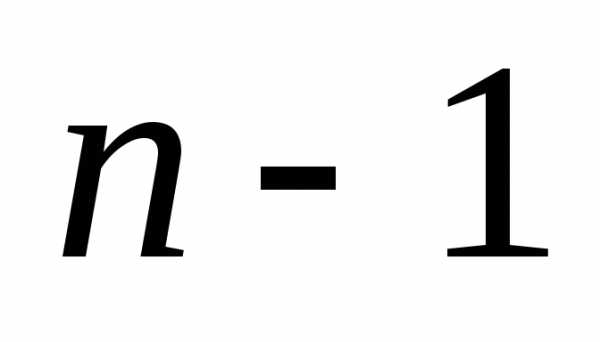 раз теорему 1 (разложим по первому
столбцу) и получим
раз теорему 1 (разложим по первому
столбцу) и получим
.
Замечание.Определитель треугольного вида равен произведению элементов главной диагонали.
6.3. Основные операции над матрицами
Определение 5.Две матрицы 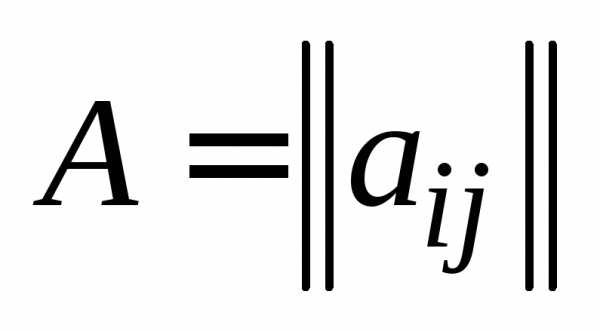 , , , и
, , , и 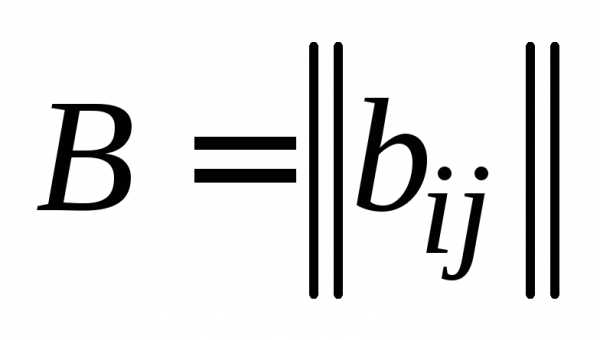 , , , будем называть равными, если
.
, , , будем называть равными, если
.
Краткая запись: 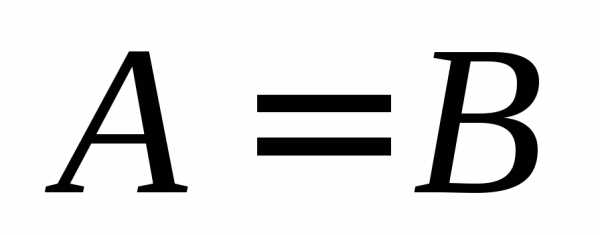 .
.
Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.
Определение 6.Суммой двух матриц 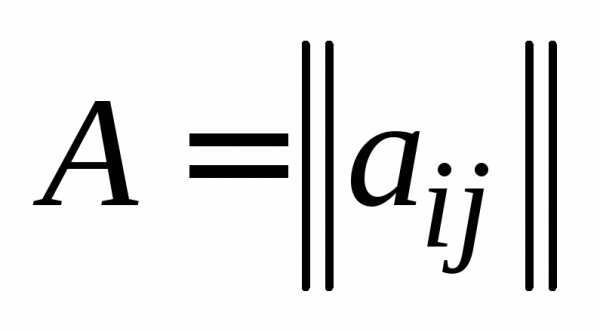 , , , и
, , , и 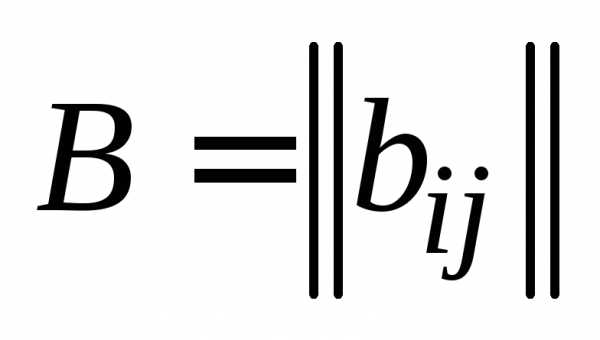 , , , называется такая матрица
, , , называется такая матрица 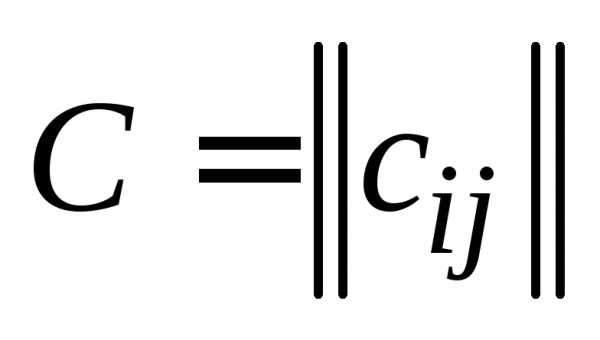 , , , что
.
, , , что
.
Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.
Пример 8.Найти сумму матриц
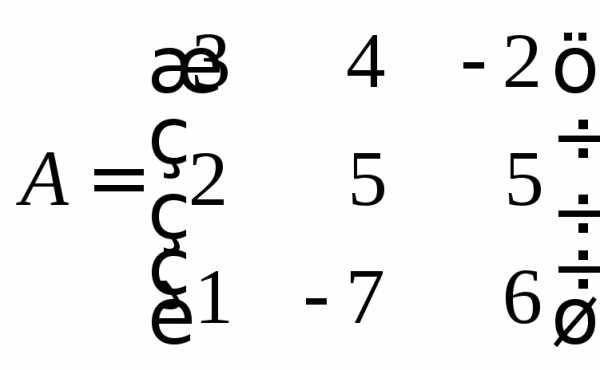 и
и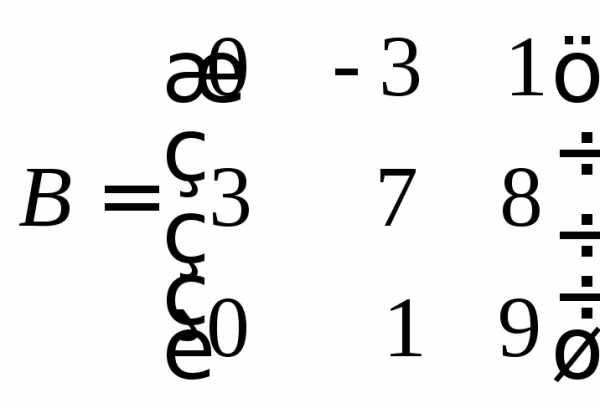 .
.
В соответствии с определением 6 найдем
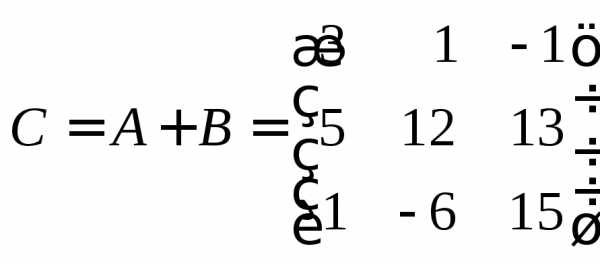 .
.
Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.
Определение 7.Произведением
матрицы 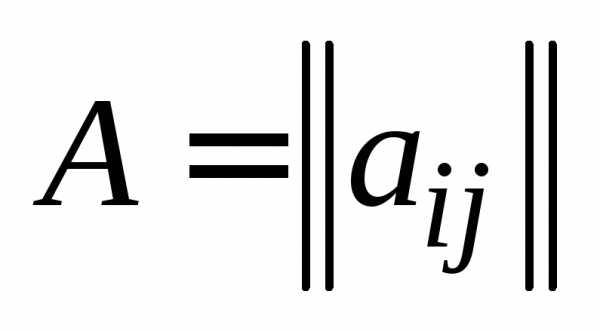 , , , на вещественное число
, , , на вещественное число 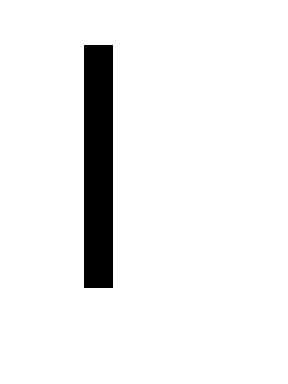 называется такая матрица
называется такая матрица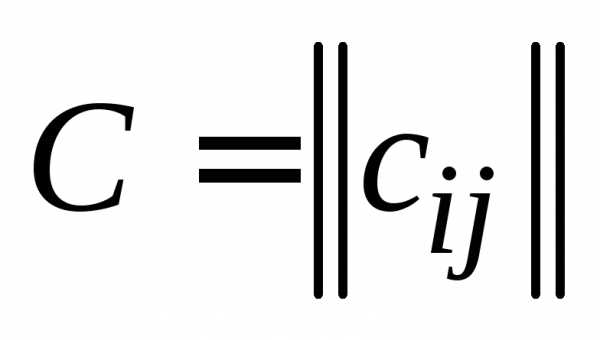 , , , для которой
.
, , , для которой
.
Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.
Пример 9.Найти линейную комбинациюматриц
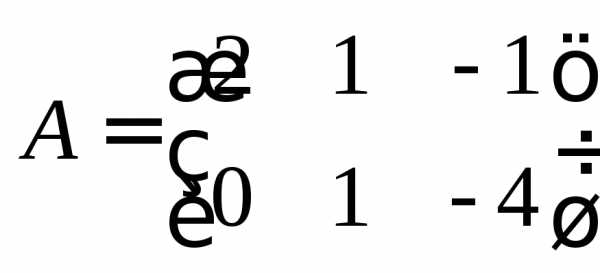 и
и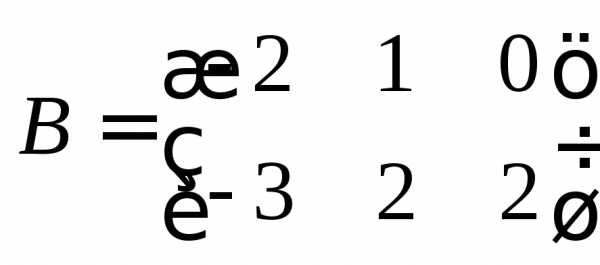 .
.
Пользуясь определением 7, получаем
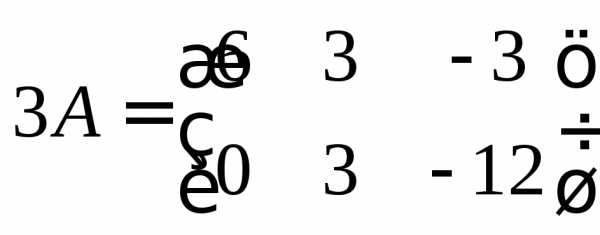 ,
,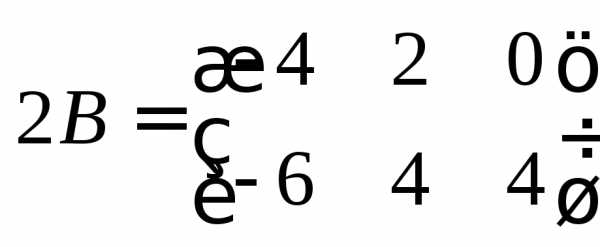 ,
,
далее привлекаем определение суммы матриц (определение 6):
.
Свойства операций сложения матриц
и умножения на число:
1. Сложение коммутативно: .
2. Сложение ассоциативно:.
3. Существует нулевая матрица  ,
удовлетворяющая условиюдля всехА.
,
удовлетворяющая условиюдля всехА.
4. Для любой матрицы Асуществует противоположная матрицаВ, удовлетворяющая условию.
Для любых матриц А иВи любых
действительных чисел имеют место равенства:
имеют место равенства:
5. .
6. .
7. .
8. .
Проверим свойство 1. Обозначим
,.
Пусть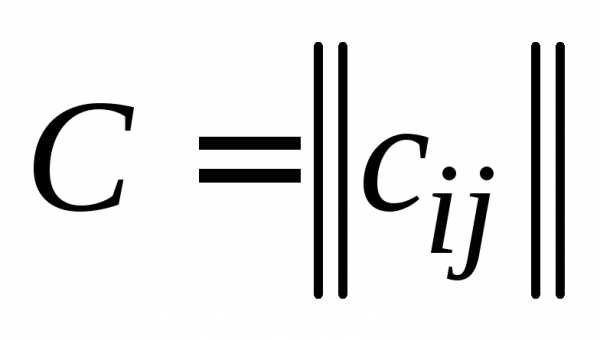 ,
,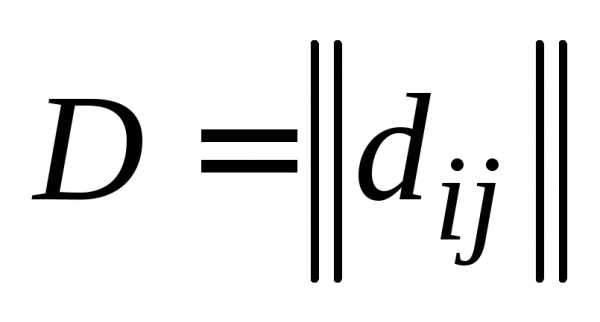 ,.
Имеем
,.
Имеем
,
и так как равенство доказано для
произвольного элемента, в соответствии
с определением 5 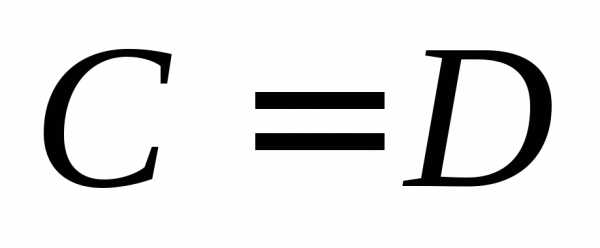 .
Свойство 1 доказано.
.
Свойство 1 доказано.
Аналогично доказывается свойство 2.
В качестве матрицы  возьмем матрицу порядка
возьмем матрицу порядка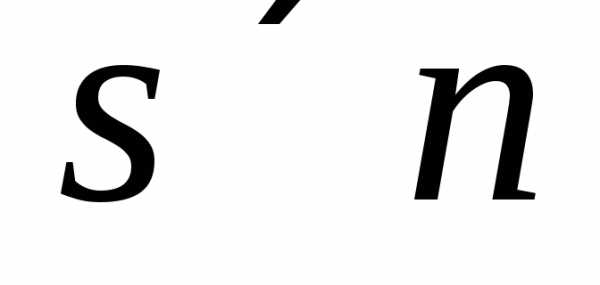 ,
все элементы которой равны нулю.
,
все элементы которой равны нулю.
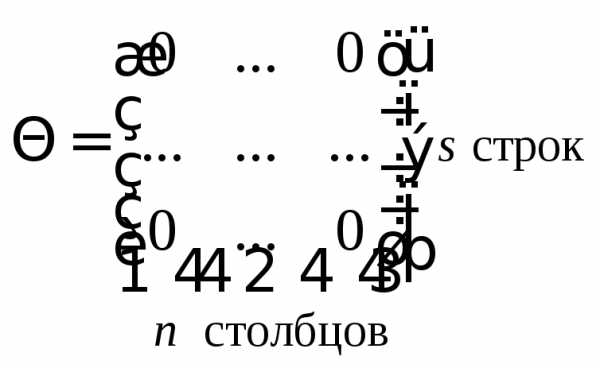
Сложив  с любой матрицей
с любой матрицей по правилу, данному в определении 6, мы
матрицу
по правилу, данному в определении 6, мы
матрицу не изменим, и свойство 3 справедливо.
не изменим, и свойство 3 справедливо.
Проверим свойство 4. Пусть  .
Положим
.
Положим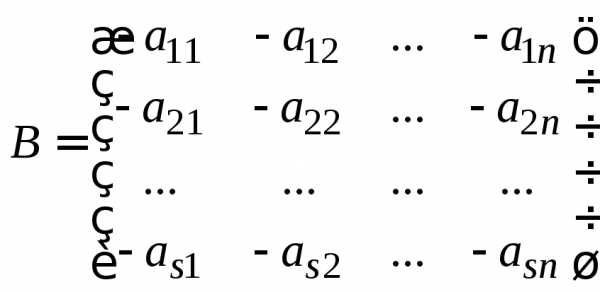 .
Тогда,
следовательно, свойство 4 справедливо.
.
Тогда,
следовательно, свойство 4 справедливо.
Проверку свойств 5 — 8 опустим.
Определение 8. Произведением
матрицы 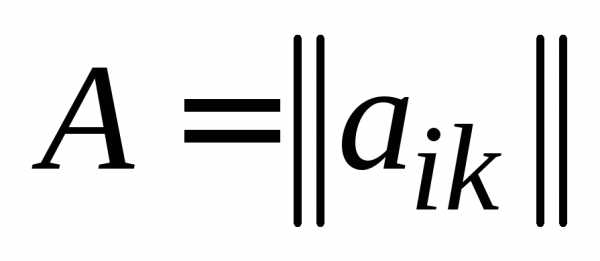 , , , на матрицу
, , , на матрицу 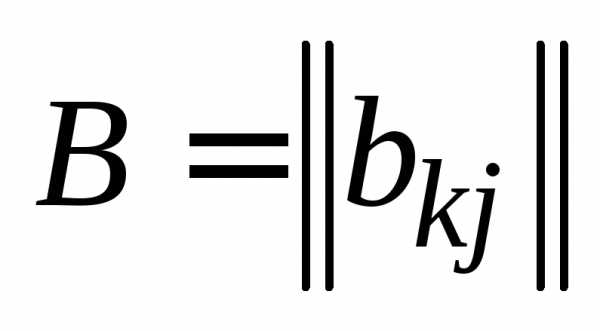 , , , называется матрица
, , , называется матрица 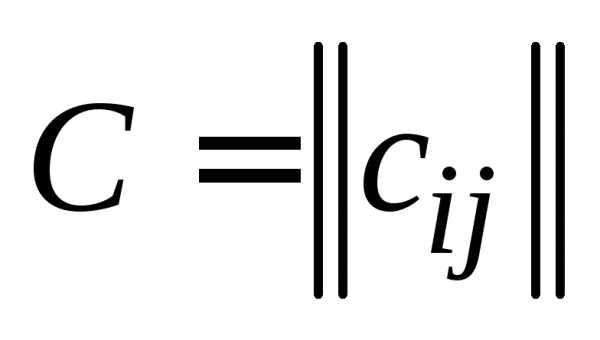 , , , с элементами
.
, , , с элементами
.
Краткая запись: 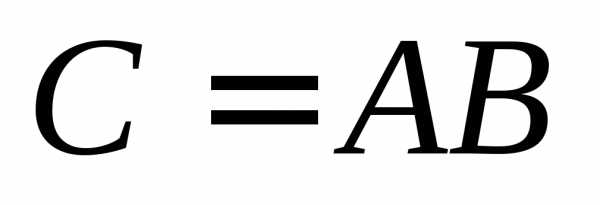 .
.
Пример 10. Найти произведение матриц
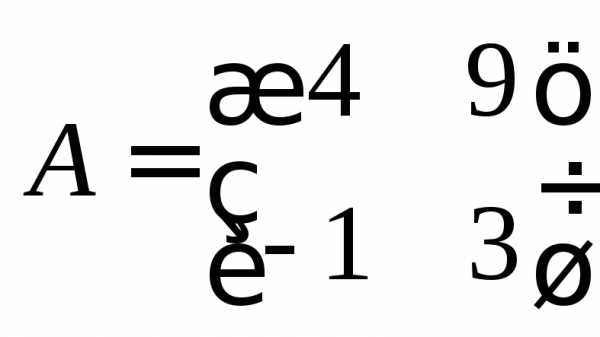 и
и .
.
В соответствии с определением 8 найдем
.
Пример 11.Перемножить матрицы
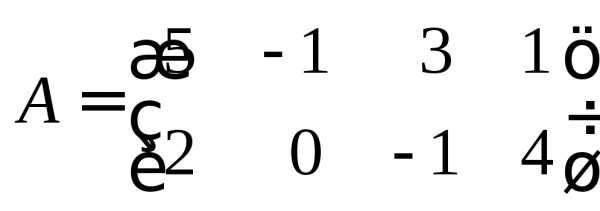 и
и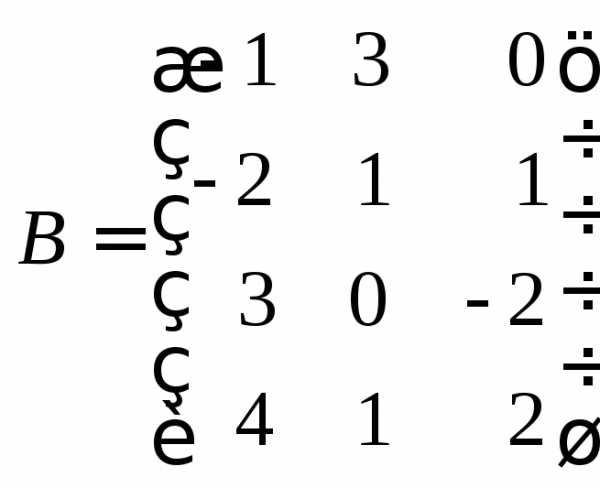 .
.
Имеем
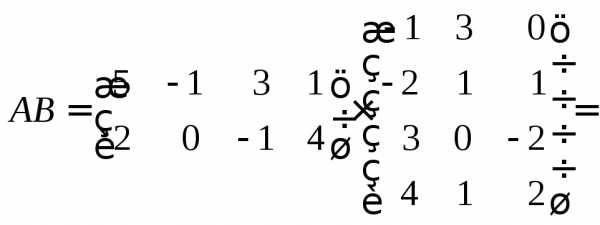
.
Замечание 1.Число элементов в строке матрицы равно числу элементов в столбце матрицы
равно числу элементов в столбце матрицы (число столбцов матрицы
(число столбцов матрицы равно числу строк матрицы
равно числу строк матрицы ).
).
Замечание 2.В матрице строк столько же, сколько в матрице
строк столько же, сколько в матрице ,
а столбцов столько же, сколько в
,
а столбцов столько же, сколько в .
.
Замечание 3. Вообще говоря,(умножение матриц некоммутативно).
Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.
Пример 12.Перемножим в обратном порядке матрицы и
и из примера 10.
из примера 10.
,
таким образом, в общем случае .
Отметим, что в частном случае равенство возможно.
Матрицы  и
и ,
для которых выполняется равенство,
называютсяперестановочными,иликоммутирующими.
,
для которых выполняется равенство,
называютсяперестановочными,иликоммутирующими.
Упражнения.
1. Найти все матрицы, перестановочные с данной:
а) 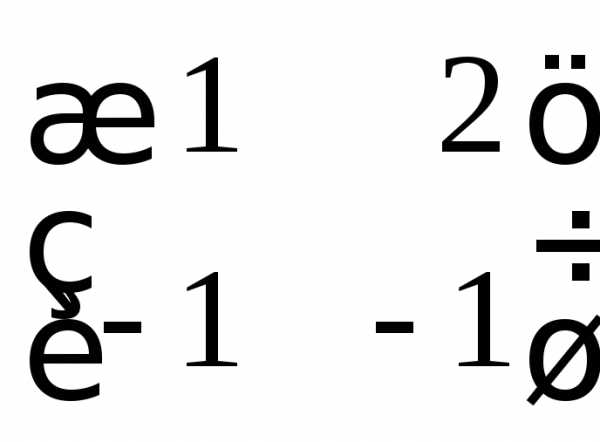 ;
б)
;
б) .
.
2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.
3. Доказать, что .
Свойства умножения матриц:
Умножение дистрибутивно:
studfiles.net
Глава 5. Определители высших порядков
Введем понятие определителя N–го порядка.
Определение
Определителем матрицы A N–го порядка называется Алгебраическая сумма N! произведений N–го порядка элементов этой матрицы, причем в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы.
Заметим, что с ростом N резко увеличивается число членов определителя (N!). Например, для N = 4 определитель содержит 24 слагаемых. Поэтому на практике при вычислении определителей высоких порядков используют другие формулы.
Свойства определителей, рассмотренные в разделе 4, справедливы и для определителей любого порядка. Поэтому для вычисления определителей 4–го, 5–го и более высоких порядков можно воспользоваться свойством 9, сформулированное в общем случае определителя произвольного порядка носит название Теоремы Лапласа. Как нетрудно убедиться, вычисление определителя 4–го порядка сводится к вычислению четырех определителей 3–го порядка. Для облегчения решения этой задачи определитель преобразуют, используя свойство 8, стремясь получить в одном из рядов максимальное число нулей.
Теорема (Теорема Лапласа)
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
, | (1.5.1) |
Формула (1.5.1) называется Разложением определителя по I–ой строке. Аналогичное утверждение имеет место и для Разложения по любому столбцу.
Определение
Квадратная матрица называется Вырожденной если ее определитель равен нулю.
Пример
Вычислить определитель матрицы A 4–го порядка:
Решение
По свойству 9 вычислим detA, разлагая его, например, по элементам 3–го столбца:
Преобразуем детерминант следующим образом: умножим 2–ю строку на 2 и прибавим к 3–й строке; умножим 2–ю строку на –6 и прибавим к 4–й строке. Получаем
| < Предыдущая | Следующая > |
|---|
matica.org.ua

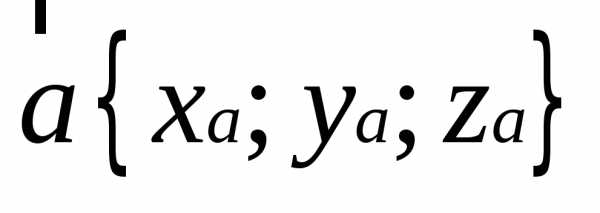 — координатами.
— координатами. в виде,
тогда можно написать:,
или в виде системы двух уравнений:
в виде,
тогда можно написать:,
или в виде системы двух уравнений: