Определитель матрицы системы – CGI script error

Содержание

Определители матрицы и системы линейных алгебраических уравнений

Реферат

по дисциплине: «Математика»

на тему:

«Определители матрицы и системы линейных алгебраических уравнений»

Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij , где i- номер строки, а j- номер столбца.

А =

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида:

= E,

называется единичной матрицей.

Определение. Если a_mn = a_nm , то матрица называется симметрической.

Пример.

— симметрическая матрица

Определение. Квадратная матрица вида

называется диагональной матрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij ± b_ij

С = А + В = В + А.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

a (А+В) =aА ±aВ

А(a±b) = aА ±bА

матрица алгебраический линейный уравнение

Пример. Даны матрицы А =

; B = , найти 2А + В.

2А =

, 2А + В = .

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить едини чная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O,

где О – нулевая матрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ, то определено произведение В^Т А^Т и выполняется равенство:

(АВ)^Т = В^Т А^Т , где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.

Понятие det (определитель, детерминант) будет рассмотрено ниже.

Определение. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А =

; В = А^Т =;

другими словами, b_ji = a_ij .

В качестве следствия из предыдущего свойства (5) можно записать, что:

(ABC)^T = C^T B^T A^T ,

при условии, что определено произведение матриц АВС.

Пример. Даны матрицы А =

, В = , С = и число a = 2. Найти А^Т В+aС.

A^T =

; A^T B = × = = ;

aC =

; А^Т В+aС = + = .

Пример. Найти произведение матриц А =

и В = .

АВ =

× = .

ВА =

× = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

Пример. Найти произведение матриц А=

, В =

АВ =

×= = .

Определение. Определителем квадратной матрицы А=

называется число, которое может быть вычислено по элементам матрицы по формуле: det A = , где

М_1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.

Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det A =

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

detA = , i = 1,2,…,n.

Очевидно, что различные матрицы могут иметь одинаковые определители.

Определитель единичной матрицы равен 1.

Для указанной матрицы А число М_1к называется дополнительным минором элемента матрицы a_1k . Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Определение. Дополнительный минор произвольного элемента квадратной матрицы a_ij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.

Свойство1. Важным свойством определителей является следующее соотношение:

det A = det A^T ;

Свойство 2. det (AB) = detA×detB

Свойство 3. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.

mirznanii.com

Вычислим определитель основной матрицы системы:

Обозначим через Δ_i определитель, получающийся из определителя Δ основной матрицы системы уравнений заменой его i-го столбца столбцом из свободных членов b₁,b₂,…,b_n (с сохранением без изменения всех остальных столбцов).

Квадратная система линейных уравнений с определителем основной матрицы, отличным от нуля, имеет и притом единственное решение, определяемое следующей формулой:

Эта формула называется формулой Крамера, а алгоритм решения системы линейных уравнений — методом Крамера или правилом Крамера.

Метод главных элементов

Пусть дана система линейных алгебраических уравнений.

(1)

Рассмотрим расширенную прямоугольную матрицу, состоящую из коэффициентов системы a[i,j] и свободных членов b[i].

Выбираем ненулевой наибольший по модулю элемент, не принадлежащий столбцу свободных членов. Пусть это будет . Этот элемент называется главным элементом, а строка, в которой он находится, называется главной строкой.

Вычисляются множители:

для всех .Далее производим следующие преобразования: к каждой неглавной строке прибавим главную строку, умноженную на соответствующий множитель для этой строки. В результате мы получим матрицу, у которой q-й столбец состоит из нулей. Отбросим этот столбец и главную p-ю строку, получим новую матрицу с меньшим на единицу числом строк и столбцов. Над матрицей повторяем те же операции, после чего получаем матрицу и т.д. Таким образом, мы построим последовательность матриц

, последняя из которых представляет двучленную матрицу — строку, её также будем считать главной строкой. Для определения неизвестных объединяем в систему все главные строки, начиная с последней. После надлежащего изменения нумерации неизвестных получается система с треугольной матрицей, из которой легко шаг за шагом найти неизвестные данной системы. Заметим, что метод Гаусса является частным случаем метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. Запрограммировать метод главных элементов непросто, поэтому чтобы уменьшить вычислительную погрешность, применяют метод Гаусса с выбором главного элемента. Необходимое условие применения метода главных элементов: определитель системы не равен нулю.

Метод квадратных корней

Пусть дана линейная система:

Ax=b

где — симметрическая матрица. Тогда матрицуА можно представить в виде произведения двух транспонированных между собой треугольных матриц

где

Производя перемножение матриц , для определения элементов матрицыТ получим следующие уравнения:

Отсюда последовательно находим:

(3)

При наличии соотношения (2) уравнение (1) эквивалентно двум уравнениям:

Отсюда последовательно находим:

Изложенный способ решения линейной системы носит название метода квадратных корней.

Схема Халецкого

Для удобства рассуждений систему линейных уравнений запишем в матричном виде:

Ax=b, (1)

где — квадратная матрица порядкаn и

А=ВС, (2)

Тогда элементы определяются по формулам:

Ву=b, Cx=y

Отсюда

Этот метод получил название схемы Халецкого.

studfiles.net

Матрицы, определители и системы линейных уравнений

Министерство образования и науки РФ

–––––––——————————–––––––

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

————————————————————

Матрицы, определители

и системы линейных уравнений

Методические рекомендации к решению задач

Санкт-Петербург

2006

УДК 00000000

Матрицы, определители и системы линейных уравнений: Методические указания к решению задач / Сост.: Е.А. Толкачева, М.Н. Абрамова, А.И. Куприянов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2006. 32 с.

Содержат решения основных типов задач элементарной линейной алгебры. Разобраны различные методы решения этих задач.

Предназначены для студентов-заочников всех специальностей.

Утверждено редакционно-издательским советом университета в качестве методических указаний

 СПбГЭТУ «ЛЭТИ», 2004

Методические указания предназначены для студентов-заочников младших курсов. При изучении курса высшей математики делается упор на умение решать задачи. Основные методы решения тех или иных задач целиком переносятся на самостоятельную проработку. Программа курса высшей математики включает в себя, наряду с другими разделами, и определители, матрицы, системы линейных уравнений. Студент в своей работе может ориентироваться на любые источники, содержащие сведения по линейной алгебре. В качестве основного источника выбрана книга Писменного [3] – наиболее доступная, с точки зрения авторов. В начале каждого параграфа дается ссылка на этот учебник. Ответы каждого примера либо подчеркнуты, либо, при необходимости выделены отдельно.

Настоящие указания являются составной частью цикла методических разработок кафедры высшей математики №2 СПбГЭТУ «ЛЭТИ», и призванных помочь студентам-заочникам в самостоятельной работе.

Глава 1. Матрицы и определители §1. Алгебра матриц

Основные определения и утверждения по данному разделу можно найти на стр.10-14, ч.1, [3]. Матрицу, по главной диагонали которой стоят единицы, а остальные элементы – нули, называют единичной и обозначают E.

При решении задач в параграфе, будем использовать матрицы:

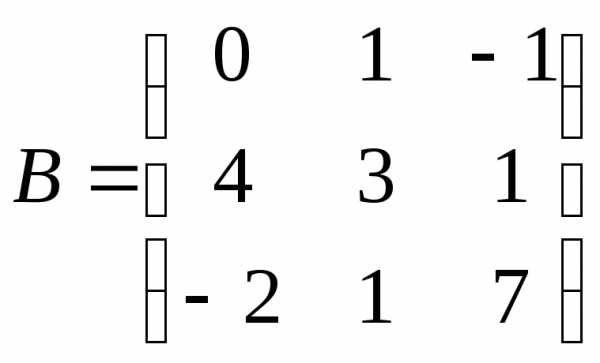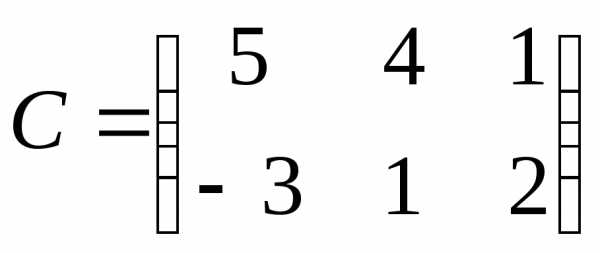, ,и. ()

Вычислите A+Bдля матриц из ().

Решение:

Суммой матриц будет матрица, элементы которой получены суммированием элементов слагаемых. Складывать и вычитать можно только матрицы одинаковой размерности, причем результат будет той же размерности.

Вычислите 3A+2B для матриц из ().

Решение:

Найдем сначала матрицы 3Aи 2B. При умножении матрицы на число необходимо каждый элемент матрицы умножить на это число.

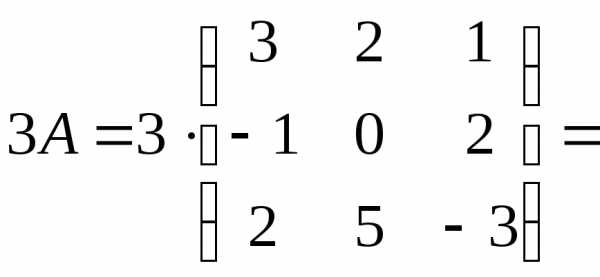Для матрицы Bаналогично:.

Сложим результаты: .

Вычислите A∙BиB∙A для матриц из ().

Решение:

Перемножить матрицы можно, если количество столбцов первого сомножителя совпадает с количеством строк второго сомножителя. Если умножается матрица порядка m×kна матрицу порядкаk×n, то в результате получится матрица порядкаm×n. Для получения ее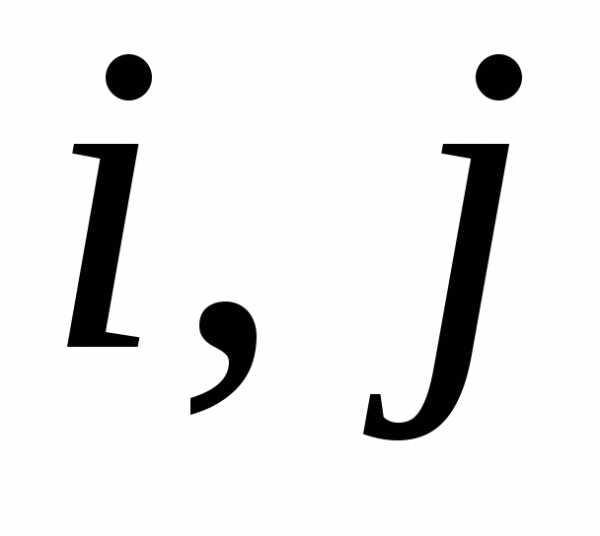—го элемента необходимо элементыi—ой строки левой матрицы умножить на соответствующие элементыj—го столбца правой матрицы и сложить полученные результаты.

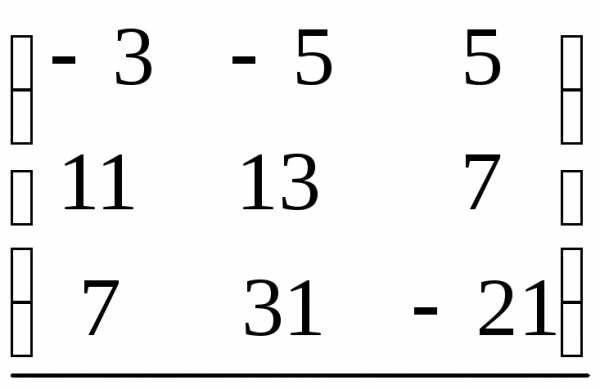. =. Произведение матриц не коммутативно, то есть для любых матрицAиB:A∙BB∙A, что и показывают полученные результаты.

Вычислите A²для матрицы из ().

Возвести матрицу в n—ую степень, значит умножить ее на себяnраз.

==.

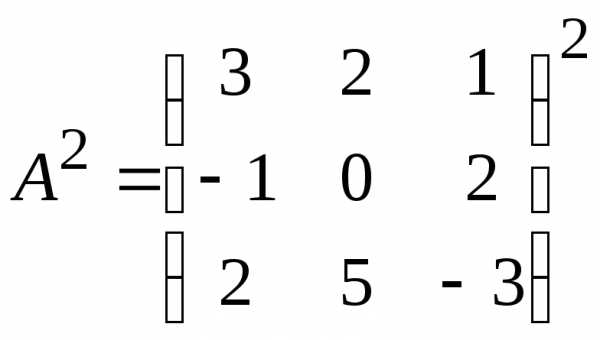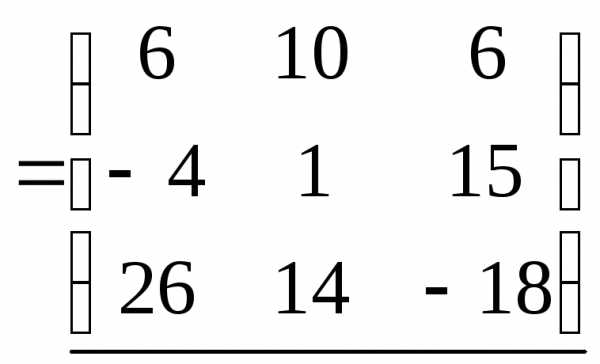
Вычислите C∙D иD∙Cдля матриц из ().

Решение:

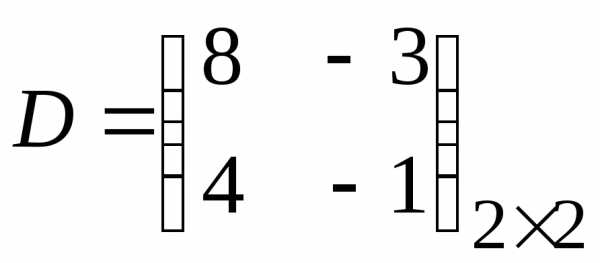Произведение C∙D не определено, так как число столбцов матрицы, которых три, не совпадает с числом строк матрицы, которых два. Напоминаем, что перемножить матрицы можно, если количество столбцов первого сомножителя совпадает с количеством строк второго сомножителя.

Если умножается матрица порядка 2×2на матрицу порядка2×3, то в результате получится матрица порядка 2×3.

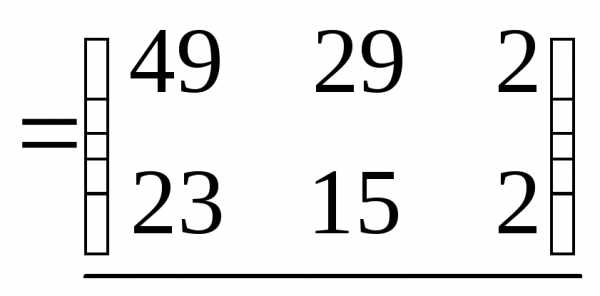Вычислите C^T∙Dдля матриц из ().

Решение:

При выполнении операций над матрицами в первую очередь выполняется транспонирование, затем умножение матриц. Для того чтобы найти транспонированную матрицу надо строки матрицы записать в столбцы (или наоборот, столбцы в строки).

Вычислите D∙Eдля матриц из ().

Решение:

На главной диагонали матрицы Eстоят 1, другие элементы равны нулю.

Легко проверить, что E∙D=D. Полученные равенства верны для произвольных матриц. Единичная матрицаEпри умножении матриц играет роль числа 1 при умножении чисел.

Найти значение многочлена f(x)=x²+x+2для матрицы∙D().

Решение:

Запись f(D)=D²+D+2будет не корректна: выражениеD²+Dесть матрица размера 2×2, к которой нельзя прибавить число 2. А потомуf(D)=D²+D+2E, гдеE— единичная матрица подходящего размера.

=== .

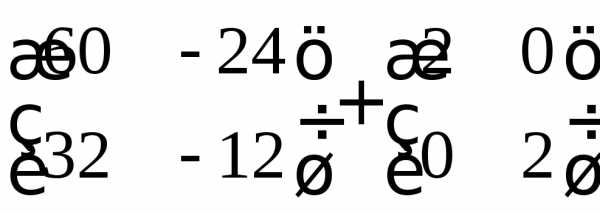
Вычислите: .

Решение:

При вычислениях следует помнить о последовательности выполнения действий: сначала умножение матриц и умножения матрицы на число, потом сложение матриц.

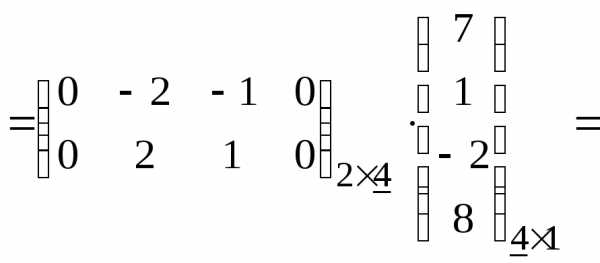
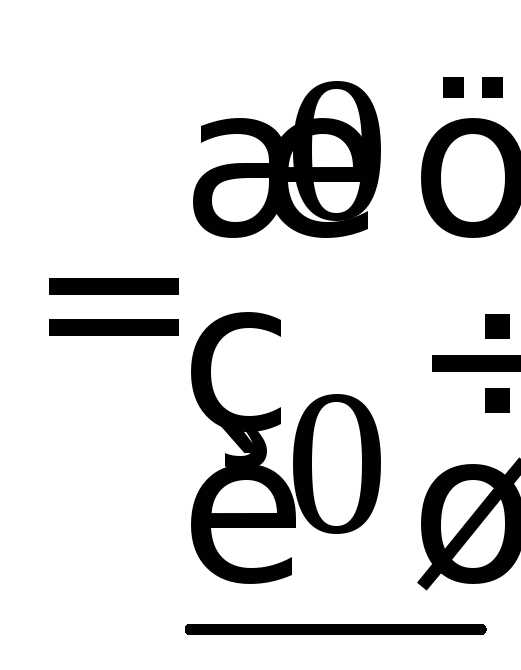studfiles.net

Вспомогательный определитель — Документ

Системы линейных уравнений

Система уравнений следующего вида:

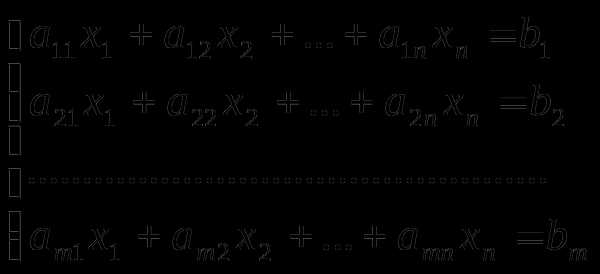где а_ij, b_i – числовые коэффициенты, x_i – переменные, называется системой линейных уравнений.

Решить систему линейных уравнений – значит указать все решения системы, то есть такие наборы значений переменных, которые обращают уравнения системы в тождества.

Система линейных уравнений называется:

совместной, если она имеет хотя бы одно решение;
несовместной, если она не имеет решений;
определенной, если она имеет единственное решение;
однородной, если все b_i = 0;
неоднородной, если все b_i ≠ 0.

Правило Крамера

(Габриель Крамер (1704-1752) швейцарский математик)

Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.

Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

 = det A  0;

Теорема. (Правило Крамера):

Система из n уравнений с n неизвестными

В случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам:

х_i_{= _;}

где  — главный определитель, составленный из числовых коэффициентов при неизвестных, а _i – вспомогательный определитель, получаемый из главного заменой i -го столбца столбцом свободных членов b_i.

_i =

Пример. Решить систему, используя правило Крамера.

;

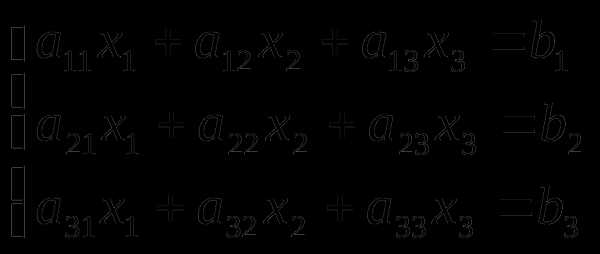
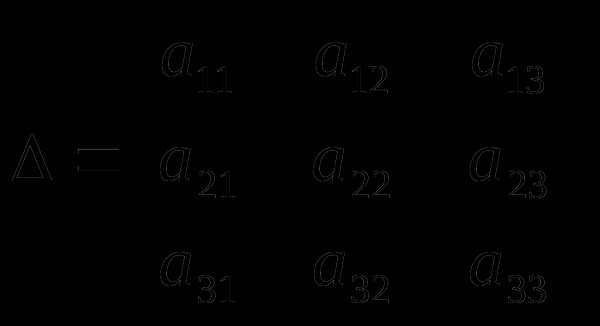₁= ; ₂= ; ₃= ;

x₁ = ; x₂ = ; x₃ = ;

Пример. Найти решение системы уравнений:

 = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

₁ = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

x₁ = = 1;

₂ = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x₂ = = 2;

₃ = 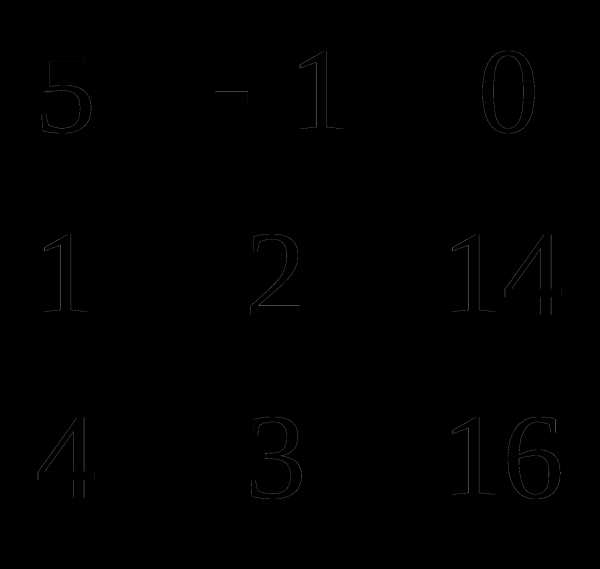= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x₃ = = 3.

Если система однородна, т.е. b_i = 0, то при 0 система имеет единственное нулевое решение x₁ = x₂ = … = x_n = 0.

Матричный метод

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Этот метод удобен для решения систем невысокого порядка. Он основан на применении свойств умножения матриц.

Пусть дана система уравнений:

Введем обозначения:

A = — матрица коэффициентов системы;

B = 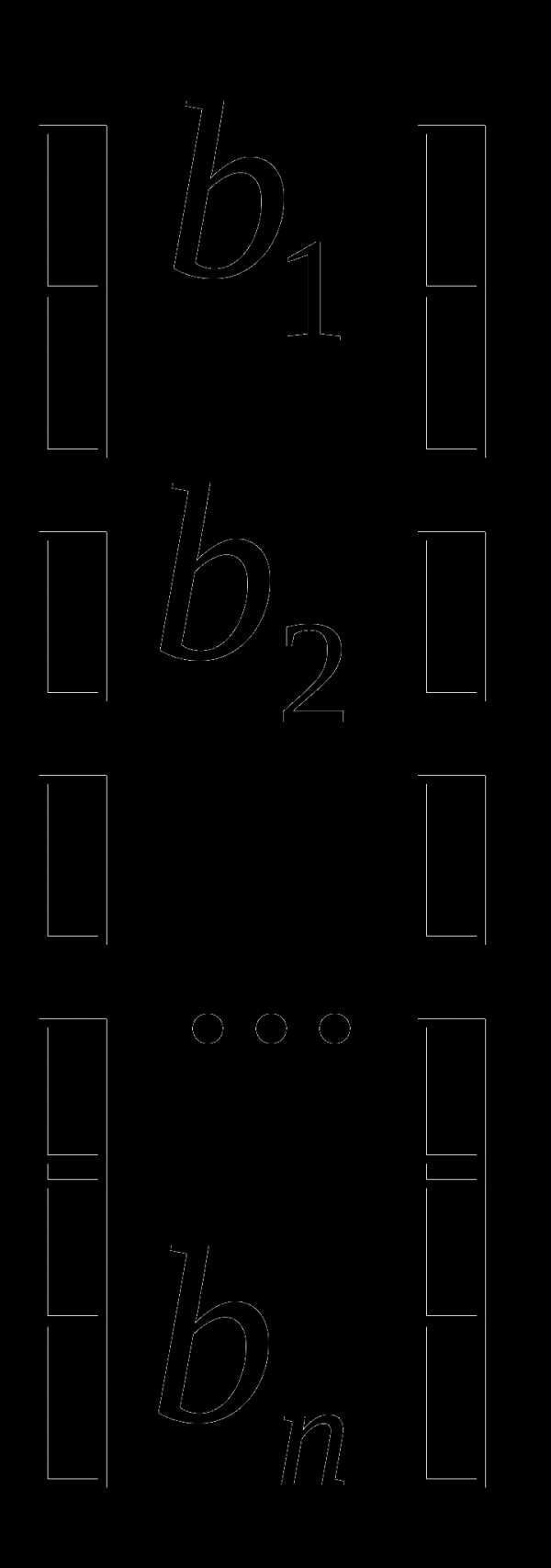матрица – столбец свободных членов;

X = — матрица – столбец неизвестных.

Систему уравнений можно записать в матричной форме:

AX = B.

Сделаем следующее преобразование: A^-1AX = A^-1B,

т.к. А^-1А = Е, то ЕХ = А^-1В, получим

Х = А^-1В — решение матричного уравнения

Пример. Решить систему матричным методом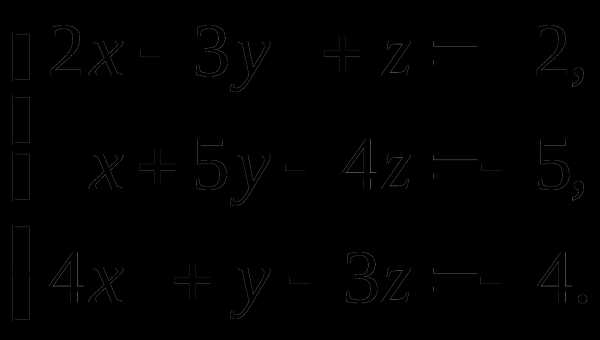

Решение. Обозначим:

, , .

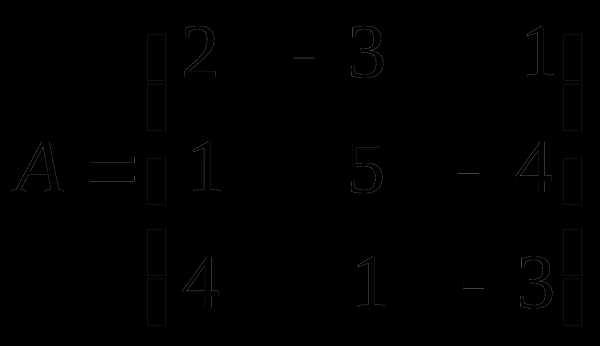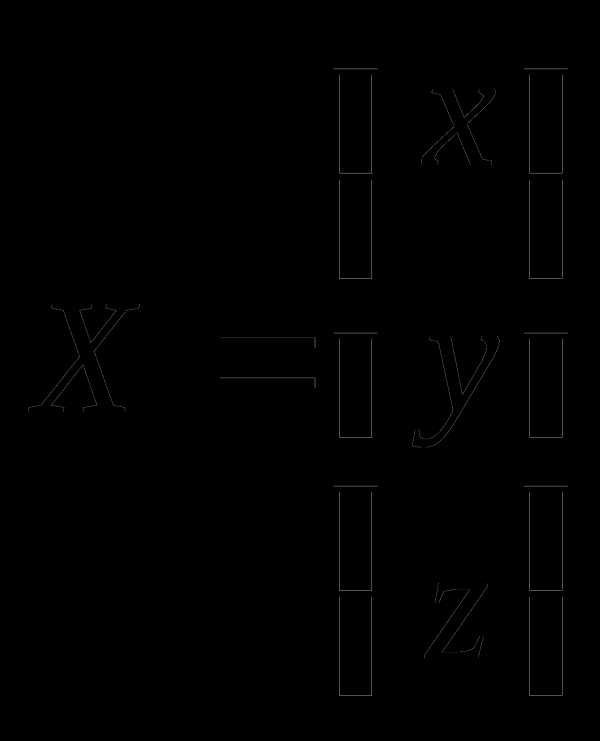Получаем матричное уравнение .

Его решение , т.е.

(Нахождение обратной матрицы было рассмотрено ранее).

Ответ:

Метод Гаусса

(Карл Фридрих Гаусс (1777-1855) немецкий математик)

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

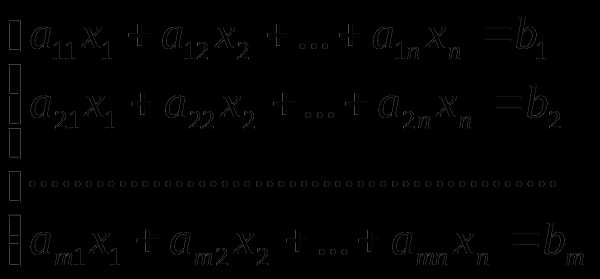
Определение: Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение: Матрица называется расширенной матрицей системы, если к матрице А присоединить столбец свободных членов системы.

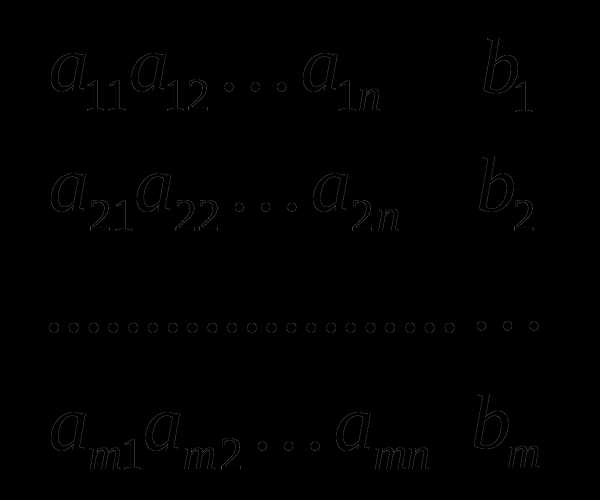
Расширенная матрица – это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями можно заменить работой со строками матрицы.

Определение: Матрицу А называют ступенчатой, если:

А) любая ее строка имеет хотя бы один отличный от нуля элемент,

Б) первый отличный от нуля элемент каждой ее строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.

Метод Гаусса является эффективным методом решения и исследования систем линейных уравнений. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида, которая легко решается и исследуется. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Разберем идею метода Гаусса на конкретных примерах.

Пример. Решить систему линейных уравнений методом Гаусса.

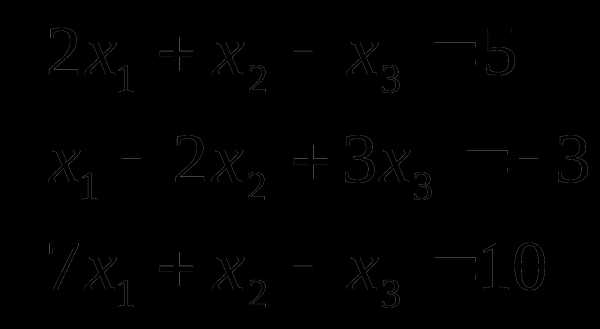
Составим расширенную матрицу системы и с помощью элементарных преобразований приведем к виду:

Таким образом, исходная система может быть представлена в виде:

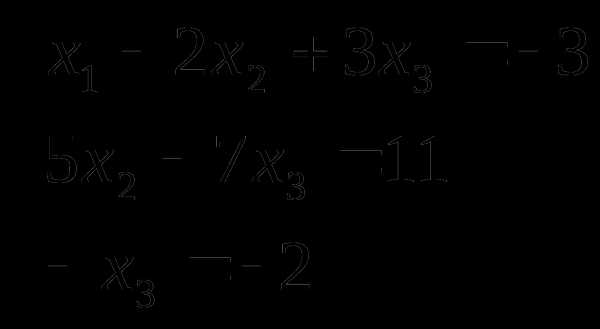, откуда получаем: x₃ = 2; x₂ = 5; x₁ = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы.

Таким образом, исходная система может быть представлена в виде:

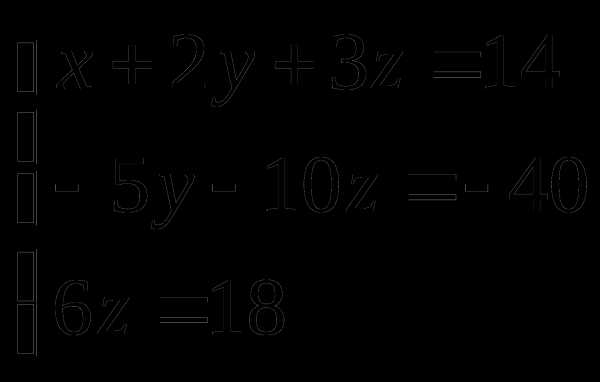, откуда получаем: z = 3; y = 2; x = 1.

gigabaza.ru

Матрицы и определители. Системы линейных уравнений

Стр 1 из 2Следующая ⇒

Матрицы и определители. Системы линейных уравнений

Матрицы

Матрицей размера m ´ n называется совокупность mn чисел, расположенных в виде таблицы из m строк и n столбцов:

Числа называются элементами матрицы. Таким образом, первый индекс элемента указывает на номер строки, второй – на номер столбца, на пересечении которых стоит этот элемент. Если m=n, т.е. число строк матрицы равно числу столбцов, то матрица называется квадратной матрицей порядка n.

Диагональ квадратной матрицы, составленная из элементов a₁₁, a₂₂, …, a_nn, называется главной диагональю.

Квадратная матрица называется единичной, если на главной диагонали у нее стоят единицы, а остальные элементы – нули.

Пусть дана произвольная матрица .Матрица , у которой каждая строка является столбцом матрицы А с тем же номером (и, следовательно, каждый столбец является строкой матрицы А), называется транспонированной к матрице А. Переход от матрицы А к В называется транспонированием. Будем обозначать транспонированную матрицу А^Т.

Заметим, что .

Определители

Для квадратных матриц существует численная характеристика, которая также имеет и многочисленные другие приложения. Прежде чем сформулировать определение определителя матрицы, введем одно вспомогательное понятие.

Пусть (s₁, s₂, … ,s_n) – строка из n различных чисел от 1 до n. Будем говорить, что в строке имеется нарушение, если существует такая пара чисел (s_i, s_j), что i < j, а s_i> s_j. Другими словами, если в этой строке большее число стоит раньше меньшего. Например, в строке (1, 4, 2, 3) имеется два нарушения (4, 2) и (4, 3).

Определителем матрицы порядка n (или определителем n-го порядка) называется сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце и расположенных по возрастанию номеров строк, причем член берется со знаком плюс, если строка из номеров столбцов его элементов имеет четное число нарушений, и со знаком минус – в противном случае.

Для обозначения определителя будем употреблять запись:

или det A .

Основываясь на определении, мы можем записать явные формулы для вычисления определителей второго и третьего порядков:

(1.1)

(1.2)

Примеры:

1) ,

2) .

Выражение определителя третьего порядка является достаточно громоздким. Для запоминания формулы существуют два удобных способа. Первый способ вычисления определителя третьего порядка схематично можно изобразить следующим образом:

Второй способ заключается в том, что под элементами матрицы выписываются снова первая и вторая строки. Тогда вычисление определителя схематично можно изобразить следующим образом:

Свойства определителей

Перечислим некоторые простейшие свойства определителей.

1. Определитель не меняется при транспонировании матрицы.

Пример.

2. Если матрица содержит строку, состоящую из нулей, то ее определитель равен нулю.

3. Если в матрице поменять местами какие-нибудь две строки, то ее определитель изменит знак.

Пример.

4. Если в матрице есть две одинаковые строки, то ее определитель равен нулю.

5. При умножении строки матрицы на число, ее определитель умножается на это число.

6. Если все элементы i-й строки матрицы представлены в виде суммы двух слагаемых , то ее определитель равен сумме определителей двух матриц, у которых все строки, кроме i-й, такие же, как и в заданной матрице, а i-я строка в первой матрице состоит из элементов b_j, а во второй – из элементов c_j.

Прежде чем перейти к следующему свойству, сформулируем важное определение.

Будем говорить, что строка является линейной комбинацией строк

если существуют некоторые числа a₁, …, a_m, такие, что для любого i = 1, …, n выполняется следующее: , или то же самое можно записать в обозначениях строк:

7. Если одна из строк матрицы есть линейная комбинация остальных строк этой матрицы, то ее определитель равен нулю.

Пример.

Этот определитель равен нулю, так как третья строка есть сумма первой строки и второй строки, умноженной на 2.

8. Определитель матрицы не изменится, если к какой-нибудь ее строке прибавить линейную комбинацию остальных строк этой матрицы.

Пример.

Второй определитель получен из первого прибавлением к первой строке второй и третьей строк, затем общий множитель первой строки был вынесен за знак определителя по свойству 5 и получился определитель, имеющий две одинаковые строки, который по свойству 4 равен нулю.

Заметим, что из первого свойства вытекает, что все остальные свойства могут быть сформулированы не только для строк матрицы, но и для ее столбцов.

Алгебра матриц

Понятие матрицы, благодаря своим многочисленным применениям, стало предметом самостоятельной теории, в основе которой лежат алгебраические операции над матрицами: сложение и умножение.

Определим сначала равенство и сложение матриц.

Матрицы А и В одинаковых размеров n´m с элементами и называются равными, если для i = 1, 2, …, n, j = 1, 2, …, m. Равенство матриц обозначается А = В.

Суммой двух матриц А и В одинаковых размеров n´m с элементами и называется матрица С = А + В, элементы которой получаются путем сложения соответствующих элементов данных матриц: для i = 1, 2, …, n, j = 1, 2, …, m.

Определенное таким образом сложение будет, очевидно, коммутативным и ассоциативным.

Для сложения существует и обратная операция – вычитание матриц А – В. Роль нуля играет при этом нулевая матрица, составленная из одних нулей.

Введем операцию умножения матрицы на число.

Произведением матрицы А на число lназывается матрица С = l × А, элементы которой получаются умножением элементов матрицы А на число l: , где i = 1, 2, …, n, j = 1, 2, …, m.

Все перечисленные выше операции над матрицами аналогичны операциям над числами и являются вполне естественными.

Следующая операция умножения матриц на первый взгляд покажется не столь очевидной.

Произведением матрицы А размера m´n с элементами и матрицы В размера n´p с элементами называется матрица С = АВ размера m´p c элементами , если

, (1.7)

где i = 1, 2, …, m, j = 1, 2, …, p.

Пример.

Теперь можно легко составлять и вычислять матричные выражения.

Пример. Если , то .

Нахождение обратной матрицы

Существует два способа нахождения обратной матрицы.

1.Первый способ основан на теореме о существовании обратной матрицы.

Пример. Найти обратную матрицу к матрице .

Вычислим определитель этой матрицы . Так как detA ¹ 0, то обратная матрица существует. Найдем алгебраические дополнения всех элементов (см. форулу (1.3):

Составим присоединенную матрицу

Находим обратную матрицу, поделив каждый элемент присоединенной матрицы на определитель матрицы А:

2.Метод элементарных преобразований.

Элементарными преобразованиями матрицы А называются следующие преобразования этой матрицы:

а) перестановка двух строк или двух столбцов,

б) умножение строки или столбца на отличное от нуля число,

в) прибавление к одной строке или столбцу другой строки или столбца.

Заметим, что если матрица А получается из матрицы В элементарными преобразованиями, то, обратив эти преобразования, можно и матрицу В получить из матрицы А.

Две матрицы называются эквивалентными, если одна из этих матриц получается из другой элементарными преобразованиями.

Пусть – матрицы, выражающие элементарные преобразования, которые данную матрицу А приводят к единичной матрице, т.е.

Умножив левую и правую части этого матричного равенства справа на матрицу , получим

Таким образом, одни и те же элементарные преобразования приводят матрицу А к единичной, а единичную матрицу к матрице .

Метод элементарных преобразований нахождения обратной матрицы заключается в том, что к данной матрице А справа приписывается единичная матрица такого же порядка. Затем над строками полученной прямоугольной матрицы производятся элементарные преобразования такие, чтобы на месте матрицы А получилась единичная матрица. При этом на месте единичной матрицы получится матрица, которая будет как раз обратной к матрице А.

Пример. Найти обратную к матрице .

Припишем справа единичную матрицу

Разделив первую строку на три и обнулив элемент в первом столбце ниже тройки, получим

Умножив вторую строку на три и обнулив элемент во втором столбце выше , получим

Таким образом,

Метод Крамера

Изложенная выше теория определителей позволяет исследовать на совместность системы, имеющие одинаковое количество уравнений и неизвестных.

Теорема 1.3. (Крамера).Система n уравнений с n неизвестными

(1.10)

имеет единственное решение, если определитель матрицы системы отличен от нуля. Это решение находится по формулам Крамера:

, (1.11)

где D – определитель матрицы системы, а D_k – определитель матрицы, полученной из матрицы системы заменой k-го столбца столбцом свободных членов.

Доказательство. Выберем произвольное число k = 1,…,n. Умножим левую и правую части первого уравнения системы (1.10) на , второго уравнения – на , …, последнего – на . Затем сложим левые и правые части полученных равенств, сгруппировав слагаемые с одинаковыми переменными х_i. Получим равенство

или

При х_k получим коэффициент . Это есть определитель матрицы системы D. Коэффициенты при остальных х_j, j ¹ k, имеют вид и будут равны нулю, так как сумма представляет собой определитель матрицы, имеющей два одинаковых столбца (вместо k-го столбца в определителе D стоит j-й столбец).

Таким образом, получили равенство

Выражение справа, очевидно, является разложением по k-му столбцу определителя

получающегося из определителя D заменой k-го столбца столбцом из чисел b₁, b₂, …, b_n, т.е. D_k. Тогда имеем . Отсюда, так как D ¹ 0, получаем .

Пример. Решить систему.

Вычислим определители:

Так как определитель матрицы системы Δ отличен от нуля, то система совместна, тогда решения системы находятся по формулам (1.11):

Матрицы и определители. Системы линейных уравнений

Матрицы

Матрицей размера m ´ n называется совокупность mn чисел, расположенных в виде таблицы из m строк и n столбцов:

Диагональ квадратной матрицы, составленная из элементов a₁₁, a₂₂, …, a_nn, называется главной диагональю.

Заметим, что .

Определители

Для обозначения определителя будем употреблять запись:

или det A .

(1.1)

(1.2)

Примеры:

1) ,

2) .

Свойства определителей

Перечислим некоторые простейшие свойства определителей.

1. Определитель не меняется при транспонировании матрицы.

Пример.

2. Если матрица содержит строку, состоящую из нулей, то ее определитель равен нулю.

3. Если в матрице поменять местами какие-нибудь две строки, то ее определитель изменит знак.

Пример.

4. Если в матрице есть две одинаковые строки, то ее определитель равен нулю.

5. При умножении строки матрицы на число, ее определитель умножается на это число.

Прежде чем перейти к следующему свойству, сформулируем важное определение.

Будем говорить, что строка является линейной комбинацией строк

Пример.

Этот определитель равен нулю, так как третья строка есть сумма первой строки и второй строки, умноженной на 2.

Пример.

Рекомендуемые страницы:

lektsia.com

Особенности вычисления определителя матрицы

Содержание

Введение…………………………………………………………………………………………….. 2

1. Постановка задачи………………………………………………………………………….. 3

2. Математические и алгоритмические основы решения задачи……………… 5

2.1 Определитель матрицы………………………………………………………………….. 5

2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6

2.3 Метод Гаусса для вычисления определителя……………………………………. 8

3. Функциональные модели и блок-схемы решения задачи…………………….. 9

4. Программная реализация решения задачи………………………………………. 11

5. Пример выполнения программы…………………………………………………….. 16

Заключение………………………………………………………………………………………. 18

Список использованных источников и литературы……………………………… 19

Введение

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.

Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.

1. Постановка задачи

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.

Пример 1.

Вычислить определитель матрицы методом A исключения Гаусса.

Решение:

Приведем матрицу к диагональному виду методом Гаусса.

Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

Знак определяется количеством обменов строк, следовательно определитель матрицы

Пример 2.

Вычислить определитель матрицы методом A исключения Гаусса.

Решение:

Приведем матрицу к диагональному виду методом Гаусса.

Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

Знак определяется количеством обменов строк, следовательно определитель матрицы

2. Математические и алгоритмические основы решения задачи

2.1 Определитель матрицы

Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.

Определитель квадратной матрицы A будем обозначать

или det A.

Определение. Определителем квадратной матрицы

второго порядка называется число

Определителем

квадратной матрицы порядка n,

, называется число

где

— определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.

2.2 Метод Гаусса для решения систем линейных уравнений

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Воспользуемся идеями метода Гаусса решения систем линейных уравнений.

Дана система:

a11 x1 + a12 x2 + … + a1n xn = b1

a21 x1 + a22 x2 + … + a2n xn = b2

…

an1 x1 + an2 x2 + … + ann xn = bn

Выполним следующий алгоритм.

На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.

На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.

Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).

В конце концов, мы приведём систему к так называемому диагональному виду:

c11 x1 = d1

c22 x2 = d2

…

cnn xn = dn

Т.е. мы нашли решение системы.

Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.

Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.

2.3 Метод Гаусса для вычисления определителя

Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).

Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).

Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.

3. Функциональные модели и блок-схемы решения задачи

Блок-схема решения задачи представлена на рисунке 1.

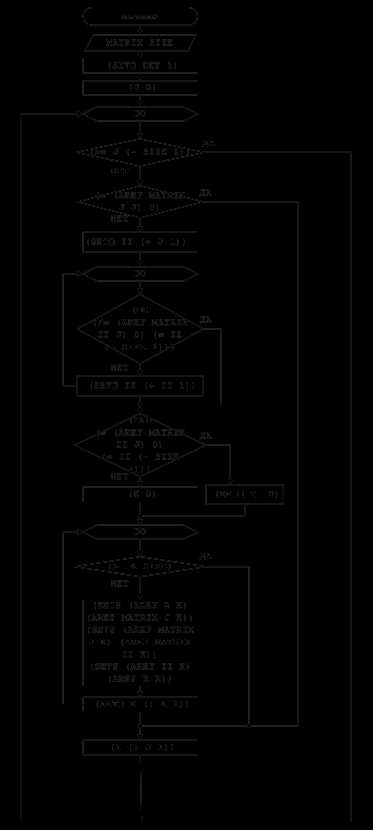
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE

4 Программная реализация решения задачи

;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ

(DEFUN DETERMINANT (MATRIX SIZE)

;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ

;ОПРЕДЕЛИТЕЛЬ

(DECLARE (SPECIAL DET))

;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ

(DECLARE (SPECIAL PAR))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL T_))

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL II))

;*********************

(SETQ R (MAKE-ARRAY SIZE :ELEMENT-TYPE ‘FLOAT :INITIAL-ELEMENT 0))

(SETQ T_ 1)

(SETQ DET 1)

(DO

((J 0))

((>= J (- SIZE 1)))

;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0

(IF (= (AREF MATRIX J J) 0)

(PROGN

(SETQ II (+ J 1))

;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0

(DO

(())

((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))

(SETQ II (+ II 1))

)

;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0

(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))

mirznanii.com

Матрицы, определители, системы линейных уравнений

МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

^ квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу ^ называют транспонированной матрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице ^ , обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или

Примеры. Найти сумму матриц:

.
— нельзя, т.к. размеры матриц различны.
.

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному ^ и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

Примеры.

.
Найти 2A-B, если , .

Найти C=–3A+4B.

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице ^ ) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

Примеры.

Пусть

Найти элементы c₁₂, c₂₃ и c₂₁ матрицы C.

Найти произведение матриц.

.
— нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
Пусть

Найти АВ и ВА.

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы ^ на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

^ , соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

.
Вычислить определитель матрицы D, если D= -А+2В и

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

^ , соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

.
.
Решите уравнение..

(x+3)(4x-4-3x)+4(3x-4x+4)=0.

(x+3)(x-4)+4(-x+4)=0.

(x-4)(x-1)=0.

x₁ = 4, x₂ = 1.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

te.zavantag.com

Определители матрицы и системы линейных алгебраических уравнений

Вычислим определитель основной матрицы системы:

Метод главных элементов

Метод квадратных корней

Матрицы, определители и системы линейных уравнений

Глава 1. Матрицы и определители §1. Алгебра матриц

Вспомогательный определитель — Документ

Матрицы и определители. Системы линейных уравнений

Особенности вычисления определителя матрицы

Матрицы, определители, системы линейных уравнений

МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Добавить комментарий Отменить ответ