Xa b матричное уравнение – Решение матричных уравнений

4. Решение матричных уравнений

Чтобы решать матричные уравнения, нужно уметь строить обратную матрицу. Матрица А^-1 называется обратной для матрицы А, если справедливы равенства А^-1А = АА^-1 = Е, где Е — единичная матрица. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля, то есть матрица была невырожденной. Чтобы построить обратную матрицу для матрицы А, нужно выполнить следующие операции:

1. вычислить определитель матрицы А, обозначаемый det А,

2. если det А не равен нулю, то найти матрицу А^т, для чего поменять местами строки и столбцы матрицы А,

3. затем в матрице А^т каждый элемент заменить на его алгебраическое дополнение. Полученную матрицу обозначают

   Ã^т,

4. разделить матрицу Ã^т на det А, т.е. каждый элемент матрицы Ã^т разделить на det А. В результате получится матрица обратная матрице А. Чтобы решить матричное уравнение АХ=В, нужно умножить слева обе части уравнения на А^-1, тогда Х=А^-1В. Для решения уравнения ХА=В, нужно обе части уравнения умножить справа на А^-1, тогда Х=ВА^-1. Напомним, что порядок умножения важен, так как, вообще говоря, A^-1B ≠ BA^-1.

Итак,

AX=B => X=A^-1B,

XA=B =>

X=BA^-1.

Пример 9

Решить матричное уравнение:

12 0

Х∙ 3 -1 1 = 1 4 -3

1 0 -1

Обозначим матрицы буквами:

1 2 0

А = 3 -1 1 , В= 1 4 -3 .

1 0 -1

Тогда данное уравнение примет вид: XA = B. Следовательно, Х = ВА^-1.

Вычислим определитель матрицы А.

det А=1·(-1)·(-1)+2·1·1+3·0·0-1·(-1)·0-0·1·1-3·2·(-1)=1+2+0-0-

-0+6=9.

Т.к. det А ≠ 0, то А^-1 существует.

Построим А^т. Для этого поменяем местами строки и столбцы.

1 3 1

А^т= 2 -1 0

0 1 -1

Заменим каждый из элементов матрицы его алгебраическим дополнением.

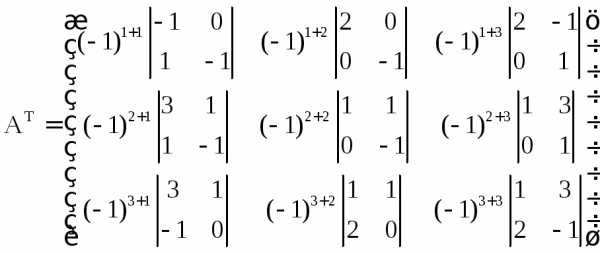
1 2 2

= 4 -1 -1

1 2 -7

Разделив каждый элемент этой матрицы на det А, получим обратную матрицу А^-1. Итак,

12 2

А^-1=1/9· 4 -1 -1

1 2 -7

НайдёмХ = ВА^-1.

1 2 2

Х = 1/9· 1 4 -3 4 -1 -1 =

1 2 -7

=1/9 · (1·1+4·4+(-3)·1 1·2+4·(-1)+(-3)·2 1·2+4·(-1)+(-3)·(-7)) =

=1/9 · (14 -8 19).

Проверим правильность решения. Для этого подставим матрицу Х в

Уравнение ХА = В.

1 2 0

1/9· 14 -8 19 · 3 -1 1 =

1 0 -1

= 1/9 · (14·1-8·3+19·1 14·2+8·1+19·0 14·0-8·1-19·1) =

= 1/9·(9 36 -27) = (1 4 -3).

Т.е. уравнение решено, верно. Итак, .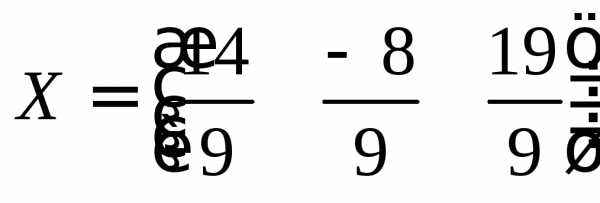

5. Вычисление ранга системы векторов

Ранг системы векторов равен числу линейно независимых векторов этой системы, он совпадает с рангом матрицы, строками которой являются координаты векторов в заданной системе координат. Рангом матрицы называется максимальный порядок отличного от нуля минора этой матрицы. Если векторы заданы своими координатами, то, чтобы найти ранг системы векторов, нужно составить матрицу A, строками которой являются координаты векторов. Затем, с помощью элементарных преобразований (умножения строки на число, перестановки строк, прибавление к строке другой строки, умноженной на число), следует все элементы ниже главной диагонали превратить в нули. То есть алгоритм тот же, что и в методе Гаусса решения системы линейных алгебраических уравнений. В результате получим матрицу эквивалентную матрицеA.

Определитель, у которого все элементы ниже главной диагонали равны нулю, равен произведению элементов главной диагонали. Следовательно, выделенный определитель, порядок которого равен

k, равняется. Любой определитель(k+1)порядка содержит нулевую строку, следовательно, равен нулю. Итак, если все элементы главной диагонали полученной матрицы отличны от нуля, то ранг матрицы и системы векторов равенk. Если же несколько элементов главной диагонали равны нулю, то для подбора ненулевого определителя максимального порядка, следует переставить столбцы матрицы.

studfiles.net

Матричные уравнения

												22
		3	1	1		4
54.			4	10		1						0
	A	1	7	17		3	.
		2	2	4		1
	1				3		3
55.		0	1		2		7					3
	A	1	0		3		2		.
		1	2		1		1
	4		3				1
		0	3	2				1			1 2, 2	1,5
56.	A	6	1		3			2		.
		1			0		1

	Для каждого значения параметра найти ранг матрицы
	2		1			1			1		При 0	равен 2, при 1 ранг
57.		1	1			0			1		равен 3, при 0, 1 ранг
		2	1		2	1		2	1	.		равен 4.
		1	1			0			1
58.	Как изменяется ранг матрицы при ее транспонировании? Обосновать.											Не изменяется
59.	Как связаны между собой ранги исходной матрицы и обратной? Обосновать.											Равны.
60.	Как будет меняться ранг матрицы при добавлении в матрицу строк										Увеличиваться на 1, или не
	или столбцов. Обосновать.											изменяться.
61.	Как будет меняться ранг матрицы при удалении из матрицы строк										Уменьшаться на 1 или не
	или столбцов. Обосновать.											изменяться.
	Чему равен ранг матрицы С, составленной из двух матриц с
62.	рангами r A иr B приписыванием к строкам матрицыА строк										max r A , r B r C r A r B

	матрицы В?
	Чему равен ранг матрицы C A B , полученной из двух матриц с
63.	рангами r A иr B ?
64.	Чему равен ранг матрицы C A B , полученной из двух матриц с
	рангами r A иr B ?
65.	Чему равен ранг матрицы C AT A , если матрицаА имеет рангr A ?
66.	Определить ранги матриц А иВ, если		(	).
67.	Найти все возможные значения ранга матрицы			, если	.
68.	Для матриц	A , иE доказать, чтоAE EA A.
		3×3 3×3
69.	Для матриц	A , B , C доказать равенство( AB )C A( BC ) .
		2×2 2×2 2×2

r A r B r C r A r B

0 r C min r A , r B

	Пусть матрица C A B .
70.		Доказать, что	C		A	B	.
	2×2 2×2 2×2

Решить матричное уравнение, полагая все матрицы коэффициентов, участвующие в преобразованиях, невырожденными.

71.	AX BX X E .	X ( A B E ) 1
72.	XA 2E X A2E.	X A A E 1
73.	( A 1 )T X ( BA )1 B.		X AT B2 A
74.	( A 1 )T X ( AB )1 A.		X AT A2 B
75.	A B X C X D X 0 .	X A B C E 1 CD
76.	X A B X B C X C A A B 1 .	X 1 A B2
				1
		2
77.	2AX3X A1 .			1
		X 2A2 3A

24

Найти xi , гдеi 1,2 ,

из матричного уравнения A X B , считая

b1a22

b2a12

a11b2

a21b1

96.

2×2 2×1

2×1

x1

, x2

A

0 .

a11a22

a12a21

a11a22a12a21

Найти xij , гдеi, j 1,2 , из матричного уравненияA X B ,

x11

b11a22b21a12

,x21

a11b21a21b11

a11a22a12a21

97.

2×2 2×2 2×2

a11a22a12a21

0 .

x12

b12a22b22a12

,x22

a11b22a21b12

считая

A

a11a22a12a21

a11a22a12a21

В некоторой отрасли m заводов выпускаютn видов продукции. Матрица

A задает объемы

mxn

A B ;

продукции на каждом заводе в первом квартале, матрица

B — на втором. МатрицаC — стоимости

1)

2)

B A ;

98.

mxn

nx1

единиц каждого из видов продукции. Найти 1) объемы выпущенной продукции за оба квартала; 2)

3) A B C

прирост объемов во втором квартале по видам продукции и заводам; 3) стоимость продукции,

выпускаемой каждым заводом.

Предприятие выпускает три вида продукции, используя два вида сырья, нормы расхода сырья на единицу

1

2

3

продукции задаются матрицей A

. Определить денежные расходы предприятия на выпуск

0

1

1

99.

1

27

товаров, задаваемый матрицей C

1

, если стоимость единицы каждого вида сырья выражается

2

матрицей P 2,

3 .

Предприятие производит мебель трех видов и продает ее в четырех регионах.

Матрица B b		2		5	1	2
			1	8	3	4	задает количество реализованной мебели m-го	1000	3300 1000 1900
34			2	4	1	3
100.
типа (строки) в n-мрегионе (столбцы). Определить выручку предприятия в каждом
регионе, если цена реализации единицы мебели m -готипа задана матрицей
A 100 200	300 .

Предприятие за определенный период производит n типов продукции

	x
	1
X x2			, используя m видов ресурсов. Нормы затратi-горесурса (строки)
nx1	…
	xn

101. на производство единицыj-готипа (столбцы) задается матрицей затрат

	a	a	…	a
	11	12		1n
A a21		a22	…	a2n		. Определить матрицу	S полных затрат каждого
mxn	…	…	…	…			mx1
		am2	…
	am1			amn

вида на производство всей продукции за этот период.

S AX

a11x1

a12x2

….

a1nxn

a

x

a

22

x

2

….

a

2n

x

n

21 1

…………………………………….

a

x

a

m2

x

2

….

a

mn

x

m1 1

n

studfiles.net

Пакет аналитических вычислений Maple, страница 7

Существует ровно один многочлен, такой, что f(Λ_A) = r(Λ_A) и deg r < m, который определяется интерполяционными условиями:

Этот многочлен называется интерполяционный многочлен Лагранжа-Сильвестра. Тогда мы можем дать новое определение f(A).

Определение 7.2. Пусть функция f определена на спектре матрицы A, тогда f(A) = r(A), где r(λ) — интерполяционный многочлен Лагранжа-Cильвестра.

Свойства функции от матрицы:

1. Пусть λ₁,…, λ_n— все собственные значения матрицы A  C_n,n, тогда f(λ₁₎,…, f(λ_n)- собственные значения f(A).

2.  Пусть матрицы A и B подобны, причем B=  S^-1AS, тогда f(B) = S^—1f(A)S.

3. Если A = diag{A₁, …, A_k}, то f(A) = diag{f(A₁), …, f(A_k)}.

В пакете LinearAlgebra содержатся функции позволяющие вычислять различные функции от матриц. Рассмотрим эти функции.

Пример 7.1. Возвести матрицу A в степени 2 и 0,5, где A =

Пример 7.2. Найти е^A и е^{Ax, где A =}

Пример 7.3. Найти A², cos(A) и е^A, где A =

Глава 8

Матричные уравнения

8.1 Уравнение вида AХ=ХB

Рассмотрим матричное уравнение AX= XB, где ,,.

Теорема 8.1. Общее решение уравнения AX= XB, где , . ,,

может быть найдено по формуле: .

Где  — общее решение уравнения ,, , , .

Если , то , если  , то  — произвольная правильная верхняя треугольная матрица.

Матрица X зависит от N произвольных параметров , , где, , .

Пример 8.1. Решить матричное уравнение AX= XB,

где  A=  , B=

 

Ввод матрицы A:

Ввод матрицы B:

Найдем жорданову форму J1 матрицы A и преобразующую матрицу U:

Найдем жорданову форму J2 матрицы B и преобразующую матрицу V:

Найдем решение уравнения :

Вычисления выполняются вручную.

8.2 Уравнение вида AХ = ХA

Пусть дана матрица . Будем решать следующую задачу: найти все матрицы , перестановочные с A. Для этого необходимо найти общее решение уравнения AX= XA. Так как уравнение AX= XA является частным случаем уравнения AX= XB, то для его решения воспользуемся теоремой 8.1 и сформулируем новую теорему:

Теорема 8.2. Общее решения уравнения AX= XA, где , , 

может быть найдено по формуле: ,

Где  — общее решение уравнения ,, , .

Если , то , если  , то  — произвольная правильная верхняя треугольная матрица. Матрица X зависит от N произвольных параметров , , где, .

Пример 8.2. Решить матричное уравнение AX= XA, где A =

 

Ввод матрицы A:

Найдем жорданову форму J1 матрицы A и преобразующую матрицу U:

Найдем решение уравнения :

Вычисления выполняются вручную.

8.3 Решение уравнения AX – XB= C

Пусть дано уравнение AX – XB= C, где ,,. Это матричное уравнение эквивалентно системе m∙n линейных уравнений относительно элементов матрицы X.

Рассмотрим соответствующее однородное уравнение AX – XB= 0. Если матрицы A и B не имеют одинаковых собственных значений, то уравнение AX – XB=0 имеет единственное решение; если же матрицы A и B имеют одинаковые собственные значения, то в зависимости от C возможны два варианта:

1. Уравнение не имеет решения.

2. , где — произвольное частное решение уравнения AX—XB=C, — общее решение уравнения AX – XB= C.

Алгоритмизация данного типа уравнений отводится в качестве упражнения.

Глава 9

Нормы матриц

Определение 9.1. Неравенство A ≤  B  между  матрицами   A = [ а_ij]и   B =[ b_ij]одинаковых  типов   обозна­чает, что   а_ij  ≤b_ij .  В этом смысле   не   всякие  две матрицы сравнимы между собой.

Определение 9.2. Под абсолютной величиной (модулем)матрицы  A= [ а_ij] будем понимать матрицу       |A| = [ | а_ij| ]

где |а_ij| — модули элементов матрицы A.

Если A и B— матрицы, для которых операции A + B  и AB имеют смысл, то:

 а) | A + B | ≤ | A | + | B |;

б) | A B | ≤ | A | · | B |;

в)  | α A | = | α | · | A |;              

(α — число).

Определение 9.3. Под нормой матрицы A = [ а_ij] понимается действительное число || A ||, удовлетворяющее условиям:

а)  || A|| ≥ 0, причем   ||A|| =0  тогда и только тогда, когда A = 0;

б)   || α A ||  = | α | ·  || A || (α — число)   и,   в   частности, || –A || = || A ||;

в)   || A + B || ≤ || A || + || B ||;

г)   || AB || ≤ || A || · || B ||;

 (A и B — матрицы,   для   которых   соответствующие операции имеют смысл).

В дальнейшем для матрицы   A = [ а_ij]произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы;

1)   || A ||_m  = | а_ij|       (т-норма);       

2)   || A ||_l   = | а_ij|        (l-норма);        

3) || A ||_k   =              (k -норма).

Далее представлены алгоритмы для нахождения нормы матрицы каждого вида:

Пример 9.1. Найти m—норму для матрицы A, где A =

Пример 9.2. Найти l-норму для матрицы A, где A =

       

Пример 9.3. Найти k-норму для матрицы A, где A =

Приложение 1

Генерация задач

Часто возникают проблемы с подготовкой контрольных и проверочных работ по данному курсу, что связано с недостатком имеющихся в учебных пособиях типовых заданий для индивидуальной работы группе студентов.

Используя Maple нетрудно решить эту проблему.

Возьмем, к примеру, наиболее легкий тип задач. Пусть у нас дана матрица A:

и необходимо найти собственные значения этой матрицы.

Решая поставленную задачу находим:

где этот столбец – вектор собственных значений, равных -1 кратности 3.

Необходимо растиражировать эту задачу, сохранив данные собственные значение и их кратность.

vunivere.ru

No related posts.