[Зачет 76] Применение векторного произведения векторов для вычисления площади параллелограмма, треугольника и выпуклого четырёхугольника, а также вектора нормали к плоскости.
Применение векторного произведения векторов для вычисления площади параллелограмма, треугольника и выпуклого четырёхугольника, а также вектора нормали к плоскости.Для параллелограмма
Найти площадь параллелограмма, построенного на векторах .Решение.
По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение , а потом его модуль. Согласноимеем
а модуль
Искомая площадь параллелограмма
S = 19,26 кв. ед.
Для треугольника
Пример 4. Найти площадь треугольника , если известны координаты его вершин: Решение. Найдём векторы и : тогда . Находим .Имеем
Для выпуклого четырехугольника
площадь выпуклого четырехугольника АВСD
равна половине длины векторного произведения [AC BD]
Для вектора нормали к плоскости
Определение. Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора -вектор нормали к плоскости.fizmatinf.blogspot.com
Векторное произведение коллинеарных векторов — КиберПедия
Определение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение: Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ:
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ:
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце.
Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называютантикоммутативностью. Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные илидистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ:
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение: Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор. О длинах пока ни слова!
(1) Поставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ:
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце.
Векторное произведение векторов в координатах
С векторами, заданными в координатах, всё тоже просто и прозрачно. Сразу обращаю внимание на то, что разговор пойдёт о координатах ортонормированного базиса. В общем случае аффинного базиса нижеприведённая формула будет нерабочей.
Векторное произведение векторов , заданных в ортонормированном базисе , выражается формулой:
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «в», затем координаты вектора «дубль-в». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Согласно свойствам определителя, если в определителе две строки переставить местами, то он сменит знак. Этот факт полностью соответствует свойству антикоммутативности векторного произведения.
Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше.
Что получается в результате раскрытия определителя?
В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.
Пример 6
Найти векторное произведение векторов и его длину.
Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.
1) Найдём векторное произведение:
В результате получен вектор , или, ещё можно записать .
Существует очень хороший способ проверки: как следует из определения, вектор должен быть ортогонален векторам . Ортогональность векторов, как мы разбирались, проверяется с помощью скалярного произведения:
Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.
2) Вычислим длину векторного произведения.
Ответ:
В плане технических обозначений здесь, наоборот, вместо громоздкой конструкции выгодно использовать букву , поскольку она сокращает запись
Аналогичный пример для самостоятельного решения:
Пример 7
Даны векторы . Найти и вычислить .
Решение с ответом в конце!
Пример 8
Даны вершины треугольника . Найти его площадь.
Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:
Ответ:
Рассмотренную задачу можно решить ещё двумя способами – было не обязательно выбирать стороны . Решение также допустимо провести через векторы либо . Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. Настоятельно рекомендую выполнить схематический рисунок, чтобы лучше понять вышесказанное.
Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить , то получим противоположно направленный вектор , но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Примерах №№6,7, поскольку там требовалось найти вполне конкретный вектор.
Пример 9
Вычислить площадь параллелограмма, построенного на векторах , если
Это пример для самостоятельного решения.
В заключение первого раздела рассмотрим обещанную задачу Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение: Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Значит,
Ответ: а) не коллинеарны, б)
cyberpedia.su
ИСПОЛЬЗОВАНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ФИГУР Исследовательская работа по математике ученика 10 Б класса МОУ СОШ №73 Перевозникова Михаила
Использование векторного произведения ВЕКТОРОВ
для вычисления площади
некоторых геометрических фигур
Исследовательская работа по математике
Ученика 10 Б класса
МОУ СОШ №73
Перевозникова Михаила
Руководители:
Ассистент каф. математического анализа механико-математического факультета СГУ им. Н.Г. Чернышевского Бердников Глеб Сергеевич
Саратов, 2015
Содержание
Введение.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трёхмерном Евклидовом пространстве: определение понятия.
1.5. Координаты векторного произведения векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма. Выведение формулы и геометрический смысл векторного произведения векторов.
2.2. Зная только координаты точек, найти площадь треугольника. Доказательство теоремы
2.3. Проверка на примерах правильности формулы.
2.4. Практическое использование векторной алгебры и произведения векторов.
Заключение
Введение
Как известно, многие геометрические задачи имеют два ключевых способа решения – графический и аналитический. Графический метод связан с построением графиков и чертежей, а аналитический предполагает решение задач преимущественно с помощью алгебраических действий. В последнем случае алгоритм решений задач связан с аналитической геометрией. Аналитическая геометрия – это область математики, а точнее линейной алгебры, которая рассматривает решение геометрических задач средствами алгебры на основе метода координат на плоскости и в пространстве. Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо скалярного произведения векторов иногда применяется векторное произведение векторов.
В связи с широким распространением трехмерных пространственных технологий, изучение свойств некоторых геометрических фигур с использованием векторного произведения представляется актуальным.
В связи с этим была обозначена цель данного проекта – использование векторного произведения векторов для вычисления площади некоторых геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и дать определение векторному произведению векторов в системе координат;
2. Проанализировать наличие связи векторного произведения с площадью треугольника и параллелограмма;
3. Вывести формулу площади треугольника и параллелограмма в координатах;
4. Проверить на конкретных примерах верность выведенной формулы.
1. Теоретический обзор.
Векторы и вычисления с векторами
Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка А, концом отрезка – точка В. Сам вектор обозначен через  или
или  . Чтобы найти координаты вектора
. Чтобы найти координаты вектора  , зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
 = {Bx — Ax ; By — Ay}
= {Bx — Ax ; By — Ay}
Коллинеарными называются векторы, лежащие на параллельных прямых или на одной прямой. При этом вектор отрезок, характеризующийся длиной и направлением.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
.
Длина вектора | | в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
С векторами можно совершать различные действия.
Например, сложение. Чтобы их сложить, нужно провести сначала второй вектор из конца первого, а потом соединить начало первого с концом второго (рис. 1). Суммой векторов является другой вектор с новыми координатами.
Сумму векторов  = {ax ; ay} и
= {ax ; ay} и  = {bx ; by} можно найти воспользовавшись следующей формулой:
= {bx ; by} можно найти воспользовавшись следующей формулой:
 +
+  = {ax + bx; ay + by}
= {ax + bx; ay + by}
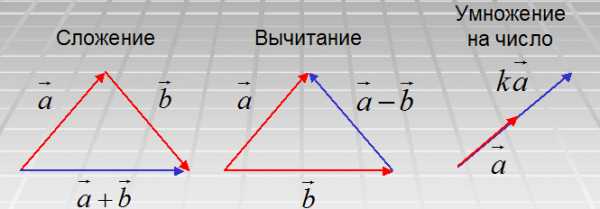
Рис. 1. Действия с векторами
Вычитая векторы, нужно сначала провести их из одной точки, а потом соединить конец второго с концом первого.
Разность векторов  = {ax ; ay} и
= {ax ; ay} и  = {bx ; by} можно найти по формуле:
= {bx ; by} можно найти по формуле:
 —
—  = {ax — bx; ay — by}
= {ax — bx; ay — by}
Также, векторы можно умножать на число. Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Произведение вектора  = {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
= {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
k ·  = {k · ax; k · ay}
= {k · ax; k · ay}
А можно ли умножать вектор на вектор? Конечно, и даже двумя вариантами!
Первый вариант – скалярное произведение.
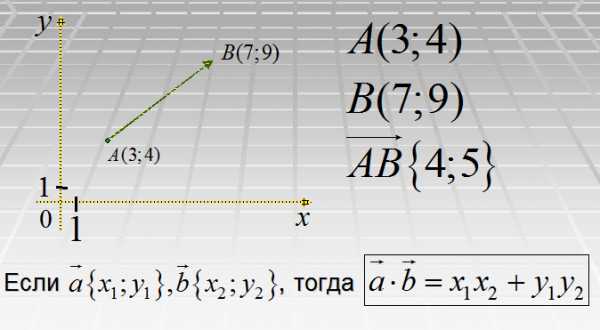
Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов можно использовать угол между данными векторами, показанный на рисунке 3.
Из формулы следует, что скалярное произведение равно произведению длин данных векторов на косинус угла между ними, его результатом является число. Важно, что если векторы перпендикулярны, то их скалярное произведение равно нулю, т.к. косинус прямого угла между ними равен нулю.
В координатной плоскости вектор также имеет координаты. Вектора, их координаты и скалярное произведение являются одними из самых удобных методов вычисления угла между прямыми (или их отрезками), если введена система координат. И если координаты , то их скалярное произведение равно:
В трехмерном пространстве существует 3 оси и, соответственно, у точек и векторов в такой системе будет по 3 координаты, а скалярное произведение векторов вычисляется по формуле:
.
1.2. Векторное произведение векторов в трехмерном пространстве.
Вторым вариантом вычисления произведения векторов является векторное произведение. Но, чтобы его определить требуется уже не плоскость, а трехмерное пространство, в котором начало и конец вектора имеют по 3 координаты.
В отличие от скалярного произведения векторов в трёхмерном пространстве операция «векторное умножение» над векторами приводит к иному результату. Если в предыдущем случае скалярного умножения двух векторов результатом было число, то в случае векторного умножения векторов результатом будет другой вектор, перпендикулярный обоим вступившим в произведение векторам. Поэтому это произведение векторов называется векторным.
Очевидно, что при построении результирующего вектора  , перпендикулярного двум, вступившим в произведение —
, перпендикулярного двум, вступившим в произведение —  и
и 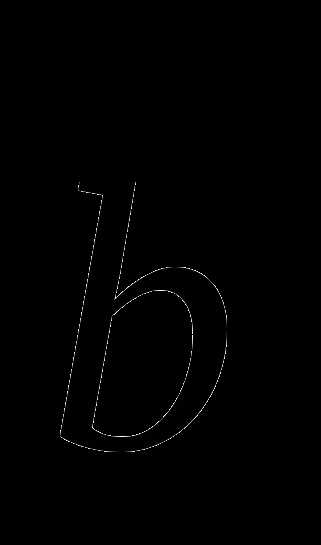 , может быть выбрано два противоположных направления. При этом направление результирующего вектора
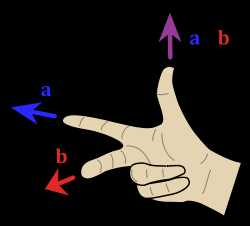
, может быть выбрано два противоположных направления. При этом направление результирующего вектора  определяется по правилу правой руки, или правилу буравчика. Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
определяется по правилу правой руки, или правилу буравчика. Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
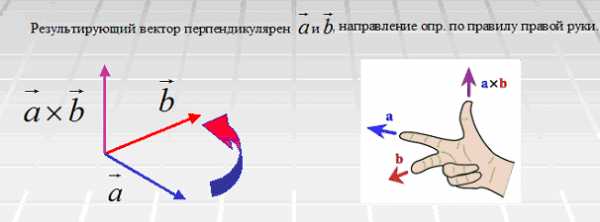
Рис. 7. Правило правой руки
1.3. Свойства векторного произведения векторов.
Длина результирующего вектора определяется по формуле
.
При этом 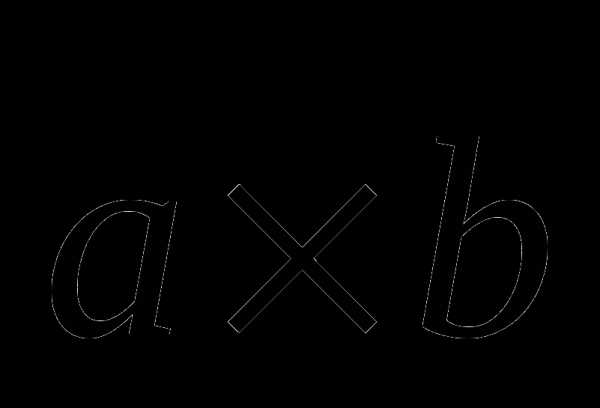 векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен
векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен 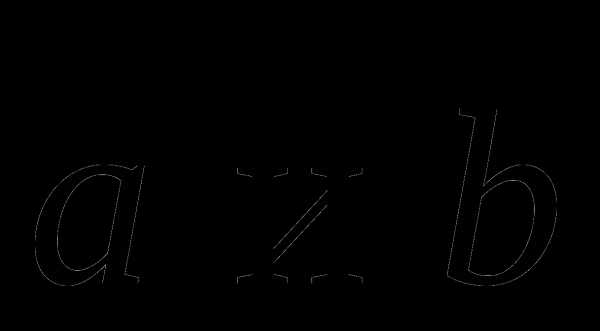 , а его направление определяется по правилу правой руки.
, а его направление определяется по правилу правой руки.
Векторное произведение зависит от порядка сомножителей, именно:
.
Векторное произведение ненулевых векторов равно 0, если они коллинеарны, тогда синус угла между ними будет равен 0.
Координаты векторов в трехмерном пространстве выражаются следующим образом: . Тогда координаты результирующего вектора находим по формуле
.
Длина результирующего вектора находится по формуле:
.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма в плоскости. Геометрический смысл векторного произведения векторов.
Пусть нам дан треугольник ABC (рис. 8). Известно, что .
Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника мы находим выражение векторного произведения векторов:
Из выше сказанного можно определить геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки.
Другими словами, длина векторного произведения векторов и равна площади параллелограмма, построенного на векторах и , со сторонами и и углом между ними, равным .
.
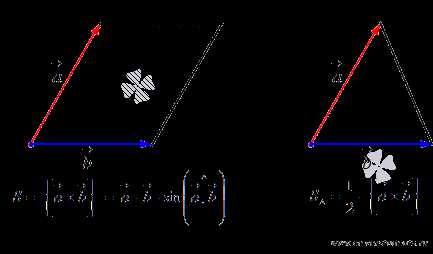
Рис. 9. Геометрический смысл векторного произведения векторов
В связи с этим, можно привести еще одно определение векторного произведения векторов:
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , длина которого численно равна площади параллелограмма построенного на векторах
, длина которого численно равна площади параллелограмма построенного на векторах  и
и  , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от
, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от  к
к  вокруг вектора
вокруг вектора  осуществлялось против часовой стрелки, если смотреть с конца вектора
осуществлялось против часовой стрелки, если смотреть с конца вектора  (рис. 10).
(рис. 10).
Рис. 10. Определение векторного произведения векторов
с использованием параллелограмма
2.2. Вывод формулы для нахождения площади треугольника в координатах.
Итак, нам дан треугольник АВС в плоскости и координаты его вершин. Найдем площадь этого треугольника (рис. 11).
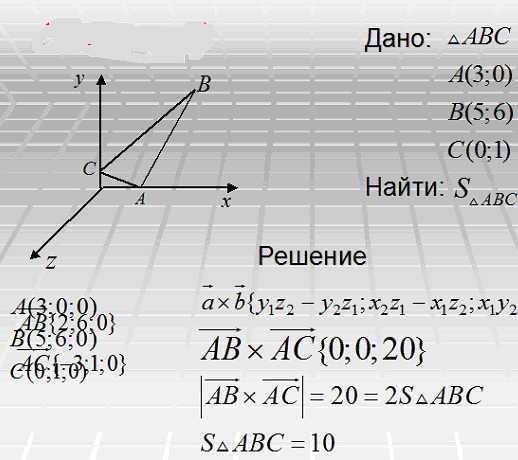
Рис. 11. Пример решения задачи на нахождение площади треугольника по координатам его вершин
Решение.
Для начала, рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и АС.
По данной прежде формуле подсчитаем координаты их векторного произведения. Длина этого вектора равна 2 площадям треугольника АВС. Площадь треугольника равна 10.
Более того, если мы рассмотрим треугольник на плоскости, то первые 2 координаты векторного произведения всегда будут равны нулю, поэтому мы можем сформулировать следующую теорему.
Теорема: Пусть дан треугольник АВС и координаты его вершин (рис. 12).
Тогда .
 Рис. 12. Доказательство теоремы
Рис. 12. Доказательство теоремы
Доказательство.
Рассмотрим точки в пространстве и вычислим координаты векторов ВС и ВА. . По приведенной раньше формуле вычислим координаты векторного произведения этих векторов. Обратим внимание, что все члены, содержащие z1 или z2, равны 0, т.к. z1и z2 = 0. УБРАТЬ!!!
Итак, следовательно,
2.3. Проверка правильности формулы на примерах
Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
a × b=
i
j
k
=
-1
2
-2
2
1
-1
= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
1
|a × b| =
1
√02 + 52 + 52 =
1
√25 + 25 =
1
√50 =
5√2
2
2
2
2
2
Ответ: SΔ = 2.5√2.
Заключение
2.4. Приложения векторной алгебры
и скалярного и векторного произведения векторов.
Где же нужны векторы? Векторное пространство и векторы носят не только теоретический характер, но и имеют вполне реальное практическое применение в современном мире.
В механике и физике многие величины имеют не только численное значение, но и направление. Такие величины называются векторными. Вместе с использованием элементарных механических понятий, опираясь на их физический смысл, многие величины рассматриваются как скользящие векторы, а их свойства описываются как аксиомами, как это принято в теоретической механике, так и при помощи математических свойств векторов. Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, момент импульса и сила Лоренца математически записываются с помощью векторов.
В физике важны не только сами вектора, но в большой степени важны и их произведения, которые помогают вычислять некоторые величины. Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Еще один пример: скалярное произведение используется для вычисления работы по приведенной ниже формуле, где F – вектор силы, а s – вектор перемещения.
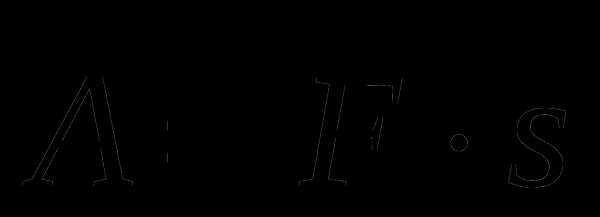
Одним из примеров использования произведения векторов является момент силы, равный произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое из того, что вычисляется в физике по правилу правой руки является векторным произведением. Найти подтверждения, привести примеры.
Стоит еще заметить, что двухмерным и трехмерным пространством не исчерпываются возможные варианты векторных пространств. Высшая математика рассматривает пространства большей размерности, в которых также определяются аналоги формул для скалярного и векторного произведения. Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
В то же время результатом векторного произведения векторов в трёхмерном Евклидовом пространстве является не число, а результирующий вектор со своими координатами, направлением и длиной.
Направление результирующего вектора определяется по правилу правой руки, что является одним из самых удивительных положений аналитической геометрии.
Векторное произведение векторов может быть использовано в нахождении площади треугольника или параллелограмма по заданным координатам вершин, что было подтверждено выведением формулы, доказательством теоремы и решением практических задач.
Векторы широко используются в физике, где такие показатели как скорость, импульс и сила могут быть представлены в виде векторных величин и вычисляются геометрически.
Список использованных источников
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: Просвещение, 2013. 383 с.
Атанасян Л.С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10-11 классы: учебник для общеобразовательных организаций: базовый и профильный уровни. М.: Просвещение, 2013. 255 с.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
????Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
http://a-geometry.narod.ru/problems/problems_32.htm
Математика. Клевер.
http://www.cleverstudents.ru/vectors/vector_product_of_vectors.html
——Изучение математики онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm
——Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5
infourok.ru
Векторное произведение — Википедия
 Векторное произведение в трёхмерном пространстве.
Векторное произведение в трёхмерном пространстве.Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Определение и история[править]
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводится остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве[править]
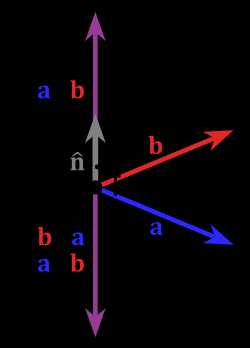
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной плоскости, так как векторы некомпланарны.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если с конца вектора кратчайший поворот от вектора к вектору виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Существует также аналитический способ определения тройки векторов. Для этого надо составить матрицу, первой строкой которой будут координаты первого вектора, второй строкой координаты второго вектора и третьей строкой координаты третьего вектора. Затем в зависимости от значения определителя можно сделать следующие выводы:
- Если определитель строго положителен, то тройка векторов правая.
- Если определитель строго отрицателен, то тройка векторов левая.
- Если определитель равен нулю, то векторы компланарны и, следовательно, линейно зависимы.
Геометрические свойства векторного произведения[править]
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.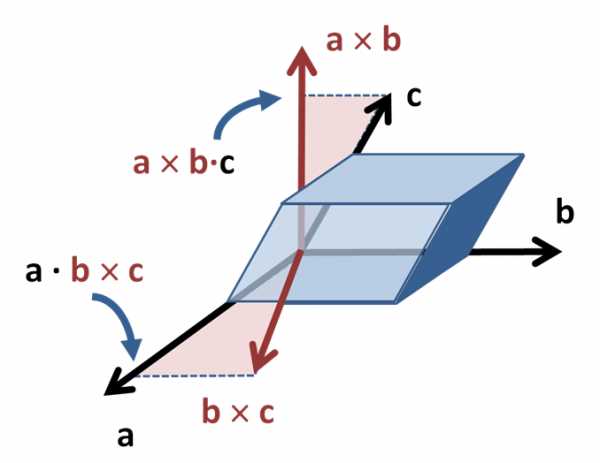 Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения[править]
Выражение для векторного произведения в декартовых координатах[править]
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Кватернионы[править]
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме[править]
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы[править]
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём[править]
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов[править]
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
Произведения векторов
Другое
- Кочин Н. Е. Введение в векторный и тензорный анализ.
www.wiki-wiki.ru
