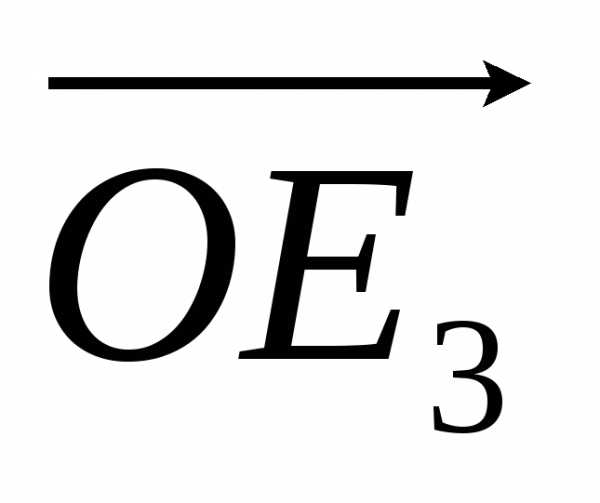Как узнать направление вектора – —

Направление вектора и направляющие косинусы

Направление вектора: основные понятия и определения

Первая точка называется началом вектора, а вторая – его концом.

Расстояние между началом и концом вектора называется длиной или модулем вектора.

Вектор, начало и конец которого совпадают, называется нулевым и обозначается ; его длина считается равной нулю. В противном случае, если длина вектора положительна, то его называют ненулевым.

Замечание. Если длина вектора равна единице, то он называется ортом или единичным вектором и обозначается .

Ненулевой вектор также можно определить как направленный отрезок.

Замечание. Направление нулевого вектора не определено.

Направляющие косинусы вектора

Замечание. Однозначно направление вектора задают его направляющие косинусы.

Чтобы найти направляющие косинусы вектора необходимо вектор нормировать (то есть вектор поделить на его длину):

   

Замечание. Координаты единичного вектора равны его направляющим косинусам.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

1. Пространство геометрических векторов

1. Геометрический вектор. Длина и направление вектора. Равенство векторов

Из школьного курса геометрии известно, что через две различные точки

A и B можно провести прямую и при том только Точки A и B, а также все точки, лежащие между ними, называют отрезком. Расстояние между точками A и B, называют длиной отрезка.

A C D B Рис. 1.1. Отрезок прямой (AB). Вектор .

Определение 1.1. Геометрическим вектором называют направленный отрезок, то есть отрезок, конечные точки которого упорядочены: одна из них является

началом, а вторая – концом отрезка.

Чтобы отличать вектор от отрезка, у конца вектора ставят стрелку. Вектор имеет две характеристики:

1. длина,

2. направление.

Длина вектора определяется путем измерения: выбрав единичный отрезок, устанавливаем, сколько раз этот единичный отрезок или какая-либо его часть укладывается в данном отрезке. (Например, =1,38 см. означает, что в качестве единичного отрезка выбран отрезок длиной в 1 сантиметр и в отрезкеPQ 138 раз укладывается сотая доля такого отрезка). Далеко не всегда единичный отрезок или любая его часть укладывается в измеряемый отрезок целое число раз. Например, если построить квадрат, сторона которого имеет длину, равную 1, то на какие бы доли мы ни дробили сторону, в диагональ квадрата не может уложиться целое число таких долей. Это означает, что сторона и диагональ квадрата

несоизмеримы и длина диагонали выражается иррациональным числом.

Существование несоизмеримых отрезков было установлено древнегреческим математиком и философом-мистиком Пифагором ( VI в. до н.э). Необходимость выражать числом длины всех отрезков потребовала введения, наряду с рациональными, иррациональных чисел. Множество, включающее в себя все рациональные и иррациональные числа, называют множеством действительных чисел и обозначают символом «R». Теория действительных чисел в своем современном виде существует благодаря трудам выдающихся европейских математиков второй половины XIX в. Р. Дедекинда (1831-1916), Г. Кантора (1845-1918), К. Вейерштрасса (1815-1897).

Теория действительного числа позволила строго обосновать возможность установления взаимно однозначного соответствия между действительными числами и точками прямой (аксиома непрерывности Кантора-Дедекинда). Если на прямой выбрать направление и эталон длины (отрезок

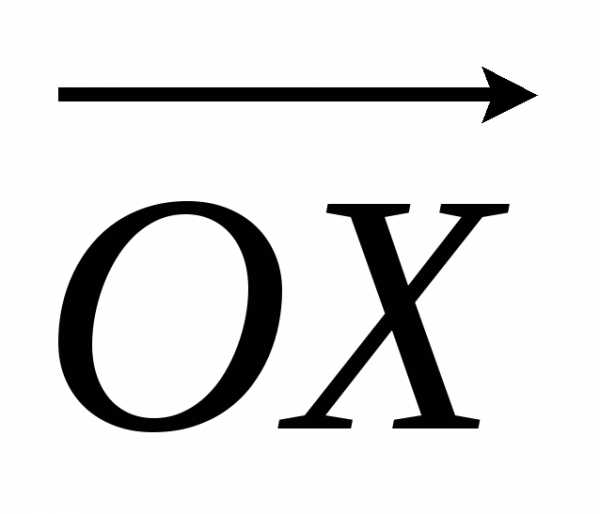OE на рис. 1.2.), то каждой точке X этой прямой соответствует действительное число x равное длине отрезка OX со знаком “+”, если направление вектора совпадает с направлением прямой, и со знаком “ — “ , если направления прямой и вектора противоположны. С другой стороны, каждому действительному числу, соответствует вполне определенная точка такой прямой. Из школьного курса математики известно, что описанную выше прямую называютчисловой осью. Связь между действительными числами и точками числовой оси столь глубока, что конкретные числа в математике часто называют “точками”.

X« O E X`     x« x` Рис. 1.2. Числовая ось.

Определение 1.2. Векторы называют коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Определение 1.3. Два коллинеарных вектора называют сонаправленными, если после приложения их к какой-либо одной точке конец одного из векторов оказывается лежащим между началом и концом второго вектора или совпадать с ним, и

противонаправленными , если концы их оказываются лежащими по разные стороны от общего начала.

На рис. 1.2. и, а также. Здесь символами «» и «» обозначены сонаправленность и противонаправленность векторов.

Отметим, что величина угла между сонаправленными векторами равна 0, между противонаправленными — .

Определение 1.4. два вектора называют равными, если они сонаправлены и длины их равны. Два вектора называют противоположными, если они противонапрвлены и длины их равны.

Аналогично тому, как длина вектора определяется путем сравнения с длиной заранее выбранного единичного отрезка,

направление вектора определяется путем сравнения с заранее выбранными «базисными» направлениями. Базисные направления указываются с помощью базисных векторов.

Пусть V₁ — множество всех направленных отрезков, лежащих на одной числовой прямой и приложенных к точке О (рис. 1.2). Каждый из этих отрезков определяет длину и направление всех, равных ему векторов, как лежащих на той же прямой, но приложенных к другим точкам, так и лежащих на любой из параллельных ей прямых. Поэтому, определив направления векторов из множества V₁ , мы определим направления всех, коллинеарных им векторов.

Очевидно, что векторы из множества V₁ имеют лишь 2 возможных направления: они могут быть сонаправленныи или противонаправленными единичному вектору 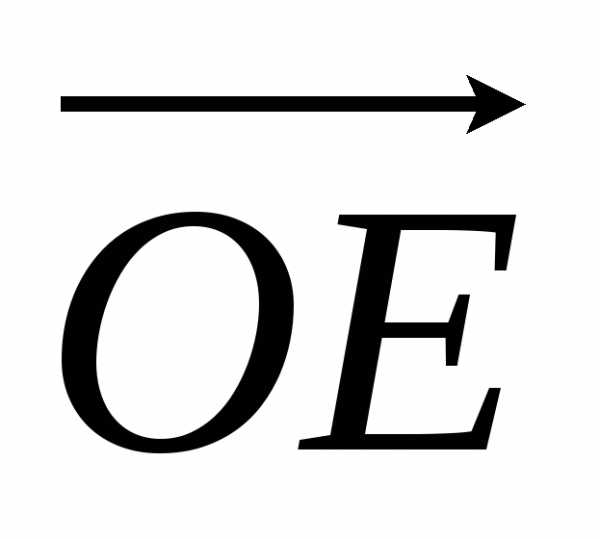. Это означает, что выбрав

в качестве базисного вектора, и приняв его направление за положительное, можно описать направления всех, коллинеарных ему векторов либо как положительное, либо как отрицательное.

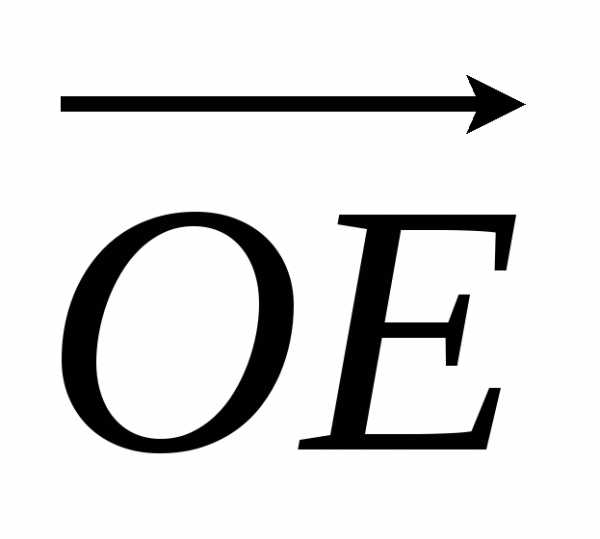
Определение 1.6. Векторы называют компланарными, если они лежат в одной плоскости или параллельных плоскостях.

Отметим, что два вектора всегда компланарны (см. рис 1.3 и рис. 1.4). Действительно два направленных отрезка могут быть либо коллинеарны либо неколлинеарны. Если они коллинеарны, то они лежат либо на одной прямой, либо на параллельных прямых (рс.1.3.). Как известно из школьного курса геометрии через прямую можно провести бесконечно много плоскостей, для которых эта прямая является линией пересечения. Через две параллельные прямые также всегда можно провести плоскость. Это и означает, что коллинеарные отрезки являются также и компланарными.

Пусть теперь два направленных отрезка неколлинеарны (рис 1.4). Начала этих векторов могут быть приложены либо к одной точке, либо к разным точкам. В первом случае направленные отрезки определяют три точки: общее начало и два различных конца, а через три точки можно провести плоскость. Во втором случае к каждому из начал этих отрезков можно приложить векторы, равные другому направленному отрезку. Таким образом, получим два параллельных треугольника, которые определят две параллельные плоскости.

D A A B B C С D Рис.1.3. Коллинеарные векторы всегда компланарны

A B A B D` C C B` D Рис.1.4. Два неколлинеарных вектора всегда компланарны

O` A` O E2 V2 E1 A O« A«	A E2   O E2
Рис.1.5.Направления всех компланарных друг другу векторов можно задать указав величины углов, которые образует представитель этого вектора вV2с базисными векторамиOE1 и OE2

Пусть V² — множество всех направленных отрезков, лежащих в одной плоскости и приложенных к какой-либо «удобной» точке плоскости (точке О на рис 1.5). Проведем через эту точку две взаимно перпендикулярные числовые оси с единичными векторами и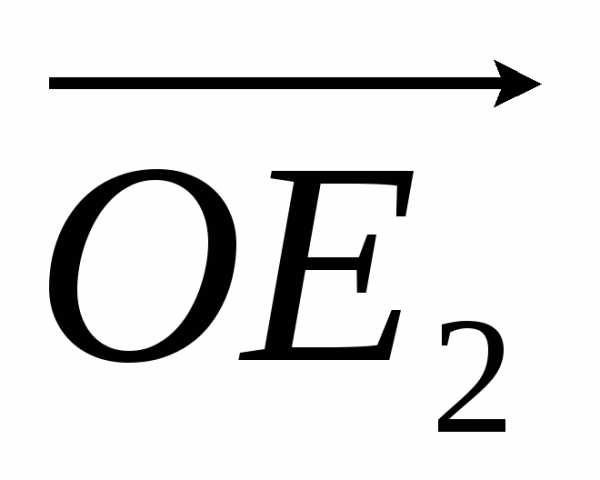. Каждый из направленных отрезков множества V₂ определяет длину и направление всех, равных ему векторов, как лежащих в той же плоскости, но приложенных к другим точкам, так и лежащих на любой из параллельных ей плоскостей. Поэтому, определив направления векторов из множества V² , мы определим направления всех, компланарных им векторов.

Очевидно, что направление любого вектора из V² можно задать, указав углы, которые образует этот вектор с двумя базисными векторам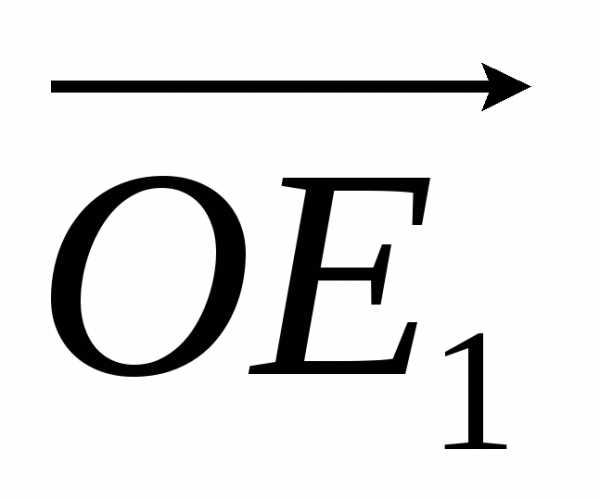и и(рис 1.5). Таким образом, имея два базисных вектора, можно задать направление любого направленного отрезка, компланарного им. Для этого достаточно найти в V² вектор, равный интересующему нас направленному отрезку, и указать величины углов, которые он образует с базисными векторами

O	E3  E1 O E2
Рис.1.6. Три вектора могут быть компланарны или некомпланарны. Направление вектора в пространстве задают величинами углов, которые этот вектор образует с базисными векторами ,,

Три вектора могут быть как компланарны, так и некомпланарны (рис. 1.6). Пусть V³ – множество всех направленных отрезков в пространстве, приложенных к какой-либо «удобной» точке пространства – точке О. проведем через эту точку три взаимно перпендикулярных оси и приложим к ней три единичных вектора отрезкам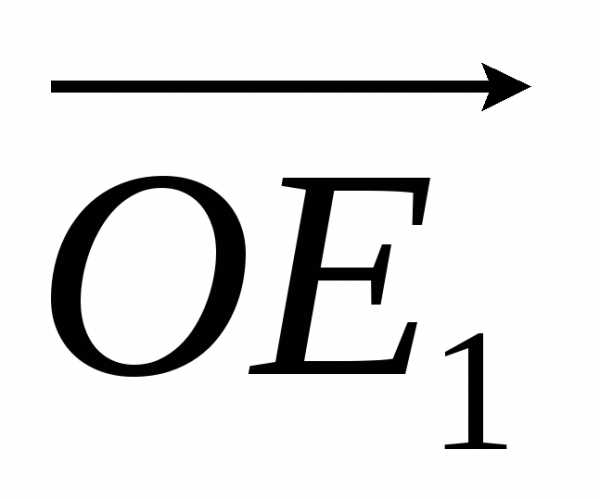и,и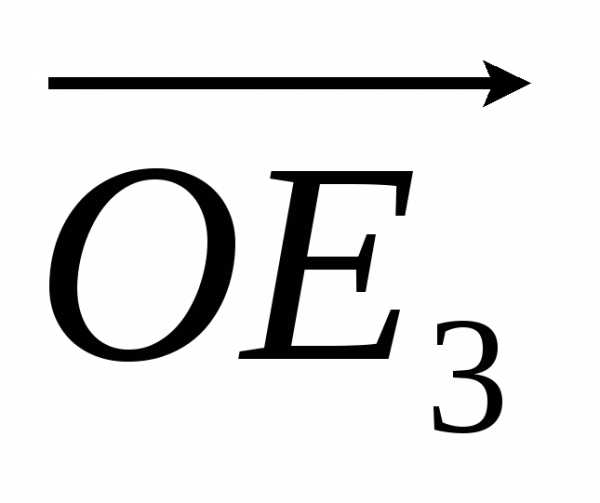(рис. 1.6), направление которых совпадает с направлениями осей. Тогда направление любого вектора из V³ можно задать, указав величины углов, которые данный вектор образует с ,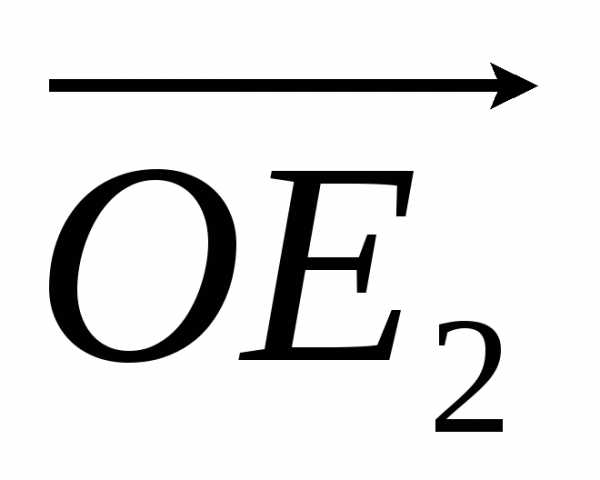и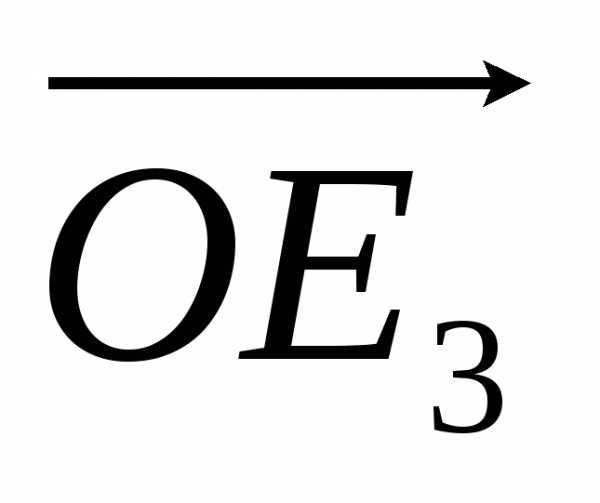(рис. 1.6). Любой направленный отрезок пространства имеет своего «представителя» во множестве V³ . Его направление можно задать, указав направление равного ему вектора из V³.

Таким образом, направление и длина любого геометрического вектора может быть задана, если известны длина и направление равного ему отрезка, приложенного к «удобной» точке, к которой приложены также и базисные векторы. Для описания всех коллинеарных векторов достаточно рассмотреть множество V¹, всех компланарных – V², всех векторов пространства – V³ .

Определение 1.5. Множество всех равных друг другу векторов называют свободным вектором.

Свободные векторы обозначают символами: ,и т.п. Свободный вектор будем рассматривать через его представителя: направленный отрезок, приложенный к «удобной» точке. Таким образом, изучение всех геометрических векторов будет сведено к изучению пространств V¹, V² и V³.

Но пространства эти будут неполны, если в каждое из них не ввести нуль-вектор.

Определение 1.6. Нуль-вектор – это вектор, длина которого равна 0.

Обозначение нуль-вектора: 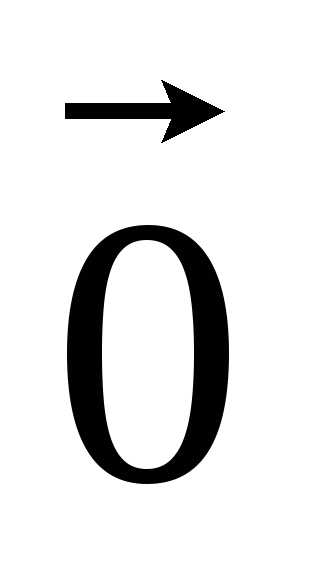. В пространствах V¹, V² и V³нуль-вектором принято считать точку приложения базисных векторов.

studfiles.net

как найти направление вектора

Вы искали как найти направление вектора? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как определить направление вектора, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти направление вектора».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как найти направление вектора,как определить направление вектора,как узнать направление вектора,направление вектора,направление вектора как найти,направление вектора как определить. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как найти направление вектора. Просто введите задачу в окошко и нажмите «решить» здесь (например, как узнать направление вектора).

Где можно решить любую задачу по математике, а так же как найти направление вектора Онлайн?

Решить задачу как найти направление вектора вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru

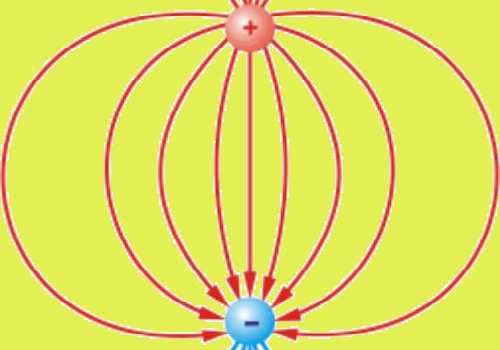
Как определить направление вектора напряженности

Заряженные тела могут влиять друг на друга без соприкосновения через электрическое поле. Поле, которое создается статичными электрическими частицами, именуется электростатическим.

Инструкция

1. Если в электрическое поле, создаваемое зарядом Q, разместить еще один заряд Q0, то оно будет влиять на него с определенной силой. Это колляция именуется напряженностью электрического поля E. Она представляет собой отношение силы F, с которое поле действует на правильный электрический заряд Q0 в определенной точке пространства, к значению этого заряда: E = F/Q0.

2. В зависимости от определенной точки пространства, значение напряженности поля E может меняться, что выражается формулой Е = Е (x, y, z, t). Следственно напряженность электрического поля относится к векторным физическим величинам.

3. От того что напряженность поля зависит от силой, действующей на точечный заряд, то вектор напряженности электрического поля E идентичен с вектором силы F. Согласно закону Кулона, сила, с которой взаимодействуют две заряженные частицы в вакууме, направлена по прямой линии, которая соединяет эти заряды.

4. Майкл Фарадей предложил наглядно изображать напряженность поля электрического заряда с поддержкой линий напряженности. Эти линии совпадают с вектором напряженности во всех точках по касательной. На чертежах их принято обозначать стрелками.

5. В том случае, если электрическое поле однородно и вектор его напряженности непрерывен по своему модулю и направлению, то линии напряженности параллельны с ним. Если электрическое поле создается правильно заряженным телом, линии напряженности направлены от него, а в случае с негативно заряженной частицей – по направлению к нему.

Для того дабы обнаружить напряженность электрического поля , внесите в него вестимый пробный заряд. Измерьте силу, которая действует на него со стороны поля и рассчитайте значение напряженности. Если электрическое поле создается точечным зарядом либо конденсатором, рассчитайте его по особым формулам.

Вам понадобится

• электрометр, динамометр, вольтметр, линейку и транспортир.

Инструкция

1. Определение напряженности произвольного электрического поля Возьмите заряженное тело, размеры которого незначительны по сопоставлению размерами тела, генерирующего электрическое поле. Отлично подойдет заряженный металлический шар с малой массой. Измерьте величину его заряда электрометром и внесите в электрическое поле. Уравновесьте силу, действующую на заряд со стороны электрического поля динамометром и снимите с него показания в ньютонах. Позже этого значение силы, поделите на величину заряда в Кулонах (E=F/q). Итогом будет напряженность электрического поля в вольтах на метр.

2. Определение напряженности электрического поля точечного заряда Если электрическое поле генерируется зарядом, величина которого знаменита, для определения его напряженности в некоторой точке пространства удаленной от него, измерьте это расстояние между избранной точкой и зарядом в метрах. Позже этого величину заряда в Кулонах, поделите на измеренное расстояние, возведенное во вторую степень (q/r?). Полученный итог умножьте на показатель 9*10^9.

3. Определение напряженности электрического поля конденсатора Измерьте разность потенциалов (напряжение) между пластинами конденсатора. Для этого параллельно ним присоедините вольтметр, итог зафиксируйте в вольтах. После этого измерьте расстояние между этими пластинами в метрах. Поделите значение напряжения на расстояние между пластинами, итогом будет напряженность электрического поля . Если между пластинами размещен не воздух, определите диэлектрическую проницаемость данной среды и поделите итог не ее значение.

4. Определение электрического поля , сделанного несколькими поля ми Если поле в данной точке является итогом наложения нескольких электрических полей, обнаружьте векторную сумму значений этих полей, с учетом их направления (тезис суперпозиции полей). Если надобно обнаружить электрическое поле, образованное двумя поля ми, постройте их векторы в данной точке, измерьте угол между ними. После этого возведите всякое из их значений в квадрат, обнаружьте их сумму. Вычислите произведение значений напряженности полей, умножьте его на косинус угла, тот, что равен 180? минус угол между векторами напряженностей, а итог умножьте на 2. Позже этого от суммы квадратов напряженностей отнимите полученное число (E=E1?+E2?-2E1E2*Cos(180?-?)). При построении полей рассматривайте, что силовые линии выходят из правильных зарядов и входят в негативные.

Видео по теме

Объектами векторной алгебры являются отрезки прямой, имеющие направление и длину, называемую модулем. Дабы определить модуль вектора , следует извлечь квадратный корень из величины, представляющей собой сумму квадратов его проекций на координатные оси.

Инструкция

1. Векторы характеризуются двумя основными свойствами: длиной и направлением. Длина вектора именуется модулем либо нормой и представляет собой скалярное значение, расстояние от точки начала до точки конца. Оба свойства используются для графического изображения разных величин либо действий, скажем, физических сил, движения элементарных частиц и пр.

2. Местоположение вектора в двухмерном либо трехмерном пространстве не влияет на его свойства. Если перенести его в другое место, то изменятся лишь координаты его концов, впрочем модуль и направление останутся бывшими. Эта автономность разрешает применять средства векторной алгебры в разных вычислениях, скажем, определения углов между пространственными прямыми и плоскостями.

3. Весь вектор дозволено задать координатами его концов. Разглядим для начала двухмерное пространство: пускай предисловие вектора находится в точке А (1, -3), а конец – в точке В (4, -5). Дабы обнаружить их проекции, опустите перпендикуляры на ось абсцисс и ординат.

4. Определите проекции самого вектора , которые дозволено вычислить по формуле:АВх = (xb – xa) = 3;ABy = (yb – ya) = -2, где:ABx и ABy – проекции вектора на оси Ох и Оу;xa и xb – абсциссы точек А и В;ya и yb – соответствующие ординаты.

5. В графическом изображении вы увидите прямоугольный треугольник, образованный катетами с длинами, равными проекциям вектора . Гипотенузой треугольника является величина, которую необходимо вычислить, т.е. модуль вектора . Примените теорему Пифагора:|АВ|? = ABx? + ABy? ? |AB| = ?((xb – xa)? + (yb – ya)?) = ?13.

6. Видимо, что для трехмерного пространства формула усложняется путем добавления третьей координаты – аппликат zb и za для концов вектора :|AB| = ?((xb – xa)? + (yb – ya)? + (zb – za)?).

7. Пускай в рассмотренном примере za = 3, zb = 8, тогда:zb – za = 5;|AB| = ?(9 + 4 + 25) = ?38.

Видео по теме

Для того дабы определить модуль точечных зарядов идентичной величины, измерьте силу их взаимодействия и расстояние между ними и произведите расчет. Если же необходимо обнаружить модуль заряда отдельных точечных тел, вносите их в электрическое поле с вестимой напряженностью и измеряйте силу, с которой поле действует на эти заряды.

Вам понадобится

• – крутильные весы;
• – линейка;
• – калькулятор;
• – измеритель электростатического поля.

Инструкция

1. Если есть два идентичных по модулю заряда, измерьте силу их взаимодействия при помощи крутильных весов Кулона, которые единовременно являются эмоциональным динамометром. Позже того, как заряды придут в баланс, и проволока весов скомпенсирует силу электрического взаимодействия, на шкале весов зафиксируйте значение этой силы. Позже этого при помощи линейки, штангенциркуля, либо по особой шкале на весах обнаружьте расстояние между этими зарядами. Рассматривайте, что разноименные заряды притягиваются, а одноименные отталкиваются. Силу измеряйте в Ньютонах, а расстояние в метрах.

2. Рассчитайте значение модуля одного точечного заряда q. Для этого силу F, с которой взаимодействуют два заряда, поделите на показатель 9•10^9. Из полученного итога извлеките квадратный корень. Итог умножьте на расстояние между зарядами r, q=r•?(F/9•10^9). Заряд получите в Кулонах.

3. Если заряды неодинаковые, то один из них должен быть предварительно знаменит. Силу взаимодействия знаменитого и неведомого заряда и расстояние между ними определите при помощи крутильных весов Кулона. Рассчитайте модуль неведомого заряда. Для этого силу взаимодействия зарядов F, поделите на произведение показателя 9•10^9 на модуль знаменитого заряда q0. Из получившегося числа извлеките квадратный корень и умножьте итог на расстояние между зарядами r; q1=r•?(F/(9•10^9•q2)).

4. Определите модуль незнакомого точечного заряда, внеся его в электростатическое поле. Если его напряженность в данной точке заблаговременно незнакома, внесите в нее датчик измерителя электростатического поля. Напряженность измеряйте в вольтах на метр. Внесите в точку с вестимой напряженностью заряд и с поддержкой эмоционального динамометра измерьте силу в Ньютонах, действующую на него. Определите модуль заряда, поделив значение силы F на напряженность электрического поля E; q=F/E.

Видео по теме

Обратите внимание!
Вектор напряженности имеет лишь одно направление в всякой точке пространства, следственно линии напряженности никогда не пересекаются.

jprosto.ru

Направление вектора магнитной индукции

Магнитное поле характеризуют при помощи вектора магнитной индукции ().

Если свободно вращающуюся магнитную стрелку, которая является небольшим магнитом, обладающим полюсами (северным (N) и южным(S)), поместить в магнитное поле, то она будет поворачиваться до тех пор, пока не установится определённым образом. Аналогично ведет себя рамка с током, повешенная на гибком подвесе, имеющая возможность поворачиваться. Способность магнитного поля ориентировать магнитную стрелку используют для того, чтобы определить направление вектора магнитной индукции.

Направление вектора магнитной индукции

Так, направлением вектора магнитной индукции считают направление, которое указывает северный полюс магнитной стрелки, которая может свободно поворачиваться в магнитном поле.

Такое же направление имеет положительная нормаль к замкнутому контуру с током. Направление положительной нормали определяют при помощи правила правого винта (буравчика): положительная нормаль направлена туда, куда поступательно перемещался бы буравчик, если бы его головку вращали по направлению течения тока в контуре.

Применяя контур с током или магнитную стрелку, можно выяснить, как направлен вектор магнитной индукции магнитного поля в любой точке.

Для определения направления вектора иногда удобно использовать так называемое правило правой руки. Его применяют следующим образом. Пытаются в воображении охватить правой рукой проводник таки образом, чтобы при этом большой палец указывал направление силы тока, тогда кончики остальных пальцев направлены так же как вектор магнитной индукции.

Частные случаи направления вектора магнитной индукции прямого тока

Если магнитное поле в пространстве создается прямолинейным проводником с током, то магнитная стрелка будет в любой точке поля устанавливаться по касательной к окружностям, центры которых лежат на оси проводника, а плоскости перпендикулярны проводу. При этом направление вектора магнитной индукции определим, используя правило правого винта. Если винт вращать так, что он будет поступательно двигаться по направлению силы тока в проводе, то вращение головки винта совпадает с направлением вектора . На рис. 1 направлен от нас, перпендикулярно плоскости рисунка.

Ориентируясь на местности при помощи компаса, мы каждый раз проводим опыт по определению направления вектора Земного поля.

Пусть в магнитном поле движется заряженная частица, тогда на нее действует сила Лоренца (), которая определена как:

   

где q – заряд частицы; – вектор скорости частицы. Сила Лоренца и вектор магнитной индукции всегда взаимно перпендикулярны. Для заряда большего нуля (), тройка векторов и связана правилом правого винта (рис.2).

Линии магнитного поля и направление вектора B

Визуализировать картину магнитного поля можно при помощи линий магнитной индукции. Линиями магнитной индукции поля называют линий, для которых касательными в любой точке являются векторы магнитной индукции рассматриваемого поля. Для прямого проводника с током линиями магнитной индукции являются концентрические окружности, плоскости их перпендикулярны проводнику, центры на оси провода. Специфика линий магнитного поля заключена в том, что они бесконечны и являются всегда замкнутыми (или уходящими в бесконечность). Это означает, что магнитное поле является вихревым.

Принцип суперпозиции вектора B

Если магнитное поле создано не одним, а совокупностью токов или движущихся зарядов, то оно находится как векторная сумма отдельных полей, создаваемых каждым током или движущимся зарядом отдельно. В виде формулы принцип суперпозиции записывают как:

   

Или:

   

Примеры решения задач

ru.solverbook.com

4.3 Проекция вектора на направление другого вектора

Рассмотрим два вектора и.

О

К

Отрезок ОК является проекцией вектора на направление вектора. Из полученного прямоугольного треугольника очевидно, что:

.

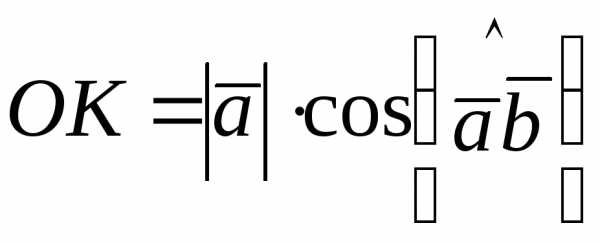Из формулы (4.1) следует:

,

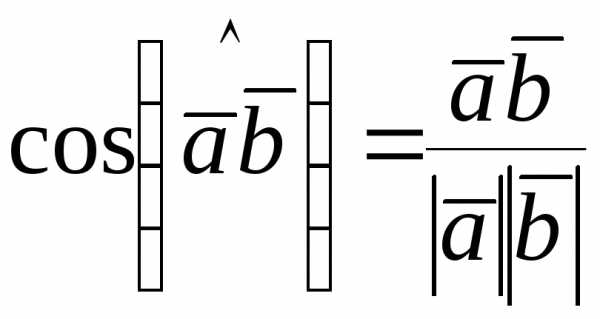следовательно, можем записать:

.

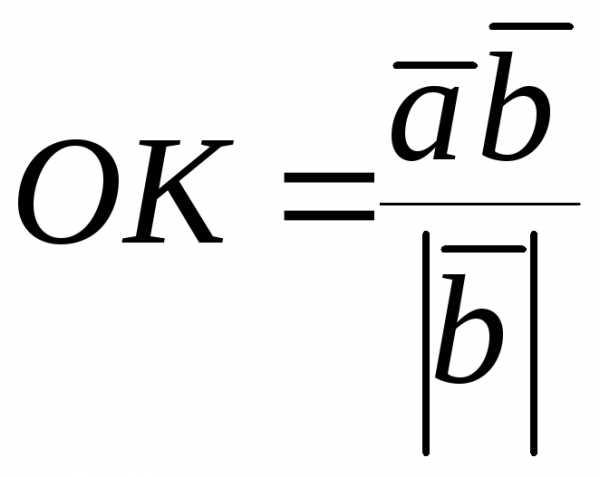Окончательно, проекция вектора на направление другого вектора вычисляется по формуле:

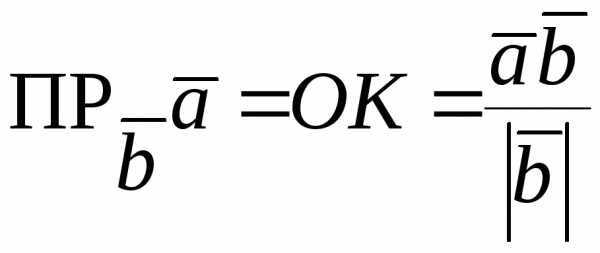(4.6)

ЛЕКЦИЯ 5

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

5.1 Определение векторного произведения

Векторным произведением двух векторов иназывается третийвектор , обладающий свойствами:

1. Вектор перпендикулярен плоскости, в которой расположены векторыи.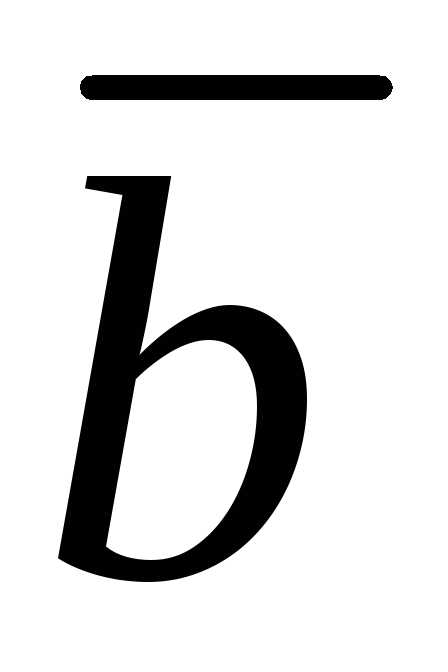

.

2. Длина вектора равна площади параллелограмма, построенного на векторахи, как на сторонах.

(5.1)

3. Векторы ,,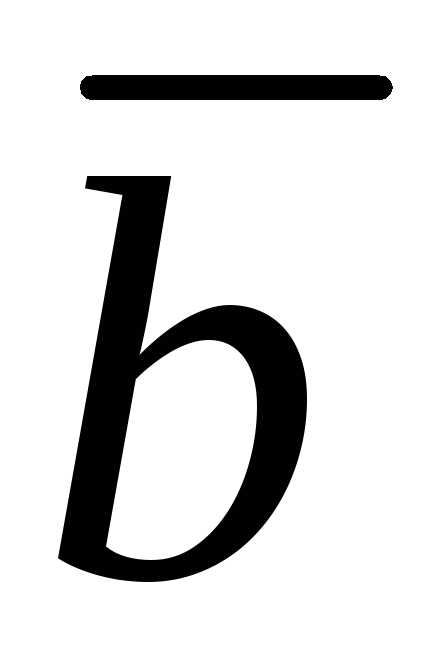, в том порядке, как они записаны, образуютправую тройку векторов.

Обозначения:

.

5.2 Вычисление векторного произведения двух векторов

Рассмотрим векторы: и. Векторное произведение этих векторов равноопределителю третьего порядка, элементами первой строки которого являются единичные орты , элементами второй и третьей строк – координаты векторовисоответственно.

(5.2)

Запишем разложение определителя в формуле (5.2) по элементам первой строки:

Таким образом, координаты векторного произведения векторов и, т.е. вектораесть:

Т.е.

Из определения векторного произведения следует, что длина вектора равна площади параллелограмма, построенного на векторах

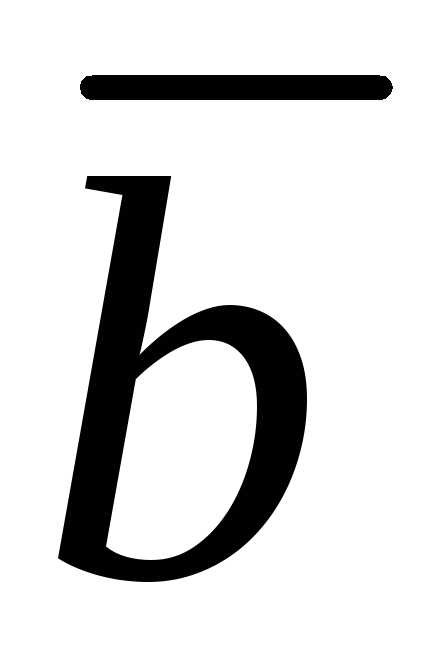и , значит,

(5.3)

Равенство (5.3) является геометрическим смыслом векторного произведения.

5.3 Свойства векторного произведения

1.

2.

3.

Векторное произведение коллинеарных векторов равно нулю. Это следует из определения векторного произведения.

5.4 Векторные произведения единичных орт

Рассмотрим векторы 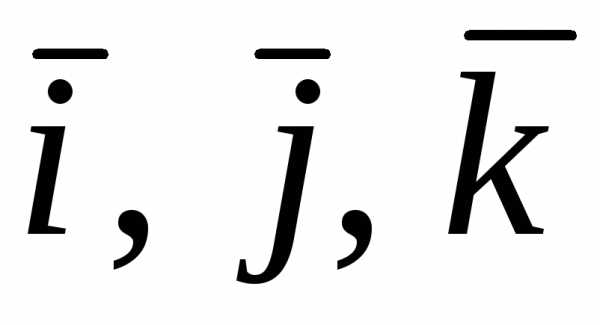. Из определения векторного произведения следует, что:

(5.4)

Очевидны равенства:

(5.5)

Чтобы определить другие векторные произведения векторов 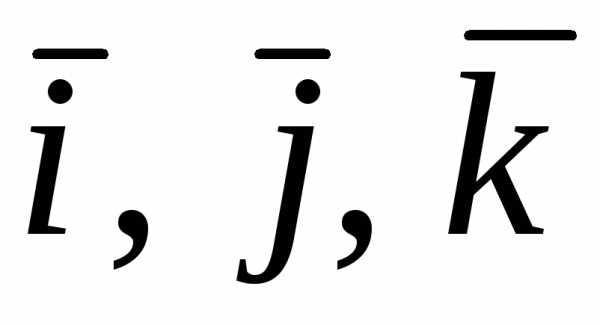, пользуются схемой:

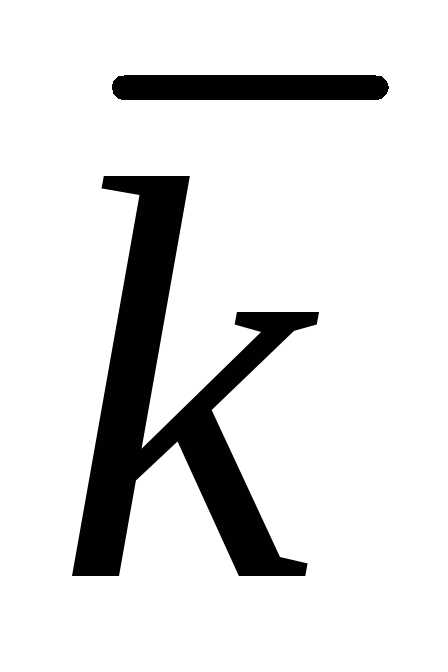
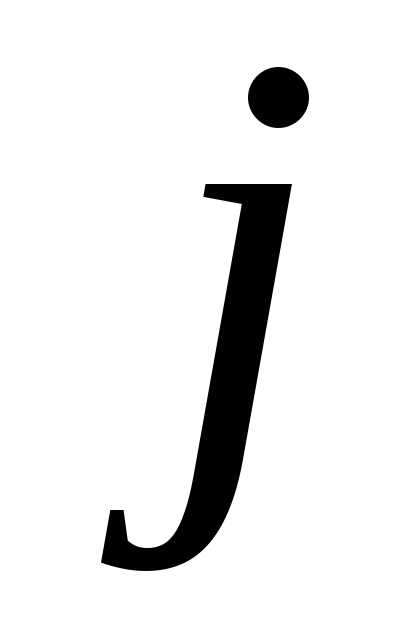
Из схемы видно, что

5.5 Условия коллинеарности и перпендикулярности векторов

Исходя из определения скалярного и векторного произведения векторов, учитывая свойства и приложение этих операций, делаем выводы:

(5.6)

Т.е. скалярное перпендикулярных векторов равно нулю.

Если векторы коллинеарны, то их координаты пропорциональны, т.е. выполняются равенства:

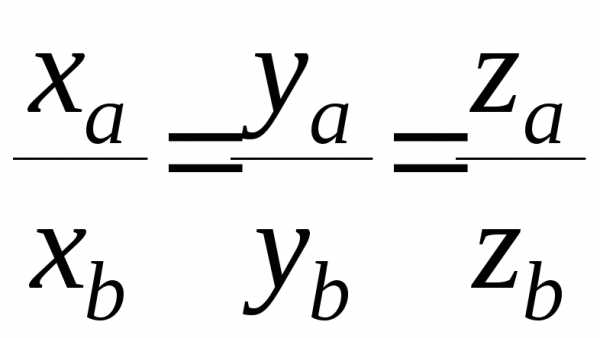(5.7)

ЛЕКЦИЯ 6

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

6.1 Определение смешанного произведения векторов

Смешанным произведением трёх векторов называется число, равное скалярному произведению векторного произведения первых двух векторов на третий.

(6.1)

Обозначение .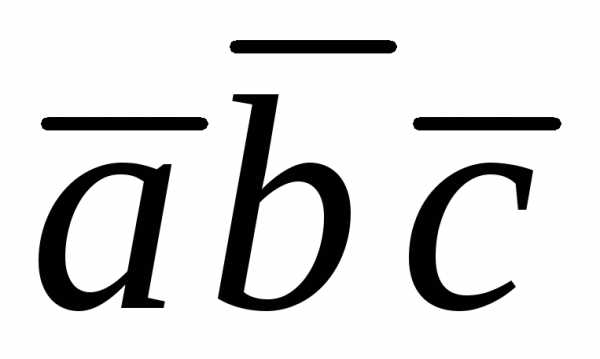

6.2 Смешанное произведение векторов в координатной форме

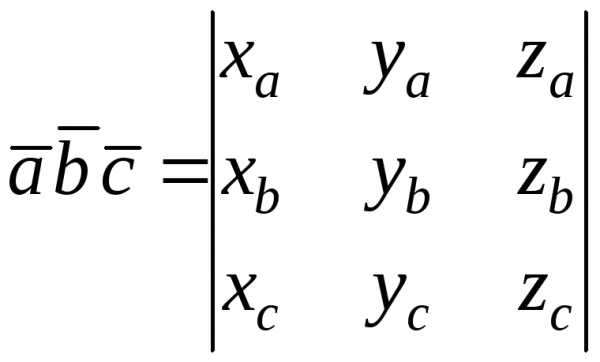(6.2)

6.3 Свойства смешанного произведения

1.

2.

6.4 Геометрический смысл смешанного произведения

Смешанное произведение трёх векторов по абсолютной величине равно объему параллелепипеда, построенного на этих векторах.

ЛЕКЦИЯ 7

Элементы аналитической геометрии

7.1 Прямая на плоскости

Уравнение прямой линии, проходящей через точку перпендикулярно вектору:

(7.1)

Уравнение пучка прямых, проходящих через заданную точу :

(7.2)

Уравнение прямой линии, проходящей через

Две заданные точки и:

(7.3)

Уравнение прямой линии с заданным угловым коэффициентом:

(7.4)

Уравнение прямой линии в отрезках на осях:

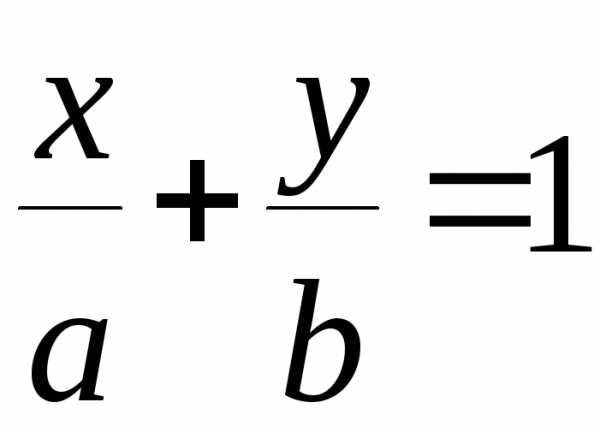(7.5)

Общее уравнение прямой линии на плоскости:

(7.6)

В уравнении (7.6) вектором-нормалью прямой является вектор: .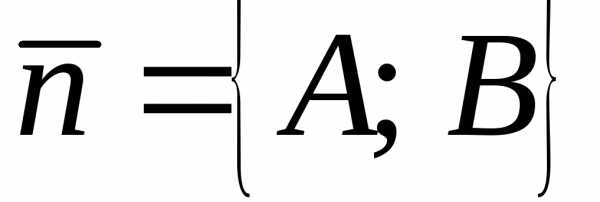

Уравнение прямой, проходящей через точку , параллельно вектору(каноническое уравнение прямой на плоскости):

(7.7)

Параметрические уравнения прямой линии на плоскости:

(7.8)

Расстояние от точки до прямой:

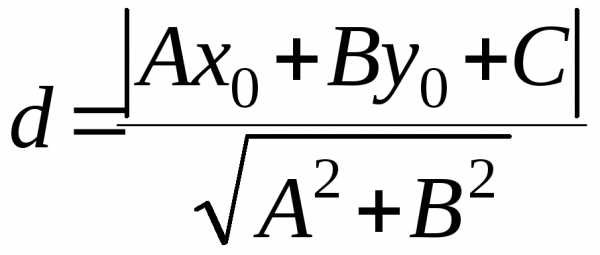(7.9)

studfiles.net

Направление — вектор — Большая Энциклопедия Нефти и Газа, статья, страница 1

Направление — вектор

Cтраница 1

Направление вектора е зависит только от расположения излучающих поверхностей относительно точки пространства. Определив величину и направление этого вектора, мы тем самым определяем и величину углового коэффициента с этой площадки для любой ее ориентации. Из векторной алгебры известно, что задание проекций искомого вектора — на три заданных направления вполне определяет вектор. Поэтому задание величин угловых коэффициентов для трех различных направлений элементарной площадки вполне определяет величину и направление единичного вектора излучения.  [1]

Направления векторов, соответствующих комплексам Z и У, являются зеркальным изображением друг относительно друга в оси вещественных, так как аргументы комплексов Z и У равны и противоположны по знаку.  [2]

Направления векторов о, Щ и г4 показаны на рие.  [3]

Направления векторов, соответствующих комплексным величинам Z и К, являются зеркальным изображением относительно друг друга в оси вещественных, так как аргументы комплексных величин Z и Y равны и противоположны по знаку.  [4]

Направления векторов показаны на рис. 351, г. Вектор w p направлен перпендикулярно к А Р в сторону вращения колеса / / вокруг полюса Р, так как вращение этого колеса ускоренное.  [5]

Направления вектора wc в моменты t1 и / 2 показаны на рисунках.  [6]

Направление векторов, представляющих расположенные кон-сольно грузы, должно быть изменено на обратное при подсчете максимального прогиба вала, необходимого для вычисления первого критического числа оборотов.  [7]

Направление вектора at однозначно связано с направлением движения точки по кругу. Выбирают направление ю так: если смотреть на движущуюся точку с острия вектора а, то точка должна двигаться против часовой стрелки.  [8]

Направления векторов a, b и с можно использовать для обозначения осей кристалла, а величины векторов могут быть наименьшими из тех, которые удовлетворяют изложенным выше требованиям.  [9]

Направления векторов Я4 и чв не могут быть противоположны, так как при этом не выполнялась бы теорема о проекциях скоростей.  [10]

Направление вектора Н в однородной и изотропной среде совпадает с направлением вектора В.  [11]

Направление вектора задается углами, которые он образует с осями координат. В трехмерном случае направление вектора однозначно определяется заданием двух углов, в двухмерном — одного. Углы эти называются направляющими, а отвечающие им косинусы — направляющими косинусами.  [12]

Направление вектора е зависит только от расположения излучающих поверхностей относительно точки пространства. Определив величину и направление этого вектора, мы тем самым определяем и величину углового коэффициента с этой площадки для любой ее ориентации. Из векторной алгебры известно, что задание проекций искомого вектора, на три заданных направления вполне определяет вектор. Поэтому задание величин угловых коэффициентов для трех различных направлений элементарной площадки вполне определяет величину и направление единичного вектора излучения.  [13]

Направления векторов vxy и v тоже совпадают, так как направляющие косинусы их одинаковы.  [14]

Направления векторов Е в электрическом толе изображаются силовыми линиями. Так называются линии, в каждой точке которых вектор Е направлен по касательной. В неравномерном поле Е изменяется от точки к точке.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru