Пи на 6 на окружности – Тригонометрическая окружность. Подробная теория с примерами.

alexxlab / / Школьная жизнь

Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение sin(45)
3 Найти точное значение sin(60)
4 Найти точное значение sin(30 град. )
5 Найти точное значение sin(60 град. )
6 Найти точное значение tan(30 град. )
7 Найти точное значение arcsin(-1)
8 Найти точное значение sin(pi/6)
9 Найти точное значение cos(pi/4)
10 Найти точное значение sin(45 град. )
11 Найти точное значение sin(pi/3)
12 Найти точное значение arctan(-1)
13 Найти точное значение cos(45 град. )
14 Найти точное значение cos(30 град. )
15 Найти точное значение tan(60)
16 Найти точное значение csc(45 град. )
17 Найти точное значение tan(60 град. )
18 Найти точное значение sec(30 град. )
19 Преобразовать из радианов в градусы (3pi)/4
20 График y=sin(x)
21 Преобразовать из радианов в градусы pi/6
22 Найти точное значение cos(60 град. )
23 Найти точное значение cos(150)
24 Найти точное значение tan(45)
25 Найти точное значение sin(30)
26 Найти точное значение sin(60)
27 Найти точное значение cos(pi/2)
28 Найти точное значение tan(45 град. )
29 График y=sin(x)
30 Найти точное значение arctan(- квадратный корень 3)
31 Найти точное значение csc(60 град. )
32 Найти точное значение sec(45 град. )
33 Найти точное значение csc(30 град. )
34 Найти точное значение sin(0)
35 Найти точное значение sin(120)
36 Найти точное значение cos(90)
37 Преобразовать из радианов в градусы pi/3
38 Найти точное значение sin(45)
39 Найти точное значение tan(30)
40 Преобразовать из градусов в радианы 45
41 Найти точное значение tan(60)
42 Упростить квадратный корень x^2
43 Найти точное значение cos(45)
44 Упростить sin(theta)^2+cos(theta)^2
45 Преобразовать из радианов в градусы pi/6
46 Найти точное значение cot(30 град. )
47 Найти точное значение arccos(-1)
48 Найти точное значение arctan(0)
49 График y=cos(x)
50 Найти точное значение cot(60 град. )
51 Преобразовать из градусов в радианы 30
52 Упростить ( квадратный корень x+ квадратный корень 2)^2
53 Преобразовать из радианов в градусы (2pi)/3
54 Найти точное значение sin((5pi)/3)
55 Упростить 1/( кубический корень от x^4)
56 Найти точное значение sin((3pi)/4)
57 Найти точное значение tan(pi/2)
58 Найти угол А tri{}{90}{}{}{}{}
59 Найти точное значение sin(300)
60 Найти точное значение cos(30)
61 Найти точное значение cos(60)
62 Найти точное значение cos(0)
63 Найти точное значение arctan( квадратный корень 3)
64 Найти точное значение cos(135)
65 Найти точное значение cos((5pi)/3)
66 Найти точное значение cos(210)
67 Найти точное значение sec(60 град. )
68 Найти точное значение sin(300 град. )
69 Преобразовать из градусов в радианы 135
70 Преобразовать из градусов в радианы 150
71 Преобразовать из радианов в градусы (5pi)/6
72 Преобразовать из радианов в градусы (5pi)/3
73 Преобразовать из градусов в радианы 89 град.
74 Преобразовать из градусов в радианы 60
75 Найти точное значение sin(135 град. )
76 Найти точное значение sin(150)
77 Найти точное значение sin(240 град. )
78 Найти точное значение cot(45 град. )
79 Преобразовать из радианов в градусы (5pi)/4
80 Упростить 1/( кубический корень от x^8)
81 Найти точное значение sin(225)
82 Найти точное значение sin(240)
83 Найти точное значение cos(150 град. )
84 Найти точное значение tan(45)
85 Вычислить sin(30 град. )
86 Найти точное значение sec(0)
87 Упростить arcsin(-( квадратный корень 2)/2)
88 Найти точное значение cos((5pi)/6)
89 Найти точное значение csc(30)
90 Найти точное значение arcsin(( квадратный корень 2)/2)
91 Найти точное значение tan((5pi)/3)
92 Найти точное значение tan(0)
93 Вычислить sin(60 град. )
94 Найти точное значение arctan(-( квадратный корень 3)/3)
95 Преобразовать из радианов в градусы (3pi)/4
96 Вычислить arcsin(-1)
97 Найти точное значение sin((7pi)/4)
98 Найти точное значение arcsin(-1/2)
99 Найти точное значение sin((4pi)/3)
100 Найти точное значение csc(45)

www.mathway.com

cos (pi / 6)

Существует множество способов, как найти значение функции cos (pi / 6). Рассмотрим некоторые из них.

  1. Этот способ очень часто используют при решении тригонометрических заданий в школе. Вычисляются значения тригонометрических функций при помощи таблицы значений функций синуса, косинуса, тангенса и котангенса от основных аргументов.


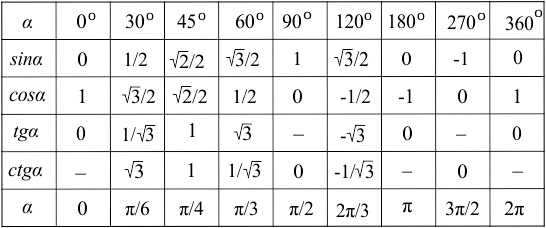
Будем использовать удобный вид таблицы. Удобна она тем, что в ней значения углов представлены как в градусах, так в радианах.
Например, угол pi/6 представлен в радианах. Найдем соответствующий ему столбец таблицы. В строках таблицы найдем функцию cos. Итак, при пересечении эти значения дают результат — корень из 3 / 2.
Математическая запись результата:

   

  1. Способ требует некоторых знаний, но тоже очень простой. Вычисляются значения тригонометрических функций с помощью тригонометрического круга (или окружности).


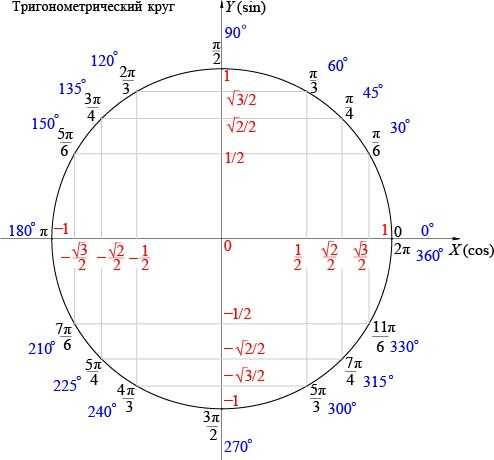
На осях координат лежат значения косинуса (ось абсцисс) и синуса (ось ординат), а значения углов — на самой окружности.
В данном случае значение угла функции косинус равен pi / 6. Найдем эту точку на окружности. Затем проведем перпендикулярную прямую на ось Ох, где лежат значения косинусов. Прямая пройдет через точку корень из 3 / 2. Следовательно, косинус от pi / 6 равен корень из 3 / 2.

  1. Быстрым и удобным способом является использование графика функции косинус — косинусоиды.


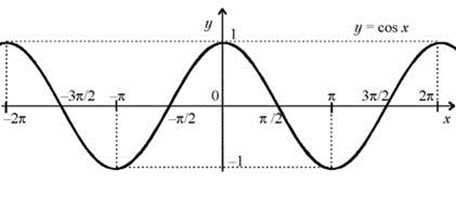
Несколько затруднительно применять его при таких неудобных значениях, как Пи / 6, но если запомнить очередность значений функций (от минимального к максимальному), то график — это самый быстрый способ узнать значение функции, не прибегая к техническим средствам или специальным таблицам.

ru.solverbook.com

Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение cos((5pi)/12)
3 Найти точное значение arctan(-1)
4 Найти точное значение sin(75)
5 Найти точное значение arcsin(-1)
6 Найти точное значение sin(60 град. )
7 Найти точное значение sin(pi/3)
8 Найти точное значение arctan(- квадратный корень 3)
9 Найти точное значение cos(pi/3)
10 Найти точное значение sin(0)
11 Найти точное значение cos(pi/12)
12 Найти точное значение sin(30 град. )
13 Найти точное значение cos(60 град. )
14
Найти точное значение		 cos(30 град. )
15 Найти точное значение sin((2pi)/3)
16 Найти точное значение arcsin(1)
17 Найти точное значение sin(pi/2)
18 График f(x)=x^2
19 Найти точное значение sin(45 град. )
20 Найти точное значение sin(15)
21 Упростить квадратный корень x^2
22 Найти точное значение arccos(-1)
23 Найти точное значение tan(60 град. )
24 Найти точное значение cos(45 град. )
25 Вычислить логарифм по основанию 2 от 8
26 Упростить квадратный корень x^3
27 Найти точное значение arcsin(-1/2)
28 Найти точное значение cos(45)
29 Найти точное значение tan(30 град. )
30 Найти точное значение tan(30)
31 Найти точное значение arcsin(1)
32 Найти точное значение arctan( квадратный корень 3)
33 Найти точное значение sin(45)
34 Найти точное значение cos(0)
35 Найти точное значение tan(45 град. )
36 Найти точное значение arctan(0)
37 Преобразовать из радианов в градусы pi/3
38 График y=x^2
39 Вычислить натуральный логарифм 1
40 Вычислить логарифм по основанию 3 от 81
41 Найти точное значение cos(15)
42 Вычислить логарифм по основанию 5 от 125
43 Упростить кубический корень из квадратного корня 64x^6
44 Вычислить логарифм по основанию 3 от 81
45 Вычислить логарифм по основанию 2 от 8
46 Найти точное значение arcsin(-( квадратный корень 2)/2)
47 Найти точное значение cos(75)
48 Найти точное значение sin((3pi)/4)
49 Упростить (1/( квадратный корень x+h)-1/( квадратный корень x))/h
50 Упростить кубический корень x^3
51 Найти точное значение sin((5pi)/12)
52 Найти точное значение arcsin(-1/2)
53 Найти точное значение sin(30)
54 Найти точное значение sin(105)
55 Найти точное значение tan((3pi)/4)
56 Упростить квадратный корень s квадратный корень s^7
57 Упростить корень четвертой степени x^4y^2z^2
58 Найти точное значение sin(60)
59 Найти точное значение arccos(-( квадратный корень 2)/2)
60 Найти точное значение tan(0)
61 Найти точное значение sin((3pi)/2)
62 Вычислить логарифм по основанию 4 от 64
63 Упростить корень шестой степени 64a^6b^7
64 Вычислить квадратный корень 2
65 Найти точное значение arccos(1)
66 Найти точное значение arcsin(( квадратный корень 3)/2)
67 График f(x)=2^x
68 Найти точное значение sin((3pi)/4)
69 Преобразовать из радианов в градусы (3pi)/4
70 Вычислить логарифм по основанию 5 от 25
71 Найти точное значение tan(pi/2)
72 Найти точное значение cos((7pi)/12)
73 Упростить 1/( кубический корень от x^4)
74 Найти точное значение sin((5pi)/6)
75 Преобразовать из градусов в радианы 150
76 Найти точное значение tan(pi/2)
77 Множитель x^3-8
78 Упростить корень пятой степени 1/(x^3)
79 Упростить корень пятой степени 1/(x^3)
80 Найти точное значение sin(135)
81 Преобразовать из градусов в радианы 30
82 Преобразовать из градусов в радианы 60
83 Найти точное значение sin(120)
84 Найти точное значение tan((2pi)/3)
85 Вычислить -2^2
86 Найти точное значение tan(15)
87 Найти точное значение tan((7pi)/6)
88 Найти точное значение arcsin(( квадратный корень 3)/2)
89 Найти точное значение sin(pi/2)
90 Преобразовать из радианов в градусы (5pi)/6
91 Упростить кубический корень 8x^7y^9z^3
92 Упростить arccos(( квадратный корень 3)/2)
93 Упростить i^2
94 Вычислить кубический корень 24 кубический корень 18
95 Упростить квадратный корень 4x^2
96 Найти точное значение sin((3pi)/4)
97 Найти точное значение tan((7pi)/6)
98 Найти точное значение tan((3pi)/4)
99 Найти точное значение arccos(-1/2)
100 Упростить корень четвертой степени x^4

www.mathway.com

Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение cos((5pi)/12)
3 Найти точное значение arctan(-1)
4 Найти точное значение sin(75)
5 Найти точное значение arcsin(-1)
6 Найти точное значение sin(60 град. )
7 Найти точное значение sin(pi/3)
8 Найти точное значение arctan(- квадратный корень 3)
9 Найти точное значение cos(pi/3)
10 Найти точное значение sin(0)
11 Найти точное значение cos(pi/12)
12 Найти точное значение sin(30 град. )
13 Найти точное значение cos(60 град. )
14 Найти точное значение cos(30 град. )
15 Найти точное значение sin((2pi)/3)
16 Найти точное значение arcsin(1)
17 Найти точное значение sin(pi/2)
18 График f(x)=x^2
19 Найти точное значение sin(45 град. )
20 Найти точное значение sin(15)
21 Упростить квадратный корень x^2
22 Найти точное значение arccos(-1)
23 Найти точное значение tan(60 град. )
24 Найти точное значение cos(45 град. )
25 Вычислить логарифм по основанию 2 от 8
26 Упростить квадратный корень x^3
27 Найти точное значение arcsin(-1/2)
28 Найти точное значение cos(45)
29 Найти точное значение tan(30 град. )
30 Найти точное значение tan(30)
31 Найти точное значение arcsin(1)
32 Найти точное значение arctan( квадратный корень 3)
33 Найти точное значение sin(45)
34 Найти точное значение cos(0)
35 Найти точное значение tan(45 град. )
36 Найти точное значение arctan(0)
37 Преобразовать из радианов в градусы pi/3
38 График y=x^2
39 Вычислить натуральный логарифм 1
40 Вычислить логарифм по основанию 3 от 81
41 Найти точное значение cos(15)
42 Вычислить логарифм по основанию 5 от 125
43 Упростить кубический корень из квадратного корня 64x^6
44 Вычислить логарифм по основанию 3 от 81
45 Вычислить логарифм по основанию 2 от 8
46 Найти точное значение arcsin(-( квадратный корень 2)/2)
47 Найти точное значение cos(75)
48 Найти точное значение sin((3pi)/4)
49 Упростить (1/( квадратный корень x+h)-1/( квадратный корень x))/h
50 Упростить кубический корень x^3
51 Найти точное значение sin((5pi)/12)
52 Найти точное значение arcsin(-1/2)
53 Найти точное значение sin(30)
54 Найти точное значение sin(105)
55 Найти точное значение tan((3pi)/4)
56 Упростить квадратный корень s квадратный корень s^7
57 Упростить корень четвертой степени x^4y^2z^2
58 Найти точное значение sin(60)
59 Найти точное значение arccos(-( квадратный корень 2)/2)
60 Найти точное значение tan(0)
61 Найти точное значение sin((3pi)/2)
62 Вычислить логарифм по основанию 4 от 64
63 Упростить корень шестой степени 64a^6b^7
64 Вычислить квадратный корень 2
65 Найти точное значение arccos(1)
66 Найти точное значение arcsin(( квадратный корень 3)/2)
67 График f(x)=2^x
68 Найти точное значение sin((3pi)/4)
69 Преобразовать из радианов в градусы (3pi)/4
70 Вычислить логарифм по основанию 5 от 25
71 Найти точное значение tan(pi/2)
72 Найти точное значение cos((7pi)/12)
73 Упростить 1/( кубический корень от x^4)
74 Найти точное значение sin((5pi)/6)
75 Преобразовать из градусов в радианы 150
76 Найти точное значение tan(pi/2)
77 Множитель x^3-8
78 Упростить корень пятой степени 1/(x^3)
79 Упростить корень пятой степени 1/(x^3)
80 Найти точное значение sin(135)
81 Преобразовать из градусов в радианы 30
82 Преобразовать из градусов в радианы 60
83 Найти точное значение sin(120)
84 Найти точное значение tan((2pi)/3)
85 Вычислить -2^2
86 Найти точное значение tan(15)
87 Найти точное значение tan((7pi)/6)
88 Найти точное значение arcsin(( квадратный корень 3)/2)
89 Найти точное значение sin(pi/2)
90 Преобразовать из радианов в градусы (5pi)/6
91 Упростить кубический корень 8x^7y^9z^3
92 Упростить arccos(( квадратный корень 3)/2)
93 Упростить i^2
94 Вычислить кубический корень 24 кубический корень 18
95 Упростить квадратный корень 4x^2
96 Найти точное значение sin((3pi)/4)
97 Найти точное значение tan((7pi)/6)
98 Найти точное значение tan((3pi)/4)
99 Найти точное значение arccos(-1/2)
100 Упростить корень четвертой степени x^4

www.mathway.com

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.

Обозначаем числа \(2π\), \(π\), \(\frac{π}{2}\), \(-\frac{π}{2}\), \(\frac{3π}{2}\)

Как вы знаете из прошлой статьи, радиус числовой окружности равен \(1\). Значит, длина окружности равняется \(2π\) (вычислили по формуле \(l=2πR\)). С учетом этого отметим \(2π\) на числовой окружности. Чтобы отметить это число нужно пройти от \(0\) по числовой окружности расстояние равно \(2π\) в положительном направлении, а так как длина окружности \(2π\), то получается, что мы сделаем полный оборот. То есть, числу \(2π\) и \(0\) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.


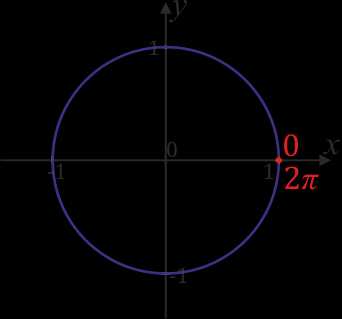
Теперь обозначим на числовой окружности число \(π\). \(π\) – это половина от \(2π\). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от \(0\) в положительном направлении половину окружности.


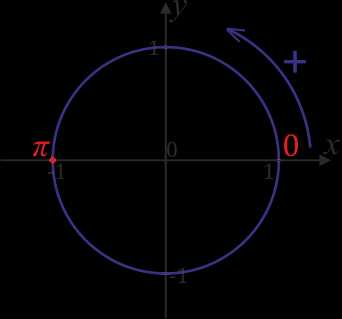
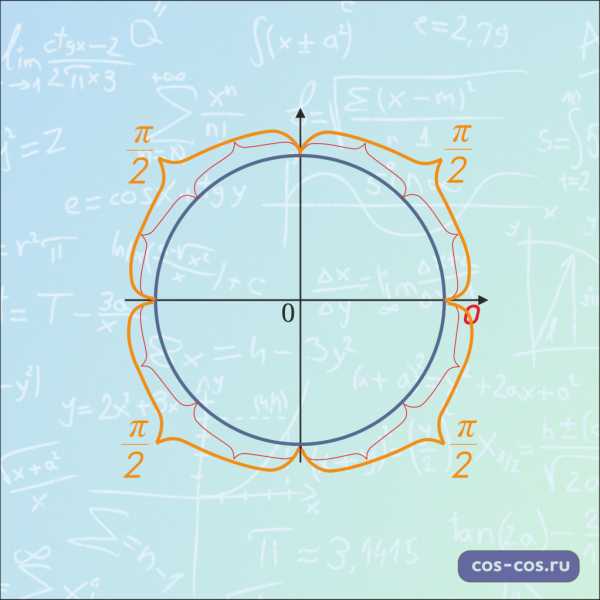
Отметим точку \(\frac{π}{2}\). \(\frac{π}{2}\) – это половина от \(π\), следовательно чтобы отметить это число, нужно от \(0\) пройти в положительном направлении расстояние равное половине \(π\), то есть четверть окружности.


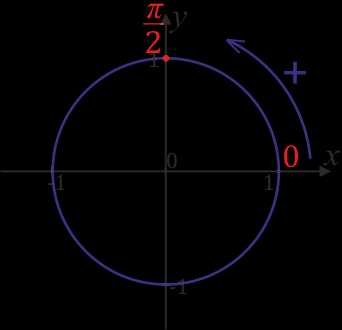
Обозначим на окружности точки \(-\)\(\frac{π}{2}\). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.


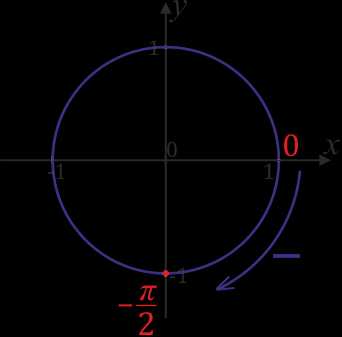
Нанесем \(-π\). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.


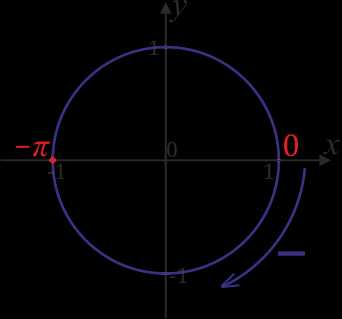
Теперь рассмотрим пример посложнее. Отметим на окружности число \(\frac{3π}{2}\). Для этого дробь \(\frac{3}{2}\) переведем в смешанный вид \(\frac{3}{2}\)\(=1\)\(\frac{1}{2}\), т.е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

                                    

 

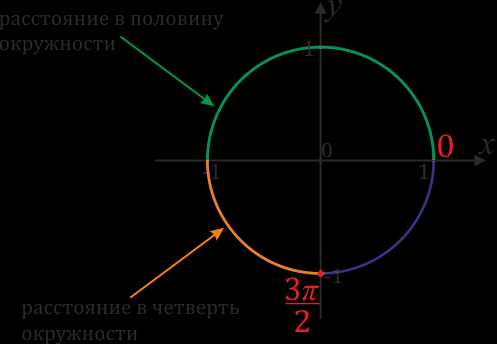
Задание 1. Отметьте на числовой окружности точки \(-2π\),\(-\)\(\frac{3π}{2}\).

Обозначаем числа \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\)

Выше мы нашли значения в точках пересечения числовой окружности с осями \(x\) и \(y\). Теперь определим положение промежуточных точек. Для начала нанесем точки \(\frac{π}{4}\), \(\frac{π}{3}\) и \(\frac{π}{6}\).
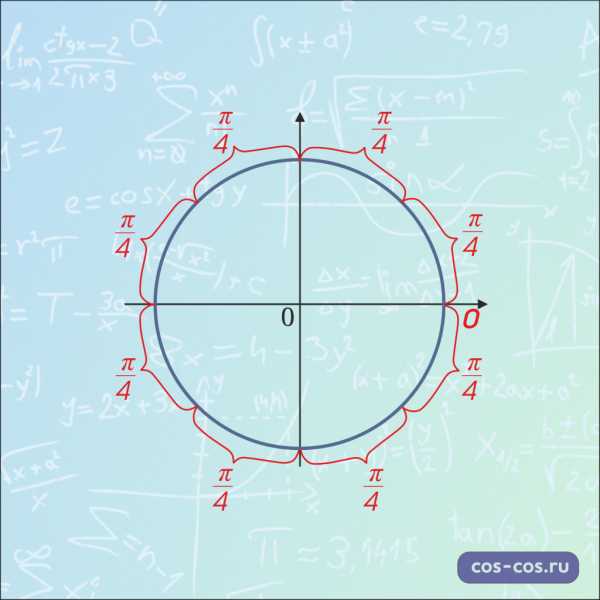
\(\frac{π}{4}\) – это половина от \(\frac{π}{2}\) (то есть, \(\frac{π}{4}\) \(=\)\(\frac{π}{2}\)\(:2)\) , поэтому расстояние \(\frac{π}{4}\) – это половина четверти окружности.

                                   

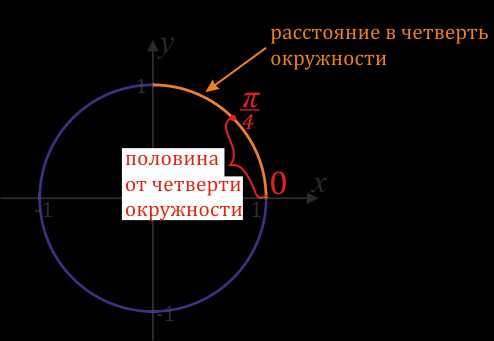
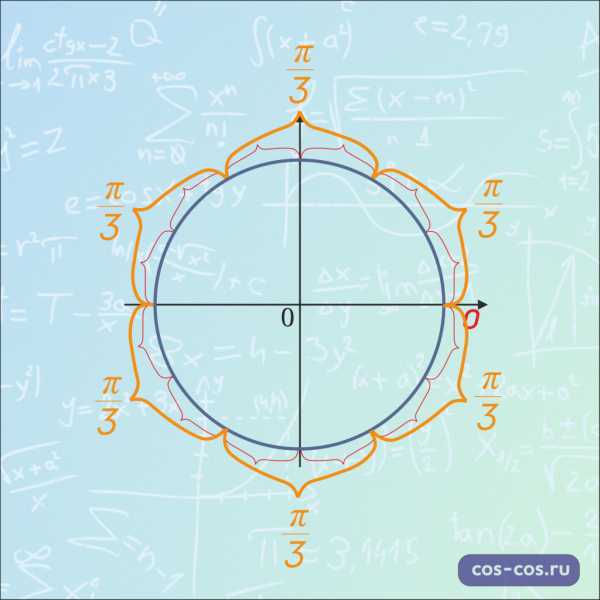
\(\frac{π}{4}\) – это треть от \(π\) (иначе говоря,\(\frac{π}{3}\)\(=π:3\)), поэтому расстояние \(\frac{π}{3}\) – это треть от полукруга.

           

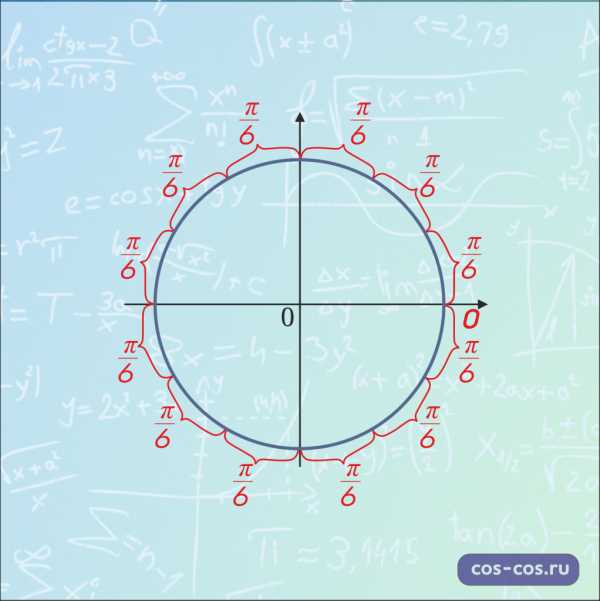
\(\frac{π}{6}\) – это половина \(\frac{π}{3}\) (ведь \(\frac{π}{6}\)\(=\)\(\frac{π}{3}\)\(:2\)) поэтому расстояние \(\frac{π}{6}\) – это половина от расстояния \(\frac{π}{3}\).


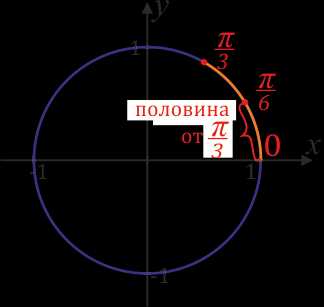
Вот так они расположены друг относительно друга:

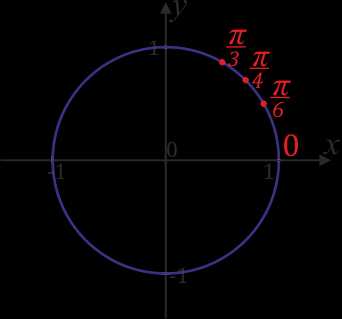
Замечание: Расположение точек со значением \(0\), \(\frac{π}{2}\),\(π\), \(\frac{3π}{2}\), \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

     

     

 

Обозначаем числа \(\frac{7π}{6}\), \(-\frac{4π}{3}\), \(\frac{7π}{4}\)

Обозначим на окружности точку \(\frac{7π}{6}\), для этого выполним следующие преобразования: \(\frac{7π}{6}\)\(=\)\(\frac{6π + π}{6}\)\(=\)\(\frac{6π}{6}\)\(+\)\(\frac{π}{6}\)\(=π+\)\(\frac{π}{6}\). Отсюда видно, что от нуля в положительную сторону надо пройти расстояние \(π\), а потом еще \(\frac{π}{6}\).

                                  

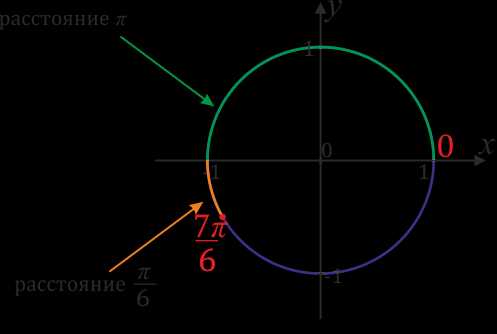
Отметим на окружности точку \(-\)\(\frac{4π}{3}\). Преобразовываем: \(-\)\(\frac{4π}{3}\)\(=-\)\(\frac{3π}{3}\)\(-\)\(\frac{π}{3}\)\(=-π-\)\(\frac{π}{3}\). Значит надо от \(0\) пройти в отрицательную сторону расстояние \(π\) и еще \(\frac{π}{3}\).

                               

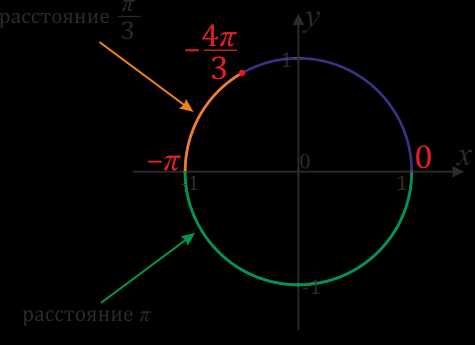
Нанесем точку \(\frac{7π}{4}\), для этого преобразуем \(\frac{7π}{4}\)\(=\)\(\frac{8π-π}{4}\)\(=\)\(\frac{8π}{4}\)\(-\)\(\frac{π}{4}\)\(=2π-\)\(\frac{π}{4}\). Значит, чтобы поставить точку со значением \(\frac{7π}{4}\), надо от точки со значением \(2π\) пройти в отрицательную сторону расстояние \(\frac{π}{4}\).

                     

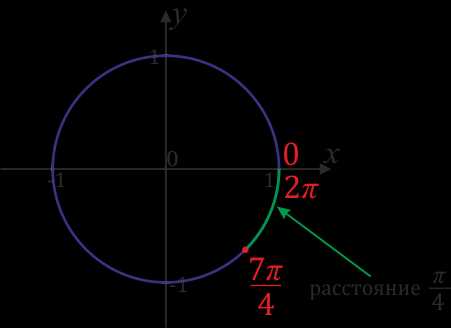
Задание 2. Отметьте на числовой окружности точки \(-\)\(\frac{π}{6}\),\(-\)\(\frac{π}{4}\),\(-\)\(\frac{π}{3}\),\(\frac{5π}{4}\),\(-\)\(\frac{7π}{6}\),\(\frac{11π}{6}\), \(\frac{2π}{3}\),\(-\)\(\frac{3π}{4}\).

Обозначаем числа \(10π\), \(-3π\), \(\frac{7π}{2}\) ,\(\frac{16π}{3}\), \(-\frac{21π}{2}\), \(-\frac{29π}{6}\)

Запишем \(10π\) в виде \(5 \cdot 2π\). Вспоминаем, что \(2π\) – это расстояние равное длине окружности, поэтому чтобы отметить точку \(10π\), нужно от нуля пройти расстояние равное \(5\) окружностям. Нетрудно догадаться, что мы окажемся снова в точке \(0\), просто сделаем пять оборотов.


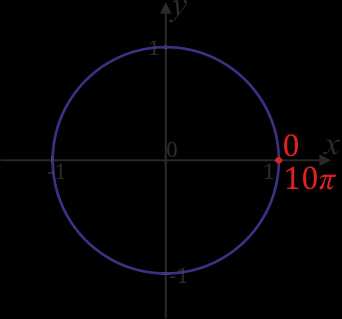
Из этого примера можно сделать вывод:

Числам с разницей в \(2πn\), где \(n∈Z\) (то есть \(n\) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше \(2π\) (или меньше \(-2π\)), надо выделить из него целое четное количество \(π\) (\(2π\), \(8π\), \(-10π\)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Еще один вывод:

Точке, которой соответствует \(0\), также соответствуют все четные количества \(π\) (\(±2π\),\(±4π\),\(±6π\)…).

Теперь нанесем на окружность \(-3π\). \(-3π=-π-2π\), значит \(-3π\) и \(–π\) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в \(-2π\)).


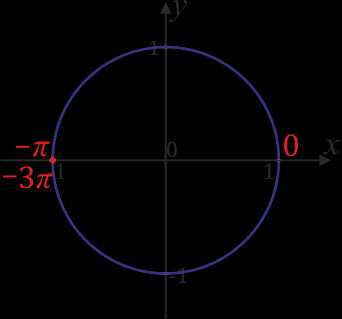
Кстати, там же будут находиться все нечетные \(π\).

Точке, которой соответствует \(π\), также соответствуют все нечетные количества \(π\) (\(±π\),\(±3π\),\(±5π\)…).

Сейчас обозначим число \(\frac{7π}{2}\). Как обычно, преобразовываем: \(\frac{7π}{2}\)\(=\)\(\frac{6π}{2}\)\(+\)\(\frac{π}{2}\)\(=3π+\)\(\frac{π}{2}\)\(=2π+π+\)\(\frac{π}{2}\). Два пи – отбрасываем, и получается что, для обозначения числа \(\frac{7π}{2}\) нужно от нуля в положительную сторону пройти расстояние равное \(π+\)\(\frac{π}{2}\) (т.е. половину окружности и еще четверть).


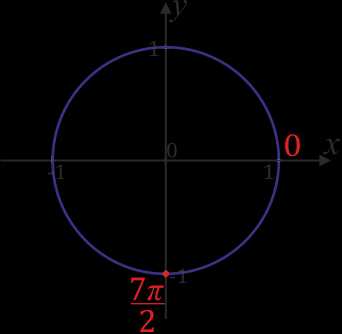
Отметим \(\frac{16π}{3}\). Вновь преобразования: \(\frac{16π}{3}\)\(=\)\(\frac{15π + π}{3}\)\(=\)\(\frac{15π}{3}\)\(+\)\(\frac{π}{3}\)\(=5π+\)\(\frac{π}{3}\)\(=4π+π+\)\(\frac{π}{3}\). Ясно, что от нуля надо пройти расстояние равное \(π+\)\(\frac{π}{3}\) – и мы найдем место точки \(\frac{16π}{3}\).


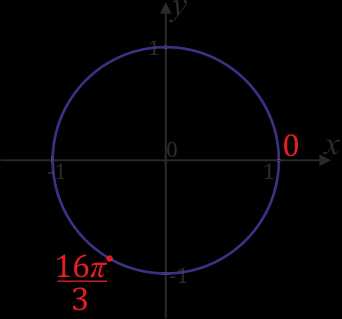
Нанесем на окружность число \(-\)\(\frac{21π}{2}\).
\(-\)\(\frac{21π}{2}\)\(= -\)\(\frac{20π}{2}\)\(-\)\(\frac{π}{2}\)\(=-10π-\)\(\frac{π}{2}\). Значит, место \(-\)\(\frac{21π}{2}\) совпадает с местом числа \(-\)\(\frac{π}{2}\).


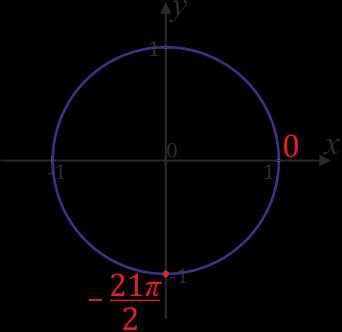
Обозначим \(-\)\(\frac{29π}{6}\).
\(-\)\(\frac{29π}{6}\)\(=-\)\(\frac{30π}{6}\)\(+\)\(\frac{π}{6}\)\(=-5π+\)\(\frac{π}{6}\)\(=-4π-π+\)\(\frac{π}{6}\). Для обозначение \(-\)\(\frac{29π}{6}\), на числовой окружности надо от точки со значением \(–π\) пройти в положительную сторону \(\frac{π}{6}\).


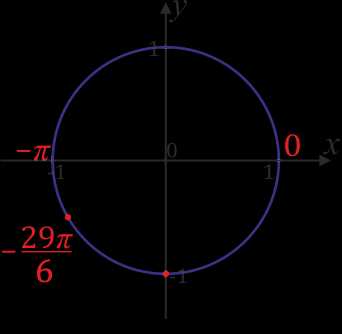
Задание 3. Отметьте на числовой окружности точки \(-8π\),\(-7π\), \(\frac{11π}{4}\),\(-\)\(\frac{7π}{3}\),\(\frac{17π}{6}\),\(-\)\(\frac{20π}{3}\),\(-\)\(\frac{11π}{2}\).

Скачать статью

cos-cos.ru

Точки на числовой окружности

При изучении тригонометрии в школе каждый ученик сталкивается с весьма интересным понятием «числовая окружность». От умения школьного учителя объяснить, что это такое, и для чего она нужна, зависит, насколько хорошо ученик пойдём тригонометрию впоследствии. К сожалению, далеко не каждый учитель может доступно объяснить этот материал. В результате многие ученики путаются даже с тем, как отмечать точки на числовой окружности

. Если вы дочитаете эту статью до конца, то научитесь делать это без проблем.

Итак, приступим. Нарисуем окружность, радиус которой равен 1. Самую «правую» точку этой окружности обозначим буквой O:

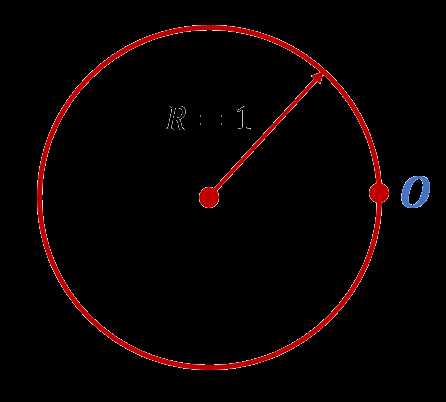
Поздравляю, вы только что нарисовали единичную окружность. Поскольку радиус этой окружности равен 1, то её длина равна .

Каждому действительному числу можно поставить в соответствие длину траектории вдоль числовой окружности от точки O. За положительное направление принимается направление движения против часовой стрелки. За отрицательное – по часовой стрелке:

Расположение точек на числовой окружности

Как мы уже отмечали, длина числовой окружности (единичной окружности) равна . Где тогда будет располагаться на этой окружности число ? Очевидно, от точки

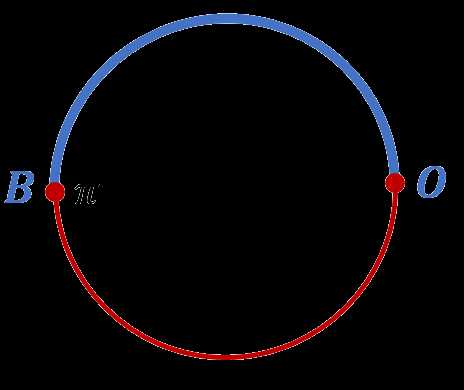
O против часовой стрелки нужно пройти половину длины окружности, и мы окажемся в нужной точке. Обозначим её буквой B:

Обратите внимание, что в ту же точку можно было бы попасть, пройдя полуокружность в отрицательном направлении. Тогда бы мы отложили на единичной окружности число . То есть числам и соответствует одна и та же точка.

Причём этой же точке соответствуют также числа , , , и, вообще, бесконечное множество чисел, которые можно записать в виде , где , то есть принадлежит множеству целых чисел. Всё это потому, что из точки B можно совершить «кругосветное» путешествие в любую сторону (добавить или вычесть длину окружности

yourtutor.info

Помогите с тригонометрией. на единичной окружности равны точки 11 пи/ 6 и -пи/ 6 ?

Прочее образование Varvara_nar 3 (445) Помогите с тригонометрией. на единичной окружности равны точки 11 пи/ 6 и -пи/ 6 ? 7 лет

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *