Площадь треугольника это – Все формулы площади треугольника — найти онлайн

Площадь треугольника — Циклопедия

Треугольник Математика. Урок 8. Площадь треугольника // novykrug [5:54]

Площадь треугольника — это положительное действительное число, характеризующее треугольник в единицах измерения площади.

Введём обозначения:

a — первая сторона;

b — вторая сторона;

c — третья сторона;

h_a — высота, опущенная на сторону a;

h_b — высота, опущенная на сторону b;

h_c — высота, опущенная на сторону c;

α — угол напротив стороны a

;

β — угол напротив стороны b;

γ — угол напротив стороны c;

p — полупериметр треугольника;

r — радиус вписанной окружности;

R — радиус описанной окружности;

S_Δ — площадь треугольника.

[править] Формулы в векторной и координатной форме

Введём обозначения:

[math]\bar r_1=(x_1,y_1,z_1)[/math] — радиус-вектор первой точки;

[math]\bar r_2=(x_2,y_2,z_2)[/math] — радиус-вектор второй точки;

[math]\bar r_3=(x_3,y_3,z_3)[/math] — радиус-вектор третьей точки;

[math]\bar n=(A,B,C)[/math] — нормаль к плоскости, проходящей через заданные точки;

p — отклонение начала координат от плоскости, проходящей через заданные точки;

S_Δ — площадь треугольника, построенного по трём заданным точкам.

• Формула с параметром p применима, только когда p≠0.

Если третью точку взять в начале координат, то можно применять следующую формулу:

[править] Формула Герона

Введём обозначения:

a — длина стороны треугольника, расположенной между второй и третьей точками;

b — длина стороны треугольника, расположенной между первой и третьей точками;

c — длина стороны треугольника, расположенной между первой и второй точками;

p — полупериметр треугольника, построенного по трём заданным точкам.

где

[править] Другие многоугольники:

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970. стр.75.
• Бронштейн М. Н., Семендяев К. А., Справочник по математике — М., 1956, стр.166, стр.187.

cyclowiki.org

Как найти площадь треугольника |

Содержание:
Треугольники.
Прямоугольный треугольник и его площадь.
Равнобедренный треугольник и его площадь.

Треугольники.

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно. (См. также: Как найти свое призвание)
Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:
S – это площадь треугольника,
a, b, c – это стороны треугольника,

h – это высота треугольника, (См. также: Как найти легальную работу за границей)
R – это радиус описанной окружности,
p – это полупериметр.
Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:

В нашем случае площадь треугольника равна: S = ? * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.). (См. также: Как найти богатого жениха…)

Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.
В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.
2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:
S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Равнобедренный треугольник и его площадь.

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:

Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы. По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете. Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.

altaiinter.org

Чему равна площадь треугольника

Чтобы ответить наиболее полно на вопрос: «Чему равна площадь треугольника» рассмотрим все возможные варианты (или основные). Каждый вариант отличается от других тем, какие данные известны для треугольника.
 
Вариант 1. Дана высота и сторона треугольника.
В этом случае площадь треугольника равна половине основания, умноженного на высоту:

   

 
Вариант 2. Даны все 3 стороны треугольника.

   

Рассмотренная формула называется формулой Герона. В ней p — это полупериметр, который находят по формуле:

   

 
Вариант 3. В треугольнике даны 2 стороны и угол между ними.
В этом случае площадь треугольника равна произведению этих сторон на синус угла, деленного на 2:

   

 
Вариант 4. Даны все 3 стороны треугольника и радиус описанной вокруг него окружности.

   

 
Вариант 5. Даны все 3 стороны треугольника и радиус вписанной в него окружности.

   

Эту же формулу можно записать в более сокращенном виде, используя полупериметр:

   

 
Это полный набор формул для площади произвольного треугольника.
Теперь достаточно только подставить известные величины в нужную формулу и найти площадь треугольника.
 

ru.solverbook.com

Площадь треугольника по двум сторонам

Выясним, как найти площадь треугольника по двум сторонам.

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Формула площади треугольника по двум сторонам:

 

   

 

 

 

 

Дано:

∆ ABC.

 

Доказать:

   

Доказательство:

 

Проведем в треугольнике ABC высоту BD.

Площадь треугольника

равна половине произведения его стороны на высоту, проведенную к этой стороне:

   

Рассмотрим треугольник ABD — прямоугольный (так как BD — высота по построению).

По определению синуса острого угла в прямоугольном треугольнике,

   

Отсюда

   

Таким образом,

   

 

Если в треугольнике ABC

угол A тупой,

 

 

 

 

 

 

 

то в треугольнике ABD

 

 

 

   

(как смежные).

По формуле

   

имеем:

   

   

То есть, и в случае тупого угла A выполняется равенство

   

а значит, верна формула

   

Что и требовалось доказать.

www.treugolniki.ru

Как найти площадь треугольника? :: SYL.ru

Школьная программа предусматривает обучение детей геометрии с раннего возраста. Одно из самых базовых знаний этой области — это нахождение площади различных фигур. В этой статье мы постараемся привести все возможные способы получения этой величины, от простейших до самых сложных.

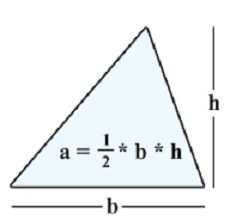
Основа

Первая формула, которую изучают дети в школе, предусматривает нахождение площади треугольника через длину его высоты и основания. Высота — это отрезок, проведённый из вершины треугольника под прямым углом к противолежащей стороне, которая будет являться основанием. Как найти площадь треугольника по этим величинам?

Если V — высота, а O — основание, тогда площадь S=V*O:2.

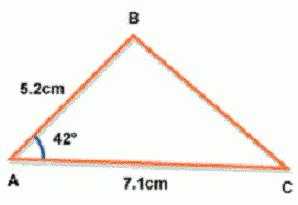
Другой вариант получения искомой величины требует от нас знания длин двух сторон, а также величины угла между ними. Если у нас L и M — длины сторон, а Q — угол между ними, тогда вы можете получить площадь по формуле S=(L*M*sin(Q))/2.

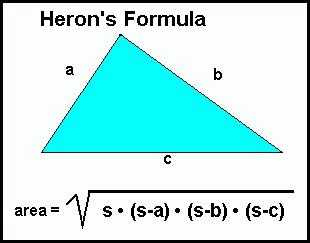
Формула Герона

Кроме всех прочих ответов на вопрос о том, как вычислить площадь треугольника, есть формула, позволяющая получить необходимое нам значение, зная исключительно длины сторон. То есть, если нам известны длины всех сторон, то нам нет необходимости проводить высоту и вычислять её длину. Мы можем воспользоваться, так называемой формулой Герона.

Если M, N, L — это длины сторон, тогда мы можем найти площадь треугольника, следующим образом. P=(M+N+L)/2, тогда необходимая нам величина S²=P*(P-M)*(P-L)*(P-N). В итоге, нам останется только вычислить корень.

Для прямоугольного треугольника формула Герона немного упрощается. Если M, L -это катеты, тогда S=(P-M)*(P-L).

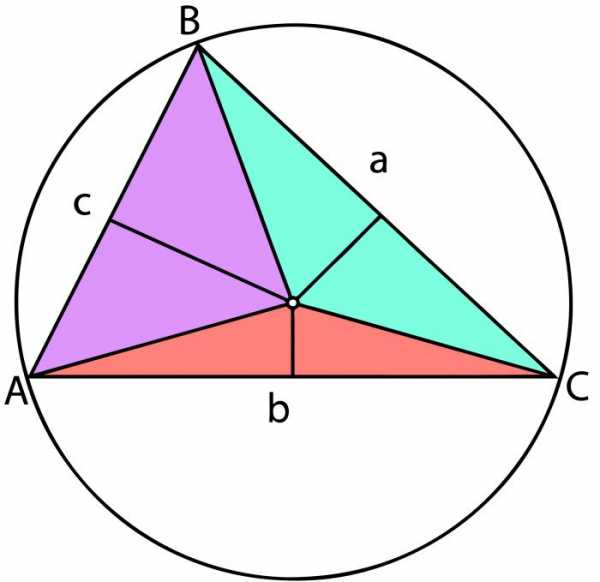
Окружности

Другой способ, с помощью которого можно найти площадь треугольника, предусматривает использование вписанных и описанных окружностей. Чтобы получить необходимую нам величину с помощью вписанной окружности, нам потребуется узнать её радиус. Обозначим его «r». Тогда формула, по которой мы будем проводить вычисления, примет следующий вид: S=r*P, где P — это половина от суммы длин всех сторон.

В прямоугольном треугольнике эта формула немного преобразуется. Конечно, вы можете использовать и указанную выше, однако лучше взять для вычислений другое выражение. S=E*W, где E и W — это длины отрезков, на которые делится гипотенуза, точкой касания окружности.

Говоря об описанной окружности, найти площадь треугольника, также не составит труда. Введя обозначение R, как радиус описанной окружности, можно получить следующую формулу, необходимую для вычисления искомой величины: S= (M*N*L):(4*R). Где три первые величины — это стороны треугольника.

Говоря о равностороннем треугольнике, за счет ряда простейших математических преобразований можно получить немого изменённые формулы:

S=(3^1/2*M²)/4;

S=(3*3^1/2*R²)/4;

S=3*3^1/2*r².

Во всяком случае, любая формула, позволяющая найти площадь треугольника, может быть изменена в соответствии с данными поставленной задачи. Так что все написанные выражения не являются абсолютами. При решении задач поразмышляйте, чтобы найти наиболее подходящий способ решения.

Координаты

При изучении координатных осей задачи, стоящие перед учениками, усложняются. Однако не настолько, чтобы впадать в панику. Для того чтобы найти площадь треугольника по координатам вершин, вы можете воспользоваться всё той же, но немного изменённой формулой Герона. Для координат она приобретает следующий вид:

S=((x₂-x₁)²*(y₂-y₁)²*(z₂-z₁)²)^1/2.

Впрочем, никто не запрещает, используя координаты, вычислить длины сторон треугольника и затем, по формулам, которые были написаны выше, посчитать площадь. Для преобразования координат в длину пользуйтесь следующей формулой:

l=((x₂-x₁)²+(y₂-y₁)²)^1/2.

Примечания

В статье использовались стандартные обозначения величин, которые применяются в условиях большинства задач. При этом степень «1/2» означает, что вам необходимо извлечь корень из всего выражения под скобками.

При выборе формулы будьте внимательнее. Некоторые из них теряют свою актуальность в зависимости от начальных условий. Например, формула описанной окружности. Она способна высчитать вам результат в любом случае, однако может быть такая ситуация, когда треугольника с заданными параметрами может вообще не существовать.

Если вы сидите дома и делаете домашнее задание, тогда можете воспользоваться онлайн-калькулятором. Многие сайты предоставляют возможность вычисления различных величин по заданным параметрам, причем не суть важно, каким именно. Вы просто можете вписать начальные данные в поля, и компьютер (сайт) посчитает за вас результат. Таким образом, вы сможете избежать ошибок, допущенных по невнимательности.

Надеемся наша статья ответила все ваши вопросы касательно вычисления площади самых разных треугольников, и вам не придётся искать допонительную информацию в другом месте. Удачи с учебой!

www.syl.ru