Матричный метод решения системы линейных уравнений
Задана система линейных алгебраических уравнений (СЛАУ) с неизвестными,коэффициентами при которых элементы матрицы , а свободными членами являются числа
Обозначим через – матрицу-столбец неизвестных, через –матрицу-столбец свободных членов. Тогда впереди систему уравнений можно записать в виде матричного уравнения:
Если квадратная матрица имеет отличный от нуля определитель ,то для нее существует обратная . Умножив слева в этом уравнении на , получим
Учитывая, что и, получим матричный решение системы
Нахождение матричного решения называется матричным способом решения системы линейных алгебраических уравнений (СЛАУ).
—————————————————————
Пример 1.
Решить СЛАУ матричным методом.
Решение.
Обозначим матрицу и векторы
Матричный решение системы уравнений ищем по формуле
Для нахождения обратной матрицы вычислим определитель
Поскольку , то заданная система уравнений совместная и имеет единственное решение.
Найдем транспонированную матрицу
Найдем алгебраические дополнения к элементам заданной матрицы:
Обратную матрицу вычисляем по формуле
Найдем решение СЛАУ
Решение СЛАУ:
Посмотреть материалы:
yukhym.com
Решение систем линейных уравнений матричным методом — Мегаобучалка
Определители
Определитель второго порядка, соответствующий таблице элементов определяется разностью и обозначается:
.
Определитель третьего порядка, соответствующий таблице элементов
определяется равенством:
Минором любого элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие этот элемент.
Алгебраическим дополнением данного элемента называется его минор, умноженный на где – сумма номеров строки и столбца этого элемента.
Определитель третьего порядка можно вычислить диагональным способом. Для этого к определителю последовательно приписываются справа первый и второй столбцы. Произведения элементов, стоящих на главной диагонали, а также на двух параллелях к ней, берутся со знаком плюс; произведения элементов побочной диагонали и на двух параллелях к ней берутся со знаком минус. Алгебраическая сумма этих шести произведений дает определитель третьего порядка
.
Примеры. Вычислить определители:
а)
б)
в)
Решение систем линейных уравнений по формулам Крамера
Решение данной системы находится по формулам:
где
.
При этом предполагается, что
Пример. Решить систему линейных уравнений по формулам Крамера
Решение: Вычислим определитель системы
следовательно данная система имеет единственное решение.
Вычислим дополнительные определители:
По формулам Крамера находим:
Следовательно, решение данной системы.
Матрицы
Прямоугольная таблица чисел, расположенных в m строках и n столбцах называется матрицей размера m x n. Обозначается буквами А, В, С.
,
где элемент матрицы, i – номер строки, j – номер столбца.
Виды матриц
1. Если в матрице число строк равно числу столбцов ( m = n), то она называется квадратной.
2. — матрица – строка.
3. матрица-столбец. 4. единичная матрица.
Операции над матрицами
1. Сложение матриц.
Сумма двух матриц А и В одинаковых размеров называется матрица
С = А + В, элементы которой определяются равенством .
2. Умножение матрицы на число.
При умножении матрицы А на число , все элементы данной матрицы умножатся на это число.
3. Умножение матриц.
Условия умножения матриц: число столбцов матрицы А должно быть равно числу строк матрицы В.
Матрица В называется обратной по отношению к квадратной матрице А, если АВ = ВА = Е. Для матрицы, обратной по отношению к матрицеА, принято обозначение
Обратная матрица находится по формуле:
где – алгебраические дополнения элементов определителя.
Решение систем линейных уравнений матричным методом
Пример. Решить систему матричным методом
Решение: Перепишем систему в виде АХ = В, где
Решение матричного уравнения имеет вид Х = А-1В.
Найдем обратную матрицу А-1, для чего вычислим определитель системы:
Вычислим алгебраические дополнения элементов определителя:
Следовательно,
Тогда матрица Х:
.
Ответ:
megaobuchalka.ru
Найти решение системы линейных уравнений третьего, четвертого порядка матричным методом
Для решения системы линейных алгебраических уравнений ее записывают в матричной форме
где -матрица, составленная из коэффициентов при неизвестных; — столбец неизвестных; — столбец свободных членов. После того, если для матрицы существует обратная матрица ( ) то система линейных уравнений имеет единственное решение и он находится за формулой
Поскольку перемножить матрицу на вектор столбец не складывает особенных трудностей, то большая проблема при вычислениях — найти обратную матрицу
В нахождении решения за приведенной формулой и заключается суть матричного метода.
Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика І.І. «Высшая математика»
————————————
Задача.
Решить систему линейных алгебраических уравнений.
1) (1. 183)
2) (4. 182)
Решение.
1) Запишем систему трех линейных уравнений в матричной форме
Найдем обратную матрицу. Напомним, что
где — определитель матрицы , а — транспонированная матрица алгебраических дополнений элементов определителя матрицы.
Вычислим определитель матрицы
Матрица алгебраических дополнений состоит из элементов , которые вычисляются через миноры по правилу
Миноры — это определители на порядок меньшие от определителя , которые образуются вычеркиванием в нем -й строки и — го столбца. На первый взгляд звучит слишком запутано, но при вычислениях все станет понятно и просто.
Найдем алгебраические дополнения к определителю
Запишем найденную матрицу алгебраических дополнений
и протранспонируем ее
Находим обратную матрицу
С помощью обратной матрицы находим решение системы линейных уравнений
На етом решения примера завешено. Как видите никаких сложных вычислений в етом задании мы не делали.
2) Запишем систему линейных уравнений четвертого порядка в матричной форме
Поскольку все коэффициенты ненулевые то вычислять ее будет трудно. Выполним над системой линейных уравнений элементарные превращения чтобы превратить в нуль некоторые из коэффициентов.
От второй строки отнимем первую и последнюю строки
От третьей строки отнимем сумму первой и четвертой строки начальной системы
От четвертой строки отнимем первый
Из последней строки уже можем сказать что но будем придерживаться правил чтобы научиться решать большие системы уравнений.
Поскольку матрица стала разреженной то вычисление определителя и матрицы алгебраических дополнений упростятся. Найдем определитель матрицы, разложив его за четвертой строкой
Найдем матрицу алгебраических дополнений, раскладывая искомые детерминанты за строками и столбцами которые содержат больше всего нулей. Для самопроверки выпишу Вам вычисление только первой строки. Остальные попробуйте вычислить самостоятельно
После нахождения всех значений получим следующую матрицу дополнений
Поскольку определитель равен единице то обратная матрица с транспонированной матрицей дополнений совпадают
Подставим в матричную запись и найдем решение
При вычислениях систем линейных алгебраических уравнений третьего, четвертого порядка матричным методом придется находить большое количество алгебраических дополнений , которые собой являют определители второго и третьего порядка соответственно. Именно ошибки при их вычислении чаще всего становятся причиной неверного решения. Для избежания таких ситуаций нужно хорошо знать правила нахождения определителей второго, третьего порядка, а также правила чередования знаков возле миноров.
Изучайте их и получайте лишь верные решения !
———————————————-
Посмотреть материалы:
yukhym.com
Примеры решения систем линейных алгебраических уравнений матричным методом
Матричный метод решения систем линейных алгебраических уравнений — вывод формулы.
Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравнения слева на (порядки матриц A ⋅ X и Впозволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как , а по определению обратной матрицы (E – единичная матрица порядка n на n), поэтому
Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле . Другими словами, решение СЛАУ находится с помощью обратной матрицы .
Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ
К началу страницы
Примеры решения систем линейных алгебраических уравнений матричным методом.
Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы.
Пример.
С помощью обратной матрицы найдите решение системы линейных уравнений .
Решение.
В матричной форме исходная система запишется как , где . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем , следовательно, для матрицы А может быть найдена обратная матрица . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как . Итак, задача свелась к построению обратной матрицы . Найдем ее.
Мы знаем, что для матрицы обратная матрица может быть найдена как , где — алгебраические дополнения элементов .
В нашем случае
Тогда
Выполним проверку полученного решения , подставив его в матричную форму исходной системы уравнений . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.
Следовательно, решение найдено верно.
Ответ:
или в другой записи .
Пример.
Решите СЛАУ матричным методом.
Решение.
Первое уравнение системы не содержит неизвестной переменной x2, второе –x1, третье – x
Построим обратную матрицу с помощью матрицы из алгебраических дополнений:
тогда,
Осталось найти решение СЛАУ:
Рекомендуем выполнить проверку.
Ответ:
.
При переходе от обычного вида системы линейных алгебраических уравнений к ее матричной форме следует быть внимательным с порядком следования неизвестных переменных в уравнениях системы. К примеру, СЛАУ НЕЛЬЗЯ записать как . Нужно сначала упорядочить все неизвестные переменные во всех уравнениях системы, а потом переходить к матричной записи:
или
Также будьте внимательны с обозначением неизвестных переменных, вместоx1, x2, …, xn могут быть любые другие буквы. Например, СЛАУ в матричной форме запишется как .
Разберем пример.
Пример.
Найдите решение системы линейных алгебраических уравнений с помощью обратной матрицы.
Решение.
Упорядочив неизвестные переменные в уравнениях системы, запишем ее в матичной форме . Вычислим определитель основной матрицы:
Он отличен от нуля, поэтому решение системы уравнений может быть найдено с помощью обратной матрицы как . Найдем обратную матрицу по формуле :
Получим искомое решение:

Ответ:
x = 0, y = -2, z = 3.
Пример.
Найдите решение системы линейных алгебраических уравнений матричным методом.
Решение.
Определитель основной матрицы системы равен нулю
поэтому, мы не можем применить матричный метод.
Нахождение решения подобных систем описано в разделе решение систем линейных алгебраических уравнений.
Пример.
Решите СЛАУ матричным методом, — некоторое действительное число.
Решение.
Система уравнений в матричной форме имеет вид . Вычислим определитель основной матрицы системы и убедимся в том, что он отличен от нуля:
Квадратных трехчлен не обращается в ноль ни при каких действительных значениях , так как его дискриминант отрицателен , поэтому определитель основной матрицы системы не равен нулю ни при каких действительных . По матричному методу имеем . Построим обратную матрицу по формуле :

Тогда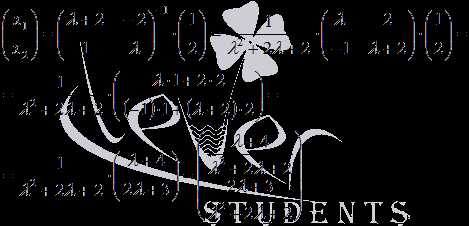
Рекомендуем выполнить проверку полученного результата.
Ответ:
.К началу страницы
Подведем итог.
Матричный метод подходит для решения СЛАУ, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы отличен от нуля. Если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
megaobuchalka.ru
